金融科技的发展使人们获得了更为便捷的交易方式, 其中, 信用卡交易成为了线上和线下最为流行的支付方式之一, 随着信用卡交易数量的增加, 信用卡欺诈也时常发生. 根据2019年中国银行业协会发布的《中国银行卡产业发展蓝皮书》数据显示, 截至2018年末, 我国信用卡累计发卡量为9.7亿张, 同比增长22.8%; 信用卡交易总额为38.2万亿元, 同比增长24.9%; 信用卡未偿信贷总额为6.85万亿元, 同比增长23.2%; 信用卡损失率为1.27%, 较上一年度1.17%略有提升; 银行卡欺诈率为1.16基点, 较上年下降0.2基点.
信用卡欺诈是一种为获取经济利益为目的的犯罪欺骗行为, 它会扰乱正常的金融发展秩序, 制约金融行业的普惠目标和创新发展, 对金融业的稳定发展产生深远影响. 因此, 对信用卡欺诈的检测已经成为金融机构核心能力之一. 中国银行业协会在《中国银行卡产业发展蓝皮书(2019)》中提到, 要完善欺诈风险防控体系建设, 提升银行卡欺诈防范水平, 构建“银行+持卡人”风控体系, 提升欺诈监控精准度. 可见, 对信用卡欺诈的识别已经成为银行风险控制的关键因素.
信用卡欺诈检测是通过挖掘持卡人的征信数据中所蕴含的信息, 从中找出规律判断其是否存在欺诈行为, 其实质是一个二分类问题. 然而在构建信用卡欺诈检测模型时, 样本数据分布极度不平衡, 欺诈样本的数量远少于非欺诈样本数量, 这会使得模型在进行训练时不能有效挖掘欺诈样本信息, 容易造成对欺诈样本的误判. 对于金融机构来说, 对欺诈客户误判造成的损失通常比对非欺诈客户的误判造成的损失大. 因此, 如何通过处理不平衡数据以使模型高效而稳定地识别具有欺诈性的交易, 成为信用欺诈检测领域亟需解决的问题.
1 文献回顾 1.1 信用卡欺诈检测对信用卡欺诈检测模型的研究一直以来备受学术界关注. Srivastava等人[1]使用隐马尔可夫模型 (HMM) 对信用卡交易处理中的操作序列进行建模, 并展示如何将其用于欺诈检测. Özçelik等人[2]使用遗传算法对银行信用卡欺诈检测, 该算法能够很好地解决信用卡欺诈检测的可变错误分类成本的分类问题. Şahin等人[3]提出了C50, CART、CHAID三种决策树算法和支持向量机(SVM)分类器对银行信用卡欺诈进行检测, 四种算法均取得较好的检测效果. Bahnsen等人[4]提出了一种基于贝叶斯最小风险的成本敏感方法检测发生欺诈时造成的实际财务成本, 以此构建一个成本敏感的信用卡欺诈检测系统. Carneiro等人[5]将由多层感知器组成的人工神经网络和聚类分析应用于信用卡欺诈预防. Fu等人[6]首次提出了使用卷积神经网络(CNN)用于信用卡欺诈的检测, 模型显示出了优越的分类性能. Jurgovsky等人[7]首次将信用卡欺诈检测问题描述为序列分类任务, 并采用长短期记忆(LSTM) 网络来合并交易序列进行欺诈检测, 提高了持卡人离线交易的检测准确性. Carcillo等人[8]提出了一种混合有监督学习和无监督学习的方法, 对欺诈样本出现的异常值分数定义的不同粒度级别进行评估来提高欺诈检测的准确率. Hussein等人[9]提出了通过堆叠集成技术将多个分类器组合用于信用卡欺诈检测, 改进了模型最终检测结果.
1.2 类别不平衡的欺诈分类重采样方法是当前一个主流的解决类不平衡的方法, 它包括欠采样和过采样两种方法. 其中, 过采样是通过增加少数样本数量使其接近多数样本数量以达到样本均衡的目的, 其以合成少数类技术(SMOTE)为代表. Almhaithawi等人[10]使用SMOTE过采样方法来处理类不均衡问题, 发现SMOTE平衡数据后, 所有模型的欺诈检测结果都有所增强. 然而, 当样本数据极度不平衡, 或者样本存在一定数量的噪声、离群点时, SMOTE方法在某种程度上会放大无效样本的影响, 进而降低分类精[11]. 琚春华等人[12]整合SMOTE算法和K最邻近算法筛选生成欺诈样本, 克服了SMOTE算法在生成新样本时的盲目性和局限性, 在一定程度上提高欺诈检测模型的分类性能.
为了进一步提高信用卡欺诈识别率, 本文构建了一个基于CNN网络的信用卡欺诈检测的基分类器, CNN算法可以完全逼近任何复杂的非线性关系, 鲁棒性和容错性强, 可以高速找到处理数据的优化方案. 针对信用卡交易数据的不平衡性, 本文利用K-means算法聚类的优点, 结合SVMSMOTE算法对数据进行平衡处理.
2 KM-SVMSMOTE-CNN信用卡欺诈检测模型 2.1 K-means算法K-means算法[13]的核心思想是将样本集按照样本间的距离划分为K个簇, 簇内间各个样本尽量紧密连在一起, 而簇间的距离尽量远离. K-means聚类流程如下:
1) 从样本中中随机选择k个样本作为初始聚类质心.
2) 计算其余样本到各质心中心的距离, 并将其归类到距离最近的簇中.
3) 重新计算每个类别簇的聚类中心.
4) 重复步骤2)和步骤3), 直到每个簇的聚类中心不再改变.
K-means聚类的目标函数如式(1)所示:
| $ E = \sum\limits_{i = 1}^k {\sum\nolimits_{{x_i} \in {c_i}} {||{x_i} - {\mu _i}|{|^2}} } $ | (1) |
其中, xi表示数据集中第i个数据样本; ci 表示第i个聚类簇; μi表示第i个聚类簇的簇心.
2.2 SVMSMOTE算法SVMSMOTE算法是SMOTE的改进算法, 传统的SMOTE算法通过随机线性插值的方法在两个少数类样本间合成新的样本, 从而实现数据均衡化的目的[14]. 其在合成新的样本时存在盲目性, 当少数类样本占比及其小时, 新生成的少数类样本会出现重叠问题[15]. 除此之外, SMOTE算法生成的样本是基于原始少数样本而来, 这些少数样本包含了一些噪音数据, 容易造成分布边缘化问题.
针对传统SMOTE算法出现的以上问题, Han等人[16]提出关注边界附近的少数样本并进行采样, 可以使模型取得更好的分类效果. 同时, 在对边界样本进行分类时, 容易将其类别错分, 而边界样本的正确分类对估计最佳分类边界尤为重要, 通过沿分类边界合成少数类样本, 可以避免对所有少数样本进行采样而存在的数据分布边缘化和随机生成数据的盲目性问题, 对此, Tang等人[17]使用SVMSMOTE 算法在边界附近创建新的少数类样本.
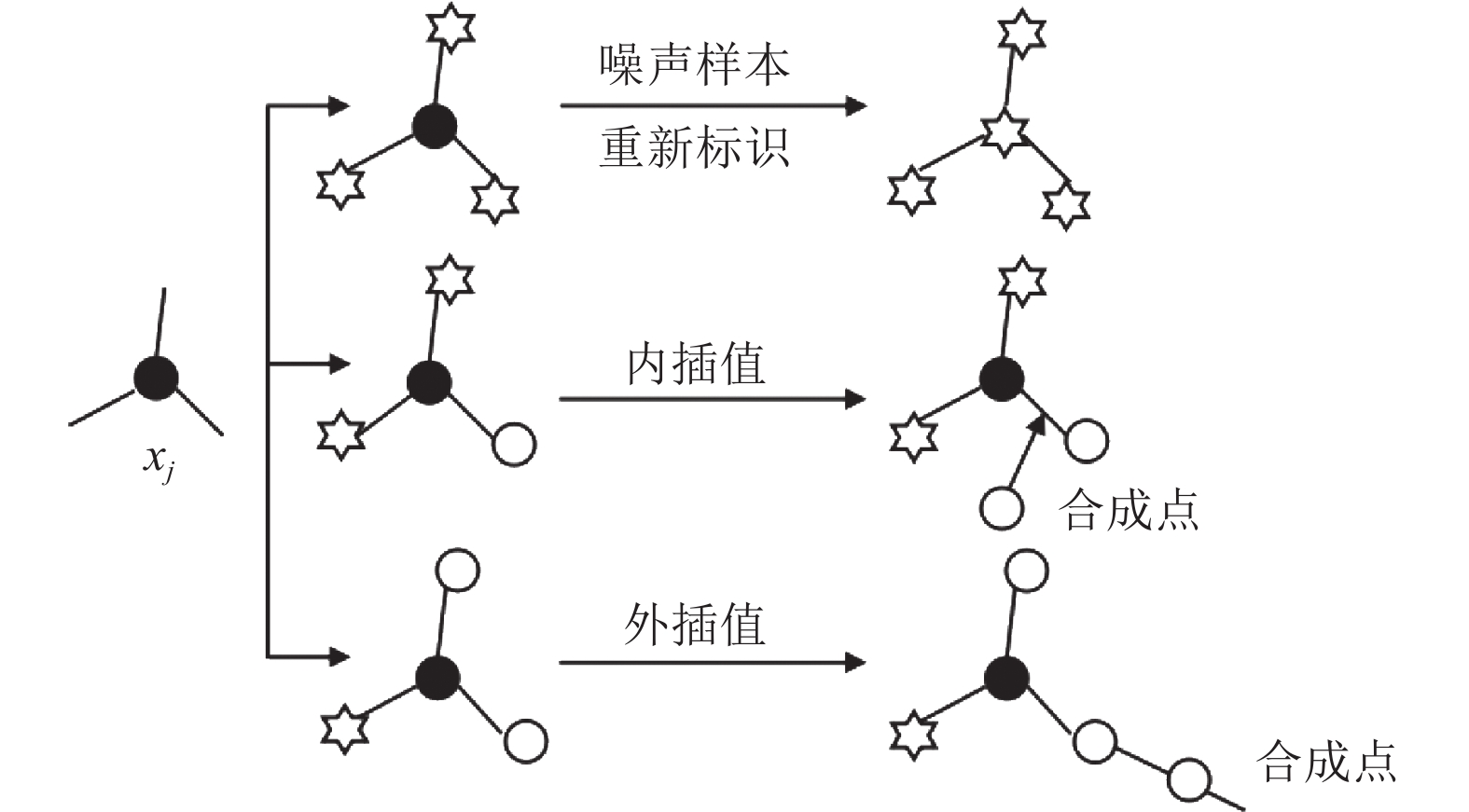
SVMSMOTE算法是一种基于支持向量的过采样方法, 它通过在训练集上训练标准的SVM分类器后获得支持向量来近似边界线区域, 并在边界附近生成新的少数类样本数据. SVMSMOTE的最近邻决策机制如图1所示. 若某一少数类样本xj的k个邻近样本中, 少数类样本的数量为s (s≤k), 多数类样本的数量为t (t≤k), 当k=t 时, 则将本xj归类为噪声样本; 若s<t, 则通过内插值法对xj生成新的少数样本, 若s>t, 则通过外插值法对xj生成新的少数样本.
2.3 KM-SVMSMOTE算法将K-means聚类算法和SVMSMOTE算法融合, 形成一个全新的过采样改进算法KM-SVMSMOTE. 其核心思想为: 利用K-means算法对少数类样本进行精确聚类, 然后使用SVMSMOTE算法基于精确聚类簇进行插值, 达到增加少数样本数量的目的使正负样本得以平衡.
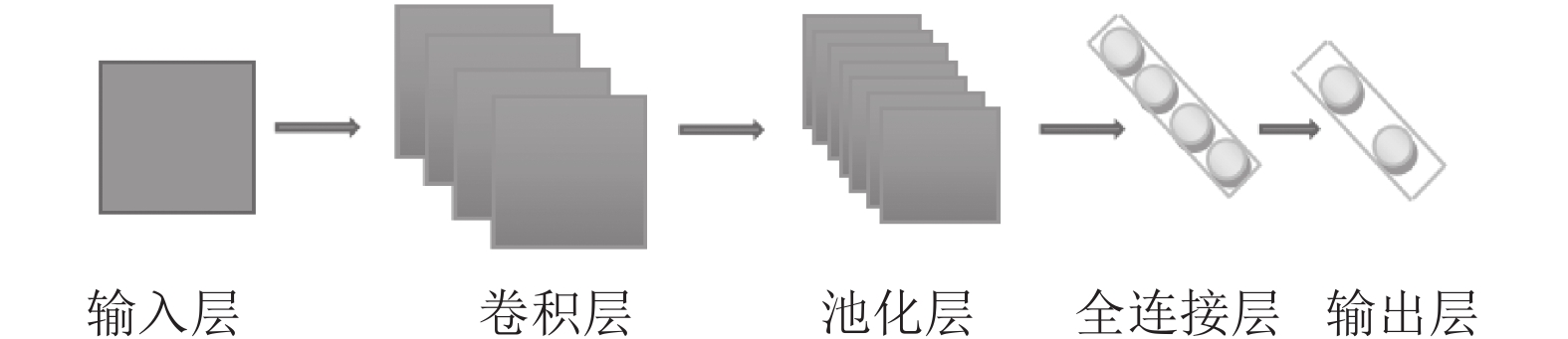
2.4 CNN建模卷积神经网络(CNN)被广泛应用于图像处理领域, 是图像处理领域的主流模型. 随着深度学习的发展, 近年来CNN也被应用于各类大型数据的处理之中, 其通过网络中的卷积层对整体数据进行特征提取, 再通过池化等操作对数据进行降维, 故其适合训练大量数据, 并且具有避免模型过拟合的机制. CNN模型基础结构如图2所示.
|
图 1 SVMSMOTE的最近邻决策机制 |
|
图 2 卷积神经网络结构 |
CNN的第i层特征图的计算过程为:
| $ {C_i} = f({C_{i - 1}}*W + {b_i}) $ | (2) |
其中,
得到第i层特征图
| $ {H_i} = subsampling({C_i}) $ | (3) |
其中,
原始数据经过卷积层-池化层的转化后, 被输送到全连接层实现对提取特征的分类识别, 通常使用Softmax 函数接收这个N维数据作为输入, 然后将每一维的值转换成(0, 1)之间的一个实数作为识别概率, 它的公式为:
| $ {P_i} = {e^{{a_i}}}/\sum\nolimits_{k = 1}^N {e_k^a} $ | (4) |
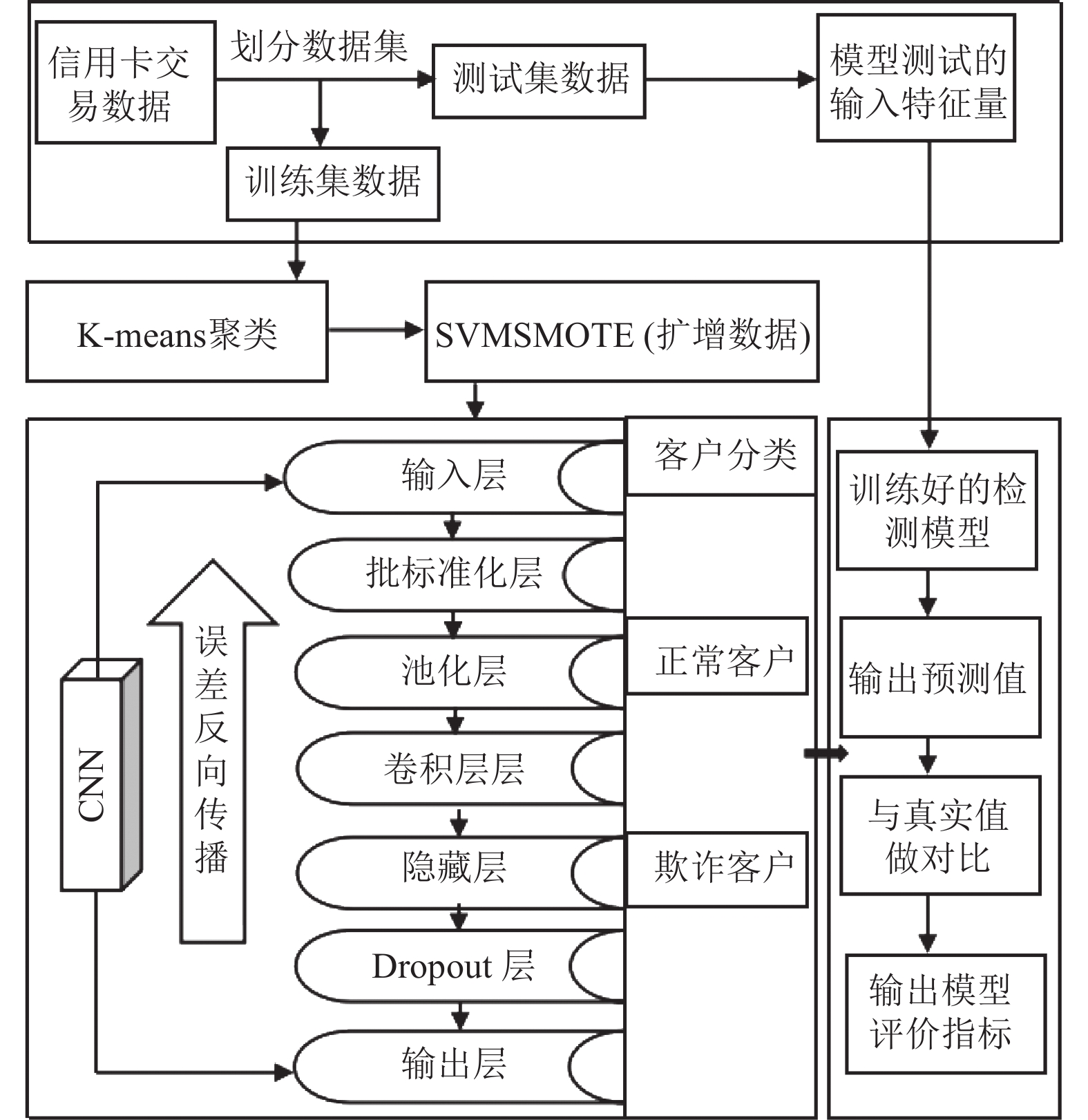
KM-SVMSMOTE-CNN信用卡欺诈检测模型是通过改进传统SMOTE算法的CNN模型, 其通过K-means聚类算法将少数类样本聚类, 然后使用 SVM 在分类边界附近生成新少数类样本数据来提升CNN模型检测性能, 模型构建及实现过程如图3所示.
|
图 3 KM-SVMSMOTE-CNN信用卡欺诈检测模型 |
信用卡交易数据样本规模较大, 计算复杂程度高, 针对这一问题, 本文采用基于CNN的信用卡欺诈检测模型对是否欺诈进行分类. 其通过卷积核不断提取数据特征, 不同区域的数据都共享一个卷积核, 即共享同一组参数, 这便是CNN的参数共享机制, 参数的共享使得网络参数数量大幅减少, 同时池化层提取经过卷积运算后的数据的主要特征, 进一步减少参数数量, 减少了计算复杂度的同时防止模型出现过拟合现象. 针对信用卡交易数据的极端不平衡性, 即欺诈样本仅占总样本的很小部分, 本文采用KM-SVMSMOTE算法对少数样本进行扩充, 解决数据不平衡带来的对欺诈交易识别率较低问题.
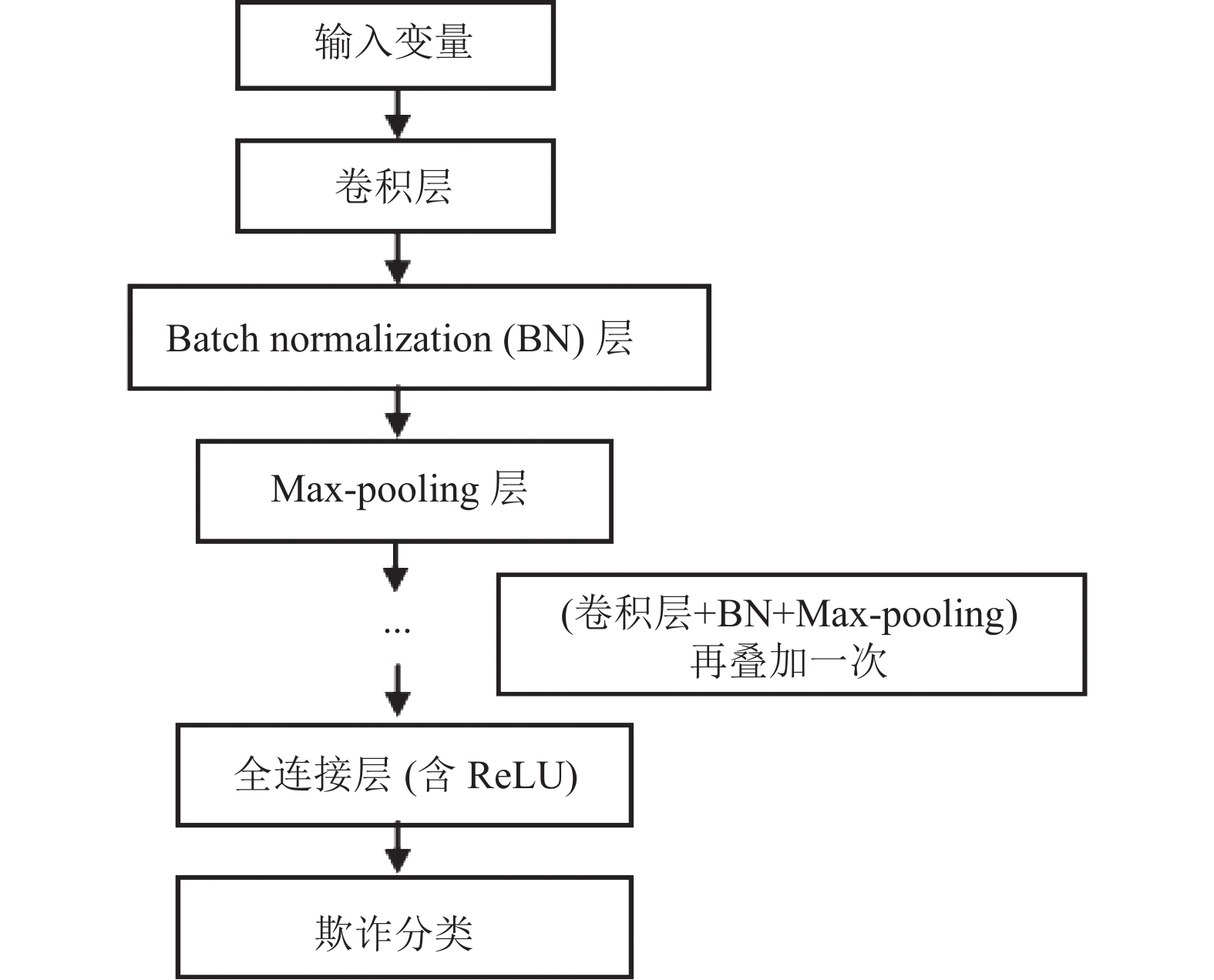
2.6 CNN网络结构本文所使用的CNN模型结构包括两个用于提取数据特征的卷积层、两个用于解决过拟合问题的batch normalization (BN)层、两个用于提高模型捕获边缘信息能力的max-pooling层、一个全连接层和一个用于预测客户是否欺诈的节点, 模型的整体连接结构如图4所示.
|
图 4 CNN模型结构 |
3 实证研究 3.1 数据来源
本文实验的数据集采用了Kaggle平台上发布的信用卡欺诈数据, 该数据集由源讯科技(Worldline)公司和布鲁塞尔自由大学(Université Libre de Bruxelles)机器学习小组合作收集整理而来, 包含了2013年9月欧洲部分信用卡持卡人两天内发生的交易信息. 本文使用的实验数据包含了24627条交易记录, 其中有492条欺诈数据, 约占实验数据集的2%, 数据及其不平衡. 数据共包含30个特征数据和一个标签数据, V1–V28 28个特征出于保密原因, 已由主成分分析方法进行了处理, 无法获取其原始数据的特征信息. 其余的两个特征中, time表示每笔交易与数据集中第一笔交易间隔的秒数; amount表示每笔交易发生的金额; 标签数据class表示类别, 0表示交易正常, 1表示欺诈交易.
3.2 数据预处理本文首先将time特征删除, 同时由于amount列数值与其他特征数值范围差异较大, 故对amount列数据做归一化处理, 归一化规则如式(5)所示.
| $ {x{'}} = \frac{{x - \min (x)}}{{\max (x) - \min (x)}} $ | (5) |
其中, max(x)和min(x)分别表示amount列数据中的最大值与最小值, x'表示数据在进行归一化后的值.
由于欺诈数据的极不平衡, 采用了KM-SVMSMOTE算法对训练数据进行平衡处理, 本文的训练样本占总样本的70%, 包含17238个交易数据, 其中345个数据为欺诈数据, 16893个数据为正常交易数据. 通过KM-SVMSMOTE算法生成欺诈类数据后, 样本达到平衡状态.
3.3 CNN模型输入数据的排布深度学习模型输入的实验数据为3D数组, 信用卡交易数据通常被视为横截面数据, 本文试图让模型识别包含29个特征信息的欺诈客户, 原始训练集数据经过KM-SVMSMOTE算法平衡后, 最终数据形状为33786×29 (33786行, 29列). 为了适应模型的输入, 本文对平衡后的数据进行3D数组的转化, 转化后整个“新数据集X”的形状为33786×1×29, 输出的目标“数据集Y”的形状为33786×1, 对于测试集也做同样的处理.
3.4 模型训练除了使用CNN模型进行训练外, 本文还训练了逻辑斯蒂回归(Logistic)、决策树、随机森林、梯度提升决策树(GBDT)、极限梯度提升(XGBoost)等基础模型, 各模型经过交叉验证选择的参数如表1所示.
| 表 1 模型参数表 |
本文采用准确率(accuracy)、精确率(precision)、召回率(recall)、F1值(F1_score)、AUC值(area under curve)作为模型评价指标. 而根据样本数据的真实类别与欺诈检测模型检测的类别可得到如表2所示的混淆矩阵, 其中, TP指被正确分类的正类样本, FN指被错误分类的正类样本, FP指被错误分类的负类样本, TN指被正确分类的负类样本. 则准确率accuracy=(TP+TN)/( TP+TN+FP+FN), 精确率precision=TP/(TP+FP), 召回率recall=TP/(TP+FN), F1值F1_score=2×precision×recall/(precision+recall).
| 表 2 混淆矩阵 |
由混淆矩阵可得到真正例率(TPR)和假正例率(FPR), 其中, TPR=TP/(TP+FN), FPR=FP/(FP+TN). 以FPR为横轴, TPR为纵轴便可绘制出ROC (receiver operating characteristic)曲线, 可以通过ROC曲线所覆盖的范围评价模型性能的好坏.
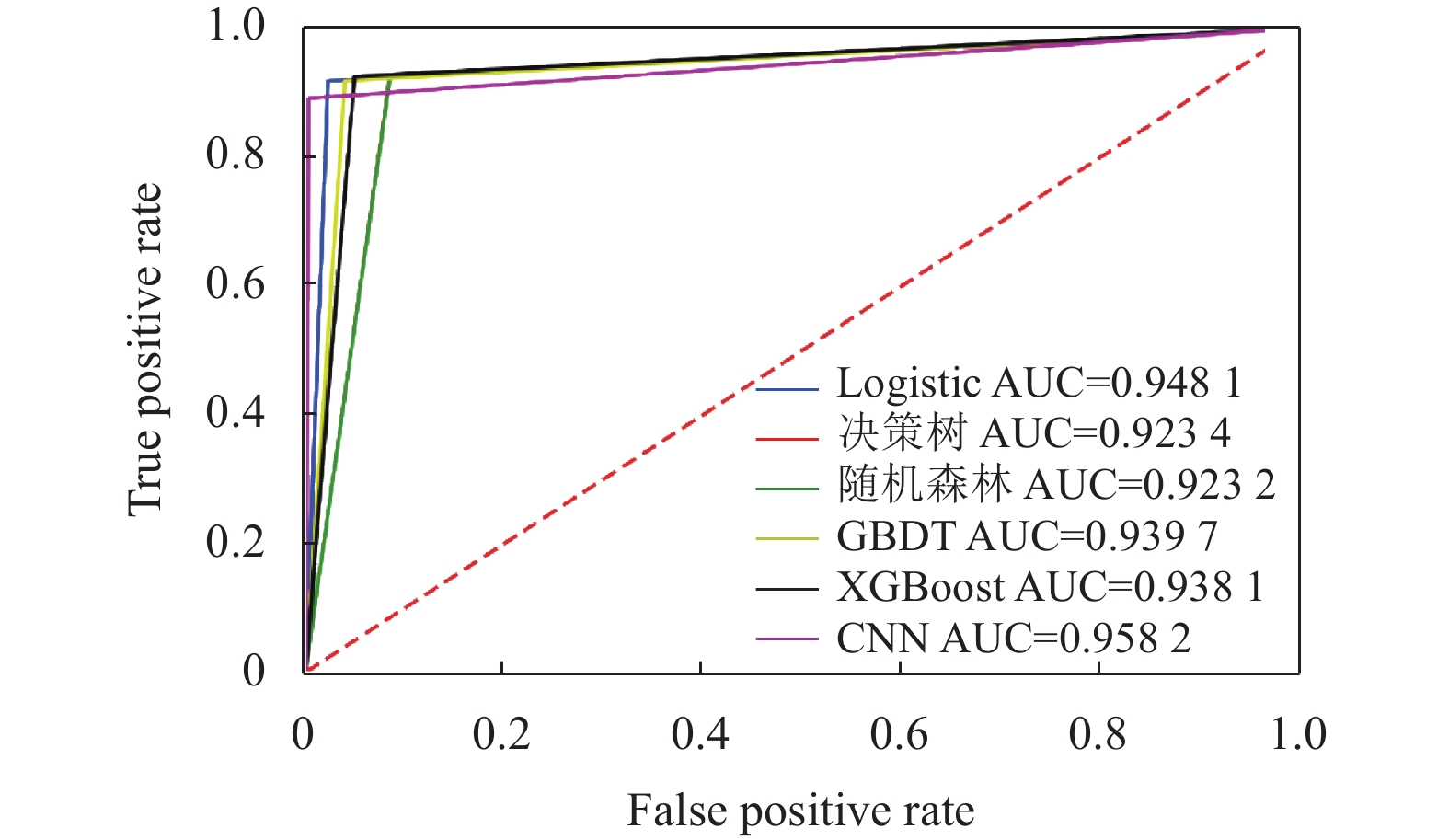
3.5 实验结果分析本文将数据集按照7:3比例划分为训练集和测试集之后, 将CNN模型和逻辑斯蒂回归、决策树、随机森林、GBDT、XGBoost等基础模型进行对比, 实验结果如表3所示, 各模型ROC曲线如图5所示.
| 表 3 各模型欺诈检测结果 |
|
图 5 各模型ROC曲线与AUC值 |
从表3可以看出, 决策树和随机森林两种传统树模型的预测结果极为接近, 他们结果比当前更有效的树模型GBDT和XGBoost的预测结果略逊一筹, 且GBDT模型和XGBoost模型算法评估结果也较为接近. Logistic模型和CNN模型表现出了比上述4个模型更好的综合分类能力, 其中Logistic模型作为传统的分类模型却得到了较好的评估结果, 可能的原因是引入l2惩罚项后, 模型的泛化能力得到增强. 进一步分析发现, CNN模型的各项评价指标的结果均达到90%以上, 其中准确率和AUC值更是分别达到了99.76%和0.9582, 表明了深度学习模型CNN的抗噪能力和泛化能力均优于其他机器学习模型. 综上所述, 本文采用CNN模型作为信用卡欺诈检测的基础模型.
为了进一步分析KM-SVMSMOTE-CNN信用卡欺诈模型的有效性, 本文还使用了未平衡数据下得CNN模型, 以及平衡采样算法中的随机欠采样(RandomUnderSampler)、随机过采样(RandomOverSampler)、SMOTE、BorderlineSMOTE对数据平衡处理后结合CNN模型对信用卡欺诈进行检测并作对比, 实验结果如表4所示.
| 表 4 不同平衡算法下欺诈检测结果 |
从表中可以看出, KM-SVMSMOTE-CNN信用卡欺诈检测模型拥有更为优秀的检测性能, 未平衡数据下CNN模型的AUC值最低, 为0.8427. 其他平衡算法下模型的F1值最高为0.8889, 最低的是RandomUnderSampler-CNN模型, 仅为0.6702, 而KM-SVMSMOTE-CNN模型的F1值高达0.9389, 除此之外, 其拥有最高的AUC值, 再次说明KM-SVMSMOTE-CNN模型拥有较强的泛化能力和分类性能.
4 结论样本极不均衡是信用卡欺诈检测需要解决的问题, 它能影响模型对信用欺诈评估的精确度. 本文通过对平衡算法和深度学习模型的研究, 提出了KM-SVMSMOTE-CNN信用卡欺诈检测模型. 一方面, 提出了KM-SVMSMOTE对样本进行平衡, 克服传统SMOTE算法在生成少数样本存在的边缘化和盲目性等问题. 另一方面, 为了充分挖信用卡交易数据中所包含的信息, 使用深度学习技术构建模型并对信用卡欺诈进行检测. 实证结果得出模型的准确率为99.76%, AUC值达到0.9582, 表明KM-SVMSMOTE-CNN模型能够很好地处理信用欺诈中不均衡数据问题, 显著提高企业对信用卡欺诈检测的效率, 能够为金融机构和监管机构在有效管理信用卡风险方面提供参考. 可将更为复杂的信用卡欺诈数据应用于此算法, 也可以将其应用于其他需要平衡数据的研究领域中.
未来可将此模型与多种机器学习算法融合, 构建更为强大的欺诈检测分类器, 以获得更好的预测性能.
| [1] |
Srivastava A, Kundu A, Sural S, et al. Credit card fraud detection using hidden Markov model. IEEE Transactions on Dependable and Secure Computing, 2008, 5(1): 37-48. DOI:10.1109/TDSC.2007.70228 |
| [2] |
Özçelik MH, Duman E, Işik M, et al. Improving a credit card fraud detection system using genetic algorithm. 2010 International Conference on Networking and Information Technology. Manila: IEEE, 2010. 436–440.
|
| [3] |
Şahin YG, Duman E. Detecting credit card fraud by decision trees and support vector machines. Proceedings of the International MultiConference of Engineers and Computer Scientists 2011. Hong Kong: International Association of Engineers, 2011. 442–447.
|
| [4] |
Bahnsen AC, Stojanovic A, Aouada D, et al. Cost sensitive credit card fraud detection using Bayes minimum risk. 2013 12th International Conference on Machine Learning and Applications. Miami: IEEE, 2013. 333–338.
|
| [5] |
Carneiro EM, Dias LAV, da Cunha AM, et al. Cluster analysis and artificial neural networks: A case study in credit card fraud detection. 2015 12th International Conference on Information Technology-New Generations. Las Vegas: IEEE, 2015. 122–126.
|
| [6] |
Fu K, Cheng DW, Tu Y, et al. Credit card fraud detection using convolutional neural networks. International Conference on Neural Information Processing. Kyoto: Springer, 2016. 483–490.
|
| [7] |
Jurgovsky J, Granitzer M, Ziegler K, et al. Sequence classification for credit-card fraud detection. Expert Systems with Applications, 2018, 100: 234-245. DOI:10.1016/j.eswa.2018.01.037 |
| [8] |
Carcillo F, Le Borgne YA, Caelen O, et al. Combining unsupervised and supervised learning in credit card fraud detection. Information Sciences, 2021, 557: 317-331. DOI:10.1016/j.ins.2019.05.042 |
| [9] |
Hussein AS, Khairy RS, Najeeb SMM, et al. Credit card fraud detection using fuzzy rough nearest neighbor and sequential minimal optimization with logistic regression. International Journal of Interactive Mobile Technologies, 2021, 15(5): 24-42. DOI:10.3991/ijim.v15i05.17173 |
| [10] |
Almhaithawi D, Jafar A, Aljnidi M. Correction to: Example-dependent cost-sensitive credit cards fraud detection using SMOTE and Bayes minimum risk. SN Applied Sciences, 2020, 2(12): 1995. DOI:10.1007/s42452-020-03810-y |
| [11] |
刘颖, 杨轲. 基于深度集成学习的类极度不均衡数据信用欺诈检测算法. 计算机研究与发展, 2021, 58(3): 539-547. DOI:10.7544/issn1000-1239.2021.20200324 |
| [12] |
琚春华, 陈冠宇, 鲍福光. 基于kNN-Smote-LSTM的消费金融风险检测模型——以信用卡欺诈检测为例. 系统科学与数学, 2021, 41(2): 481-498. DOI:10.12341/jssms14145 |
| [13] |
戴月明, 王明慧, 张明, 等. SVD优化初始簇中心的K-means中文文本聚类算法. 系统仿真学报, 2018, 30(10): 3835-3842. |
| [14] |
Chawla NV, Bowyer KW, Hall LO, et al. SMOTE: Synthetic minority over-sampling technique. Journal of Artificial Intelligence Research, 2002, 16: 321-357. DOI:10.1613/jair.953 |
| [15] |
翟云, 王树鹏, 马楠, 等. 基于单边选择链和样本分布密度融合机制的非平衡数据挖掘方法. 电子学报, 2014, 42(7): 1311-1319. DOI:10.3969/j.issn.0372-2112.2014.07.011 |
| [16] |
Han H, Wang WY, Mao BH. Borderline-SMOTE: A new over-sampling method in imbalanced data sets learning. International Conference on Intelligent Computing. Hefei: Springer, 2005. 878–887.
|
| [17] |
Tang YC, Zhang YQ, Chawla NV, et al. SVMs modeling for highly imbalanced classification. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 2009, 39(1): 281-288. DOI:10.1109/TSMCB.2008.2002909 |
 2022, Vol. 31
2022, Vol. 31


