阀冷系统是换流阀的一个重要组成部分, 它将阀体上各元件的功耗发热量排放到阀厅外, 保证晶闸管运行结温在正常范围内. 阀冷系统运行数据主要用于监测采用水冷的换流阀的冷却效果是否有效, 分为内冷水系统和外冷水系统. 其中冷却水进阀温度是反映阀冷系统换热性能的重要指标, 若换热性能出现异常, 将引起冷却水进阀温度上升, 严重时将达到换流阀运行允许温度的最大值, 导致换流阀强迫停运事件的发生. 进阀温度都是以时间序列形式存储, 可以使用时序分析方法对其进行预测, 实现对设备异常运行状态的提前预警, 将有效提高阀冷系统内设备运行的安全性和可靠性.
时间序列预测在帮助人们进行资源管理和科学决策的过程中扮演着非常重要的角色, 其目的在于研究如何根据历史观测数据对未来进行准确预测. 经典的时间序列预测模型通过给定最近一段时间的历史数据来预测未来. 常用的方法包括Box-Jenkins方法[1]和ARIMA模型[2]. 在实践中, 预测问题通常更为复杂, 例如, 输入通常包含动态历史特征和长期依赖, 输入和输出之间存在线性和非线性关系等. 然而, 传统的自回归方法[3-5]难以捕获序列数据中存在的这些关系. 解决现有方法在时间序列预测中的这种局限性是本文的重点.
最近, 深度神经网络已经在时间序列预测中得到了广泛应用, 常用于预测多个时间步以后的数据, 预测的时间步越远, 预测难度越大. 循环神经网络(RNN)和它的变体长短期记忆网络(LSTM)被提出用于对复杂序列数据建模, 例如自然语言[6], 声音信号[7]和视频信息[8]. LSTM已经被广泛运用在了预测任务中[9-11], 在捕获动态时间序列中的重复模式方面表现出强大的能力. 对于大多数深度学习实践者来说, 序列建模等同于循环神经网络, 然而文献[12]通过大量实验表明, 基于卷积架构的时间卷积网络(TCN)在多个序列建模任务上表现得比循环神经网络更好. TCN由于其简单性和适用于长时间序列的特点在时间序列建模任务上受到了广泛关注[13, 14]. 本文试图将LSTM和TCN结合起来使用, 以综合它们的优势.
大多数神经网络模型没能有效地将时间本身作为特征, 通常假设数据是同步的, 即按相等时间间隔采集. 为了帮助神经网络更好地利用时间特征, 一些研究者针对特定问题提出了手动提取时间特征的方法[15, 16], 但这些方法代价高且需要问题相关的专业领域知识. 最近许多研究旨在提出通用的时间序列表示学习方法[17-19], 通过模型自动提取时间特征, 从而避免手工提取带来的问题.
此外, 在各种确定性的点预测方法的基础上, 考虑到多种不确定性因素, 开展了大量概率性区间预测的研究工作, 即预测目标的完整分布来量化预测的不确定性, 从而估计决策的风险. 对于换流站内的数据来说, 如果预测值高于阈值就需要提前报警, 从预测分布中选取不同程度的估计值依赖于阈值设定的严格程度. 分位数回归已被广泛用于对不同的分位数进行预测, 以便在不做分布假设的情况下对目标分布进行估计. 均值回归又称最小二乘法, 是分位数回归的一种特殊情况, 它关注的是条件平均数, 而分位数回归可以扩展到任意分位数. 最近的许多预测模型[20, 21]都通过分位数损失函数来实现分位数估计.
本文基于表示学习和组合网络的思想, 结合时间序列的预测分析方法, 提出了一个深度学习框架T2VNN (Time2Vec neural network)并将其应用于阀冷系统进阀温度的预测研究, 如图1所示. 首先使用经典的时间表示学习方法Time2Vec[22]对进阀温度的周期信息进行特征提取, 其次将TCN和双向LSTM构成组合网络对提取后的信息进行编码. 在结果的输出部分添加了传统的自回归线性模型, 使得非线性神经网络对于进阀温度数据规模的变化具有更强的鲁棒性. 最后使用分位数损失函数对模型进行评估, 从而产生不同分位数的预测结果. 实验表明本文方法在真实阀冷系统进阀温度数据集上的预测效果优于传统的时间序列预测方法.
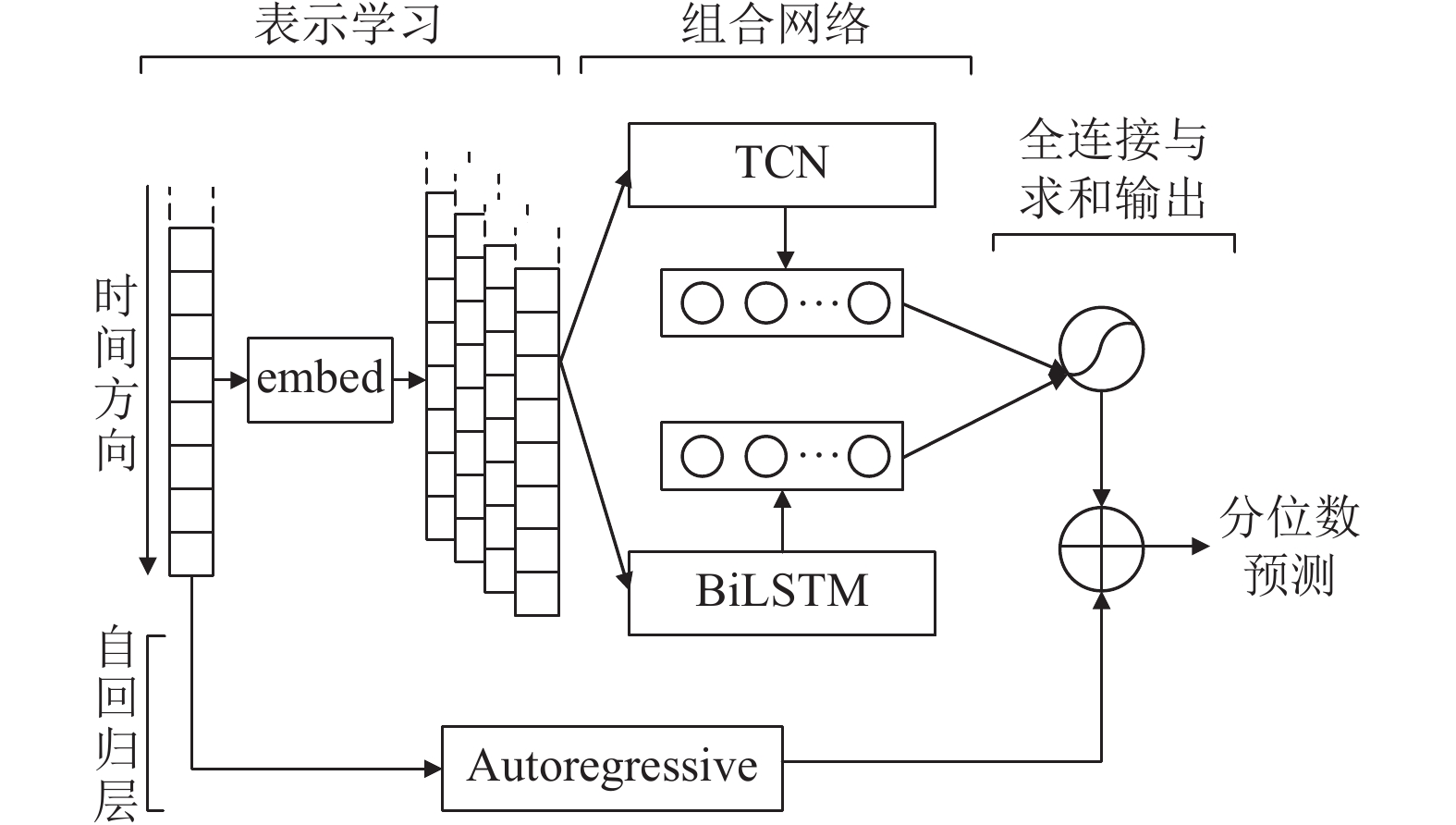
|
图 1 T2VNN架构图 |
1 相关工作
在自然语言处理领域已经存在了大量关于表示学习的研究成果[23, 24], 当处理对象变成时间序列的时候, 许多研究者同样提出了一些通用的表示学习方法, 进一步提升了模型对于时间序列的处理能力. Fortuin等[25]对时间序列的演化进行表示, 同时关注了表示的可解释性. Hyvärinen等[26]通过表征对时间序列中大小均匀的分项来区分它们. Wu等[27]提出一种基于核的估计方法来计算特征嵌入.
深度神经网络使用过去观察到的时间序列来预测未来未知的时间序列. 其中, 循环神经网络在多个时间步中维持隐含状态信息, 早期的成果主要包括使用原生的RNN模型[28]和组合了ARIMA和多层感知机的混合模型[29]等. Dasgupta等[30]将RNN和动态玻尔兹曼机组合在一起. 随着基于卷积架构的TCN及其相关模型被提出, 一些研究开始将TCN用于时间序列预测. Hewage等[13]将TCN用于天气预测, 实验表明TCN对比LSTM和其他经典的机器学习方法表现更好. Li等[31]结合胶囊网络和TCN用于城市交通预测.
Salinas等[32]提出了DeepAR概率预测模型, 通过事先假设分布来预测未来. DeepAR以LSTM作为基础模型, 通过最大化似然函数来训练. 在预测的过程中, 需要从估计的参数分布中多次抽取样本, 作为预测的经验分布. 本文方法与DeepAR的不同之处在于, 使用了更贴近实际的分位数回归[33], 这是一种更高效的训练策略, 通过将预测问题表示为分位数回归来直接生成目标变量的分位数估计. Zheng[34]使用梯度提升方法[35]来最小化分位数回归的损失函数.
2 框架在这一部分中, 首先对阀冷系统进阀温度预测问题进行形式化的建模, 然后在接下来的部分中讨论本文提出的T2VNN模型的架构细节(图1). 最后, 对分位数回归的目标函数和优化策略进行介绍.
2.1 问题建模中国南方电网阀冷监测设备有很多, 每个设备都有各自的监测数据, 需要对所有的监测数据按设备进行划分, 并按照时间日期进行排列, 筛选出拥有完整时序性的进阀温度数据列表. 首先给定一系列通过采集得到的进阀温度序列数据
表示学习方法Time2Vec[22]作为T2VNN模型的embed层, 目的是对进阀温度中的周期性和非周期性特征进行特征提取, 使神经网络更好地捕获其中的规律性特征. 对于给定时间序列
| $ {t} 2v(\tau )[i] = \left\{ {\begin{array}{*{20}{l}} {{\omega _i}\tau + {\varphi _i}, }&{{\text{if }}i = 0} \\ {F({\omega _i}\tau + {\varphi _i}), }&{{\text{if }}1 \leqslant i \leqslant k} \end{array}} \right. $ | (1) |
其中,
将组合网络TCN的输出向量记为
| $ h_t^D = {W^T}h_t^T + {W^B}h_t^B + b $ | (2) |
其中,
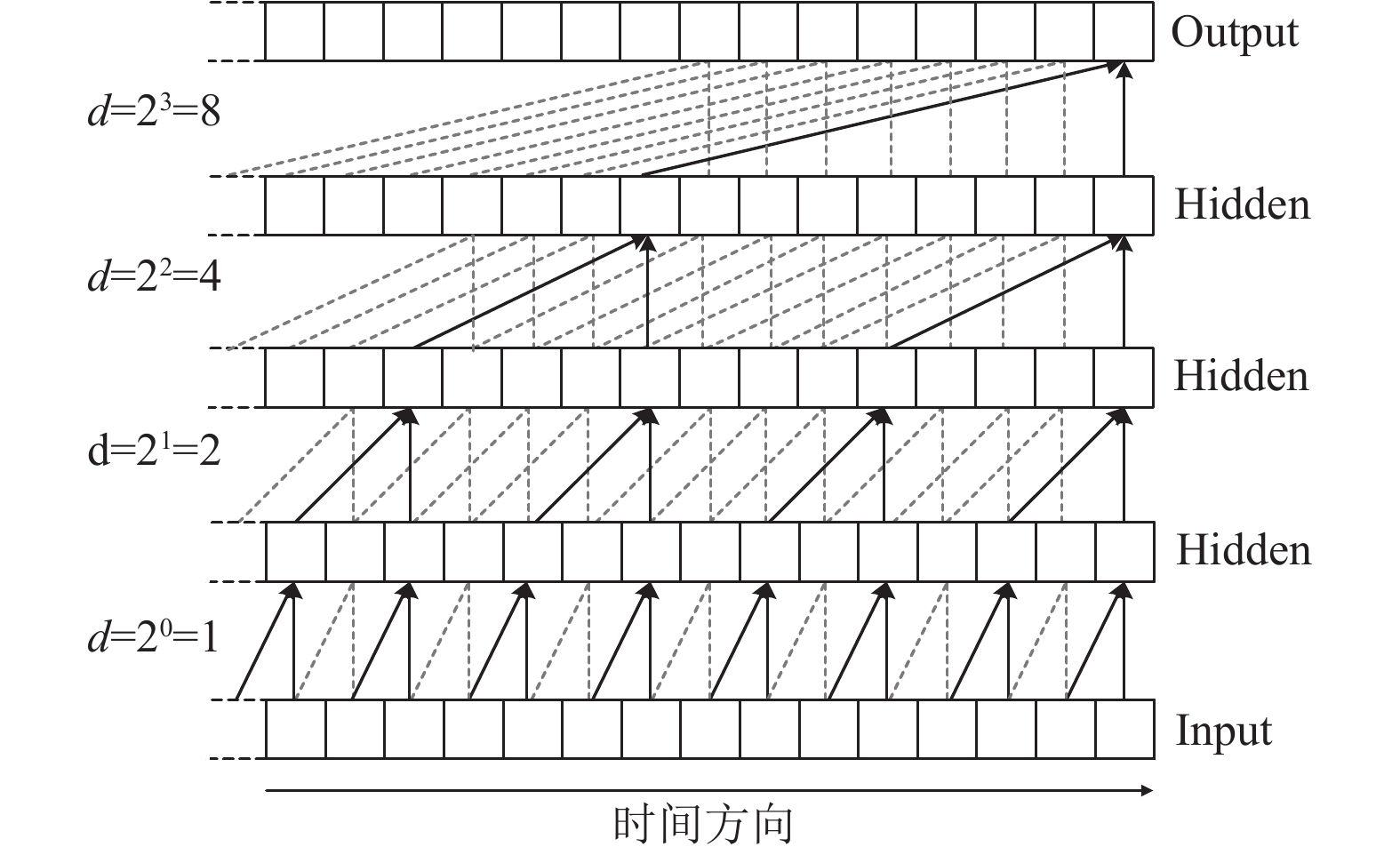
|
图 2 TCN模型 |
(1) 时间卷积网络TCN
TCN由扩张因果卷积构成. 其中, 卷积操作使用一维卷积, 通过在空缺位置补零将任意长度的多维特征映射为相同长度的输出向量, 并且使用因果卷积在映射的过程中确保当前时间点的数据只能通过历史数据计算得到. 为了在不增加网络复杂度的情况下扩大对进阀温度历史数据的接受范围, 进一步融合了扩张卷积的思想形成扩张因果卷积. 更形式化地来说, 对于多维序列特征输入
| $ F(s) = ({{x}}{ * _d}f)(s) = \sum\limits_{i = 0}^{k - 1} {f(i) \cdot {{{x}}_{s - d \cdot i}}} $ | (3) |
其中,
(2) 双向长短期记忆网络BiLSTM
LSTM能够缓解RNN训练时产生的梯度消失问题, 更好地捕获时间序列的长期依赖模式. 因为进阀温度时间序列不仅存在正向的依赖关系, 还有可能存在相应的逆向关系, 所以在这里使用了双向LSTM(BiLSTM), 可以让输入特征在正序和逆序两个方向上进行传播, 从而为预测建立更多的潜在特征. 形式上, 将每个时间点的输入记为
| $ {i_t} = \sigma ({W_{ix}}{x_t} + {W_{ih}}{h_{t - 1}}) $ | (4) |
| $ {f_t} = \sigma ({W_{fx}}{x_t} + {W_{fh}}{h_{t - 1}}) $ | (5) |
| $ {o_t} = \sigma ({W_{ox}}{x_t} + {W_{oh}}{h_{t - 1}}) $ | (6) |
| $ {c_t} = f \cdot {c_{t - 1}} + {i_t} \cdot \tanh ({W_{cx}}{x_t} + {W_{ch}}{h_{t - 1}}) $ | (7) |
| $ {h_t} = {o_t} \cdot \tanh ({c_t}) $ | (8) |
对于双向LSTM, 如图3所示, 时间点
| $ \overrightarrow {{h_t}} = \overrightarrow {LSTM} ({x_t};\overrightarrow {{h_{t - 1}}} ) $ | (9) |
| $ \overleftarrow {{h_t}} = \overleftarrow {LSTM} ({x_t};\overleftarrow {{h_{t - 1}}} ) $ | (10) |
| $ {h_t} = [\overrightarrow {{h_t}} ;\overleftarrow {{h_t}} ] $ | (11) |

|
图 3 BiLSTM模型 |
在模型的输出部分, 为了有选择性地关注到每个时间点的输出信息, 引入了Attention机制[36]. 在当前时间点
| $ {\alpha _t} = {\textit{AttnScore}}({H_t}, {h_{t - 1}}) $ | (12) |
其中,
| $ h_t^B = W[{c_t};{h_{t - 1}}] + b $ | (13) |
由于神经网络的非线性性质, 输出尺度对于输入尺度的变化不敏感, 并且由于进阀温度时间序列存在线性和非线性的多种上下文关系, 数据规模随时间也会发生较明显的变化. 本文借鉴LSTNet[37]将序列分解成线性和非线性部分, 非线性部分通过Time2Vec进一步提取其中的周期性和非周期性模式, 线性部分通过自回归(AR)模型进行特征提取. 将AR部分的预测结果记为
| $ h_t^L = \sum\limits_{k = 0}^{w - 1} {W_k^{ar}{y_{t - k}} + {b^{ar}}} $ | (14) |
最后将组合网络部分的输出和AR部分的输出相加得到T2VNN模型在时间点
| $ {{\widehat Y_t}} = h_t^D + h_t^L $ | (15) |
进阀温度本身存在众多非线性特性以及非均匀分布的残差, 不适合使用平均绝对误差(MAE)作为损失函数, 所以本文使用平均绝对偏差(MAD)损失函数作为模型训练的目标函数, 以实现分位数预测, 定义为每个未来时间点
| $ {L^{MAD}} = \sum\limits_t {[q{{({y_t} - {{\widehat y}_t}})^ + } + (1 - q){{( {{\widehat y_t}} - {y_t})}^ + }]} $ | (16) |
其中,
本文使用5种方法(包括本文方法)在电网领域数据集上针对时间序列预测任务展开实验. 所有的数据和实验代码可以从网站
本文使用如下方法展开对比实验:
(1) Benchmark直接使用历史输入最后一个时间点的值作为预测值.
(2) Autoregressive自回归模型是传统时间序列预测方法的典型代表.
(3) Gradient-Boosting是一个经典的机器学习算法, 可用于回归和分类问题. 为了对比这里使用分位数损失函数.
(4) DeepAR是基于LSTM的概率预测模型, 为了对比使用其基于分位数回归的形式.
3.2 评估指标本文使用两个传统的评估指标, 定义如下:
(1) 相对平方根误差(RSE):
| $ {\textit{RSE}} = \frac{{\sqrt {\displaystyle\sum\nolimits_t {{{({Y_t} - {{\widehat Y_t}})}^2}} } }}{{\sqrt {\displaystyle\sum\nolimits_t {({Y_t} - {\rm{mean}}(Y))} } }} $ | (17) |
(2) 经验相关系数(CORR):
| $ CORR{\text{ = }}\frac{{\displaystyle\sum\nolimits_t {({Y_t} - {\rm{mean}}(Y))( {{\widehat Y_t}} - {\rm{mean}}(\widehat Y))} }}{{\sqrt {\displaystyle\sum\nolimits_t {{{({Y_t} - {\rm{mean}}(Y))}^2}{{( {{\widehat Y_t}} - {\rm{mean}}(\widehat Y))}^2}} } }} $ | (18) |
其中,
实验数据集valve (
为了更直观地展示进阀温度随时间的变化情况, 绘制如图4所示的折线图. 从图4中可以看出, 除了一些明显的极端值外, 进阀温度随时间的变化呈现出一定的周期性. 为了使用更清晰的方式对重复模式进行检验, 进一步绘制自相关函数(ACF)图如图5所示. 自相关函数描述了进阀温度当前值与其过去值之间的相关程度, 包括直接和间接的相关性信息. 时间序列包含长期趋势变动、季节变动、循环变动和不规则变动, ACF在寻找相关性时会综合考虑所有这些变动, 它的函数定义如下:
| $ R(\tau ) = \frac{{{E} [({y_t} - \mu )({y_{t + \tau }} - \mu )]}}{{{\sigma ^2}}} $ | (19) |
其中,

|
图 4 进阀温度折线图 |
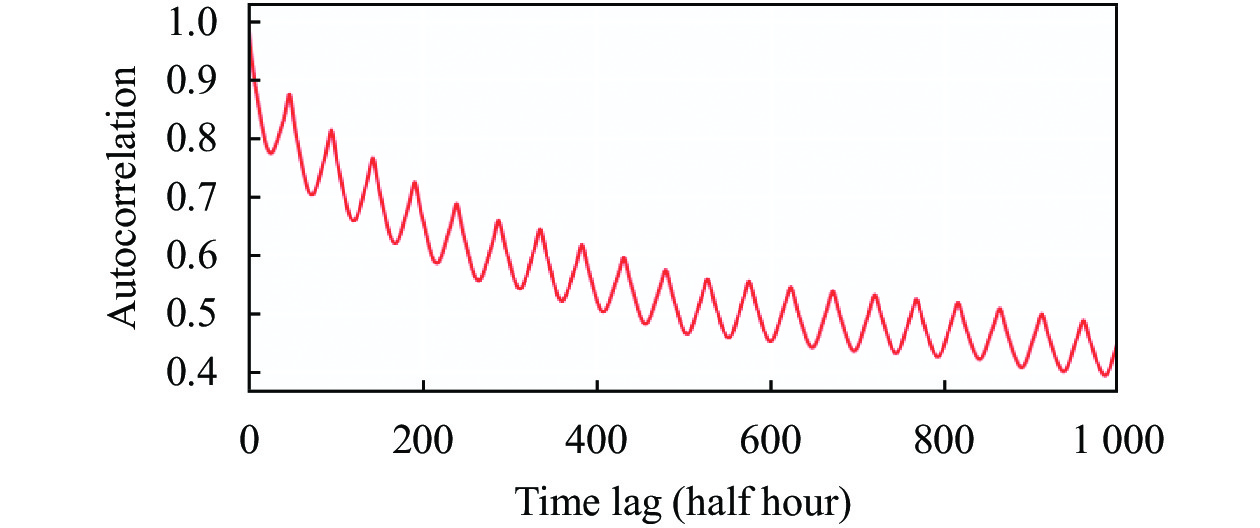
|
图 5 进阀温度自相关函数图 |
在将数据输入模型之前, 还需要一些预处理操作. 从图中可以看出进阀温度随时间变化幅度较大, 需要将它们整合到统一的范畴下, 然后才能进行后续的建模操作. 这里使用标准化的方式, 目的是将原始数据分布转化为均值为0方差为1 的标准正态分布. 之后将原数据集依据6:2:2的比例按时间顺序划分为训练集、验证集和测试集. 接下来将对实验过程中涉及的一些细节进行说明.
3.4 实验细节所有方法首先都需要通过滑动窗口的方式批量采集数据, 形成<输入, 输出>的数据对, 滑动窗口的长度
| 表 1 超参数配置 |
3.5 实验结果
本文使实验从两个角度出发, 一个是不同的预测时间步
| 表 2 对比实验不同预测时间步评估结果 |
| 表 3 对比实验不同分位数评估结果 |
表3总结了所有方法在不同分位数上损失函数的值, 此时的预测时间步统一设置为3. 从表中可以看出, Benchmark和Autoregressive由于缺乏分位数预测能力在所有分位数上表现都是最差的. Gradient-Boosting和DeepAR由于拥有较强的分位数感知能力性能有所提升. 本文方法T2VNN在所有分位数上损失函数的值都是最低的, 说明T2VNN在多种不同的分位数下适应能力更强, 表明使用平均绝对偏差(MAE)作为损失函数的正确性. 为了将预测结果可视化, 便于形象地观察预测效果, 在测试集中选取500个连续时间点的数据, 将预测结果绘制如图6和图7所示. 图6中展示了分位数为0.5 (即自回归预测), 预测时间步为3的预测结果, 其中蓝线代表预测值, 黑线代表真实值. 图7展示了不同分位数的预测结果. 红色区域的下界和上界分别表示分位数0.25和0.75的预测结果; 黄色区域的边界表示分位数0.01和0.99的预测结果. 从图中可以看出, 本文方法T2VNN能够捕获到未来序列数据中的时间模式和趋势变化.
3.6 消融实验为了衡量本文T2VNN框架中一些部分对于模型整体性能的贡献, 设计了相应的消融实验, 即每次从原方法中移除某一个组件进行实验. 首先, 将移除了不同组件后的T2VNN命名如下.

|
图 6 进阀温度自回归预测结果 |
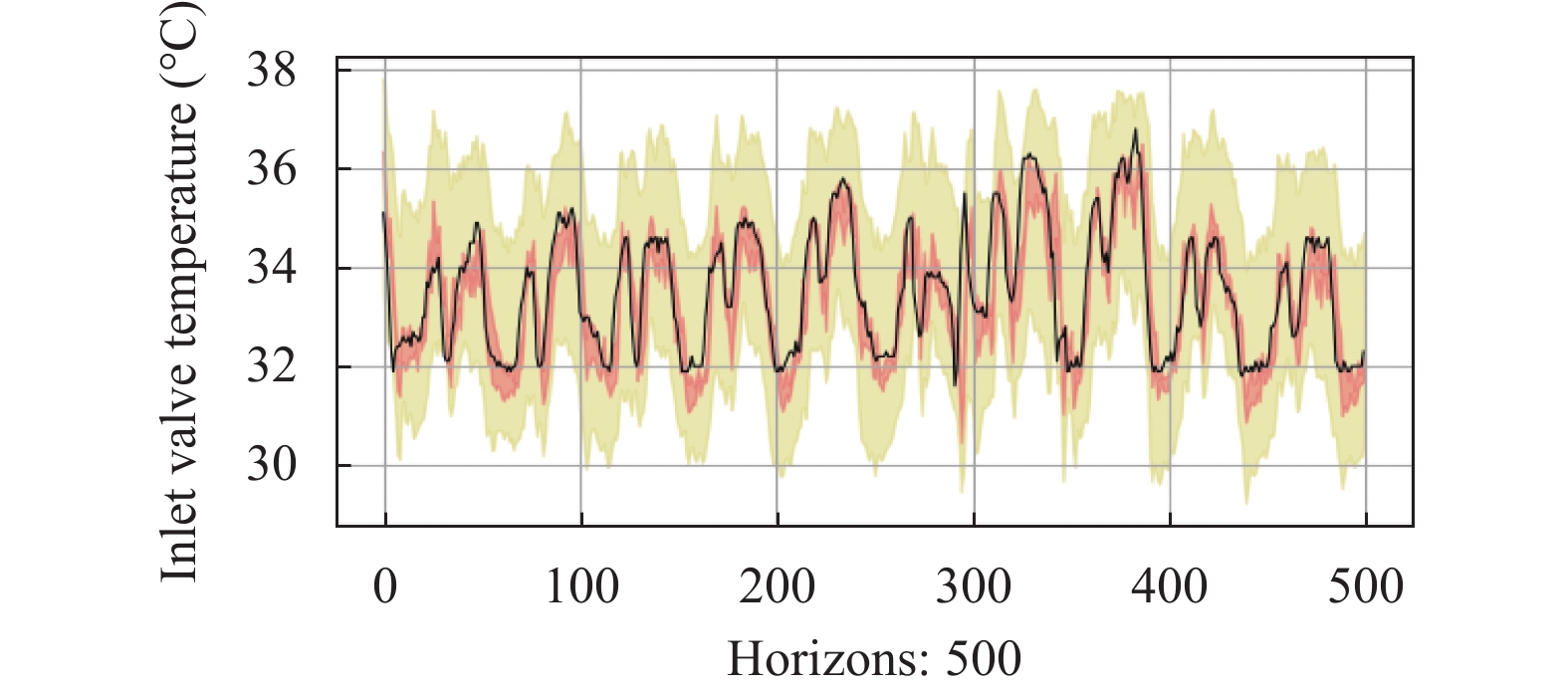
|
图 7 进阀温度分位数预测结果 |
(1) T2VNNw/oT2V: T2VNN模型移除时间序列表示学习方法Time2Vec.
(2) T2VNNw/oAttention: T2VNN模型组合网络部分移除双向LSTM中的Attention层.
(3) T2VNNw/oAR: T2VNN模型移除与表示学习和组合网络并行的自回归层.
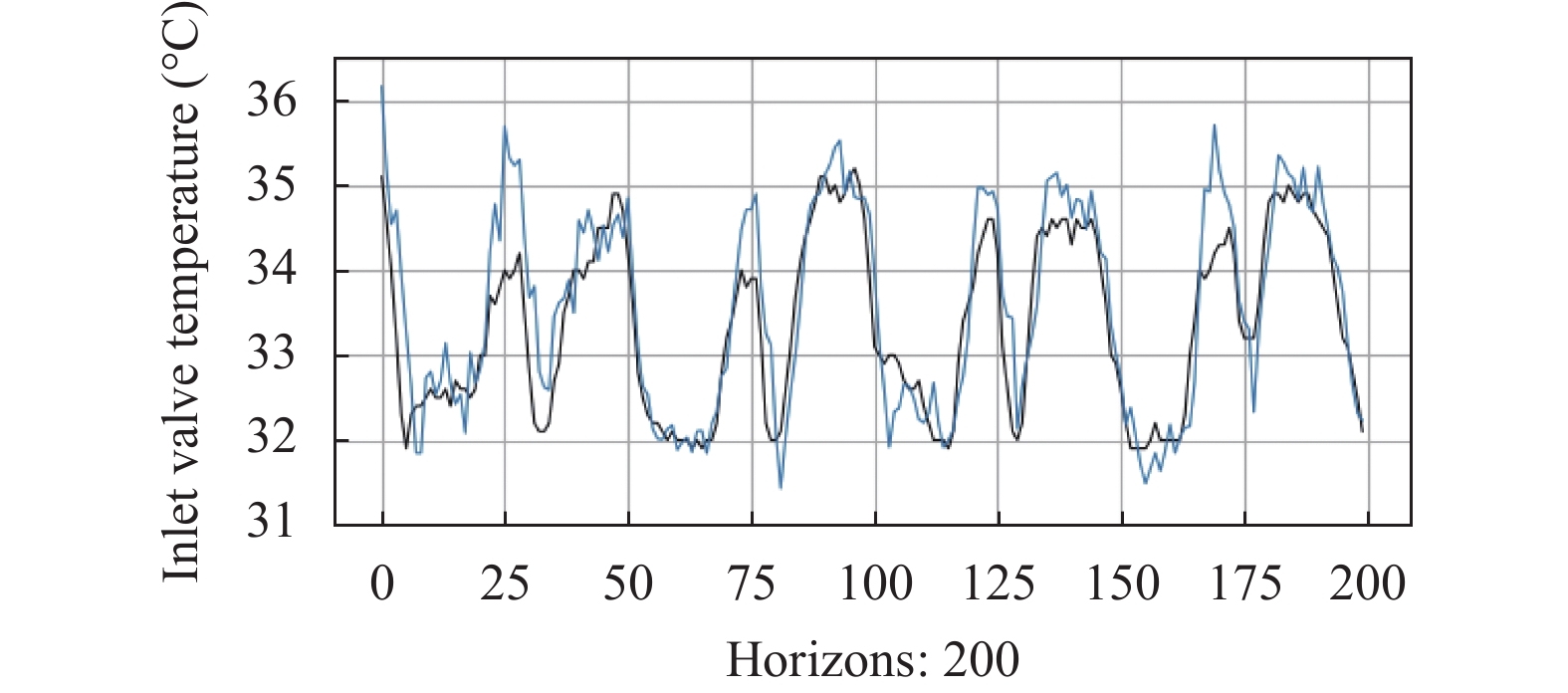
移除部分组件会减少模型的参数量, 需要调整部分超参数使得所有模型的参数量相似. 表4总结了所有方法在不同预测时间步上的评估结果, 分位数设置为0.5, 粗体为两个评估指标在每列中最好的结果. 从表中可以看出, 去除Attention或AR部分后, 模型的性能在所有预测时间步上均出现一定程度的下滑. 去除T2V部分后, 除了预测时间步为12时RSE的值外, 其他情况下也都出现了下滑. 最后, 为了进一步验证本文模型中添加自回归层的必要性, 选取200个连续时间点的数据将T2VNNw/oAR和T2VNN的预测结果绘制如图8和图9所示, 其中蓝线代表预测值, 黑线代表真实值. 从图中可以看出两者预测的差异主要体现在峰值处, 除去自回归层后模型对于数据趋势的变化不敏感, 自回归层能够在一定程度上改善模型对于数据趋势的捕获能力. 综上所述, 本文方法中的几个关键组成部分对模型整体性能均存在贡献.
| 表 4 消融实验不同预测时间步评估结果 |

|
图 8 T2VNNw/oAR预测结果 |
|
图 9 T2VNN预测结果 |
4 结论与展望
本文针对阀冷系统进阀温度预测问题提出了一个深度学习框架T2VNN模型. 通过结合表示学习方法Time2Vec和组合网络的思想, 同时在输出部分添加了自回归模型, 将模型预测过程分解为线性和非线性部分, 用于电网领域阀冷系统中进阀温度的预测研究. 其中组合网络部分结合了TCN和双向LSTM的优势, 共同捕获序列中存在的依赖关系. 本文方法在多个预测时间步和分位数预测中性能均超过多个典型模型, 成功捕获到了进阀温度历史数据中的周期性与非周期性重复模式, 以及相应的趋势变化. 最后, 通过消融实验证明了本文方法中一些关键组件对整体性能均存在贡献.
| [1] |
Holt CC. Forecasting seasonals and trends by exponentially weighted moving averages. International Journal of Forecasting, 2004, 20(1): 5-10. DOI:10.1016/j.ijforecast.2003.09.015 |
| [2] |
Box GEP, Jenkins GM, MacGregor JF. Some recent advances in forecasting and control. Journal of the Royal Statistical Society: Series C (Applied Statistics), 1974, 23(2): 158-179. |
| [3] |
Janacek G. Time series analysis forecasting and control. Journal of Time Series Analysis, 2010, 31(4): 303. |
| [4] |
Li JH, Chen WY. Forecasting macroeconomic time series: LASSO-based approaches and their forecast combinations with dynamic factor models. International Journal of Forecasting, 2014, 30(4): 996-1015. DOI:10.1016/j.ijforecast.2014.03.016 |
| [5] |
Zhang GP. Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing, 2003, 50: 159-175. DOI:10.1016/S0925-2312(01)00702-0 |
| [6] |
Sutskever I, Vinyals O, Le QV. Sequence to sequence learning with neural networks. Proceedings of the 27th International Conference on Neural Information Processing Systems. Montreal: MIT Press, 2014. 3104–3112.
|
| [7] |
van den Oord A, Dieleman S, Zen H, et al. WaveNet: A generative model for raw audio. arXiv: 1609.03499, 2016.
|
| [8] |
Donahue J, Hendricks LA, Guadarrama S, et al. Long-term recurrent convolutional networks for visual recognition and description. 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Boston: IEEE, 2015. 2625–2634.
|
| [9] |
Trung CV, Dinh MN, Dimla E. Predicting phase-field behavior of brittle fracture model based on LSTM time series forecasting model. 2020 RIVF International Conference on Computing and Communication Technologies (RIVF). Ho Chi Minh City: IEEE, 2020. 1–6.
|
| [10] |
Yadav A, Jha CK, Sharan A. Optimizing LSTM for time series prediction in Indian stock market. Procedia Computer Science, 2020, 167: 2091-2100. DOI:10.1016/j.procs.2020.03.257 |
| [11] |
Karevan Z, Suykens JAK. Transductive LSTM for time-series prediction: An application to weather forecasting. Neural Networks, 2020, 125: 1-9. DOI:10.1016/j.neunet.2019.12.030 |
| [12] |
Bai SJ, Kolter JZ, Koltun V. Trellis networks for sequence modeling. arXiv: 1810.06682, 2019.
|
| [13] |
Hewage P, Behera A, Trovati M, et al. Temporal convolutional neural (TCN) network for an effective weather forecasting using time-series data from the local weather station. Soft Computing, 2020, 24(21): 16453-16482. DOI:10.1007/s00500-020-04954-0 |
| [14] |
Lin L, Xu BL, Wu WC, et al. Medical time series classification with hierarchical attention-based temporal convolutional networks: A case study of myotonic dystrophy diagnosis. arXiv: 1903.11748, 2019.
|
| [15] |
Baytas IM, Xiao C, Zhang X, et al. Patient subtyping via time-aware LSTM networks. Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Halifax: ACM, 2017. 65–74.
|
| [16] |
Kwon BC, Choi MJ, Kim JT, et al. RetainVis: Visual analytics with interpretable and interactive recurrent neural networks on electronic medical records. IEEE Transactions on Visualization and Computer Graphics, 2019, 25(1): 299-309. DOI:10.1109/TVCG.2018.2865027 |
| [17] |
Neil D, Pfeiffer M, Liu SC. Phased LSTM: Accelerating recurrent network training for long or event-based sequences. arXiv: 1610.09513, 2016.
|
| [18] |
Zhu Y, Li H, Liao YK, et al. What to do next: Modeling user behaviors by time-LSTM. Proceedings of the 26th International Joint Conference on Artificial Intelligence. Melbourne: AAAI Press, 2017. 3602–3608.
|
| [19] |
Mei HY, Eisner J. The neural hawkes process: A neurally self-modulating multivariate point process. arXiv: 1612.09328, 2017.
|
| [20] |
Wen RF, Torkkola K, Narayanaswamy B, et al. A multi-horizon quantile recurrent forecaster. arXiv: 1711.11053, 2018.
|
| [21] |
Xu QF, Liu X, Jiang CX, et al. Quantile autoregression neural network model with applications to evaluating value at risk. Applied Soft Computing, 2016, 49: 1-12. DOI:10.1016/j.asoc.2016.08.003 |
| [22] |
Kazemi SM, Goel R, Eghbali S, et al. Time2Vec: Learning a vector representation of time. arXiv: 1907.05321, 2019.
|
| [23] |
Church WK. Word2Vec. Natural Language Engineering, 2017, 23(1): 155-162. DOI:10.1017/S1351324916000334 |
| [24] |
Young T, Hazarika D, Poria S, et al. Recent trends in deep learning based natural language processing. arXiv: 1708.02709, 2018.
|
| [25] |
Fortuin V, Hüser M, Locatello F, et al. Deep self-organization: Interpretable discrete representation learning on time series. arXiv: 1806.02199, 2019.
|
| [26] |
Hyvärinen A, Morioka H. Unsupervised feature extraction by time-contrastive learning and nonlinear ica. Proceedings of the 30th International Conference on Neural Information Processing Systems. Barcelona: Curran Associates Inc., 2016. 3772–3780.
|
| [27] |
Wu LF, Yen IEH, Yi JF, et al. Random warping series: A random features method for time-series embedding. Proceedings of the 21st International Conference on Artificial Intelligence and Statistics. Lanzarote: PMLR, 2018. 793–802.
|
| [28] |
Connor J, Atlas LE, Martin DR. Recurrent networks and NARMA modeling. Proceedings of the 4th International Conference on Neural Information Processing Systems. Denver: Morgan Kaufmann Publishers Inc., 1991. 301–308.
|
| [29] |
Jain A, Kumar AM. Hybrid neural network models for hydrologic time series forecasting. Applied Soft Computing, 2007, 7(2): 585-592. DOI:10.1016/j.asoc.2006.03.002 |
| [30] |
Dasgupta S, Osogami T. Nonlinear dynamic Boltzmann machines for time-series prediction. Proceedings of the AAAI Conference on Artificial Intelligence, 2017, 31(1): 1833-1839. |
| [31] |
Li DZ, Lin C, Gao W, et al. Capsules TCN network for urban computing and intelligence in urban traffic prediction. Wireless Communications and Mobile Computing, 2020, 2020: 6896579. |
| [32] |
Salinas D, Flunkert V, Gasthaus J, et al. DeepAR: Probabilistic forecasting with autoregressive recurrent networks. International Journal of Forecasting, 2020, 36(3): 1181-1191. DOI:10.1016/j.ijforecast.2019.07.001 |
| [33] |
Koenker R, Bassett GW. Regression quantiles. Econometrica, 1978, 46(1): 211-244. |
| [34] |
Zheng SF. Boosting based conditional quantile estimation for regression and binary classification. 9th Mexican International Conference on Artificial Intelligence, MICAI 2010. Pachuca: Springer, 2010. 67–79.
|
| [35] |
Friedman JH. Greedy function approximation: A gradient boosting machine. The Annals of Statistics, 2001, 29(5): 1189-1232. DOI:10.1214/aos/1013203450 |
| [36] |
Bahdanau D, Cho K, Bengio Y. Neural machine translation by jointly learning to align and translate. arXiv: 1409.0473, 2016.
|
| [37] |
Lai GK, Chang WC, Yang YM, et al. Modeling long- and short-term temporal patterns with deep neural networks. The 41st International ACM SIGIR Conference on Research & Development in Information Retrieval. Ann Arbor: ACM, 2018. 95–104.
|
| [38] |
Kingma D, Ba J. Adam: A method for stochastic optimization. arXiv: 1412.6980, 2017.
|
 2022, Vol. 31
2022, Vol. 31



