燃气轮机的运行是一个多变量影响的复杂系统, 运行产生的烟气包含大量污染物, 是造成环境污染主要的来源之一[1]. 氮氧化物(NOx)是烟气污染物中最常见的一种, 容易引发化学烟雾、温室效应等环境问题. 选择性催化还原(SCR)是燃气轮机运行中的一项重要技术, 由于SCR脱硝系统入口NOx浓度测量具有一定的滞后特性, 而且受不同因素的影响, 燃气轮机排放的氮氧化物浓度会有较大的波动[2]. 如果能够提前准确预测NOx排放的入口浓度及确定关键特征变量, 能够为建立精确的预测模型, 实现燃烧控制工艺参数优化效率打下基础.
基于物理分析的影响NOx排放的关键运行参数, 往往是针对某一具体型号或工况, 适用范围差. 近年来, 基于数据驱动建模的方法因其具有良好的预测稳定性和非线性处理能力, 在电厂中得到了广泛应用. 吕游等[3]首先利用偏最小二乘法(PLS)对变量进行降维以及消除彼此间的相关性, 然后建立NOx排放的最小二乘支持向量机(LS-SVM)模型, 经过与其他模型对比分析, 验证了PLS特征提取能够降低模型的复杂性. Li等[4]建立基于改进的粒子群算法优化支持向量机(SVM)的NOx预测模型, 以此降低预测误差和提高预测结果的稳定性. 赵刚等[5]在保证燃气轮机运行稳定的情况下利用BP神经网络模型对影响燃气轮机NOx排放的变量因素进行敏感性分析, 确定它们的影响大小及正负相关性. 伦智梅等[6]建立神经网络回归算法模型(RNN), 在此基础上利用平均影响值(MIV)算法定量分析各输入变量对发动机NOx的影响大小. 朱钰森等[7]为了解决锅炉非线性、多工况、多耦合等特点, 提出了一种多模型方法预测NOx的排放量, 根据输入变量对输出变量的影响程度来评价样本之间的差异性, 并把计算出的平均影响值(MIV)作为与多模型连接的权系数, 克服了由于特征变量波动较大使得预测模型不稳定的缺陷. 于静等[8]为了避免由于变量数目的原因造成预测模型精度降低, 采用互信息(MI)筛选出5个特征变量作为预测模型的输入, 降低模型训练的复杂性.
综上所述, 除了预测模型的选择之外, 特征变量的选择也将直接影响预测模型的精确度. 由实验确定的NOx排放规律的泛化性能较差, 不能很好地预测特定燃气轮机的NOx排放以及影响NOx排放的特征变量. 因此, 本文首先利用PLS确定应选择影响燃气轮机NOx排放的特征变量个数, 克服了由于经验和机理分析选取的主观性, 再利用MI选择相关性较大的变量, 确定预测模型的基础数据集. 为了验证PLS-MI组合特征选择模型的有效性, 将其与常用的特征选择方法进行对比分析.
1 氮氧化物与SCR脱硝系统目前, 电站选择降低NOx排放主要有两种方式, 分别为燃烧优化控制和SCR脱硝处理[9]. 但无论哪种减排方式都需要对燃气轮机运行过程中NOx的排放量进行准确监测. SCR脱硝系统的工作原理是在催化剂的作用下, 通过还原剂氨将NOx转化为氮气和水, 如图1所示. 在适当的温度和催化剂条件下, SCR脱硝系统效率主要由氨的量决定, 发生的化学反应如式(1)–式(4)[10]. 从反应原理可以看出若喷氨量不足会降低SCR系统的脱硝效率, 导致NOx浓度排放超标; 若喷氨量过多, 会提高SCR系统的脱硝效率, 但是会造成还原剂氨的浪费和增加成本, 甚至会造成二次污染[11]. 为了减少NOx的排放, 避免氨流量过多导致资源浪费以及氨流量过少造成排放的NOx浓度超标, 必须实时测量和监控SCR脱硝系统的入口NOx排放浓度, 并对燃气轮机的运行实施优化控制[12].
| $ {\rm{4NH_3}} + {\rm{4NO}} + {\rm{O_2}} \to {\rm{4{N_2}}} + {\rm{6{H_2}O}} $ | (1) |
| $ {\rm{4N{H_3}}} + {\rm{6NO}} \to {\rm{5{N_2}}} + {\rm{6{H_2}O}} $ | (2) |
| $ {\rm{2N{H_3}}} + {\rm{NO}} + {\rm{N{O_2}}} \to {\rm{2{N_2}}} + {\rm{3{H_2}O}} $ | (3) |
| $ {\rm{8N{H_3}}} + {\rm{6N{O_2}}} \to {\rm{7{N_2}}} + {\rm{12{H_2}O}} $ | (4) |

|
图 1 SCR系统反应示意图 |
燃气轮机难以通过机理建模的方式实现对NOx排放浓度的精确描述. 相比于机理建模, 数据建模不需要深入了解对象机理特性. 它主要是以大数据为驱动, 统计学原理为基础, 利用先进人工智能算法获得对象的动态特性[13]. BP神经网络是非线性过程建模的常用数据驱动模型, 若没有对数据集进行特征选择, 容易带来模型过拟合及建模时间变长等问题, 而且基于BP神经网络等方法建立SCR脱硝系统的入口NOx浓度预测模型参数的设置过多, 准确性受噪音影响较大, 这些模型对于小样本数据集的训练具有泛化性差和过拟合的缺陷.
综上所述, 准确的测量燃气轮机NOx排放以控制氨注入量是需要解决的关键问题. 我国电厂主要是通过在燃气轮机后接入了SCR脱硝反应器系统, 与NH3反应生成氮和水, 减少NOx排放, 但SCR系统的工作温度必须满足一定的范围和NH3适量使用. 另一种可行的方式是通过调整控制相关变量来保证燃气轮机健康运行的情况下, 对影响NOx排放的变量进行敏感性分析, 确定它们对燃气轮机NOx排放的影响大小以及正负相关性, 这一方法没有附加产物, 更加安全有效, 具有良好的应用前景.
2 燃气轮机NOx特征选择的模型理论 2.1 偏最小二乘法偏最小二乘法(partial least squares, PLS)是一种多元统计数据分析方法, 在成分提取中, 通过将高维空间相关变量投影到一个低维空间变量[14]. 通过信息综合与筛选技术, 既可以从原始数据集中选择适当数量的可以较好地概括自变量系统x中的信息的潜在变量, 也可以消除变量间的共线问题, 尽可能准确的解释因变量y的变化[15].
令Rdx表示第h个成分th对x的解释能力, 自变量个数为p, 第i个自变量xi与第h个成分th的相关系数为r(xi;th), 如式(5):
| $ Rdx = \frac{1}{p}\sum\limits_{i = 1}^p {{r^2}({x_i};{t_h})} $ | (5) |
用m表示利用交叉有效性提取的主要成分个数, 则m个成分对x的累计解释能力CRdx为:
| $ CRdx = \sum\limits_{h = 1}^m {\left[ {\frac{1}{p}\sum\limits_{i = 1}^p {{r^2}({x_i};{t_h})} } \right]} $ | (6) |
令q表示因变量个数, Rdy表示第h个成分th对y的解释能力:
| $ Rdy = \frac{1}{q}\sum\limits_{j = 1}^q {{r^2}({y_j};{t_h})} $ | (7) |
则m个成分对y的累计解释能力CRdy为:
| $ CRdy = \sum\limits_{h = 1}^m {\left[ {\frac{1}{q}\sum\limits_{j = 1}^q {{r^2}({y_j};{t_h})} } \right]} $ | (8) |
PLS中的变量投影重要性(variable importance in projection, VIP)通过相关自变量综合的主成分解释特征变量xi (i=1, 2, …, n)对自变量y的重要性, 并根据VIP值筛选影响较大的特征变量, 可以克服特征变量xi间的多重相关性, 计算简单, 应用广泛. 它每个变量xi的VIP值是通过PLS加载权重的平方和(
| $ VI{P_i} = \sqrt {\frac{p}{{CRdy}}\sum\limits_{h = 1}^m {Rdy\omega _{ih}^2} } $ | (9) |
其中,
信息熵是由美国科学家香农提出, 主要是用来度量随机变量的不确定性程度. 其值越大, 所蕴含的信息量越大[16]. 用H(X)表示信息源X={x1, x2, …, xn}对应的信息熵, 每个信息源xi所对应的概率为p(xi), 则:
| $ \begin{split} H(X)= \sum\limits_{i = 1}^n {p({x_i})} {\log _2}\frac{1}{{p({x_i})}} = - \sum\limits_{i = 1}^n {p({x_i})} {\log _2}p({x_i}) \end{split} $ | (10) |
在条件Y确定的情况下, 信息源X可以用条件熵来描述:
| $ H(X|Y) = - \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^m {p({x_i}, {y_j})} } {\log _2}p({x_i}|{y_j}) $ | (11) |
| $ H(X, Y) = - \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^m {p({x_i}, {y_j})} } {\log _2}p({x_i}, {y_j}) $ | (12) |
互信息(mutual information, MI)用于分析每个可能的输入变量与目标输出变量之间的非线性关系, 从中选择最相关的变量作为模型的输入变量[17]. 对于给定目标变量Y后, 特征变量X的不确定性减少程度为:
| $ \begin{split} I(X ; Y) &=\mathop \iint_{Y X} p_{X Y}(x, y) \log \left(\frac{p_{XY}(x, y)}{p_{X}(x) p_{Y}(y)}\right) d x d y \\ &=\sum_{i=1}^{n} \sum_{j=1}^{m} p\left(x_{i}, y_{j}\right) \log _{2} \frac{p\left(x_{i}, y_{j}\right)}{p\left(x_{i}\right) p\left(y_{j}\right)} \end{split} $ | (13) |
其中, p(xi)为X的边缘概率分布, p(yj)为Y的边缘概率分布.
偏最小二乘法既能较好地概括自变量系统中的信息, 又能很好的解释因变量的变化并排除系统中的噪声干扰[18]. 互信息不仅能反应线性关系, 也能反应其非线性关系, 因此互信息在反应变量之间的相关性比相关系数更加全面[19]. 因此, 本文采用PLS特征提取和MI特征选择混合算法(PLS-MI)选取燃气轮机氮氧化物的影响变量.
3 仿真结果分析 3.1 数据获取与预处理燃气轮机的运作过程是一个复杂的化学反应过程, 国内外学者对基于数据的氮氧化物的特征变量均有所研究, 从不同参数条件下进行了分析, 发现控制燃料流量、燃料组分、环境温度、燃烧温度和燃气轮机的进出口压力差等都可以影响NOx的产生. 燃气轮机NOx排放特性主要与燃烧室内燃烧模式及燃烧特性相关, 影响因素主要有燃料流量、空气流量、燃气轮机负荷、燃烧室温度等. 燃气轮机燃烧室温度主要由燃料流量和空气流量决定.
为了研究影响NOx排放情况的关键因素, 文献[5]中选取电厂稳态数据的环境温度、天然气温度、透平出口温度、IGV开度、值班火焰燃料质量流量、预混火焰燃料质量流量、燃烧室进口压力、燃烧室压降等8个变量作为模型的输入变量. 本文基于试验过程中积累的先验知识, 以冗余的选择原则, 选取影响燃气轮机NOx排放水平的19个性能参数作为燃气轮机的影响因素, 分别为: 环境温度(AT)、环境压力(AP)、环境湿度(AH)、空气过滤器压差(AFDP)、燃气轮机排放压力(GTEP)、燃气轮机轴转矩(GTT)、燃气发生器转速(GGn)、GT压缩机进出口空气温度差T、涡轮进口温度(TIT)、涡轮后温度(TAT)、涡轮能量产率(TEY)、高压涡轮出口压力(P1)、燃气轮机废气压力(Pexh)、燃气轮机压缩机进出口空气压力差(P2)、涡轮出口高压(HP)温度(T)、压缩机排气压力(CDP)、燃料流量(mf)、涡轮注入控制(TIC)、一氧化碳(CO)等, 在此基础上提取对燃气轮机NOx影响较大的特征变量.
偏最小二乘法的特征变量个数是通过残差阈值来确定. 当特征变量个数增加时, 方差解释信息的变化小于一定的阈值就停止分解, 如图2的特征变量的方差解释. 从图2中可以看出当特征变量个数为7时, 因变量中约有95%的方差信息被解释. 此时提取新的特征变量得到的方差解释信息的变化较小, 因此剩余的残差可被认为是噪声干扰. 若再增加特征变量个数, 会引入噪声并且使模型的复杂度增加, 从而降低模型的精确度.
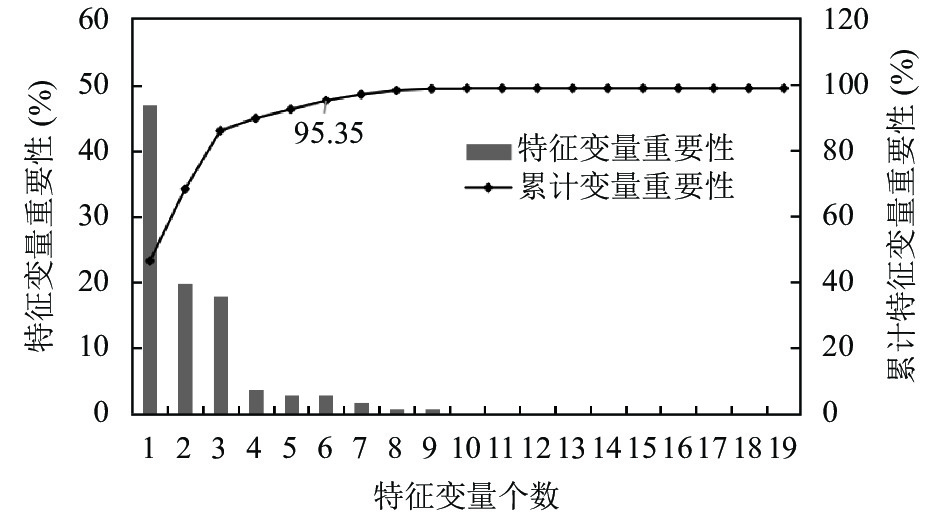
为了验证PLS在选择NOx特征变量个数的有效性, 选择特征提取中最常用的主成分分析(principal component analysis, PCA)和随机森林(random forest, RF)方法作为对比[20, 21]. 利用主成分分析(PCA)对燃气轮机氮氧化物的影响因素个数进行分析, 计算主成分因子的累计方差贡献率, 如图3所示. 为了减少信息的丢失, 选择累计方差贡献率95%为阈值, 把方差贡献率的累加值超过95%的因子数作为特征变量的选取数[20]. 从图3中可以看出, 当第5个特征因子出现的时候, 其总体的累计方差贡献率为95.06%, 超过了95%, 则可以选取5个特征变量代替原变量作为预测模型的输入. 在随机森林中, 为了选择哪些特征更重要, 需要考虑的是特征的累加重要性, 通常以95%为阈值, 当其特征重要性的累加值超过该阈值时, 就选择其特征变量个数代替原来的数据集[21]. 从图4可以看出, 当特征变量个数为6时, 特征变量的累加重要性达到了95.35%, 因此应该选取6个特征变量.

|
图 2 PLS分析因变量方差解释与特征变量个数变化关系 |

|
图 3 PCA分析因变量方差解释与特征变量个数变化关系 |
综上, 不同方法选择的特征变量的数目不同, 利用PLS、PCA、RF应选择的特征变量分别是7个、5个和6个. 为了更好地证明所选用模型在燃气轮机特征变量选择中具有较好的适用性, 把单一模型PLS、MI、RF和组合模型RF-MI、PCA-MI、PCA-RF、PCA-PLS、PLS-MI的预测仿真结果对比分析.
|
图 4 RF分析特征变量重要性与特征变量个数之间的关系 |
3.2 不同变量选择方法的仿真结果
为了更好地验证预测模型的仿真效果, 采用度量建立模型与样本数据拟合程度的均方根误差(RMSE)、平均绝对值百分比误差(MAPE)、平均绝对误差(MAE) 3个评价指标, 如式(14)–式(16).
| $ RMSE = \sqrt {\frac{1}{N}\sum\limits_{t = 1}^N {{{({y_t} - {{\hat y}_t})}^2}} } $ | (14) |
| $ MAPE = \frac{1}{N}\frac{{\displaystyle\sum\limits_{t = 1}^N {\left| {{y_t} - {{\hat y}_t}} \right|} }}{{{y_t}}} $ | (15) |
| $ MAE = \frac{1}{N}\sum\limits_{t = 1}^N {\left| {{y_t} - {{\hat y}_t}} \right|} $ | (16) |
其中,
利用Matlab R2018a的开发环境进行仿真实验, 求出各个特征变量的互信息值、偏最小二乘法的重要性值、随机森林的重要性值, 如表1所示.
从表1中可以看出, 利用PLS选取的7个变量为X1、X4、X9、X11、X14、X16、X19, 利用随机森林应该选取6个特征变量为X1、X3、X4、X5、X10、X19, 利用主成分分析法应该选择5个特征变量. 单一的PLS、MI、RF特征选择方法选择影响较大的变量, 并进行预测仿真分析, 组合模型是利用PLS、PCA、RF确定出应选择出的特征变量数目, 然后再利用MI选择出相关性较强冗余性小的变量, 代入BP神经网络的预测模型, RF-MI、PCA-MI、PCA-RF、PCA-PLS、PLS-MI的预测仿真结果如表2所示.
| 表 1 NOx排放量的多模型特征变量选择结果 |
| 表 2 BP神经网络预测模型的仿真结果 |
为了防止BP神经网络预测模型存在偶然性问题, 再利用遗传算法(GA)优化BP神经网络的GABP模型和天牛须搜索算法(BAS)优化BP神经网络的BASBP模型进行预测仿真实验, 结果如表3和表4所示.
| 表 3 GA-BP网络模型预测的仿真结果 |
研究问题时将BP神经网络、GABP、BASBP网络预测模型分别在进行特征变量处理和不同特征变量选择方法下进行实验并对预测结果进行了统计, 通过表2–表4中的评价指标分析, 利用随机森林和主成分分析时, 选择的特征变量较PLS的较小, 不具有代表性, 缺失了一部分信息. 在实际问题中, 每一类方法都有一定的局限性. 采用PLS-MI组合的特征选择优于单一的PLS、MI特征选择, 说明PLS和MI在提取特征时只估计单个特征的得分, 未评估特征子集的性能, 导致提取特征变量时丢失大量有用信息, 降低模型的预测性能. 把PLS和MI模型组合对影响燃气轮机氮氧化物的特征变量选取实践中, 通过不同的仿真模型证明了PLS-MI组合模型较单一的PLS、MI、RF和组合的PCA-MI、RF-MI、PCA-RF、PCA-PLS特征变量选择方法提取的特征变量更具有代表性且能提高模型预测性能.
| 表 4 BAS-BP网络模型预测的仿真结果 |
3.3 灵敏度分析
首先利用PLS-MI的组合特征选择方法选择出燃气轮机NOx的影响因素, 根据表1选择出MI值较大的特征变量为: X1 、X5、X4、X3、X16、X9、X11.
特征选择的目的是准确预测燃气轮机NOx的排放, 则需要对影响NOx排放的变量进行敏感性分析, 确定特征变量对NOx的影响大小以及正负相关性, 如图5所示. 选取的7个变量中, X1、X4、X3为环境变量不可调, 调整SCR系统的入口NOx浓度应着眼于X5、X16、X9和X11的4个独立变量进行调整.

|
图 5 相关性分析 |
4 结论
在对燃气轮机运行的系统分析研究前, 需要对工艺流程中的各个变量进行评估, 选择数据价值高的变量. 目前研究常用的方法大多都是以多元线性回归作为基础进行分析, 以特征与目标的相关性作为变量选择的条件, 但是在研究中并没有考虑多重线性的影响.
通过研究发现, 在对燃气轮机NOx数据分析和特征提取的过程中, 为了得到更多的有用信息, 都是尽可能多的选择有价值的特征. 但当收集的样本数据集变量过多时会具有高度非线性, 导致建立的预测模型会耗费大量的时间, 也易出现过拟合的现象, 特征变量选择在建模过程中成为了一个非常重要的部分. 本文在选择燃气轮机NOx排放量的影响因素时, 兼得了单一模型稳定的泛化性能与多模型较好的跟踪能力, 克服了由于存在非线性、多工况、输出变量波动较大而使得建模效果不稳定的难题.
| [1] |
唐振浩, 柴向颖, 曹生现, 等. 考虑时延特征的燃煤锅炉NOx排放深度学习建模
. 中国电机工程学报, 2020, 40(20): 6633-6643. |
| [2] |
董泽, 闫来清. SCR脱硝系统NOx排放浓度建模与仿真
. 系统仿真学报, 2020, 32(2): 172-181. |
| [3] |
吕游, 刘吉臻, 杨婷婷, 等. 基于PLS特征提取和LS-SVM结合的NOx排放特性建模
. 仪器仪表学报, 2013, 34(11): 2418-2424. |
| [4] |
Li QW, Zhou KY, Yao GH. Combustion optimization model for NOx reduction with an improved particle swarm optimization
. Journal of Shanghai Jiaotong University (Science), 2016, 21(5): 569-575. DOI:10.1007/s12204-016-1764-6 |
| [5] |
赵刚, 朱华昕, 李苏辉, 等. 基于数据和神经网络的燃气轮机NOx排放预测与优化
. 动力工程学报, 2021, 41(1): 22-27. |
| [6] |
伦智梅, 张振京, 宋业栋, 等. 基于回归神经网络的柴油机NOx排放预测及影响分析
. 山东理工大学学报(自然科学版), 2021, 35(3): 81-86. |
| [7] |
朱钰森, 金晓明, 张泉灵. 基于聚类与加权连接的锅炉NOx排放量多模型建模
. 控制工程, 2019, 26(4): 688-693. |
| [8] |
于静, 金秀章, 刘岳. 基于结构改进RBF神经网络的NOx预测模型比较. 控制工程. https://doi.org/10.14107/j.cnki.kzgc.20210150. (2021-06-05)[2021-07-05].
|
| [9] |
余印振, 韩哲哲, 许传龙. 基于深度卷积神经网络和支持向量机的NOx浓度预测. 中国电机工程学报. https://doi.org/10.13334/j.0258-8013.pcsee.210077. (2021-04-01)[2021-06-23].
|
| [10] |
许壮, 康英伟. 基于随机森林的火电机组SCR脱硝反应器建模. 动力工程学报, 2020, 40(6): 486-491, 501. |
| [11] |
Yang WJ, Ren JN, Zhang HW, et al. Single-atom iron as a promising low-temperature catalyst for selective catalytic reduction of NOx with NH3: A theoretical prediction
. Fuel, 2021, 302: 121041. DOI:10.1016/j.fuel.2021.121041 |
| [12] |
Yan LQ, Dong Z, Jia H, et al. Dynamic inferential NOx emission prediction model with delay estimation for SCR de-NOx process in coal-fired power plants
. Royal Society Open Science, 2020, 7(2): 191647. DOI:10.1098/rsos.191647 |
| [13] |
Lv Y, Yang TT, Liu JZ. An adaptive least squares support vector machine model with a novel update for NOx emission prediction
. Chemometrics & Intelligent Laboratory Systems, 2015, 145: 103-113. |
| [14] |
Dong Z, Ma N, Li CQ. NOx emission model for coal-fired boilers using partial least squares and extreme learning machine
. Journal of Southeast University (English Edition), 2019, 35(2): 179-184. |
| [15] |
Li Z, Lee YS, Chen JH, et al. Developing variable moving window PLS models: Using case of NOx emission prediction of coal-fired power plants
. Fuel, 2021, 296: 120441. DOI:10.1016/j.fuel.2021.120441 |
| [16] |
吴雨, 刘媛华. 基于最近最远邻和互信息的特征选择方法. 计算机应用研究, 2017, 34(12): 3713-3716. DOI:10.3969/j.issn.1001-3695.2017.12.044 |
| [17] |
杨志淳, 靖晓平, 乐健, 等. 基于MI-PSO-BP算法的配电设备状态实时评估方法. 电力自动化设备, 2019, 39(12): 108-113. |
| [18] |
Zhang C, Peng T, Zhou JZ, et al. An improved autoencoder and partial least squares regression-based extreme learning machine model for pump turbine characteristics. Applied Sciences, 2019, 9(19): 3987. DOI:10.3390/app9193987 |
| [19] |
Gao LY, Wu WG. Relevance assignation feature selection method based on mutual information for machine learning. Knowledge-Based Systems, 2020, 209: 106439. DOI:10.1016/j.knosys.2020.106439 |
| [20] |
李郅琴, 杜建强, 聂斌, 等. 特征选择方法综述. 计算机工程与应用, 2019, 55(24): 10-19. DOI:10.3778/j.issn.1002-8331.1909-0066 |
| [21] |
Simsekler MCE, Alhashmi NH, Azar E, et al. Exploring drivers of patient satisfaction using a random forest algorithm. BMC Medical Informatics and Decision Making, 2021, 21(1): 157. DOI:10.1186/s12911-021-01519-5 |
 2022, Vol. 31
2022, Vol. 31


