2. 华南师范大学 网络教育学院, 广州 510631
2. School of Distance Education, South China Normal University, Guangzhou 510631, China
目前常用的室内定位技术包括蓝牙[1]、超宽带(UWB)[2]、射频识别(RFID)[3]、红外[4]、Zigbee[5]、视觉[6]和可见光[7]等, 这些技术需要部署特定的基础设施, 方法复杂且昂贵, 很难大规模推广. 随着智能手机的普及, 手机配备的各种传感器可以采集各种信号, 为室内定位技术的研究提供了方便. WiFi的普及使得很多的室内定位研究基于WiFi信号进行, 但WiFi信号受到多径效应的影响, 衰减会比较快. 在全局空间, WiFi具有较高的区分度, 但对于距离相近的位置点, 采集的RSSI数据较为相似, 在局部空间上缺乏唯一性. 在室内环境的局部空间, 地磁场具有较高的区分度, 但在定位空间很大时, 多个相距较远的位置可能具有非常相似的地磁特征, 在全局空间上缺乏唯一性. 因此仅使用WiFi或地磁场等单一定位源进行定位, 都难以达到较高的精度.
针对单一定位源存在较大误差的现象, 多源信息融合定位应运而生. 目前, 国内外对于多源信息融合定位方面有较多的研究. Pham等[8]将WiFi信号和视觉信号进行融合进行定位, 文献[9]融合了WiFi、蓝牙以及光学传感器三维坐标和磁传感器旋转属性来定位, Shu等[10]采用双向粒子滤波过程融合地磁信号和WiFi信号, 余刘勇等[11]采用地磁和惯性导航的联合定位. 实验数据表明, 多源信息融合都要比单信号方法进行定位的效果好. 基于WiFi和地磁场信号具有一定互补性的特点, 本文通过指纹匹配的方式来实现WiFi和地磁场信号的融合定位.
指纹匹配定位的离线阶段主要完成指纹库的构建, 在线阶段则是通过KNN[12]、WKNN[13]、机器学习[14]、深度学习[15]等匹配算法将待定位点与指纹库中的指纹进行匹配, 然后估计其位置. 如何解决指纹数据和物理坐标的映射关系是需要考虑的首要问题. BP神经网络因其有较强的非线性映射能力[16] , 能建立指纹数据和物理坐标之间的非线性关系被广泛应用于定位预测. 但BP神经网络因随机产生权值和阈值易出现收敛时间长, 迭代次数多, 精度不高等现象[17, 18]. 差分进化算法是一个全局优化算法, 有收敛速度快、控制参数少且设置简单、优化结果稳健等优点[19]. 利用差分进化算法的全局搜索能力, 能够有效改进BP模型的性能.
在BP神经网络中, 神经网络层之间的初始权值和偏差是随机初始化的, 这不仅增加了收敛时间, 还有陷入局部最优的可能性. 因此, 为提高BP神经网络的学习能力, 充分发挥其强大的非线性映射能力, 文献[20]利用DE差分进化算法(differential evolution, DE)来优化BP神经网络的参数, 但标准的DE算法有控制参数、进化策略选择困难[21]等诸多问题. 为了提高差分进化算法的优化能力, 本文提出了一种改进的差分进化算法来优化BP神经网络, 有助于BP模型更好地学习WiFi和地磁指纹数据的特征, 以此来提高定位精度和网络的收敛速度.
2 改进的自适应差分进化算法DE算法主要过程包括种群初始化、变异、交叉和选择等步骤, 其中变异操作是生成具有较好适合度值的新向量操作, 以获得更好的搜索能力[22]. 目前最常用的变异策略DE/rand/1[23]操作如式(1)所示:
| $ {v}_{i, G}={x}_{{r_1}, G}+F\cdot({x}_{{r_2}, G}-{x}_{{r_3}, G}) $ | (1) |
其中, G为进化代数;
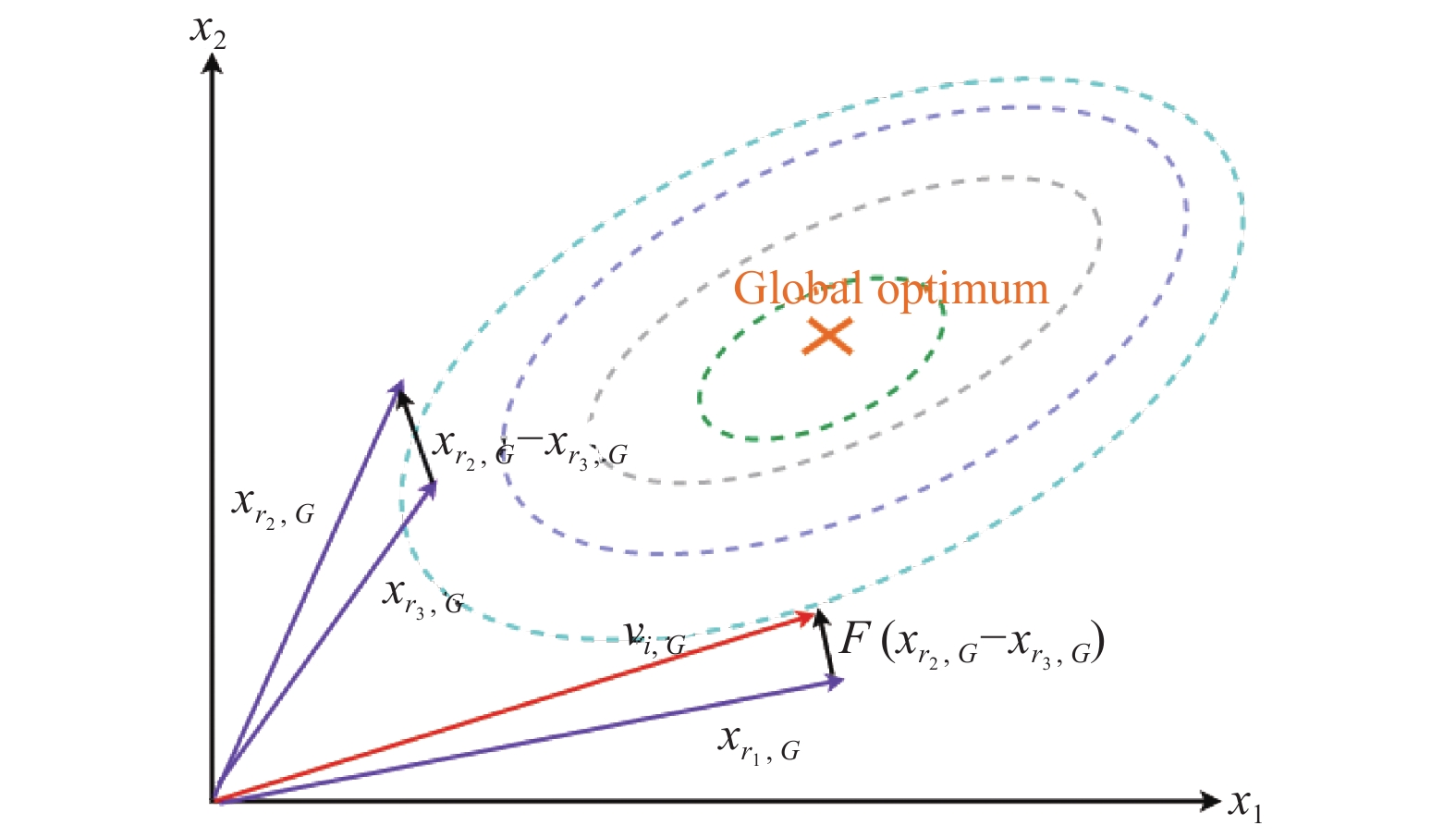
|
图 1 DE/rand/1的突变策略过程图 |
2.1 改进的变异操作
集体智能(collective intelligence, CI) 是可以为种群进化提供更好搜索方向的突变算子, 能引导种群走向一个更好的搜索区域, 该算子由混合了部分适应性较好的向量和随机选择的向量的集合信息来生成.
| $ {x}_{mix\_mbest, G}={{\displaystyle\sum }_{k=1}^{m}}{w}_{k}\cdot{x}_{k, G} $ | (2) |
其中,
| $ {w_k} = \frac{{m - k + 1}}{{1 + 2 + \cdots + m}} \begin{array}{*{20}{c}} {},\;{k \in (1, 2, \cdots , m)} \end{array} $ | (3) |
基于CI的突变策略可以表示为:
| $ \begin{split} {v}_{mix, G}=&{x}_{{r}_{1}, G}+F\cdot({x}_{{r}_{2}, G}-{x}_{{r}_{3}, G})\\ & +F\cdot({x}_{mix\_mbest, G}-{x}_{{r}_{1}, G})\end{split} $ | (4) |
如图2所示, 在二维参数空间上, 基于CI的突变策略过程在种群进化的搜索方向
DE算法的变异因子F和交叉概率因子CR (crossover rate) 在整个种群进化过程中控制着种群多样性和收敛速度.
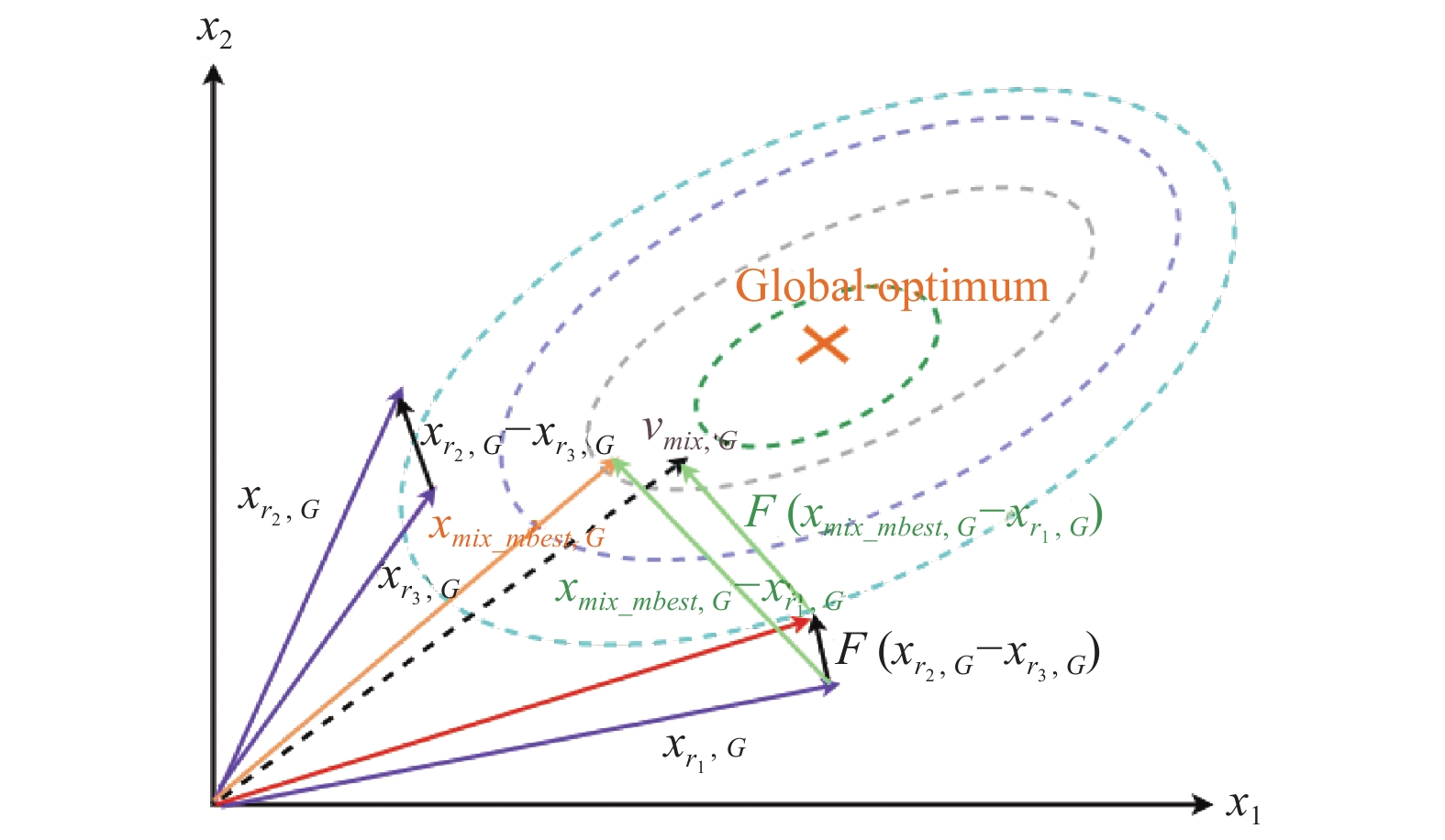
|
图 2 基于CI的突变策略的过程图 |
当进化代数G小时, 较大的F值才能保证个体的多样性, 跳出局部极值找到全局最优值, 但其收敛速度会降低; 当G变大时, 群体的多样性需求降低, 较小的F值更易于保持搜索局部最优值的稳定性. 为此, 本文用改进的Logistic函数作为自适应变异因子F(G), 随着种群的进化, 变异因子F会慢慢变小, 即:
| $ CR(G)={C}_{\mathrm{min}} \cdot \frac{{F}_{\min}}{1+\left(\dfrac{{F}_{\min}}{{F}_{\max}}-1\right){\rm{exp}}(-aG)} $ | (5) |
其中,
根据交叉概率因子的特点, CR值越大, 算法局部搜索能力越强, 收敛越快; CR值越小, 全局搜索能力越强, 有利于保持种群多样性. 为保持种群前期的多样性和后期的收敛速度, 利用Sigmoid函数作为自适应交叉概率因子CR(G), 可以兼顾种群的多样性和收敛速度, 故:
| $ \begin{split} CR(G)=&C{R}_{\min}\\ &+(C{R}_{\max}-C{R}_{\min})\cdot\frac{1-{\rm{exp}}(-\beta G/{G}_{\max})}{1+{\rm{exp}}(-\beta G/{G}_{\max})}\end{split} $ | (6) |
其中,
IDEBP定位算法主要包括离线阶段和在线定位阶段. 离线阶段需要完成指纹库的构建和IDEBP模型的训练. 在线定位阶段将测试数据集输入到训练好的模型中, 然后得到最终的定位结果.
3.1 离线阶段 3.1.1 指纹库的构建在离线阶段首先需要对定位区域进行网格划分, 然后借助智能手机采集每个网格点的RSSI值、地磁场强度值以及该点对应的物理坐标值, 并且将数据写入后台数据库中. 每条指纹数据的格式如下:
| $ \begin{split} {D_{i, j}} =& \{ {\textit{RSSI}}{_1}, {\textit{RSSI}}{_2}, {\textit{RSSI}}{_3}, \cdots , {\textit{RSSI}}{_n}, {m_x}, {m_y}, {m_{\textit{z}}}\} \end{split} $ | (7) |
其中,
指纹库D的结构图如表1所示, 表中t为指纹点的个数.
| 表 1 指纹库D的结构表 |
3.1.2 模型训练
模型训练过程如下:
(1)本文以n个AP在各个参考点的RSSI值以及三维的地磁场强度值作为BP神经网络的输入, 以各个参考点位置的坐标(i, j)作为输出, 中间层为隐含层. 确定神经网络的结构之后, 对种群中个体进行编码, 编码长度
(2)训练集样本输入到BP模型中进行训练, 计算出模型输出与样本输出之间的误差. 通过误差来计算种群个体的适应度, 并用适应度函数判断种群中个体的优劣程度:
| $ f(x) = \frac{C}{{E(x)}} $ | (8) |
其中, x是与BP神经网络的权重和偏差相对应的种群个体, E(x)是相应的BP神经网络输出的均方误差. C是一个常数.
(3)种群中个体进行变异、交叉以及选择操作之后, 判断种群进化次数是否满足种群的最大迭代要求. 若满足要求, 则得到最优个体; 反之, 则更新BP神经网络的权值和偏差.
(4)得到最优个体后, 利用最优个体给BP神经网络的权值和偏差赋值并进行BP神经网络模型的训练.
3.2 定位阶段将测试集数据归一化后输入到训练好的BP模型中, 模型根据测试数据, 输出预测结果. 然后将得到的数据进行反归一化, 得到最终的定位结果, 即每个测试数据所对应的(i, j)坐标.
4 实验设计与结果分析为验证算法的性能, 项目组开发了一套以Android智能手机为终端的室内定位APP, 实验中, 通过智能移动设备上的室内定位APP采集数据. 实验采集数据所用的智能移动设备为红米K30.
4.1 实验环境实验环境选在华南师范大学计算机学院3楼空间信息研究中心实验室, 该实验室是一个长约为23 m, 宽约为8 m的室内空间. 图3是实验环境的平面图, 图4是数据采集的实景图, 图5是实验应用系统图. 实验者在实验场所中划了11×35个网格点, 每个网格点的边长为0.6 m, 其中长方形的小方块为学生工位, 小圆点为采集数据的网格点, 五角星为WiFi接入点, 共有16个. 除去学生工位、会议桌以及墙体等有障碍物的网格点外, 有效的网格点共有283个. 为保证实验数据的可靠性, 每台设备在每个网格点上, 以1 s作为时间间隔, 采集120次数据. 在整个实验过程中, 十几个实验室成员在该区域内正常活动学习.
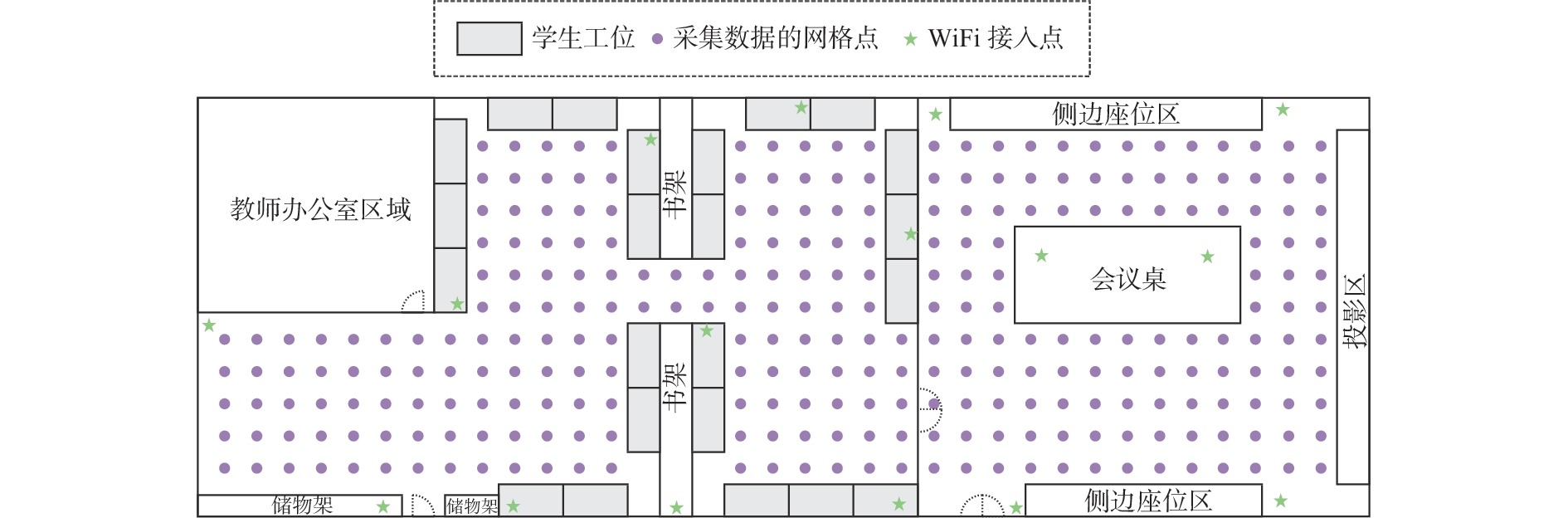
|
图 3 实验环境平面图 |

|
图 4 数据采集实景图 |

|
图 5 实验应用系统图 |
4.2 IDEBP 定位算法实验与对比分析
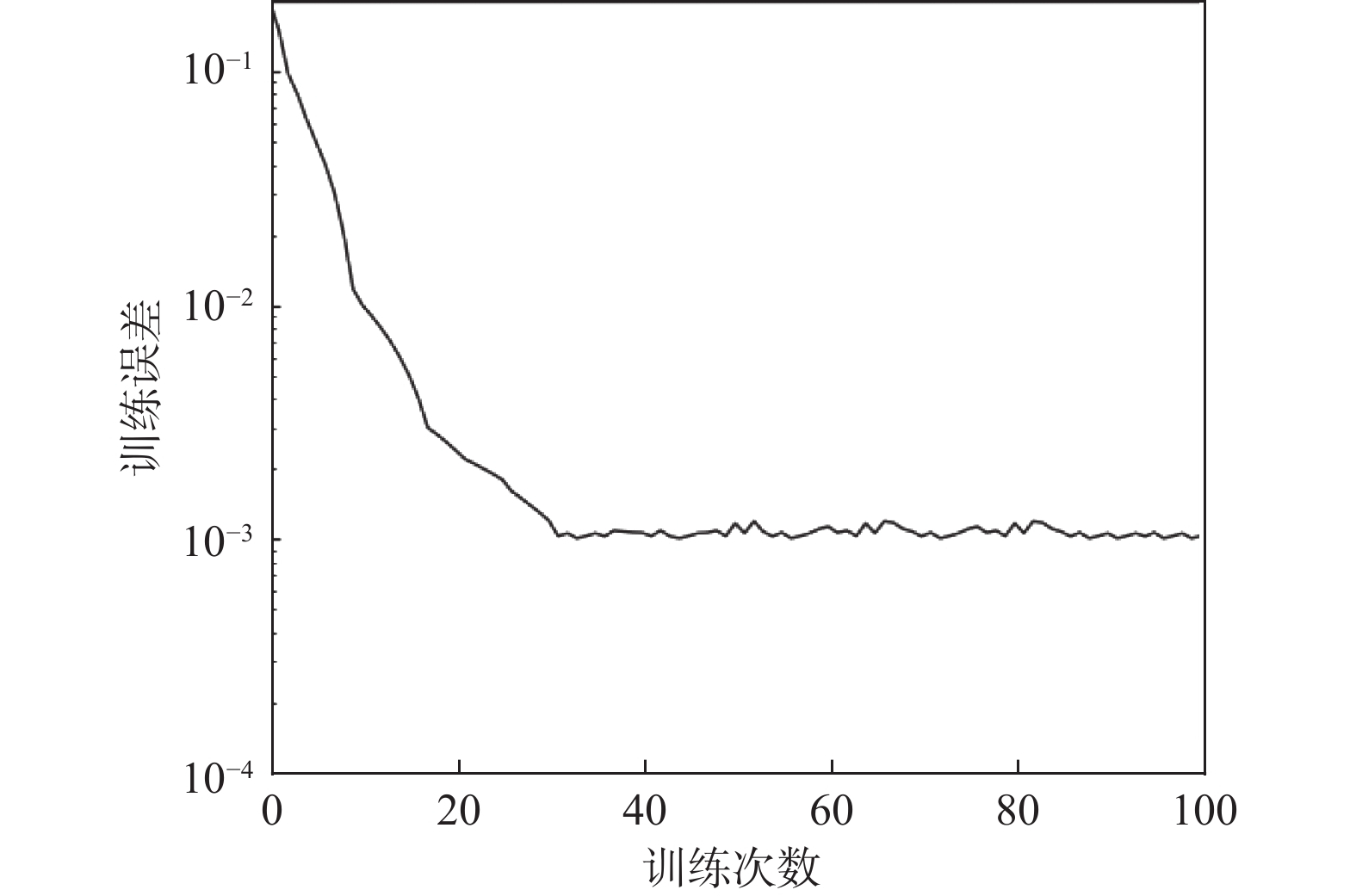
将训练集数据输入到程序中进行训练, 训练结束得到BP神经网络和IDEBP模型的训练误差曲线分别如图6和图7所示. 图中横坐标表示训练次数, 纵坐标表示训练误差. 从图6可以看出, BP神经网络在100步时训练误差仍然大于0.1, 且整体的迭代误差下降速度慢. 这是因为BP神经网络存在迭代次数多, 训练时间长, 误差精度大等问题. 从图7中可以看出, IDEBP神经网络在第28次迭代时就已经到达了所设定的目标误差, 即0.001. 由上可知, 差分进化算法优化BP神经网络的算法在一定程度上可以改进传统BP算法收敛时间长, 迭代次数多, 精度不高等缺点.
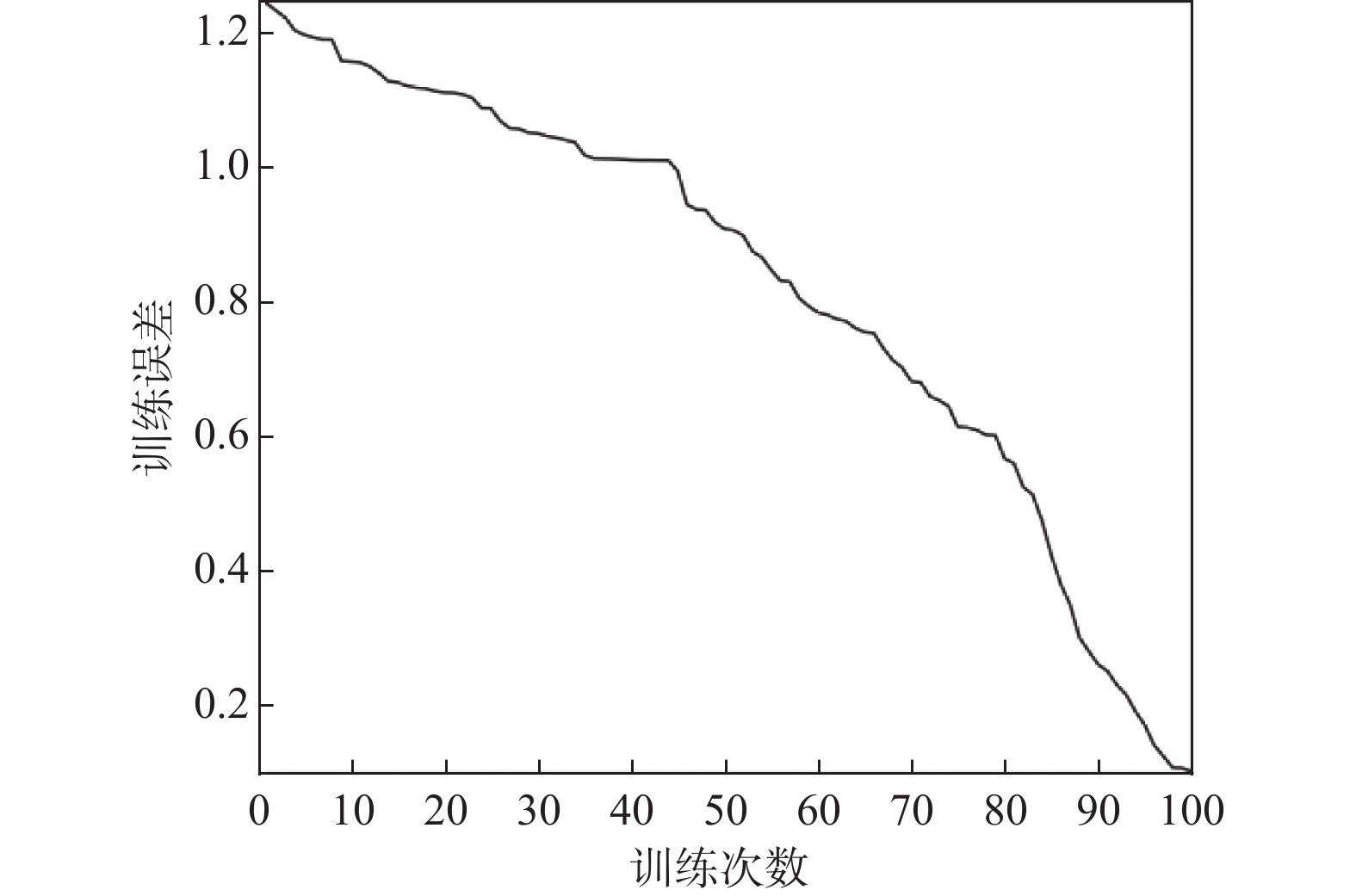
|
图 6 BP神经网络训练误差曲线 |
|
图 7 IDEBP神经网络训练误差曲线 |
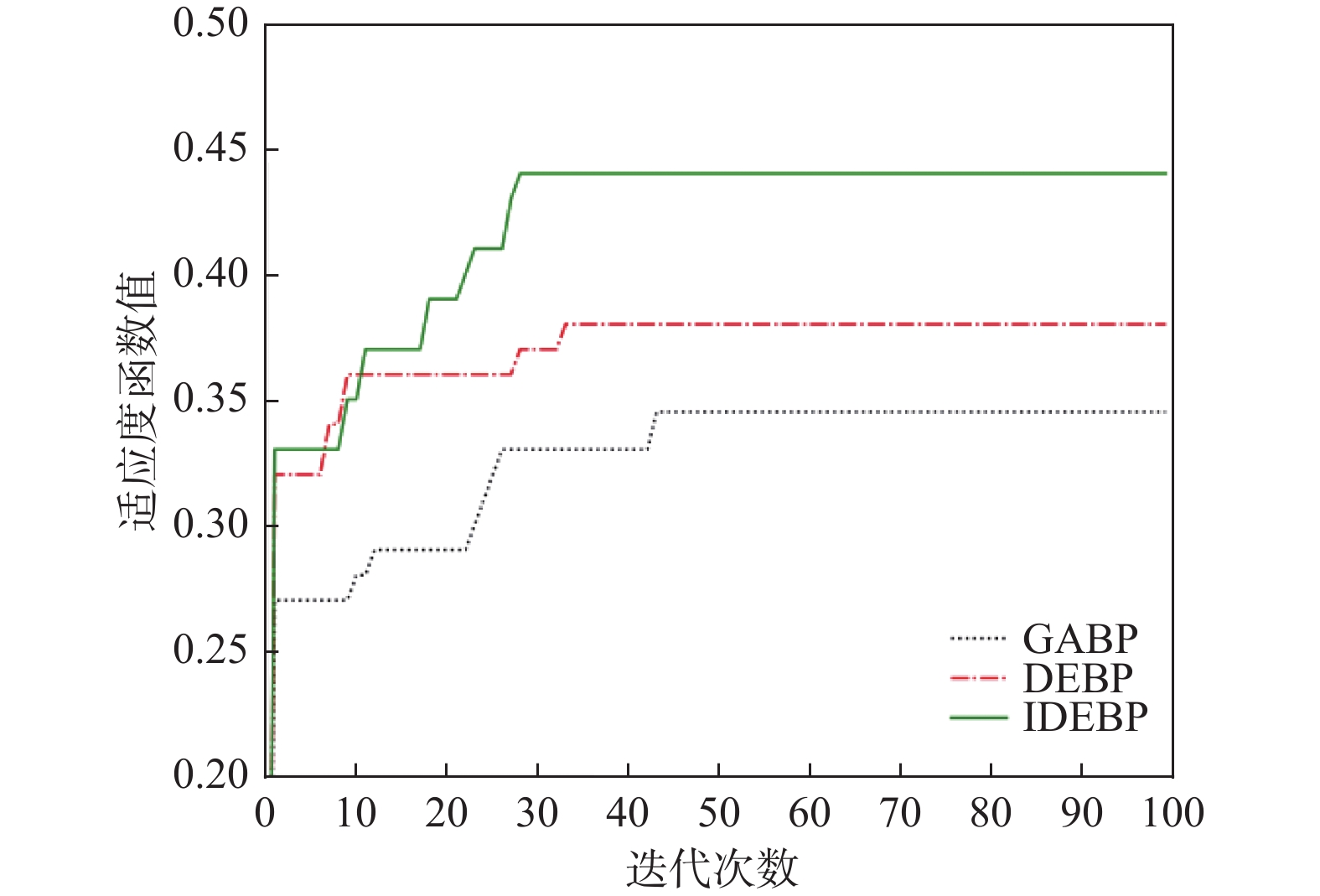
针对BP神经网络随机初始化权值和阈值易出现收敛时间长, 迭代次数多等问题, 文献[24]提出了GABP (genetic algorithm BP)算法, 文献[25] 提出了DEBP (differential evolution BP)算法对BP神经网络进行优化. 图8对GABP 算法, DEBP算法和IDEBP算法中种群适应度曲线随着迭代次数增加的变化情况进行了比较. 图中横坐标表示迭代次数, 纵坐标表示种群适应度. 由图可知, GABP算法和DEBP算法分别在第43次和第33次迭代中趋于稳定, 而IDEBP算法在第28次迭代中就能趋于稳定, 算法加快了种群的收敛速度. 同时GABP算法和DEBP算法的适应度水平分别约为0.34和0.38, IDEBP约为0.44, 而较高的适应度水平可以找到更好的权重和偏差.
|
图 8 优化的BP神经网络适应度图 |
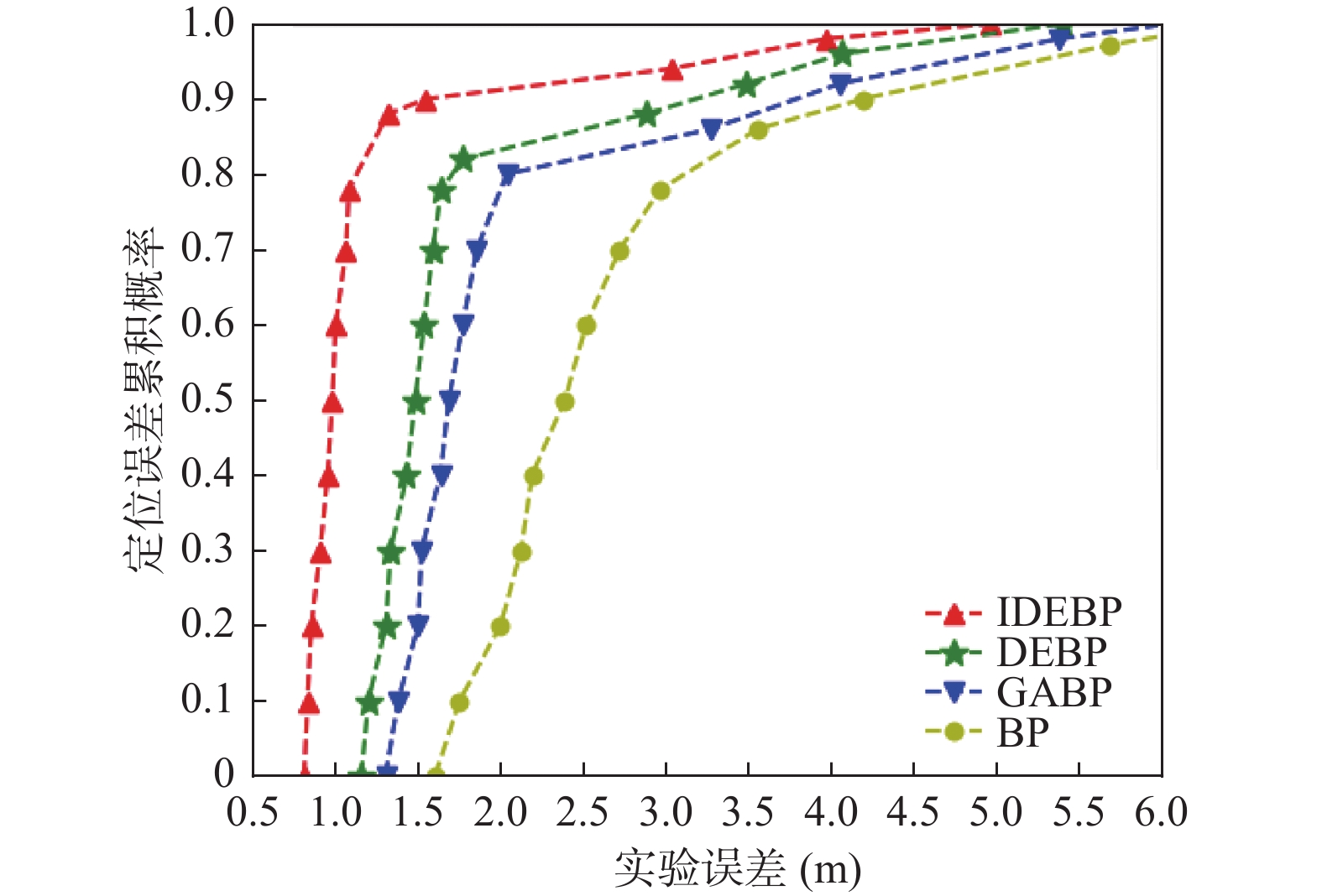
图9比较了BP算法[26]、GABP算法、DEBP算法和IDEBP算法的定位误差累积分布曲线. 由图可知, 因为IDE算法较强的全局搜索能力可以优化BP神经网络的初始权值和偏差, 所以IDEBP算法具有最优的定位效果, DEBP算法的定位效果次之, GABP算法与BP算法的定位精度依次排在其后面.
|
图 9 定位误差百分比图 |
考虑上述4种定位算法的平均定位误差和最大最小误差, 如表2所示, IDEBP算法平均误差为1.14 m, 相对于其他定位算法的定位精度分别提高了1.88 m, 0.92 m, 0.55 m.
| 表 2 不同模型的定位性能比较 (m) |
5 结论
针对标准的DE算法进化策略、控制参数选择困难等诸多问题, 本文改进了差分进化算法, 并与BP神经网络相结合, 克服了BP神经网络迭代次数多, 训练时间长, 误差精度大等缺点, 提出了应用于WiFi和地磁场的联合指纹定位的IDEBP算法. 实验结果表明, IDEBP算法可以有效地提高指纹定位的精度, 加快神经网络的收敛速度.
| [1] |
de Blasio G, Quesada-Arencibia A, García CR, et al. A protocol-channel-based indoor positioning performance study for Bluetooth low energy. IEEE Access, 2018, 6: 33440-33450. DOI:10.1109/ACCESS.2018.2837497 |
| [2] |
Alarifi A, Al-Salman AM, Alsaleh M, et al. Ultra wideband indoor positioning technologies: Analysis and recent advances. Sensors, 2016, 16(5): 707. DOI:10.3390/s16050707 |
| [3] |
Ni LM, Liu YH, Lau YC, et al. LANDMARC: Indoor location sensing using active RFID. Proceedings of the 1st IEEE International Conference on Pervasive Computing and Communications, 2003. Fort Worth: IEEE, 2003. 407–415.
|
| [4] |
Yucel H, Edizkan R, Ozkir T, et al. Development of indoor positioning system with ultrasonic and infrared signals. 2012 International Symposium on Innovations in Intelligent Systems and Applications. Trabzon: IEEE, 2012. 1–4.
|
| [5] |
Huang CN, Chan CT. ZigBee-based indoor location system by k-nearest neighbor algorithm with weighted RSSI
. Procedia Computer Science, 2011, 5: 58-65. DOI:10.1016/j.procs.2011.07.010 |
| [6] |
Wolf J, Burgard W, Burkhardt H. Robust vision-based localization by combining an image-retrieval system with Monte Carlo localization. IEEE Transactions on Robotics, 2005, 21(2): 208-216. DOI:10.1109/TRO.2004.835453 |
| [7] |
Yasir M, Ho SW, Vellambi BN. Indoor positioning system using visible light and accelerometer. Journal of Lightwave Technology, 2014, 32(19): 3306-3316. DOI:10.1109/JLT.2014.2344772 |
| [8] |
Pham TTT, Le TL, Dao TK. Fusion of WiFi and visual signals for person tracking. Proceedings of the 7th Symposium on Information and Communication Technology. Ho Chi Minh City: ACM, 2016. 345–351.
|
| [9] |
Bargshady N, Garza G, Pahlavan K. Precise tracking of things via hybrid 3-D fingerprint database and kernel method particle filter. IEEE Sensors Journal, 2016, 16(24): 8963-8971. DOI:10.1109/JSEN.2016.2616758 |
| [10] |
Shu YC, Bo C, Shen GB, et al. Magicol: Indoor localization using pervasive magnetic field and opportunistic WiFi sensing. IEEE Journal on Selected Areas in Communications, 2015, 33(7): 1443-1457. DOI:10.1109/JSAC.2015.2430274 |
| [11] |
余刘勇, 单志龙. 基于可信度的地磁与惯导联合室内定位系统. 传感技术学报, 2019, 32(5): 728-734. DOI:10.3969/j.issn.1004-1699.2019.05.016 |
| [12] |
戴志诚, 李小年, 陈增照, 等. 基于KNN算法的可变权值室内指纹定位算法. 计算机工程, 2019, 45(6): 310-314. |
| [13] |
Alfakih M, Keche M. An enhanced indoor positioning method based on Wi-Fi RSS fingerprinting. Journal of Communications Software and Systems, 2019, 15(1): 18-25. |
| [14] |
Zou H, Lu XX, Jiang H, et al. A fast and precise indoor localization algorithm based on an online sequential extreme learning machine. Sensors, 2015, 15(1): 1804-1824. DOI:10.3390/s150101804 |
| [15] |
Lee N, Ahn S, Han D. AMID: Accurate magnetic indoor localization using deep learning. Sensors, 2018, 18(5): 1598. DOI:10.3390/s18051598 |
| [16] |
Tsai JT, Chou JH, Liu YK. Tuning the structure and parameters of a neural network by using hybrid Taguchi-genetic algorithm. IEEE Transactions on Neural Networks, 2006, 17(1): 69-80. DOI:10.1109/TNN.2005.860885 |
| [17] |
Dai CH, Chen WR, Zhu YF, et al. Seeker optimization algorithm for tuning the structure and parameters of neural networks. Neurocomputing, 2011, 74(6): 876-883. DOI:10.1016/j.neucom.2010.08.025 |
| [18] |
Liu HR, Zhao CX, Li X, et al. Study on a neural network optimization algorithm based on improved genetic algorithm. Chinese Journal of Scientific Instrument, 2016, 37(7): 1573-1580. |
| [19] |
Das S, Mullick SS, Suganthan PN. Recent advances in differential evolution—An updated survey. Swarm and Evolutionary Computation, 2016, 27: 1-30. DOI:10.1016/j.swevo.2016.01.004 |
| [20] |
张义民. 基于DEBP算法的模糊神经网络在轻汽油醚化系统中的应用研究[硕士学位论文]. 青岛: 青岛科技大学, 2018.
|
| [21] |
Das S, Suganthan PN. Differential evolution: A survey of the state-of-the-art. IEEE Transactions on Evolutionary Computation, 2011, 15(1): 4-31. DOI:10.1109/TEVC.2010.2059031 |
| [22] |
Tian L, Li ZC, Yan XF. Potential-based differential evolution algorithm with joint adaptation of parameters and strategies. IEEE Access, 2020, 8: 100562-100577. DOI:10.1109/ACCESS.2020.2997355 |
| [23] |
Zhang JQ, Sanderson AC. JADE: Adaptive differential evolution with optional external archive. IEEE Transactions on Evolutionary Computation, 2009, 13(5): 945-958. DOI:10.1109/TEVC.2009.2014613 |
| [24] |
Cui XR, Yang J, Li J, et al. Improved genetic algorithm to optimize the Wi-Fi indoor positioning based on artificial neural network. IEEE Access, 2020, 8: 74914-74921. DOI:10.1109/ACCESS.2020.2988322 |
| [25] |
Han JW, Li QX, Wu HR, et al. Prediction of cooling efficiency of forced-air precooling systems based on optimized differential evolution and improved BP neural network. Applied Soft Computing, 2019, 84: 105733. DOI:10.1016/j.asoc.2019.105733 |
| [26] |
朱轶峰. 基于WiFi-BP的室内定位算法. 电子科技, 2020, 33(8): 74-79. |
 2022, Vol. 31
2022, Vol. 31



