无线传感器网络(wireless sensor network, WSN)由大量的微型传感器节点组成, 它们通过无线电进行通信, 形成了一个具有无中心、自组织、多跳路由特点的网络系统[1]. 1978年, 美国的卡耐基-梅隆大学最早成立了分布式传感器网络工作组[2]. 2003年, 美国《技术评论》杂志将WSN评选为未来十大新兴科技中的第一项. 2006年, 我国在《国家中长期科学与技术发展规划纲要》中, 提出的3个信息领域的前沿方向, 有两项与WSN有关. 由此可见, WSN的发展是必然趋势. 因其可以分布在人员无法到达的区域, 所以WSN可广泛应用于国防军事、环境监测、卫生保健等领域[3].
由于节点抛洒的随机性, 在WSN的应用中节点采集的信息数据只有结合与之对应的位置信息才有意义, 比如森林突发火灾时需要确定节点监测到火源的位置信息; 军事活动中需要确定节点监测到敌方活动信息的位置信息; 海底探测时需要确定节点监测到海底环境的位置信息. 同时, WSN为了节约成本并且降低功耗, 只有少部分锚节点携带GPS, 其他大部分节点都是不知道具体位置的未知节点, 如何通过已知位置的锚节点得到未知节点的位置信息是WSN定位技术面临的一大难点[4]. 所以, 节点定位技术一定程度上决定了WSN的实际应用前景, 这项技术也是众多学者研究WSN的重点方向之一.
在WSN的定位算法中, 质心定位算法能耗低、实现简单, 但是定位精度易受到锚节点密度的影响. 所以, 很多学者为了减少定位误差将其与RSSI定位算法相结合进行研究: 文献[5]使用均值滤波、中值滤波对RSSI进行预处理, 然后对过滤后的信号进行高斯滤波并进行加权, 得到较精确的RSSI值. 该算法通过结合多种滤波方法, 减小了使用单一滤波造成的测率误差, 但是该算法在定位环节没有考虑到由质心造成的误差. 文献[6]提出了一种改进的加权质心定位算法, 首先使用中值滤波对RSSI进行预处理, 然后对权值进行距离的差分修正. 该算法在原始的加权质心定位算法基础上有效地提高了定位精度, 但是能耗过高, 计算量过大. 文献[7]引入迭代的思想, 将已定位成功的未知节点升级为锚节点辅助计算. 该算法可以在锚节点占比小的情况下, 降低无法定位的节点比例, 但是该算法没有考虑在测距过程中存在的误差. 文献[8]在原有锚节点的基础之上, 利用余弦定理增加了虚拟静态锚节点参与定位. 该算法降低了定位所需要的硬件成本, 但是没有考虑到定位过程中将距离作为权重带来的误差.
针对上述研究中的缺点和不足, 本文在质心定位算法的基础之上进行改进, 提出了一种改进的加权质心定位算法, 并通过仿真验证算法的有效性.
1 质心定位算法 1.1 RSSI定位算法接收信号强度指示(received signal strength indicator, RSSI)表示发射端向接收端发送能量信号的信号强度数值[9]. 其定位过程的实现步骤, 依次是信号发射、信号采集、信号转换以及定位计算[10]. 其中, 第3步信号转换最为重要, 该过程通过空间传播模型来计算锚节点和未知节点间的距离. 本文采用对数——常态分布模型[11], 公式如下:
| $ {P_L}(d) = {P_L}({d_0}) + 10\eta \lg \left(\frac{d}{{{d_0}}}\right) + {X_\sigma } $ | (1) |
其中, PL(d)为距离为d(m)时的信号路径损耗; PL(d0)为距离信号发射端d0(m)处的信号损耗, 其中d0为参考距离, 一般为1 m; η为路径损耗指数; d为发送端到接收端的距离; Xσ为均值为零, 方差为σ的高斯随机变量. 则接收信号强度如下:
| $ {\textit{RSSI}} = {P_T} - {P_L}(d) $ | (2) |
其中, PT为发送信号强度; RSSI为接收信号强度.
由式(1)、式(2)可得, 锚节点到未知节点之间的距离为:
| $ d = {10^{\frac{{{P_T} - {P_L}({d_0}) - {\textit{RSSI}} - {X_\sigma }}}{{10\eta }}}} $ | (3) |
RSSI定位算法不需要增加多余的硬件模块, 在实际应用中容易实现, 但是极易受到多径效应等环境因素的影响, 导致其定位精度不高.
1.2 质心定位算法质心定位算法[12]是一种不需要测距的定位算法, 通过计算网络连通性进行定位. 其原理是以锚节点为圆心, 以通过路径损耗模型计算出的距离为半径画圆, 计算出形成的公共区域的质心坐标. 可得出未知节点A(x, y)的质心算法公式为:
| $ (x, y) = \left( {\frac{{\displaystyle\sum\limits_{i = 1}^n {{x_i}} }}{n}} \right., \left. {\frac{{\displaystyle\sum\limits_{i = 1}^n {{y_i}} }}{n}} \right) $ | (4) |
其中, (x, y)为未知节点坐标; (xi, yi)为未知节点通信范围内第i个锚节点坐标; n为未知节点通信范围内锚节点数量.
质心定位算法计算简单、开销小、容易实现. 但是定位误差大, 而且定位精度极易受到锚节点数量和均匀程度的影响.
1.3 基于RSSI的加权质心定位算法通过文献[13]可知, 传统的质心定位算法不能反映出锚节点在节点定位时位置的影响, 因此, 将RSSI值作为权重因子引入质心定位算法中, 以此来反映锚节点的位置对质心坐标的影响. 如果RSSI值越大, 代表节点之间的距离越近, 则该锚节点的位置对质心坐标有更大的影响. 可得出未知节点A(x, y)的加权质心算法公式为:
| $ (x, y) = \left( {\frac{{\displaystyle\sum\limits_{i = 1}^n {{{\textit{RSSI}}_i} \cdot {x_i}} }}{{\displaystyle\sum\limits_{i = 1}^n {{{\textit{RSSI}}_i}} }}} \right., \left. {\frac{{\displaystyle\sum\limits_{i = 1}^n {{{\textit{RSSI}}_i} \cdot {y_i}} }}{{\displaystyle\sum\limits_{i = 1}^n {{{\textit{RSSI}}_i}} }}} \right) $ | (5) |
其中, (x, y)为未知节点坐标; (xi, yi)为未知节点通信范围内第i个锚节点坐标; RSSIi 为第i个锚节点的信号强度值; n为未知节点通信范围内锚节点数量.
虽然这种改进方法明显提高了质心定位算法的定位精度, 但是在实际应用中, 外界环境比较复杂, RSSI值极易受到环境干扰, 单纯使用RSSI值作为权值不易修正误差值, 影响定位精度.
1.4 基于RSSI测距校正的加权质心定位算法由于实际环境中使用RSSI作为权值会影响到未知节点的定位精度, 因此, 有学者提出利用信号的空间传输模型计算出锚节点到未知节点间的距离, 用该距离的倒数作为影响质心的权重因子. 可得出未知节点A(x, y)的加权质心算法公式为:
| $ (x, y) = \left( {\frac{{\displaystyle\sum\limits_{i = 1}^n {\frac{1}{{{d_i}}}{x_i}} }}{{\displaystyle\sum\limits_{i = 1}^n {\frac{1}{{{d_i}}}} }}} \right., \left. {\frac{{\displaystyle\sum\limits_{i = 1}^n {\frac{1}{{{d_i}}}{y_i}} }}{{\displaystyle\sum\limits_{i = 1}^n {\frac{1}{{{d_i}}}} }}} \right) $ | (6) |
其中, (x, y)为未知节点坐标; (xi, yi)为未知节点通信范围内第i个锚节点坐标; di为未知节点A与第i个锚节点经距离校正后的距离值; n为未知节点通信范围内锚节点数量.
式(5)和式(6)都是在RSSI算法的基础之上对质心定位算法进行权值修正, 而式(6)考虑到了RSSI的系统环境误差, 采用距离加权修正定位误差, 提高了质心定位算法的定位精度. 因此本文保留其优点, 对权值能否继续优化展开研究.
2 增强型质心定位改进算法 2.1 RSSI值预处理在节点定位过程中, 信号传输过程很容易受到多径效应等环境因素的影响, 使得未知节点接收到的RSSI具有较大的波动性. 因此, 本文针对这个问题对接收到的RSSI值进行滤波处理, 得到优化后的RSSI值, 用于测距阶段的距离计算. 具体实现过程如下:
首先, 设置阈值k, 对未知节点接收到的RSSI值进行计数, 当接收到的RSSI值达到阈值时停止接收, 否则将继续接收.
然后, 对接收到的RSSI值进行降序排序, 得到集合RSSIsort, 将该集合分别进行均值滤波和中值滤波, 公式如下:
| $ {{\textit{RSSI}}_{\rm{sort}}} = sort\{ {{\textit{RSSI}}_1}, {{\textit{RSSI}}_2}, \cdots , {{\textit{RSSI}}_k}\} $ | (7) |
| $ {{\textit{RSSI}}}_{\rm{mid}}=\left\{ {\begin{array}{l}{{\textit{RSSI}}}_{\frac{k+1}{2}}\begin{array}{cc}, & k为奇数\end{array}\\ \frac{{{\textit{RSSI}}}_{\frac{k+1}{2}+\frac{k}{2}}}{2}\begin{array}{cc}, & k为偶数\end{array}\end{array}} \right. $ | (8) |
| $ {{\textit{RSSI}}_{\rm{AVG}}} = \frac{1}{k}\sum\limits_{i = 1}^k {{{\textit{RSSI}}_i}} $ | (9) |
其中, k为未知节点接收到的RSSI值个数, RSSIk为未知节点接收到的第k个RSSI值, RSSIsort为降序排列后的RSSI集合, RSSImid为中值滤波处理后的RSSI值, RSSIAVG为均值滤波处理后的RSSI值.
最后, 对RSSImid和RSSIAVG取平均值, 得到较为准确的RSSI值. 公式如下:
| $ {\textit{RSSI}} = \frac{{{{\textit{RSSI}}_{\rm{mid}}} + {{\textit{RSSI}}_{\rm{AVG}}}}}{2} $ | (10) |
在加权质心定位算法中, 权值的选取对节点定位精度影响很大, 式(6)的算法以距离的倒数作为权值来修正误差, 进一步提高了未知节点的定位精度. 因此, 本文将在此基础上继续对质心权值进行改进.
由式(3)的变形可得:
| $ \frac{1}{d} = {10^{\frac{{{P_L}({d_0}) + {\textit{RSSI}} + {X_\sigma } - {P_T}}}{{10\eta }}}} $ | (11) |
可以看出, 在其他参数确定的前提下, 测距值d和RSSI之间更接近于指数关系. 所以, 结合上述距离加权的质心定位算法, 将权值由距离的倒数升级为距离倒数的t次幂. 改进后的公式为:
| $ (x, y) = \left( {\frac{{\displaystyle\sum\limits_{i = 1}^n {{\omega _i} \cdot {x_i}} }}{{\displaystyle\sum\limits_{i = 1}^n {{\omega _i}} }}} \right., \left. {\frac{{\displaystyle\sum\limits_{i = 1}^n {{\omega _i} \cdot {y_i}} }}{{\displaystyle\sum\limits_{i = 1}^n {{\omega _i}} }}} \right) $ | (12) |
其中,
对于t的取值, 根据文献[14]的研究可知, t的取值主要受到锚节点密度的影响, 与环境干扰和定位区域大小无关. 因此, 接下来将通过仿真探寻t的最优取值. 仿真中t的取值范围为[0.5, 2.5], 以0.1为步长遍历区间全部数值, 将算法的定位误差作为评判标准, 分别寻找不同锚节点密度下t的最优取值, 即定位误差最小时对应t的取值.
仿真实验中, 实验环境和实验条件详见第3节. 在200 m×200 m的区域中, 随机部署300个节点, 通信半径为45 m, 改变锚节点密度, 实验结果如表1. 由此可见, 其他条件不变, 当锚节点密度不同时, 随着锚节点密度的增大, t的最优取值分布在(1.8, 2.2)区间. 因此, 式(12)中的t值将会依据锚节点密度来确定, 比如锚节点密度为20%, 则t取值为2.
| 表 1 不同锚节点密度下的t值 |
2.3 迭代式加权质心定位算法
质心定位算法在定位过程中受锚节点的密度影响很大, 当锚节点密度较低时, 会产生大量无法进行定位的节点, 导致节点的覆盖率较低. 因此本文引入迭代的思想, 实现过程如下.
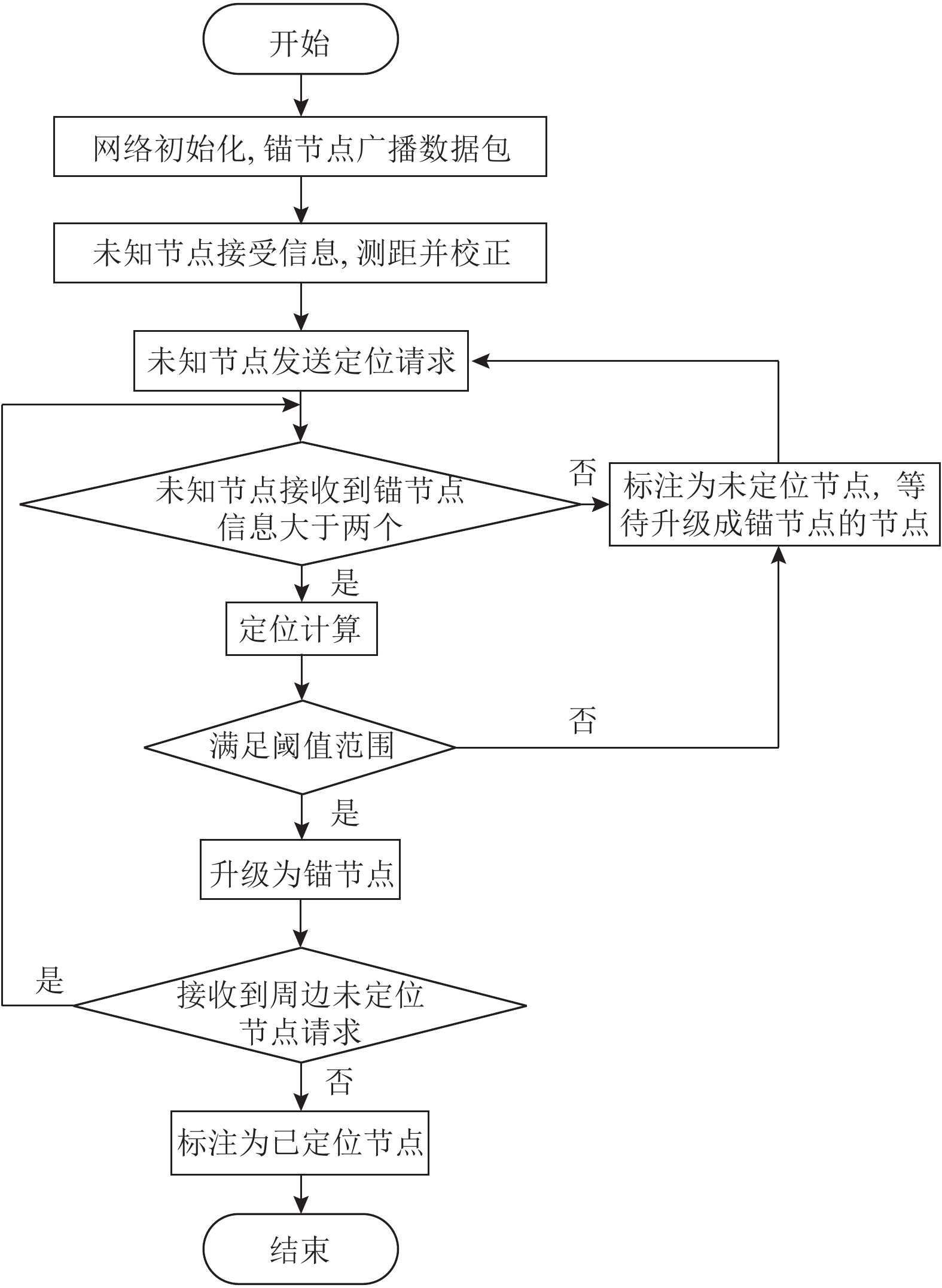
当未知节点通信范围内的锚节点数量大于或等于3个时, 则使用原有锚节点进行定位; 当未知节点通信范围内的锚节点数量小于3个时, 则需要接收已定位节点所携带的位置信息, 将其升级为锚节点参与未定位节点的定位. 由于距离越远节点接收到的RSSI值误差越大, 使用升级为锚节点的节点参与后续定位运算, 将会产生更大的定位误差. 因此, 如果该节点要用到升级节点, 需要先判断其接收到的升级节点所携带的RSSI值是否满足阈值N, 如果满足阈值N则接收, 否则丢弃该节点. 改进后的算法流程图如图1所示.
2.4 改进算法的具体实现步骤1)锚节点周期性的广播自身id、位置坐标、RSSI值等信息.
2)每个未知节点分别接收并记录下多个来自邻居锚节点发送的信息, 如邻居锚节点的id、坐标信息和RSSI值. 将每组RSSI值分别进行均值滤波和中值滤波处理, 取二者均值作为该锚节点的RSSI值.
3)使用对数——常态分布模型, 利用上述预处理后的RSSI值计算出每个锚节点到未知节点之间的距离d.
4)若未知节点周围的锚节点数大于两个, 则根据改正过的加权质心定位算法式(12), 计算出该未知节点的坐标.
5)逐一检查未定位的节点, 重新接收邻居锚节点以及已定位的未知节点的信息, 判断接受到的RSSI值是否满足阈值条件, 如果满足, 则将已定位好的未知节点升级为锚节点, 重新对剩余的未知节点进行定位.
6)计算所有节点的平均定位误差, 公式为:
| $ {E_i} = \frac{{\sqrt {{{({x_o} - {x_{\rm{best}}})}^2} + {{({y_o} - {y_{\rm{best}}})}^2}} }}{R} $ | (13) |
| $ {E_{\rm{AVG}}} = \frac{1}{N}\sum\limits_{i = 1}^N {{E_i}} $ | (14) |
其中, (xo, yo)为第i个未知节点的真实坐标, (xbest, ybest)为第i个未知节点的估计坐标, R为节点的通信半径, Ei为第i个节点的定位误差, N为未知节点的总数, EAVG为所有未知节点的平均定位误差.
|
图 1 迭代式加权质心定位算法流程图 |
3 实验仿真结果分析
使用Matlab R2020b实验平台分别对传统质心定位算法、基于RSSI的(距离)加权质心定位算法以及本文提出改进算法进行仿真, 在不同的锚节点比例、不同的通信半径这两种情况下分别进行对比.
3.1 仿真条件将300个节点随机部署在200 m×200 m的正方形区域中, 根据实验要求设定锚节点比例和节点通信半径. 信号传播模型采用对数——常态分布模型, 路径损耗指数在不同环境下取值不同, 具体可根据表2进行参考取值, 仿真中以室内空间为定位环境, 因此将η设为4. 为了提高算法的稳定性, 采用多次重复实验, 实验次数为50次, 最终的结果取50次的平均值.
| 表 2 各应用场景下路径损耗系数η的取值 |
根据表2参数设置, 形成最初的节点分布图, 如图2所示, 圆形代表未知节点, 星形代表锚节点, 均匀分布在定位区域内.

|
图 2 节点分布图 |
3.2 锚节点比例的影响
在总节点数为300, 通信半径45 m, 锚节点比例分别为10%、15%、20%、25%、30%、35%、40%的情况下对质心定位算法、基于RSSI的加权质心定位算法和本文改进后的算法进行仿真, 得到的仿真结果如图3所示, 可以看出这3种算法的平均定位误差都随着锚节点比例的增加而减小.
当锚节点比例为10%时, 质心定位算法平均定位误差最大, 这是由于未知节点周围的锚节点过少, 导致质心定位算法暴露其弊端, 在锚节点密度小的情况下无法精准定位, 而其他两种算法的平均定位误差都有明显的减小, 其中, 基于RSSI的加权质心定位算法平均定位误差为36.53%, 本文改进算法的平均定位误差为34.50%, 由此可见这两种算法都可以有效改善质心定位算法的弊端, 而且本文的改进算法效果更好; 随着锚节点比例的逐渐增大, 可以看出基于RSSI的加权质心定位算法和本文的改进算法表现出巨大的优越性, 定位精度有着显著的提升, 而本文的改进算法在同等条件下定位精度最高, 同时平均定位误差减小的最快; 当锚节点比例大于20%时, 可以看出3种定位算法的平均定位误差减少缓慢, 这是由于随着锚节点的比例逐渐增大, 锚节点到达了一定数量, 足够提供较为准确的位置辅助信息; 在其他条件相同的情况下, 锚节点比例为25%时, 本文改进的算法平均定位误差19.24%, 比质心定位算法降低了38.23%, 比基于RSSI的加权质心定位算法降低了14.49%, 由此可见本文的改进算法定位精度明显优于前两种算法.

|
图 3 不同锚节点密度的平均定位误差图 |
3.3 节点通信半径的影响
在总节点数为300, 锚节点密度占总节点数20%, 节点通信半径分别为30 m、35 m、40 m、45 m、50 m、55 m、60 m的情况下对质心定位算法、基于RSSI的加权质心定位算法和本文改进后的算法进行仿真, 得到的仿真结果如图4所示, 可以看出这3种算法的平均定位误差都随着节点通信半径的增大而减小.
当节点通信半径为30 m时, 质心定位算法平均定位误差为45.30%, 在3种算法中定位误差最大, 这是由于通信半径过小, 导致未知节点无法与更多的锚节点进行通信, 从而无法精确定位, 而基于RSSI的加权质心定位算法和本文改进算法的平均定位误差都有明显减小, 二者平均定位误差分别为36.05%和34.07%, 由此可见, 这两种算法都可以有效改善节点通信距离过短时质心定位算法造成的误差, 而且本文的改进算法效果更好; 随着通信半径的逐渐增大, 可以看出基于RSSI的加权质心定位算法和本文的改进算法表现出巨大的优越性, 这两种算法的定位精度比质心定位算法有着显著的提升, 而本文的改进算法在同等条件下定位精度最高, 同时平均定位误差减小的最快; 当通信半径大于45 m时, 3种算法的平均定位误差减少缓慢, 这是由于通信半径越大, 节点能收获到的定位精度越多, 定位越精确; 当通信半径为50 m时, 本文改进的算法平均定位误差19.24%, 比质心定位算法降低了40.70%, 比基于RSSI的加权质心定位算法降低了18.27%, 由此可见本文的改进算法定位精度明显优于前两种算法.

|
图 4 不同节点通信半径的平均定位误差图 |
4 结论
本文对质心定位算法及加权质心定位算法进行研究, 在此基础之上提出了一种改进的基于RSSI的加权质心定位算法. 首先在测距阶段对RSSI值进行预处理, 然后在定位阶段对质心定位算法进行加权改进, 进而引入迭代的思想将已定位的未知节点升级为锚节点辅助定位, 最后将其与质心定位算法以及基于RSSI的加权质心定位算法一同进行仿真分析, 结果表明, 本文提出的改进算法相较于其他两种算法定位精度有明显的提高.
| [1] |
Zhao YK, Xu J, Jiang JL. RSSI based localization with mobile anchor for wireless sensor networks. Proceedings of the 5th International Conference on Geo-Spatial Knowledge and Intelligence. Chiang Mai: Springer, 2017. 176–187.
|
| [2] |
Borges LM, Velez FJ, Lebres AS. Survey on the characterization and classification of wireless sensor network applications. IEEE Communications Surveys & Tutorials, 2014, 16(4): 1860-1890. |
| [3] |
吕淑芳. 无线传感器网络节点定位研究综述. 传感器与微系统, 2016, 35(5): 1-3, 8. |
| [4] |
Savvides A, Han CC, Strivastava MB. Dynamic fine-grained localization in ad-hoc networks of sensors. Proceedings of the 7th Annual International Conference on Mobile Computing and Networking. Rome: ACM, 2001. 166–179.
|
| [5] |
吴斌. WSN节点定位技术的质心定位算法优化策略. 通信技术, 2020, 53(12): 2983-2988. DOI:10.3969/j.issn.1002-0802.2020.12.016 |
| [6] |
Ru LL, Zhang LH. A weighted centroid localization algorithm for wireless sensor networks based on weight correction. Proceedings of the 9th International Conference on Advanced Infocomm Technology. Chengdu: IEEE, 2017. 165–169.
|
| [7] |
谢桦. 基于RSSI的无线传感器网络加权质心定位算法[硕士学位论文]. 赣州: 江西理工大学, 2017.
|
| [8] |
Li YK, Shao HG, Ni SZ. A weighted centroid localization algorithm based on RSSI and virtual static beacon nodes. Advanced Materials Research, 2015, 1077: 252-256. |
| [9] |
Zeng ZL, Gao JM, Wang JH. Corrected range weighted centroid localization algorithm based on RSSI for WSN. Proceedings of the 2011, International Conference on Informatics, Cybernetics, and Computer Engineering (ICCE2011). Berlin: Springer, 2010. 453–460.
|
| [10] |
李海啸, 于东, 胡毅, 等. 改进的无线传感器网络三边质心定位算法. 小型微型计算机系统, 2020, 41(6): 1216-1223. DOI:10.3969/j.issn.1000-1220.2020.06.017 |
| [11] |
许红艳, 王经卓, 董自健, 等. MDS-MAP算法在不同传播模型中定位误差的比较. 淮海工学院学报(自然科学版), 2012, 21(1): 15-19. |
| [12] |
Bulusu N, Heidemann J, Estrin D. GPS-less low-cost outdoor localization for very small devices. IEEE Personal Communications, 2000, 7(5): 28-34. DOI:10.1109/98.878533 |
| [13] |
陈维克, 李文锋, 首珩, 等. 基于RSSI的无线传感器网络加权质心定位算法. 武汉理工大学学报(交通科学与工程版), 2006, 30(2): 265-268. |
| [14] |
尹亚波, 徐晴. 基于RSSI测距的无线传感器网络质心定位算法优化. 计算机与数字工程, 2018, 46(12): 2425-2429, 2462. DOI:10.3969/j.issn.1672-9722.2018.12.009 |
 2022, Vol. 31
2022, Vol. 31


