海浪预报是海洋环境预报中的难题. 海浪的预报在沿海城市居民的日常生活中占有着重要的地位. 海浪会因为海风的随机性变得更加随机和复杂. 风浪能改变表面的风场结构, 导致海浪的生成机制和过程更加繁琐[1]. 近岸沿海城市的海洋经济经常受到海浪等灾害的威胁, 建立海浪智能精细化预报业务对于预防并减少海洋灾害和发展海洋经济具有重大的意义.
目前海浪预报大致分为经验模型、数值预报和机器学习法[2]这3类方法. 经验模型类预测海浪是利用假设先验模型的方式, 但是预测效果一般, 比如自回归移动平均方法. 数值模型类预测海浪是利用求解海浪谱控制方程的方式来拟合、预测, 该预测法对海域宽阔的海浪有较好的预测效果, 但对地形繁杂的近岸、沿岸海域则预测效果较差, 例如海浪模型、近岸海浪数值模型、第三代海浪模型和海浪数值模式[3]等. 支持向量机(SVM)[4]和人工神经网络[5]等机器学习技术方法由于它们具备更好的自适应学习和非线性映射的特点, 适宜解决那些复杂的物理机制, 难以确定推理规则的非线性问题. 因而在海浪预测中人工神经网络有着广阔的发展前景[6]. 目前机器学习中有关海浪预测的方法有支持向量机、BP神经网络、长短期记忆神经网络等相关算法, 例如利用支持向量机预测海浪数据, 通过人工神经网络来预测南海硇洲岛的海浪数据[5], 利用BP神经网络预测上海沿海浮标站的海浪数据[7], 利用长短期记忆[8, 9]模型进行海浪预测[10]等. 对于具有非线性和弱规律性的海浪波高数据, BP神经网络能够表现出较好的预测特性. 然而, BP神经网络自身存在误差收敛慢、训练周期长、泛化能力差、容易陷入局部极小等缺陷. 长短期记忆神经网络(LSTM)[11]是RNN的进阶版本, 它优化了RNN的细胞结构, 能够对时间序列数据进行记忆的优点的同时还解决了传统RNN自身存在的缺陷, 比如梯度爆炸、梯度消失和长期记忆能力不足.
为了解决上述问题, 本文提出了一种结合随机森林(random forest, RF)算法[12]和注意力机制[13]的双向长短期记忆神经网络(BiLSTM)的海浪预测模型, 并在基础上选取2017–2018年北海小麦岛海洋站点的海洋环境数据作为海浪预测的实验数据. 首先使用随机森林[9]能够进行特征重要性度量的特点, 在众多海洋环境数据中筛选出与风速、海浪波高关联性较高的影响因素作为模型的输入, 然后将双向长短期记忆[14]神经网络与注意力机制[15]相结合, 并搭建预测模型, 即RF-BiLSTM海浪预测模型. 双向长短期记忆 (bidirectional LSTM, BiLSTM)[16]神经网络是在长短期记忆的基础上添加了反向隐含层, 这样就可以让模型在前向隐含层使用过去数据, 在反向隐含层使用将来数据, 这样预测效果会更加精确. 最终实验证明, 该模型比其他模型的学习效果要好, 特别是面对数据量规模较大的多变量时间序列数据时, 该模型的准确性更高和收敛速度也更快. 海浪的准确预测对沿海城市经济发展和海洋灾害防范具有重要意义, RF-BiLSTM模型比其他预测模型的性能更好, 在海浪波高预测上有重要的战略意义和运用价值[17, 18].
1 神经网络模型 1.1 长短期记忆神经网络循环神经网络(recurrent neural network, RNN)能挖掘并分析数据中的时序信息, 因此对具备序列性质的数据作用甚好. 图1为循环神经网络结构图. RNN还具有时间反馈循环和存储记忆数据的特点, 而且在时序数据分析中有着很好的效果. 因为RNN能够记录每时刻的数据信息, 每时刻的输入层和上一时刻的隐藏层共同决定该时刻的隐藏层, 所以RNN对解决时间序列问题有着超前的优越性. 而且不同顺序的输入序列最后的结果也是完全不同的. 因此RNN处理序列数据时效果又好又敏感.

|
图 1 循环神经网络结构图 |
|
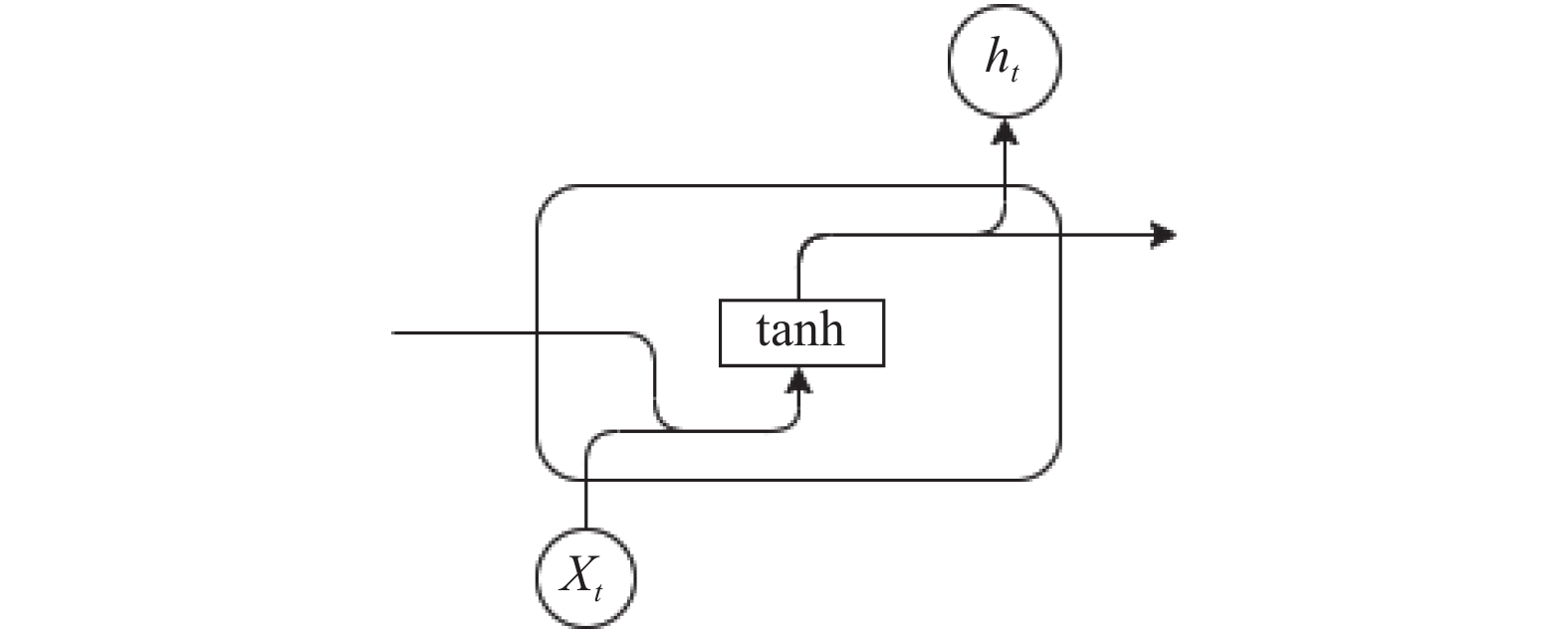
图 2 RNN单元结构 |
图2所示为RNN的神经单元结构, 由于RNN的神经单元仅有这一个函数, 因此在训练中会多次叠加函数, 容易造成梯度消失和梯度爆炸的结果, 所以RNN 在跨度大的时间序列数据方面处理效果不是很理想.
LSTM是RNN的进阶版本, 比普通的RNN高级, RNN因为没有筛选的特点, 所以全部信息它都记录、保存下来, 但是LSTM能够筛选存储信息, 留下所需要的信息, 这就可以有效避免梯度消失问题. LSTM能够筛选信息, 能够选择性的遗忘或保留输入信息, 皆是因为它具有遗忘门、记忆门和输出门这3大门控系统.
标准RNN中, 重复神经网络模块的处理层通常为单tanh层, 较为简单, 与标准RNN相比, LSTM有着更加繁琐的4层架构的重复模块. LSTM的核心思想就是记忆块, 主要包含了1个记忆单元和3个门(遗忘门、输入门、输出门), 如图3所示.

|
图 3 LSTM单元结构 |
LSTM的第1步: 决定通过单元状态筛选信息, 遗忘门通过Sigmoid函数来控制这个决定, 依据上一时刻的输出通过或部分通过, 也可以理解为从之前所学习的很多东西中将没用的东西就对它进行选择性过滤. 其表达式如下:
| $ {f_t} = \sigma \left( {{W_f}\left[ {{h_{t - 1}}, {x_t}} \right] + {b_f}} \right) $ | (1) |
第2步: 生成需要更新的新信息. 这个过程分为两个环节, 一是哪些值用来更新由输入门通过Sigmoid函数来决定的, 二是新的候选值通过tanh函数生成, 两者相加, 得到了新信息.
第3步: 将前两步联合, 将需要的信息保留, 不需要的信息过滤, 新信息添加的过程. 第2步、第3步的公式如下:
| $ {i_t} = \sigma \left( {{W_i}\left[ {{h_{t - 1}}, {x_t}} \right] + {b_i}} \right) $ | (2) |
| $ {\bar C_t} = \tanh \left( {{W_C}\left[ {{h_{t - 1}}, {x_t}} \right] + {b_C}} \right) $ | (3) |
| $ {C_t} = {f_t}{C_{t - 1}} + {i_t}{\bar C_t} $ | (4) |
第4步: 决定模型的输出, 首先初始输出由Sigmoid函数得到, 其次利用tanh函数将
| $ {o_t} = \sigma \left( {{W_o}\left[ {{h_{t - 1}}, {x_t}} \right] + {b_o}} \right) $ | (5) |
| $ {h_t} = {o_t}\tanh \left( {{C_t}} \right) $ | (6) |
以上公式中,
模型采用神经网络中常用函数的tanh和Sigmoid函数作为
| $ s\left( x \right) = \frac{1}{{1 + {{\rm{e}}^{ - x}}}} $ | (7) |
| $ \tanh \left( x \right) = \frac{{{{\rm{e}}^x} - {{\rm{e}}^{ - x}}}}{{{{\rm{e}}^x} + {{\rm{e}}^{ - x}}}} $ | (8) |
单向LSTM能够很好地处理和预测时间序列过长数据的特点, 然而它进行预测只能利用以往的数据信息, 例如预测未来几个小时甚至一天的海浪预报预测数据需要利用过去若干天的海浪预报预测数据. 只利用了距离预测数据较近的若干个历史数据, 这就将较早的历史数据信息遗忘了. 双向LSTM神经网络具有利用过去和未来的海浪预报预测数据来更好的模拟预测海浪数据. BiLSTM的基本思想是每一个训练的序列向前和向后分别是两个长短期记忆神经网络, 同时这两个层均与输入层、输出层相连接. 过去(前向)和未来(反向)相结合得到了输出. 在海浪波高预测中, 是利用过去和未来的风速海浪预测数据实现对波高的预测.
BiLSTM的神经元由输入层、隐含层(前向、反向)、输出层组成. 图4为BiLSTM的结构图, 能够观察出前向隐含层和反向隐含层均与输出层相连.

|
图 4 BiLSTM神经网络示意图 |
每个时刻向前隐含层的输出由前向隐含层从1时刻到
| $ {\dot h_t} = f\left( {{w_1}{x_t} + {w_2}{{\dot C}_{t - 1}} + {w_3}{{\dot h}_{t - 1}}} \right) $ | (9) |
| $ {h_t} = f\left( {{w_4}{x_t} + {w_6}{C_{t - 1}} + {w_7}{h_{t - 1}}} \right) $ | (10) |
| $ {\dot h_t} = f\left( {{w_5}{{\dot h}_t} + {w_8}{h_t}} \right) $ | (11) |
一般在神经网络模型中, 模型的参数与表达能力和存储信息是成正比的. 所以当大量的信息被模型存储时, 就会造成信息过载的问题. 在大量的输入数据中, 注意力机制能够找到对当下任务最重要的数据信息, 对其他数据的重要程度能够降低, 甚至可以过滤一些无效信息, 这样信息过载的困扰就可以解决, 也能提升任务处理的工作效率和准确性. 它关注输入数据中更关键的信息, 即可以更好地学习有用的信息去影响结果, 而且模型的计算和存储也不会扩大, 能够提高效率. 注意力机制主要应用在循环神经网络框架中的隐藏状态矩阵
| $ {v_t} = \sum\nolimits_{i = 1}^{t - 1} {{\alpha _i}} {h_i} $ | (12) |
| $ {\alpha _i} = \frac{{\exp \left( {f\left( {{h_i}, {h_t}} \right)} \right)}}{{\displaystyle\sum\nolimits_{j = 1}^{t - 1} {\exp \left( {f\left( {j, {h_t}} \right)} \right)} }} $ | (13) |
其中,
本文选取北海观测站点小麦岛观测站点的观测数据集作为样本数据集, 其中采集了从2017年1月1日0时到2018年12月31日24时的相关海洋观测数据. 表1为原始观测数据中某时间段的数据.
| 表 1 部分原始海洋气象数据表 |
表1数据可以看出, 该海洋观测站点的观测数据是每小时记录、更新一次, 该观测数据要素包括采集数据的区站号(StationId)、年/月/日(YY/MM/DD)、时(Hour)、温度(Tem)、海盐(SSalt)、湿度(Hum)、海浪(WV)、风速(Win_S)、风向(Win_D)、模式风速(MWin_S)、气压(AP)、降水量(PreH).
2.1.2 数据预处理(1)数据清洗. 数据清洗的工作比较复杂, 数据清洗成功与否决定数据的质量的好坏, 所以数据清洗是预测实验的重要保障. 首先需要处理的是原始数据中冗杂、无效的数据, 如观测站编号均是小麦岛站点的编号01116, 因而去掉这一列对海浪预测实验无用的数据; 第二就是查看数据表中是否有缺省值(null或999)并加以处理, 本文中的缺省值通过fillna函数进行填充处理, 选择各项数据的中位数将其代替; 最后将日期、时间两项整合为一项.
(2)数据归一化. 本文的输入数据为上表中的海洋气象数据, 由表1可知每种气象数据都有着对应的数量级和数量级单位, 这种无序化的数量规则将对最终海浪的预测结果造成很大的误差. 本文将对样本数据进行规范化操作, 即归一化处理, 来消除这种不利因素. 对此, 本文将样本数据的取值限定在[0, 1]这个区间之内, 计算公式如下:
| $ {X^*} = \frac{{X - {X_{\min }}}}{{{X_{\max }} - {X_{\min }}}} $ | (14) |
其中,
(3)数据转化. 因为处理好的基础数据集中有输入数据和输出数据, 所以将其看作成监督学习问题. 输入数据是与海浪相关的各种影响因素在
针对海浪预测为例, 提出了RF-BiLSTM海浪预测模型, 即基于随机森林的注意力机制和双向长短期记忆神经网络相结合的海浪预测模型. 首要工作是对海浪影响因素数据归一化处理, 也就是预处理不同的数量级和数量级单位的样本数据, 而后将其转变为监督学习数据; 其次利用随机森林进行特征的重要性度量并筛选出与风浪关联程度较高的影响因素作为输入数据; 然后利用训练数据对带有注意力机制的BiLSTM模型进行训练, 最后利用测试数据对训练成功的注意力机制的BiLSTM模型进行测试.
2.2.1 随机森林选择特征为了去掉一些冗余的数据, 并保留对海浪预测相关性比价大的特征. 本文对样本数据的特征通过随机森林算法进行重要性度量, 选择出对海浪预测过程中相关性较高的影响因素, 以此来避免输入变量过多带来的数据冗余的问题. 具体分为以下两个步骤:
(1) 计算影响因素
1) 袋内数据是由随机有放回抽样海浪数据构成的, 袋外数据(OOB)是由未被抽取的样本数据构成的, 测试集是袋外数据组成; 将抽取的样本数据用来搭建随机森林模型, 利用袋外数据对该模型的性能进行评估, 从而计算袋外数据误差, 记为errOOB1;
2) 随机对袋外数据OOB所有样本的随机改变某个影响因素
3) 假设随机森林中有
| $ W=\sum({errOOB} 2-{errOOB} 1) / N $ | (15) |
(2)按照上述操作能够得到样本数据中每个影响因素
1) 根据式(15)计算每个影响因素
2) 根据特征重要性在当前的影响因素中确定一个剔除的比例并剔除对应部分, 留下的影响因素组成一个新特征集;
3) 利用新特征集重新搭建随机森林模型, 计算其中各个影响因素的
4) 重复上述步骤, 直到剩下
5) 依据上述操作, 能够得到所有特征集和特征集相应的随机森林模型的袋外误差率. 因此, 决定神经网络的输入数据集是袋外误差率最低的特征集.
图5为使用随机森林在海浪预测过程中进行特征重要性度量的结果. 由图能够看出, 在海浪预测的特征重要性度量过程中, 温度、湿度、风向、风速、模式风速这几种因素对海浪的关联性在所有的影响因素中相对而言更高, 所以输入变量便由温度、湿度、风速、风向、模式风速组成, 同时样本数据集由输入变量的特征集组成.

|
图 5 随机森林特征选择结果 |
|
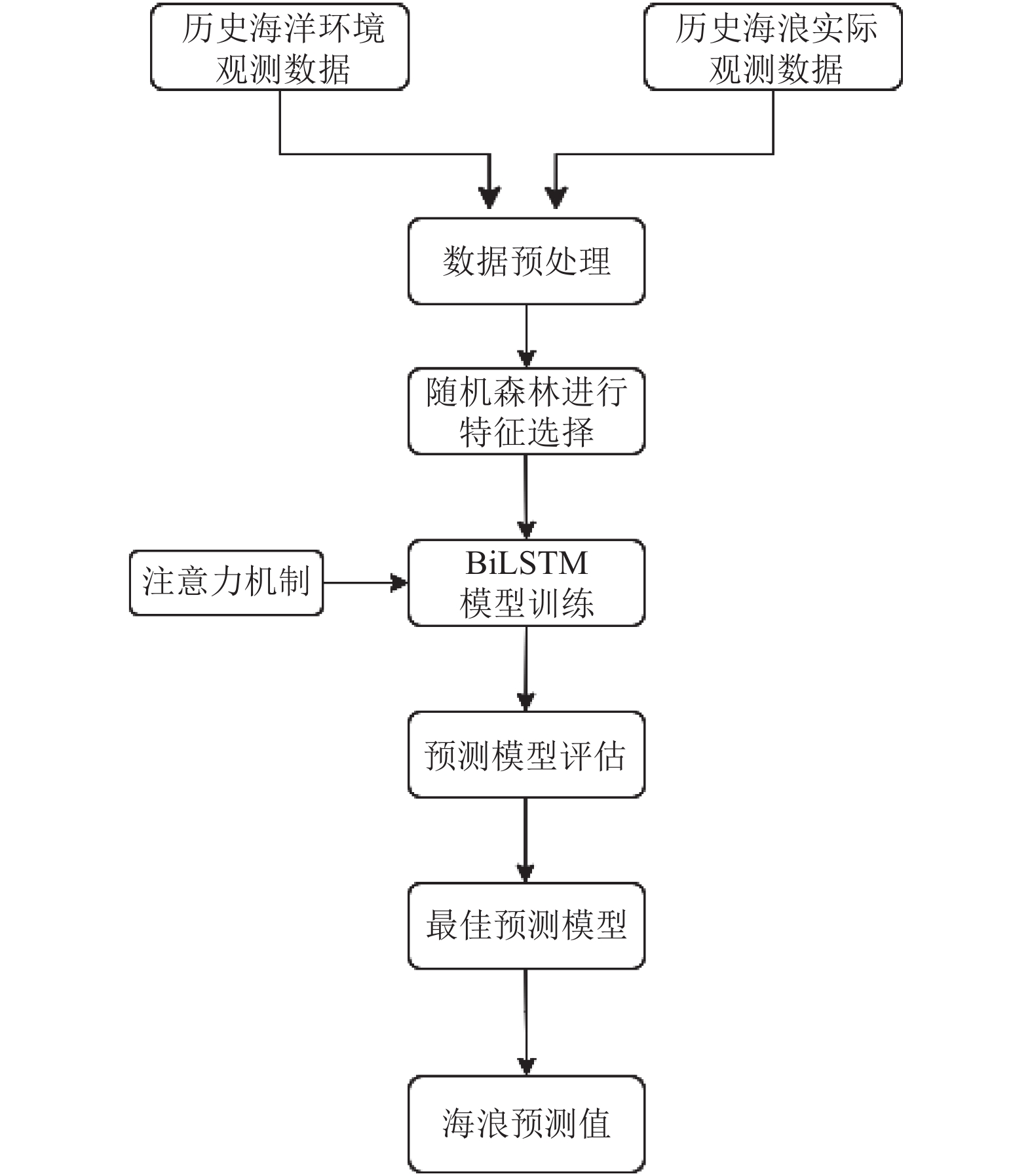
图 6 RF-BiLSTM海浪结构框图 |
2.2.2 RF-BiLSTM神经网络风浪预测模型
神经网络预测模型大多是训练若干历史数据, 从而建立输入和输出的关系, 训练成功后, 通过现有的输入数据来预测未来数据. 本文分析了历史海洋环境和风浪数据, 发现风速和海浪的波高大小有着最密切的关系, 因此建立风速、海浪与海洋风浪的相关数据建立联系. 由于利用过去的风速数据预测海浪会有一些局限性, 因此, RF-BiLSTM模型是利用过去的风速数据信息和未来的风速数据信息进行预测更加准确的风速数据进而预测的海浪数据会更加精确.
基于随机森林的BiLSTM的风浪预测模型结构如图6所示. 首先处理海洋站观测数据, 提取风速、海浪观测值和其他观测值; 其次, 对众多特征使用随机森林进行特征度量并筛选, 并作为输入数据; 然后, 建立注意力机制和BiLSTM相结合的预测模型, 将做好的特征数据集输入预测模型进行训练; 再根据设置的评估指标选取最佳预测模型, 得到更精确的海浪波高预测值.
2.3 评估指标选择的模型预测不同得到的结果也是不一样的. 如BiLSTM神经网络、BP神经网络、LSTM神经网络、等. 因此, 对预测结果使用常用的两种指标进行评估, 并对此进行适用性分析.
(1)均方根误差RMSE评价指标, 指标数值越小, 预测误差越小, 预测效果越好.
| $ {\textit{RMSE}} = \sqrt {\frac{1}{n}{{\sum\nolimits_{i = 1}^n {\left( {{{\hat Y}_i} - Y} \right)} }^2}} $ | (16) |
(2)平均绝对百分比误差MAPE评价指标, 指标数值越小, 预测误差越小, 预测效果越好.
| $ MAPE = \frac{1}{n}\sum\nolimits_{i = 1}^n {\left| {\frac{{{{\hat Y}_i} - {Y_i}}}{{{Y_i}}}} \right|} $ | (17) |
为了验证本文提出的基于RF-BiLSTM海浪预测模型的优越性, 采用了小麦岛2017–2018两年的海洋观测数据作为训练样本, 预测样本为2019年前半年的观测数据. 并分别用BP、LSTM和BiLSTM模型作为对比试验.
图7显示模型训练和模型测试过程中迭代50次的损失函数变化曲线图, 由图可知, 当损失函数迭代15次时, 损失函数基本收敛, 在迭代36次以后, 损失值变动幅度极小, 基本保持不变, 并且测试的损失函数比训练损失函数值还低, 说明在测试集上该模型表现出了更好的效果, 展现出了较强的泛化能力.

|
图 7 RF-BiLSTM模型损失函数曲线图 |
由于数据量较大, 本文随机在数据集中选取了连续数据, 即连续5天的数据作为训练和测试输出的展示数据, 得到图8和图9的拟合效果图.

|
图 8 RF-BiLSTM与BiLSTM训练输出对比图 |

|
图 9 RF-BiLSTM与BiLSTM测试输出对比图 |
从图8和图9能够看出, 用RF-BiLSTM模型和BiLSTM模型得到的海浪预测趋势不仅在训练过程中而且在测试过程中都与实际海浪趋势基本一样, 说明BiLSTM模型比较适合海浪预测. 但是相对于单纯的BiLSTM模型来讲, 本文提出的基于RF-BiLSTM的海浪预测模型得出的结果和实际数据值拟合的更好一点, 曲线与真实值对应的曲线更贴合, 趋势更一致.
为了验证海浪预测模型的预测精度, 表2中列出测试过程中BiLSTM和RF-BiLSTM的RMSE、MAPE的值.
| 表 2 RF-BiLSTM与BiLSTM模型误差对比 |
由表2可知: RF-BiLSTM海浪预测模型的RMSE、MAPE值均小于BiLSTM, 说明RF-BiLSTM海浪预测模型预测精度更高, 海浪的预测值与实际海浪数据值之间具有更小的误差.
综上表明, 对于数据量规模大的多变量时间序列而言, 使用本文的RF-BiLSTM模型, 拟合程度更好, 预测结果更精确.
为了进一步的验证本文提出的RF-BiLSTM海浪预测模型的优越性. 于是将RF-BiLSTM模型训练测试结果与LSTM、BP模型预测的结果相比较, 选择连续4天的数据作为训练测试数据展示, 最终结果对比图如图10和图11所示.
|
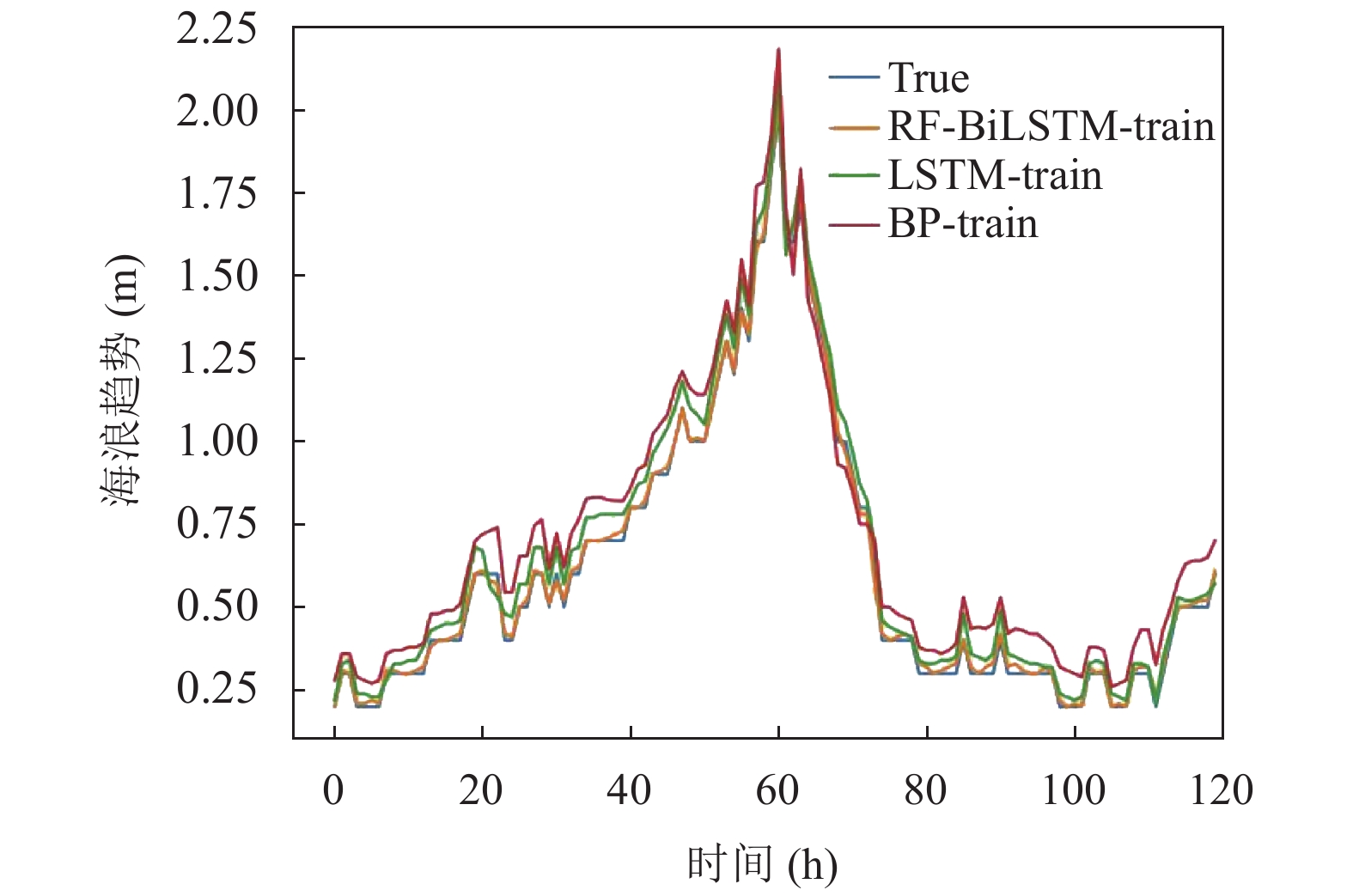
图 10 RF-BiLSTM与其他模型训练输出对比图 |
图10和图11中显示了RF-BiLSTM、BP、LSTM这3种模型在训练和测试中海浪预测值和海浪真实值的对比结果. 从图10可以看出, 在训练过程中LSTM模型的预测值与真实值之间的拟合程度与RF-BiLSTM模型的拟合程度相差不大. 而在图11中可以看出, 是LSTM模型在海浪波动较大的时候拟合效果没有那么好, 比如在第32和第37个数据点时, 预测出得海浪值与海浪真实值之间偏离程度较大. 相反, RF-BiLSTM模型不管是在训练还是在测试过程中, 海浪的预测值和实际值之间的拟合效果都比较好, 比如在第24个、第32个和第44个数据点时, 海浪预测值和实际值简直完全重合. 因此, RF-BiLSTM海浪预测模型与LSTM、BP这两种模型相比较, 海浪的预测值和实测值之间拟合效果更好, 尤其是在海浪波动较大的地方, RF-BiLSTM也能够表现出较好的拟合效果.

|
图 11 RF-BiLSTM与其他模型测试输出对比图 |
表3显示了RF-BiLSTM与BP、LSTM模型之间的测试误差对比. 由图可知, RF-BiLSTM模型预测的误差最小, 预测精度更高. 由此说明本文提出的RF-BiLSTM模型能够更好地描述海浪的非线性变化, 在海浪预测上有较好的发展和重要意义.
| 表 3 不同预测模型测试误差对比 |
4 结论与展望
本文搭建了RF-BiLSTM模型, 即基于随机森林的BiLSTM海浪预测模型, 介绍了随机森林、注意力机制、LSTM和BiLSTM的数学模型, 搭建基于随机森林的注意力机制与双向长短期记忆神经网络相结合的海浪预测模型, 以小麦岛站点的海洋数据进行预测分析. 实验研究显示, RF-BiLSTM模型与BP, LSTM模型相比, 更加健壮, 预测准确度高, 性能更加优越, 能够准确有效地预测海浪, 并成功解决了传统模型所存在的准确度不高的问题. 因此对于数据量规模较大的多变量的时间序列数据预测分析时, 基于随机森林的注意力机制与双向长短期记忆神经网络相结合的预测模型具有实用性和优越性, 并在海洋预测领域中有着广大的运用前景.
| [1] |
管长龙. 我国海浪理论及预报研究的回顾与展望. 青岛海洋大学学报, 2000, 30(4): 549-556. |
| [2] |
许富祥. 海浪预报知识讲座——第九讲 海浪预报技术及预报方法(2). 海洋预报, 2003, 20(2): 79-83. DOI:10.3969/j.issn.1003-0239.2003.02.013 |
| [3] |
李本霞, 吴淑萍, 邢闯, 等. 近海近岸高精度海浪业务化数值预报系统. 海洋预报, 2010, 27(5): 1-6. DOI:10.3969/j.issn.1003-0239.2010.05.001 |
| [4] |
金权, 华锋, 杨永增. 基于SVM的海浪要素预测试验研究. 海洋科学进展, 2019, 37(2): 199-209. DOI:10.3969/j.issn.1671-6647.2019.02.004 |
| [5] |
陈希, 沙文钰, 李妍, 等. 人工神经网络技术在海浪预报中的应用. 海洋通报, 2002, 21(2): 11-15. DOI:10.3969/j.issn.1001-6392.2002.02.002 |
| [6] |
金权. 基于机器学习算法对海浪波高的预测及优化研究[硕士学位论文]. 青岛: 自然资源部第一海洋研究所, 2019.
|
| [7] |
朱智慧, 曹庆, 徐杰. 神经网络方法在上海沿海海浪预报中的应用. 中国海洋学会2019海洋学术(国际)双年会论文集. 三亚: 海洋出版社, 2019. 54–61.
|
| [8] |
高丽斌, 郭民权, 张少涵, 等. 基于长短期记忆网络的波高预报. 福建电脑, 2018, 34(8): 105-107. |
| [9] |
陶晔, 杜景林. 基于随机森林的长短期记忆网络气温预测. 计算机工程与设计, 2019, 40(3): 737-743. |
| [10] |
Bento AR, Salvação N, Soares CG. Validation of a wave forecast system for Galway Bay. Journal of Operational Oceanography, 2018, 11(2): 112-124. DOI:10.1080/1755876X.2018.1470454 |
| [11] |
李清, 高春燕, 胡长骁, 等. 基于长短期记忆网络与注意力机制的短期光伏发电预测. 电气自动化, 2020, 42(5): 19-21, 37. DOI:10.3969/j.issn.1000-3886.2020.05.006 |
| [12] |
Callens A, Morichon D, Abadie S, et al. Using Random forest and Gradient boosting trees to improve wave forecast at a specific location. Applied Ocean Research, 2020, 104: 102339. DOI:10.1016/j.apor.2020.102339 |
| [13] |
郭汉, 帅仁俊, 马力, 等. 基于AB-CNN-BiLSTM心衰死亡率预测模型. 计算机应用与软件, 2021, 38(4): 37-42. DOI:10.3969/j.issn.1000-386x.2021.04.007 |
| [14] |
刘永强, 续毅, 贺永辉, 等. 基于双向长短期记忆神经网络的风电预测方法. 天津理工大学学报, 2020, 36(5): 49-54, 59. DOI:10.3969/j.issn.1673-095X.2020.05.011 |
| [15] |
龚飘怡, 罗云峰, 方哲梅, 等. 基于Attention-BiLSTM-LSTM神经网络的短期电力负荷预测方法. 计算机应用, 2021, 41(S1): 81-86. |
| [16] |
熊玄辰, 曹俊兴, 周鹏, 等. 基于双向长短期记忆神经网络的岩相预测方法. 成都理工大学学报(自然科学版), 2021, 48(2): 226-234. |
| [17] |
高丽斌. 基于深度学习的台湾海峡及周边海域波浪预报研究[硕士学位论文]. 福州: 福建农林大学, 2019.
|
| [18] |
张蔺廉, 陈淑琴, 陈梅汀. 基于舟山多年风浪资料的近海海浪预报研究. 海岸工程, 2018, 37(3): 25-33. DOI:10.3969/j.issn.1002-3682.2018.03.003 |
 2022, Vol. 31
2022, Vol. 31


