2. 北京迪普迅智能信息技术有限公司, 北京100089
2. Deepsim Intelligent Information Technology Co. Ltd., Beijing 100089, China
水是生命体最重要的组成部分, 是生命繁衍的基本条件. 随着经济的迅速发展, 工业和生活排放废水量增加, 大量未处理污水排入河流或地下水中, 不仅导致水体使用功能大幅下降, 还加剧了水资源匮乏问题[1]. 据相关文献[2, 3]的研究, 世界上只有很少的部分河流未受污染的影响. 水污染也是造成一些发展中国家疾病和死亡的重要原因之一[4]. 联合国发表的资料表明, 全球有11亿人缺乏安全饮用水, 每年有500多万人死于与水有关的疾病[5]. 水质的恶化, 已经构成制约和引发一个地区或城市经济发展甚至社会不安定的重要因素[6]. 因此, 建立水质模型预测水质变化是保障饮用水安全和人类健康的关键.
水质数据通常是按时间顺序排列的时间序列数据.循环神经网络(RNN)是一种适合于时间序列数据预测的方法[7, 8]. 如Kumar等人[7]对河流月流量数据进行了预测研究, 并将RNN与前馈神经网络进行了比较, 预测效果较好. Jia 等人[8]使用RNN对湖泊温度和水质数据进行建模, 并通过与ANN模型的对比, 证明RNN在时间序列数据预测中具有更高的准确性. 然而, RNN模型存在梯度消失、梯度爆炸和对长距离序列数据的信息依赖性较差等问题. 为了解决这些问题, Hochreiter[9]提出了LSTM模型, 并证明了LSTM在预测时间序列数据方面具有独特的优势, 与RNN相比有效地提高了预测精度. Hu 等人[10]对ANN和LSTM模型对降雨径流量的预测进行了比较, 结果表明LSTM模型具有更好的仿真性和更高的智能性. Hu等人[11]和Liu等人[12]使用LSTM分别对海水养殖区的海水质量和长江的饮用水质量进行了研究, 证明LSTM能更准确地反映水质变化的发展趋势. 然而, 对于波动范围大的数据, 单一的LSTM模型难以确保预测的准确性[13].
为了提高模型的泛化能力和预测精度, Vinyals等人[14]提出了用于时间序列预测的序列对序列(Seq2Seq)模型. Seq2Seq是一种具有编解码结构的网络模型, 不限制输入序列和输出序列的长度, 使模型更加灵活. 同时, 引入注意机制, 减少了早期序列信息的压缩, 进一步提高了远程信息依赖能力. Xiang等人[15]运用Seq2Seq模型估算每小时降雨径流量, 结果表明其预测精度优于试验中所有其他对比模型. Kao等人[16]以台湾石门水库流入量为预测对象, 证明了Seq2Seq模型的可靠性. 然而, 目前Seq2Seq模型在水质数据预测中的研究还处于起步阶段.
此外, 其他研究将LSTM和小波分解相结合, 以提高单一LSTM模型的精度. 孙铭等人[17]建立了水质小波分解和LSTM时间序列预测模型(W-LSTM), 与传统的LSTM模型相比, 此模型具有更高的预测精度和泛化能力. Barzegar等人[18]提出了一种用于多尺度湖泊水位预测的混合CNN-LSTM深度学习和边界校正最大重叠离散小波变换(DWT)模型, 成功地提高了湖泊水位预测的精度. Du等人[19]提出了一种DWT、主成分分析(PCA)预处理技术和LSTM结合的混合模型, 用于需水量预测, 与其他参照预测模型的结果比较, 证明了其所提出混合模型的优越性. Xie等人[20]提出了一种结合LSTM和DWT的深度学习方法(WA-LSTM)来预测长江6个代表性河段的日水位, 结果表明该方法在应用中稳定可靠.
基于以上研究, 本文提出了一种更为先进的小波(Wavelet) Seq2Seq模型(W-Seq2Seq), 通过小波分解去噪和LSTM双层双向Seq2Seq模型(BiSeq2Seq)相结合来的方法来预测水质变化. 通过与其他5种不同结构的模型的对比实验, 验证了所提出方法的有效性.
1 模型算法 1.1 离散小波变换傅里叶变换是信号处理中广泛使用的分析工具, 它将时域信号转换为频域信号; 但傅里叶变换在时域上缺乏辨别能力[21]. 小波变换的发展解决傅里叶变换时域信息丢失的现象, 小波利用一系列带通滤波器用于将原始时域信号分解为二维时频信息, 这大大提高了局部信号的性能, 并提高了模型的抗噪声性能[22, 23].
小波变换是一种数据分解和重构的方法, 使用低通滤波器和高通滤波器将原始数据分解为低频小波系数cAn和高频小波系数cD1, …, cDn [24].
小波变换包括连续小波变换(CWT)和离散小波变换(DWT)两种. 其中, CWT基小波
| $ {\psi _{ab}}(t) = \frac{1}{{\sqrt a }}\psi \left(\frac{{t - b}}{a}\right) $ | (1) |
其中, a为尺度因子(a>0),b为位移因子(b∈R). 小波变换尺度通过调整a和b的值, 把实现时间序列信号分解高频时间和低频时间系数.
CWT公式如下所示:
| $ W{T_f}(a, b) = \int_{ - \infty }^{ + \infty } {f(t)\overline {{\psi _{ab}}(t)} } dt $ | (2) |
其中, WTf (a, b)代表连续小波系数, f(t)表示原始数据,
连续小波变换的缺点在于连续小波变换会计算所有尺度的小波系数, 不仅浪费资源, 也产生大量冗余数据.因此, 通常使用DWT. DWT是连续小波变换在尺度和位移上以2的幂离散化而得到; 其基小波
| $ a = a_0^j, b = ka_0^j{b_0} $ | (3) |
| $ {\psi _{jk}}(t) = {a_0}^{ - \frac{j}{2}}\psi ({a_0}^{ - j}t - k{b_0}) $ | (4) |
其中, a0>0, b0∈R, ∀j,k = 0, 1, 2, …, m∈Z,
DWT公式如下所示:
| $ W{T_f}(j, k) = \int_{ - \infty }^{ + \infty } f (t)\overline {{\psi _{j, k}}(t)} dt $ | (5) |
其中,
分别重构低频和高频小波系数, 得到低频信号rAn和高频信号rD1, …, rDn ; 其中低频信号表示近似信息, 高频信号表示详细信息.
最后, 低频信号和高频信号相加, 实现原始信号的重构, 其重构公式如下.
| $ f(t) = c{A_n}l({\psi _{ik}}(t)) + \sum\nolimits_{n = 1} {c{D_n}h({\psi _{ik}}(t))} $ | (6) |
其中, f(t)表示重构信号,
小波分解的两个重要任务是选择最优小波和确定分解层数. 常用的小波有Haar、Daubechies、Sym、Bior、Coif、Morlet、Mexican Hat和Meyer. 本文选取Daubechies5 (db5)作为基小波, 其原因db5是dbN小波族中常用的小波之一, 比较适合相对平滑数据集的分解[17].
根据文献[25], 小波变换的最大分解层数用式(7)计算得出.
| $ leve{l_{{\text{max}}}} = floor({\log _2}(L/(wl - 1))) $ | (7) |
其中, levelmax表示最大分解层数, floor表示向下取整函数, L用来表示数据长度, wl表示小波分解低通滤波器的长度.
1.2 Seq2Seq模型Seq2Seq模型由编码器和解码器两部分组成, 每部分相当于一个独立的LSTM模型. 不同之处在于编码器将时间序列数据作为输入(每个LSTM对应于一个时间步长), 生成指定长度的向量C作为输出. 向量C由编码器中最后一个LSTM的隐藏层状态和单元状态组成. 在解码器中, 向量C解码为隐藏层状态和单元状态作为输入时, 每个LSTM单元将产生预测结果作为输出. 实验对两层双向Seq2Seq模型(Bi2)结果与一层单向Seq2Seq模型(Uni1)、一层双向模型(Bi1)和两层单向模型(Uni2)的结果进行了对比.
Uni1是最基础的Seq2Seq模型, 其中编码器中只有一个正向层. 对于Bi1, 与Uni1的区别在于其编码器包含两个独立的循环结构(LSTM), 一个正向, 一个反向. 与Uni1的编码器类似, Bi1的前向结构用于计算隐藏层信息和单元状态, 而反向结构用来反向读取序列数据(从n到1), 并计算反向结构生成的一组隐藏层和单元状态. 正向结构产生的隐层和单元状态与反向结构不同, 最后通过连接两种结构的相应部分得到向量C. 反向结构允许网络先学习后续数据, 并根据反向数据调整其参数, 这可能有助于网络获得前向LSTM不具备的依赖性.

|
图 1 两层双向Seq2Seq模型(Bi2) |
在Uni2中, 两个层堆叠在一起, 其中编码器和解码器的第一层LSTM的输出被传递到第2层作为其输入.理论上, 具有更多隐藏层的深层Seq2Seq体系结构可以有效地学习复杂模式, 并逐步建立输入序列数据的更高级别表示. Bi2的编码器和解码器与Uni2类似的方式堆叠, 而区别在于第1层的正向和反向结构的输出分别传递给第2层的正向和反向结构(图1). 在理论上, 由于具有更多的隐藏层和前后向层, Bi2比其他3种Seq2Seq模型结构具有更强大的能力, 学习较复杂的模式.
1.3 数据处理 1.3.1 均值平滑运用均值平滑方法, 通过取缺失数据或异常值左右相邻值的平均值来替换数据集中的缺失值和异常值, 如式(8)所示.
| $ {x_t} = \frac{{{x_{t - 1}} + {x_{t + 1}}}}{2} $ | (8) |
其中, xt是数据t时刻缺失或异常值的替代值, xt–1是时间t–1上的数据值, xt+1是时间t+1上的数据值.
1.3.2 标准化为加快模型训练收敛速度, 提高预测精度, 通常将数据集归一化为[−1, 1]或[0, 1]之间的值. 本文使用了最大-最小归一化方法, 其计算方法为式(9).
| $ {x_{\rm{norm}}} = \frac{{x - {x_{\min }}}}{{{x_{\max }} - {x_{\min }}}} \times ({{{max}} _{\rm{new}}} - {{{min}} _{\rm{new}}}) + {{{min}} _{\rm{new}}} $ | (9) |
其中, xnorm表示归一化后的数据; x为原始数据; xmax和xmin分别代表原始数据的最大值和最小值; maxnew和minnew表示范围的上限和下限, 分别等于1和0.

|
图 2 W-Seq2Seq模型原理流程图 |
1.4 W-Seq2Seq模拟流程
小波分解去燥和Seq2Seq结合的混合预测建模方法(W-Seq2Seq) (图2), 使用小波将数据集分解为高频信号和低频信号; 其中仅保留低频信号作为原始数据的近似值进行建模, 而高频信号细节作为噪声去除. 所提出的W-Seq2Seq建模方法不仅继承了Seq2Seq模型强大的预测精度, 而且通过有效降低数据噪声, 为高频复杂数据集提供了一个更优化、更通用的操作系统.
2 研究数据 2.1 数据描述本文的研究数据来自山东省烟台市福山区门楼镇以西2000 m处青岩河下游的门楼水库, 该水库面积约为14.65平方公里, 是烟台市区主要水源地, 烟台市区70%以上工业生产和居民生活用水都来自这里[26]. 水库总库容2亿立方米, 是一座防洪、灌溉、发电、饲鱼、参观、游览的综合性水库. 然而, 随着当地经济的发展, 水库水质也在逐年恶化, 富营养化已成为水库所面临的主要生态问题. 因此, 控制水库污染, 防止水质进一步恶化已迫在眉睫.
2.2 数据样本选择pH、氨氮(NH3-N)、电导率和浊度4项水质指标, 用无线传感器每3 s自动采集数据一次. 采样时间为2020年3月6日至2020年4月24日, 每项指标共采集数据1440000. 最后, 采取每1200个数据的平均值, 把数据转化为小时数据来分析和建模, 每项指标的小时数据集有1200个值. 4项指标的可视化图清楚地显示了pH值和电导率数据系列中存在异常值(图3), 使用式(8)的平均平滑法替换数据集中的异常值. 清洗后的数据集作为最后实际使用数据, 其中每项指标数据的前1080个值(90%)用于模型训练, 最后120个值(10%)用于模型的测试.
数据集划分及其统计分析如表1所示, 浊度测试数据集的平均值为152.195、最小值为100.42、最大值为232.974、第25个百分位数、50个百分位数和75个百分位分别为120.897、145.721和178.031, 都远大于训练数据集中相应数据, 这意味着测试数据拥有序列的最大值, 且变化幅度较大, 这表明训练数据可能难以训练一个模型来准确预测测试数据值. 然而, 氨氮和电导率的测试数据集和训练数据集之间没有太大差异, 表明训练数据集足以训练一个模型来准确预测测试数据值.关于pH值, 统计分析结果和数据可视化结果显示数据集具有高频特征, 所以需要更复杂的模型来准确预测其测试数据.
3 实验分析 3.1 实验环境实验中使用的计算机环境配置如下: Windows 10 (64位), 采用Intel Core I5-6500中央处理器, CPU频率为3.2 GHz, 内存为4 GB. 编程语言采用Python 3.6; 科学计算库采用Numpy 1.18.5、数据分析库采用Pandas 1.1.0、数据可视化库采用Matplotlib 3.3.0. 机器学习库采用TensorFlow 2.0、集成开发环境(IDE)是PyCharm Professional Edition 2020.1.1.
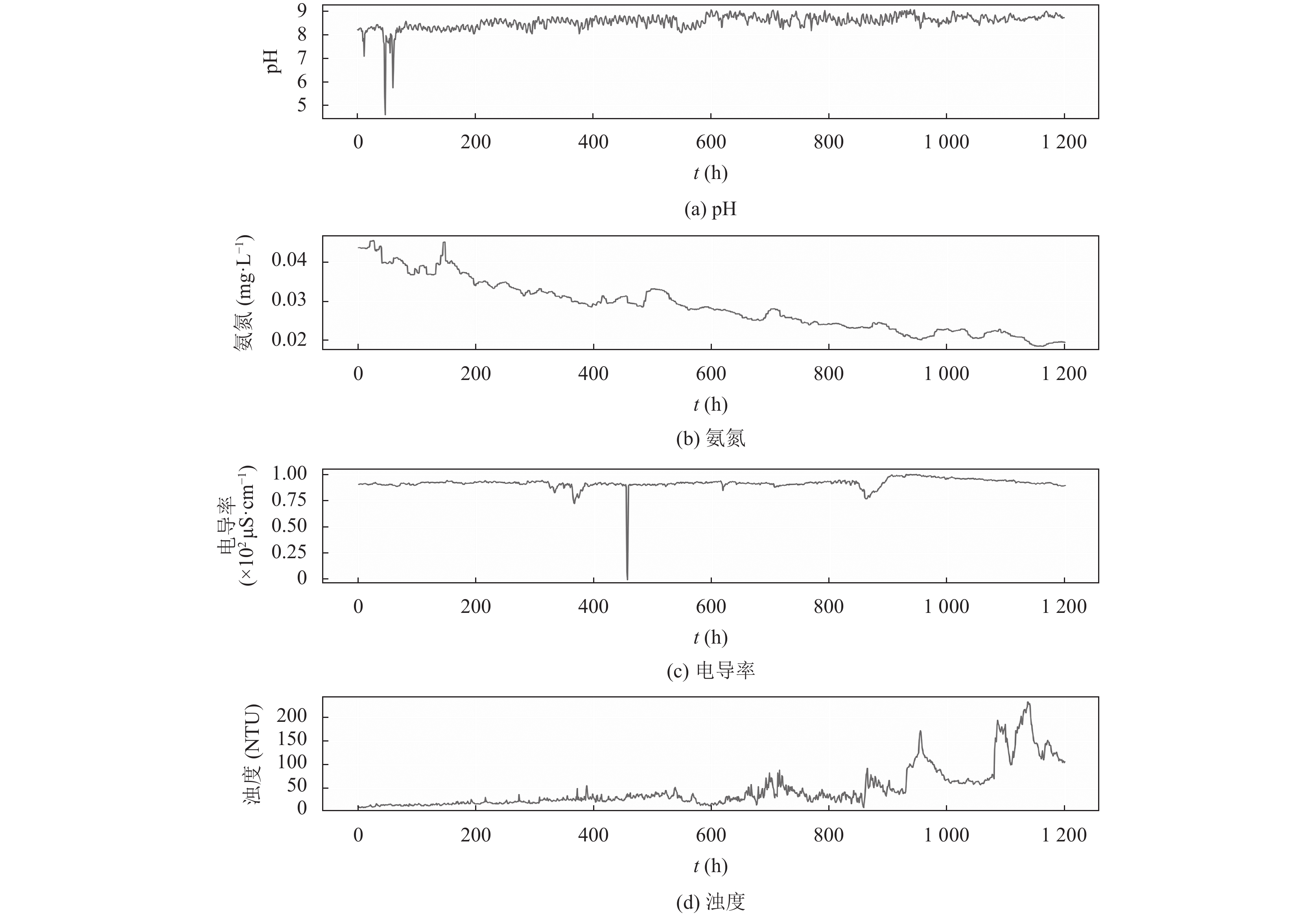
|
图 3 清洗前的数据集曲线图 |
| 表 1 清理后数据的统计分析结果 |
3.2 模型评估指标
选取MSE, RMSE 和 MAPE作为模型训练和预测精度的评价指标. 3个评价指标的计算方法用式(10)、式(11)和式(12)表示.
| $ {\textit{MSE}} = \frac{1}{N}\sum\nolimits_{t = 1}^N {{{({y_t} - \overline {{y_t}} )}^2}} $ | (10) |
| $ {\textit{RMSE}} = \sqrt {\frac{1}{N}\sum\nolimits_{t = 1}^N {{{({y_t} - \overline {{y_t}} )}^2}} } $ | (11) |
| $ MAPE = \frac{1}{N}\sum\nolimits_{t = 1}^N {\left| {\frac{{{y_t} - \overline {{y_t}} }}{{{y_t}}}} \right|} $ | (12) |
其中, N表示数据长度, yt表示实际数据,
每项指标的长度为1200, 所以根据式(7), db5小波对各指标序列最大分解层数为7层. 然而, 根据实际经验最大分解层的一半通常是最佳分解层数[19]. 因此在实验中选择了4个分解层.
表2显示了实际数据和db5小波分解的四阶低频信号(rA4)之间的差异. 氨氮的rA4比其他3个指标的误差更小, 如MSE≈1.65E–07, RMSE≈0.00046和MAPE≈0.0085. 电导率的rA4和实际数据值之间的误差也非常小, MSE≈0.000082, RMSE≈0.0091和MAPE≈0.0091. 相对氨氮和电导率, pH值的rA4值和实际数据值之间的误差较大, MSE≈0.018, RMSE≈0.133, 但是MAPE (≈ 0.012)表明pH的rA4值代表实际数据集的准确率也非常高, 约为98.8%.对于浊度, rA4的MSE (60.38)和RMSE (7.77)非常大, 而MAPE (< 0.109)表明浊度rA4代表其实际数据集的准确率也达到89.1%. 图4显示了4个指标的实际数据集与其分解后的rA4之间的比较结果, 进一步表明了低频信号rA4在降低数据噪声影响的同时很好地保持了原数据变化的趋势.
| 表 2 db5小波分解的四阶低频信号(即近似值)与每个指标的实际数据值之间的误差 |
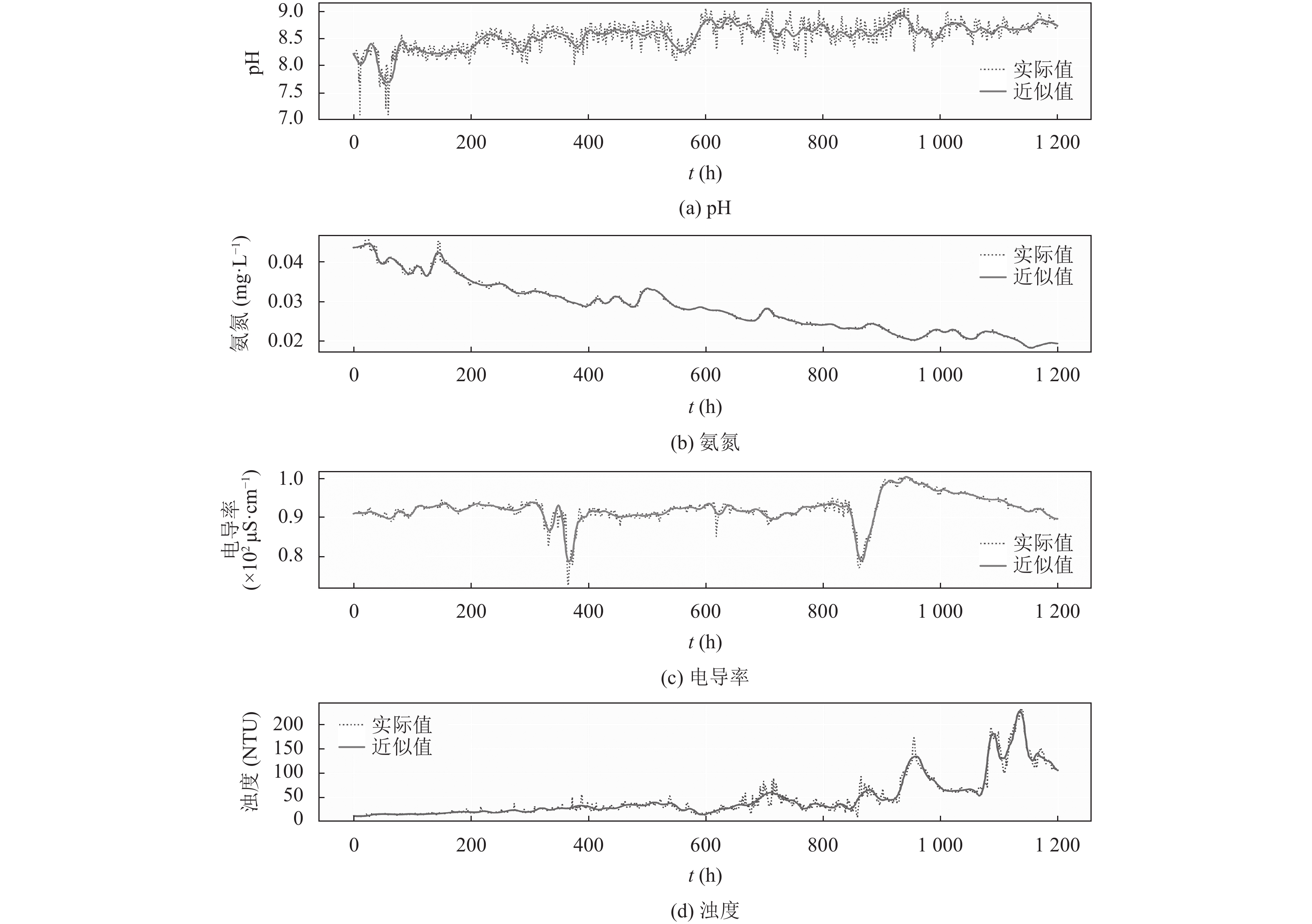
|
图 4 db5小波分解近似值曲线(rA4)和实际数据集比较图 |
3.4 训练结果
此项研究中, Bi2模型和其他5个比较模型(Uni1、Bi1、Uni2、LSTM、W-LSTM)都在相同的实验平台和环境下运行. 为了避免实验中的随机因素, 每个模型均训练10次, 每次运行100轮次(epoch), 最后取结果的平均值. 在训练过程中, 训练数据集的10%进一步用于模型验证, 表3总结了4种Seq2Seq模型和传统LSTM模型, 以及孙铭等人[17]提出的基于小波分解的LSTM模型(W-LSTM)的训练评估对比结果.
对于pH值, 训练的比较结果显示Bi2模型在训练和验证数据集上具有最小误差值(MSE≈0.0002, RMSE≈0.014和MAPE≈0.00002), 表明此模型对历史数据的拟合性能最好. 对于氨氮, Bi1具有最佳的拟合和验证误差, 其MSE、RMSE和MAPE分别约为0.0001, 0.01和0.0001. 关于电导率, 与Bi2相比, 虽然Uni1具有略小的训练误差 MSE (≈0.0025)和RMSE (≈0.0501); 但Bi2具有较小的训练误差MAPE (≈0.000083)和验证误差MSE (0.0037)、RMSE (0.0608)和MAPE (0.000093), 并且与LSTM和W-LSTM模型相比, Bi2具有更小的误差值. 此结果表明, 在训练过程中Bi2具有最佳的模拟性能. 对于浊度, 在训练和测试集上Uni1具有相对较小评估误差, 但是总体而言, Bi2和其他两个Seq2Seq模型的评估误差也非常小, 如MSE (0.000187–0.000467)、RMSE (0.0137–0.0216)和MAPE (0.000016–0.000064), 此外4种Seq2Seq模型与LSTM和W-LSTM相比总体上误差较小. 训练集和验证集上的评估比较结果表明4个Seq2Seq模型都具有非常好的性能, 能够高精度地拟合4项水质指标的历史数据集, 与其他模型相比具有更好的性能.
| 表 3 4种Seq2Seq模型和LSTM、小波LSTM (W-LSTM) 的训练评估对比结果 |
3.5 测试结果
6种模型的测试结果的对比如表4和图5所示, 具体而言, 在pH值测试数据集上, Bi2具有最佳的预测性能, 预测精度极高, 其MSE、RMSE和MAPE分别为7.33E–04、0.0271和0.0025 (表4). 然而, 其他5个对比模型Uni1、Bi1、Uni2、LSTM以及W-LSTM的MSE、RMSE和MAPE测试误差较大, 表明其他5个对比模型的预测性能相对较低. 模型的预测对比曲线图(图5(a))进一步显示, Bi2对pH的预测曲线与实际数据变动趋势吻合较好; 而Uni1的预测值图却是一条直线, 表明该模型的预测能力不足. 虽然Bi1、Uni2、LSTM和W-LSTM都可以预测到pH指标的波动趋势, 但它们放大了其波动幅度(图5(a)).
就氨氮而言, Uni2和Bi2都具有非常好的预测性能, 因其较小测试误差, MSE (3.30E–07和4.16E–07)、RMSE (5.75E–04和6.45E–04)和MAPE (0.0197和0.0239) (表4). Uni1和Bi1虽也预测到氨氮的趋势, 但这两个模型的误差远大于Uni2和Bi2 (图5(b)), LSTM和W-LSTM与Uni1和Bi1相比, 误差较大, 不能很好地预测氨氮的趋势. 至于电导率, 测试评估结果显示Bi2具有最小的MSE (6.84E–05)、RMSE (0.0083)和MAPE (0.0074), 表明Bi2具有最好的预测性能; 而Uni1和Bi1的预测值曲线几乎是线性的, 其分别低估和高估了氨氮测试数据曲线的波动(图5(c)).
就浊度而言, MSE、RMSE和MAPE测试评估误差较大, 表明6个模型对浊度的整体预测精度不如对其他3个指标的预测精度高(表4). 因为浊度测试数据集含有整个数据集中的最大值, 且变化浮动较大, 所以模型可能难以准确预测测试数据集, 没有捕捉到测试数据集的波动(图5(d)). 然而, 与其他5个模型相比, Bi2的MSE和RMSE评估误差较小; 表明Bi2也有良好的预测结果. 较小的MAPE (0.1142)误差, 进一步表明Bi2模型的预测准确率为88.6% (表4). 评估比较曲线图直观地显示了Bi2较好的预测性能, 其能够捕捉测试数据的波动行为; 而其他5个模型预测结果仅为平滑的递减曲线, 不能很好地预测测试数据(图5(d)).
4 结论本文提出一种新颖的小波分解去噪和双层双向Seq2Seq的混合水质预测模型(W-Bi2Seq2Seq). 小波分解的结果证实, 最大分解层数的一半是最佳分解层数, 即在这种情况下的四阶低频信号(rA4): (1)是实验实际数据集的最佳近似值; (2)降低数据复杂性和噪声对实验数据影响的有效方法; (3)提高模型的泛化能力.
| 表 4 4种小波Seq2Seq模型和LSTM、小波W-LSTM的测试评估结果 |
所采用的小波双层双向模型(Bi2)的评估结果与小波单层单向模型(Uni1)、小波单层双向模型(Bi1)、小波双层单向模型(Uni2)、LSTM模型以及W-LSTM模型的结果进行比较. 训练评估结果表明, 提出4种Seq2Seq模型整体上优于LSTM和W-LSTM模型, 并且对不同复杂程度的水质数据都有良好的拟合能力. 然而, 测试比较结果表明, Bi2与其他3种Seq2Seq模型相比, 在预测复杂性程度较高的水质数据时更具优势. 因为其复杂的建模结构, 能够显著提高模型的预测精度和泛化能力.

|
图 5 4种Seq2Seq模型、LSTM、W-LSTM模型预测结果对比曲线 |
| [1] |
余周, 胡志伟, 吴佳, 等. 我国水污染现状、危害及处理措施研究. 环境与发展, 2019, 31(6): 61, 63. |
| [2] |
Woznicki SA, Nejadhashemi AP, Ross DM, et al. Ecohydrological model parameter selection for stream health evaluation. Science of the Total Environment, 2015, 511: 341-353. DOI:10.1016/j.scitotenv.2014.12.066 |
| [3] |
Chen YM, Xia JH, Cai WW, et al. Three-phase-based approach to develop a river health prediction and early warning system to guide river management. Applied Sciences, 2019, 9(19): 4163. DOI:10.3390/app9194163 |
| [4] |
Wang Q, Yang ZM. Industrial water pollution, water environment treatment, and health risks in China. Environmental Pollution, 2016, 218: 358-365. DOI:10.1016/j.envpol.2016.07.011 |
| [5] |
张静, 孙晓杰. 水资源环境与人类健康相关性研究. 建材与装饰, 2016(48): 124-125. |
| [6] |
高荣伟. 我国水资源污染现状及对策分析. 资源与人居环境, 2018(11): 44-51. DOI:10.3969/j.issn.1672-822X.2018.11.009 |
| [7] |
Kumar DN, Raju KS, Sathish T. River flow forecasting using recurrent neural networks. Water Resources Management, 2004, 18(2): 143-161. DOI:10.1023/B:WARM.0000024727.94701.12 |
| [8] |
Jia XW, Karpatne A, Willard J, et al. Physics guided recurrent neural networks for modeling dynamical systems: Application to monitoring water temperature and quality in lakes. arXiv: 1810.02880, 2018.
|
| [9] |
Hochreiter S. Untersuchungen zu dynamischen neuronalen Netzen[Master’s thesis]. Munich: Technical University of Munich, 1991.
|
| [10] |
Hu CH, Wu Q, Li H, et al. Deep learning with a long short-term memory networks approach for rainfall-runoff simulation. Water, 2018, 10(11): 1543. DOI:10.3390/w10111543 |
| [11] |
Hu ZH, Zhang YR, Zhao YC, et al. A water quality prediction method based on the deep LSTM network considering correlation in smart mariculture. Sensors, 2019, 19(6): 1420. DOI:10.3390/s19061420 |
| [12] |
Liu P, Wang J, Sangaiah AK, et al. Analysis and prediction of water quality using LSTM deep neural networks in IoT environment. Sustainability, 2019, 11(7): 2058. DOI:10.3390/su11072058 |
| [13] |
Lin SL, Huang HW. Improving deep learning for forecasting accuracy in financial data. Discrete Dynamics in Nature and Society, 2020, 2020: 5803407. |
| [14] |
Vinyals O, Bengio S, Kudlur M. Order matters: Sequence to sequence for sets. 4th International Conference on Learning Representations. San Juan, Puerto Rico, 2015.
|
| [15] |
Xiang ZR, Yan J, Demir I. A rainfall-runoff model with LSTM-based sequence-to-sequence learning. Water Resources Research, 2020, 56(1): e2019WR025326. |
| [16] |
Kao IF, Zhou YL, Chang LC, et al. Exploring a long short-term memory based encoder-decoder framework for multi-step-ahead flood forecasting. Journal of Hydrology, 2020, 583: 124631. DOI:10.1016/j.jhydrol.2020.124631 |
| [17] |
孙铭, 魏守科, 王莹洁, 等. 基于小波分解的LSTM水质预测模型. 计算机系统应用, 2020, 29(12): 55-63. DOI:10.15888/j.cnki.csa.007695 |
| [18] |
Barzegar R, Aalami MT, Adamowski J. Coupling a hybrid CNN-LSTM deep learning model with a boundary corrected maximal overlap discrete wavelet transform for multiscale lake water level forecasting. Journal of Hydrology, 2021, 598: 126196. DOI:10.1016/j.jhydrol.2021.126196 |
| [19] |
Du BG, Zhou QL, Guo J, et al. Deep learning with long short-term memory neural networks combining wavelet transform and principal component analysis for daily urban water demand forecasting. Expert Systems with Applications, 2021, 171: 114571. DOI:10.1016/j.eswa.2021.114571 |
| [20] |
Xie ZQ, Liu Q, Cao YL. Hybrid deep learning modeling for water level prediction in Yangtze River. Intelligent Automation & Soft Computing, 2021, 28(1): 153-166. |
| [21] |
郭彤颖, 吴成东, 曲道奎. 小波变换理论应用进展. 信息与控制, 2004, 33(1): 67-71. DOI:10.3969/j.issn.1002-0411.2004.01.015 |
| [22] |
Mustière F, Bolić M, Bouchard M. Speech enhancement based on nonlinear models using particle filters. IEEE Transactions on Neural Networks, 2009, 20(12): 1923-1937. DOI:10.1109/TNN.2009.2033367 |
| [23] |
刘凯, 李文权, 赵锦焕. 短时公交客流小波预测方法研究. 交通运输工程与信息学报, 2010, 8(2): 111-117. DOI:10.3969/j.issn.1672-4747.2010.02.021 |
| [24] |
Zhao JD, Wei SK, Wen XB, et al. Analysis and prediction of big stream data in real-time water quality monitoring system. Journal of Ambient Intelligence and Smart Environments, 2020, 12(5): 393-406. DOI:10.3233/AIS-200571 |
| [25] |
Lee GR, Gommers R, Waselewski F, et al. PyWavelets: A Python package for wavelet analysis. Journal of Open Source Software, 2019, 4(36): 1237. DOI:10.21105/joss.01237 |
| [26] |
王国群, 王怡, 门世臣. 同心曲——山东烟台门楼水库增容建设纪事. 中国水利, 1991(4): 43-44. |
| [27] |
孙铭. 基于深度学习算法的水质预测模型研究[硕士学位论文]. 烟台: 烟台大学, 2021.
|
 2022, Vol. 31
2022, Vol. 31



