蜡染是指将蜡作为抗染介质应用于织物上, 通过染色获得图案的技术, 是我国历史悠久的传统纺织印染手工艺, 古称“蜡缬”[1]. 作为一种技术与艺术, 在过去与现在都是一种优秀的民族文化, 承载了少数民族独特的历史与文化内涵; 其图案具有高度的艺术价值与文化内涵, 常被应用于现代设计中. 由于蜡染图案组成复杂, 其构型与纹样的排布往往是根据设计师的审美经验与设计经验来进行排列组合, 费时费力且受设计水平制约. 在图案设计方面, Cui等[2]提取形状特征通过形状文法计算系统生成系列图形模板; Muslimin[3]提出了一种基于形状文法的设计方法来分析和综合结构设计中的表示机制; Nasri等[4] 提出一种自动生成原始和新形式的周期性摩尔几何图案的建模方法; Tian等[5]提出了基于分形几何的蜡染花卉图案自动生成方法, 实现传统手工蜡染图案的计算机自动模拟生成; 张欣蔚等[6]通过建立本体模型与形状文法之间的关系实现复杂图案的快速设计; 李华飙等[7]通过对不同传统纹样进行特征分析, 找出其生成规则的异同, 提出了一种传统纹样统一生成模式; 章义来等[8]提出了基于分形规则的陶瓷图案构图模型, 实现图案的快速生成; Strobbe等[9]研究了形状语法在计算机上的实现. 本文在上述研究的基础上提出一种基于构型规则重用的设计方法, 通过对构型规则的提取与重用, 实现蜡染图案快速设计.
本文研究流程如图1所示. 首先对蜡染图案的构图进行分析与表征, 将蜡染图案层次分为主要纹样、修饰纹样、填充纹样与边框纹样. 然后提取蜡染图案元素, 通过轮廓匹配获取元素空间位置, 建立拓扑构型规则. 随后收集蜡染知识了解纹样语义; 对蜡染纹样进行表征并构建蜡染图像数字资源库; 提出基于标识矩阵法的图案嵌入方法, 在拓扑构型规则的节点上嵌入合适纹样, 生成设计方案.
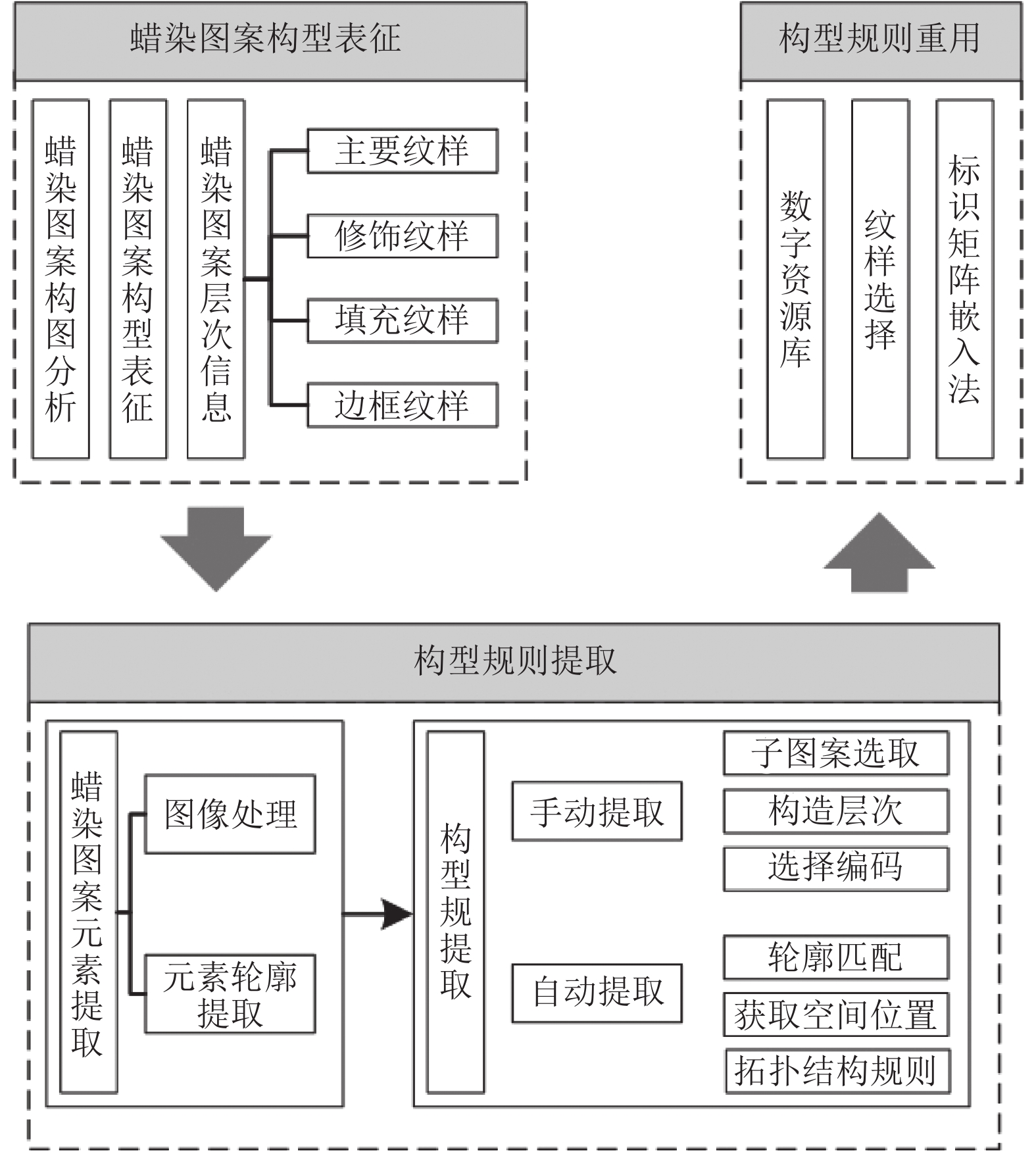
|
图 1 研究流程图 |
1 蜡染图案构型表征 1.1 蜡染图案构图分析
平面化是蜡染图案的主要构图形式[10], 任何纹样都可置于同一幅画面中. 蜡染制作者认为“满即多, 全即美”, 因而在绘制时为了显示出图案的视觉冲击力, 纹样的种类、数量、造型都不受制约, 纹样种类繁多却不混乱, 给人一种均衡、秩序的视觉感受. 蜡染图案主要布局方式有以下3种.
1)秩序布局: 在构图时选取一种纹样作为主要图案, 其余纹样根据主要图案的走势进行分布, 如图2(a)所示.

|
图 2 蜡染图案主要布局形式 |
2)零散布局: 把纹样无规则的放置在画面中, 但纹样与纹样之间留有一定的留白区域, 大量的留白区域使得没有关联的纹样营造出一种自然和谐的视觉感受, 如图2(b)所示.
3)分区布局: 使用几何图形来划分整个画面, 每个区域都是一幅完整画面, 在整体上形成一种秩序, 如图2(c)所示.
构型是建筑学中的概念, 常用来表达元素与元素、元素与整体之间的关系[11]; 在蜡染图案中用建筑学的理论难以对其进行描述, 需要寻找其他方式对蜡染图案的布局进行描述. 对于图案组成方式, 人们常通过视觉观察后使用自然语言对其进行描述, 如图3(a)所示, 人们会给出“八个鱼纹环绕一个铜鼓纹”这样的语言描述, 其中“八个”“环绕”“一个”则揭露了该图案的排布规律, 这种规律用形式化的方式表达为构型; 图3(b)和图3(c)则展示出即使纹样相同, 构成的不同图案给人的视觉感受也不一样. 因此把轮廓c定义为由n个点组成的一条封闭曲线c=[a1, a2, …, an]; 图元e定义为由m个有限轮廓组成的复合轮廓e=[ f1, f2, …, fm]; 构型k定义为有限个图形变换组合的布局规则 k=[λ1, λ2, …, λr]; 这里的变换包含但不限于基本图形的变换.

|
图 3 图案构型和相同图案在不同构型下的视觉观感 |
如图3(a)所示, 图中有9个纹样, 但图元却可以有很多种, 例如4个鱼纹可以看作1个图元, 1个鸟纹可以看作1个图元, 4个鸟纹可以看作1个图元, 1个铜鼓纹也可以看作1个图元. 图元是图案组成的基本单元, 也是图形变换的最小对象. 为了更好地描述蜡染图案中纹样的层次关系, 提出一种基于蜡染图案的层次表达方法.
1.2 蜡染图案层次信息图元是图案的一部分, 一幅完整的蜡染图案是图元与图元间的相互作用, 和语义的深层次组合形成的一个有意义的整体. 将整幅蜡染图案表达为一种树状结构, 节点由有限个图元按照构型组合的子图案, 子图案u={e1, k1, e2, k2, …, en, kn}; 子图案u也可以是有限个子图案{uc1, uc2, …, ucn}, 按照构型组合为u={uc1, kc1, uc2, kc2, …, ucn, kcn}; 图元层次按照主要纹样(Z)、修饰纹样(X)、填充纹样(T)和边框纹样(B)进行划分, 蜡染图案的层次表达信息如表1所示.
| 表 1 蜡染图案的层次表达信息表 |
2 图案与构型规则提取 2.1 蜡染图案提取 2.1.1 蜡染图像形态学预处理
本文通过图像采集设备获得蜡染图案的数字图像, 图像中纹样轮廓清晰可见. 然而, 由于织物结构和蜡染制作过程中产生的冰裂纹较为明显, 这些因素极大地干扰了蜡染图案轮廓提取, 因此有必要去除图像中的纹理.
(1)图像梯度计算
为了提高蜡染图案轮廓的边缘检出率, 使用形态学[12]梯度运算增强图像中得极值对比度, 同时保留图像中相对平滑的区域, 对于图像f (x, y), 梯度图像g (x, y)定义为:
| $ {\text{g}}\left( {x, y} \right) = f\left( {x, y} \right) \oplus b\left( {x, y} \right) - f\left( {x, y} \right)\Theta b\left( {x, y} \right) $ | (1) |
其中, ⊕为膨胀运算, Θ为腐蚀运算; 经过梯度计算后, 图像中的灰度过渡得到明显增强, 并消除了梯度对边缘方向的依赖性.
(2)形态学重建
为消除梯度图像中由于噪声造成的局部极值, 使用形态学中的开闭重构算法对梯度图像进行重构, 保留重要的轮廓极值信息. 通过开闭重构将图像中的纹理和噪声一并去除, 并在重建过程中恢复纹样轮廓, 在保持纹样形状信息的同时简化了图像. 形态学重建运算是在测地膨胀的基础上展开的, 因此对于梯度图像g (x, y)和参考图像f (x, y), 其形态学测地膨胀定义为:
| $ \left\{ {\begin{array}{*{20}{l}} {D_B^{i + 1}\left( {g, r} \right) = \min \left[ {\left( {D_B^i \oplus B} \right), r} \right]} \\ {D_B^i\left( {g, r} \right) = \min \left[ {\left( {{{g}} \oplus B} \right), r} \right]} \end{array}} \right., \left( {i = 1, 2, \cdots } \right) $ | (2) |
其中, B为盘形结构元, 盘形结构元具有旋转不变的特性, 因此不会造成图像特征值的失真. 形态学测地膨胀是一种迭代运算, 当迭代次数到达
| $ O_B^{\left( {{\rm{rec}}} \right)}\left( {g, r} \right) = D_B^{\left( {{\rm{rec}}} \right)}\left[ {g \circ B, r} \right] $ | (3) |
其中,
| $ \left\{\begin{array}{l} E_{B}^{j+1}(g, r)=\max \left[\left(E_{B}^{j} \Theta B\right), r\right] \\ E_{B}^{j}(g, r)=\max [({g} \Theta B), r] \end{array}, (j=1, 2, \cdots)\right. $ | (4) |
| $ C_B^{\left( {{\rm{rec}}} \right)}\left( {g, r} \right) = E_B^{\left( {{\rm{rec}}} \right)}\left[ {{{g}} \cdot B, r} \right] $ | (5) |
将形态学混合开闭重建运算
| $ {{g}}_B^{\left( {{\rm{rec}}} \right)} = C_B^{\left( {{\rm{rec}}} \right)}\left[ {O_B^{\left( {{\rm{rec}}} \right)}\left( {{\text{g}}, r} \right), r} \right] $ | (6) |
通过对蜡染数字图像进行闭运算、腐蚀、开运算等形态学处理, 不仅能有效去除图像中的纹理和噪声, 而且得到的二值图像也能清楚地反映图像中纹样的整体特征; 然后对蜡染图像进行阈值分割, 并转换成二值图像, 用于后续的边缘提取.
2.1.2 蜡染图案轮廓提取蜡染图案轮廓提取包括整体轮廓提取和元素轮廓提取. 轮廓也被称为边缘, 它包含了关于图像的大量信息, 也是图像的一个重要特征. 边缘是图像中灰度变化剧烈或在小范围内不连续的点的集合, 可以理解为两条灰度相对不同的边界线. 图像中的物体与背景在灰度或纹理上存在一定的差异, 边缘检测利用这种差异来提取目标和背景之间的边界线, 最终将目标与背景区分开来.
与传统的微分算子相比, Canny边缘检测算子因其抑噪比大、检测精度高的优点而得到了广泛的应用[13]. 使用Python-OpenCV模块中的Canny算子对经过形态学调整的蜡染图案元素进行提取, 提取结果见图4. 为后续重用设计提供数字素材. 本实验在Windows 10操作系统, Python 3.7和OpenCV 4.5.1环境下进行.

|
图 4 Canny算子提取效果 |
2.2 蜡染图案提取 2.2.1 用户交互手动提取规则
(1)选择子图案
用户根据对蜡染图案中纹样的视觉感知程度, 选取一个或多个蜡染纹样作为子图案; 由于不同用户对纹样的感知程度不同, 即使是同一幅蜡染图案也存在多种选择结果, 如表2所示.
(2)构造层次
用户对纹样进行选择判断, 若主要纹样Z中U1唯一存在, 则该纹样自身为父图案, 即可进行下一阶段纹样的选取; 若U1不是唯一存在, 则选取相似子图案; 通过用户选择结果构建自底向上的子图案层次表达模型.
(3)选择编码
用户根据选择结果对图元进行从左到右、从上到下依次标注.
(4)重复步骤(1)–(3), 用户将所有想要提取的子图案都编码完成后, 即可选择退出构型规则提取界面, 系统自动根据用户编码结果自动生成构型规则, 以结果一为例的构型规则如图5所示.
2.2.2 构型规则自动提取由于蜡染图案组成复杂, 有较多相似轮廓, 手动提取规则的话需要大量的时间和操作, 因此需要对蜡染轮廓进行分类. 轮廓分类从距离和相似两个维度来进行考虑. 相似轮廓往往存在旋转、阵列、对称等特征, 而距离则会产生集群感或有一定的特殊意义. 综上考虑, 自动提取主要有以下3个过程.
| 表 2 手动选取子图案的不同结果 |
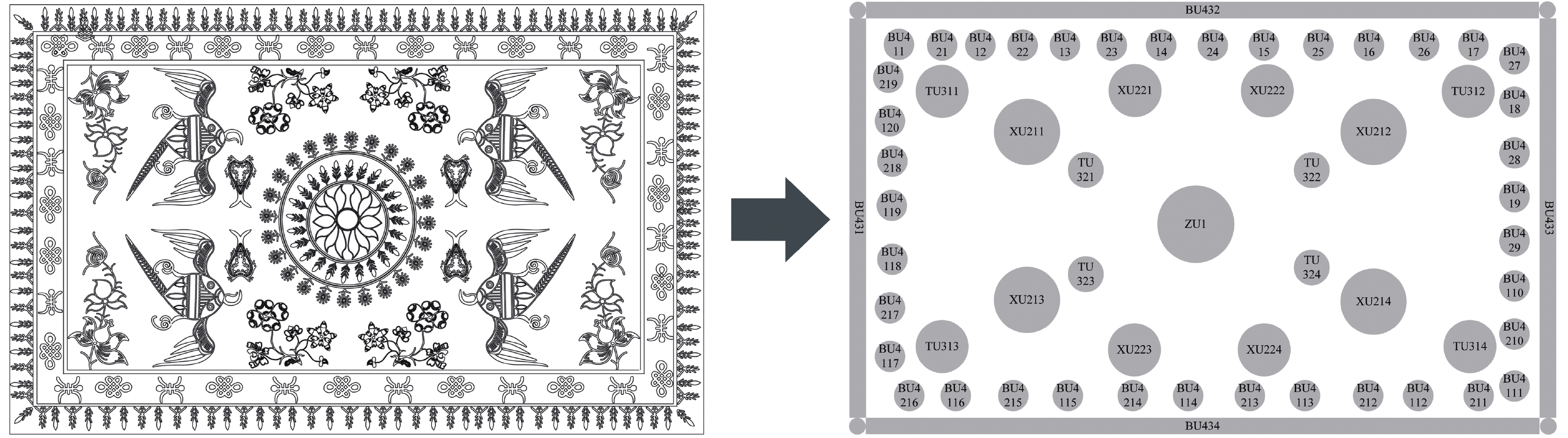
|
图 5 结果1的构型规则示例 |
1)基于Hu矩的相似性轮廓聚类
统计学中常用矩来统计随机变量的分布情况, HuMK在1962年提出, 将矩特征应用于图像处理中, 主要用来表征图像的几何特征, 又称为几何矩; 由于图像在进行旋转、缩放、平移等操作后, 仍能保持矩的不变性, 因此又称不变矩, 在该方法被广泛采用后用HuMK的名字来对其进行命名为Hu矩[14]. 本文利用Hu矩的不变特性来实现纹样轮廓的匹配分类. 对于轮廓A, 轮廓
| $ m_i^A = {{\rm{sign}}}\left( {h_i^A} \right){\text{log}}h_i^A $ | (7) |
| $ m_i^B = {{{\rm{sign}}}}\left( {h_i^B} \right){\text{log}}h_i^B $ | (8) |
A, B间的轮廓差异性计算函数公式为:
| $ I\left( {A, B} \right) = \mathop \sum \limits_{i = 1}^7 \left| {\frac{1}{{m_i^A}} - \frac{1}{{m_i^B}}} \right| $ | (9) |
经多次试验发现, 当I(A, B)<0.02时, 几乎可以识别所有相似轮廓. 将识别出的相似轮廓归入相似轮廓群, F=[f1, f2, f3, …, fn], 将不相似轮廓归入不相似轮廓群, D=[d1, d2, d3, …, dn], 聚类过程如图6所示.
2)凝聚层次聚类
不相似的轮廓大多数在空间位置上有一定的隐喻, 在视觉上构成子图案. 因此在面对不规则的图案时, 采用凝聚层次聚类(agglomerative nesting)算法对非相似类集群进行自底向上聚合策略的层次聚类轮廓分离, 由于集群中是形状, 因此使用边缘最小距离来衡量, 则轮廓Ci和轮廓Cj的最小边缘距离计算公式为:
| $ d_{\min }\left(C_{i}, C_{j}\right)=\min _{x \in C_{i}, {\textit{z}} \in C_{j}} {dist}(x, {\textit{z}}) $ | (10) |
使用凝聚层次聚类方法对不相似轮廓群D进行分类, 得到J个集群轮廓类J1, J2, …, Jn, 和P个彼此独立轮廓类P1, P2, …, Pn. 经过凝聚层次聚类后将d1的内圈与外圈分离开来, 将聚类结果构造层次表达模型, 如图7所示.

|
图 6 基于Hu矩匹配的蜡染纹样相似性聚类 |
3)构型规则拓扑表达
使用Hu矩进行轮廓匹配时, 运用其中的一阶矩和零阶矩来计算纹样的中心坐标, 计算公式如下:
| $ M_{00}=\sum_{I} \sum_{J} V(i, j) $ | (11) |
| $ M_{10}=\sum_{I} \sum_{J} i{ \times }(i, j) $ | (12) |
| $ M_{01}=\sum_{I} \sum_{J} j{ \times } V(i, j) $ | (13) |
| $ i_{c}=\frac{M_{10}}{M_{00}}, j_{c}=\frac{M_{01}}{M_{00}} $ | (14) |
| $ i_{c}=\frac{M_{10}}{M_{00}}, j_{c}=\frac{M_{01}}{M_{00}} $ | (15) |
其中, M00 是零阶矩, M10 、M01 是一阶矩, ic 和 jc是图像的中心坐标. 将每个子图案的中心点抽象成在图案中的坐标点, 按照空间位置将每个点连接, 构建子图案的邻域关系图, 这些点与线的拓扑关系称为构型规则. 蜡染图案中子图案U的总个数集合为U={U1, U2, …, Ue}, 其中e为不同纹样的总个数; 例如图中某个子图案Ue={Ue1, Ue2, …, Uef }, f为该子图案在该图案中出现的次数. 根据上述规则在蜡染图案中从左往右依次对图案进行标注, 如图8所示; 基于上述方法进行构型规则大量提取, 构建构型规则库, 以便后续设计服务.

|
图 7 非相似类图案层次表达模型 |

|
图 8 纹样位置分布及拓扑结构表达 |
3 基于构型规则重用的蜡染图案创新设计 3.1 蜡染纹样表征与数字资源库建设 3.1.1 蜡染知识收集
本文的知识来源于各个方面, 例如文献书籍查阅、田野走访等, 其中最主要的来源于贵州省民间蜡染的制作者、使用者、研究者等多方面专家提供的知识和经验. 通过大量的资料收集与梳理, 对贵州省蜡染知识进行分类, 分类概念表如图9(a)所示; 并将收集的蜡染图片进行编码保存便于后期调用, 见图9(b)所示.
苗族蜡染的图案内容不仅是对所选题材的表示, 更是透过所选题材展示其中的内涵与本质. 蜡染图案是对生活现象、历史文化和生活环境的反映, 苗家人往往通过图案的单一或是组合来表达更深层次的内涵. “图必有意, 图必吉祥”, 他们把对生活事物的观察和美好生活的向往呈现在蜡染图案中, 从某种意义来说, 图案是蜡染艺术的灵魂; 常见纹样语义归类如表3所示.

|
图 9 蜡染知识分类概念表及蜡染图片编码方式 |
| 表 3 纹样语义归类表 |
3.1.2 蜡染纹样表征与数字资源库建设
可拓学[15]采用形式化语言表达事、物、关系和问题, 建立了以基元(物元、事元和关系元)为可拓学逻辑细胞的形式化模型. 基元概念把质与量统一在一个三元组中, 可以形式化描述物、事和关系即B=(O, C, V); 建立了形式化描述复杂事物和关系的复合元, 并利用它们描述事与物的问题、信息、知识和策略. 其中O为基元B的研究对象, C为特征, V为量值, 即可拓区间, 即c=[c1, c2, c3, …, cn]T对应的特征量值v=[v1, v2, v3, …, vn]T定义B的研究对象O的n维物元, 多维物元所构成的阵列表示如下:
| $ B=(O, C, V)=\left[\begin{array}{ccc} O & C_{1} & V_{1} \\ & C_{2} & V_{2} \\ & \vdots & \vdots \\ & C_{n} & V_{n} \end{array}\right]=\left[\begin{array}{c} R_{1} \\ R_{2} \\ \vdots \\ R_{n} \end{array}\right] $ | (16) |
为实现对蜡染纹样的计算机识别与复杂图形设计, 本文使用可拓学的基元方法, 对蜡染纹样进行表征. 以矢量纹样为对象载体, 以文化语义(历史、文化、采集地、创作人、风格等)、量化信息、可视化图形、编码信息等为特征量, 进行可拓基元形式化与量化表征. 根据基元理论, 将上述知识抽象为物元、事元与关系元, 把对象、特征以及量值放置在一个整体中进行考虑, 其基元表达式为:
| $ B=\left[\begin{array}{ccc}蜡染纹样& 特征1& {V}_{1}\\ & 特征2& {V}_{2}\\ & 特征3& {V}_{3}\end{array}\right]=\left[\begin{array}{c}{R}_{1}\\ {R}_{2}\\ {R}_{3}\end{array}\right] $ | (17) |
通过对以上知识整理, 建立每个纹样的表征模型, 结合收集的蜡染图像构建数字资源库, 并从中选取部分代表纹样进行矢量化工作, 建立蜡染纹样矢量图库, 以便于为后续设计服务.
3.2 构型规则重用方法子图案在图案中的分布称为图案的构型, 将图案中的构型规则提取之后, 在拓扑节点上嵌入适合的纹样, 即可生成新的图案. 纹样的嵌入不是机械的置入, 而是语义更深层次的组合, 在艺术价值与语义内涵上可以创造更多的组合与选择. 构型规则重用步骤如下:
1)选择构型规则和子图案: 用户从规则库中选择要重用的构型规则, 如图10(a)中的构型规则R; 从纹样矢量图库中选择要嵌入的子图案, 如图10(a)中的子图案集A.
2)子图案嵌入: 把已选择的子图案, 按照主要纹样、修饰纹样、填充纹样和边框纹样的层次信息, 嵌入到构型规则拓扑节点上.
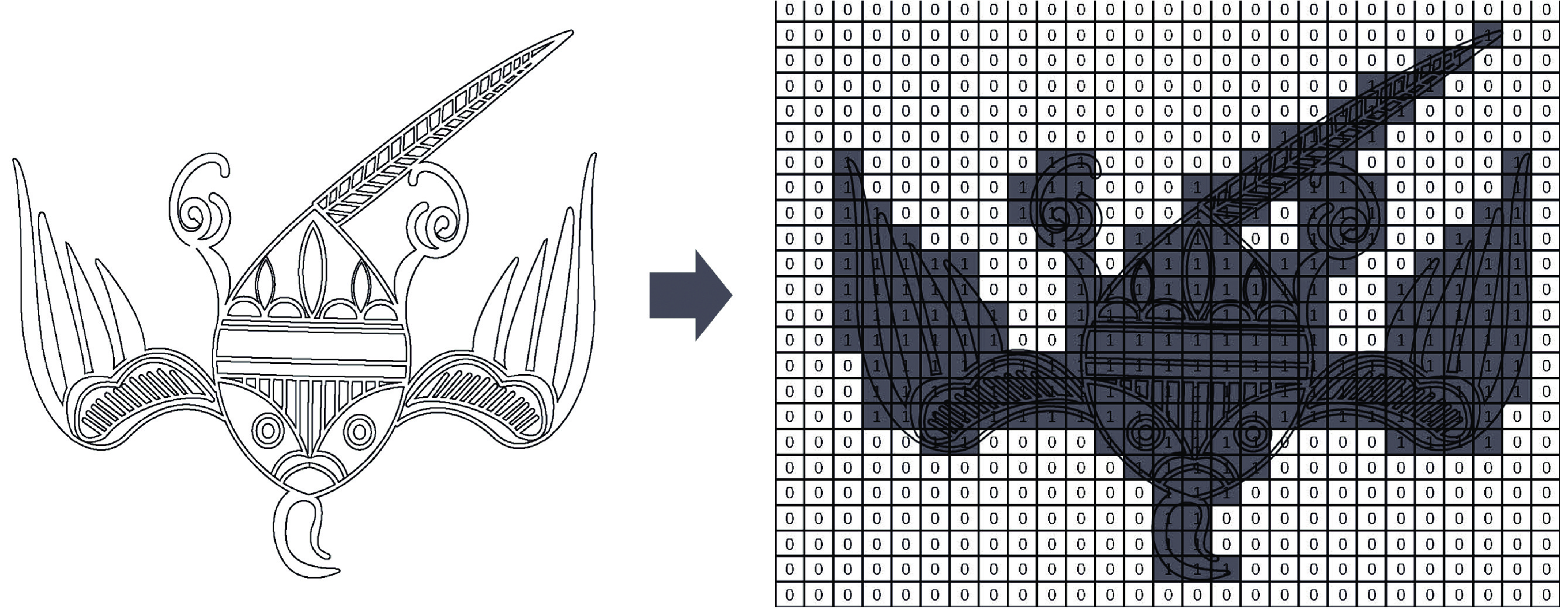
3)消除重叠: 子图案在嵌入过程中, 由于拓扑结构的空间位置会出现纹样重叠的情况, 本文提出一种基于标识矩阵法的子图案嵌入方法来解决纹样的重叠情况. 首先建立一个初始值为0的蜡染画布大小的标识矩阵, 当有图案嵌入时, 标识元素由0改为1, 基于标识矩阵法的纹样嵌入方法如图11所示.

|
图 10 纹样嵌入构型过程与相同纹样在同一构型中的嵌入结果 |
|
图 11 基于标识矩阵约束的图案嵌入 |
4)局部调整: 用户对嵌入结果进行局部调整, 直到满意为止.
构型规则嵌入子图案具体过程见图10(b), 构型规则R与子图案集A的嵌入结果如图10(c); 其他子图案在构型规则R中的嵌入结果如图12所示. 基于构型规则重用的设计方法, 可以快速生成大量保持蜡染图案布局特点和视觉特性的蜡染图案设计方案.
3.3 构建蜡染图案设计原型系统在Windows 10系统下搭建蜡染图案设计原型系统实现图案轮廓、图案构型提取和转移, 具有轮廓提取、构型规则提取、矢量图元库、蜡染数字资源库、规则库管理、蜡染图案生成与修改、资源上传等功能, 如图13所示.
用户可以在该系统自行选择中意的构型规则与纹样, 也可以根据自己期望的图案语义来进行纹样的深层次语义组合. 设计师可以在现有的资源库中选择适合的构型规则与纹样进行重新组合, 可以大幅提高设计效率.

|
图 12 子图案在构型规则R中的嵌入结果 |

|
图 13 蜡染图案定制系统部分界面 |
一位用户从规则库中选取偏好的构型规则, 从系统的纹样库中通过语义筛选出关于“幸福”“兴旺”的纹样元素, 随后进入详细定制界面, 如图14所示.

|
图 14 详细定制界面 |
4 总结与展望
针对蜡染图案的创新问题, 本文提出一种构型提取与重用的方法, 从构型和图元的定义出发对蜡染图案进行描述, 使用OpenCV计算机视觉库的相关函数和Python语言进行蜡染图案的轮廓提取与匹配, 根据轮廓中心位置构建邻域关系拓扑结构图, 然后使用标识矩阵法对纹样进行嵌入. 该方法在实现了蜡染图案的重用, 在一定程度上提高了蜡染图案的创新效率. 基于构型规则重用的图案创新设计方法可以为其他传统图案的创新提供一定的参考. 当前研究仅从蜡染图案的构型方向进行图案创新研究, 后续将在蜡染图案的其他方向进行创新研究, 并结合大数据技术提升蜡染图案创新设计效率.
| [1] |
王天凤. 苗族蜡染艺术研究——以贵州安顺地区为对象[硕士学位论文]. 昆明: 昆明理工大学, 2014.
|
| [2] |
Cui J, Tang MX. Integrating shape grammars into a generative system for Zhuang ethnic embroidery design exploration. Computer-Aided Design, 2013, 45(3): 591-604. DOI:10.1016/j.cad.2012.08.002 |
| [3] |
Muslimin R. Parametric, grammatical, and perceptual iterations on structural design synthesis. Artificial Intelligence for Engineering Design, Analysis and Manufacturing, 2018, 32(3): 269-281. DOI:10.1017/S0890060417000580 |
| [4] |
Nasri A, Benslimane R. Parametric shape grammar formalism for moorish geometric design analysis and generation. Journal on Computing and Cultural Heritage, 2017, 10(4): 19. |
| [5] |
Tian GD, Yuan QN, Hu T, et al. Auto-generation system based on fractal geometry for batik pattern design. Applied Sciences, 2019, 9(11): 2383. DOI:10.3390/app9112383 |
| [6] |
张欣蔚, 王进, 陆国栋, 等. 基于本体和形状文法的图案构形提取与重用. 浙江大学学报(工学版), 2018, 52(3): 461-472. DOI:10.3785/j.issn.1008-973X.2018.03.007 |
| [7] |
李华飙, 侯小刚, 王婷婷, 等. 基于规则学习的传统纹样统一生成模式研究. 浙江大学学报(理学版), 2020, 47(6): 669-676. |
| [8] |
章义来, 彭永康. 基于分形规则的陶瓷图案构图模型研究与应用. 陶瓷学报, 2014, 35(1): 71-77. DOI:10.3969/j.issn.1000-2278.2014.01.015 |
| [9] |
Strobbe T, Eloy S, Pauwels P, et al. A graph-theoretic implementation of the Rabo-de-Bacalhau transformation grammar. Artificial Intelligence for Engineering Design, Analysis and Manufacturing, 2016, 30(2): 138-158. DOI:10.1017/S0890060416000032 |
| [10] |
汪美谕. 苗族蜡染纹样艺术研究——以丹寨苗族地区为例[硕士学位论文]. 西安: 西安建筑科技大学, 2016.
|
| [11] |
张晓瑞, 程志刚, 白艳. 空间句法研究进展与展望. 地理与地理信息科学, 2014, 30(3): 82-87. |
| [12] |
Chen DL, Cheng PP. A method to extract batik fabric pattern and elements. The Journal of the Textile Institute, 2021, 112(7): 1093-1099. DOI:10.1080/00405000.2020.1802885 |
| [13] |
冯文倩, 李新荣, 杨帅. 人体轮廓机器视觉检测算法的研究进展. 纺织学报, 2021, 42(3): 190-196. |
| [14] |
李洪安, 杜卓明, 李占利, 等. 基于双特征匹配层融合的步态识别方法. 图学学报, 2019, 40(3): 441-446. |
| [15] |
杨春燕, 蔡文, 涂序彦. 可拓学的研究、应用与发展. 系统科学与数学, 2016, 36(9): 1507-1512. DOI:10.12341/jssms12905 |
 2022, Vol. 31
2022, Vol. 31