近年来, 智慧社区、智慧养老^[1]的理念在全国内被广泛研究, 社区快速发展建设, 绿化、公共设施、车辆等使得社区内结构越来越复杂, 当幼儿或老人独自进入危险区域或与家人失去联系时, 监护人很难第一时间获取他们的具体情况, 一种高效准确的定位措施便显得格外重要. 智慧社区与传统社区的区别在于其结合大数据、云计算等技术, 通过全分布的物联感知系统对居民的生活、工作、安全、健康等需求作出智能响应, 而不是通过简单的社区监控和物业人员进行管理^[2]. 获取社区人员的位置信息, 有助于对网络中突发事件进行事前预警、事中决策以及事后处理, 不仅能预测、及时感知用户的当前安全情况, 还可融合他们的出行频率、行为轨迹等信息预测出用户的行为习惯、喜爱偏好, 进而对社区的智能、智慧建设提供参考.

智慧定位方法同样需要通过数据融合方法来实现, 且大多定位方法是利用的无线射频识别(RFID)技术, 其通过电磁波进行通信, 利用基于测距的定位算法, 将传播过程中的信号值或信号接收角度等转换为信号传播的距离, 具有方便快捷、识别速度快等优点, 并且基于RFID的定位方案成本低、易部署, 故该类定位系统目前在国内外广泛研究, 如董长春等^[3]结合蚁群算法和正反馈机制对Chan算法进行改进, 提出了基于RFID技术的商品车无线定位方法, 可精准定位商品车的实际位置, 但该方法没有考虑到环境因素的影响. 陈龙鹏^[4]提出的以RFID融合计算机视觉的室内定位算法, 解决了因室内环境的障碍物干扰, 实时性差的问题, 通过计算机视觉定位显著提高了定位实时性, 但这种算法在非视距环境下的定位精度并不理想. 兰庆庆等^[5]结合了网格聚类算法和密度峰值聚类算法各自的特点设计了基于网格的密度峰值聚类算法, 通过获取最高密度的网格对象来确定簇心, 可处理大规模数据集并定位误差均值在0.128 m左右, 稳定性较高, 不足之处是该算法对动态标签作用不大, 仅作用于静态标签.

由于Kalman滤波在非视距环境中有一定的鲁棒性, 所以被广泛用于目标的跟踪定位中, 该理论假设跟踪过程是线性的, 而这也符合居民的运动特性. Yi 等^[6]为解决室内复杂环境下超宽带定位精度波动大、定位结果偏差等问题, 在数据后期引入自适应Kalman滤波方法, 并用AGV小车进行对比实验, 结果表明在测量数据缺失的情况下, 该方法可完成实时高精度室内定位. Suo 等^[7]针对WIFI定位中容错能力低、抗噪声能力弱等缺点, 提出一种基于Kalman滤波的WIFI室内定位方法, 得到RSSI值后, 通过Kalman滤波估计出最优距离, 然后通过三角质心法计算出最优距离, 算法效果较优. Ning^[8]研究了一种基于交互式多模Kalman滤波的无线定位方法, 解决了蜂窝网络中定位精度差的问题, 具有良好的定位性能和滤波性能.

本文首先确定了以RSSI值确认目标标签的坐标的方法, 针对RFID数据交换时计算量大, 过程噪声、观测噪声、环境因素等影响着测量坐标值的准确度等问题, 提出了改进的密度峰值聚类算法(DPC)和Kalman滤波相融合的定位方法, 结合Kalman滤波和DPC的优点, 将DPC聚类结果作为Kalman滤波的观测信号, 通过迭代得出最终轨迹, 最终实现社区内动态人员实时定位, 并通过实验进行了验证.

在社区内实现定位要求精度较高, 社区内部环境不同于外部, 社区内树木、公共设施、车辆等较多, 不利于定位, GPS精度往往不达标, 故采用RFID标签定位而不是GPS, 社区内的RFID感知网络与目标标签的信息交换即可确定用户的位置, 再调取该区域的监控能快速准确地获取用户的具体情况.

RFID阅读器的区域布置与标签的定位方法相关, 常用的基于测距的定位方法: 基于接受信号强度(RSSI)^[9]、基于信号传输时间(TOA)^[10]、基于信号传输时间差(TDOA)^[11]和基于信号到达角度(AOA)^[11]. 其中RSSI测距法无须增加硬件成本和严格的网络同步, 故应用较多^[12]. 为了减少成本, 使用较少的阅读器, 使得阅读器感应范围全覆盖社区区域, 本文使用结合接收信号的强度(RSSI)的方法, 借助社区内布置的参考标签确认目标标签的位置. RFID阅读器布置的原则就是感知范围对社区公共区域全覆盖, 再布置一些确定位置的参考标签形成定位网络.

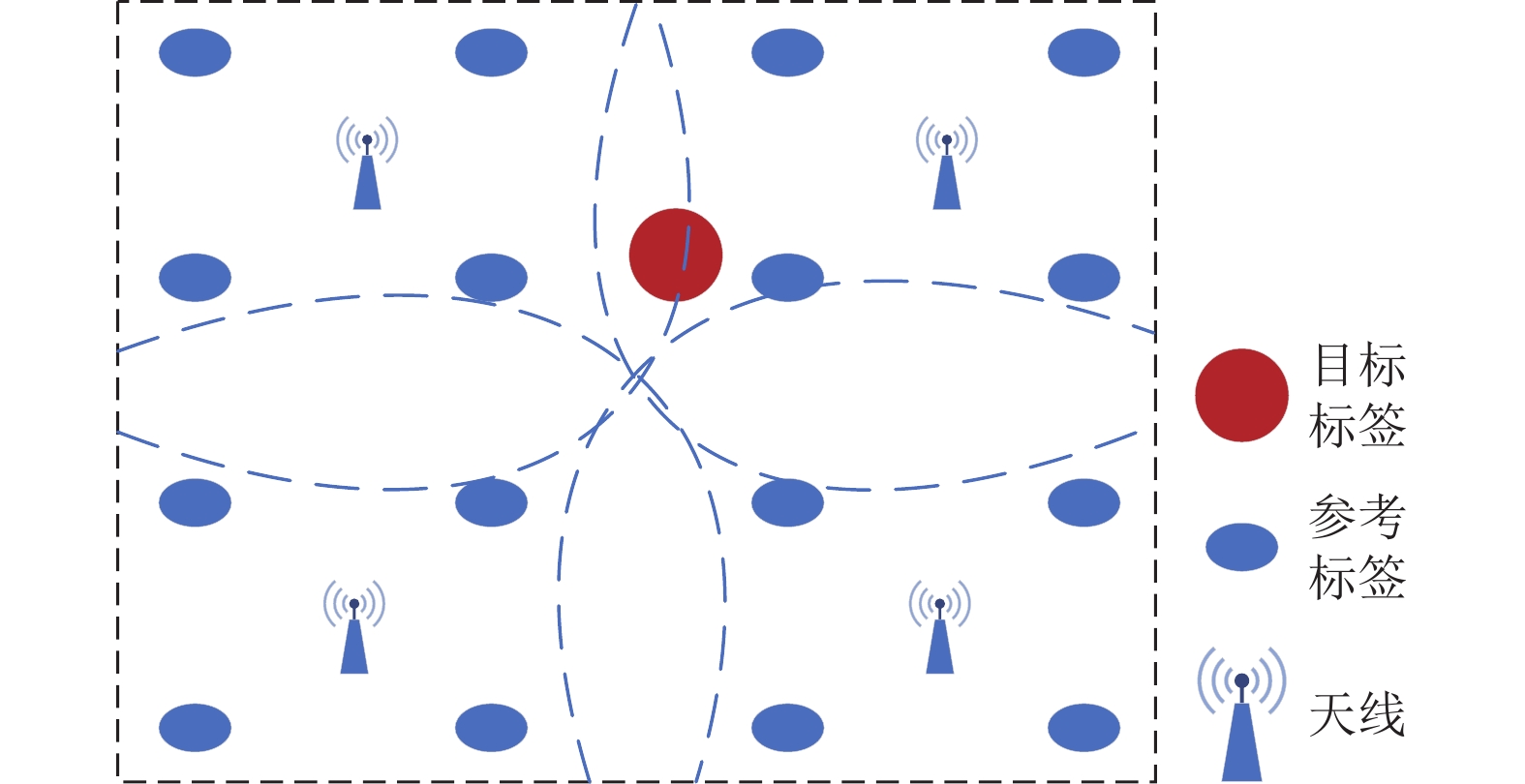
在如图1所示的数据采集网络中, 包括天线、参考标签和目标标签, 阅读器通过多个天线获取标签同一时刻的RSSI值. 当信号在社区内传输时, 其功率会根据距离产生一定的损耗, 通过传输损耗模型即可将信号强度转换为天线与标签的距离, 传输损耗模型如式(1)所示. 得出各天线与目标标签距离之后, 根据天线间的距离, 即可求出估计标签的坐标.

其中, d为天线到标签的实际距离, ${{R}}(d)$ 为距离为d时天线接收到的信号强度值, $R({d_o})$ 为某一确定距离 ${d_o}$ 下天线接收到的信号强度值, n是当前环境下的传输损耗因子, ${N_o}$ 与环境相关, 是一个满足均值为0, 标准差为 $\sigma $ 的高斯分布的随机变量.

图 1

Fig. 1

图 1 数据采集网络

在实际系统中, 由于障碍物、物体形态不规则、人或物体的移动等因素导致信号在传播过程中存在着反射、折射、多径传播等现象, 导致采集到的信号强度具有很大的不确定性^[13]. 存在当目标位置固定时, 获取的RSSI值分布情况不集中甚至分散, 造成同一个RSSl值可能对应多个通信距离, 最终计算出不同的坐标值. 故本文提出一种结合IDPC的Kalman滤波定位方法(K-IDPC), 将DPC和Kalman滤波的优点相结合以解决上述问题.

通过聚类算法实现静态目标的定位, DPC算法^[14]全称为基于快速搜索和发现密度峰值的聚类算法, 该算法能够快速发现多数据点的簇中心, 无须提前设置簇的数量和参数, 可实现任意形状数据的高效聚类.

DPC的基本思想是计算任意两个数据点间的距离, 根据截断距离计算出数据点的局部密度 $\;{\rho _i}$ 和相对距离 ${\delta _i}$ ( $\;{\rho _{\text{i}}}$ 为节点间距离小于截断距离的节点个数, ${\delta _i}$ 为数据点到局部密度比他大且距离近的另一数据点间的欧式距离). 再绘制出聚类决策图, 将局部密度和相对距离值较高的点标记为聚类中心, 而局部密度较小和相对距离较高的点标记为噪声点, 最后分配其余数据点到相应的簇并剔除噪声点, 最后的结果使得聚类中心的局部密度大于该簇内所有其余数据点的局部密度, 如图2(a)为实验过程中初始状态时的数据点的散点图, 大多数据在(100 m, 100 m)附近, 图2(b)为以这些数据点的局部密度和相对距离绘制出的决策图, 图中偏右上的数据点为簇心, 偏左上的数据点为噪声点, 簇心已在图中标出.

图 2

Fig. 2

图 2 IDPC决策结果示例

由于RFID定位系统交换数据量不大, 频率在每秒60–90次, 相对于DPC其他案例相比数据集较小. 而改进的DPC算法(improved-DPC, IDPC)针对DPC处理小数据集时聚类效果差的问题, 提出了新的局部密度计算公式, 使用高斯核定义样本数据点的局部密度^[15], 如式(2)、式(3)所示为改进的局部密度和相对距离的计算公式.

其中, ${d_{ij}}$ 为数据点 ${x_i}$ 与 ${x_j}$ 之间的距离, ${d_c}$ 为横断距离.

除了环境影响数据精度外, 当阅读器与标签数据交换时, 由于设备的原因会产生观测噪声和过程噪声, 最终导致阅读器收到的数据不够准确, 卡尔曼滤波(Kalman filter)^[12]是根据上一状态的预测值和当前状态的观测值预测运动系统当前状态, 可以通过多次预测修正来校正目标位置并感知噪声的统计特性, 故经常用来降低设备的观测噪声和过程噪声.

本文设计的K-IDPC即结合DPC算法的Kalman滤波定位, 首先将某时间段内的数据分为若干份(以1 min内RFID天线与标签交换数据约4200次为例, 将数据按时序排列后分为60份, 每份约70个数据值, 因为阅读器的数据传输速率在每秒1600字节左右), 每份的数据代表目标在同一时刻的位置. 然后计算两两数据间的相对距离, 根据相对距离计算出每个数据点的局部密度, 以局部密度和相对距离为横纵坐标绘制决策图并找出每份数据的簇心, 最后将这一系列的簇心值作为Kalman滤波的观测值z. 图3为Kalman滤波部分的原理图.

图 3

Fig. 3

图 3 Kalman滤波原理

本章通过实验来验证K-IDPC的效果, 实验前提是社区内的居民会佩戴封装有RFID目标标签的装置, 如手环、门禁卡等, 当需要对某位居民定位跟踪时, 首先获取该标签最近时间内在社区公共设施或建筑的通行记录, 以该设施的位置作为参考, 确定接收数据的天线和阅读器, 减少搜索范围.

具体实验在作者所在学校某一路段进行并获取相关数据, 该路段途径图书馆、教学楼、若干停车位等设施, 实验时将目标标签佩戴于被测者身上, 阅读器以及参考标签按图1所示布置, 通过天线增益后超高频阅读器读取范围为30 m左右, 被测者的移动范围在阅读器感知范围之内, 并安排行人与车辆经过. 本实验中存在对信号值的影响因素有: 图书馆和教学楼内任何可发射电磁波的小型设施, 如门禁、PC、广播系统; 来往车辆与行人的电子产品; 以及阅读器间的相互干扰等.

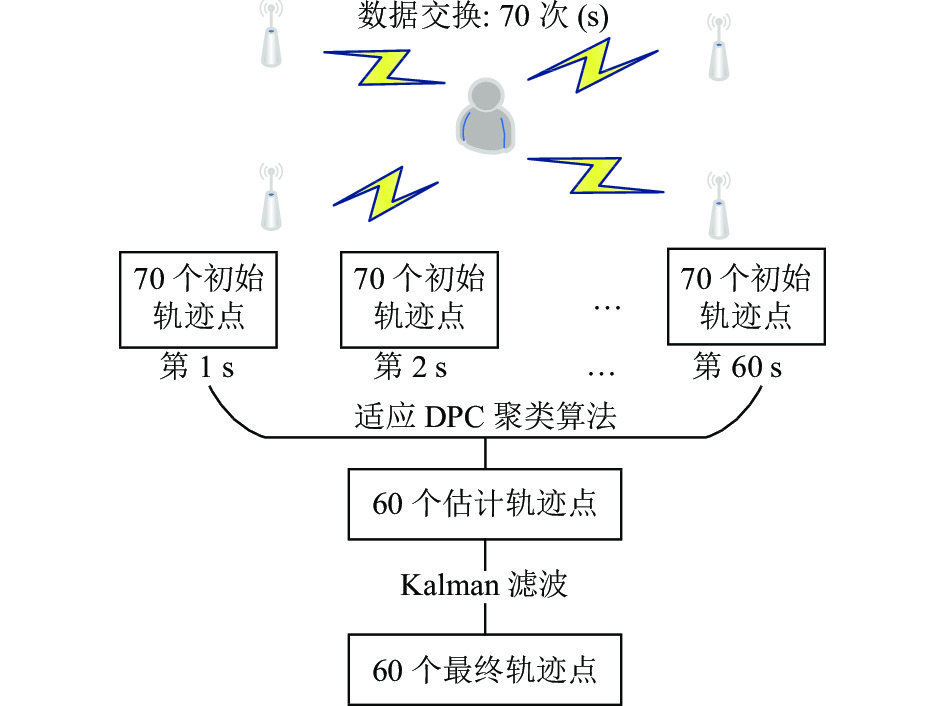
实验设定目标标签以匀速移动, 阅读器与目标标签传输数据率为11 KB/s, 即1375 B/s, 数据内容包括标签名、时间、信号值约20个字节, 亦即每秒传输约70次数据, 通过RSSI计算出受环境和观测噪声影响的估计标签初始轨迹点, 通过IDPC算法消除环境影响得出聚类中心点. 而后经过60次实验得出一分钟内目标标签的估计轨迹点, 再通过Kalman滤波消除观测噪声和过程噪声的影响, 得出目标标签的最终轨迹点, 图4为实验验证过程.

图 4

Fig. 4

图 4 实验过程

首先设置参数, 设置初始居民的位置坐标为(100 m, 100 m), 并以(0.75 m/s, 0.75 m/s)的正常速度匀速直线前进, 计算初始轨迹点坐标和相对距离后作升序排列, 设置10%处的距离值为横断距离, 通过决策图筛选出的估计轨迹点如图5中观测轨迹所示, 初始位置(100 m, 100 m)到最终位置(145 m, 145 m)的轨迹点大致为匀速直线运动, 但误差依旧很大. 而后进行Kalman滤波, 设置状态预测过程存在均值为0、方差为 $4 \times {{\text{e}}^{ - 4}}$ 的正态扰动, 观测过程存在均值为0、方差为2的正态扰动, 滤波后的定位结果如图5中滤波轨迹所示.

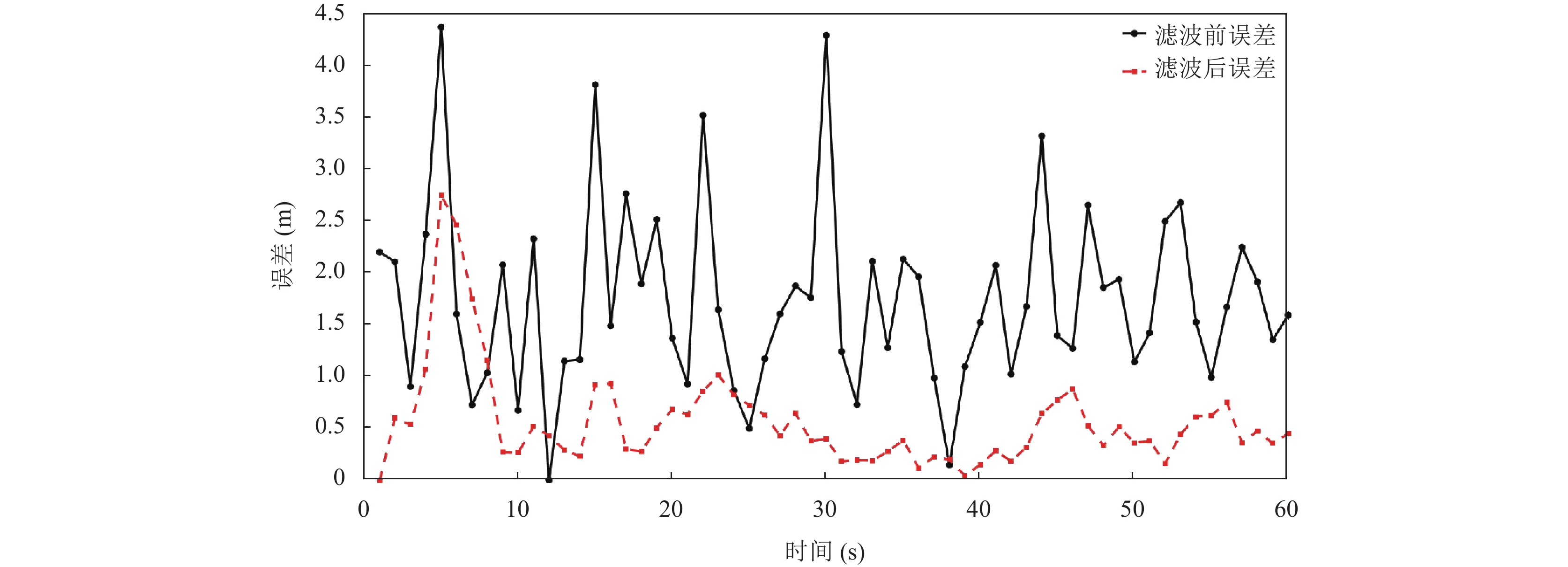
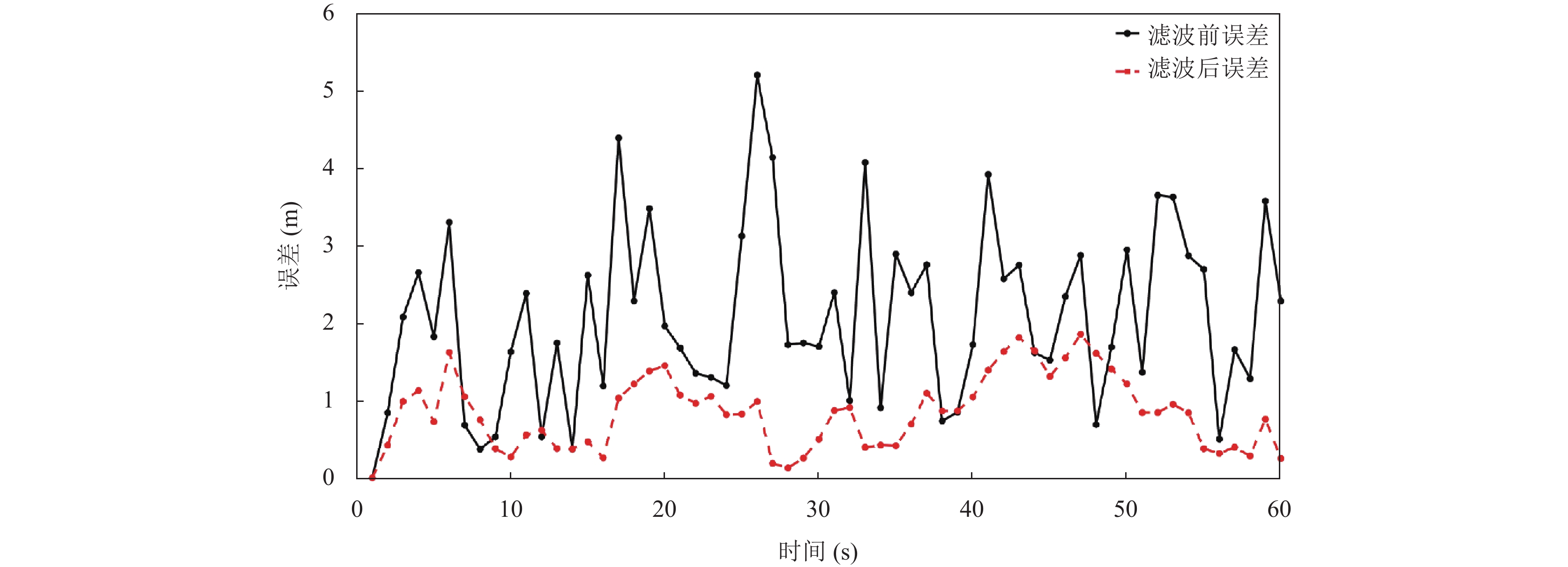
本文以定位误差作为衡量标准, 即每秒时定位点与真实点的欧氏距离, K-IDPC与Kalman滤波定位的误差如图6和图7虚线所示, 实线为滤波前的误差, 使用K-IDPC定位平均误差为0.565 m, Kalman滤波定位的平均误差为0.842 m, 精度提高了约49%, 定位稳定性大幅提高.

作为智慧社区建设的重要部分, 智慧定位使得居民在社区内的位置随时被获取, 并可及时处理紧急情况. 除此之外, 通过居民的行为轨迹还可分析得到用户的行为习惯、喜爱偏好等行为特征. 实验时发现, 当数据点较多且噪声较大时, Kalman滤波效果会大幅减弱, 在定位后期会出现误差逐渐增大, 即滤波轨迹偏离真实轨迹的情况, 故将目标轨迹的观测值使用DPC算法处理以减少数据点数量, 增大观测数据与原轨迹的拟合度. Kalman滤波与DPC算法的融合, 将前者对白噪声和观测噪声的处理能力、后者对复杂环境噪声的消除能力相结合, 实现了对目标的动态实时定位. 通过本文定位方法和Kalman滤波定位误差结果可看出, K-IDPC定位精度比Kalman定位提高了约49%, 定位误差控制在了0.5 m左右, 具有更好的稳定性.

图 5

Fig. 5

图 5 K-IDPC轨迹定位结果

图 6

Fig. 6

图 6 K-IDPC定位误差图

图 7

Fig. 7

图 7 Kalman滤波定位误差图