聚类是一种无监督学习方法, 它基于给定的相似性评价措施将数据集划分成若干簇, 使得在同一个簇中的对象彼此具有高相似性, 处于不同簇中的对象具有低相似性^[1]. 聚类被广泛应用在许多领域, 如机器学习、模式识别等^[2]. 对于传统的聚类算法, 属性值的缺失导致部分实例之间的距离无法有效的度量, 所以不能直接应用到不完整的数据集上. 因此, 在不完整数据集上的聚类研究是非常有意义的.

目前针对不完整数据的处理, 主要采用以下方法: (1) 在聚类之前直接删除包含缺失值的实例, 尽管它很简单, 但是当缺失比例较小时, 删除是非常有效的方法^[3]. (2) 对缺失的数据集进行填充, 通过填充的方式获取完整的数据集, 然后使用传统聚类算法进行聚类分析, 算法的性能往往受限于预估填充值的准确性^[4]. (3) 在聚类过程中采用非填充的方式, 在聚类之前没有对缺失部分进行填充处理, 而是在不完整状态下减少缺失值对聚类过程的影响. 如利用数据包含的背景知识, 通过在实例之间添加少量“软约束”^[5]引导包含缺失值的实例进行簇的划分, 减少数据填充过程中不可靠的填充值对聚类的影响.

针对不同的问题, 研究人员提出了多种结合不完整数据的聚类算法. 文献[6]提出一种删除策略, 当数据集缺失比例较小时, 一般小于10%, 直接将包含缺失值的实例删除, 数据缺失比例较小时, 对于最终的聚类分析结果不会产生较大的影响. 文献[7] 提出K-Pod算法, 采用迭代填充的方式处理不完整数据, 填充的过程中使用期望最大化算法(expectation maximization)预估缺失属性值, 每一次迭代过程中使用K-means对填充后的实例进行标记, 直到算法收敛, 但是迭代过程中重复使用K-means方法进行更新, 消耗了大量时间. 文献[5]提出SLIM算法, 在聚类过程中添加基于距离的成对约束, 引导包含缺失值的实例进行簇的划分. 文献[8]提出k_m-means算法, 该算法将缺失值的处理结合到聚类过程中, 通过调整局部距离计算方式, 减少实例中缺失值对目标函数的影响.

k_m-means是对K-means的扩展, 仍然受到K-means算法固有缺陷的限制^[9]. 该算法采用K-means++^[10]的初始化方式获取k个聚类中心, 使得中心之间距离尽可能的大. 由于缺失值的存在, 导致聚类中心的可靠性存在较大的不确定性. 主要表现在两方面: 直接不确定性和间接不确定性. 初始化过程中选择的聚类中心, 在标记阶段引导簇的划分起到十分关键的作用, 所以增大初始化阶段选取聚类中心的可靠性研究具有重要意义.

可信度来源于He在EKM算法^[11]中, 描述成对约束在簇划分过程中的满足度, 即某个簇中, 实例的划分结果满足成对约束的个数占成对约束总个数的比例. EKM算法中认为满足度高, 则该簇可信度高; 满足度低, 则该簇的可信度低. 因此, 受He工作的启发, 为了描述不完整数据集中实例之间距离的可信度, 结合实例的完整性, 本文将实例中属性值的完整性称为实例可信度, 实例中缺失值的比例越小, 则计算出的局部距离可信度的越高; 反之, 实例中缺失值比例越高, 则计算出的局部距离可信度的越低.

为了解决k_m-means初始化阶段选取聚类中心的可靠性问题, 本文在初始化过程中引入可信度, 通过可信度调整距离的计算, 减小选取聚类中心的直接不确定性, 增大初始化完成后选取聚类中心的可靠性, 使得聚类中心能够更好地引导标记阶段的簇划分. 本文第1节介绍不完整数据的缺失机制和符号定义, 第2节介绍k_m-means算法, 第3节介绍改进的k_m-means算法, 第4节先对初始化阶段选取聚类中心的可靠性问题进行实验与分析说明, 然后对改进后的k_m-means进行实验并分析结果, 第5节对所做的工作进行总结.

1 不完整数据集 1.1 不完整数据的缺失机制

不完整数据的缺失机制^[12]有3种不同的类型. 完全随机缺失, 是指缺失部分独立于本身, 与数据集的其他属性无关; 随机缺失, 是指缺失部分独立于本身, 与数据集中其他属性有关; 非随机不可忽略缺失, 是指缺失部分与本身有关, 与数据集中的其他属性也有关. 完全随机缺失和随机缺失被称作可忽略缺失, 目前处理不完整数据集主要针对可忽略缺失.

1.2 符号定义

现有文献中有许多关于缺失度(missing rate) ^{[12, 13]}的定义. 本文采用属性值缺失度和实例缺失度, 从不同维度描述缺失程度. 属性值缺失度衡量数据集中缺失的属性值比例, 实例缺失度衡量含有缺失属性值的实例比例.

设数据集 $D = \{ {X_1}, {X_2}, \cdots, {X_n}\} \in {R^{n \times p}}$ , n是数据集D的规模, p是属性个数. ${X_i}$ 的部分属性值可能会出现缺失, 用?表示缺失值. 假设 $Y = \{ {Y_1}, {Y_2}, \cdots, {Y_n}\} $ 是一个p维的缺省信息矩阵, ${Y_i}$ 的第j个属性 ${Y_{ij}} = I({X_{ij}}\; {\rm{ is\; recorded}})$ , ${X_{ij}}$ 是 ${X_i}$ 的第j个属性, $I( \cdot )$ 是一个指示函数, 当自变量为真时为1, 否则为0.

定义1. 属性值缺失度(value missing rate, VMR).设D中属性值出现缺失的个数为 ${n_v} = \displaystyle\sum\nolimits_{i = 1}^n {\displaystyle\sum\nolimits_{j = 1}^p {(1 - {Y_{ij}})} }$ , 则数据集D的属性值缺失度为 $VMR = {{{n_v}} \mathord{\left/ {\vphantom {{{n_v}} {np}}} \right. } {np}}$ .

定义2. 实例缺失度(instance missing rate, IMR).设D中含有缺失属性值的实例个数为 ${n_i}$ , 则数据集D的实例缺失度为 $IMR = {{{n_i}} \mathord{\left/ {\vphantom {{{n_i}} n}} \right. } n}$ .

在不完整数据集中, 属性值缺失度和实例缺失度描述数据集的整体缺失程度.

2 k_m-means算法简介

k_m-means算法又被称为结合不完整数据集处理的K-means类型算法, 在Hartigan等人^[14]提出的K-means算法框架基础上改进, 使其能够高效的结合缺失值的处理. 该算法的主要思想是: 通过修正实例与聚类中心之间的相似性度量方式, 将缺失值的处理结合到算法中, 减少实例中的缺失值对目标函数的影响, 使得算法准确度有不错的提升.

给定数据集 $D = \{ {X_1}, {X_2}, \cdots, {X_n}\} \in {R^{n \times p}}$ . 假设K是已知的, 算法的目标寻找划分集 $C = \{ {C_1}, {C_2}, \cdots, {C_K}\} $ 和聚类中心 $\;\mu {\text{ = \{ }}{\mu _1}{\text{, }}{\mu _2}{\text{, }}\cdots{\text{, }}{\mu _K}{\text{\} }}$ , 优化目标是使得每个实例到它所在聚类中心的距离总和最小, 优化目标函数如式(1):

$ {W_\kappa } = \sum\nolimits_{k = 1}^K {\sum\nolimits_{i = 1}^n {\sum\nolimits_{j = 1}^p {I\left( {{X_i} \in {C_k}} \right)} } } {Y_{ij}}{\left( {{X_{ij}} - {{\hat \mu }_{kj}}} \right)^2} $

(1)

对于每一个划分集合C, 聚类中心的更新如式(2):

$ {\hat \mu _{kj}} = \frac{{\displaystyle\sum\nolimits_{i = 1}^n {I\left( {{X_i} \in {C_k}} \right){Y_{ij}}{X_{ij}}} }}{{\displaystyle\sum\nolimits_{i = 1}^n {I\left( {{X_i} \in {C_k}} \right){Y_{ij}}} }} $

(2)

实例 ${X_i}$ 和聚类中心 $ \;{\hat \mu _k} $ 之间的距离可表示为式(3):

$ \delta _{i, {C_k}}^2 = {\left\| {{X_i} - {{\hat \mu }_{\text{k}}}} \right\|^2}{\text{ = }}\sum\nolimits_{j = 1}^p {{Y_{ij}}} {\left( {{X_{ij}} - {{\hat \mu }_{kj}}} \right)^2} $

(3)

k_m-means在不完整数据集上对实例标记时依赖于指标 $\Delta _{k, i}^ - $ 和 $\Delta _{l, i}^ + $ , 分别表示将 ${X_i}$ 从簇 ${C_k}$ 中移除WSS (within-cluster sum of squares)的减少值和将 ${X_i}$ 加入簇 ${C_l}$ 中WSS的增加值, 其中 $\Delta _{k, i}^ - $ 和 $\Delta _{l, i}^ + $ 的计算如式(4)和式(5)所示:

$ \Delta _{k, i}^ - = \sum\nolimits_{j = 1}^p {\frac{{{n_{kj}}}}{{{n_{kj}} - {Y_{ij}}}}} \delta _{i, {C_{_k}}}^2 $

(4)

$ \Delta _{l, i}^{\text{ + }} = \sum\nolimits_{j = 1}^p {\frac{{{n_{lj}}}}{{{n_{lj}} + {Y_{ij}}}}} \delta _{i, {C_l}}^2 $

(5)

其中, ${n_{kj}} = \displaystyle\sum\nolimits_{i = 1}^n {I({X_i} \in {C_k})} {Y_{ij}}$ , ${n_{kj}}$ 表示簇 ${C_k}$ 的所有实例中第j个属性值未缺失的个数. 同时k_m-means算法引入辅助向量 $\xi _i^{(t)}$ (t表示迭代次数), 表示实例 ${X_i}$ 到所有聚类中心的最短距离时, 对应的簇索引, 具体计算如式(6):

$ \xi _{\text{i}}^{\left( t \right)} = \arg {\mathop {\min }\nolimits_{1 \leqslant k \leqslant K}}\delta _{i, {C_k}}^2 $

(6)

k_m-means类似于K-means的思想, 首先通过算法2初始化得到K个聚类中心, 使用式(6)对实例的所属簇进行初始化标记, 然后比较将 ${X_i}$ 移除簇 ${C_k}$ 和加入簇 ${C_l}$ 后对 ${W_\kappa }$ 的贡献度大小, 分别用 $\Delta _{k, i}^ - $ 和 $\Delta _{l, i}^ + $ 表示, 确定 ${X_i}$ 应该归属于那个簇使得目标函数(式(1))最小, 每次迭代完n个实例后, 再通过式(2)更新聚类中心, 如此循环直到最后聚类中心不再改变, 算法终止. 其中, 活动集 $L$ 表示上一次迭代过程发生变化的簇, 结合不完整数据集的聚类中心初始化过程本文将在算法2中讨论, k_m-means算法框架如算法1所示.

算法1. k_m-means算法

输入: 数据集D, 聚类数K

输出: 聚类簇的划分 $\scriptstyle C = \{ {C_1}, {C_2}, \cdots, {C_K}\}$ , 聚类中心 $\scriptstyle\;\mu {\text{=\{}}{\mu _1}{\text{, }}{\mu _2}{\text{, }}\cdots{\text{, }}{\mu _K}{\text{\} }}$

1)采用算法2初始化得到K个簇中心, $\scriptstyle\{ \hat \mu _k^{(0)};k = 1, 2, \cdots, K\}$

2)采用式(6)初始化每一个实例的所属簇, $\scriptstyle {\xi ^{(0)}} = \{ \xi _1^{(0)}, \xi _2^{(0)}, \cdots, \xi _n^{(0)}\}$

3)初始化活动集 $\scriptstyle{\cal{L}} = \{ 1, 2, \cdots, K\}$ 和迭代次数 $\scriptstyle t = 0$

4) while $\scriptstyle {\cal{L}} \ne \varnothing$ do

5) for each $\scriptstyle {X_i} \in D$

6) 获取距离 $\scriptstyle{X_i}$ 最近的簇 $\scriptstyle k = \xi _i^{(t)}$ , 采用式(4)计算 $\scriptstyle \Delta _{k, i}^ -$ . // t表示迭代次数

7) if $\scriptstyle k \in {\cal{L}}$

8) 计算 $\scriptstyle l = \arg {\min _{b \ne k}}\Delta _{b, i}^ +$

9) else

10) 计算 $\scriptstyle l = \arg {\min _{b \in L}}\Delta _{b, i}^ +$

11) if $\scriptstyle \Delta _{l, i}^ + < \Delta _{k, i}^ -$

12) 将 $\scriptstyle {X_i}$ 从 $\scriptstyle {C_k}$ 移入 $\scriptstyle {C_l}$ , 更新 $\scriptstyle \xi _i^{(t + 1)} = l$

13) 采用式(2)更新聚类中心 $\scriptstyle \hat \mu _k^{(t + 1)}$ 和 $\scriptstyle \hat \mu _l^{(t + 1)}$ , 并将 $\scriptstyle k$ 和 $\scriptstyle l$ 放入 $\scriptstyle {\cal{L}}$ 中

14) else

15) $\scriptstyle {X_i}$ 仍属于 $\scriptstyle {C_k}$ , 设置 $\scriptstyle \xi _i^{(t + 1)} = \xi _i^{(t)}$

16) end for

17) 从 $\scriptstyle {\cal{L}}$ 中移除本轮迭代过程中没有更新的簇索引, 更新迭代次数t=t+1

18) end while

步骤(8)和步骤(10)中的 $\Delta _{b, i}^ + $ 采用式(5)计算得出. 下面我们将讨论结合不完整数据集的聚类中心初始化过程, 本文将k_m-means算法中初始化聚类中心的部分称作KMIWMD (K-means++ initialization with missing data)具体流程如算法2所示.

算法2. KMIWMD算法

输入: 数据集D, 聚类数量K

输出: K个聚类中心

1) $\scriptstyle \;\mu \leftarrow$ 随机选取 $\scriptstyle \;{\hat \mu _1}{\text{ = }}{X_i}$ 作为第1个聚类中心

2) while $\scriptstyle |\mu | < K$ do // |·|表示集合的个数

3) 计算概率 $\scriptstyle pr{o_i} = {{d_i^2} / {\sum\nolimits_{y = 1}^n {d_y^2} }}, \; i \in \{ 1, 2, \; \cdots, \; n\}$

4) 通过概率 $\scriptstyle pr{o_i}$ 选取第k个(k=2, 3, …, K)聚类中心 $\scriptstyle{\hat \mu _k}$

5) $\scriptstyle\;\mu \leftarrow \mu \cup {\hat \mu _k}$

6) end while

步骤(3)中 $d_i^2 = {{\min}_{l = 1, 2, \cdots, k - 1}}\tilde d_{i, {C_l}}^2$ , $ \tilde d_{i, {C_l}}^2 $ 通过式(7)计算. KMIWMD初始化聚类中心的过程中使用K-means++的框架, 在实例之间的距离计算中结合了缺失值的处理. 在结合缺失值的处理的过程中, 重新定义了初始化聚类中心过程中距离的计算方式, 如式(7)所示:

$ {{\tilde {{d}}}}_{i, {{\text{C}}_k}}^2 = \tilde \delta _{i, {C_k}}^2 = {{\delta _{i, {C_k}}^2} \mathord{\left/ {\vphantom {{\delta _{i, {C_k}}^2} {\sum\nolimits_{j = 1}^p {{Y_{ij}}{Y_{kj}}} }}} \right. } {\sum\nolimits_{j = 1}^p {{Y_{ij}}{Y_{kj}}} }} $

(7)

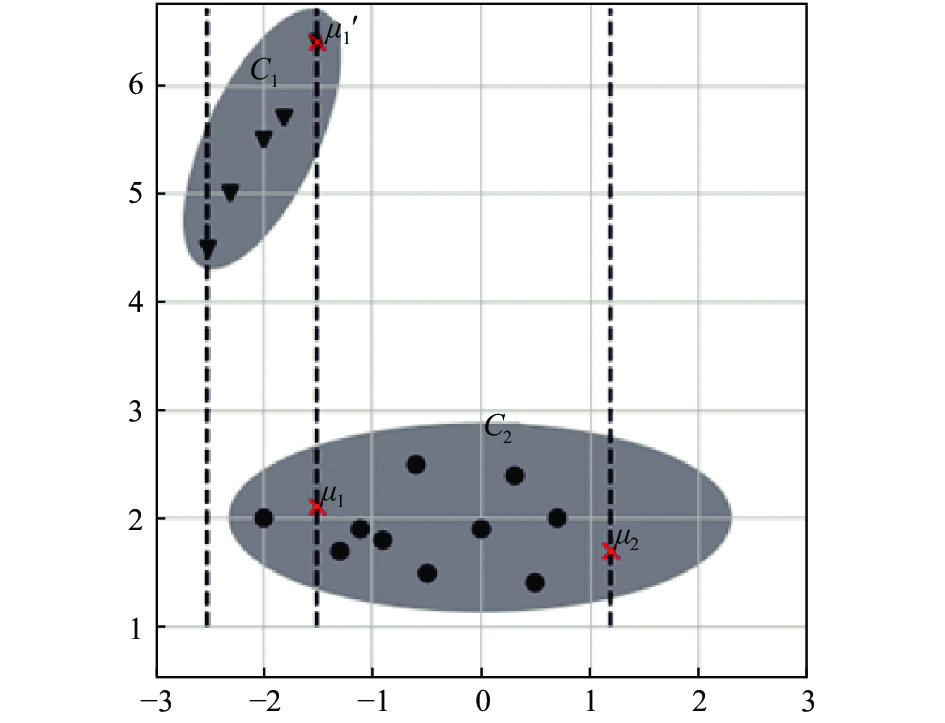
在KMIWMD算法初始化完成后, 选取的聚类中心存在不可靠性, 这种不可靠性具体表现在两方面: (1) 直接不确定性, 被选为簇中心的实例存在缺失值时, 它所处的空间位置并不确定, 在缺省值被填充为某些值时, 它不适合作为簇中心. (2) 间接不确定性, 在度量实例之间的距离时, 由于缺失值的存在, 可能出现原本距离较近的实例, 得出的距离较大, 导致相距较远的实例不会被选作下一个聚类中心, 如图1所示. 我们将其他包含缺失值的实例, 导致聚类中心的不确定性称作间接不确定性. 上述两种不确定性会导致聚类中心在标记阶段对簇的划分产生错误的引导, 容易陷入局部最优解.

如图1所示, 存在两个大小不同的簇 ${C_1}$ 和 ${C_2}$ , 假设使用KMIWMD初始化选择的第一个聚类中心 $\;{\mu _1}$ . 当 $\;{\mu _1}{\text{ = }}( - 1.5, ?)$ 存在缺失值时, 由于缺失值的存在, 导致原本二维平面上的点与点之间的距离变成了点与直线之间的距离, 即其他实例到 $\;{\mu _1}$ 的距离变成了到直线x=–1.5的距离. 此时 ${\mu _2}$ 与直线x=–1.5距离最远, 由算法2中的步骤(3)计算得, 概率 $pr{o_2}$ 最大, 所以选择 $\;{\mu _2}$ 为下一个聚类中心. 由图1可知此时选择的两个聚类中心均在簇 ${C_2}$ 中, 这会导致在接下来的实例标记过程中, 初始中心无法有效的引导簇的划分. 当 $\;{\mu _1}{\text{=}} ( -1.5, 2.1)$ 不存在缺失值时, 距离 $\;{\mu _1}$ 最远的实例为 $\;{\mu _1}^\prime $ , 通过计算可知 $pr{o_1}^\prime $ 最大, $\;{\mu _1}^\prime $ 作为下一个聚类中心. 因为 $\;{\mu _1}^\prime $ 和 $\;{\mu _1}$ 分布在不同的簇中, 所以和 $\;{\mu _2}$ 相比 $\;{\mu _1}^\prime $ 是一个更好的聚类中心. 上述过程中, 我们将 $\;{\mu _1}$ 是否包含缺失值称作直接不确定性; 将 $\;{\mu _1}$ 存在缺失值时, 导致选取下一个聚类中心的发生变化称作间接不确定性. 针对上述存在的问题, 我们将在第3节讨论解决方案.

3 结合可信度的k_m-means聚类算法

针对k_m-means算法初始化(KMIWMD算法)过程中, 选取聚类中心的不可靠性问题, 受He等人的工作启发^{[11, 15]}, 本文在式(7)的计算过程中引入可信度, 如定义3和定义4, 通过可信度优化不完整数据集的初始化过程, 减少初始化完成后, 多个聚类中心位于同一个簇中, 使得聚类中心能够更好地引导簇的划分. 结合式(7)和可信度, 推出新的结合缺失值处理的初始化方式, 式(8)为结合实例可信度的距离计算, 当实例 ${X_i}$ 中存在缺失值, 即 $I{C_i} < 1$ , 在计算实例与聚类中心之间的距离时, 实例可信度通过减少该实例被选做下一个聚类中心的概率 $pr{o_i}$ , 尽量保证选取较完整的实例作为下一个聚类中心, 从而增大选取聚类中心可靠性. 式(9)为结合公共属性可信度的距离计算, 式(9)与公共属性可信度的结合方式和式(8)类似.

定义3. 实例可信度(instance credibility, IC).设D中某个实例 ${X_i}$ 的属性值未缺失的个数为 ${n_{in}} = \displaystyle\sum\nolimits_{j = 1}^p {{Y_{ij}}}$ , 则 ${X_i}$ 的实例可信度为 $IC = {{{n_{in}}} \mathord{\left/ {\vphantom {{{n_{in}}} p}} \right. } p}$ .

定义4. 公共属性可信度(public attribute credibility, PAC).设实例 ${X_i}$ 与实例 ${X_k}$ , 两实例中同一个属性均未缺失的属性值个数为 ${n_c} = \displaystyle\sum\nolimits_{j = 1}^p {{Y_{ij}}{Y_{kj}}}$ , 则 ${X_i}$ 与 ${X_k}$ 的公共属性可信度为 $PAC = {{{n_c}} \mathord{\left/ {\vphantom {{{n_c}} p}} \right. } p}$ .

在不完整数据集中, 实例可信度描述单个实例的缺失程度, 实例可信度越小, 表示该实例包含缺失属性值越多, 实例越不可信. 公共属性可信度描述任意两个实例之间, 同一个属性均未缺失的属性值比例, 公共属性可信度越小, 表示两个实例之间公共缺失的属性值越多, 实例越不可信.

$ {{\hat {{d}}}}_{i, {{\text{C}}_k}}^2 = I{C_i}\frac{{\delta _{i, {C_k}}^2}}{{\displaystyle\sum\nolimits_{j = 1}^p {{Y_{ij}}{Y_{kj}}} }} $

(8)

$ {{\bar {{d}}}}_{i, {{\text{C}}_k}}^2 = PA{C_{i{\text{, }}k}}\frac{{\delta _{i, {C_k}}^2}}{{\displaystyle\sum\nolimits_{j = 1}^p {{Y_{ij}}{Y_{kj}}} }} $

(9)

式(8)中的 $I{C_i}$ 表示 ${X_i}$ 的实例可信度, 式(9)中的 $PA{C_{i, k}}$ 表示 ${X_i}$ 与 ${C_k}$ 的公共属性可信度. 结合上文对算法2的分析与改进, 本文提出优化后的KMIWMD算法, 即结合可信度的不完整数据集聚类中心初始化算法, 记作KMIWMD++, 具体的流程如算法3所示.

算法3. KMIWMD++算法

输入: 数据集D, 聚类数K, 可信度阈值 $\scriptstyle \theta '$

输出: K个聚类中心

1) 采用定义3计算各个实例 $\scriptstyle IC = \{ I{C_1}, I{C_2}, \cdots, I{C_n}\}$

2) $\scriptstyle\; \mu \leftarrow$ 随机选取 $\scriptstyle\;{\hat \mu _1}{\text{ = }}{X_i}$ 作为第一个聚类中心, 其中, $\scriptstyle I{C_i} > \theta '$

3) while $\scriptstyle |\mu | < K$ do // ||表示集合的个数

4) 使用式(8)计算 $\scriptstyle d_i^2 = {{\rm{min}}_{l = 1, 2, \cdots, k - 1}}\hat d_{i, {C_l}}^2$

5) 计算概率 $\scriptstyle pr{o_i} = {{d_i^2} \mathord{\left/ {\vphantom {{d_i^2} {\sum\nolimits_{y = 1}^n {d_y^2} }}} \right. } {\sum\nolimits_{y = 1}^n {d_y^2} }},\; i \in \{ 1, 2, \cdots, n\}$

6) 通过概率 $\scriptstyle pr{o_i}$ 选取第k个(k=2, 3, …, K)聚类中心 $\scriptstyle {\hat \mu _k}$

7) $\scriptstyle\; \mu \leftarrow \mu \cup {\hat \mu _k}$

8) end while

步骤(4)中我们可以使用式(8)或式(9)结合不同的可信度, 调整初始化过程中的距离计算. KMIWND++算法确定下一个聚类中心的时, 在局部距离计算的过程中引入可信度(实例可信度或公共属性可信度), 步骤(2)中通过实例可信度选择包含较完整信息的实例作为第一个聚类中心, 减小簇中心包含缺失值对第k(k=2, 3, …, K)个中心选取的影响. 步骤(4)、步骤(5)通过实例可信度(或者公共属性可信度)调整距离计算, 减少包含缺失值的实例被选作下一个中心的概率, 尽可能地减少直接不确定性对中心选取的影响, 使得初始化完成后多个中心分布在不同的簇中. 最后, 本文将使用算法3初始化的算法1称作KMMC (k_m-meanswith credibility), 接下来在第4节通过实验分析对比k_m-means和KMMC在结合不完整数据集的处理效果.

4 实验与分析

如表1 所示, 实验阶段使用7个UCI 数据集和3个UCR 数据集. Seeds, Ceramic, Wine, Wdbc, CCBR, Iris和Column来自于UCI 数据集. Plane, CBF和Trace来自于UCR 数据集. Wdbc 表示的是Breast Cancer Wisconsin (Diagnostic)数据集, CCBR表示Cervical Cancer Behavior Risk数据集, Ceramic表示Chemical Composition of Ceramic Samples数据集, Column表示的是Vertebral Column 数据集. 每组数据都采用了Z-Score标准化.

本文对实验需要的缺失数据集进行如下处理, 构建随机缺失机制下的不完整数据集. 在完整数据集基础上, 分别构建不同实例缺失度(IMR)的不完整数据集, 构建过程中分别取IMR为0、10%和20%. 首先通过随机数发生器在n个实例中随机选取miss=IMR×n个实例作为缺失部分, 然后通过随机数发生器依次在miss个实例中随机选取m个属性, 将该属性对应的值设置为空值, 每个实例的随机种子为该实例在数据集中的序号, 最后将miss个包含缺失值的部分和n–miss个完整部分组合成实验所需的不完整数据集. 公共属性可信度存在为0的情况, 如 ${X_1} = (?, ?, 6), {X_2} = (1, 5, ?)$ , 此时 $PA{C_{1, 2}}{\text{ = }}0$ , 为了避免这种情况, 构建过程中保证每个实例中属性值缺失的个数m<p/2. 针对不同的实例缺失度进行实验分析, 聚类准确性使用调整兰德里系数ARI (adjusted rand index)衡量, 实验结果为5折交叉验证的平均值. 通过实验发现算法3中可信度阈值 $\theta '$ 取0.8时, 初始化选择的聚类中心效果较好, 故本文实验中 $\theta '$ 统一取0.8.

第一组实验, 如表2和表3所示, 通过实验分析KMIWMD (算法2)和KMIWMD++ (算法3)初始化完成后聚类中心包含缺失值的情况和初始完成后聚类中心出现在同一个簇中的情况, 其中算法2为k_m-means算法中的初始化聚类中心部分.

第2组实验, 如表4所示, 通过实验对比k_m-means算法结合不同的聚类中心初始化算法(算法2和算法3)对聚类准确度的影响.

表2和表3分别表示对Iris数据集, 采用KMIWMD和KMIWMD++算法进行1 000次实验, 初始化完成后选取的聚类中心包含缺失值的次数和聚类中心在同一个簇中的次数(表2和表3中的数据统计在同一组实验中完成). 表2中的 ${m_i}\;(i = 1, 2, \cdots, k)$ 表示选择k个聚类中心包含缺失值的次数, 如 ${m_1} = 239$ 表示1 000次实验中, 选取的k聚类中心里有1个聚类中心包含缺失值出现239次, 表3中 ${s_i}\;(i = 2, 3, \cdots, k)$ 表示选择的k个聚类中心在同一个簇中的次数, 如 ${s_3} = 8$ 表示1 000次试验中, 选取的k聚类中心有3个聚类中心在同一个簇中出现了8次.

结合表2和表3中统计数据分析可知, 随着数据集中的实例缺失度增大, 选取的聚类中心包含缺失值的概率在升高, 同时, 每一次实验选取的聚类中心在同一个簇中的概率也在升高. 由算法2可知, 第一个聚类中心是随机从n个实例中选取的, 随着实例缺失度的增大, 选取的第一个聚类中心包含缺失值的可能自然在升高. 从式(7)计算实例与聚类中心之间的距离可知, 当聚类中心包含缺失值时, 式(7)得出的局部距离可能比真实的距离大. 如某一次选取的聚类中心点 ${\mu _1}{\text{ = }}(6, ?, 8)$ , 真实的聚类中心为 ${\mu _1}^\prime = (6, 2, 8)$ , 使用公式(7)计算实例 ${X_1}{\text{ = }}(2, 4, 3)$ 与 ${\mu _1}$ 之间局部距离 $\tilde d_{1, {C_1}}^2 = {{[{{(6 - 2)}^2} + 0 + {{(8 - 3)}^2}]} \mathord{\left/ {\vphantom {{[{{(6 - 2)}^2} + 0 + {{(8 - 3)}^2}]} 2}} \right. } 2} = 20.5$ , 而实际中真实的距离为 $d_{1, {C_1}}^2 = {{[{{(6 - 2)}^2} + {{(2 - 4)}^2} + {{(8 - 3)}^2}]} \mathord{\left/ {\vphantom {{[{{(6 - 2)}^2} + {{(2 - 4)}^2} + {{(8 - 3)}^2}]} 3}} \right. } 3} = 15$ . 由于聚类中心中缺失值的存在, 增大了该实例被选做下一个聚类中心的可能, 而实际该实例距离上一个聚类中心较近, 属于同一簇内的可能大. 随着数据集的实例缺失度增大, 多个聚类中心在同一个簇的概率增大.

表4是KMMC与k_m-means对比实验结果, KMMC算法中每一行两个值分别表示采用实例可信度和公共属性可信度优化的实验结果. 从实验数据分析可知, 当数据集不存在缺失值时, 通过定义3和定义4可知, 实例可信度 $I{C_i} \equiv 1, \forall i \in (1, n)$ , 公共属性可信度 $PA{C_{i, k}} \equiv 1, \forall i, k \in (1, n), i \ne k$ , 文中引入的可信度对于KMMC算法与k_m-means算法初始化聚类中心不存在影响, 所以表4中KMMC算法与k_m-means算法在完整数据集的情况下ARI值均相等. 在相同的缺失机制和实例缺失度的情况下, KMMC的ARI值普遍要比k_m-means的值要高, 说明了减少初始化中心的直接不确定性, 即减少包含缺失属性值的实例作为初始样本中心, 可以提高结合缺失值处理的聚类算法性能. 但是在高维数据集(CBF), 传统的距离度量方式难以准确找出实例之间的差异性, 导致聚类效果不佳; 同样, 在Trace数据集上, 当实例缺失度为20%时, 优化初始中对聚类结果几乎没有提升. 在高维数据集中随着实例缺失度增大, 通过优化初始化聚类中心, 无法有效的改善聚类准确度.

5 总结与展望

针对不完整数据集初始化聚类中心问题, 提出了结合可信度的不完整数据集聚类算法KMMC, 将实例可信度和公共属性可信度运用到聚类中心初始化过程中, 减少实例中属性值的缺失对实例之间距离度量的影响, 增大初始化阶段选取聚类中心的可靠性. 通过可信度调整距离计算, 有效减少了簇划分过程中, 不可靠的聚类中心对实例标记阶段产生的错误引导. 最后, 通过UCI和UCR数据集对比KMMC与k_m-means算法的聚类准确度, 实验结果表明, 改进初始化聚类中心的KMMC算法的准确度优于k_m-means算法, 验证了KMMC算法的有效性. 未来工作将致力于如何在不完整数据集上引入成对约束, 引导聚类过程中的簇划分, 减少不完整数据对实例标记阶段的影响.