在物质生活不断提高的同时, 人们对西装完美搭配的追求也愈加强烈了, 西装个性化定制成为了人们追求高质量生活最直接的表达方式之一[1]. 选择西装与搭配西装将会有一系列的问题需要注意, 比如: 面料、色彩、版型、款式和衣扣等其他细节内容的选择, 这些细节内容之间的搭配对于普通用户是一个比较困难的问题[2, 3]. 随着西装定制企业与互联网应用的相结合, 企业定制平台已存在大量的西装定制订单信息数据, 其中包括了上衣各部位的表仕样、里仕样、特殊辅料、特殊加工、指定色以及指定色位置等信息, 挖掘其中的关联关系对企业发展有一定的促进作用, 对西装企业在服装定制意愿不断加强的消费趋势下, 从批量生产向定制生产转型的重要技术支持. 挖掘频繁项集是数据挖掘过程中的一个重要的步骤, 在许多应用环境中都非常有用, 但是, 在服装定制领域的应用少之甚少. 传统算法以最小支持度作为输入, 输出内容至少是在该相对事务数据库中出现的全部项集, 一般都会发现成千上万甚至更多的频繁项集, 无法从中容易获取到准确有价值的信息.
目前国内外众多学者在数据挖掘方面做了深入的应用研究, 并应用到了很多不同的领域方向, 为其发展做出了巨大的贡献. 文献[4]利用邻接矩阵记录所有数据项的支持度计数, 删除不满足最小支持度计数的数据项, 从而进行对FP-tree的剪枝, 降低对存储资源的占用浪费; 文献[5]结合挖掘目标筛选出相关的特定数据项进行分析, 减少频繁模式挖掘的次数; 文献[6]通过引入权重来区分数据项在事务中的重要性程度; 文献[7]采用哈希表替代项头表, 并将最小支持度计数相同的节点合并在一起实现压缩FP-tree; 文献[8]采用有序树代替传统FP-tree并采用列表记录项的频繁度, 从而降低对存储空间资源的占用以及减少对FP-tree的遍历次数; 文献[9]通过设置最小支持度并剔除不频繁出现的项目集, 以提高操作效率; 文献[10]增加每个维度属性的权重设置, 以避免由于属性分布不均匀而产生冗余的虚假规则.
本文结合目前对FP-growth算法的各步骤改进技术点, 新增不平衡比评价指标过滤频繁项集中用户不感兴趣的关联规则, 融合K-means聚类算法将挖掘到的频繁项集进行共性分组, 将具有相同共性的关联规则划分在一个簇中, 简化对频繁项集的分析. 综上所述, 将FP-growth算法、K-means聚类算法与西装定制搭配工作相结合, 通过挖掘西装定制项目之间隐藏的规则, 为企业工作人员提供可行的决策建议, 更好地为用户提供高水平的服务, 满足用户的不同需求, 进而提升用户的回购率. 实验选择日本最大的西装销售商青山洋服的某定制生产商的定制数据为研究对象, 对算法的改进从不同方面进行验证.
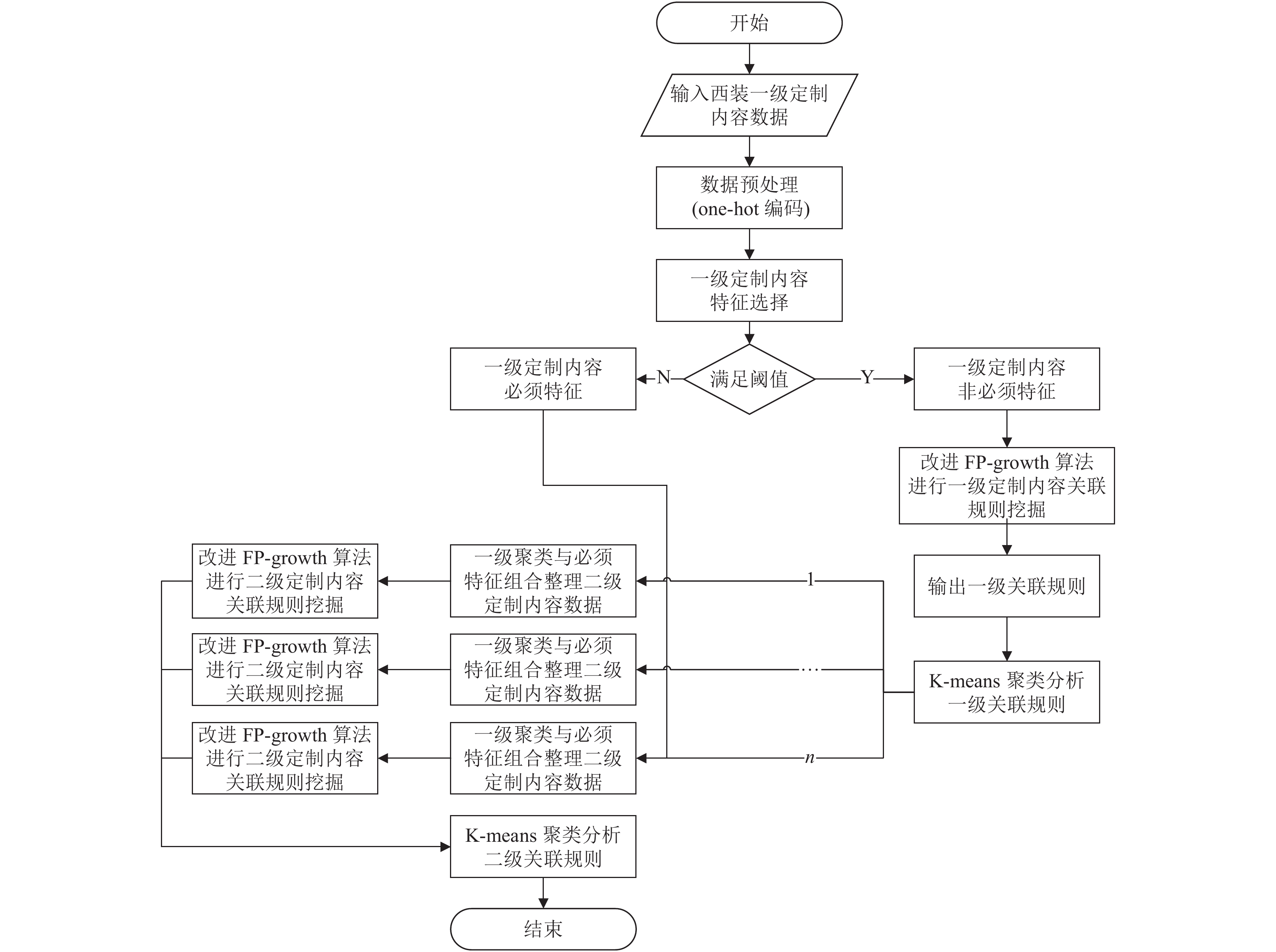
1 西装定制搭配问题模型 1.1 西装定制搭配模型建立为了高效、准确分析西装定制内容搭配之间的关系, 结合某西装定制企业实际情况, 本文通过将改进FP-growth算法、K-means算法和西装定制内容搭配相互融合的方式, 建立挖掘算法模型, 如图1所示.
1.2 对一级定制内容特征选择处理深入企业和公司人员沟通、交流, 可以了解到一级定制内容中存在必须特征和非必须特征, 挖掘必须特征与非必须特征或者必须特征与必须特征之间的关系, 没有实际的意义. 通过方差选择方法对一级定制内容进行特征选择. 结合实际场景, 可以总结出特征值全为1的特征为必须特征, 不存在特征值全为0的特征, 故设置条件阈值为0. 通过特征选择, 能够将一级定制内容分为必须特征和非必须特征, 从而为一级定制和二级定制内容频繁项集的挖掘提供准确的数据基础.
1.3 对频繁项集的聚类处理通过关联规则算法进行数据挖掘将会产生大量的频繁项集, 为了降低对频繁项集理解的复杂性, 本文使用K-means算法对挖掘的频繁项集进行聚类处理, 将具有相同共性的样本划分在一个簇中, 每一簇内的规则前件之间存在共同的特征, 簇内规则的相似性很高, 不同簇之间的趋势不同. 采用SSE (误差平方和)评价指标选取最佳聚类数, 可以高效地得到聚类簇数k. 为后续实验提供数据基础, 同时用户在得到聚类分组规则集时, 容易通过聚类规则集内的规则找出规则之间的共同点, 快速得到有价值的信息, 对无意义的规则直接进行删除.
2 算法概述 2.1 关联规则概念(1) 支持度(support): 指事务数据库中同时包含事件A和事件B的概率, 如式(1)所示:
| $ {\textit{Sup}}(A \Rightarrow B) = P(A \cup B) $ | (1) |
其中, A和B表示不同的事件. 将项集在事务数据库中出现的频数, 称为支持度计数. 能够作为衡量关联规则[11]是否是强关联性的条件, 可以筛选出事务数据库中满足条件的频繁项集[11, 12].
(2) 置信度(confidence): 指由项集的条件推出后件的可信度, 体现了规则的确定性, 如式(2)所示.
| $ Con(A\Rightarrow B)=\frac{P(A\cup B)}{P(A)}\approx \frac{AB出现的次数}{{A}出现的次数} $ | (2) |
置信度能够作为衡量关联规则是否有实际意义和价值的条件.
|
图 1 西装定制内容搭配算法模型 |
(3) 不平衡比(imbalance ratio): 是指关联规则“
| $ {{IR(A, B) = }}\frac{{|Sup(A) - Sup(B)|}}{{Sup(A) + Sup(B) - Sup(A \Rightarrow B)}} $ | (3) |
其中, Sup表示的是支持度. 能够很好地评估关联规则的真实性, 当不平衡比值无线接近于零时, 就可以说明项集之间的关联规则是非常平衡的、用户感兴趣的, 反之亦然.
2.2 K-means算法K-means聚类算法, 是一种通过划分方法的迭代求解的分析算法, 时间复杂度和空间复杂度都是O(n). 其优点是原理通俗易懂; 算法实现过程比较简单; 聚类效果也比较优越. 缺点是簇数k值的选取是随机的、经验化的, 初始质心的选择也很难抉择; 对于非凸的事务数据集不容易收敛; 最终聚合结果和初始质心的选择有很大的关系, 其容易取得某个局部最优的结果.
本文通过手肘法来选择聚类最佳的簇数k, 其中误差平方和是最为核心的评价方法, 简称SSE (sum of the squared errors), SSE是全部样本点数据的聚类误差结果, 反映着聚合效果的优劣.
2.3 FP-growth算法FP-growth算法的数据挖掘过程是根据建立的FP-tree树节点, 按照项头表中支持度计数从小到大的顺序依次遍历, 采用了分而治之的搜索思想, 确定每一个项的条件模式基[13], 从而将存在的频繁项集挖掘出来.
与传统Apriori算法分析对比: FP-growth算法优点是没有候选集的产生; 仅需要两次对数据集进行遍历访问, 很大程度上降低了程序挖掘的时间[14]. 但是, 由于这个过程是基于事务数据集整体进行构建FP-tree树节点, 在处理多维度大型数据集的过程中, 算法将会表现出内存资源消耗急速增加的问题, 而且程序中存在递归调用过程, 程序的执行效率有所下降[15, 16].
FP-growth算法进行挖掘的关键步骤是构建FP-tree树节点. 首次对数据集进行遍历, 设定最小支持度计数min_sup=3, 可以将所有的频繁1项集挖掘出; 将每个事务中非频繁1项集的项全部删除, 并按照数据项的支持度计数对其进行降序排列, 如表1所示.
| 表 1 第一次扫描原始数据库处理 |
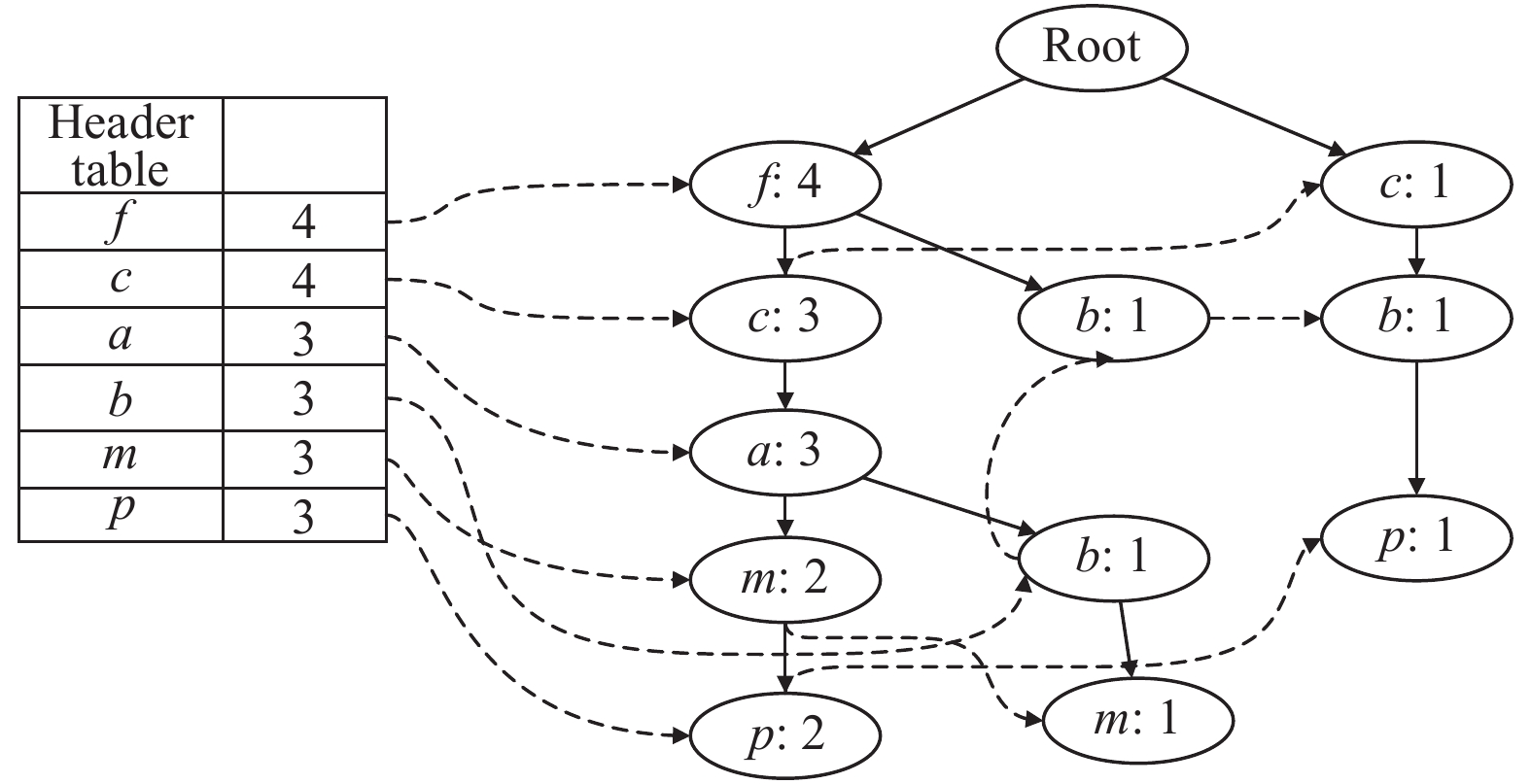
第2次遍历数据集, 创建项头表并构建FP-tree树节点, 初始设置树的根节点为null, 并依次为每个事务创建一个分支, 如图2所示.
|
图 2 FP-tree节点 |
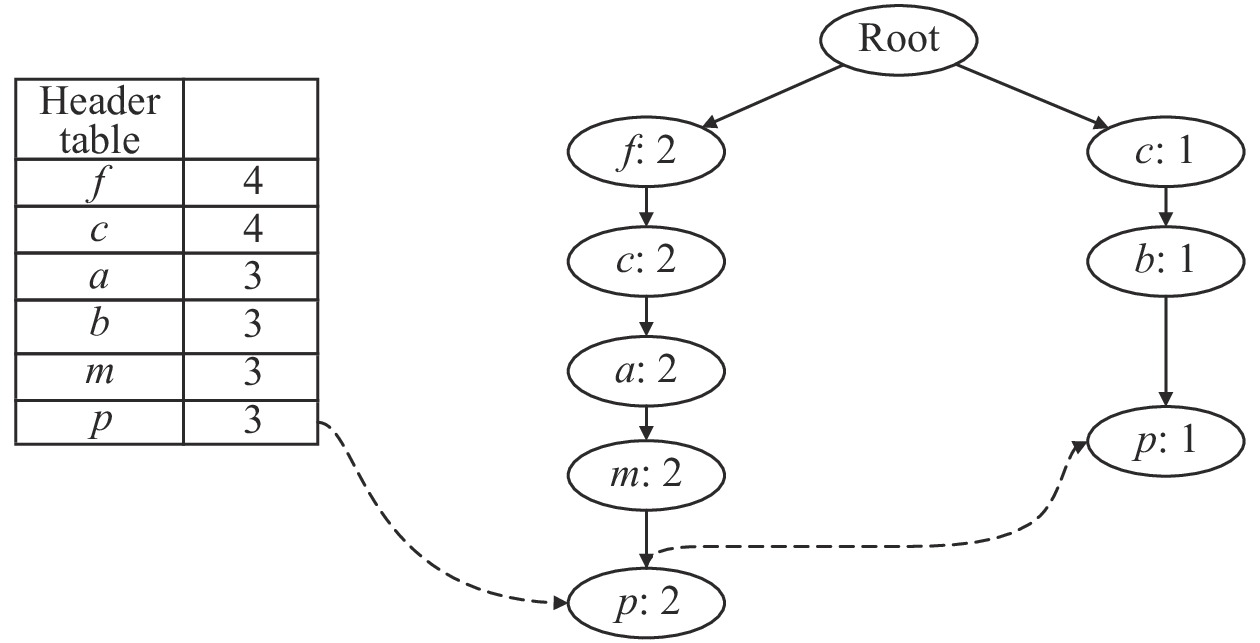
FP-tree的挖掘方式是自底向上, 如图3, 根据项头表中的数据项依次遍历其条件模式基进行挖掘, 设定最小支持度计数为2. 从节点p开始挖掘, 直到挖掘完所有节点, 就得到了可以挖掘到的事务数据库中全部频繁项集. 其中, 节点f的条件模式基为空, 故不用进行挖掘.
3 改进FP-growth算法 3.1 改进算法的主要思想本文在继承FP-growth算法优点的前提下针对其存在的内存资源浪费、执行效率不高和频繁项集数量庞大的问题进行优化改进. 综合已有的几项优势技术, 提出3点优化改进思路: (1) 采用哈希表, 只需要扫描事务数据集一次, 把相关信息存入哈希表和对象数组中, 可以通过哈希函数高效定位需要的项, 提高查询效率. (2) 采用有序FP-tree结构代替FP-tree, 由于树结构中节点是有顺序的, 可以有效地使挖掘事务项的数量减少, 降低浪费存储空间、加快程序执行效率. (3) 增加不平衡比评估方法来判断频繁项的不平衡程度, 使频繁项集数量得到很好的控制, 同时使有意义的项集呈现出来, 排除存在抑制的项集[17, 18].
|
图 3 节点p频繁项集挖掘 |
(1) 哈希表用来存储和处理数据集每次事务记录. 为清晰描述该效果, 使用二维矩阵结构将表1中的原始数据集表示出来, 如式(4)所示. 事务中每个数据项的位置对应二维矩阵的行或列, 但该矩阵并没有使用到算法中. 哈希函数
| $ {M_{m \times n}} = \left[ {\begin{array}{*{20}{c}} a&b&c&d&e&f&g&h&i&j&k&l&m&n&o&p&q&s\\ 1&0&1&1&0&1&1&0&1&0&0&0&1&0&0&1&1&0\\ 1&1&1&0&0&1&0&0&0&0&0&1&1&0&1&0&0&0\\ 0&1&0&0&0&1&0&1&1&1&0&0&0&0&1&0&0&1\\ 0&1&1&0&0&0&1&0&0&0&1&0&0&0&0&1&0&1\\ 1&0&1&0&1&1&0&0&0&0&0&1&1&1&0&1&0&0 \end{array}} \right] $ | (4) |
(2) 使用有序FP-tree代替传统的FP-tree, 有序FP-tree中的节点定义了4个域空间内容, 分别为name、count、pcLink和nLink. name域存放节点在哈希表中对应的哈希地址值; count域存放节点的频繁数; pcLink域在树结构建立时指向第1个孩子节点, 完成建树过程后指向父节点; nLink域在树结构建立时指向兄弟节点, 完成后指向相同name的下一个节点位置. 在相同父节点的不同子节点插入时需要按照节点的哈希地址值降序依次排列, 可以减少访问子节点的次数, 从而达到了高效建立树的目标[19]. 传统FP-tree中的节点是无序的; 有序FP-tree的节点与传统FP-tree相比较占用约为2/3的内存资源. 在建树过程可以利用横向上节点的有序性减少子节点遍历的次数, 提升建树过程的效率, 利用垂直方向上的有序性对最大频繁项集挖掘时可以减少挖掘数量, 提升挖掘过程的效率[20, 21]. 其中, name就是该项在哈希表中的哈希地址值, 不需要进行查找.
(3) 不平衡比可以有效地减少抑制项集的产生. 通过对挖掘的频繁项集计算置信度和不平衡比, 可以判断出该项集是否满足设定的最小置信度和最大不平衡比, 可以在程序中对挖掘关联规则数量进行有效的控制, 剔除抑制项集对实验结果产生偏差的可能性.
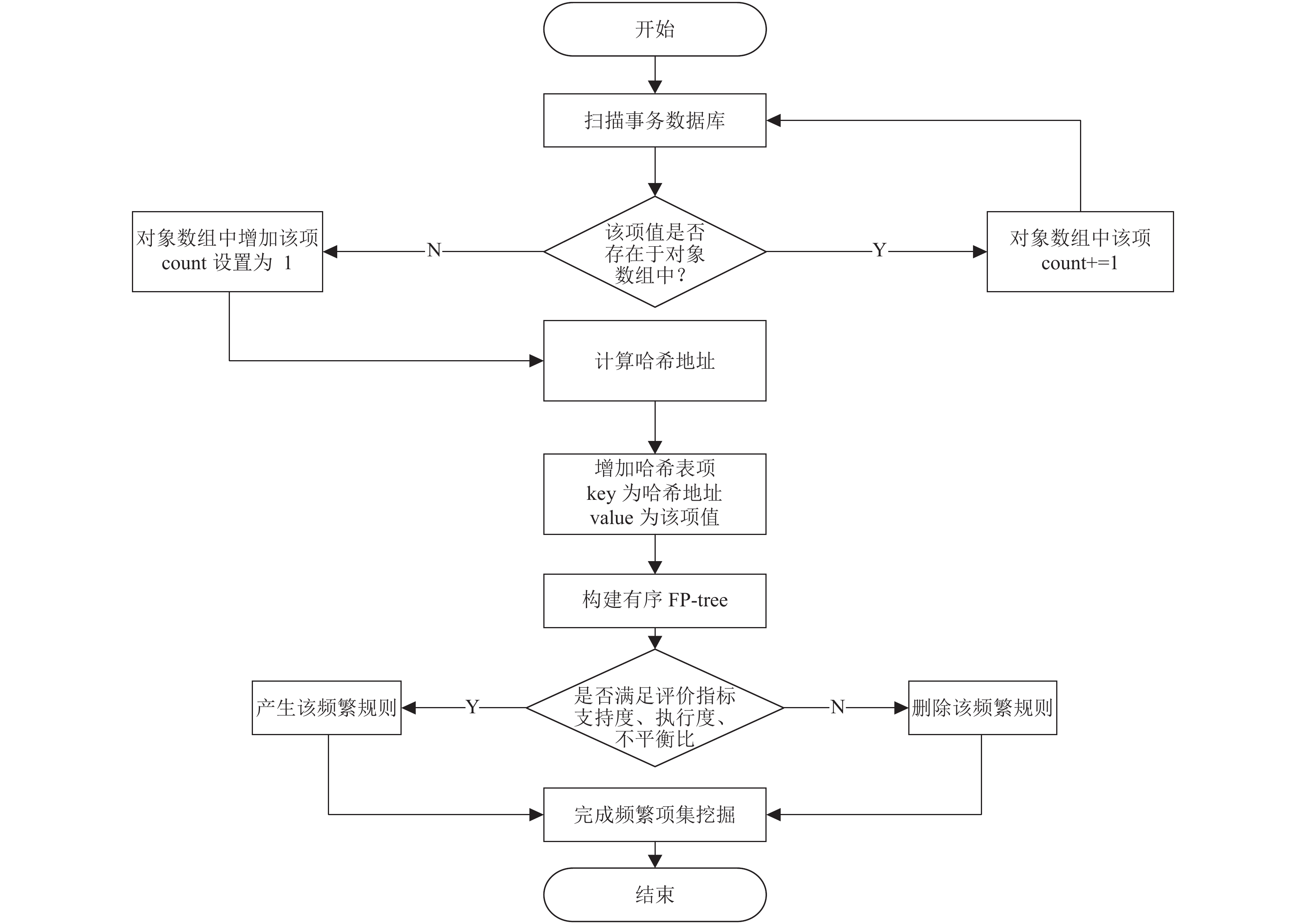
3.2 改进算法的主要流程改进FP-growth算法主要过程流程图, 如图4所示.
|
图 4 改进FP-growth算法的主要过程流程图 |
4 改进算法在西装定制搭配中的应用 4.1 实验环境
硬件环境: 英特尔 Core i5-6300HQ CPU @ 2.30 GHz处理器, 16 GB内存, 512 GB固态硬盘.
软件环境: Windows 10系统, PyCharm 2019.
编程语言: Python 3.7.
4.2 数据预处理本实验选择日本最大的西装销售商青山洋服的某定制生产商的定制数据作为分析的数据源, 选取其中的上衣数据集为研究对象. 该数据集包含2021年02月的上衣历史订单记录3 466条, 其中一级上衣定制内容特征31个, 二级上衣定制内容特征136个, 如表2.
对上衣定制内容数据集进行one-hot编码数据预处理, 存在记为1, 不存在记为0, 用于一级定制内容特征选择, 记为实验数据1, 如表3所示; 表2中上衣定制内容历史数据, 用于二级定制内容频繁项集挖掘, 记为实验数据2.
| 表 2 上衣定制内容历史记录(部分) |
| 表 3 上衣定制内容one-hot编码处理(部分) |
4.3 实验结果分析
(1) 一级定制内容特征选择
使用过滤法的去掉取值变化小的特征方法对实验数据1进行特征选择. 结果如表4所示, 其中一级定制内容中必须特征7项, 非必须特征24项.
| 表 4 一级定制内容特征选择 |
(2) 一级定制内容频繁项集
对实验数据2进行数据转换处理, 例如, 用“JK01”代替“JK0101”“JK0102”等, 并删除必须特征内容, 由于文章篇幅问题, 不展示经处理后的数据集, 记为实验数据3. 使用改进FP-growth算法挖掘一级非必须特征内容中隐含的频繁项集, 设定实验的最小支持度计数为1 400、最小置信度为0.6. 通过实验挖掘到频繁项集273组, 如表5. 经公司业务负责人审核实验结果, 273组关联规则全部都是有意义的、用户所感兴趣的, 符合西装定制搭配的实际情况, 并且不平衡比都在0.2以下.
| 表 5 一级定制内容频繁项集(部分) |
(3) 一级定制内容聚类分析
根据一级定制内容频繁项集规则进行K-means聚类实验, 通过实验发现, 最佳聚类簇数为k=5, 如图5所示. 可以将一级定制内容频繁项集根据聚类结果分组, 为二级定制内容挖掘提供实验基础.
(4) 二级定制内容频繁项集
根据一级定制内容聚类结果分别与一级定制内容必须特征进行组合, 分组使用改进FP-growth算法进行隐含的关联规则挖掘, 设定实验的最小支持度计数为800、最小置信度为0.9. 通过实验挖掘到频繁项集总计4 699组, 如表6所示. 经公司负责人员审核发现其中有1 082组关联规则是无意义的、用户不感兴趣的, 不符合西装定制的实际情况. 例如, 涤纶面料与形状记忆这个规则, 由于涤纶面料是不需要做形状记忆的, 所以这个关联规则是无意义的. 最后, 实验得出最大不平衡比为0.55.
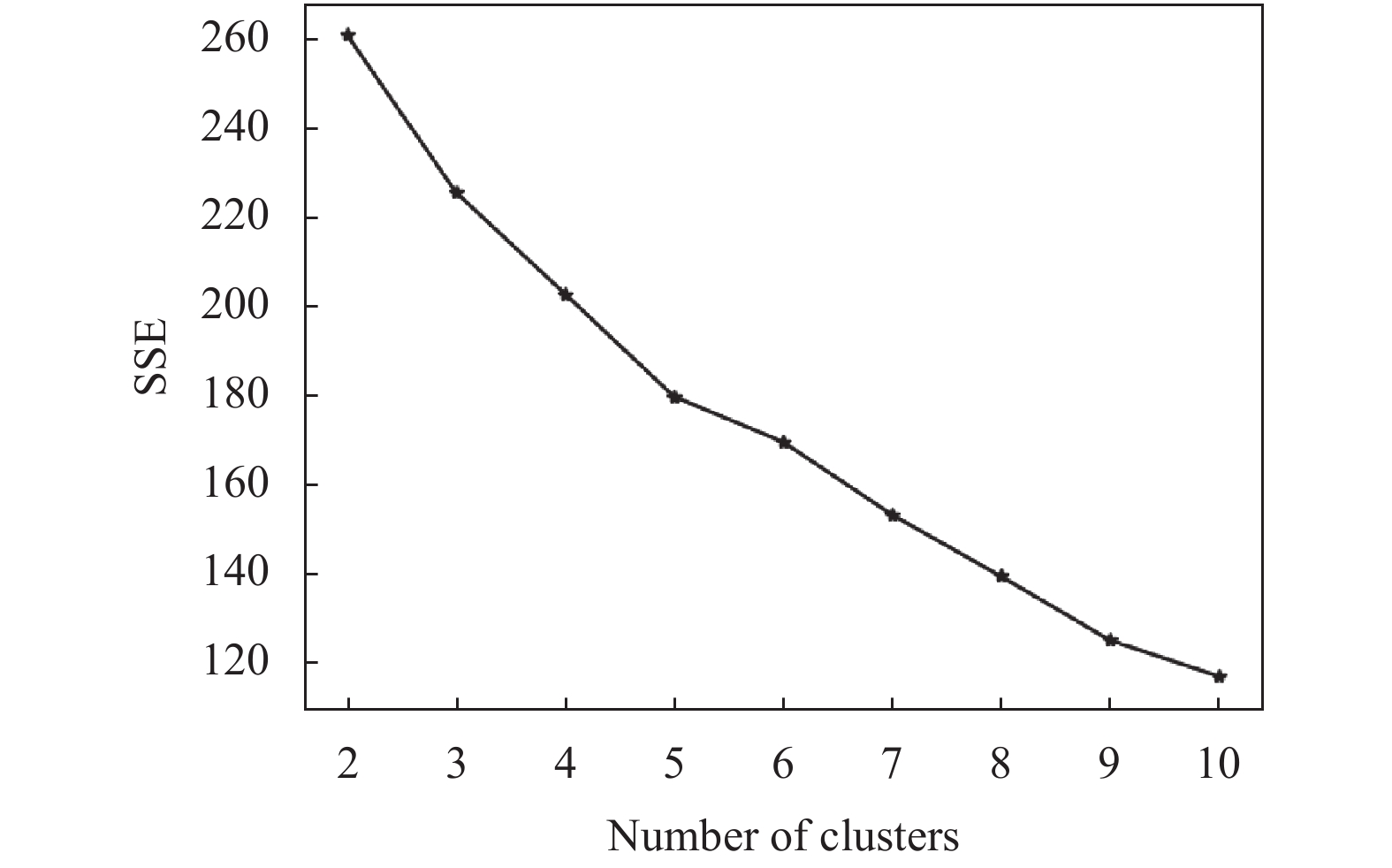
|
图 5 一级定制内容聚类K值 |
(5) 二级定制内容聚类分析
对二级定制内容频繁项集进行汇总整理, 对汇总数据进行one-hot编码处理, 然后进行K-means聚类实验分析, 通过实验可以发现, 最佳聚类簇数k=6, 如图6.
4.4 改进FP-growth算法性能测试为增进分析改进的FP-growth算法在性能方面优势, 利用实验数据3对改进FP-growth算法、传统FP-growth算法和Apriori算法进行运行时间、内存消耗以及频繁项集数比较, 设置最小置信度为0.6. 运行结果比较结果如图7(a), 内存消耗比较结果如图7(b), 频繁项集数比较结果如图7(c)所示. 可以发现: 改进的FP-growth算法相比传统算法提升了约15%的执行时间, 内存资源消耗上也相对降低6.7%左右, 并且挖掘的频繁项集也相对较少. 因此改进的FP-growth算法是一个相对高效、可行的数据挖掘算法.
| 表 6 二级定制内容频繁项集(部分) |
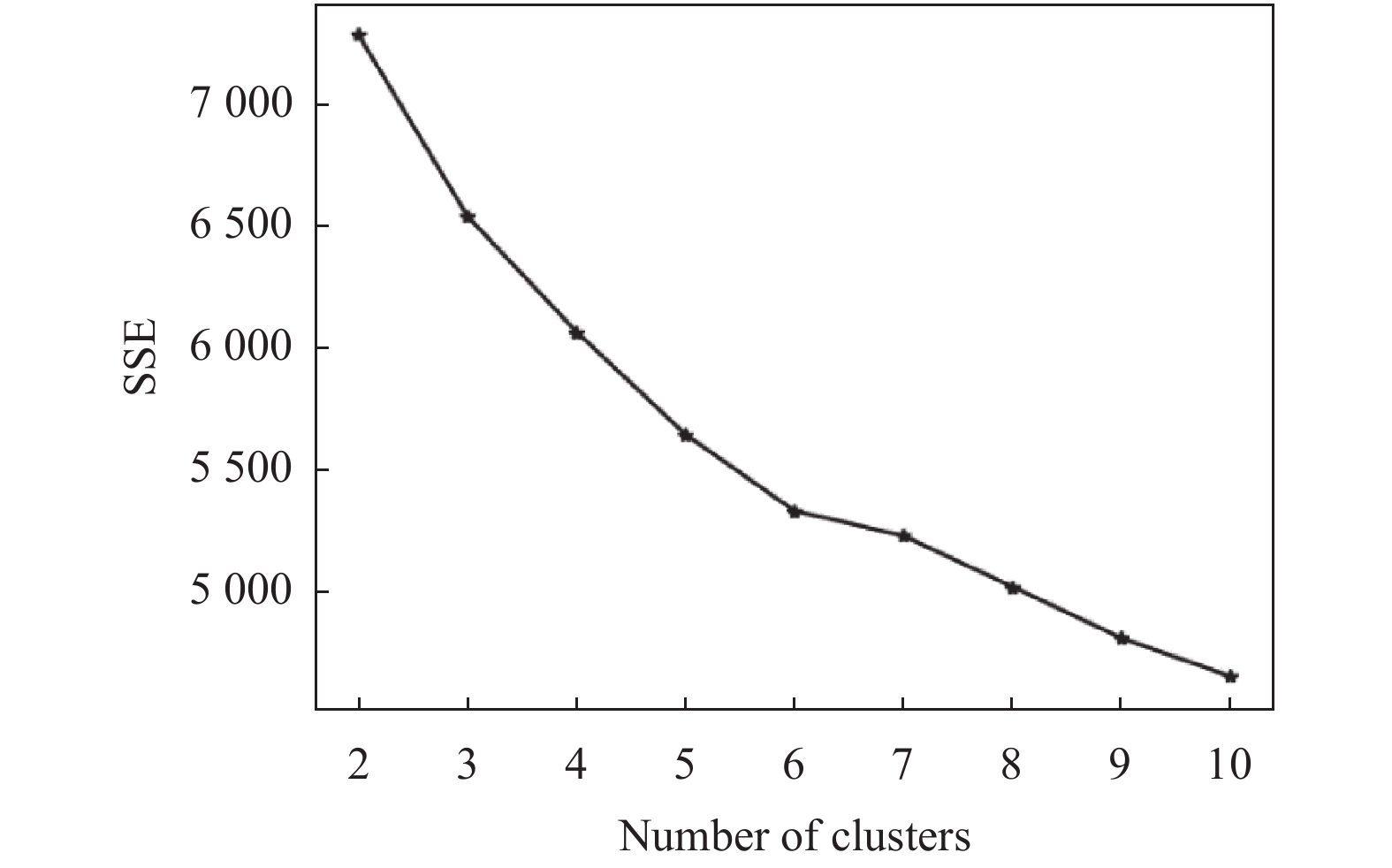
|
图 6 二级定制内容聚类k值 |
5 结束语
本文提出融合K-means与改进FP-growth的西装定制内容搭配挖掘算法. 首先, 综合相关文献中先进的技术点对FP-growth算法进行改进, 采用有序FP-tree代替FP-tree的树结构, 减少内存资源占用; 采用哈希表, 只需要对事务数据集进行一次扫描, 减少了读取I/O的开销, 存储和遍历查询所消耗的时间很明显有所降低; 采用不平衡比评价方法对抑制型的频繁项进行删除, 减少频繁项集的复杂. 然后, 融合改进FP-growth与K-means算法并结合实际应用场景, 利用该算法对西装定制一级内容、二级内容进行聚类分析和数据挖掘分析, 用户通过查看每一簇中的规则就能快速地找到自己感兴趣的规则, 并且针对簇内的规则得出结论. 通过实验证明, 该算法在挖掘关联规则上是可行的且高效的, 挖掘出的规则是用户感兴趣的且有意义的, 对企业的建设提供决策支持, 提供更切合实际、可行的建议, 更好地满足用户各类需求.
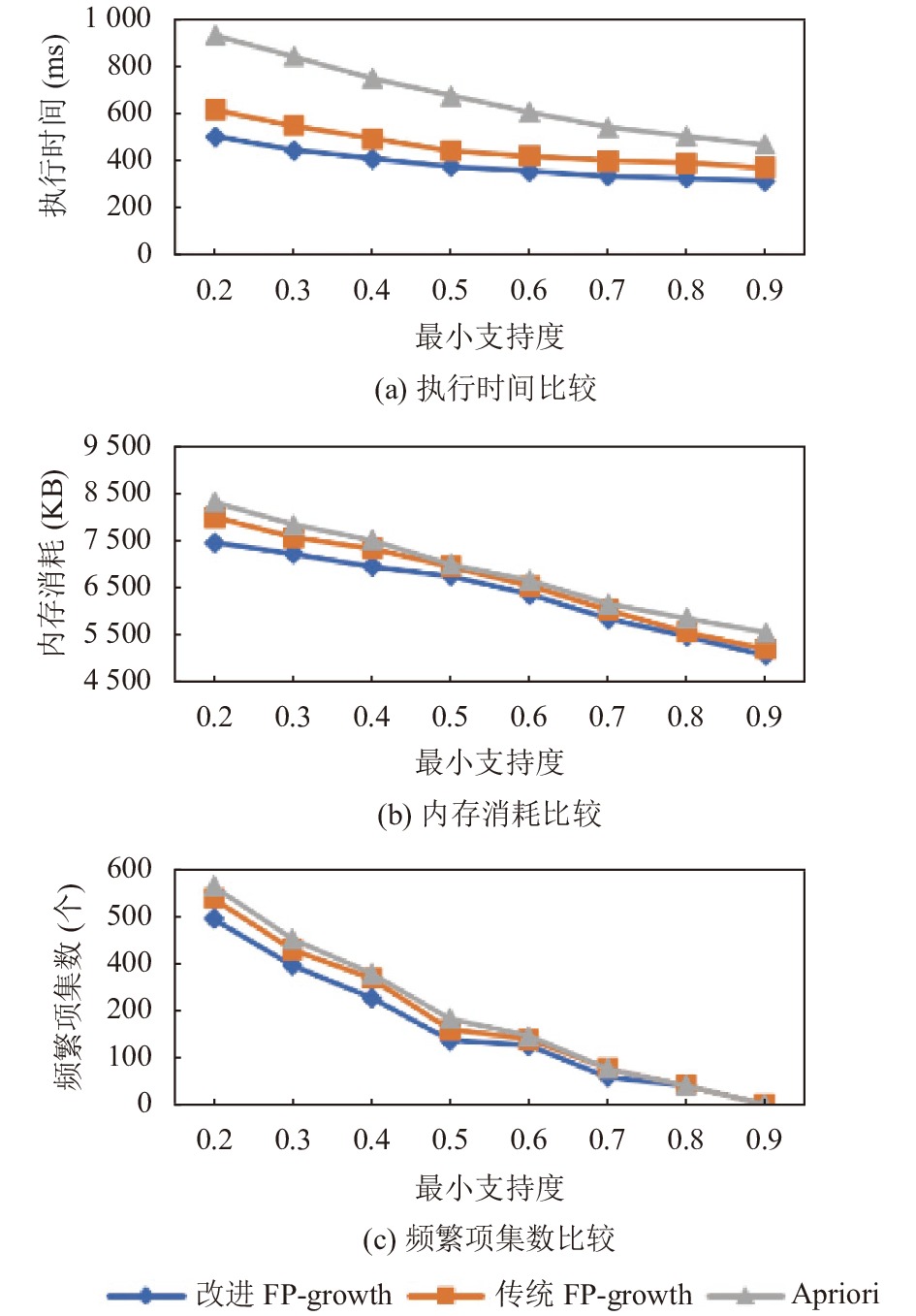
|
图 7 改进FP-growth性能比较 |
| [1] |
邵芬娟, 侯真威. 数据挖掘在服装领域的应用分析. 纺织科技进展, 2021, (2): 1–5.
|
| [2] |
金正昆. 西装的选择与搭配. 新湘评论, 2010, (8): 44–45.
|
| [3] |
纪丹丹, 戴宏钦. 服装搭配方法研究综述. 现代丝绸科学与技术, 2020, 35(4): 31–35.
|
| [4] |
字云飞, 李业丽, 孙华艳, 等. 改进FP-Growth算法在旅游线路规划中的应用研究. 计算机与现代化, 2018, (2): 17–21, 26.
|
| [5] |
杜梦欣. 基于FP-Growth的关联规则算法研究及其在高校教育大数据中的应用[硕士学位论文]. 长春: 吉林大学, 2019.
|
| [6] |
刘云翔, 韩贝. 基于改进FP算法的隧道交通事故关联分析. 现代电子技术, 2018, 41(17): 141–144.
|
| [7] |
何晴, 陆黎明. 基于哈希和合并技术的FP-Growth新算法. 上海师范大学学报(自然科学版), 2018, 47(4): 469–473.
|
| [8] |
岳帅, 尹绍宏. 基于有序FP树和二维列表的频繁模式挖掘算法. 哈尔滨商业大学学报(自然科学版), 2018, 34(6): 692–697.
|
| [9] |
Li JW, Yu N, Jiang JW, et al. Research on student behavior inference method based on FP-growth algorithm. International Conference on Geomatics in the Big Data Era (ICGBD). Guilin: ISPRS, 2020. 981–985.
|
| [10] |
Chunduri RK, Cherukuri AK. Scalable algorithm for generation of attribute implication base using FP-growth and spark. Soft Computing, 2021, 25(14): 9219–9240.
|
| [11] |
叶福兰. 基于改进的FP-growth算法的高校课程关联度实证研究. 科技和产业, 2020, 20(4): 186–190.
|
| [12] |
毛宁宁, 苏怀智, 高建新. 基于FP-growth的大坝安全监测数据挖掘方法. 水利水电科技进展, 2019, 39(5): 78–82.
|
| [13] |
Wang XY, Jiao GE. Research on association rules of course grades based on parallel FP-Growth algorithm. Journal of Computational Methods in Sciences and Engineering, 2020, 20(3): 759–769.
|
| [14] |
姬海波. 基于MapReduce框架的关联规则算法研究与优化[硕士学位论文]. 成都: 电子科技大学, 2018.
|
| [15] |
李敏波, 丁铎, 易泳. 基于FP-Growth改进算法的轮胎质量数据分析. 中国机械工程, 2019, 30(2): 244–251.
|
| [16] |
Yang XD, Lin XX, Lin XL, et al. Application of Apriori and FP-growth algorithms in soft examination data analysis. Journal of Intelligent & Fuzzy Systems, 2019, 37(1): 425–432.
|
| [17] |
殷茗, 王文杰, 张煊宇, 等. 一种基于邻接表的最大频繁项集挖掘算法. 电子与信息学报, 2019, 41(8): 2009–2016.
|
| [18] |
文芳, 黄慧玲, 李腾达, 等. 基于FP-growth关联规则的图书馆数据快速挖掘算法研究. 重庆理工大学学报(自然科学版), 2020, 34(6): 189–194.
|
| [19] |
Wang TY, Hou JX, Yu ZH. Analysis of hierarchical and time-phased model of large-scale power grid based on FP-growth algorithm. IOP Conference Series: Earth and Environmental Science, 2018, 192: 012031. DOI:10.1088/1755-1315/192/1/012031 |
| [20] |
倪德, 马传香. FP-growth算法及其优化在税务系统中的应用. 计算机应用, 2018, 38(S2): 140–143.
|
| [21] |
王利军, 唐立. 基于有序FP-tree结构和投影数据库的最大频繁模式挖掘算法. 淮阴师范学院学报(自然科学版), 2020, 19(1): 35–39, 44.
|
 2022, Vol. 31
2022, Vol. 31


