2. 山东大学高效洁净机械制造教育部重点实验室, 济南 250061;
3. 山东大学 机械工程国家级实验教学示范中心, 济南 250061
2. Key Laboratory of High Efficiency and Clean Mechanical Manufacture Shandong University, Ministry of Education, Jinan 250061, China;
3. National Experimental Teaching Demonstration Center of Mechanical Engineering, Shandong University, Jinan 250061, China
图像增强技术是数字图像处理的一个重要分支. 然而复杂的工业环境会影响到图像采集的质量, 特别是光照环境或物体表面反光等原因造成图像整体光照不均. 因此引入图像增强技术平衡整个图像的受光问题, 同时也能突出图像中目标物的特征信息, 进而得到一种更加实用的图像或者转换成一种更适合人或机器进行分析处理的图像[1]. 图像增强现已在诸多的领域中得到应用, 如: 自动驾驶、智能监控系统、工业检测系统以及航天航空领域等
传统的图像增强方法可粗略分为3类分别为: 空域、频域以及混合域. 其中, 以直方图均衡[2]、伽马变换[3]为主的空域方法主要是直接对图像像素值进行处理; 以小波变换[4]为例的频域方法是在某种变换域内进行操作; 将空域和频域的一些方法结合就构成了混合域. 传统的方法所取得效果不是很理想, 一方面是采用的方法过于简单, 另外是没有结合图像中的上下文信息等.
近年来, 卷积神经网络在图像超分辨率[5]、去模糊[6]、去雾[7]、降噪[8]和图像增强等许多低层次计算机视觉任务中取得了长足的进步. 与传统方法相比, 一些基于 CNN 的方法显著提高了图像增强的质量[9]. 大多数现有训练方法都依赖配对数据去学习原始图像与目标图像的映射关系, 得到最终的增强图像[10].
而文章基于对Zero-DCE-Net图像增强网络算法的研究[11]. 该网络相比于同类研究的优势是消除了配对数据进行训练, 实现了零参考, 同时通过设计一组损失函数来避免过拟合的风险[12]. 此外该网络模型考虑到像素值的范围、单调性和可微性, 因此特别设计了曲线估计, 通过将低光像素迭代至高阶曲线, 首次实现像素级的动态调整. 从而在保持增强图像范围的同时也保留了相邻像素的对比度. 整个网络由7层全卷积组成, 经过每一层卷积后, 噪声一步步地被消除, 噪声等级减小, 图像内容的细节也随之丢失[13].
但随着深度学习在图像分类和目标检测的广泛应用[14], 训练需要高质量的图像作为训练集, 同时检测过程光线影响也是非常大. 而检测和分类就是依靠图像的细节特征[15], 因此不仅需要对低光照图像增强, 并且增强后的图像应该保留大部分的细节信息[16], 这有助于提升图像分类准确性以及目标检测的精度.
1 网络结构 1.1 Zero-DCE网络结构原Zero-DCE图像增强网络由对称级联的7个卷积层的普通CNN, 前6层卷积层由Conv和ReLU函数组成, 最后一层卷积层由Conv和tanh函数组成, 其中第1/2/3层输出和第4/5/6层进行通道级联. 每层卷积的通道数32, 卷积核大小3×3, 最后输出R/G/B三个通道8次迭代的值, 因此是24通道, 网络结构图如图1.

|
图 1 Zero-DCE网络结构 |
1.2 改进后的网络结构
改进后的网络核心架构由7层卷积和3层反卷积组成, 此外增加两个残差块. 第4/5/6层为增加的反卷积层[17], 实现对图像细节丢失的补偿, 2层残差块实现每层反卷积后与2/3层求差, 通过去学习一个残差值来平衡图像细节信息, 达到降噪和提升图像的清晰度[18]. 1/2/3/7/8/9层由Conv和ReLU函数组成, 最后一层由Conv和tanh函数组成, 反卷积层和卷积层的通道数为互相对应的, 都为32, 卷积核大小3×3, 最后输出R/G/B三通道是经过了10次迭代后的值, 输出通道为30. 改进后网络结构如图2所示. 为方便书写, 改进后的网络命名为IMZD-DevRd.
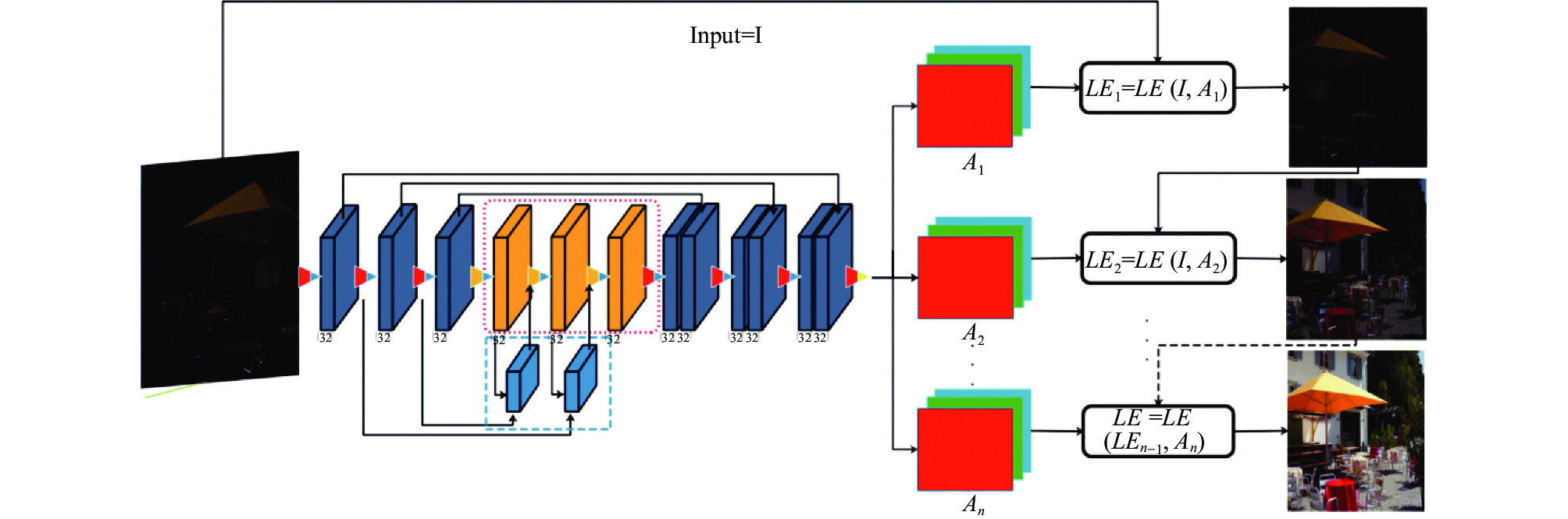
2 网络功能实现零参考深度曲线估计网络主要通过设计一组可微分的非参考损失来实现将深度网络与光增强作为图像特定曲线估计任务, 从而对给定的图像实现更精准的动态调整, 改进网络总体实现过程如图3所示. 零参考深度曲线估计网络由3个部分组成: LE-curve (光增强曲线)、DCE-Net (估算最佳拟合的光增强曲线)、Loss (损失函数)[19].
2.1 光增强曲线第1部分LE-curve (光增强曲线)设计的非线性映射曲线有3个点[20]: 1)为了避免由于截断溢出而导致图像信息的丢失, 需将待处理图像的每个像素归一到[0, 1]范围内; 2)为使得相邻像素保留原有的差异性, 光增强曲线需为单调的; 3)在梯度反向传播过程中, 该曲线的形式尽可能简单并可微. 为了实现这3个目标, 设计了一个二阶曲线, 表示如下:
| $ LE\left(I\left(x\right)\text{; } \alpha \right)=I\left(x\right)+ \alpha I\left(x\right)\left(1-I\left(x\right)\right) $ | (1) |
其中, x为像素坐标,

|
图 2 IMZD-DevRd网络结构 |
|
图 3 改进后网络功能实现流程 |
通过式(1)的光增强曲线迭代后, 可以使得调整变得更灵活, 从而使模型能够适应各种弱光条件.
2.2 深度曲线估计网络第2部分主要为深度曲线估计网络, 也是文章提出的改进地方, 将一幅弱光图像输入, 会得到一组像素级曲线参数映射所对应的高阶曲线作为输出, 网络采用由1/2/3和7/8/9层具有对称连接的卷积网络, 4/5/6层残差层平衡图像的细节信息, 输入图像首先在1/2/3层卷积后, 然后通过残差块将2/3层的输出和4层进行整合输入到第5层反卷积层中, 依次往后推一层.
2.3 损失函数设计第3部分为损失函数的设计, 原网络损失函数由空间一致性损失[21]、曝光控制损失[22]、色彩恒常性损失[23]和光照平滑损失[24]4部分组成. 改进后的损失函数增加了内容损失[25], 主要用于每次迭代生成后的图像与上一次图像进行欧式距离计算, 保留图像的语义信息, 最后叠加一个总的损失函数.
(1)空间一致性损失(
为保持图像的空间一致性, 通过调整输入图像与增强图像相邻区域的梯度, 通过计算两个图像三通道均值, 得到两个灰度图像, 将其分解成若干个4×4的块, 最后计算每个块内中心像素与相邻像素的插值并求其均值. 其公式如下:
| $ {L_{\text{spa}}} = \frac{1}{K}\mathop \sum \limits_{i = 1}^K \mathop \sum \limits_{j \in \Omega \left( i \right)} {\left( {\left| {\left( {{Y_i} - {Y_j}} \right)} \right| - \left| {\left( {{I_i} - {I_j}} \right)} \right|} \right)^2} $ | (2) |
其中, K为局部区域的数量, Ω(i)是以区域i为中心的4个相邻域(上、下、左、右), Y和I分别为增强图像和输入图像的局部区域平均强度值, 这个值根据经验设置为4×4大小, 如果设置为其他大小, 损失函数将变得稳定.
(2)曝光控制性损失(
为了抑制曝光不足或过度曝光区域, 所以设计了曝光控制性损失函数来控制曝光水平. 曝光损失控制是指局部区域的平均强度值与良好曝光级别E之间的距离[26]. 按照现有惯例, E为三原色空间的灰度级别, 在本实验中将取E=0.6. 将图像增强转化为灰度图, 分级为若干16×16个块, 计算每块内的均值[27]. 公式如下:
| $ {L_{\rm{exp}}} = \frac{1}{M}\mathop \sum \nolimits_{k = 1}^M \left| {{Y_k} - E} \right| $ | (3) |
其中, M为大小16×16的不重叠局部区域的数量, Y为增强图像中局部区域的平均强度值.
(3)色彩恒常性损失(
根据灰色世界颜色恒常性假设[28], 即将每个传感器通道的颜色平均到整个图像, 通过色彩恒常性损失来纠正增强图像中潜在的颜色偏差, 并建立三通道之间的联系, 尽可能使得增强后的颜色相关. 函数设计如下:
| $ {L_{\rm{col}}} = \mathop \sum \limits_{\forall \left( {p, q} \right) \in \varepsilon } {\left( {{J^p} - {J^q}} \right)^2}, \varepsilon = \left\{ {\left( {R, G} \right), \left( {R, B} \right), \left( {G, B} \right)} \right\} $ | (4) |
其中,
(4)光照平滑损失(
在每个曲线参数映射中添加光照平滑损失以保持相邻像素之间的单调关系, 这样所有通道、迭代次数A (网络输出)的水平、垂直方向梯度平均值应该很小. 光照损失函数如下:
| $ {L_{\rm{tvA}}} = \frac{1}{N}\mathop \sum \limits_{n = 1}^N \mathop \sum \limits_{c \in \mu } {\left( {\left| {{\nabla _x}A_n^c} \right| + \left| {{\nabla _y}A_n^c} \right|} \right)^2}, \mu = \left\{ {R, G, B} \right\} $ | (5) |
其中, N为迭代次数,
(5)内容损失(
分别将每次迭代增强后的图像与上一次迭代生成的图像输入到预训练好VGG网络[29]中提取特种, 然后计算像素之间的欧式距离来判别增强前后的差异性, 可用来保持图片的语义信息[30]. 其公式如下:
| $ {L_{\rm{content}}} = \frac{1}{{{C_j}{H_j}{W_j}}}{\emptyset _j}\left( {{F_W}\left( {{I_o}} \right)} \right) - {\emptyset _j}\left( {{I_t}} \right) $ | (6) |
其中,
总的损失
| $ {{{L}}_{{\text{total}}}} = {{{L}}_{{\text{spa}}}} + {{{L}}_{{\text{exp}}}} + {w_{\rm{col}}}{{{L}}_{{\text{col}}}} + {w_{\rm{tvA}}}{{{L}}_{{\text{tvA}}}} + {{{L}}_{{\text{content}}}} $ | (7) |
其中,
实验设备: CPU为Intel Xeon(R)W-2155, GPU为GeForce RTX 2080 Ti/PCle/SSE2, 内存64 GB的台式电脑. 实验数据: 训练采用3 022张不同曝光程度图片, 如图4所示, 其大小为512×512. 所有的程序都是在Linux系统下进行编译、链接与运行, 其中网络训练在PyTorch平台上, 图像质量评估在Matlab上进行的测试.

|
图 4 不同曝光图片 |
在得到训练好的权重后, 首先对部分低光照图像进行了增强处理, 对比网络改进前后的图像, 结果如图5所示.
增强后的图像无法仅仅通过肉眼去判别好坏, 因此通过在PSNR和SSIM两种图像质量评估方法[31]中进行了测试, 此外对传统的拉普拉斯、直方图均衡化、Retinex-Net[32]和Enlighten-GAN[33]作为对比. 测试结果如表1所示.
通过表1发现, 改进后的图像质量相比原来提升是比较明显的. 另外通过对改进前后的图像进行傅里叶变换[34]来验证改进后图像细节是否增加. 如图6所示.
傅里叶谱主要将图像的时域转成频域, 图像边缘的灰度值变换快, 就对应这频率高, 即高频显示图像边缘, 而图像细节处也就是属于灰度值急剧变化的区域, 正是因为灰度值的急剧变化才会出现细节. 因此对改进先后的图片做傅里叶变换, 分析改进先后图像细节信息是否增加

|
图 5 改进网络前后图像对比 |
由于改进后的网络在原网络的基础上, 增加了3层反卷积和两层残差, 因此计算量势必会有所增加, 为了清晰的了解网络改进前后的一个时间开销, 本实验通过表2记录了改进网络前后训练以及测试耗时对比.
通过对比发现, 改进后的网络后计算量明显增加, 训练时间也相应增加, 但是在测试上面耗时不是相差很大, 对于应用在大多的工业领域还是基本能够满足它的速度要求, 同时增加的图像细节信息也能提高检测的精度.
| 表 1 几种图像增强方法的图像质量评估结果 |
通过图6(i) (原图傅里叶谱减去Zero-DCE的傅里叶谱)和图6(j) (原图傅里叶谱减去IMZD-DevRd傅里叶谱)可以看出, 图6(j)中的低频部分是高于图6(i)的, 说明原图中高频部分和改进后增加的高频部分抵消了, 从而说明改进后的网络确实可以增加图像的细节信息. 图6(i)和图6(l) (原图傅里叶谱减去去原图噪后的傅里叶谱, 即认为噪声)可以说明Zero-DCE的去噪效果, 此外通过图6(k)可以说明改进后的也达到了和原网络去噪的效果.
此外, 通过比较目前主流的几种图像增强方法后图像的视觉感知[35], 如图7所示. 主要对室内和室外两种环境进行比对, 可以发现改进后的算法在室内和室外视觉感知是优于其他方法的, 其他几种方法增强后图像会出现失真、模糊和伪影的现象.

|
图 6 图像傅里叶变换对比 |
| 表 2 网络改进前后的训练以及测试耗时对比 |
最后为了检验改进后的算法是否能提高目标检测的精度, 其中目标检测算法采用SSD, 数据集为VOC2017和VOC2012, 基于上述环境和配置中训练的网络模型.

|
图 7 视觉感知对比 |
在目标检测和图像分类训练中最主要是根据图像的细节特征来分类训练得到所对应的目标网络权重, 进而检测和分类的图像细节信息应尽可能多与之对应. 具体检测效果如图8所示.

|
图 8 改进前后目标检测情况 |
通过图8结果所示, 明显改进后对于目标检测的精度提高了很多, 这可以应用在很多方面.
4 结论与展望在对Zero-DCE-Net图像增强网络的研究基础上, 针对卷积后图像细节信息的丢失问题, 提出了结合反卷积和小残差网络解决该问题, 最后对改进后的网络进行测试, 首先通过在图像质量评估方法PSNR和SSIM中证实了改进后的图像质量是优于原网络的, 其次通过傅里叶变换和目标检测验证了改进后的网络, 不仅可以达到对图像的增强, 同时图像细节信息也能得到补偿, 这有助于在目标检测、图像分类和图像修复领域的广泛应用.
| [1] |
靳阳阳, 韩现伟, 周书宁, 等. 图像增强算法综述. 计算机系统应用, 2021, 30(6): 18–27.
|
| [2] |
Stark JA. Adaptive image contrast enhancement using generalizations of histogram equalization. IEEE Transactions on Image Processing, 2000, 9(5): 889–896.
|
| [3] |
Goossens K, Haelewyn J, Meersman F, et al. Pressure- and temperature-induced unfolding and aggregation of recombinant human interferon-gamma: A Fourier transform infrared spectroscopy study. Biochemical Journal, 2003, 370(2): 529–535.
|
| [4] |
Antonini M, Barlaud M, Mathieu P, et al. Image coding using wavelet transform. IEEE Transactions on Image Processing, 1992, 1(2): 205–220.
|
| [5] |
Yang JC, Wright J, Huang TS, et al. Image super-resolution via sparse representation. IEEE Transactions on Image Processing, 2010, 19(11): 2861–2873.
|
| [6] |
Chen XG, Yang J, Wu Q. Image deblur in gradient domain. Optical Engineering, 2010, 49(11): 117003. DOI:10.1117/1.3505868 |
| [7] |
Long J, Shi ZW, Tang W, et al. Single remote sensing image dehazing. IEEE Geoscience and Remote Sensing Letters, 2014, 11(1): 59–63.
|
| [8] |
Elad M, Aharon M. Image denoising via sparse and redundant representations over learned dictionaries. IEEE Transactions on Image Processing, 2006, 15(12): 3736–3745.
|
| [9] |
Kang C, Lai YK, Wu YX, et al. Automatic semantic modeling of indoor scenes from low-quality RGB-D data using contextual information. ACM Transactions on Graphics, 2014, 33(6): 1–12.
|
| [10] |
Wolpern AE, Burgos DJ, Janot JM, et al. Is a threshold-based model a superior method to the relative percent concept for establishing individual exercise intensity? A randomized controlled trial. BMC Sports Science, Medicine and Rehabilitation, 2015, 7(1): 16. |
| [11] |
Guo CL, Li CY, Guo JC, et al. Zero-reference deep curve estimation for low-light image enhancement. 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Seattle: IEEE, 2020. 1777–1786.
|
| [12] |
Li CY, Guo CL, Chen CL. Learning to enhance low-light image via zero-reference deep curve estimation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2021, 1. DOI:10.1109/TPAMI.2021.3063604 |
| [13] |
Neichel B, Lu JR, Rigaut F, et al. Astrometric performance of the Gemini multiconjugate adaptive optics system in crowded fields. Monthly Notices of the Royal Astronomical Society, 2014, 445(1): 500–514.
|
| [14] |
Linden DEJ, Prvulovic D, Formisano E, et al. The functional neuroanatomy of target detection: An fMRI study of visual and auditory oddball tasks. Cerebral Cortex, 1999, 9(8): 815–823.
|
| [15] |
Szoplik T, Garcia J, Ferreira C. Rank-order and morphological enhancement of image details with an optoelectronic processor. Applied Optics, 1995, 34(2): 267–275.
|
| [16] |
丁畅, 董丽丽, 许文海. 图像梯度场双区间均衡化的细节增强. 电子学报, 2017, 45(5): 1165–1174.
|
| [17] |
Ma XR, Fu AY, Wang J, et al. Hyperspectral image classification based on deep deconvolution network with skip architecture. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(8): 4781–4791.
|
| [18] |
Yang J, Li WJ, Wang RG, et al. Enhanced two-phase residual network for single image super-resolution. Journal of Visual Communication and Image Representation, 2019, 61: 188–197.
|
| [19] |
Wu CS, Liang TC, Kuan H, et al. Output power enhancement of GaN-based light-emitting diodes using circular-gear structure. Japanese Journal of Applied Physics, 2011, 50(3R): 032101. DOI:10.7567/JJAP.50.032101 |
| [20] |
Gonzalez-Izal M, Falla D, Izquierdo M, et al. Predicting force loss during dynamic fatiguing exercises from non-linear mapping of features of the surface electromyogram. Journal of Neuroscience Methods, 2010, 190(2): 271–278.
|
| [21] |
Jian Z, Craigmile PF, Cressie N. Loss function approaches to predict a spatial quantile and its exceedance region. Technometrics, 2008, 50(2): 216–227.
|
| [22] |
Kurmi Y, Chaurasia V. An image fusion approach based on adaptive fuzzy logic model with local level processing. International Journal of Computer Applications, 2015, 124(1): 39–42.
|
| [23] |
Nieves JL, Pérez-Ocón F, Hernández-Andrés J, et al. Spectral-reflectance function recovery for improved colour-constancy experiments. Displays, 2002, 23(5): 213–222.
|
| [24] |
Berloffa G, Modena F. Income shocks, coping strategies, and consumption smoothing: An application to indonesian data. Journal of Asian Economics, 2013, 24: 158–171.
|
| [25] |
Huang JC. Image super-resolution reconstruction based on generative adversarial network model with double discriminators. Multimedia Tools and Applications, 2020, 79(39): 29639–29662.
|
| [26] |
Li ZG, Zheng JH, Rahardja S. Detail-enhanced exposure fusion. IEEE Transactions on Image Processing, 2012, 21(11): 4672–4676.
|
| [27] |
Mertens T, Kautz J, Van Reeth F. Exposure fusion: A simple and practical alternative to high dynamic range photography. Computer Graphics Forum, 2009, 28(1): 161–171.
|
| [28] |
Rutherford MD, Brainard DH. Lightness constancy: A direct test of the illumination-estimation hypothesis. Psychological Science, 2002, 13(2): 142–149.
|
| [29] |
Ke HJ, Chen D, Li XL, et al. Towards brain big data classification: Epileptic EEG identification with a lightweight VGGNet on global MIC. IEEE Access, 2018, 6: 14722–14733.
|
| [30] |
Ignatov A, Kobyshev N, Timofte R, et al. DSLR-quality photos on mobile devices with deep convolutional networks. 2017 IEEE International Conference on Computer Vision (ICCV). Venice: IEEE, 2017. 3297–3305.
|
| [31] |
Sun ZH, Hoogs A. Image comparison by compound disjoint information with applications to perceptual visual quality assessment, image registration and tracking. International Journal of Computer Vision, 2010, 88(3): 461–488.
|
| [32] |
Provenzi E, Fierro M, Rizzi A, et al. Random spray retinex: A new retinex implementation to investigate the local properties of the model. IEEE Transactions on Image Processing, 2007, 16(1): 162–171.
|
| [33] |
Jiang YF, Gong XY, Liu D, et al. EnlightenGAN: Deep light enhancement without paired supervision. IEEE Transactions on Image Processing, 2021, 30: 2340–2349.
|
| [34] |
Uzun IS, Amira A, Bouridane A. FPGA implementations of fast Fourier transforms for real-time signal and image processing. IEE Proceedings-Vision, Image, and Signal Processing, 2005, 152(3): 283–296.
|
| [35] |
McNamara A. Visual perception in realistic image synthesis. Computer Graphics Forum, 2001, 20(4): 211–224.
|
 2022, Vol. 31
2022, Vol. 31



