电力是国计民生的支柱产业, 优质可靠的电力供应是现代化持续稳定发展的重要保证. 随着电力终端日益增多, 全国各地分布了大量电力终端, 定位服务的需求日益迫切. 如何对电力终端进行定位, 提供准确、安全、可靠的定位信息, 成为管理调度电力系统的关键问题之一^{[1, 2]}.

目前采用GPS授时技术和定位技术是对电力终端进行定位的常用手段. 然而, 由于GPS并不安全, 存在多种欺骗式攻击方法^{[3, 4]}, 使得GPS接收机解算出虚假的定位结果. 从攻击手段上来讲, GPS欺骗式攻击可以分为两类: 一类是转发式欺骗, 这种攻击利用了GPS通过传播时延计算伪距的原理, 通过一台接收机设备接收真实卫星信号, 经过延迟、功率放大后转发至攻击目标, 使得攻击目标接收机计算得到错误的位置^[5]. 此类攻击类似于传统的重放式攻击, 仅需转发信号, 实现难度低. 另一类是生成式欺骗, 该攻击利用了GPS民用波段信号格式公开的特点, 通过伪造真实信号发送至攻击目标, 使得导航接收机最终解算出错误的定位结果. 伪造者需要具备GPS信号编码、导航电文等相关知识, 实现难度相对较高^[6].

自2001年以来, 美国国家运输中心在其提交给美国国家运输部的技术报告中首次评估了欺骗式攻击对全球定位系统的危害性^[7], 随后, 众多学者开始对GPS的欺骗式干扰进行了系统研究. Wesson等人研制了生成式GPS欺骗器, 并成功攻击了一架无人机^[8]. Kerns等人通过建立无人机欺骗攻击的必要条件, 探讨了欺骗信号的作用范围, 研究了捕获欺骗信号与真实信号的过程^[9]. Liang等人提出了一种基于协同式网络GPS认证方法用于检测GPS攻击^[10]. 在国内, 史鹏亮等人对转发式欺骗干扰的选星方法进行了研究, 提出了一种基于常用GNSS定位选星方法和对卫星位置精度因子的贡献值选择被转发卫星的选星方法^[11]. He等人在建立多天线转发式攻击数学模型的基础上, 研究了影响攻击结果的关键因素和主要参数, 并设计开发了GPS欺骗攻击仿真系统进行欺骗原理进行验证^[12]. 梁高波等人从不同的角度研究了转发式欺骗攻击对接收机的影响^[13]. 有学者通过对目标接收机的精密定位以及转发信号的精确时延控制, 实现对授时接收机的定时偏差控制. 还有研究者通过分析伪距定位原理, 研究修改信号的导航电文信息实现转发式欺骗攻击, 并进行仿真研究^{[14, 15]}.

基站定位技术由于其覆盖范围广, 可用于室内定位, 所以基站定位也是目前常用的定位技术. 根据基站定位所采用的特征值, 可以分为基于增强小区ID (E-CID)定位、到达时间差(TDOA)定位、到达角度(AOA)定位以及混合定位^[16]. 传统的3G/4G网络下, 实际定位精度在100 m以上, 很多时候无法满足用户定位需求. 而传统的GPS静态单点定位精度一般在10 m以下^[17], 所以3G/4G基站定位在精度方面还是略显不足. 随着5G技术迅速发展, 5G引入的毫米波技术和高带宽带来了更高精度的到达角和到达时间, 同时5G布设的密集基站也为高精度、高鲁棒性的基站定位提供了硬件基础. 根据3GPP的标准, 5G定位服务1级应能达到水平精度10 m, 垂直精度3 m^[18]. 此外, 在安全方面, 目前的5G标准中引入了用户隐藏标识符 (subscription concealed identifier, SUCI)防止用户真实身份信息的泄露, 5G中终端的真实身份称为SUPI (subscription permanent identifier), 利用存放在用户终端的公钥, 将SUPI加密成用户隐藏标识符SUCI, 并经由基站上传至5G核心网. 在核心网内由统一数据管理(unified data management, UDM)解密SUCI得到用户正式身份SUPI, 然后再根据用户选择的认证方式提取对应的鉴权密钥与鉴权结果, 校验鉴权结果真伪^[19]. 由此可知, 5G网络具有较高的安全性.

基于以上内容, 本文提出了一种基于基站辅助对GPS系统进行欺骗检测的技术, 由于基站信号具备运营商的加密认证机制, 其本身可信程度较高, 因此基站定位为GPS抗欺骗提供了可信基础. 此外, 本文提出了一致性因数用于描述GPS定位结果和基站定位的一致性程度. 本文对该算法进行了全面的理论分析和实验. 实验表明, 在使用本论文模型情况下, 本算法的准确率为99.98%, 且在其他分类方法引入一致性因数的情况下, 准确率均有不同程度的提升.

1 系统模型与数据度量 1.1 系统模型

为便于后续对基于基站辅助的GPS抗欺骗技术的研究, 本节将对相关参数建立数学模型. 本文系统模型建立在WGS84 (world geodetic system)大地测量系统标准中的标准经纬坐标系中. 由于本文提出的抗欺骗方法仅与GPS定位和基站定位的位置有关, 与其他因素无关, 因此不考虑信号生成、传播、捕获的过程, 直接对解算出的定位结果进行分析. 假设GPS定位采用静态单点定位方式, 基站定位采用1级5G定位标准, 二者定位精度均为10 m^[18]. 假设地球上的某随机真实位置为 $ ({R_x}, {R_y}) $ , 正常工作下的GPS解算出的定位结果为 $ ({G_x}, {G_y}) $ , 基站定位解算出的定位结果为 $ ({B_x}, {B_y}) $ , 遭受攻击的GPS解算出的定位结果为 $({\textit S_x}, {\textit S_y})$ .

由于真实位置可为地球上任意位置, 则有 $ {R_x} $ 服从 $ [ - 180, 180] $ 上的均匀分布, 记为 $ {R_x}\sim U[ - 180, 180] $ , $ {R_y} $ 服从[−90, 90]上的均匀分布, 记为 $ {R_y}\sim U[ - 90, 90] $ .

假设攻击者意图是完全随机的, 同理有 $ {S_x} $ 服从 $ [ - 180, 180] $ 上的均匀分布, 记为 ${\textit S_x}\sim U[ - 180, 180]$ 服从[−90, 90]上的均匀分布, 记为 ${\textit S_y}\sim U[ - 180, 180]$ .

GPS和基站定位误差均用高斯分布表示. 则有:

$ {G_x} = {R_x} + {D_x} $

(1)

$ {G_y} = {R_y} + {D_y} $

(2)

其中, $ {D_x} $ 和 $ {D_y} $ 为相互独立且均服从 $ N(0, {10^{ - 8}}) $ 的高斯分布. 根据高斯分布特点, 可知 $ {G_x} $ 在95%的情况下处于区间 $ ({R_x} - 2 \times {10^{ - 4}}, {R_x} + 2 \times {10^{ - 4}}) $ . 如果将地球看为一个标准球体, 使用半正矢公式计算可得到水平方向上最大误差为22.26 m, 可见误差符合满足GPS单点定位精度.

同理有:

$ {B_x} = {R_x} + D_x^{'} $

(3)

$ {B_y} = {R_x} + D_y^{'} $

(4)

其中, $ D_x^{'} $ 和 $ D_y^{'} $ 为相互独立且均服从 $ N(0, {10^{ - 8}}) $ 的高斯分布. 且误差符合1级5G定位标准精度.

1.2 数据集

目前, 通用的GPS欺骗数据集较少, 仅有TEXBAT(Texas spoofing test battery). 然而该数据集缺乏基站定位信息, 不适用于本文. 因此, 本文在实验采集的数据基础上, 根据上述建立的模型进行扩充, 生成了包含基站定位的GPS欺骗数据集, 数据集示例如表1所示, 其中, “标签”列为0代表GPS遭受欺骗, 1代表GPS工作正常.

1.3 一致性因数

为了描述GPS定位和基站定位结果的一致性程度, 本文提出了一种新的度量: 一致性因数(consistency factor, CF), 该度量的计算方法如式(5):

$ CF({G_x}, {G_y}, {B_x}, {B_y}) = | {{G_x} - {B_x}} | + | {{G_y} - {B_y}} | $

(5)

其中, $ {G_x} $ 为GPS定位经度, $ {G_y} $ 为GPS定位纬度, $ {B_x} $ 为基站定位经度, $ {B_y} $ 基站定位纬度. 使用本公式, 可将上述数据集中具有4维的输入特征组合为单维度特征. 根据经纬度范围可推导出 $ CF $ 的取值区间为 $ [0, 540] $ , 且该一致性因数 $ CF $ 越大, 则代表二者一致性程度越低, 反之, 一致性因数 $ CF $ 越小, 则二者一致性程度越高.

2 基于基站辅助的抗欺骗方法 2.1 系统总体结构

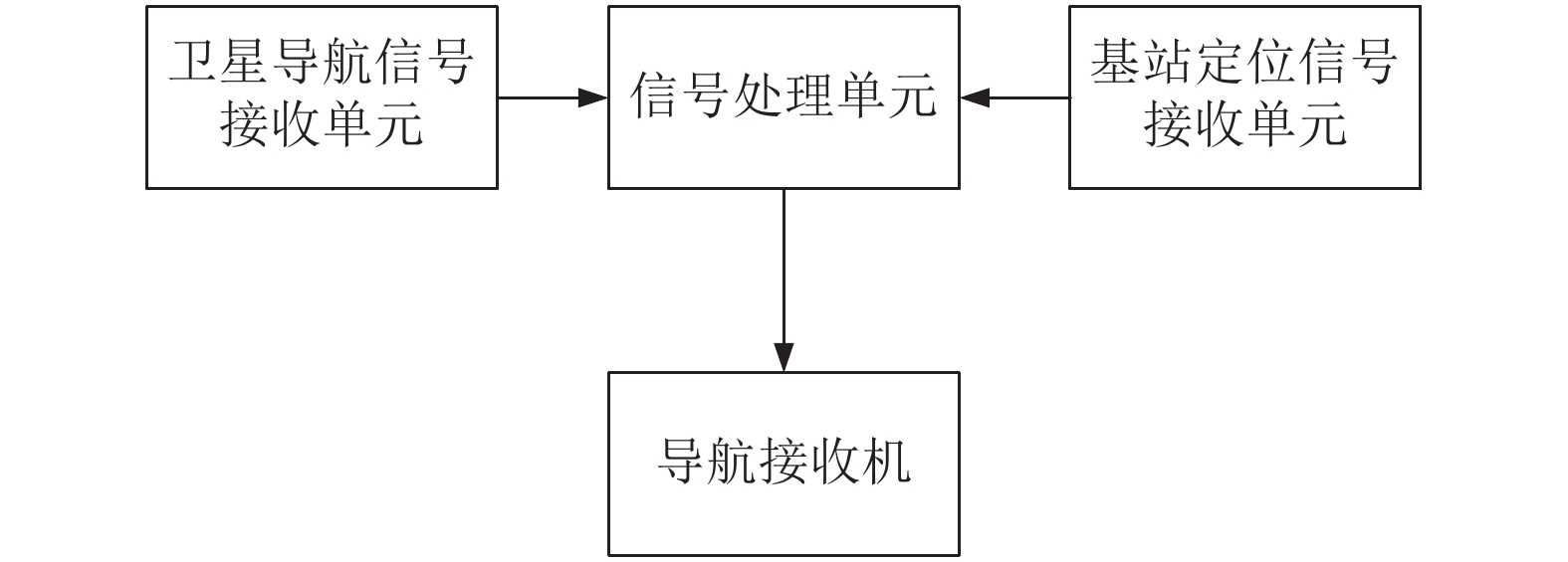
本文提出基于基站辅助的GPS欺骗检测方法, 利用可信的基站定位信号来校验可能被欺骗的GPS信号. 系统的总体结构包括GPS信号接收单元、基站信号接收单元、信号处理单元和导航接收机. 其中各单元的功能为: GPS信号接收单元负责接收GPS信号, 并将GPS信号发送至信号处理单元处理. 基站信号接收单元负责接收基站信号, 并将基站信号发送至信号处理单元. 信号处理单元将二者信号处理完毕后, 解算出定位结果, 计算一致性因数, 根据阈值判断是否遭受欺骗式攻击, 最后发送至导航接收机. 总体结构如图1.

下面分别分析正常工作情况和受到攻击情况的一致性因数.

2.2 不存在攻击情况下的一致性因数分析

当欺骗攻击不存在时, 系统的工作状况如图2所示. 首先, GPS信号接收单元接收GPS信号, 计算得定位位置为经度 $ {G_x} $ , 纬度 $ {G_y} $ , 并将以上结果发送至信号处理单元. 接着, 基站定位信号接收单元接收基站定位信号, 计算得定位位置为经度 $ {B_x} $ , 纬度 $ {B_y} $ , 并将以上结果发送至信号处理单元. 信号处理单元根据式(6)计算出一致性程度 $ CF $ .

$ CF({G_x}, {G_y}, {B_x}, {B_y}) = | {{G_x} - {B_x}} | + | {{G_y} - {B_y}} | $

(6)

根据第1.1节中的模型定义, 在正常工作情况下, 一致性程度CF的最大值推导如式(7)所示.

$ \begin{split} \max (CF) =& \max \left(\Big| {{G_x} - {B_x}} \Big|\right) + \max \left(\Big| {{G_y} - {B_y}} \Big|\right)\\ = &\max \left(\left| {{R_x} + {D_x} - {R_x} - D_x^{'}} \right|\right)\\ &+ \max \left(\left| {{R_{{y}}} + {D_y} - {R_y} - D_y^{'}} \right|\right)\\ = &\max \left(\left| {{D_x} - D_{{x}}^{'}} \right|\right) + \max \left(\left| {{D_{{y}}} - D_y^{'}} \right|\right) \end{split} $

(7)

由于 $ {D_x} $ , $D_{{x}}^{'}$ , ${D_{{y}}}$ , $ D_y^{'} $ 均为互相独立且服从 $ N(0, {10^{ - 8}}) $ , 则在95%的情况下, 他们的值域为 $ ( - 2 \times {10^{ - 4}}, 2 \times {10^{ - 4}}) $ , 因此有:

$ \max (CF) = 8 \times {10^{ - 4}} $

(8)

根据上述推导过程可以得出结论, 攻击不存在时, 即在正常工作情况下, 一致性程度最大值为 $ 8\times {10}^{-4} $ .

2.3 受到攻击的一致性因数分析

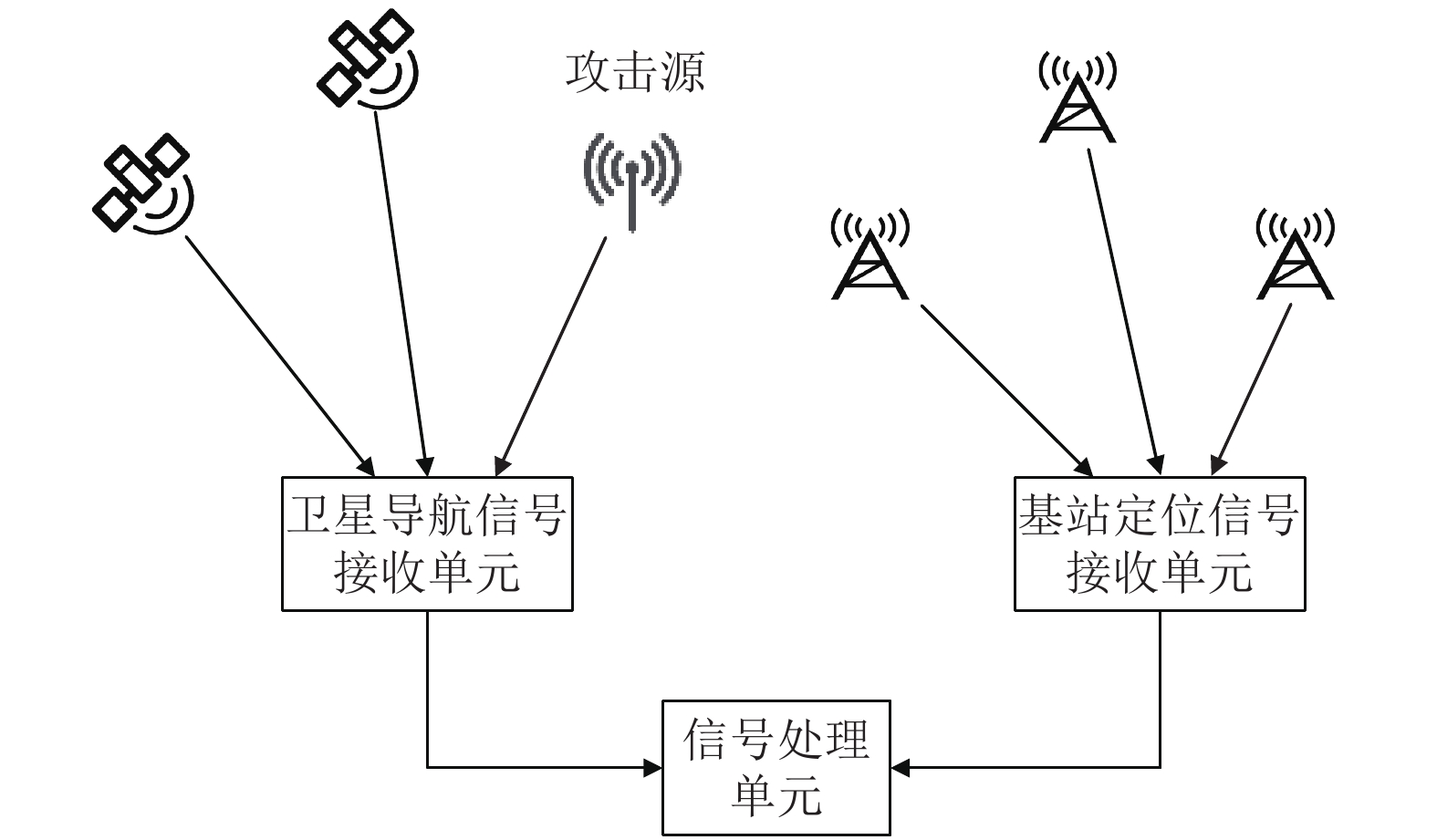
当存在欺骗攻击源信号时, 其工作状况如图3所示. 首先, GPS信号接收单元接收GPS信号和攻击源信号, 计算得攻击者设定位置为经度 $ {S_x} $ , 纬度 $ {S_y} $ , 并将以上结果发送至信号处理单元. 接着, 基站定位信号接收单元接收基站定位信号, 计算得定位位置为经度 $ {B_x} $ , 纬度 $ {B_y} $ , 并将以上结果发送至信号处理单元. 信号处理单元根据式(9)计算出一致性因数 $ CF $ .

$ CF({S_x}, {S_y}, {B_x}, {B_y}) = | {{S_x} - {B_x}} | + | {{S_y} - {B_y}} | $

(9)

下面计算CF小于正常情况下一致性因数最大值的概率, 由于CF的分布较为复杂, 采取放缩法来估计此概率值.

$ \begin{split} CF({S_x}, {S_y}, {B_x}, {B_y}) =& | {{S_x} - {B_x}} | + | {{S_y} - {B_y}} | \\ =& | {{S_x} - {R_x} - {D_x'}} | + | {{S_y} - {R_y} - {D_y'}} | \\ \approx & | {{S_x} - {R_x}} | + | {{S_{{y}}} - {R_y}} | \\ \geqslant& | {{S_x} - {R_x}} | \\ \end{split} $

(10)

根据第1.1节中的模型定义, $ {S_x}, {R_x}\sim U[ - 180, 180] $ , 且 $ {S_x}, {R_x} $ 互相独立, 则有 $ | {{S_x} - {R_x}} | $ 服从低限为0, 众数为0, 上限为360的三角分布. 计算可得该三角分布 $ | {{S_x} - {R_x}} | < 8 \times {10^{ - 4}} $ 的概率为 $ 2.22 \times {10^{ - 6}} $ . 则有:

$ P(CF < 8 \times {10^{ - 4}}) = 2.22 \times {10^{ - 6}} $

(11)

因此, 在使用本文所定义的模型时, 当GPS遭受攻击后, 可将正常情况下一致性程度的最大值作为阈值进行判决, 从而检测出欺骗攻击的存在.

2.4 算法具体流程

基于第2.2节和第2.3节的讨论, 得到算法的具体流程如算法1所示. 下面对本算法的时间复杂度和空间复杂度进行分析, 首先算法获取4个输入参数 $ {G_x}, $ $ {G_y}, {B_x}, {B_y} $ , 然后使用式(5)计算一致性因数 $ CF $ , 该公式涉及到3次加减法运算以及两次绝对值运算. 最后将 $ CF $ 与阈值 $ d $ 比较一次即得出判断结果. 对于不同的输入, 算法的执行语句数和额外存储空间均为常数, 因此本算法的时间复杂度和空间复杂度均为O(1), 故本算法具有较高的计算效率.

算法1. GPS欺骗检测算法

1) GPS接收单元接收GPS信号并发送至信号处理单元, 记为 $\scriptstyle {G_x}, {G_y} $ .

2) 基站定位信号接收基站信号并发送至信号处理单元, 记为 $\scriptstyle {B_x}, {B_y} $ .

3) 信号处理单元将步骤1)和2)中接收到的定位结果, 根据式(5)计算出一致性因数 $\scriptstyle CF $ .

4) 如果 $\scriptstyle CF $ 大于等于设定的阈值 $\scriptstyle d $ 则判定为遭受攻击. 反之, 则判定为正常工作.

5) 基于步骤4)中的判断结果, 如果GPS信号被欺骗, 则发送基站定位坐标至导航接收机, 并返回遭受攻击; 如果GPS信号工作正常, 则发送GPS定位坐标至导航接收机, 返回正常工作.

3 实验处理和分析 3.1 实验环境

为验证本文算法的实际效果, 本文使用第1节所提出的数据集, 共10万条数据, 其中5万条为攻击数据, 5万条为正常数据. 经过式(5)转化为单维的一致性因数, 并使用阈值分割法进行判决.

实验硬件为Intel(R) Core i5-9400F CPU @2.90 GHz, 内存16.0 GB的台式电脑, 软件配置为Windows 10 Professional, 工具语言采用Python 3.9.5.

3.2 评价指标

一般来说, 判断GPS接收机是否遭受欺骗攻击可以视为一个二元分类问题, 因此本文使用准确率(Accuracy)和精度(Precision)作为指标来评价本算法, 其中准确率作为主要评价指标. 计算方式如式(12)–式(13)所示. 英文缩写含义如表2所示.

$ Accuracy = \frac{{TP + TN}}{{TP + TN + FN + FP}} $

(12)

$ Precision = \frac{{TP}}{{TP + FP}} $

(13)

3.3 实验结果

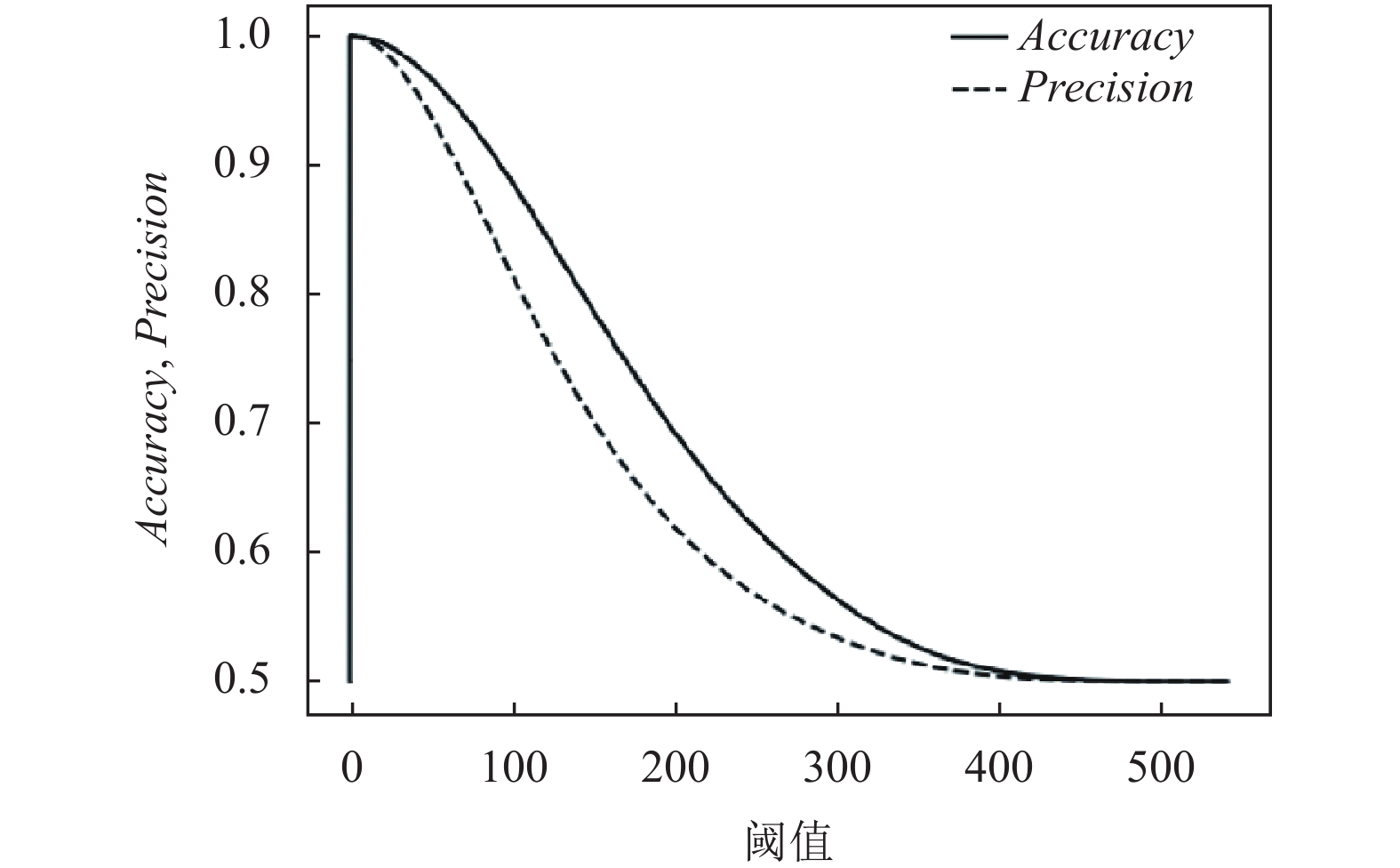
为了充分研究设定不同阈值对结果的影响, 本文采用遍历阈值法来观察各阈值的分割效果. 第1.3节已给出一致性因数CF的区间, 故遍历区间设为 $ [0, 540] $ . 考虑到服从 $ N(0, {10^{ - 8}}) $ 的分布数量级多为 $ {10^{ - 4}} $ , 故步长设置为 $ {10^{ - 4}} $ . 得到准确率、精确率的曲线分别如图4所示, 部分具体结果如表3所示. 图5表明准确率在(0, 2×10^–4)区间内为单调递增, 再结合图4可知准确率在 $ (2 \times {10^{ - 4}}, 540) $ 区间单调递减. 由此可见, 设定合适的阈值可以有效检测GPS欺骗的发生. 第1节中推导出的阈值为 $ 8 \times {10^{ - 4}} $ 接近极大值点, 可见理论和实际符合的很好. 另外, 在准确率相近的情况下, 应选取较小的阈值, 以检测距离基站定位结果较近的攻击点.

本文还使用了经典的机器学习分类算法进行对比实验. 实验按7:3的比例划分训练集和测试集, 以同样的指标来评估各模型, 得到实验结果如表4所示. 可以看到, 本文使用的“阈值分割+一致性因数”进行分类后, 在准确率上和精确率上均优于其他6种机器学习分类算法. 此外, 由于本算法实现简单, 因此在运行时间上也有极大优势, 相较于传统机器学习分类算法, 运行效率有较大提升.

4 结论

本文提出了一种基于基站辅助的GPS抗欺骗技术, 通过安全性高的基站定位校验GPS定位结果, 且引入了一致性因数用于描述GPS定位结果和基站结果的一致性程度. 然后采用阈值分割法对一致性因数进行判决, 取得了较高分类准确率和精确率. 此外, 本文通过实验证明了引入一致性因数可有效提高分类算法的准确率. 与现有欺骗检测技术相比, 本文方法实现简单, 由于电力5G终端兼具GPS信号接收模块和5G基站信号接收模块, 因此本算法可有效应用在电力5G场景.