2. 山东省智能建筑技术重点实验室, 济南 250101
2. Shandong Provincial Key Laboratory of Intelligent Building Technology, Jinan 250101, China
目标跟踪作为计算机视觉中的关键问题之一, 已经被广泛应用于视频监控、人机交互、无人驾驶等领域. 目标跟踪是根据视频帧序列第一帧的目标位置来预测后续帧中的目标位置, 不仅需要把跟踪目标所在的空间位置在视频序列中标注出来还需要将连续的视频帧中标注出的目标中心点连接以得到运动轨迹[1].
目标跟踪分为生成式和判别式两类方法. 生成式方法通过最小化跟踪目标和候选目标之间的重构误差来确认目标, 比较常见的算法有卡尔曼算法、粒子滤波算法、光流法等. 而判别式方法是以当前帧目标区域为正样本、当前帧背景区域为负样本训练分类器, 下一帧用训练好的分类器寻找最优的目标区域. 判别式方法的最新发展就是相关滤波类方法和深度学习类方法, 这两个方向的算法是当前跟踪算法中的研究热点. Bolme等人开创性地将相关滤波技术引入到目标跟踪领域, 提出了一种误差平方和最小的滤波器MOSSE跟踪算法[2], 不同于只是简单使用模板跟踪的算法, 其滤波器是通过首帧的目标训练而得的, 遮挡时能够根据跟踪是否失败来决定是否更新滤波器参数, 以自适应于目标的变化. KCF算法[3]是通过基于核化的岭回归分类器使用循环移位得到的循环矩阵来采集样本, 利用循环矩阵的性质降低运算量以提高算法实时性. C-COT算法[4]将不同空间分辨率的特征图插值到连续空间域, 将多尺度与深层语义信息结合起来, 可以更好地应对尺度变化时的模型漂移.
近年来, 随着深度学习在目标检测、实例分割等多方面研究中取得了令人瞩目的成果, 基于深度学习的目标跟踪研究也越来越多. 现有的针对目标检测、实例分割等预训练的网络需要区分出较多类的目标, 但在跟踪问题中, 网络只需要区分前景和背景两类目标, 太复杂的网络会增加计算量, 降低算法的实时性. 卷积神经网络(CNN)凭借其对特征强大的表示能力和高效的提取方式, 逐渐应用于计算机视觉领域. 在目标跟踪任务中, 出现了众多基于CNN的深度学习算法, 其致力于对目标表征能力的强化, 例如树结构卷积神经网络(TCNN)[5]用了树结构来组织多个CNN构成网络, 模型按照树结构中的路径进行在线更新, 提高了模型可靠性; 结构感知网络(SANet)[6]将CNN与循环神经网络(RNN)融合, CNN用来提供目标物体和背景之间的判别性, RNN用来提供目标物体与相似物之间的判别性, 以此增强模型对相似目标的分辨能力; 全卷积孪生网络(SiamNet)[7]利用相同的两个CNN进行相似度的比较, 成功地将跟踪问题转换为相似度学习问题; 对抗学习跟踪算法(VITAL)[8]用到了生成对抗网络(GAN)算法[9]的思想, 在CNN的基础上引入了对抗特征生成器, 有效提高了网络性能, 成功将GAN应用到目标跟踪领域.
基于迁移学习[10]思想的多域卷积神经网络(MDNet)[11]是CNN应用于深度目标跟踪最具有代表性的算法之一. MDNet算法通过多域学习的网络结构, 利用网络的卷积层学习不同视频中的通用特征, 利用多分支全连接层分别学习不同视频的高层特征, 候选框的选取部分借鉴了RCNN[12], 具有很高的跟踪准确率. 但一般来说, 跟踪模型会随着目标的变化而稳定变化, 当目标出现一些复杂情况时, 模型更新会使得模型的可靠性降低, 用这样的模型去进行后续的跟踪, 很难重新准确定位目标; 跟踪问题中, 每帧的正样本在空间上高度重叠, 不能捕获丰富的外观变化, 并且正样本和负样本极度不平衡. 本文在MDNet算法基础上提出了一种基于候选框置信度与坐标方差阈值判断相结合的模型更新方法, 使其正样本在正确的基础上更加丰富, 其次将原算法的交叉熵损失函数改进为效果更好的focal loss损失函数. Focal loss最初由Lin等人[13]提出, 是一种改进的交叉熵损失函数, 用于解决目标检测领域数据极不平衡的问题, 并且在同一论文中成功应用于RetinaNet算法中, 后来逐渐被应用于语义分割、目标跟踪等任务中.
1 MDNet算法原理及损失函数 1.1 MDNet算法原理如图1所示, MDNet算法使用多域学习的网络结构, 输入是107×107的RGB图像, conv1–conv3卷积层和fc4、fc5全连接层构成网络共享层, fc61–fc6k全连接层为特定域层, 每个视频序列都对应一个域. 训练时, 用不同的视频序列训练得到网络共享层, 追踪一个新目标时, 网络结合共享层和特定域层, 只有对应该视频序列的特定域层被使用.

|
图 1 MDNet网络结构 |
MDNet采用随机梯度(SGD)的方式进行端到端的离线预训练. 在离线训练过程中, 每帧提取50个正样本和200个负样本, 正样本与目标框的重叠率≥0.7, 负样本与目标框的重叠率≤0.5. 每一帧图片, 以上一帧目标的位置为中心, 采用多维高斯分布(宽、高和尺度3个维度)的形式采样256个候选框, 然后将这256个候选框输入到网络里进行计算. 网络输出是一个二维向量, 分别表示输入的候选框是对应目标和背景的概率. 目标得分概率最高的那个候选框即确定为最终跟踪到的目标. 计算如式(1)所示.
| $ {x}^{*}=\underset{{x}^{*}}{\mathrm{arg}\mathrm{max}}{f}^+\left({x}^{i}\right) $ | (1) |
MDNet网络使用长期和短期两种方式更新. 在线跟踪时, 当前帧判断跟踪成功, 且预测边界框与真实边界框重叠率不小于0.7时, 在目标框周围按照随机高斯分布选取50个正样本和200个负样本, 提取的负样本与目标框的重叠率不大于0.3. 视频序列的第一帧中提取500个正样本和5 000个负样本. 在边界框回归中, 随机提取1 000个重叠率≥0.6的正样本. 当预测目标的分数小于0.5时, 用最近20帧所收集到的样本进行短期更新, 每隔10帧用最近100帧收集到的样本进行一次长期更新.
1.2 MDNet算法的损失函数MDNet算法中使用了交叉熵损失函数, 函数公式如式(2):
| $ L=\frac{1}{ N}{\displaystyle \sum _{i}-}\left[{y}_{i}\mathrm{log}\left({p}_{\text{i}}\right)+\left(1-{y}_{i}\right)\mathrm{log}\left(1-{p}_{i}\right)\right] $ | (2) |
其中,
本文基于MDNet算法提出了一种基于候选框置信度与坐标方差阈值判断相结合的模型更新方法, 并将原算法的交叉熵损失函数改进为效果更好的focal loss损失函数.
2.1 基于候选框置信度与坐标方差阈值判断相结合的模型更新方法不同于MDNet算法每帧无差别地在目标框周围提取50个正样本和200个负样本进行特征集合的更新, 本文算法为了丰富正样本, 采取基于候选框置信度的方法选取正负样本, 根据候选框置信度(即候选框预测得分)排列的top5, 按照随机高斯分布在5个候选框周边都分别选取10个正样本和40个负样本放入用于更新的特征集合中.
MDNet算法中, 只要当前帧预测得分top5候选框的得分均值为正, 则认为跟踪成功, 对每个跟踪成功的当前帧目标框周围都选取符合条件的样本进行特征样本集合的更新. 本文算法在判断是否进行模型更新时, 考虑到用当前帧所取样本进行更新可能会使模型可靠性降低从而导致后续跟踪性能下降的问题, 设置中心点坐标方差阈值:
| $ {\sigma ^2} = \frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {{m_i} - \overline m} \right)}^2}} $ | (3) |
其中,
跟踪检测中, 一张特征图往往会产生成千上万的候选区, 但绝大多数像素都是背景, 只有少数像素是我们要检测跟踪的对象, 而且正样本的位置比较集中, 第一帧取得的都是在标记的目标附近, 位置比较相近且数量较少, 负样本取自于图片中比较分散且数量较多, 负样本的数量远远多于正样本的数量, 正负样本极其不均衡. 交叉熵损失函数在训练过程中会倾向于样本多的类别, 导致对样本量少的类别判断性能较差, 针对此问题引入focal loss损失函数:
| $ {{FL}}\left( {{p_{{t}}}} \right) = - \alpha {\left( {1 - {p_{{t}}}} \right)^\gamma }\log \left( {{p_{\text{t}}}} \right) $ | (4) |
| $ {p_{{t}}} = \left\{ {\begin{array}{*{20}{c}} {{p_{{i}}}},&{y = 1} \\ {1 - {p_{{i}}}},&{y = 0} \end{array}} \right. $ | (5) |
其中,
本文算法基于PyTorch深度学习框架实现, 实验操作系统为 Windows, CPU 为Intel i7-7700 3.60 GHz, GPU为NVIDIA GeForce GTX 1050 Ti.
数据集使用OTB100[14]和自己采集的监控视频数据集的混合数据集, 其中包括OTB100中80个完全标注的视频序列和20个完全标注的监控视频数据, 其中涉及背景干扰、光照变化、遮挡、形变、尺度变化、快速运动、运动模糊、移出视野、低分辨率、平面内旋转和外旋转11种视频属性.
3.2 评价指标 3.2.1 成功率(Success)当预测边界框
| $ {{IOU}} = \frac{{\left| {{{{R}}_{{{tr}}}} \cap {{{R}}_{{{gt}}}}} \right|}}{{\left| {{{{R}}_{{{tr}}}} \cup {{{R}}_{{{gt}}}}} \right|}} $ | (6) |
| $ \varepsilon = \sqrt {{{\left( {{x_{tr}} - {x_{gt}}} \right)}^2} + {{\left( {{y_{tr}} - {y_{gt}}} \right)}^2}} $ | (7) |
本实验包括4部分: 基于候选框置信度的更新策略对比实验、坐标方差阈值实验、损失函数对比实验、本文算法评估实验.
3.3.1 基于候选框置信度的更新策略对比实验本实验针对本文提出的基于候选框置信度的更新策略中候选框的选择数量及分配方法进行了实验, 分配方法设置正负样本均分和由多到少分布的两类实验. 选择正负样本的总数量是参考MDNet实验中正负样本分别取50、200个, 在此基础上多次实验, 最终确定了4个策略的样本取值. 策略1–4分别为: (1)得分前5的候选框对每个框周边都取20个正样本、80个负样本; (2)得分前5的候选框依次对每个框周边取30、25、20、15、10个正样本和120、100、80、60、40个负样本; (3)得分前5的候选框依次对每个框周边取15、13、10、7、5个正样本和60、50、40、30、20个负样本; (4)得分前5的候选框对每个框周边都取10个正样本、40个负样本.
实验结果如表1所示, 可以看出, 策略1所取样本是策略4所取样本数的两倍, 精确率比策略4要低2.46%, 但是成功率只提升了0.07%不明显, 分析原因可能是, 虽然对得分前5的候选框周边取样本可以增加样本的丰富性, 但取的样本数量过多会影响精确度, 进而对成功率的提升也有影响, 此结果也侧面证明了策略4所取样本数量已足够, 样本数量过多反而影响结果; 而策略2和策略3成功率和准确率均不如策略4, 效果不够好的原因可能是, 得分越高的候选框取的样本数越多、得分越低的候选框取的样本数越少, 对模型更新影响最大的还是得分最高的候选框, 得分第5的候选框对整个模型的影响非常小, 因此提升效果不明显. 但策略1、4在精确率和成功率均优于原算法, 因此本实验可以充分证明基于候选框置信度的更新策略的有效性.
| 表 1 更新策略对比实验的测试结果 |
3.3.2 坐标方差阈值实验
图2是对数据集一个视频序列中当前帧预测得分top5候选框的位置数据的方差, 图2(a)–图2(f)依次是对候选框左上角坐标
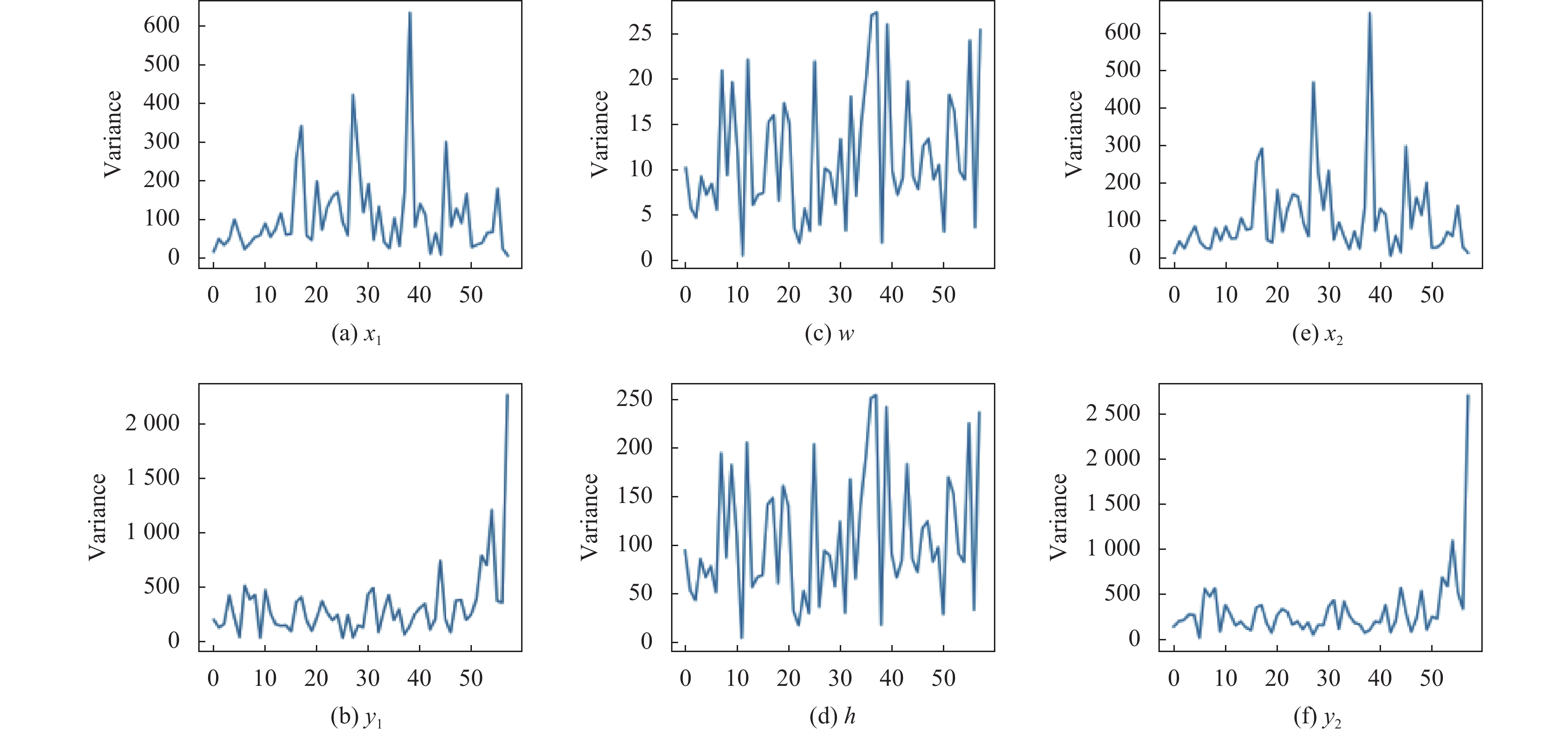
|
图 2 坐标方差 |
表2为选择方差变化明显的中心点坐标方差, 设定不同的方差阈值进行实验得到的结果, 可以看出, 加入方差阈值判断后, 在精确率与成功率上均有不同程度的提高, 其中方差阈值取前5帧方差均值的1.2倍时取得最好的结果, 精确率相比于原算法提高了2.18%, 成功率上提高了0.93%. 实验充分证明了坐标方差阈值判断方法的有效性.
| 表 2 不同坐标方差阈值实验结果 |
3.3.3 损失函数对比实验
本实验为更改损失函数为focal loss函数后在数据集上的测试结果与更改损失函数之前的测试结果对比, 实验中唯一变量为损失函数, MDNet-FL算法为MDNet算法更改交叉熵损失函数为focal loss损失函数后的算法.
实验结果如表3所示, 可以看出, MDNet-FL比起原算法在精确率和成功率上均有提高. 但精确率提高了0.83个百分点的同时, 成功率仅提高了0.20个百分点. 分析原因, focal loss的原理是通过控制不同类别对损失函数的贡献来调节类间的不平衡, 更强调错分样本, 完全丢弃易分的样本, 降低了简单负样本在训练中所占的权重. 训练中实际值与预测值差距越大, 对损失的贡献就越大, 训练趋于稳定后, 对损失函数贡献最明显的是困难样本和标签不明确两部分. 因此, 实验效果很大程度上取决于数据集的特点. 本文实验中, 设置正样本与目标框的重叠率大于0.7, 负样本与目标框的重叠率小于0.5, 因此会出现虽然预测到了真实目标但是为非正样本的情况, 这时候引入focal loss, 虽然一定程度上解决了正负样本不平衡的问题, 但是标签不明确的样本权重被增大, 影响网络训练过程, 进而导致效果提升不够明显.
| 表 3 损失函数对比实验 |
3.3.4 本文算法评估
本文算法是在MDNet算法基础上采用了基于候选框置信度与坐标方差阈值判断相结合的更新方法, 引入了focal loss损失函数.
本实验采用OPE (one-pass evaluation)评估方法, 图3为本文算法与MDNet算法在数据集上的评估结果: 准确率结果图中横坐标的阈值为预测边界框与真实边界框中心点误差距离的像素点数, 设置为20个像素点; 成功率结果图中横坐标的阈值为预测边界框与真实边界框重叠率, 跟踪问题中, 一般认为目标框与真实框重叠率大于0.5即为跟踪成功, 且本文为了对比实验效果, 将实验成功率阈值与MDNet中的实验统一设置为0.5. 可以看出, 本文算法在精确率上取得了90.87%的优异表现, 成功率上取得了68.32%的结果, 相较于MDNet算法在精确率上提高了2.80个百分点, 在成功率上提高了1.42个百分点.

|
图 3 混合数据集上的测试结果 |
在OTB100基准数据集上对本文算法和MDNet算法进行了评估对比, 图4为实验结果, 可以看出, 相比于原算法, 本文算法在精确率上提高了0.29个百分点, 成功率上提高了0.23个百分点.
图5展示了本文算法在几个视频序列中与MDNet算法测试结果的效果对比, 本文算法为红色框, MDNet算法为绿色框. 可以直观看出, 无论在OTB100视频序列中还是在监控视频序列中, 本文算法目标框更准确, 而且在部分MDNet算法跟踪失败的视频帧中本文算法跟踪成功.

|
图 4 OTB100数据集上的测试结果 |
表4列出了本文算法与MDNet算法在部分视频序列测试结果成功帧数的对比. 跟踪阈值设置为0.5, 即当前帧的预测边界框与目标真实边界框重叠率大于0.5视为当前帧跟踪成功. 其中S为视频序列的总帧数, M为MDNet算法跟踪成功的帧数, N为本文算法跟踪成功的帧数. 其中, Bolt视频序列中效果最为明显, 跟踪成功率提高了8.60%.
4 结论与展望本文在MDNet算法基础上提出了一种基于候选框置信度与坐标方差阈值判断相结合的更新方法, 引入了focal loss损失函数, 有效丰富了正样本, 提升了模型的性能, 并在实验中验证了模型的有效性, 对跟踪领域中正样本缺乏且不够丰富的问题有一定借鉴意义. 近年来, 虽然目标跟踪领域有大量研究取得了较好的效果, 但相比于计算机视觉其他领域, 当前基于深度学习的目标跟踪算法[15-17]仍面临着诸多挑战, 其中最关键的是缺乏大量准确的训练数据, 因此, 针对不同应用场景做出大量的公开数据也是推动基于深度学习的目标跟踪发展的重要途径.

|
图 5 部分视频序列测试效果 |
| 表 4 数据集部分视频在本文算法的测试结果 |
| [1] |
李玺, 查宇飞, 张天柱, 等. 深度学习的目标跟踪算法综述. 中国图象图形学报, 2019, 24(12): 2057-2080. |
| [2] |
Bolme DS, Beveridge JR, Draper BA, et al. Visual object tracking using adaptive correlation filters. Proceedings of 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Francisco: IEEE, 2010. 2544–2550.
|
| [3] |
Henriques JF, Caseiro R, Martins P, et al. High-speed tracking with kernelized correlation filters. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(3): 583-596. DOI:10.1109/TPAMI.2014.2345390 |
| [4] |
Danelljan M, Robinson A, Khan FS, et al. Beyond correlation filters: Learning continuous convolution operators for visual tracking. Proceedings of the 14th European Conference on Computer Vision. Amsterdam: Springer, 2016. 472–488.
|
| [5] |
Nam H, Baek M, Han B. Modeling and propagating CNNs in a tree structure for visual tracking. arXiv: 1608.07242, 2017.
|
| [6] |
Fan H, Ling HB. SANet: Structure-aware network for visual tracking. Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops. Honolulu: IEEE, 2017. 2217–2224.
|
| [7] |
Bertinetto L, Valmadre J, Henriques JF, et al. Fully-convolutional Siamese networks for object tracking. Proceedings of European Conference on Computer Vision. Amsterdam: Springer, 2016. 850–865.
|
| [8] |
Song YB, Ma C, Wu XH, et al. VITAL: Visual tracking via adversarial learning. Proceedings of 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018. 8990–8999.
|
| [9] |
Goodfellow IJ, Pouget-Abadie J, Mirza M, et al. Generative adversarial nets. Proceedings of the 27th International Conference on Neural Information Processing Systems. Montreal: NIPS, 2014. 2672–2680.
|
| [10] |
Pan SJ, Yang Q. A survey on transfer learning. IEEE Transactions on Knowledge and Data Engineering, 2010, 22(10): 1345-1359. DOI:10.1109/TKDE.2009.191 |
| [11] |
Nam H, Han B. Learning multi-domain convolutional neural networks for visual tracking. Proceedings of 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016. 4293–4302.
|
| [12] |
Girshick R, Donahue J, Darrell T, et al. Rich feature hierarchies for accurate object detection and semantic segmentation. Proceedings of 2014 IEEE Conference on Computer Vision and Pattern Recognition. Columbus: IEEE, 2014. 580–587.
|
| [13] |
Lin TY, Goyal P, Girshick R, et al. Focal loss for dense object detection. Proceedings of 2017 IEEE International Conference on Computer Vision. Venice: IEEE, 2017. 2999–3007.
|
| [14] |
Wu Y, Lim J, Yang MH. Object tracking benchmark. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(9): 1834-1848. DOI:10.1109/TPAMI.2014.2388226 |
| [15] |
罗元, 肖航, 欧俊雄. 基于深度学习的目标跟踪技术的研究综述. 半导体光电, 2020, 41(6): 757-767. |
| [16] |
Zhang XQ, Jiang RH, Fan CX, et al. Advances in deep learning methods for visual tracking: Literature review and fundamentals. International Journal of Automation and Computing, 2021, 18(3): 311-333. DOI:10.1007/s11633-020-1274-8 |
| [17] |
Zhu K, Zhang XD, Chen GZ, et al. Single object tracking in satellite videos: Deep siamese network incorporating an interframe difference centroid inertia motion model. Remote Sensing, 2021, 13(7): 1298. DOI:10.3390/rs13071298 |
 2022, Vol. 31
2022, Vol. 31


