电子商务的快速发展, 让我国快递数量在2017年就进入了“单日亿件”时代, 为了降低地面货运交通的压力, 提高快递服务质量, 国内外各大物流公司早早将旋翼无人机加入物流配送环节, 作为解决“最后一公里”问题的答案[1]; 另一方面, “无人机+行业细分”的发展模式也让旋翼无人机在城市内的安防和抢险救灾等方面发挥着重要作用[2].
面对复杂的城市环境, 旋翼无人机的路径规划技术格外重要. 一条好的飞行路径, 直接关系到无人机的运行效率、自身安全和对地面的安全影响[3]. 如何在复杂城市环境下, 快速找到距离更短、能耗更低、安全性更高、更符合旋翼无人机运动约束的路径, 是目前急需解决的问题.
传统的路规划如A*算法和生物启发类算法, 计算量大、规划时间长, 不能很好地应对高维复杂环境[4-5]; 数学模型法、人工势场法, 对环境和机器人的建模要求较高, 且容易陷入局部最优[6-7]; 基于采样的路径规划方法[8-10], 通过随机性的节点采样, 能快速寻找到空间中的路径, 受维度变化的影响小, 但较强的随机性和盲目的路径寻找策略, 导致求解效率较低, 较难找到高质量路径解.
LaValle教授在1999年提出了快速搜索随机树(RRT)算法[11], 以其独特的节点扩展机制, 成功应用于多种路径规划场景中, 如覆盖路径规划、机械臂路径规划、车辆路径规划等. 随后, RRT*算法[12]被提出, 在RRT算法的基础上增加了父节点重新选择和局部节点重连步骤, 弥补了RRT算法的一些不足, 且被证实能够达到路径最优[13]. 然而以上算法及其变体只能面向[0, 1]地图环境, 针对机器人在连续成本变化空间的路径规划问题, Jaillet等人提出了T-RRT算法[14], 在RRT算法的基础上引入了模拟退火的思想, 自行判断新成本节点能否被扩展, 让路径的探索偏向低成本区域, 可用于机器人在三维连续成本空间的路径规划. 紧随其后, T-RRT*算法[15]被提出, 将RRT*算法的思想与T-RRT算法相结合, 进一步降低了路径成本.
另一方面, 针对RRT算法随机性强的问题, 文献[16]提出的I-RRT算法, 以目标点概率性偏置的方式, 让搜索树的新节点扩展指向目标点; 文献[17]提出Informed-RRT*算法, 通过约束地图上的采样区域, 减少盲目性的同时, 较好地提高了路径质量; 文献[18,19]结合人工势场法的思想, 提出APF-RRT算法, 将目标点方向参与到每一次新树节点扩展中, 影响节点扩展. 然而, 在面对城市环境下的旋翼无人机路径规划工况, 上述方法还存在以下问题:
(1)空间成本类型考虑不充足;
(2)路径节点的扩展质量差;
(3)路径抖动性强.
针对这些问题, 本文在T-RRT算法的基础上, 提出基于探索、启发和转移的EHT-RRT (exploring heuristic transition-based RRT)算法, 综合全局路径规划和局部路径规划的特点, 通过多层球形危险度探索、启发式成本估计、局部节点滑移、添加节点的局部最好方向属性, 以及改进了的节点扩展机制, 让算法在三维空间中的规划路径更加稳定、平滑和安全, 减少路径后处理和轨迹规划的难度, 更适合解决旋翼无人机在复杂三维环境下的路径规划问题.
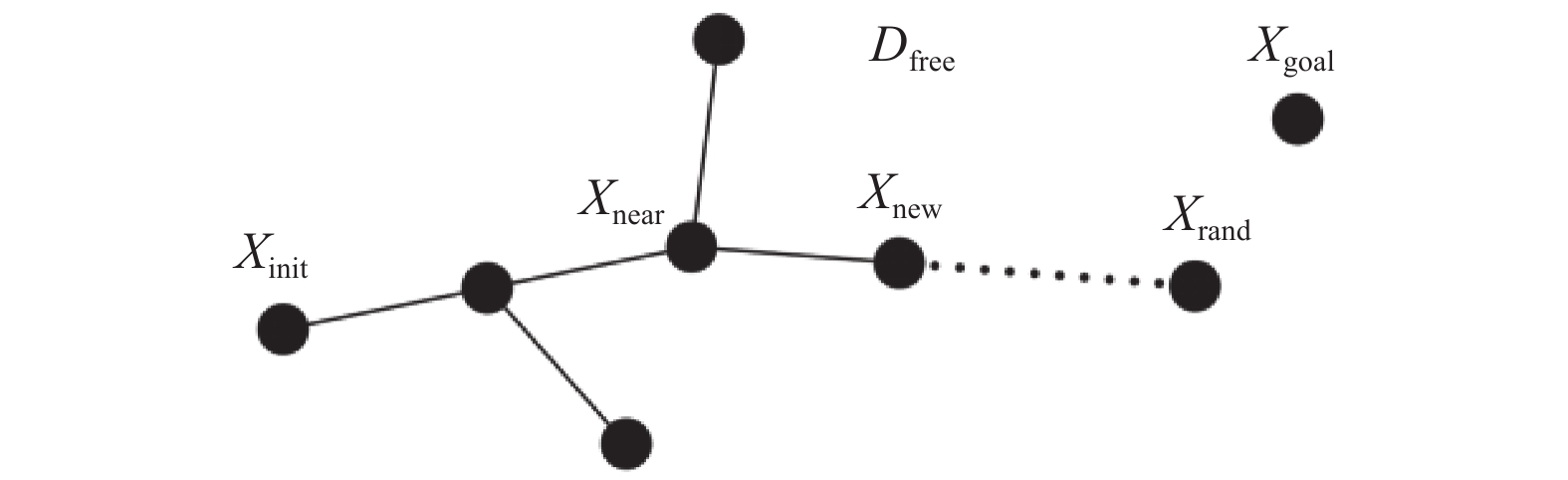
1 研究基础 1.1 RRT算法RRT算法首先将起点Xinit加入树中, 然后在无障碍空间Dfree中生成随机采样点Xrand, 遍历当前树节点, 找到离Xrand点最近的Xnear节点, 随后以Xnear–Xrand的方向, 按照固定步长d生成可行新节点Xnew, 重复以上步骤直到新节点Xnew距目标点Xgoal一定距离, 从而反向找到路径解, 原理如图1所示.
|
图 1 RRT算法扩展原理 |
1.2 T-RRT算法
T-RRT算法在RRT的框架上改进而来, 引入了模拟退火的思想, 通过对比两节点间的成本变化, 决定新节点能否被扩展. 算法在生成无碰撞的新节点Xnew后, 需要进行转移测试审核: 如果新节点成本c(Xnew)比最近点的成本c(Xnear)低, 那么通过测试, 如果比最近点的高, 需要通过模拟退火思想下的概率公式, 才可通过转移测试. 转移测试函数如算法1所示.
算法1.
begin
if c(Xnew) > cmax then return False;
if c(Xnear) > c(Xnew) then return True;
if Rand(0, 1) < p then
T = T/α;
nFail = 0;
return True;
else
if nFail
T = T×α;
nFail
else
nFail = nFail + 1;
return False;
end
算法1中, K为起始点和目标点的空间成本算数平均数; T为模拟的温度值; α为温度变化系数; nFail为失败扩展次数; nFailmax
EHT-RRT算法基于T-RRT算法改进, 保留了完整的转移测试函数, 去除节点细化/扩展审核函数, 在此基础上, 提出节点滑移策略和启发式成本探索策略, 利用球形节点结构, 将探索出的滑移方向危险度和滑移节点带来的启发式路径长度、路径偏角变化、路径高度变化, 共同组成总的启发式成本, 用于路径节点的局部滑移, 并分析出局部最好方向, 添加到扩展基点的属性中, 以改进节点的扩展过程.
2.1 启发式成本探索由于城市环境下的楼宇、信号、人流等因素的影响, 算法借鉴了车辆路径规划中的多层Morphin搜索树的局部路径规划方法[20]和A*算法中的启发式成本估计思想, 提出节点滑移策略, 对滑移方向及节点进行启发式成本探索, 为后续步骤做准备.
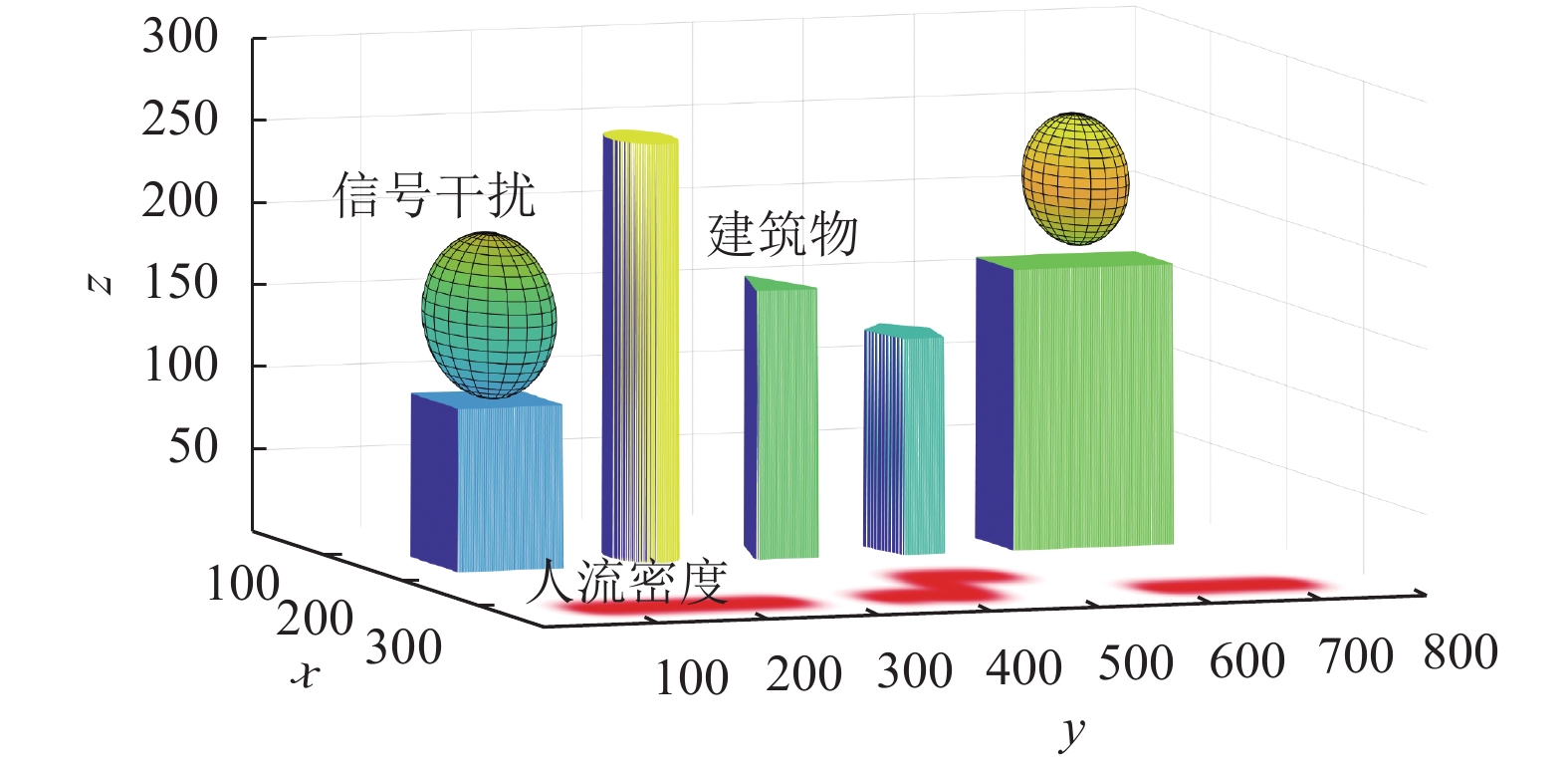
2.1.1 危险度索引和计算全局地图环境下的城市障碍危险物如图2所示, 分为楼宇障碍物、信号干扰和地面人流密度.
楼宇障碍物, 用[0, 1]模型表示, 0代表可行区域, 1代表楼宇障碍物, 则节点的楼宇危险度为:
| $ {{C} _{{b}}} = \left\{ \begin{gathered} 0{\text{ , }}{C_{{\text{building}}}}{\text{(}}{x} , y, {\textit{z}}{\text{)}} = 0 \hfill \\ {\text{inf , }}{C_{{\text{building}}}}{\text{(}}{x} , y, {\textit{z}}{\text{)}} = 1 \hfill \\ \end{gathered} \right. $ | (1) |
其中, Cbuilding为楼宇障碍物的索引矩阵.
信号干扰模型, 用干扰源三维坐标和干扰半径的列表[x,y, z, r]表示, 则节点的信号危险度为:
| $ {{C} _{{{si}}}} = \left\{ \begin{gathered} 0{\text{ , }}{{C} _{{\text{signal}}}}{\text{(}}{x} , y, {\textit{z}}{\text{)}} > {{r} _{i} } \hfill \\ {{r} _i} - {{C} _{{\text{signal}}}}{\text{(}}{x} , y, {\textit{z}}{\text{) , 0}}{\text{.2}}{{r} _i} \leqslant {{C} _{{\text{signal}}}}{\text{(}}{x} , y, {\textit{z}}{\text{)}} \leqslant {{r} _i} \hfill \\ {\text{inf , }}{{C} _{{\text{signal}}}}{\text{(}}{x} , y, {\textit{z}}{\text{)}} < 0.2{{r} _i} \hfill \\ \end{gathered} \right. $ | (2) |
| $ {{C} _{{s}}} = \sum\limits_{{{i = 1}}}^M {{{C} _{{{si}}}}} $ | (3) |
其中, Csignal为节点到信号干扰源的距离, M为信号干扰源数量.
|
图 2 城市环境模型 |
地面人流密度模型, 由地面人流密度二维矩阵表示, 等级为1–100, 则节点的人流危险度为:
| $ {{C} _{{p}}} = {C_{{\text{people}}}}{\text{(}}{x} , y{\text{)}} $ | (4) |
其中, Cpeople为地面人流密度索引矩阵.
综上, 单一空间节点的总危险度为:
| $ {{C} _x} = {p_1} \cdot {C_{{b}}} + {p_2} \cdot {C_{{s}}} + {p_3} \cdot {C_{{p}}} $ | (5) |
其中, (p1, p2, p3)为3种危险的权重.
算法在进行节点扩展时, 只是从欧式距离上选择了离Xrand更近的Xnear节点作为扩展基点, 却没有考虑Xnear节点的周围环境情况. 从文献[21]可知, 对节点的路径碰撞检查会消耗大量时间, 所以本文采用更加细密的多层球形节点结构进行危险度索引和计算, 以避免路径偏向建筑障碍物附近, 提高路径扩展的成功率, 减少碰撞检查次数.
如图3所示, 以3层结构为例, 为了保证较好的方向扩展密度, 结构的相邻方向偏角采用45°.
图3(a)显示的为探索球的二维3层结构, 共有8个方向, 每个方向按半径不同有3个节点. 首层节点因为要用于路径的局部节点滑移, 不宜过大, 所以设置为标准扩展步长d的1/3, 末层节点考虑到局部节点滑移带来的动态扩展步长, 所以设置为标准步长的4/3, 具体取值关系如式(6).
| $ \left\{ \begin{gathered} {{r} _{\text{1}}}{\text{ = 1/3}}d \hfill \\ {{r} _{\text{2}}}{\text{ = 2/3}}d \hfill \\ {{r} _{\text{3}}}{\text{ = 4/3}}d \hfill \\ \end{gathered} \right. $ | (6) |

|
图 3 多层危险度探索球 |
抽出图3(a)中的一层, 以任意方向每45°进行一次旋转复制, 即可得到图3(b)所示的探索球的三维单层结构, 共26个方向. 完整结构的每个方向有3个探索点, 则单一方向上的危险度为:
| $ {{C} _{{n}}} = {C_{\text{1}}} + {C_{\text{2}}} + {C_{\text{3}}} $ | (7) |
其中, (C1, C2, C3)分别为1–3层节点的总危险度值, 可由式(5)计算而得.
2.1.2 路径启发成本多层危险度探索, 只能了解到当前节点周围的危险度情况, 然而算法还需要考虑无人机的运动约束和能耗问题. 旋翼无人机不同于固定翼无人机, 它能实现位置的精准悬停, 亦能实现短距离刹车和转弯, 但这样的操作, 必定会浪费自身能量. 文献[22]中通过大量的实验证明, 除路径长度外, 不断的姿态改变, 也严重影响着旋翼无人机的续航.
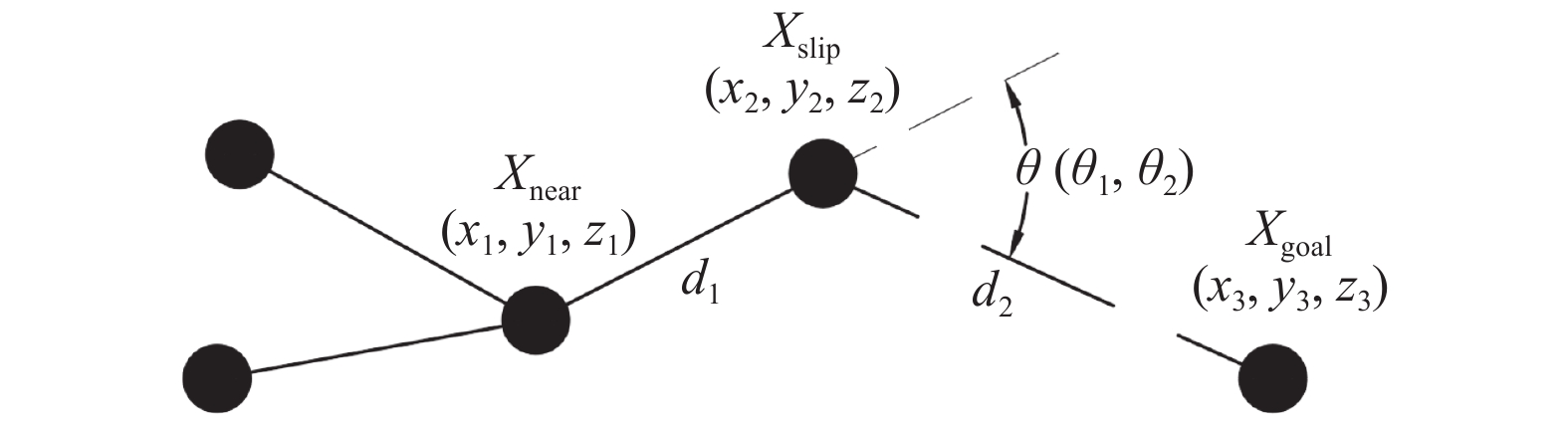
如图4所示, 对于选定滑移节点Xslip的路径, 计算最近点到滑移节点Xnear–Xslip的欧式距离d1, 滑移节点到目标点Xslip–Xgoal的欧式距离d2; 计算最近点到滑移节点到目标节点Xnear–Xslip–Xgoal的偏转角度θ(水平偏角θ1、竖直偏角θ2); 计算Xnear–Xslip和Xslip–Xgoal的高度变化绝对值(h1, h2). 则滑移节点下的启发式路径长度d、偏转角度θ和高度变化h可定义为:
| $ \left\{ \begin{gathered} {d} = {d_{\text{1}}} + {d_{\text{2}}} \hfill \\ \theta = {\theta _{\text{1}}} + {\theta _{\text{2}}} \hfill \\ {h} = {h_{\text{1}}} + {h_{\text{2}}} \hfill \\ \end{gathered} \right. $ | (8) |
综上, 由A*算法中的启发式成本估计思想, 从滑移点带来的方向危险度、路径长度、路径偏转角度和高度变化4个方面, 力求路径的平滑、安全, 减少无人机的能耗, 总的启发成本为:
| $ {{C} _{{h}}} = {w_{\text{1}}} \cdot {C_{{n}}} + {w_{\text{2}}} \cdot d + {w_{\text{3}}} \cdot \theta + {w_{\text{4}}} \cdot h $ | (9) |
其中, (w1, w2, w3, w4)为4个启发成本的权重.
|
图 4 路径启发成本 |
2.2 局部节点滑移
为了提高路径质量, 提出了局部节点滑移策略. 由上文可得滑移层26个节点的启发式估计成本, 然后找出最小成本滑移点作为新节点Xnew. 如图5所示, 选定了A点作为新节点Xnew, 路径也从临时新节点Tnew(O点)滑移到新节点Xnew上.

|
图 5 局部滑移扩展 |
以此能让路径偏向更好位置, 并实现了扩展步长的动态改变, 这有利于算法逃离陷阱区域.
2.3 局部最好方向人工势场法和RRT算法的融合, 让路径的寻找更有方向性, 但面对密集的楼宇建筑区域, 很可能让当前点的下次扩展失效, 从而进行不必要的路径碰撞检查. 所以, 为了避免上述状况的发生, 算法中对每个节点添加了局部最好方向属性best_dir, 以提高路径临时新节点的扩展质量.
在第2.1节中, 可得到临时新节点周围26个滑移点, 以及26个方向的成本. 局部最好方向的选取过程伪码如算法2所示.
算法2.
Intput: the cost vector CM;
the infinite cost quantity: cost_inf_num;
the point Tnew & Xgoal; Pmin_cost
the threshold of variance a.
Output: best_dir.
begin
if cost_inf_num = 0;
cost_var = variance(CM);
if cost_var < a
best_dir = Xgoal– Tnew;
else
best_dir = Pmin_cost–Tnew;
else
best_dir =Pmin_cost– Tnew;
end
通过矩阵中无穷大成本的数量cost_inf_num和成本均方差cost_var与阈值a的大小, 即可确定当前范围下最好扩展方向的向量best_dir, 将其加入此次扩展得到的新节点属性中, 用于未来可能的节点扩展. 局部最好方向best_dir如图5所示.
2.4 临时新节点扩展为了更好地应对复杂环境下的路径扩展寻找, 本文结合了I-RRT算法中目标点的概率性影响, 以及APF-RRT的目标点全时刻影响, 结合上文提出的best_dir属性, 对临时新节点的扩展做出改进.
如图6所示, 同样是通过随机节点Xrand找到最近节点Xnear作为扩展基点. 算法首先读取节点Xnear的局部最好方向best_dir, 然后按照式(10), 计算得出3个方向上的标准步长扩展向量.
| $ \left\{ \begin{gathered} {{\boldsymbol{n}}_1} = {d} \cdot {\text{(}}{{X} _{{\text{rand}}}}{{ – }}{{X} _{{\text{near}}}}{\text{)/}}\left\| {{{X} _{{\text{rand}}}}{{ – }}{{X} _{{\text{near}}}}} \right\| \hfill \\ {{\boldsymbol{n}}_2} = {d} \cdot {\boldsymbol{best\_dir}}/\left\| {{\boldsymbol{best\_dir}}} \right\| \hfill \\ {{\boldsymbol{n}}_3} = {d} \cdot {\text{(}}{{X} _{{\text{goal}}}}{{ – }}{{X} _{{\text{near}}}}{\text{)/}}\left\| {{{X} _{{\text{goal}}}}{{ – }}{{X} _{{\text{near}}}}} \right\| \hfill \\ \end{gathered} \right. $ | (10) |
其中, ||·||为内部向量的模, 则临时新节点可表示为:
| $ {{T} _{{\text{new}}}} = {{X} _{{\text{near}}}} + {{u} _{\text{1}}} \cdot {{\boldsymbol{n}}_{\text{1}}} + {{u} _2} \cdot {{\boldsymbol{n}}_2} + {{{\boldsymbol{u}}} _3} \cdot {n_3} $ | (11) |
其中, (u1, u2, u3)为3个向量的权重.
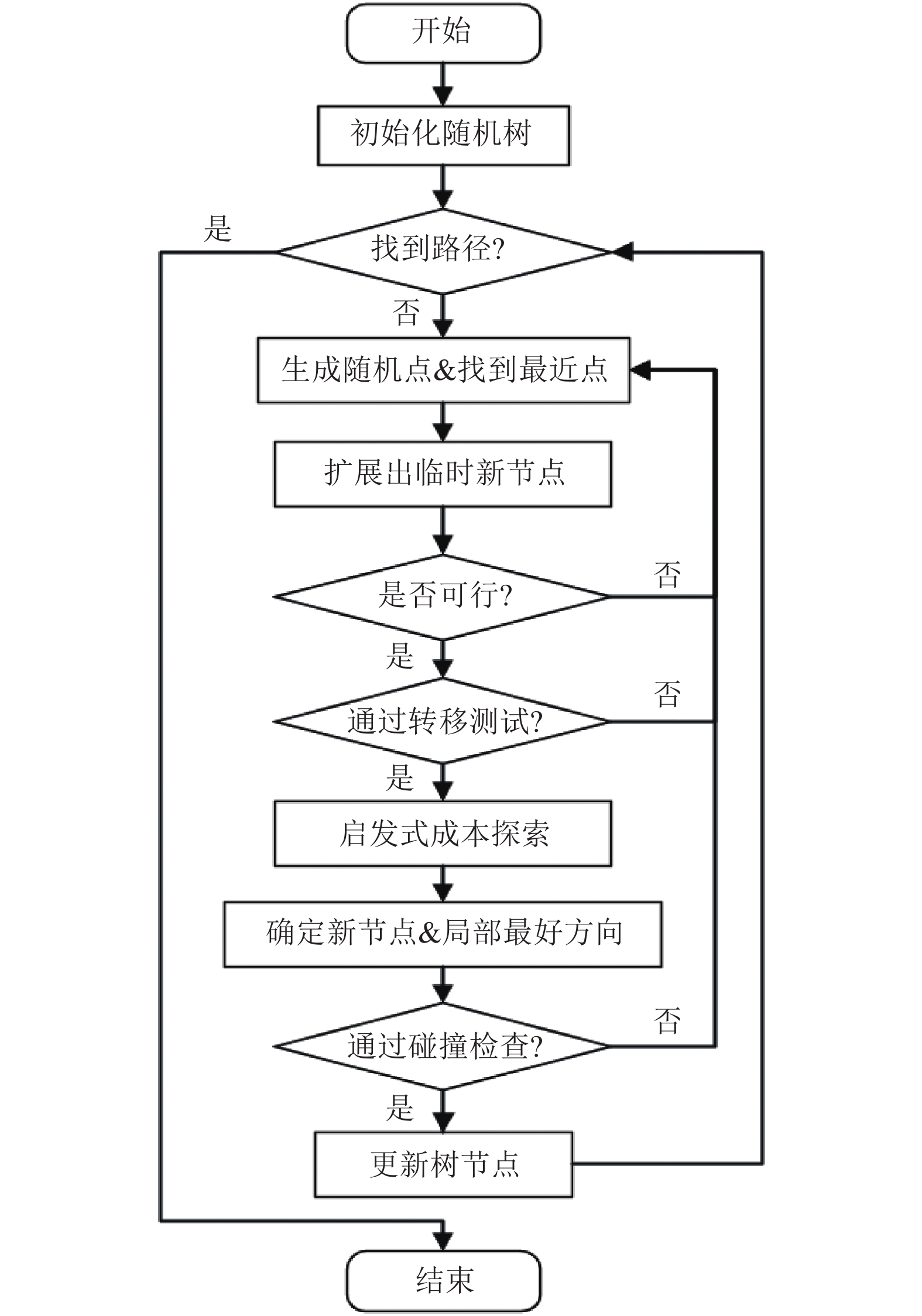
2.5 算法流程算法首先将起点Xinit加入树中, 接下来在无障碍空间Dfree中生成随机采样点Xrand, 遍历当前树节点, 找到离Xrand点最近的Xnear节点, 随后以Xnear–Xrand、Xnear–Xgoal、best_dir的3方向扩展机制, 生成可行临时新节点Tnew, 接着对节点Tnew依次进行路径碰撞检查和转移测试审核, 通过后再以节点Tnew为球心, 构建多层危险度探索球, 通过索引计算每个方向的危险度值, 将此值和滑移层节点的启发式路径长度、路径偏转角度、高度变化的权重和, 作为滑移层节点的启发式成本. 通过成本分析, 找到成本最低的滑移点作为此次扩展的新节点Xnew, 并确定新节点的局部最好方向向量best_dir属性, 接着进行路径碰撞检测, 若通过则将新节点加入树中. 重复以上步骤直到新节点Xnew距目标点Xgoal一定距离, 从而反向找到路径解. 完整的算法流程, 如图7所示.

|
图 6 临时新节点扩展 |
|
图 7 EHT-RRT算法流程图 |
3 实验仿真与分析
为了验证EHT-RRT的性能, 实验设置了如图8所示的规模较大、信号干扰较多、人流较稀疏的环境1和规模较小、信号干扰较少、人流较密集的环境2, 两种城市环境进行仿真实验, 并通过环境1来选定算法的各种参数.

|
图 8 城市环境 |
具体任务省略了起飞和降落过程, 只考虑空间中两点间的三维路径规划, 并通过多算法对比实验和消融对比实验验证EHT-RRT算法的有效性.
仿真程序在64 bit Matlab 2018平台下运行, 电脑系统环境为Windows 10, 配置为Inter(R) Core(TM) i7-1165G7 CPU @2.8 GHz, 16 GB RAM.
3.1 仿真参数设置在求解路径时, 算法中的各种参数都影响着求解性能. 算法中的终点检测半径和标准扩展步长可依据城市环境中的楼宇和道路的相关建设标准和实际情况自行设定, 本文取终点检测半径为30 m, 标准扩展步长为18 m. 转移测试函数中的各项参数与T-RRT算法设置保持一致. 其他参数的选取均由仿真环境中20次平均规划结果进行选定.
探索球层数. 探索球层数越多, 越能准确了解空间中的危险情况, 但同时也会影响算法的效率. 不同层数探索球下的路径搜索时间和路径危险度变化如图9所示. 综合两项指标, 可以看出层数为3时情况较好, 所以选取探索球层数为3.

|
图 9 不同层数的性能对比 |
路径危险度的定义为, 最终路径的平均路径节点危险度与路径长度的乘积, 计算公式为:
| $ {{C} _{{L}}} = {L} \cdot \frac{{\text{1}}}{{N} }\sum\limits_{{{i}} = 1}^{N} {{{C} _{{{{x}}_{{i}}}}}} $ | (12) |
其中, N为最终路径的节点数, L为路径长度, Cxi为单一节点的危险度, 可由式(5)计算.
危险度权重. 不同的危险对无人机的影响也有所不同, 本文利用层次分析法来确定上文所述的3种危险权值(p1, p2, p3)的大小. 由文献[23]的介绍可得如表1所示的判断矩阵, 并计算得3种权重值.
启发函数权重. 启发函数的设置, 可以从不同的侧重点去影响路径的规划结果, 文中设置了危险度、路径长度、偏转角度和高度变化, 共4个启发量, 可采用对照实验法来确定最终的权重值.
首先确定危险度的权重值. 方法为改变危险度的权重大小, 其余3项均分剩余权重, 采用平均规划时间、平均路径危险度和平均路径长度作为评判标准, 则不同权重组合下的规划结果如表2所示.
| 表 1 不同危险权重选取 |
| 表 2 危险度启发权重选取 |
从表2中可以看出, 3号实验组的路径规划结果相对较好, 所以危险度的权重定为0.4.
接着确定路径长度的权重值. 保持危险度权重不变, 改变路径长度的权重, 偏转角度和高度变化均分剩余权重, 选取同样的评判标准, 实验组别及结果如表3所示. 从表3中可以看出, 2号实验组的各项结果都较好, 所以取路径长度的权重为0.2.
| 表 3 路径长度启发权重选取 |
同理, 从表4和图10的结果可以确定偏转角度和高度变化的权重分别为0.3, 0.1.
偏转角度为每两条相邻路径线的水平偏角和竖直偏角之和; 高度变化为每相邻两个路径点间的高度变化绝对值.
3方向扩展权重. 随机方向的设置, 有助于算法摆脱陷阱区域, 所以设置其权重为0.5, 同样利用对照实验法得到如表5所示结果. 可以看出2号试验的规划效果最好, 所以权重选定为(0.5, 0.2, 0.3).
| 表 4 偏转角度和高度变化启发权重选取 |

|
图 10 不同偏转角度和高度变化权重的对比 |
| 表 5 3方向权重选取 |
由此可得EHT-RRT算法的完整参数如表6所示, 并设置算法在两个环境中的起点、终点.
| 表 6 仿真参数设置 |
3.2 仿真结果与分析 3.2.1 多算法对比实验
多算法对比实验将同样拥有20%目标偏置的T-RRT、BT-RRT (双向T-RRT)和T-RRT*算法进行比较. 4种算法均不进行路径迭代优化和路径剪枝处理, 只对比首次找到路径时的20次结果均值. 各算法的路径寻找情况俯视图如图11所示, 其中路径搜索树为蓝色, 最终路径为绿色.
为便于对比观察, 仅将各算法路径规划结果作如图12所示的立体展示.

|
图 11 各算法仿真图 |
从图11可以看出, 4种算法在两个环境下都能较好地避开人流稠密区域, 实现较为安全的路径规划, 但T-RRT和 T-RRT*算法在规划时探索了较多无效区域, BT-RRT算法路径较长且曲折, 而EHT-RRT算法能将探索范围约束在目标方向附近, 并朝向目标点. 结合图12可以看出T-RRT、BT-RRT和T-RRT*算法的规划路径抖动大, 而EHT-RRT算法规划的路径更加平滑和稳定, 便于后期处理.

|
图 12 4种算法的路径规划结果对比 |
表7为20次仿真结果中的常规路径规划参数对比, 可以反映算法的一般性能.
| 表 7 常规参数对比 |
从20次的平均结果看, 双向探索机制的BT-RRT算法规划时间最短, EHT-RRT算法的规划时间较长, 但比T-RRT*算法短, 作为全局路径规划, 这些时间都在可接受范围内; 路径长度参数上, EHT-RRT算法的平均路径长度可比T-RRT算法减少8.5%–13.9%, 可比BT-RRT算法减少12.8%–14.3%, 可比T-RRT*算法减少6.0%–11.2%; 平均路径危险度参数上, EHT-RRT算法可比T-RRT算法减少8.5%–14.5%, 可比BT-RRT算法减少12.8%–15.4%, 可比T-RRT*算法减少6.0%–11.3%.
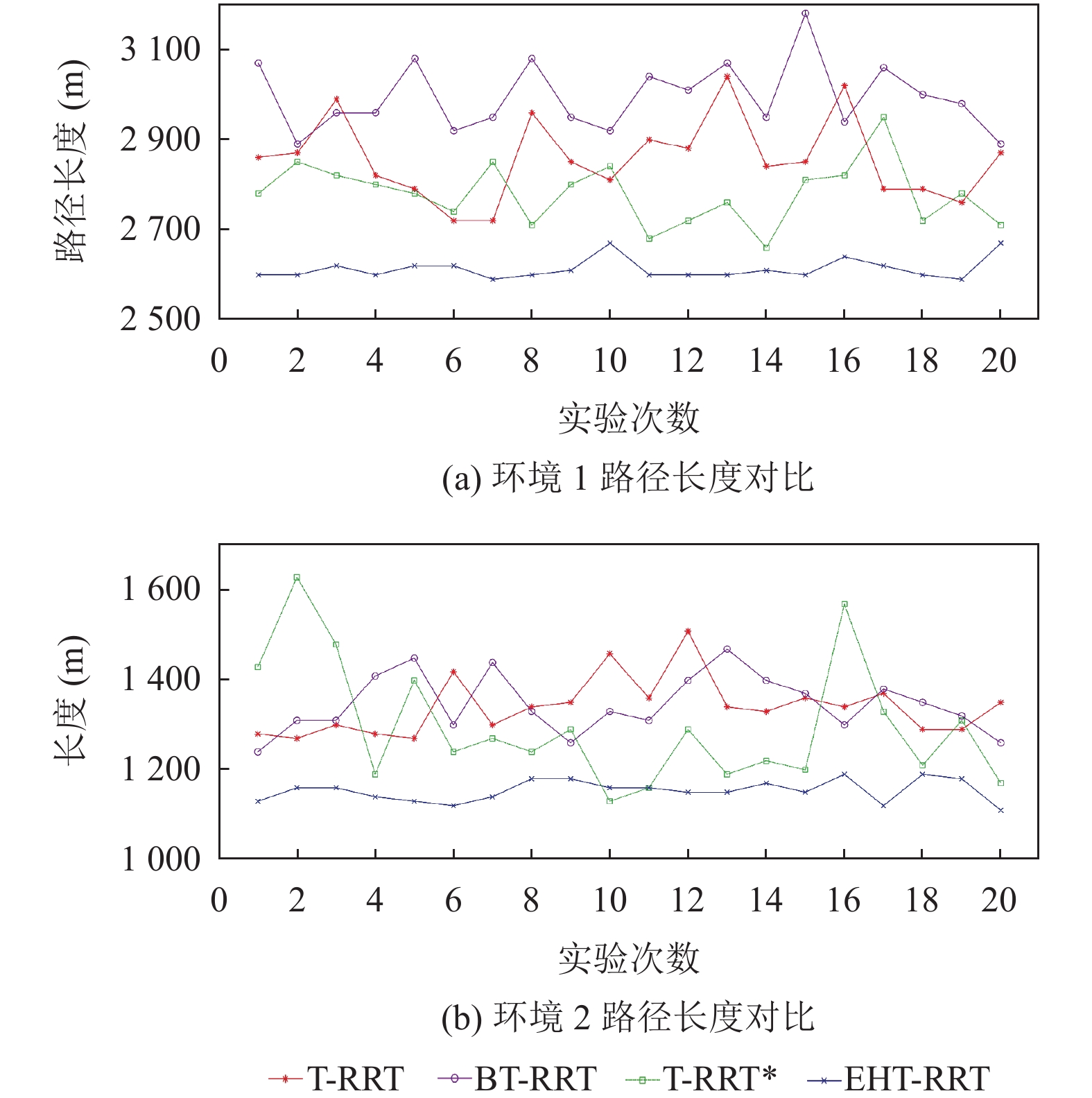
为了更好地了解算法的规划效果, 将4种算法20次的规划路径长度进行图13所示的对比展示. 结合图11和表7可以看出, EHT-RRT算法的规划结果, 路径长度更短, 一致性更好, 这有利于算法在实际中的应用.
|
图 13 不同算法路径长度对比 |
表8为20次仿真结果的路径抖动参数对比, 一定程度上能反映规划路径对无人机能耗, 以及对路径后处理工作量的影响.
| 表 8 路径抖动参数对比 |
平均偏角变化参数上, EHT-RRT算法可比T-RRT算法减少53.1%–59.7%, 可比BT-RRT算法减少35.6%–64.6%, 可比T-RRT*算法减少2.9%–51.1%; 平均高度变化参数上, EHT-RRT算法可比T-RRT算法减少54.7%–60.5%, 可比BT-RRT算法减少2.9%–47.9%, 可比T-RRT*算法减少52.2%–52.8%.
图14为4种算法20次规划路径的平均偏角变化和平均高度变化对比, 可以看出在环境2中BT-RRT算法和EHT-RRT算法大致处于一个性能上, 其余情况下, EHT-RRT算法都能保持最低的路径抖动性. 且结果相对稳定, 而 T-RRT、BT-RRT和EHT-RRT算法规划结果波动较大, 一致性较差.

|
图 14 不同算法的路径抖动参数对比 |
3.2.2 消融对比实验
为了验证EHT-RRT算法改进的有效性, 以环境1为基础, 针对算法的改进项进行了消融对比实验.
因为算法的改进项间存在继承关系(如: 启发式成本探索的结果是局部节点滑移和局部最好方向的数据基础; 局部最好方向应用于改进的节点扩展机制), 所以仅查看EHT-RRT算法在局部节点滑移和局部最好方向这两个方面的改进成效.
消融处理仅将对比项功能删减, 整体的算法流程顺序保持不变. 实验仍然采取20次的平均仿真结果作为对比数据, 具体如表9所示.
| 表 9 消融对比实验 |
从表9中数据可以看出, 完整的EHT-RRT算法能提供更好的规划效果. 消去局部节点滑移, 导致路径长度、路径危险度以及路径的抖动性都增长较大; 消去局部最好方向导致路径的扩展出现局部盲目性, 造成规划时间较长. 可以分析出: 局部节点滑移策略能更好地提升路径质量; 局部最好方向能更好地避免局部环境陷阱, 提升路径搜索效率.
综上分析, EHT-RRT相比T-RRT、BT-RRT和T-RRT*, 在平均路径长度、平均路径危险度和平均高度变化参数上, 都有较好的表现. 算法在各方面的改进也为寻找更好的路径带来积极效果, 所以EHT-RRT算法更适合在连续复杂的成本空间中, 找到一致性更好、长度更短、危险度更低且更加平滑安全的无人机飞行规划路径.
4 结论本文针对复杂城市环境下的旋翼无人机路径规划问题, 提出了EHT-RRT算法, 具体包括以下4个方面:
(1)对节点采用启发式成本探索, 利用多层球形节点结构, 从危险度、路径长度、路径偏转角度和高度变化4个方面, 共同影响路径的偏向;
(2)提出局部节点滑移策略, 可让规划路径远离障碍物和危险地区, 降低路径危险度;
(3)为节点添加局部最好方向属性, 可让每一次的节点扩展, 考虑当前节点的环境危险情况, 提高扩展质量和效率;
(4)综合随机方向、局部最好方向和目标点方向, 改进节点的扩展机制, 减少盲目性, 提高规划效率.
仿真结果表明, 本文算法能生成路径更短、安全性更高、更加平滑的三维路径, 可用于旋翼无人机在复杂成本空间中的路径规划.
| [1] |
周俊飞. 一本书读懂无人机物流. 北京: 机械工业出版社, 2018.
|
| [2] |
黄爱凤, 邓克绪. 民用无人机发展现状及关键技术. 第九届长三角科技论坛——航空航天科技创新与长三角经济转型发展分论坛论文集. 南京: 江苏省航空航天学会, 2012. 29–35.
|
| [3] |
张启钱, 许卫卫, 张洪海, 等. 复杂低空物流无人机路径规划. 北京航空航天大学学报, 2020, 46(7): 1275-1286. |
| [4] |
Šišlák D, Volf P, Pěchouček M. Accelerated A* path planning. Proceedings of the 8th International Conference on Autonomous Agents and Multiagent Systems. Budapest: International Foundation for Autonomous Agents and Multiagent Systems, 2009. 1133–1134.
|
| [5] |
Tsai CC, Huang HC, Chan CK. Parallel elite genetic algorithm and its application to global path planning for autonomous robot navigation. IEEE Transactions on Industrial Electronics, 2011, 58(10): 4813-4821. DOI:10.1109/TIE.2011.2109332 |
| [6] |
Borrelli F, Subramanian D, Raghunathan AU, et al. MILP and NLP techniques for centralized trajectory planning of multiple unmanned air vehicles. 2006 American Control Conference. Minneapolis: IEEE, 2006. 6.
|
| [7] |
尚璞. 旋翼无人机路径规划与自主避障控制系统研究[硕士学位论文]. 西安: 西安科技大学, 2019.
|
| [8] |
Solovey K, Salzman O, Halperin D. Finding a needle in an exponential haystack: Discrete RRT for exploration of implicit roadmaps in multi-robot motion planning. In: Akin HL, Amato NM, Isler V, et al. eds. Algorithmic Foundations of Robotics XI. Cham: Springer, 2015. 591–607.
|
| [9] |
Devaurs D, Siméon T, Cortés J. A multi-tree extension of the transition-based RRT: Application to ordering-and-pathfinding problems in continuous cost spaces. 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems. Chicago: IEEE, 2014. 2991–2996.
|
| [10] |
李文广, 孙世宇, 李建增, 等. 分段优化RRT的无人机动态航迹规划算法. 系统工程与电子技术, 2018, 40(8): 1786-1793. DOI:10.3969/j.issn.1001-506X.2018.08.17 |
| [11] |
LaValle SM. Rapidly-exploring random trees: A new tool for path planning. Technical Report, Alumni Hall Ames: Lowa State University, 1998.
|
| [12] |
Karaman S, Frazzoli E. Sampling-based algorithms for optimal motion planning. The International Journal of Robotics Research, 2011, 30(7): 846-894. DOI:10.1177/0278364911406761 |
| [13] |
Englot B, Hover FS. Sampling-based sweep planning to exploit local planarity in the inspection of complex 3D structures. 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems. Vilamoura-Algarve: IEEE, 2012. 4456–4463.
|
| [14] |
Jaillet L, Cortés J, Siméon T. Transition-based RRT for path planning in continuous cost spaces. 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems. Nice: IEEE, 2008. 2145–2150.
|
| [15] |
Devaurs D, Siméon T, Cortés J. Optimal path planning in complex cost spaces with sampling-based algorithms. IEEE Transactions on Automation Science and Engineering, 2016, 13(2): 415-424. DOI:10.1109/TASE.2015.2487881 |
| [16] |
蔡文涛, 邓屹, 张静, 等. 基于改进RRT算法的机械臂路径规划. 传感器与微系统, 2019, 38(5): 121-124. |
| [17] |
张玉伟, 左云波, 吴国新, 等. 基于改进Informed-RRT算法的路径规划研究. 组合机床与自动化加工技术, 2020(7): 21-25. |
| [18] |
李洋, 徐达. 基于引力自适应步长RRT的双臂机器人协同路径规划. 机器人, 2020, 42(5): 606-616. |
| [19] |
Wang H, Sun Z, Li DZ, et al. An improved RRT based 3-D path planning algorithm for UAV. 2019 Chinese Control and Decision Conference (CCDC). Nanchang: IEEE, 2019. 5514–5519.
|
| [20] |
张毅, 杜凡宇, 罗元. 基于改进Morphin搜索树的局部路径规划算法. 电光与控制, 2016, 23(7): 15-19. |
| [21] |
李耀仲, 王书亭, 蒋立泉, 等. 基于稀疏节点快速扩展随机树的移动机械臂运动规划. 中国机械工程, 2021, 32(12): 1462–1470.
|
| [22] |
Dorling K, Heinrichs J, Messier GG, et al. Vehicle routing problems for drone delivery. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2017, 47(1): 70-85. DOI:10.1109/TSMC.2016.2582745 |
| [23] |
曹茂林. 层次分析法确定评价指标权重及Excel计算. 江苏科技信息, 2012(2): 39-40. DOI:10.3969/j.issn.1004-7530.2012.02.019 |
 2022, Vol. 31
2022, Vol. 31


