2. 遵义医科大学 医学信息工程学院, 遵义 563003
2. School of Medical Information Engineering, Zunyi Medical University, Zunyi 563003, China
电子病历的发展从提升效率, 到信息集成共享, 再到提升医疗质量与安全, 发生了质的变化, 而随着远程医疗技术的发展, 学者们又对电子病历的跨区域共享展开了大量的研究. 其中, 身份验证作为信息系统安全的第一道关卡, 对于电子病历的跨区域[1]安全共享至关重要.
用户身份验证[2-7]的方法基本上可分为: 基于口令的身份验证、基于令牌的身份验证、基于生物学特征的身份验证和基于公开密钥加密算法的身份验证, 在网络通信中最常见的是基于公开密钥加密算法的身份验证. 文献[8]针对用户异地访问系统中存在用户身份鉴别和用户数字证书[9]信息交互的问题, 提出采用分布式PKI/CA架构, 通过数字证书对两地操作系统、应用系统提供统一的安全支撑, 形成面向业务应用和数据管理的统一身份、统一认证的信任体系, 实现异地信息资源的整合利用和业务协同. 但是该方案中的证书管理中心(CA)并不是完全安全, 其颁发的主密钥对都相同, 若主密钥泄露, 那么入侵者将冒充CA来颁发证书. 文献[10]提出了一种通过将大文件分块, 采用多线程传输, 并支持文件断点续传的方案, 解决了异地环境下大文件传输的稳定性问题. 该方案制定了基于SSL协议的传输安全策略, 首先, 通过数字证书和电子签名验证通信双方的身份信息, 阻止与非法用户的通信; 其次, 使用对称/非对称加密算法对密钥和数据信息加密, 防止传输过程中密钥和数据信息被非法窃取. 上述方案中都是用第三方CA认证中心颁发的数字证书来实现客户与服务器之间的双向认证, 但是证书申请成本高, 还有使用期限限制, 随着用户的增多, 证书的管理难度也越来越大. 文献[11]为触觉互联网辅助远程手术应用程序设计了一种超高效的相互认证和密钥协商协议, 外科医生和机械臂之间通过网关进行相互认证, 然后这3个实体生成一个公共的秘密会话密钥, 用于当前登录会话中的未来通信, 从而实现远程手术操作期间的安全通信. 国密SM9算法[12]也去除了以CA签发数字证书作为凭证的过程, 用户不需要通过第三方来保证其公钥来源的真实性, 这一措施极大地拓宽了PKI[13-15]的应用范围和场景, 也节省了传统PKI身份认证体制在密钥产生、证书签发、密钥管理等方面的花销. 对于认证, 私钥的分发和安全是整个流程安全性的核心, 文献[16]对SM9算法的私钥分发给出了具体的解决方案, 在安全分发私钥的同时实现了客户端与服务器的双向认证.
为保障跨区域医疗信息的安全共享, 鉴别通信双方的身份至关重要, 本文提出了一种基于SM9的双向身份验证方案(bidirectional authentication scheme based on SM9, BAS)实现了用户之间的身份信息认证, 为安全有效的实现电子病历的共享奠定基础.
1 相关工作 1.1 Diffie-Hellman (DH)密钥协议DH密钥协商算法的具体流程如下:
(1) 用户A与用户B共享一个素数
(2) 用户A产生一个私有的随机数
| $ {Y_A} = {g^x}\boldsymbolod p $ | (1) |
将式(1)计算的结果
(3) 用户B产生一个私有的随机数
| $ {Y_B} = {g^y}\boldsymbolod p $ | (2) |
将式(2)计算的结果
(4) 用户A接收到
| $ {K_A} = Y_B^x = {g^{xy}}\boldsymbolod p $ | (3) |
| $ {K_B} = Y_A^y = {g^{xy}}\boldsymbolod p $ | (4) |
(5) 式(3)和式(4)计算得到的结果满足K=KA=KB, 因此双方经过协商后得到了相同的密钥K, 达成密钥协商的目的.
本文将DH算法协商的共同密钥作为验证因子, 并将其应用到验证流程中.
1.2 双线性群双线性对定义在椭圆曲线群上, 主要有Tate对、Ate对、R-ate对和Weil对. SM9算法中使用的双线性对为R-ate对[17, 18], 其安全性和运算速率较高.
设有
(1) 双线性性: 对任意的
(2) 非退化性:
(3) 可计算性: 对任意的
表1为本文方案所用符号定义.
2.2 BAS方案本文以医院间电子病历的访问过程中用户之间的身份验证作为案例, 提出BAS方案来对跨区域信息共享中通信双方的身份验证进行分析和研究.
BAS方案采用了“验证因子+数字签名”的验证方式, 该方法区别于传统的公钥加密身份验证方式, 本文将通信双方通过DH算法产生的共同密钥作为验证因子来完成第1阶段的身份验证, 再通过数字签名完成第2阶段的身份验证. 图1为BAS方案详细认证流程图.
| 表 1 符号定义 |
认证流程具体步骤如下:
(1) 医院A向医院B申请所需患者的电子病历, 医院B收到医院A的请求后做出响应. 同时, 双方通过DH算法分别产生验证因子
(2) 医院B保存验证因子
(3) 医院A对比分析
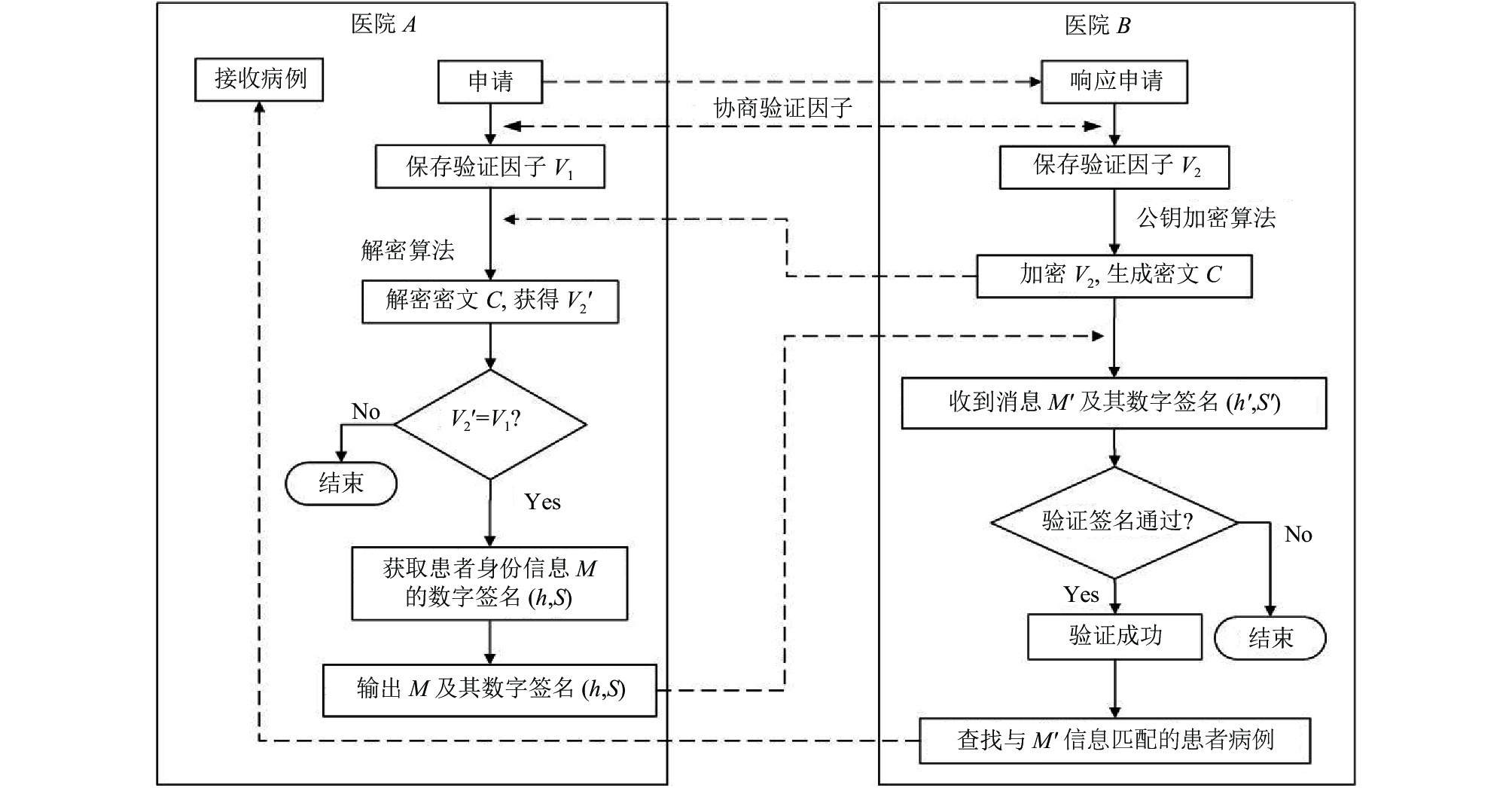
|
图 1 BAS方案认证流程图 |
2.3 方案描述
(1) 系统初始化
系统选取两个循环加法群
系统的密钥生成中心(
系统的密钥生成中心(
(2) 用户B身份验证阶段
用户A与用户B使用DH算法协商验证因子保存后, 用户B需将自己的验证因子

|
图 2 用户B身份验证 |
1) 加密验证因子
用户B使用用户A的标识
2) 验证
用户A收到密文
(3) 用户A身份验证阶段
用户B的身份验证成功后, 用户A需要获取消息

|
图 3 用户A身份验证 |
1) 数字签名
首先, 计算
2) 验证数字签名
用户B收到消息
数字签名及验签的正确性关键是考虑签名时
(1) 签名时:
| $ \begin{split} w = {g^r} = e{\left( {{P_1}, Pu{b_s}} \right)^r} = e{\left( {{P_1}, s{P_2}} \right)^r} = e{\left( {{P_1}, {P_2}} \right)^{rs}} \end{split} $ | (5) |
(2) 验签时:
| $ \begin{split} w &= ut \\ &= e\left( {S, {h_1}{P_2} + Pu{b_s}} \right) \cdot e{\left( {{P_1}, Pu{b_s}} \right)^h} \\ &= e\left( {\left( {r - h} \right)d{s_A}, {h_1}{P_2} + s{P_2}} \right) \cdot e{\left( {{P_1}, s{P_2}} \right)^h} \\ &= e\left( {\left[ {\left( {r - h} \right) \cdot s \cdot {{\left( {{h_1} + s} \right)}^{ - 1}}} \right]{P_1}, \left[ {{h_1} + s} \right]{P_2}} \right) \cdot e{\left( {{P_1}, {P_2}} \right)^{sh}} \\ &= e{\left( {{P_1}, {P_2}} \right)^{\frac{{\left( {r - h} \right)s}}{{{h_1} + s}}\left( {{h_1} + s} \right)}} \cdot e{\left( {{P_1}, {P_2}} \right)^{sh}} \\ &= e{\left( {{P_1}, {P_2}} \right)^{\left( {r - h} \right)s + sh}} \\ &= e{\left( {{P_1}, {P_2}} \right)^{rs}} \end{split} $ | (6) |
根据式(5)和式(6)推导可知, 签名和验签计算的
(1) 密钥安全
本文方案中的主密钥对都是通过随机数产生, 用户的私钥是由密钥生成中心通过主私钥与用户的标识计算生成, 且私钥由用户加密后存储在自己的设备上, 只用于数字签名和公钥加密, 既不会被泄露, 也避免被窃取.
(2) 中间人攻击
本文方案是基于DH算法和标识密码技术的双向认证方案. 在第1阶段的身份验证中, 通信双方通过DH算法协商的验证因子经过了非对称加密过后进行传输, 用户的私钥都存储在本地, 不在网络上进行传输, 可以有效地防止攻击者的窃听行为. 在第2阶段的身份验证中, 主私钥与用户标识产生的签名私钥对数据产生数字签名, 中间人即使伪造了标识, 也无法伪造数字签名. 因此, 不能通过仿冒或欺骗等手段达到窃取用户间的通信信息这一目的.
(3) 重放攻击
本文方案中验证因子和密钥对都是由随机数计算而来, 加密验证因子产生的密文也是由随机数计算而来, 可通过随机数的信息来识别和确定是否是重放信息, 从而避免重放攻击.
(4) 前向安全
本文方案中, 密钥是由KGC通过主私钥和用户的标识结合产生, 而每次加密密钥或签名密钥都是随机的、不同的, 且每次认证时必须使用对方的标识, 标识若是伪造的将造成认证失败. 密钥的随机性以及标识的全过程参与成为了系统安全的保障. 信息也都是经过加密后再进行传输, 所以不会造成以前通信时产生的会话密钥被泄露, 也不会泄露以前通信的内容.
3 实验结果及分析服务器的基本配置: CPU i3-2120U, 主频3.30 GHz, 内存4.00 GB, 硬盘931.51 GB, IP地址为202.101.72.84. 同时在服务器上部署了一个基于Java开发的双向身份验证系统, 该系统主要用于BAS方案的实验论证.
在BAS方案的可行性及正确性测试中, 选取两个用户A和B进行认证测试, 其中用户A和用户B计算验证因子后由用户B加密自己的验证因子发送给用户A进行验证. 表2为实验具体参数.
用户A收到用户B加密的密文C后, 对其进行解密并验签, 解密成功后得到用户B的验证因子
用户B的身份验证成功后, 用户A获取消息
用户B收到消息
对于电子病历的跨区域共享中通信双方身份验证的需求, 本文提出的基于SM9算法的双向身份验证方案, 改变了传统PKI身份验证的流程, 使用“验证因子+数字签名”的方式实现了用户的双向认证. 且该方案中, SM9算法无需预先与协商密码者交换CA证书, 减少了申请和验证环节, 满足跨域用户安全通讯的需求. 本文方案在满足正确性的基础上安全可靠, 在跨域医疗协同这一应用场景下具有一定的研究价值和应用前景, 能够有效的避免因用户的身份验证问题造成患者的就诊信息被泄露. 在接下来的研究中将将继续对SM9算法的相关计算进行优化, 提高验证效率.
| 表 2 BAS方案用户B加密验证因子实验参数 |
| 表 3 用户A解密实验参数 |
| 表 4 BAS方案用户A数字签名实验参数 |
| 表 5 用户B验证数字签名实验参数 |
| [1] |
刘欢. 跨域认证与授权系统的设计与实现[硕士学位论文]. 西安: 西安电子科技大学, 2014.
|
| [2] |
赵玉超. 一种基于非对称加密算法的安全高效身份认证协议. 工业技术创新, 2020, 7(6): 103-107. |
| [3] |
刘怀兰, 侯昕, 王佳. 改进的基于USBKey的动态身份认证方案. 华中科技大学学报(自然科学版), 2010, 38(11): 41-43. |
| [4] |
董艳花, 张树美, 赵俊莉. 基于深度神经网络的有遮挡身份验证. 青岛大学学报(自然科学版), 2021, 34(2): 45-52. |
| [5] |
王霏, 陈明. 完美前向安全的基于身份认证密钥协商方案. 密码学报, 2020, 7(1): 56-68. |
| [6] |
封化民, 孙轶茹, 孙莹. 基于身份认证加密的私钥共享方案及其应用. 计算机应用研究, 2014, 31(5): 1507-1510. DOI:10.3969/j.issn.1001-3695.2014.05.054 |
| [7] |
李郁林. 一种基于动态令牌的双向认证方案. 信息与电脑, 2019, 31(24): 211-212. |
| [8] |
宋芹芹, 袁泉. PKI/CA系统异地统一身份认证研究与实现. 网络安全技术与应用, 2017(6): 54-55. DOI:10.3969/j.issn.1009-6833.2017.06.033 |
| [9] |
光笑黎, 张露露, 刘继增. 一种轻量级基于证书的认证密钥协商方案. 计算机系统应用, 2021, 30(1): 264-269. DOI:10.15888/j.cnki.csa.007806 |
| [10] |
方明. 异地协同研发过程中基于分布式PLM的数据交换研究[硕士学位论文]. 武汉: 华中科技大学, 2017.
|
| [11] |
Kamil IA, Ogundoyin SO. A lightweight mutual authentication and key agreement protocol for remote surgery application in tactile Internet environment. Computer Communications, 2021, 170: 1-18. DOI:10.1016/j.comcom.2021.01.025 |
| [12] |
赖建昌, 黄欣沂, 何德彪, 等. 基于商密SM9的高效标识签密. 密码学报, 2021, 8(2): 314-329. |
| [13] |
Sharma K, Agrawal A, Pandey D, et al. RSA based encryption approach for preserving confidentiality of big data. Journal of King Saud University—Computer and Information Sciences. In Press.
|
| [14] |
Dijesh P, Babu SS, Vijayalakshmi Y. Enhancement of e-commerce security through asymmetric key algorithm. Computer Communications, 2020, 153: 125-134. DOI:10.1016/j.comcom.2020.01.033 |
| [15] |
Hoobi MM, Sulaiman SS, AbdulMunem IA. Enhanced multistage RSA encryption model. IOP Conference Series: Materials Science and Engineering, 2020, 928(3): 032068. |
| [16] |
赵奕捷. 基于标识密码(IBC)的私钥分发和双向认证研究. 江苏通信, 2020, 36(6): 70-75. DOI:10.3969/j.issn.1007-9513.2020.06.018 |
| [17] |
甘植旺, 廖方圆. 国密SM9中R-ate双线性对快速计算. 计算机工程, 2019, 45(6): 171-174. |
| [18] |
王明东, 何卫国, 李军, 等. 国密SM9算法R-ate对计算的优化设计. 通信技术, 2020, 53(9): 2241-2244. DOI:10.3969/j.issn.1002-0802.2020.09.025 |
 2022, Vol. 31
2022, Vol. 31


