2. 南宁师范大学 数学与统计学院, 南宁 530299
2. Department of Mathematics and Statistics, Nanning Normal University, Nanning 530299, China
计算机和智能通信技术的快速发展, 使得信息的传播、共享也变得越来越便捷, 但同时对信息安全的问题提出了新挑战. 而传统信息安全的保障手段——密码术能有效地保障信息安全, 但是进入移动互联网、大数据时代, 传统的加密技术也暴露出其中的不足, 因为加密数据是异常数据, 容易成为数据分析挖掘的重点目标, 从而容易引起大量的攻击. 因此大家又把目光投向一种古老的技术——信息隐写技术(信息隐藏技术)[1-10], 信息隐藏技术其实自古就有, 例如在古代为了隐秘地传递机密信息, 会把传递信息的士兵剃光头后写上军事机密, 然后等他的头发长长后传递信息, 接收时再剃光那位士兵的头发就能看到机密信息. 而在计算机时代, 则对信息隐藏技术提出更高的要求, 信息隐藏不仅要让人肉眼无法分辨, 而且要实现对抗计算机视觉识别.
混沌系统具有对初始条件和控制参数敏感、伪随机和不可预测性等一系列特性, 这些特性与密码学的要求相一致. 因此, 混沌系统经常被用在图像加密中[11-15], 利用混沌系统产生的混沌序列对图像进行扩散与混淆, 从而达到加密的效果. 而通过 2D-DCT, 可以把图像的主要能量集中在左上角, 这样只要把秘密图像的信息替换除左上角外的其它地方, 就既能减少失真度, 又达到良好的隐藏效果.
本文首先利用二维 Logistic 映射生成的混沌序列对秘密图像进行扩散, 从而改变秘密图像的像素值, 然后再利用混沌序列生成的置乱矩阵对扩散后的图像进行置乱. 接着分块对载体图像进行 2D-DCT, 并根据混沌系统产生的混沌序列自适应地把置乱后图像的信息替换每块变换DCT 后的右下角, 然后对替换后的矩阵进行 2D-IDCT, 从而得到隐密图像. 我们的算法不论在扩散与置乱阶段还是替换隐藏阶段都受到混沌系统的控制, 从而所提算法对密钥非常敏感. 在实验中, 我们采用峰值信噪比(PSNR)、均方根误差(RMSE)与结构相似性(SSIM)这3个指标, 从不同角度来衡量载体图像与隐密图像相似度, 能全面准确地反映本文算法所得隐密图像的失真度. 实验结果表明, 载体图像与隐密图像的PSNR达到62.615, RMSE 为0.188 7, 而SSIM等于0.999 7, 这些都反映了算法良好的隐藏效果. 与现有的隐藏算法相比较, 我们算法的PSNR更大, 从而说明我们算法具有更优的隐藏性能.
1 二维Logistic映射与2D-DCT 1.1 二维Logistic映射经典的二维Logistic映射[13]可表述为:
| $ \left\{ {\begin{array}{*{20}{c}} {{x_{k + 1}} = {x_k} + \lambda \left( {{x_k} - x_k^2 + {y_k}} \right)} \\ {{y_{k + 1}} = {y_k} + \lambda \left( {{y_k} - y_k^2 + {x_k}} \right)} \end{array}} \right. $ | (1) |
当
2D-DCT是与傅里叶变换相关的一种变换, 它类似于离散傅里叶变换, 但是只使用实数. 因此, 在对语音、图像信号变换中, 2D-DCT变换被认为是一种准最佳变换. 通过2D-DCT可以将图像信号从时域映射到空间频率域, 使得图像在时域所表现出的能量发散形式变换为频域能量相对集中的形式, 以便与对图像信息进行各种处理. 2D-DCT将图像的主要能量集中在左上角, 这样可以将秘密信息嵌入到中高频的右下方, 且能有效地减少载体图像的失真度.
2D-DCT的公式为:
| $ F(u, v) = c(u)c(v)\sum\limits_{x, {{y}} = 0}^{N - 1} {f(x, y)\cos \frac{{\pi (2x + 1)u}}{{2N}}\cos \frac{{\pi (2y + 1)v}}{{2N}}} $ | (2) |
其中,
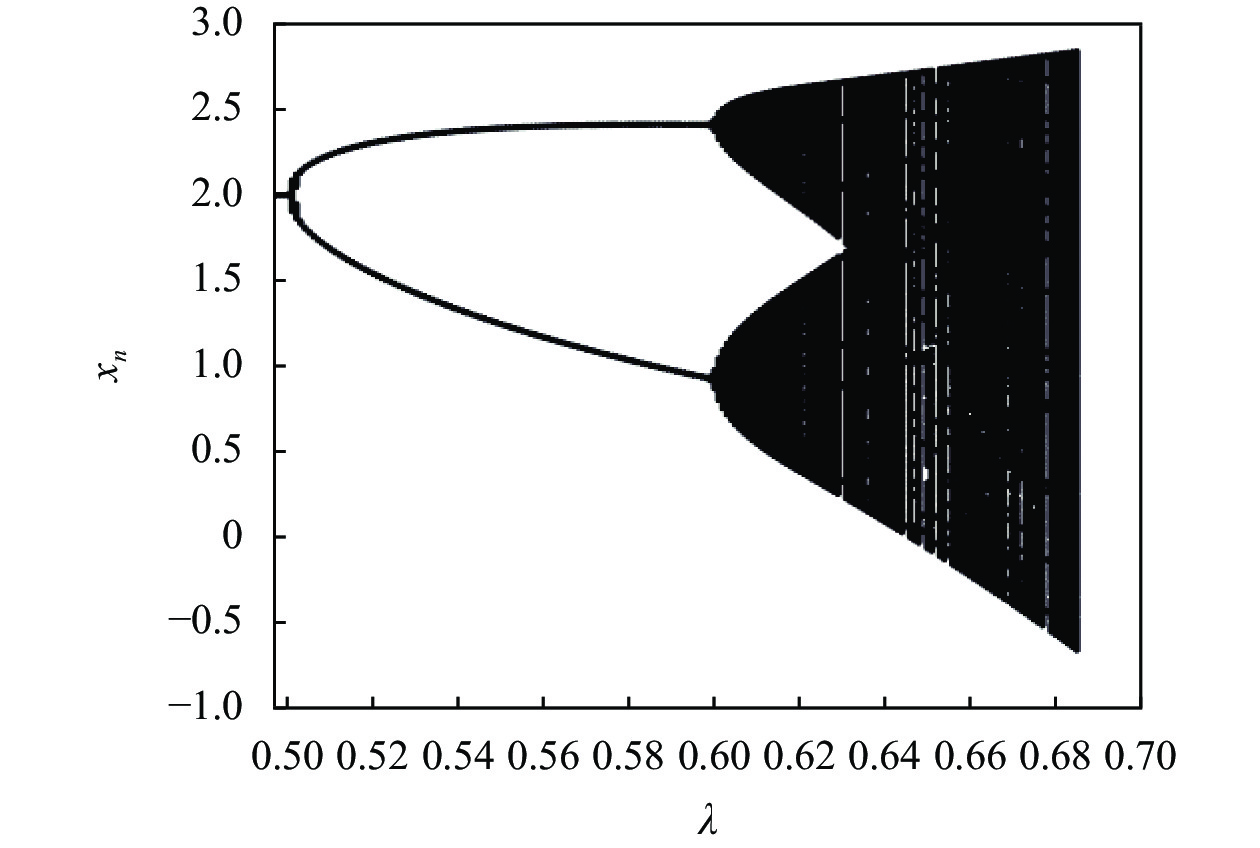
|
图 1 二维Logistic映射的分岔图 |
2D-IDCT的公式为:
| $ f(x, y) = \sum\limits_{x = 0}^{N - 1} {c(u)c(v)F(u, v)\cos \frac{{\pi (2x + 1)u}}{{2N}}\cos \frac{{\pi (2y + 1)v}}{{2N}}} $ | (3) |
其中,
图像隐藏方案包含两个步骤, 首先是对待隐藏图像的预处理, 其次是把预处理后的待隐藏图像隐藏到载体图像中. 我们先对待隐藏图像进行加密, 然后通过分块分存的方法把预处理后的图像隐藏在载体图像
步骤1. 通过迭代二维Logistic映射(1), 生成两个长度为
步骤2. 根据式(2)把混沌序列
| $ \left\{ {\begin{array}{*{20}{c}} {{w_{1i}} = \boldsymbolod (round({{10}^k}{x_i}), 256) } \\ {{w_{2i}} = \boldsymbolod (round({{10}^k}{y_i}), 256) } \end{array}} \right. $ | (4) |
其中,
步骤3. 分别从
步骤4. 利用序列
| $ \left\{ {\begin{array}{*{20}{c}} {{k_{1i}} = \boldsymbolod (round({{10}^k}{{\textit{z}}_{1i}}), 2) } \\ {{k_{2i}} = \boldsymbolod (round({{10}^k}{{\textit{z}}_{2i}}), 2) } \end{array}} \right. $ | (5) |
步骤5. 分别对序列
步骤6. 重新排列整数序列
| $ M = ((I + {H_1})\boldsymbolod 256) \oplus {H_{2}} $ | (6) |
其中, 符号
步骤7. 利用置乱矩阵
| $ F = {M_1} \times M \times {M_2} $ | (7) |
步骤8. 把载体图像分成
D=blkproc(S, [4 4], 'dct2');
for i=1:N
for j=1:N
D(l1i*4-k1i, l2j*4-k2j)=E(i, j);
end
end
步骤9. 把矩阵
记二维Logistic映射的控制参数

|
图 2 图像隐藏与恢复效果 |
众所周知, 图像的直方图反映了像素的统计特性. 因此, 若对于加密算法, 加密图像的直方图越趋于均衡则说明加密效果越好; 若对于图像隐藏技术, 嵌入秘密图像后的隐密图像与载体图像的直方图越接近则说明隐藏效果越佳. 图3(a)和图3(b)显示了秘密图像预处理前后图像的直方图, 其中, 图形底部的灰度条表示Lena图像的灰度级, 0代表黑色, 255代表白色, 而0–255之间的数值代表不同级别的灰度值. 如图可直观看出预处理后的直方图呈现均匀化, 因此窃取者无法通过密文的直方图获得秘密图像有效的统计信息. 图3(c)和图3(d) 为载体图像和隐密图像的直方图, 由图可看出载体图像与隐密图像的直方图肉眼观察几乎完全一致的, 这说明所提算法的隐藏效果非常好.

|
图 3 直方图 |
为了检测算法抗剪切能力, 对隐密图像做剪切攻击实验. 图4(a)–图4(c)分别剪切了隐密图像的1/64, 1/16与1/4 的像素, 而图4(d)–图4(f)则是它们对应恢复的图像. 由实验结果可看出所提算法能有效地把剪切攻击的影响控制在局部的范围, 从而受到攻击后仍能有效地恢复大部分秘密图像的信息.
为了进一步对检验图像隐藏的效果的性能, 从而引入峰值信噪比(PSNR)和均方根误差(RMSE)来衡量两幅图像之间的相似度[10-12]. 设两幅图像分别用
| $ {\textit{PSNR}} = 10\log 10\left[ {\frac{{M \times N \times {{255}^2}}}{{\displaystyle\sum\limits_{i = 1}^M {\displaystyle\sum\limits_{j = 1}^N {{{[S(i, j) - {S_I}(i, j)]}^2}} } }}} \right] $ | (8) |
| $ {\textit{RMSE}} = {\left[ {\frac{1}{{M \times N}}\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {{{[S(i, j) - {S_I}(i, j)]}^2}} } } \right]^{\frac{1}{2}}} $ | (9) |

|
图 4 剪切攻击及恢复的图像 |
由它们的定义, 可以看出它们的 PSNR 值越大或RMSE 值越小, 说明两幅图像越接近, 即两幅图像的相似度度越高.
结构相似性(SSIM), 也是一种有效衡量两幅图像相似度的指标. 两张图像的结构相似性可通过下式计算:
| $ {\textit{SSIM}} = \frac{{\left( {2{\mu _S}{\mu _{{S_I}}} + {c_1}} \right)\left( {2{\sigma _S}{\sigma _{{S_I}}} + {c_2}} \right)\left( {{\sigma _{S{S_I}}} + {c_3}} \right)}}{{\left( {\mu _S^2 + \mu _{{S_I}}^2 + {c_1}} \right)\left( {\sigma _S^2 + \sigma _{{S_I}}^2 + {c_2}} \right)\left( {{\sigma _S}{\sigma _{{S_I}}} + {c_3}} \right)}} $ | (10) |
其中,
利用 PSNR , RMSE 与 SSIM 定义的计算方法, 通过计算可得出4组图像的PSNR, RMSE和 SSIM 的值并列于表1 中. 4组图像有秘密图像与预处理后图像的对比, 载体图像和隐密图像的对比, 秘密图像与正确密钥恢复图像的对比, 以及错误密钥恢复图像与秘密图像的对比.
| 表 1 效果分析 |
通过表1的实验数据可以看出, 秘密图像与预处理后图像的PSNR 较小, RMSE较大, SSIM接近于0, 这些都说明秘密图像与预处理后的图像差别很大, 是完全不一样, 从而验证了对秘密图像预处理的加密效果好; 载体图像和隐密图像的PSNR大于30 (PSNR大于30时, 人眼就无法分辨), RMSE较小, 而SSIM 接近于1, 3个指标结果都说明了这两幅图像的相似度很高, 这证明了所提算法的图像隐藏效果很好; 秘密图像与正确密钥恢复图像的PSNR 趋于无穷大, RMSE的值等于0, 而SSIM接近于1 , 都说明这两幅图像是完全一样, 即秘密图像能完全恢复; 错误密钥恢复图像与秘密图像的PSNR 较小, RMSE较大, 而SSIM接近于0, 这表明错误密钥恢复的图像与秘密图像完全不一样, 即所提算法对密钥非常敏感, 密钥的微小扰动(
一般而言, 隐藏算法的嵌入容量越大, 则对应的载体图像失真越明显, 即对应的 PSNR的值越小. 因此, 对于不同的隐藏算法若其中有一种算法的嵌入容量最大, 而其对应的 PSNR 的值也最大, 说明该隐藏算法的隐藏效果比其它算法好. 从表2可以看出, 我们所提算法、林纯等的算法[16]、冯丹青等的算法[17]与翁子盛的算法[18]在采用相同大小的 Lena 作为载体图像, 不同的嵌入容量的条件下, 我们所提算法在嵌入容量比其它3种高的情况下, 对应的PSNR的值却明显高于其他算法, 这表明我们所提算法的隐藏效果更好.
| 表 2 不同算法比较 |
4 结束语
本文提出了一种基于二维 Logistic 映射与 DCT的分块图像隐藏算法. 首先对秘密图像进行预处理, 利用二维 Logistic 映射产生混沌序列对秘密图像进行扩散与置乱操作, 从而达到对秘密图像第一重保护的目的. 然后通过 DCT 把预处理后的加密图像的信息分存在载体图像中以达到信息隐藏的效果, 从而对秘密图像起到第二重保护的作用. 实验结果表明, 本文所提算法具有良好的抗剪切效果, 隐藏效果也非常好, 并且可以实现秘密图像的无损复原.
| [1] |
丁玮, 齐东旭. 数字图像变换及信息隐藏与伪装技术. 计算机学报, 1998, 21(9): 838-843. DOI:10.3321/j.issn:0254-4164.1998.09.012 |
| [2] |
王育民, 张彤, 黄继武, 等. 信息隐藏: 理论与技术. 北京: 清华大学出版社, 2006, 30-38. |
| [3] |
Zhang XP. Reversible data hiding in encrypted image. IEEE Signal Processing Letters, 2011, 18(4): 255-258. DOI:10.1109/LSP.2011.2114651 |
| [4] |
Hong W, Chen TS, Wu HY. An improved reversible data hiding in encrypted images using side match. IEEE Signal Processing Letters, 2012, 19(4): 199-202. DOI:10.1109/LSP.2012.2187334 |
| [5] |
黄慧青. 基于DCT和混沌的图像隐藏技术. 计算机系统应用, 2013, 22(6): 105-107, 118. DOI:10.3969/j.issn.1003-3254.2013.06.024 |
| [6] |
黄慧青. 基于混沌系统的图像隐藏技术. 计算机系统应用, 2013, 22(11): 183-186. DOI:10.3969/j.issn.1003-3254.2013.11.035 |
| [7] |
Ma KD, Zhang WM, Zhao XF, et al. Reversible data hiding in encrypted images by reserving room before encryption. IEEE Transactions on Information Forensics and Security, 2013, 8(3): 553-562. DOI:10.1109/TIFS.2013.2248725 |
| [8] |
柳玲, 陈同孝, 曹晨, 等. 一种随机嵌入抗SPAM检测的可逆数据隐藏算法. 计算机应用研究, 2013, 30(7): 2111-2114. DOI:10.3969/j.issn.1001-3695.2013.07.048 |
| [9] |
Qian ZX, Zhang XP, Feng GR. Reversible data hiding in encrypted images based on progressive recovery. IEEE Signal Processing Letters, 2016, 23(11): 1672-1676. DOI:10.1109/LSP.2016.2585580 |
| [10] |
Jiang RQ, Zhou H, Zhang WM, et al. Reversible data hiding in encrypted three-dimensional mesh models. IEEE Transactions on Multimedia, 2018, 20(1): 55-67. DOI:10.1109/TMM.2017.2723244 |
| [11] |
叶瑞松, 黄慧青. 基于奇Logistic映射的混沌序列的图像加密算法. 仪器仪表学报, 2008, 29(4): 109-111. |
| [12] |
黄慧青, 许鸿儒. 基于三维Arnold混沌系统的图像加密算法. 嘉应学院学报, 2012, 30(11): 23-26. DOI:10.3969/j.issn.1006-642X.2012.11.006 |
| [13] |
Huang HQ, Yang SZ. Colour image encryption based on logistic mapping and double random-phase encoding. IET Image Processing, 2017, 11(4): 211-216. DOI:10.1049/iet-ipr.2016.0552 |
| [14] |
Huang HQ. Novel scheme for image encryption combining 2D logistic-sine-cosine map and double random-phase encoding. IEEE Access, 2019, 7: 177988-177996. DOI:10.1109/ACCESS.2019.2958319 |
| [15] |
Sahari ML, Boukemara I. A pseudo-random numbers generator based on a novel 3D chaotic map with an application to color image encryption. Nonlinear Dynamics, 2018, 94(1): 723-744. DOI:10.1007/s11071-018-4390-z |
| [16] |
林纯, 吴晓新, 郭晓丽, 等. DCT域可逆图像隐藏技术研究. 微电子学与计算机, 2014, 31(7): 61-64. DOI:10.19304/j.cnki.issn1000-7180.2014.07.014 |
| [17] |
冯丹青, 陈亮. 一种改进的奇异值奇偶区间量化图像隐藏算法. 科学技术与工程, 2019, 19(26): 283-287. DOI:10.3969/j.issn.1671-1815.2019.26.044 |
| [18] |
翁子盛. 一种基于格雷码的图像隐藏算法. 科学技术创新, 2019, 2019(25): 87-88. |
 2022, Vol. 31
2022, Vol. 31


