2. 陕西交通控股集团有限公司 宝鸡分公司, 宝鸡 721399
2. Baoji Branch, Shaanxi Transportation Holding Group Co. Ltd., Baoji 721399, China
截止2021年4月, 全国汽车保有量已达到2.87亿辆, 呈逐年累加趋势. 巨大的车流量使得公路路面病害也在逐年累加, 给公路进行预防性养护工作带来了很大的困难[1, 2]. 其中, 坑槽是公路路面常见的病害之一, 其不但影响行车驾驶的舒适度, 而且会导致严重的安全隐患. 因此, 路面坑槽检测技术对进行公路预防性养护工作具有重要的意义[3].
目前检测公路路面坑槽病害的途径主要是以下3种: 一是震动法[4], 该方法利用加速度传感器的信号反馈来检测坑槽病害, 设备价格低廉, 处理速度快, 但存在漏检的缺点, 不适用于准确提取路面坑槽病害. 二是二维图像分析法[5, 6]. 王朋辉等人[6]提出了基于图像纹理特征以及灰度特征的坑槽提取算法. 该方法主要利用了坑槽与正常路面之间的灰度差异, 但其缺点在于采集图像的灰度值容易受到采集场地环境的限制, 即光照、天气变化、阴影、水渍等因素严重影响图像的灰度分布. 这样将影响到坑槽识别所获取的面积、深度等信息的精度与准确性. 三是三维重建法, 采用三维技术来重建坑槽的立体模型, 该方法包括立体视觉法[7, 8]和三维激光扫描法[9-11]. 张丰梁[7]采用车载双目识别技术的被动检测算法来实现坑槽深度的检测. 该方法易受环境光照变化、单一纹理等因素的影响, 从而导致图像匹配具有不稳定性, 并且大量的像素点计算使得算法要求较高, 故不适应于公路路面的坑槽提取. Zhang等人[8]基于立体视觉, 使用视差算法生成的视差图, 根据坑槽与拟合的二次曲面之间的距离来检测坑槽. 杨雷等人[10]以激光点云为研究对象, 提出一种剖面自适应曲线拟合的坑槽提取算法, 该方法以剖面中的高曲率点作为坑槽边界候选点, 之后进行聚类优化提取出坑槽轮廓. 该方法需要对每个点计算曲率, 计算量较大. 畅陈豪等人[11]提出了基于点云剖面特征描述的坑槽提取算法. 该方法对点云的横断剖面以及纵断剖面分别计算坑槽特征描述, 构建坑槽特征描述算子来自动识别坑槽. 基于三维激光点云, 通过分析点云特征提取坑槽. 该方法可以克服天气、光照、水渍、阴影等环境因素的干扰, 具有较高的实用性. 但是该方法受点云密度的影响, 对点云特征点的计算量大、耗时长, 对算法以及处理设备要求较高.
针对车载三维激光点云扫描计算量大的问题, 本文结合RANSAC算法思想, 快速扫描横断面数据并判断坑槽点, 并且与曲率特征检测坑槽的扫描算法进行对比. 实验结果显示, 该方法具有较高的效率, 并且由此采集到的坑槽深度、面积等数据准确程度高.
1 RANSAC算法随机抽样一致性算法RANSAC (random sample consensus)[12, 13], 是通过重复的随机选取样本集去估算出一个适用于数据集的比较好的数据模型. RANSAC算法能够很好的避开噪声数据对结果的影响, 是比较稳健的模型估计方法.
RANSAC的主要步骤分为以下几步:
(1)从数据集N中随机抽样选取建模所需最小样本集n;
(2)使用最小样本集n来计算出符合该数据集N的数据模型参数;
(3)计算所有数据与这个模型的误差, 在误差阈值内符合这个模型的数据记为“内点”, 反之则为“外点”;
(4)比较当前模型与先前计算所得最好模型的“内点”个数, “内点”数目越多则模型越好, 保存更好模型;
(5)重复步骤(1)–(4), 直到达到设定的迭代次数k, 得出最优模型参数.
1.1 RANSAC算法与最小二乘法由于最小二乘法是对所有的数据进行的整体最优策略, 容易受到异常数据的影响, 进而影响实验效果的精度. RANSAC算法不仅常用于计算机视觉领域特征点匹配问题上, 同样在路面点云数据优化处理上也有非常好的效果[14]. 在存在坑槽的路面横断面数据上, 计算横断面回归线, 采用最小二乘法与RANSAC算法计算结果示意图如图1所示.

|
图 1 RANSAC算法与最小二乘法比较示意图 |
该测试示例数据包含16个正常路面点以及4个异常点, 可以看出采用最小二乘法受到异常点的影响, 在一定程度上偏离了大部分的正常路面点, 即存在了明显的误差. 而采用RANSAC算法, 则能很好的避开异常点, 误差较小, 实验效果良好. 因此, 在存在异常数据的情况下去估计数据模型, 采用RANSAC算法要更优于最小二乘法.
2 坑槽识别算法由激光检测车采集的三维高程点云数据, 可以简化为一个个二维的横断面数据. 由于路面点云的横断面数据大多数是不存在坑槽的, 需要避免对点云中大量的正常路面点进行复杂的特征点提取判断, 节省计算量及计算时间, 首先使用RANSAC对点云横断面数据进行基准线分析, 矫正车载检测横梁带来的扰动, 并且初步判断该横断面上是否存在坑槽点及记录其位置; 对于存在坑槽的横断面, 选出存在坑槽点的局部区域, 可认为局部区域是一个平面, 使用RANSAC计算回归基准平面, 即路面所在平面; 之后由点云数据与局部基准平面的关系, 将坑槽点进行连通域提取, 从而得出属于同一个坑槽的点集; 然后对坑槽点集进行边界提取并优化, 利用点云领域内点的均匀程度来判断边界点; 最后得出坑槽轮廓, 使用三次B样条插值进行拟合, 将坑槽边界映射到二维平面上进行积分运算, 从而分析出该坑槽的面积信息. 该流程如图2所示.

|
图 2 坑槽提取流程图 |
2.1 横断面分析 2.1.1 路面三维坐标系
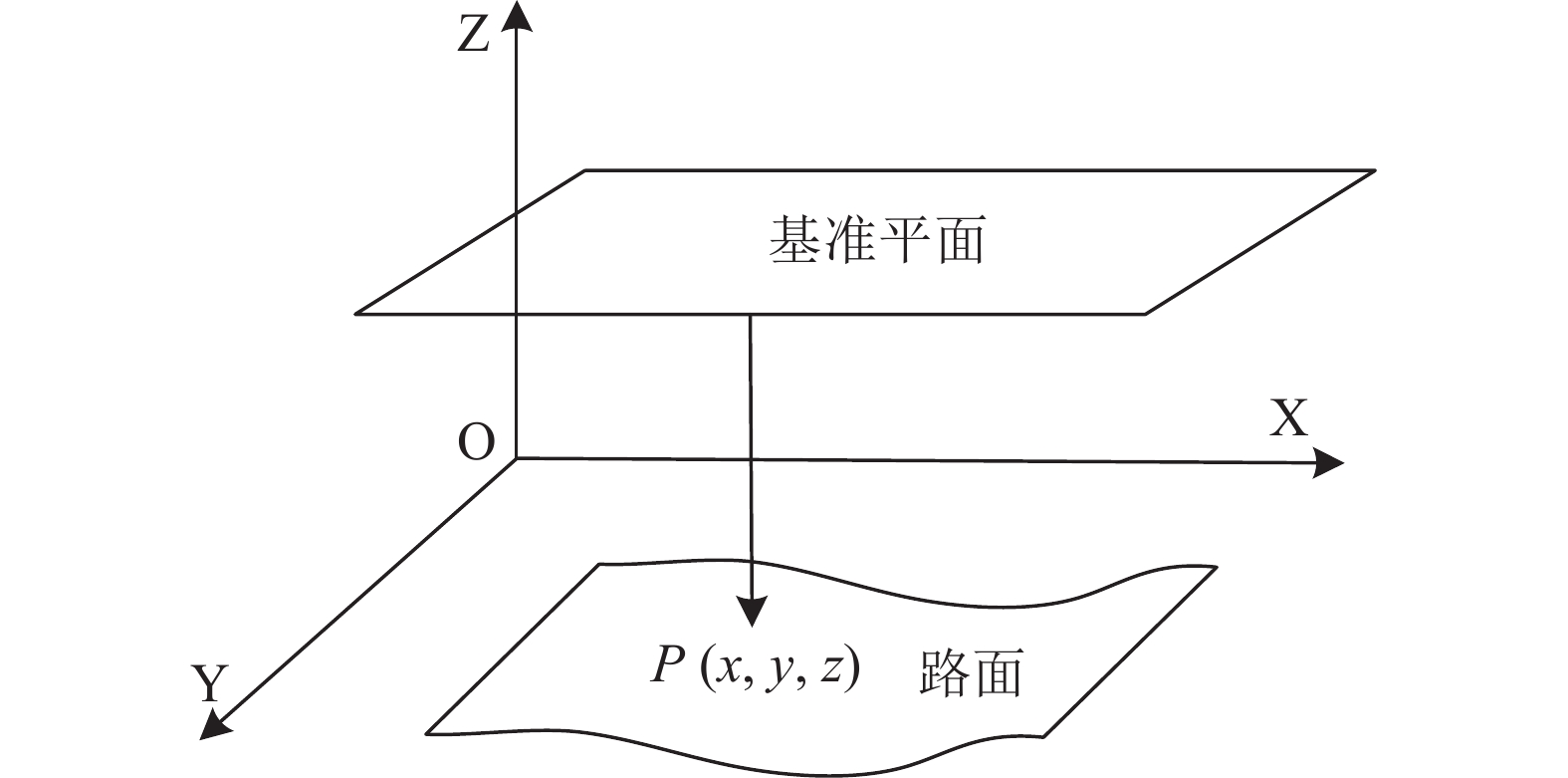
将路面三维点云数据融合到以X轴为里程、Y轴为横断面坐标、Z轴为点高程的三维坐标系[15]里, 如图3所示. 基准平面是一个平行于平面XOY, 为方便分析, 一般选取平面XOY为基准平面. 则路面上任意一点P相对于基准平面的坐标为(x,y, z), 那么整个路面R可以表示为:
| $ \boldsymbol{R} = \left\{ {\begin{array}{*{20}{c}} {\left( {{x_1}, {y_1}, {{\textit{z}}_{11}}} \right)}&{\left( {{x_1}, {y_2}, {{\textit{z}}_{12}}} \right)}& \cdots &{\left( {{x_1}, {y_m}, {{\textit{z}}_{1m}}} \right)} \\ {\left( {{x_2}, {y_1}, {{\textit{z}}_{21}}} \right)}&{\left( {{x_2}, {y_2}, {{\textit{z}}_{22}}} \right)}& \cdots &{\left( {{x_2}, {y_m}, {{\textit{z}}_{2m}}} \right)} \\ \vdots & \vdots & \ddots & \vdots \\ {\left( {{x_n}, {y_1}, {{\textit{z}}_{n1}}} \right)}&{\left( {{x_n}, {y_2}, {{\textit{z}}_{n2}}} \right)}& \cdots &{\left( {{x_n}, {y_m}, {{\textit{z}}_{nm}}} \right)} \end{array}} \right\} $ | (1) |
式(1)可以按里程X方向切割成多个横断面数据
| $ {{\boldsymbol{T}}_{\boldsymbol{i}}}{\text{ = }}\left\{ {\begin{array}{*{20}{c}} {\left( {{x_i}, {y_1}, {{\textit{z}}_{i1}}} \right)}&{\left( {{x_i}, {y_2}, {{\textit{z}}_{i2}}} \right)}& \cdots &{\left( {{x_i}, {y_m}, {{\textit{z}}_{im}}} \right)} \end{array}} \right\} $ | (2) |
因此, 对三维点云的分析可简化为对横断面数据的分析. 为了较好的分析横断面信息, 将数据点映射到二维坐标平面YOZ上, 则当前横断面数据T:
| $ \boldsymbol{T} = \left\{ {\begin{array}{*{20}{c}} {\left( {{y_1}, {{\textit{z}}_1}} \right)}&{\left( {{y_2}, {{\textit{z}}_2}} \right)}& \cdots &{\left( {{y_m}, {{\textit{z}}_m}} \right)} \end{array}} \right\} $ | (3) |
由于在道路检测车的检测过程中, 容易出现车身颠簸震动, 导致检测车的检测横梁不能始终保持在同一测量基准线上, 造成所测量的路面高程线已偏离实际高程线, 导致无准确参考基准面判断路面破损, 如图4所示.
|
图 3 路面点云三维坐标系 |

|
图 4 横梁倾斜时的横断面检测情况 |
因此, 为了使数据高程更接近实际值, 需要矫正检测数据, 使其以理想基准线为基准. 当检测横梁存在震动时, 横断面Y坐标不会改变, 而高程坐标Z则会存在一个偏移, 则偏移后的横断面数据为:
| $ \begin{split} \boldsymbol{T'} & {\text{ }} = \boldsymbol{T} + {y_i} \cdot \tan \alpha + b \\& {\text{ }} = \left\{ {\begin{array}{*{20}{c}} {\left( {{y_1}, {\textit{z}}{'_1}} \right)}&{\left( {{y_2}, {\textit{z}}{'_2}} \right)}& \cdots &{\left( {{y_m}, {\textit{z}}{'_m}} \right)} \end{array}} \right\} \end{split} $ | (4) |
其中,
| $ {{\rm{z}}}{'_i} = {y_i} \cdot {\rm tan} \alpha + b $ | (5) |
由于第1.1节采用RANSAC可以计算出k和b, 代入式(5)可得校正后的横断面数据:
| $ \boldsymbol{T''} = \boldsymbol{T'} - \left( {{y_i} \cdot \tan \alpha + b} \right) \approx \boldsymbol{T} $ | (6) |
根据实际情况需求, 本文采用RANSAC算法, 进行横断面基准线分析. 横断面上所有的点都以横断面基准线为基准, 即所有点高程都是相对于基准路面的高度. 点高程越接近于0, 则表示点越接近基准路面, 即不是坑槽点. 反之, 当点高程越小于0则表示点高程向下凹陷越深, 即坑槽点.
参照JTC 5210-2018《公路技术状况评定标准》, 对于沥青路面的坑槽破损程度, 由坑槽深度作为判定标准有: 坑槽深度小于25 mm为轻度; 坑槽深度大于或者等于25 mm为重度. 因此, 参考上述判定标准, 设定深度阈值T1, 当整个横断面数据高度值都在阈值T1以内, 则认为该横断面不存在坑槽, 或者认为坑槽特征不明显, 还未成为坑槽病害. 将超出阈值T1的点高程数据认为坑槽数据, 并且标记为坑槽点. 由阈值T1可以确定坑槽深度范围, 用以区分坑槽的严重程度. 横断面高程点经过RANSAC初步判定坑槽点, 结果示意图如图5所示.

|
图 5 RANSAC初步判定坑槽点 |
在实际情况下, 大部分路面是完好的, 少数会出现坑槽病害. 因此, 在庞大的路面点云数据中, 只有少部分数据是存在坑槽的. 使用RANSAC进行横断面初步分析, 能够很好的定位到存在坑槽的位置, 记录坑槽点云位置并且取出相邻的横断面点云, 之后再对该位置进行详细的坑槽提取分析. 该方法能够很好地解决路面点云计算量大的问题.
2.2 局部基准面计算由第2.1节横断面分析可以初步判断出坑槽的位置以及部分被标记的坑槽点. 为了减少各个横断面之间的误差, 还原更加准确的坑槽形状, 需要对坑槽附近的局部横断面数据进行整体处理. 因此, 需要计算坑槽附近的局部基准路面, 即相对高程基准路面. 局部平面上的点与该基准面的相对高程即为坑槽深度. 当相对高程接近0时, 这说明该点在基准面附近, 属于正常路面点; 当高程小于0时, 说明该点向下凹陷, 越是偏离基准面, 则其下陷程度越明显, 即属于坑槽点. 因为考虑的是局部坑槽路面, 可认为该局部路面是接近于平面而非曲面. 为此, 使用RANSAC算法计算坑槽的局部基准面, 用于计算平面模型的采样数据为坑槽周围为未被标记的路面点, 这样能够更好地估计平面模型.
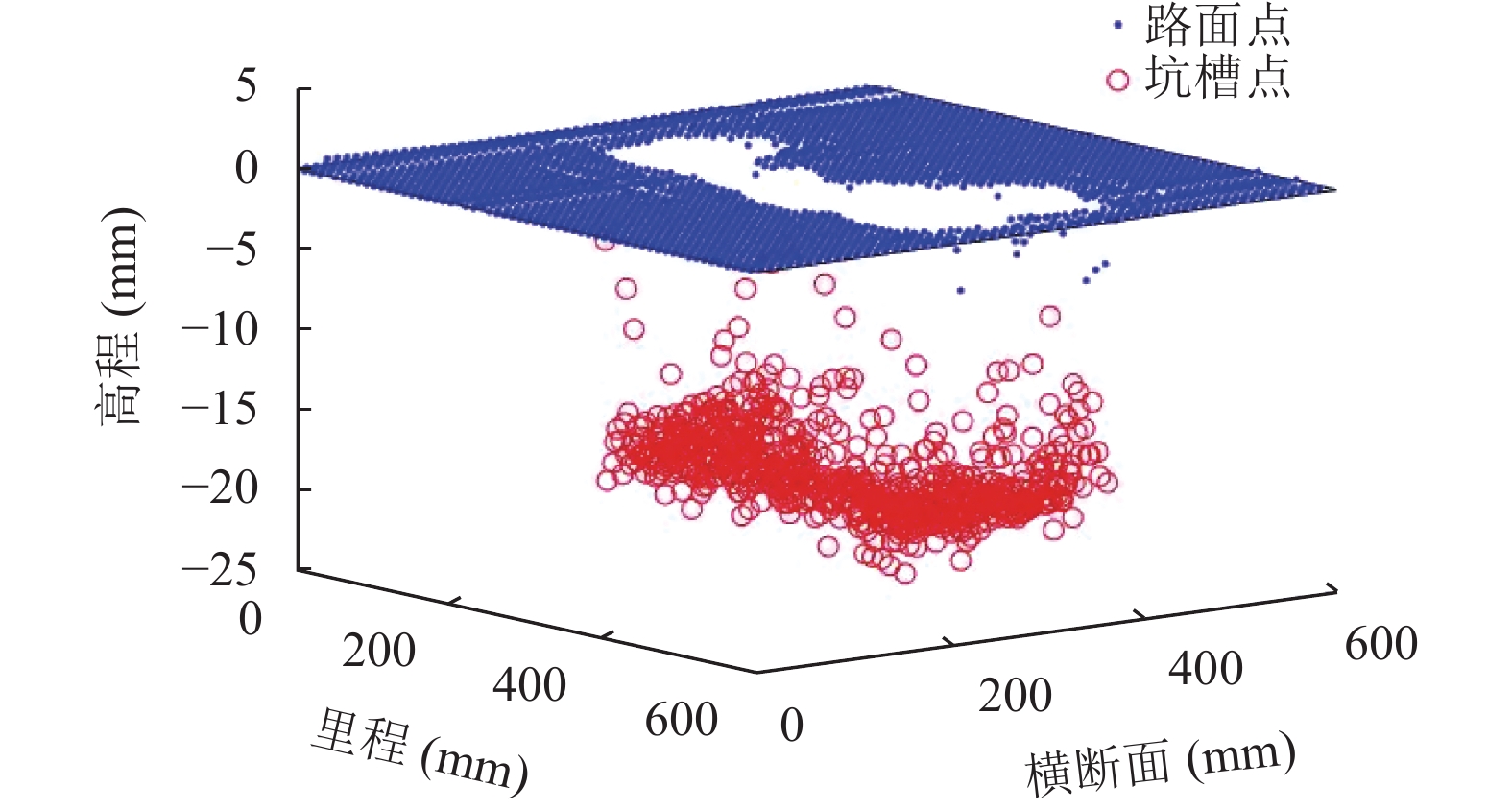
2.3 坑槽点连通域提取选出坑槽局部区域点云, 计算每个点到达局部坑槽基准面的相对高程. 设定坑槽判定规则: 当点相对高程小于设定阈值T2, 即认为当前点与基准路面差距较小, 应归类为路面点; 反之, 则认为坑槽点. 使用种子填充算法, 令其中一个坑槽点作为种子点, 如果相邻的点被判断为坑槽点, 则将其加入坑槽点集S; 重复操作, 直至没有种子点, 停止. 则点集S即为一个完整的坑槽点集. 然后在下一个坑槽种子点开始新的聚类. 点数较少的坑槽点集认为存在错误数据或者坑槽特征不明显, 应去掉. 如图6所示, 经过局部基准面计算, 并且进行坑槽点连通域提取, 可以分离出坑槽点与路面点.
|
图 6 坑槽点连通域提取 |
2.4 坑槽边界提取与优化
由于边界点一侧不存在其他的点; 而非边界点其周围均匀分布其他点. 本文采用的是文献[16]中的坑槽边界提取方法, 利用点云领域内点的均匀程度来判断边界点, 即边界点的外侧无其他坑槽点, 而其内侧则均为坑槽点. 总体方法为计算某点P与其近邻点组成的向量之间的夹角, 然后对个夹角进行排序, 计算连续夹角间的最大差值, 将这个差值与设置的阈值进行比较, 若大于则该点则为边界点, 否则不是.
计算所得的边界点为了使边界线平滑, 更接近实际形状, 并且方便与后续的面积积分操作, 需要进行插值拟合优化处理. 本文采用三次样条插值法进行边界拟合处理, 所得结果为坑槽边界点集B.
2.5 坑槽分析由第2.3节处理后得到坑槽点集, 对该点集所有数据进行遍历, 所得的高程绝对值最大者即为坑槽的最大深度
| $ {H_{\rm{max}}} = {\left| {{{\textit{z}}_i}} \right|_{\rm{max}}}, {{\textit{z}}_i} \in S $ | (7) |
其中, S为坑槽点集,
参考文献[9], 将坑槽边界集合B映射到XOY平面上, 则闭合的曲线围成的面积即为坑槽面积, 如图7所示. 将该坑槽区域沿X轴方向分n个宽度相同的梯形, 则积分计算其面积为:
| $ S{\text{ = }}\sum\limits_{i = 1}^n {\Delta {S_i} = \frac{1}{2}\sum\limits_{i = 1}^n {\Delta X\left( {{Y_i} + {Y_{i - 1}}} \right)} } $ | (8) |

|
图 7 坑槽面积积分示意图 |
3 实验分析
本文的实验数据分为室内及室外两部分. 室内数据是由激光测距仪, 固定测量高度后, 在实验室测试矩形以及圆形等规则的坑槽模型. 点云扫描横断面间距为10 mm, 横断面每个点的距离也为10 mm, 测距精度为1 mm. 室外路面数据是由低速道路检测车采集获得, 采集数据为校园沥青路段中的一条车道. 该实验路段的长度100 m, 扫描宽度为3.5 m, 点云间间距为10 mm, 扫描线间距为10 mm, 测距精度为1 mm, 每个横断面的点数量为350个, 数据总量为3 500 000个. 处理数据设备为笔记本电脑, 配置CPU为Intel 9代i7, 主频为2.6 GHz, 显卡型号为GTX1650, 并使用Matlab处理数据.
3.1 效率性分析本文方法提高点云计算效率在于进行快速的扫描, 而扫描出存在坑槽的横断面则由坑槽形状提取算法进行处理. 对横断面扫描检测坑槽算法进行效率性分析, 使用文献[10]中的曲率特征点检测方法作为对照方法. 文献[10]采用的横断面坑槽扫描算法步骤为: (1)采用最小二乘法对横断面进行曲线拟合; (2)计算横断面上每个点的曲率, 并计算高于平均曲率的高曲率点; (3)由高曲率点进一步计算并进行坑槽特征点判定. 计算横断面上的每一个点的曲率K, 计算公式为:
| $ K{\text{ = }}\frac{{\left| {y''} \right|}}{{{{\left( {1 + y{'^2}} \right)}^{\frac{3}{2}}}}} $ | (9) |
其中, y'和y''分别为当前点在横断面拟合曲线曲线上的一阶导数和二阶导数.
对照实验所使用的数据为100 m路段点云, 点云数量为3 500 000个. 使用本文横断面扫描算法与曲率特征点算法, 对该数据进行10次横断扫描检测计算, 其对照实验结果如表1所示.
| 表 1 横断面扫描检测算法实验结果比较 |
由表1结果, 采用曲率特征点算法所需要的平均时间12.554 s, 方差为0.025 6, 标准差为0.160; 采用本文方法所需的平均时间为5.466 s, 方差为0.018 9, 标准差为0.137. 采用曲率特征点方法与本文扫描方法的计算时间的平均差值为7.088 s, 使用本文方法相对于曲率特征点算法平均提升的效率为56.46%. 由此结果显示, 采用本文的扫描方法, 同一数据量的计算时间要明显低于使用曲率特征点的算法, 计算时间的分布更为收敛.
使用RANSAC算法计算横断面直线模型只需要两个样本点, 迭代多次后, 遍历每个点与最优模型的高度差, 所涉及的计算复杂度较低; 而采用计算特征点的方法, 使用最小二乘法计算横断面拟合曲线, 并求出横断面上每个点的一阶和二阶导数, 最后取平均曲率为阈值去比较每个点的曲率, 该方法计算复杂度较高, 计算量较大. 针对点云的数量到达千万甚至亿级别, 本文算法能够快速扫描出坑槽点的位置, 并将存在坑槽点的局部横断面提取出, 以供后续的坑槽详细信息提取, 使得扫描横断面点云与提取详细坑槽信息算法可以并发执行, 提高执行效率.
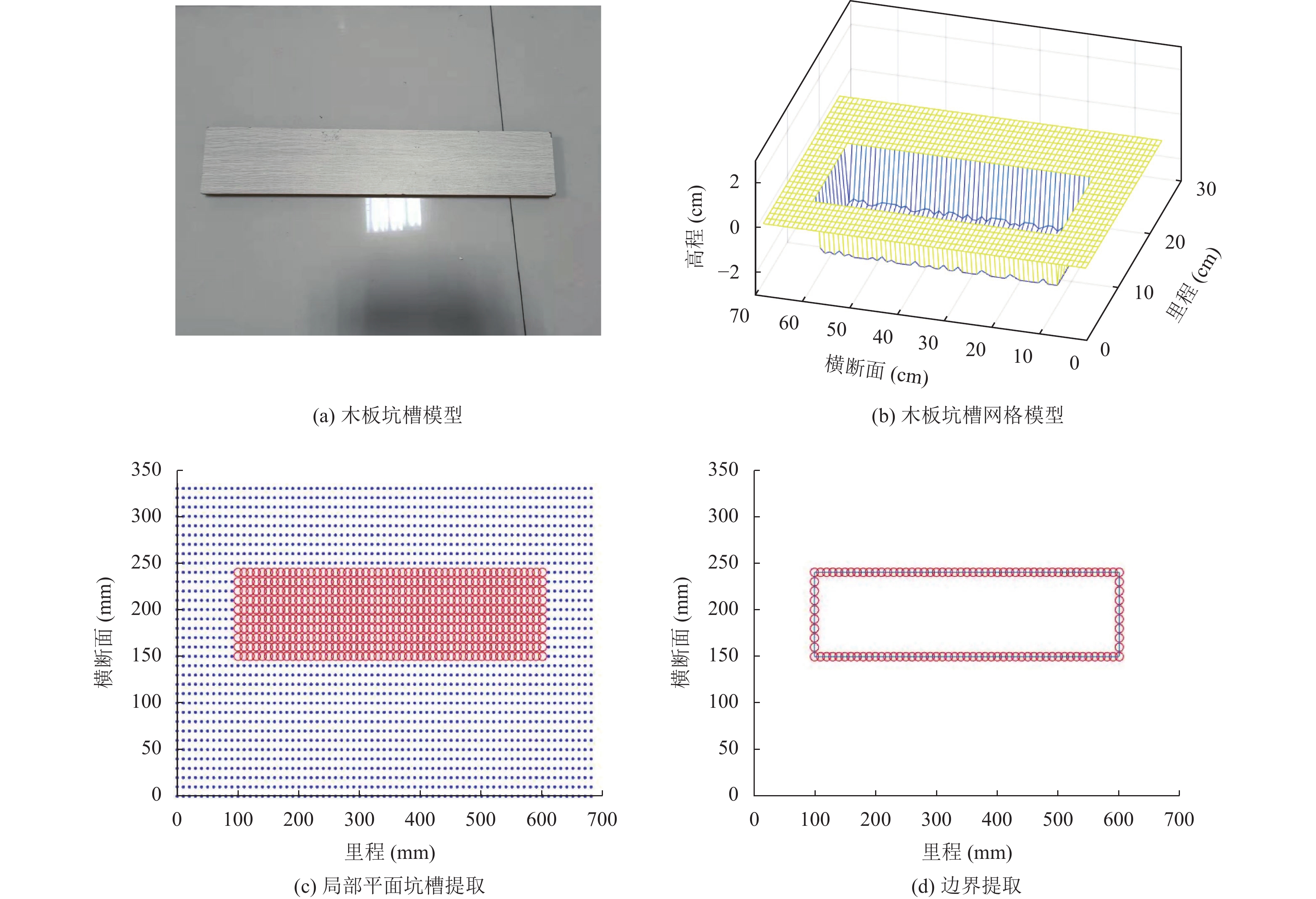
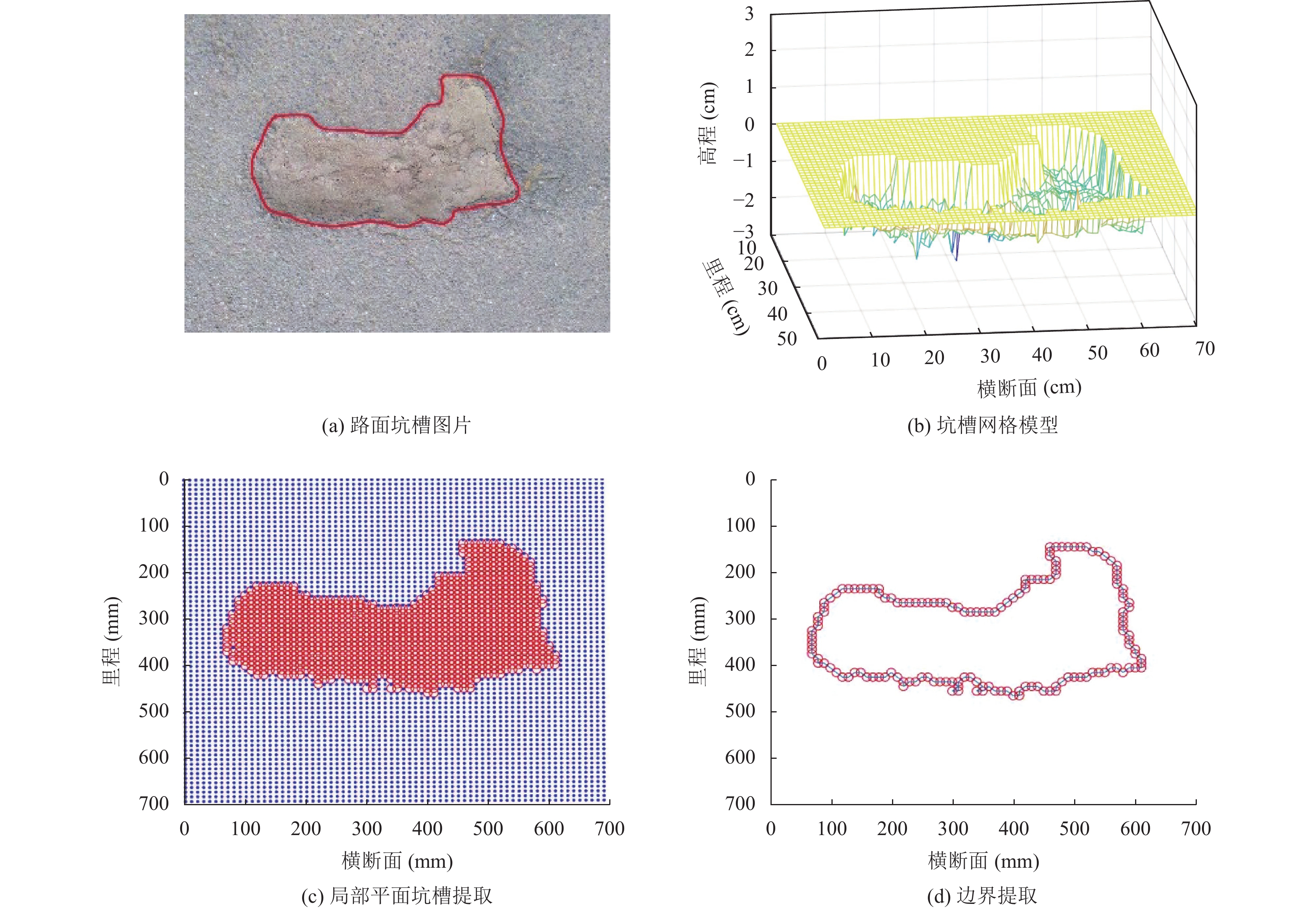
3.2 准确性分析图8所示为在室内使用木板模型采集数据处理的结果. 图9和图10为在公路采集到的坑槽及实验结果. 实验结果显示, 本文方法能够很好的提取出坑槽的形状轮廓. 本文以坑槽的深度及面积为指标验证本文方法效果, 采集到坑槽样本12个, 对每个样本进行10次计算, 结果取平均值. 用人工测量的方法与本文方法进行对比, 实验结果如表2所示.
由表2本文方法与人工方法的对比结果, 坑槽深度采集精度为1 mm, 其误差范围在0.9–2.3 mm之间, 相对误差范围在3.00%–6.59%之间, 平均相对误差为4.73%. 由坑槽面积结果显示, 其相对误差范围在2.43%–5.65%, 平均相对误差为4.50%. 由此数据可知, 本文实验结果的深度及面积平均相对误差都小于5%, 实验结果良好, 能够有效地提取出坑槽的信息.
由JC 510-2018《公路技术状况评定标准》定义坑槽标准损坏程度: 坑槽深度小于25 mm, 或面积小于0.1 m2属于轻度坑槽; 坑槽深度大于或等于25 mm, 或大于或等于0.1 m2属于重度坑槽. 由该标准, 坑槽编号为1、5、10为轻度坑槽; 其余编号的为重度坑槽. 由表结果显示, 属于重度坑槽的平均误差为4.21%, 误差较小; 而轻度坑槽平均误差为5.38%, 误差较大. 产生该结果的原因为采集间隔为10 mm, 在坑槽较小的时候, 该采集精度对计算结果的精度影响较大.
依照本文算法进行坑槽面积计算, 其结果比实际值要小. 产生该问题的原因在于计算坑槽局部0高程平面后, 聚类坑槽点云方法决定的. 因为设定距离0高程平面的阈值作为划分坑槽点与平面点, 所以部分坑槽边缘点距离0高程平面较近而被划分为路面点, 导致缺少部分边界点而计算出的面积要小于实际值.
|
图 8 室内木板实验结果 |
|
图 9 路面坑槽1实验结果 |
|
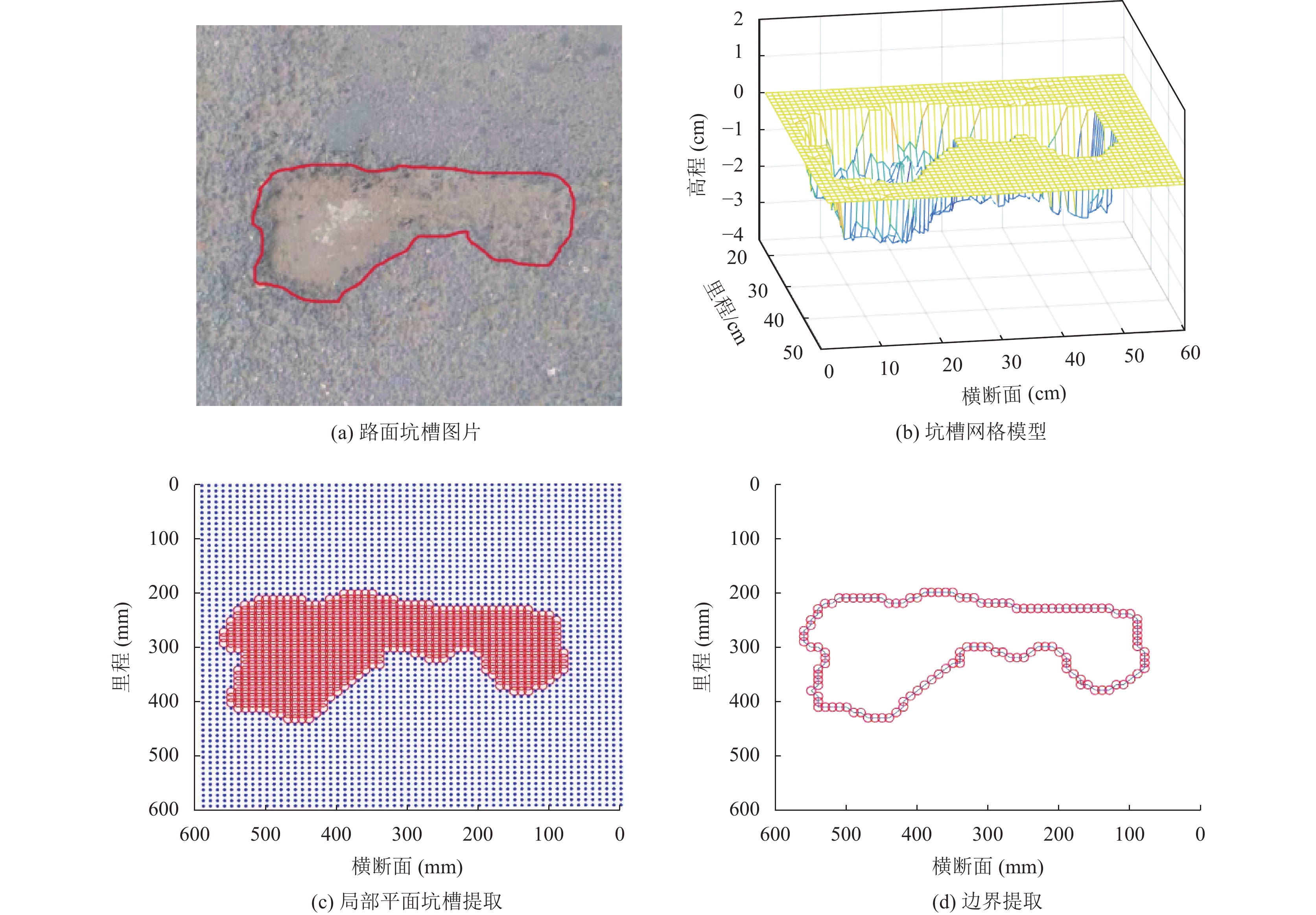
图 10 路面坑槽2实验结果 |
| 表 2 路面坑槽实验结果比较 |
4 结论
针对车载三维点云扫描提取坑槽特征点计算量大的问题, 本文使用RANSAC算法思想, 以整体基准判定异常点的方法去提取坑槽. 首先使用横断面基准线整体判断并标记坑槽点, 然后针对坑槽区域进行局部基准面整体判断坑槽点集, 之后使用种子填充算法进行坑槽连通域点集提取, 最后对坑槽点集进行边界提取以及插值拟合, 从而可以计算出坑槽有效信息.
实验结果表明, 相较于由曲率特征点判定坑槽的方法, 本文使用RANSAC扫描检测横断面方法的效率平均提升56.46%, 能够快速扫描出坑槽点的位置, 提高识别提取的效率. 采集坑槽样本12个, 深度指标平均误差为4.73%, 面积指标平均误差为4.50%. 实验结果误差较小, 具有良好的识别效果.
本文方法针对横断面扫描检测坑槽位置进行处理, 避免了在正常路面点云上的大量分析和处理, 能够准确地提取出不规则坑槽的轮廓形状、面积和深度等信息. 本文算法处理后提取的坑槽与实际路面坑槽存在一定范围的误差, 但该误差较小, 提取结果与真实结果之间具有较高的一致性.
| [1] |
丁超. 高速公路沥青路面预防性养护思考. 建筑技术开发, 2020, 47(21): 118-120. DOI:10.3969/j.issn.1001-523X.2020.21.055 |
| [2] |
袁健. 现代公路养护中预防性公路养护技术的应用. 居舍, 2021(4): 73-74. |
| [3] |
马登成. 如何让公路养护装备更智慧. 中国公路, 2021(10): 40-42. |
| [4] |
de Zoysa K, Keppitiyagama C, Seneviratne GP, et al. A public transport system based sensor network for road surface condition monitoring. Proceedings of the 2007 Workshop on Networked Systems for Developing Regions. Kyoto: ACM, 2007. 9.
|
| [5] |
Koch C, Brilakis I. Pothole detection in asphalt pavement images. Advanced Engineering Informatics, 2011, 25(3): 507-515. DOI:10.1016/j.aei.2011.01.002 |
| [6] |
王朋辉, 胡永彪, 田明锐, 等. 基于图像纹理的沥青路面坑槽识别及提取. 计算机应用研究, 2018, 35(5): 1596-1600. DOI:10.3969/j.issn.1001-3695.2018.05.069 |
| [7] |
张丰梁. 基于车载双目视觉的路面坑槽检测方法研究[硕士学位论文]. 苏州: 苏州科技学院, 2015.
|
| [8] |
Zhang Z, Ai X, Chen CK, et al. An efficient algorithm for pothole detection using stereo vision. 2014 IEEE International Conference on Acoustics, Speech and Signal Processing. Florence: IEEE, 2014. 564–568.
|
| [9] |
惠冰, 郭牧, 周博闻. 沥青路面坑槽三维重构与指标计算方法. 哈尔滨工业大学学报, 2018, 50(3): 97-102. DOI:10.11918/j.issn.0367-6234.201611104 |
| [10] |
杨雷, 刘如飞, 卢秀山, 等. 一种车载激光扫描点云中路面坑槽自动提取方法. 测绘工程, 2020, 29(1): 66-71. |
| [11] |
畅陈豪, 刘如飞, 柴永宁, 等. 点云剖面特征描述的路面坑槽提取方法. 地理空间信息, 2021, 19(2): 9-13. DOI:10.3969/j.issn.1672-4623.2021.02.003 |
| [12] |
Fischler MA, Bolles RC. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Communications of the ACM, 1981, 24(6): 381-395. DOI:10.1145/358669.358692 |
| [13] |
Chum O, Matas J. Optimal randomized RANSAC. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2008, 30(8): 1472-1482. DOI:10.1109/TPAMI.2007.70787 |
| [14] |
曹毓, 冯莹, 杨云涛, 等. RANSAC直线估计方法在路面三维点云优化中的应用. 红外与激光工程, 2012, 41(11): 3108-3112. DOI:10.3969/j.issn.1007-2276.2012.11.047 |
| [15] |
马荣贵. 路面三维检测系统原理及方法研究[博士学位论文]. 西安: 长安大学, 2008.
|
| [16] |
丁承君, 孙刚, 尹李亮, 等. 散乱点云的边界提取. 计算机技术与发展, 2017, 27(7): 83-86. DOI:10.3969/j.issn.1673-629X.2017.07.020 |
 2022, Vol. 31
2022, Vol. 31


