跑道视程(runway visual range, RVR)是指起飞/着陆时飞机与跑道内地面物体之间的视程, 表示在大雾等恶劣天气条件下跑道和跑道中心线的识别程度, 是影响飞机起飞和降落的重要因素之一. 在能见度小于800 m的情况下, 航空管制员需要根据跑道视程判断飞机是否能够起降^[1]. 随着民航航班总量的快速增长, 跑道视程对航班运行的影响愈加显著, 已经成为影响航班安全、正常、效率的主要因素^[2]. 实际机场运行管制过程中, 为了保障起降安全, 一般较低的跑道视程发生时不允许飞机起降. 相应地, 跑道视程降低将导致机场运行能力减弱, 机场航班容量降低, 进而引起航班堵塞延误, 旅客滞留, 增加机场运行成本. 因此, 机场气象或者管制人员就会特别关心未来一段时间内跑道视程的变化趋势, 跑道视程预测将能够为机场业务人员提前决策提供依据, 特别是对低跑道视程条件提前作出预警, 制定相关起降、管制预警应急方案.

跑道视程不是一个直接观测量, 目前许多机场已经布设了民航自动气象观测系统(automated weather observing system, AWOS)通过参数计算实时的跑道视程值, 但观测仅仅能够反映当前状态, 无法满足机场业务部门对未来跑道视程变化趋势的产品需求, 机场业务上至少需要提前预报未来近6个小时的跑道视程变化情况辅助业务决策.

机场跑道视程预测常用的传统方法多是基于不同天气形势的各种预报模型的知识积累和近似记忆, 但因知识更新手段的繁琐, 近年来该方法逐渐被预报员抛弃^[3]. 随着计算机计算能力以及人工智能技术的进步, 深度学习预测技术在跑道视程预测领域日益受到关注. 朱蕾等人利用3年的乌鲁木齐机场RVR观测资料, 使用SVM方法分别构建了大于800 m和小于800 m的RVR推理模型^[3]. Ku等人也采用了卷积神经网络对韩国泰安机场的跑道视程预测进行了初步尝试^[4]. 周志洋利用数据挖掘技术, 通过多个维度的气象特征首次对高高原机场的跑道视程进行了短时预测, 准确率最高达到81.14%^[5].

长短时记忆网络(long short term memory network, LSTM)是一种改进的循环神经网络, 它有效解决了循环神经网络在梯度消失和缺乏长期记忆能力等方面存在的问题, 能够从海量的长时间序列信息中自动学习其特征并保存, 适合处理时序预测问题, 近年来在气象领域已得到应用. 袁芳介绍了LSTM技术的基本原理, 并提出该方法在处理气象领域非线性分类、回归等问题应用建议^[6]. 李芬等人将LSTM方法用于细颗粒物(particle matter≤2.5 μm, PM_2.5)的短期预测^[7]. 魏昱洲等人使用LSTM方法进行超短期风速的预测试验, 均取得了一定的预报效果^[8]. 此外, 罗芳琼等人基于LSTM方法提取的特征信息, 结合随机森林和支持向量机方法, 建立了低温气象灾害预报混合模型, 取得了较高的预测精度^[9].

低跑道视程现象受多重气象和非气象因子影响, 不同因子之间也同样存在相互作用关系, 具有明显的非线性特征, 预报难度较大. 因而, 如何尽可能地提高对低跑道视程天气的预报能力, 从而实现提前预警是航空气象保障人员颇为关注的问题. 为确保飞机能够安全起降, 本文采用咸阳机场2012–2018年共7年的民航自动气象观测系统观测资料对跑道视程进行研究, 采用新型的基于长短时记忆网络方法, 建立机场跑道视程预测模型, 旨在为气象保障人员提供一定的可供参考的预测产品, 辅助决策保障飞机的安全起降.

1 跑道视程、长短时记忆网络概念解析 1.1 跑道视程

跑道视程是指在机场跑道中线上, 飞机上的飞行员能够看到跑道面上的标志或者跑道边界灯或中线灯的距离^[10]. 跑道视程不是直接测量的气象要素, 通过跑道灯光强度( $I$ )、照度阈值( $E$ )和大气消光系数( $\sigma $ ), 根据柯西米德定律(Koschmieder’s law)和阿拉德定律(Allard’s law)计算得出的数值^[2], 将两个定律计算得出的较大值作为要报告的 $RVR$ 值.

在白天无灯光的情况下, 根据柯西米德定律, $RVR$ 的计算公式为^[2]:

$ RVR = - \ln 0.05 / \sigma \approx 3 / \sigma $

(1)

在白天能见度受限或夜晚的情况下, 此时需要开启跑道灯, 依据阿拉德定律, $RVR$ 的计算公式为^[2]:

$ \sigma RVR + \ln \left( E \right) - \ln \left( I \right) = - 2\ln \left( {RVR} \right) $

(2)

其中, 跑道灯光强度可通过背景亮度仪测量的背景亮度估算得出, 照度阈值可按照设定的跑道灯光级数估算得到, 大气消光系数可由大气透射仪或前向散射仪测量的气象光学视程得出^[2].

从公式出发, 跑道视程似乎与气象无关, 但实际业务中, 照度阈值及大气消光系数的变化受到多种气象要素综合影响, 例如强降水导致能见度降低, 直观上导致大气消光系数增大, 跑道视程降低, 大雾也能导致能见度降低, 直观上导致大气消光系数增大, 跑道视程降低^[2]. 跑道灯光级数调整导致照度阈值变化也受降水、大雾等低能见度天气的影响. 气象要素对跑道视程的影响作用是极其复杂的、非线性的, 还没有任何一种数学物理公式或者模型能够完全刻画这种影响关系.

咸阳机场Ⅰ类精密进近着陆标准为主导能见度≥800 m或 $RVR$ ≥550 m, Ⅱ类精密进近着陆标准为300 m≤ $RVR$ <550 m^[11]. 对于Ⅱ类精密进近, 当跑道视程观测设备故障或无法获得跑道视程报告时不得实施Ⅱ类运行^[11]. 通常, 将 $RVR$ <550 m定义为低跑道视程, 低跑道视程下常引发大面积航班延误, 严重影响航班正常运行, 易引发不安全事件, 飞行员及各安全保障部门均需要非常谨慎地对待这种运行情况^{[1, 11]}.

1.2 长短时记忆网络

LSTM是Hochreiter等人^[12] 1997年提出的基于循环神经网络理论的具有记忆长短期信息能力的神经网络, 是一种特殊的循环神经网络(recurrent neural network, RNN), 主要是为了解决长序列训练过程中的梯度消失和梯度爆炸问题, 相比普通的RNN, LSTM在更长的序列中能够有更好的表现^{[7, 13]}. 经过若干代的发展, 已经形成了比较系统且完整的LSTM框架, 并且在语音识别、图像描述、自然语言处理、市场调研和交通预测等领域得到了广泛的应用^[14-16]. LSTM的基本节点结构如图1所示.

图1中, $ \times $ 表示缩放信息, $ + $ 表示添加信息, ${\text{σ }}$ 表示Sigmoid层, ${\text{tanh}}$ 表示tanh层(双曲正切), ${H_{t - 1}}$ 表示上一个节点的输出, ${C_{t - 1}}$ 表示上一个节点的状态, ${X_t}$ 表示输入, ${C_t}$ 表示更新后的状态, ${H_t}$ 表示输出. 贯穿图1的两条水平线代表了传输单元的状态, 通过线性变换保证了单元内部信息传输的不变性, 它是长短时记忆网络的核心^[16]. 长短时记忆网络还能通过几个结构管理信息的传输, 从而添加或删除向单元状态中传输的信息, 选择性的让信息通过, 一般将这些结构称为门限^[17]. LSTM内部主要有3个阶段(遗忘、输入、输出), 这3个阶段通过3个门限逻辑实现, “遗忘门”忘记部分过去的信息, “输入门”记住部分现在的信息, 然后将过去的记忆与现在的记忆合并后通过“输出门”决定最终输出的部分.

(1)遗忘阶段: 这个阶段主要是对上一个节点传进来的输入进行选择性忘记, 遗忘门计算逻辑:

$ {f}_{t}=\sigma \left({W}_{f}\cdot\left[{H}_{t-1}, {X}_{t}\right]+{b}_{f}\right) $

(3)

其中, ${f_t}$ 表示遗忘门输出, ${H_{t - 1}}$ 表示上一个节点的输出, ${X_t}$ 表示输入, ${W_f}$ 表示遗忘门权重, ${b_f}$ 表示遗忘门偏置, $\sigma $ 表示Sigmoid层.

(2)输入阶段: 这个阶段将这个节点的输入有选择性地进行“记忆”, 输入门计算逻辑:

$ {i}_{t}=\sigma \left({W}_{i}\cdot\left[{H}_{t-1}, {X}_{t}\right]+{b}_{i}\right) $

(4)

其中, ${i_t}$ 表示输入门输出, ${H_{t - 1}}$ 表示上一个节点的输出, ${X_t}$ 表示输入, ${W_i}$ 表示输入门权重, ${b_i}$ 表示输入门偏置, $\sigma $ 表示Sigmoid层.

当前候选节点状态计算逻辑:

$ {\tilde{C}}_{t}={\rm tanh}\left({W}_{C}\cdot\left[{H}_{t-1}, {X}_{t}\right]+{b}_{C}\right) $

(5)

其中, ${\tilde C_t}$ 表示当前候选节点状态, ${H_{t - 1}}$ 表示上一个节点的输出, ${X_t}$ 表示输入, ${W_C}$ 表示权重, ${b_C}$ 表示偏置, ${\rm tanh}$ 表示tanh层.

将前两个阶段得到的结果通过计算逻辑:

$ {C}_{t}={f}_{t}\cdot{C}_{t-1}+{i}_{t}\cdot{\tilde{C}}_{t} $

(6)

其中, ${C_t}$ 表示传输给下一个节点的状态, ${C_{t - 1}}$ 表示上一个节点的状态.

(3)输出阶段: 这个阶段将决定哪些信息将会被当成当前状态的输出, 输出门计算逻辑:

$ {o}_{t}=\sigma \left({W}_{o}\cdot\left[{H}_{t-1}, {X}_{t}\right]+{b}_{o}\right) $

(7)

其中, ${o_t}$ 表示输出门输出, ${H_{t - 1}}$ 表示上一个节点的输出, ${X_t}$ 表示输入, ${W_o}$ 表示输出门权重, ${b_o}$ 表示输出门偏置, $\sigma $ 表示Sigmoid层.

当前节点最终输出还对上一阶段得到的 ${C_t}$ , 通过tanh函数进行了放缩, 计算逻辑:

$ {H}_{t}={o}_{t}\cdot {\rm tanh}\left({C}_{t}\right) $

(8)

其中, ${H_t}$ 表示当前节点的最终输出.

2 跑道视程预测数据集构建 2.1 AWOS观测资料

本文采用了2012–2018年咸阳机场共7年的民航气象自动观测系统AWOS观测资料, AWOS每分钟记录一次各种气象要素数据, 包括风向、风速、温度、露点温度、气压、相对湿度、降水量、背景亮度、气象光学视程、跑道视程等.

咸阳机场南北两条跑道沿东北–西南方向, AWOS观测设备位于两条跑道的4个跑道端点及2个中点, 南侧跑道东北端点编号RWY23L, 中点编号SOUTH MID, 西南端点编号RWY05R, 北侧跑道东北端点编号RWY23R, 中点编号NORTH MID, 西南端点编号RWY05L.

2.2 预报因子选择

影响机场跑道视程的天气主要有雾、烟、沙尘、强降水等, 不同的天气现象具有不同的气象影响因子. 因此, 本小节主要通过对低跑道视程的时序特征分析和相关分析, 获取影响咸阳机场的典型气象因子.

通过对咸阳机场2012–2018年共7年的AWOS观测资料统计, 咸阳机场各端点低跑道视程的月际分布如图2所示.

图2中低跑道视程天气的月际变化呈双峰型分布, 集中多发于秋冬季的9–12月和2–3月, 春季和夏季发生次数较少, 这种季节分布特征表明本场低跑道视程天气主要是由雾造成. 而形成雾的相关气象因子条件有: 地面气温相对较低, 大气相对湿度较大, 接近准饱和状态, 近地层无风.

经过统计, 本场各端点低跑道视程的小时分布如图3所示.

图3中低跑道视程天气多发于凌晨至上午, 下午至傍晚较少发生, 并且在凌晨至清晨北侧跑道明显多于南侧跑道, 而上午发生的低跑道视程天气南侧跑道多于北侧跑道. 表明咸阳机场的大雾天气主要以辐射雾为主, 机场西北部平原相对东南方向的渭河河谷辐射冷却效应更强, 夜间至凌晨更容易产生辐射雾, 而日出后北部升温快于南部, 辐射雾消散更快, 另一方面和渭河河谷冷气垫的温差造成的局地环流利于河谷区域的雾自东南向西北方向输送.

此外, 针对AWOS自动观测资料中存在气象要素较多, 以及考虑到跑道视程也与仪器自身特性相关. 为了尽可能多地获取与低跑道视程相关的各类因子, 利用本场AWOS自动观测每分钟的平均风、阵风、温度、露点温度、气压、相对湿度、背景光亮度等地面观测要素进行相关性分析, 从而选择预报因子.

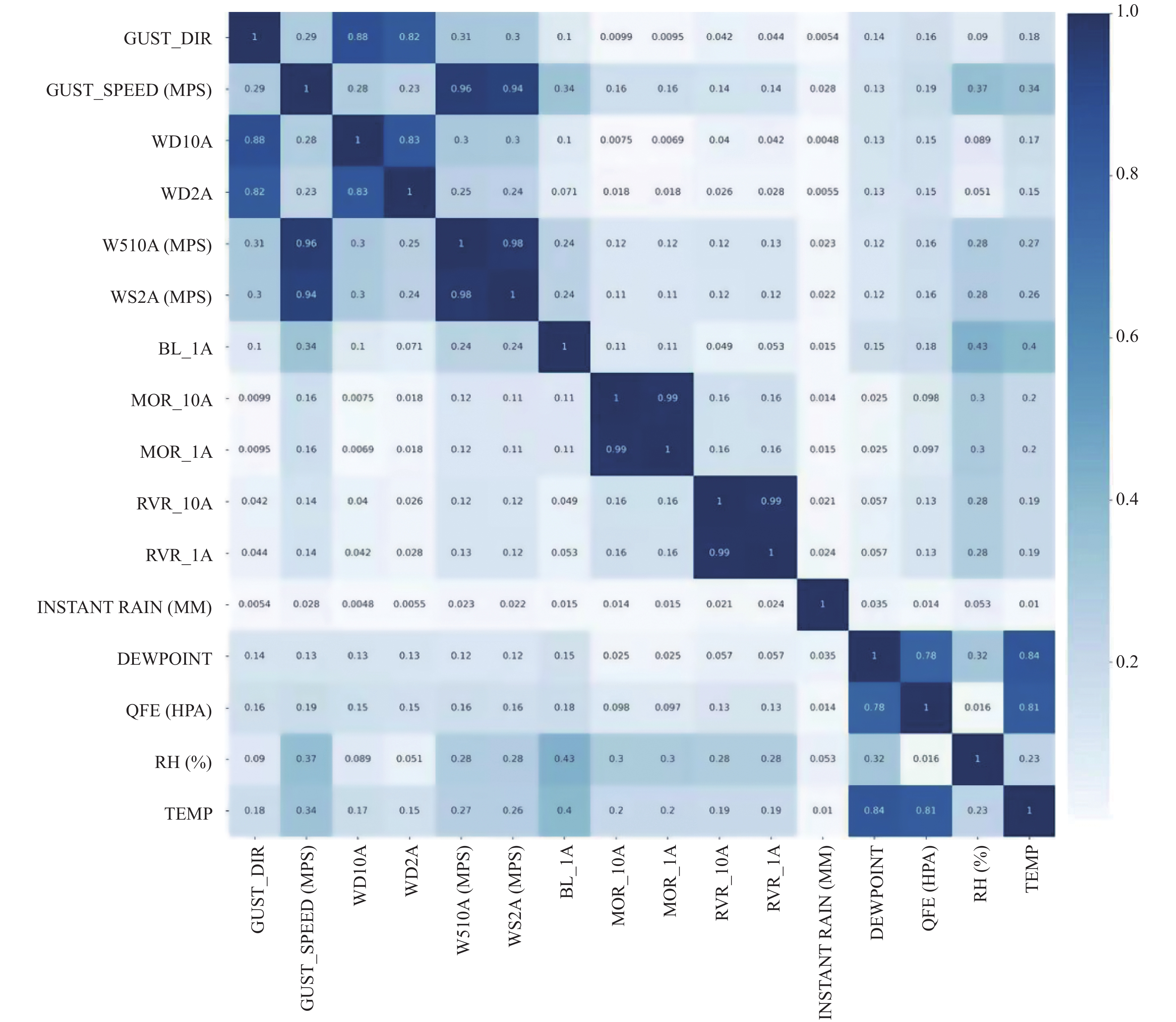
AWOS各地面观测要素之间的相互相关性特征如图4所示.

图4可见, 风类要素和温压类要素各自之间相关性较高, 其他要素间相关性不明显. 提取各要素与跑道视程的相关性(不考虑正负相关)从大到小排列, 结合专家经验, 本文选取14个相关性较强要素作为预报输入因子, 依次分别为2分钟平均风速、2分钟平均风向、10分钟平均风速、10分钟平均风向、背景亮度、10分钟平均气象光学视程、1分钟平均气象光学视程、10分钟平均跑道视程、1分钟平均跑道视程、1分钟平均降水量、露点温度、气压、相对湿度和温度. 数据格式如表1 所示.

以上输入预报因子的选取, 不仅确保了对现有观测资料的充分使用, 也能体现各要素之间的相互影响作用随时间的动态变化过程, 进而构造一个比较完备的预测数据集.

2.3 多变量时序预测

多变量时序预测问题(multivariable time series prediction problem)是指用过去的多个变量的观测值预测其中某一个或多个变量未来的观测值. 多步预测(multi-step forecasting)是指用过去的观测值预测未来一个时间序列的观测值^[18].

本文利用预报时间点前4个小时的本场AWOS自动观测的14个预报因子作为输入, 预测未来6小时每分钟的 $RVR$ 值, 即多步多变量时序预测.

时间序列数据集是由按时间索引排序的一系列数字组成, 为了能够从输入模式里学习如何预测输出模式, 需要将时间序列数据集转化为监督学习的数据格式, 即监督学习数据集由输入模式 $X$ 和输出模式 $Y$ 构成. 将跑道视程预测时间序列数据集转化为监督学习的数据格式, 如表2所示.

如表2所示, 这是多步多变量时序预测的监督学习数据格式, 表2中 $t$ 表示预报时间点, $t - 240$ 表示预报时间点过去240分钟, 即过去4个小时, $t + 359$ 表示预报时间未来359分钟, 即未来6个小时. 表2左半部分即监督学习数据集中的输入模式 $X$ , 其中包括过去4个小时的14个预报因子观测值; 表2右半部分即监督学习数据集中的输出模式 $Y$ , 未来6个小时的 $RVR$ 观测值.

将跑道视程预测的时间序列数据集转化为监督学习数据集之后, 对数据集进行数据预处理, 包括缺省值处理、归一化、样本均衡等.

由于各输入的预报因子存在量级和单位上的差异, 为了消除各个预报因子之间的差异带来的数据不均一性, 需要对跑道视程预测数据集作标准的归一化处理, 使每一个预报因子的数据落在区间 $\left[ { - 1, 1} \right]$ 内.

由于低跑道视程天气在整个数据集中所占比例较小, 样本均衡就格外重要, 本文采用了分层抽样法进行样本均衡. 分层抽样法就是将总体单位按其属性特征分成若干类型或层, 然后在类型或层中随机抽取样本单位. 分层抽样的特点是由于通过划类分层, 增大了各类型中单位间的共同性, 容易抽出具有代表性的调查样本^[19]. 该方法适用于总体情况复杂, 各单位之间差异较大, 单位较多的情况.

将跑道视程预测数据集输出模式 $Y$ 中的 $t$ 时刻 $RVR$ 值, 按照表3 $RVR$ 等级进行划分^[20], 分成5层, 然后在这5层中进行随机抽样, 从而使跑道视程预测数据集中的样本均衡.

将经过数据预处理(缺省值处理、归一化、样本均衡)的跑道视程预测数据集按照6:2:2的比例进行随机抽样, 并将样本分组为训练集、验证集和测试集. 训练集被用于预测模型构建, 验证集被用于模型参数最优调试和测试集被用于模型预测效果检验, 从而保障模型的可信性和科学性.

3 机场跑道视程预测实证分析 3.1 LSTM预测模型构建

机场跑道视程预测问题为多步多变量时序预测问题, 因此本文采用了适合处理时序数据的长短时记忆网络, 提出了一种基于LSTM的机场跑道视距预测模型.

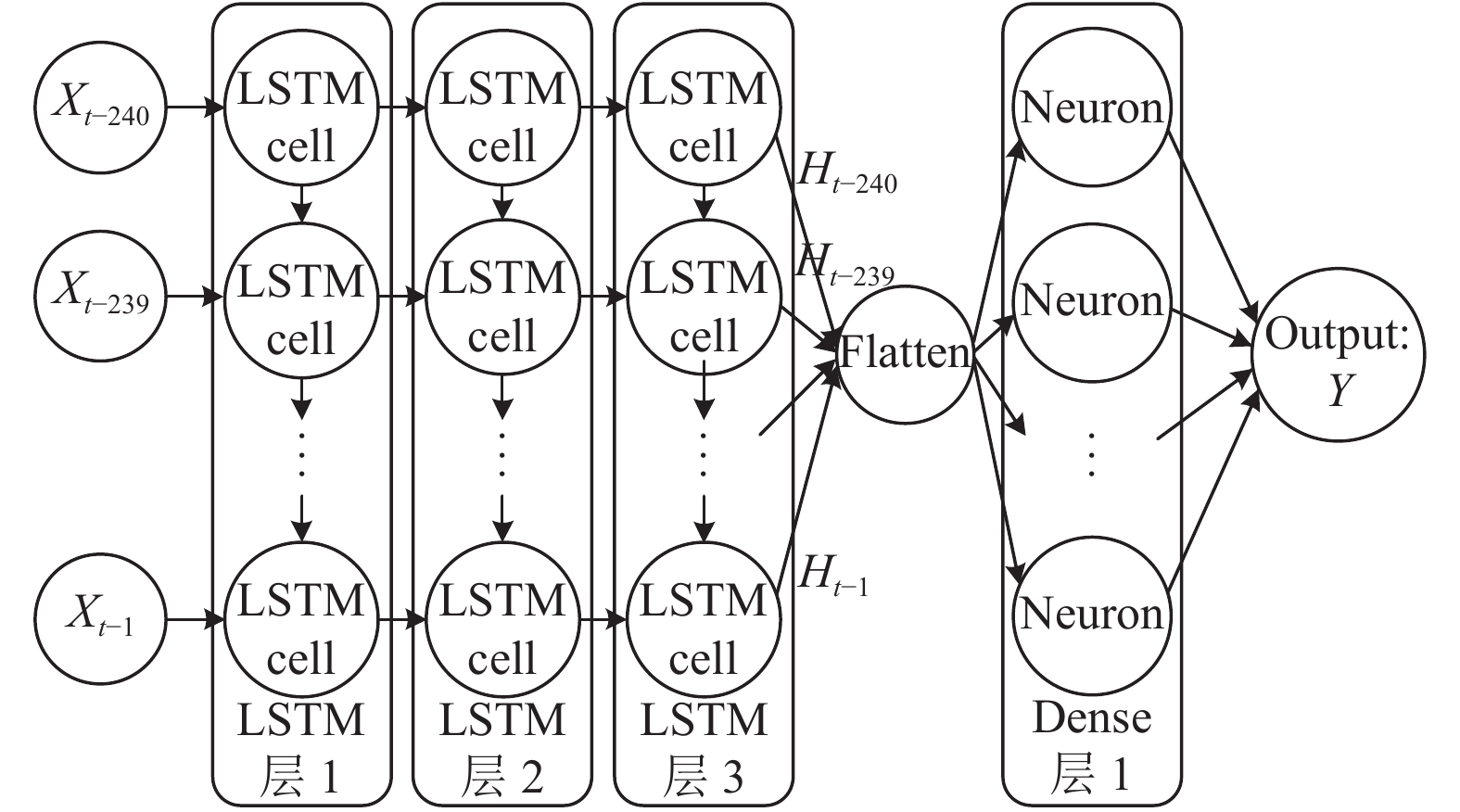
根据柯尔莫哥洛夫理论(Kolmogorov theory), 当前馈型神经网络具有3层及以上结构时可实现以任意精度逼近任意非线性连续函数^[13,21,22]. 因此, 本文的预测模型由3个LSTM层和1个全连接的神经网络层组成, 且为了避免过拟合, 在每个LSTM层后面添加了dropout层, 结构图如图5所示. 过去4个小时的气象要素(风速、温度、湿度和跑道视程等)被输入网络, 预测跑道未来6个小时的视程.

图5中 ${X_{t - i}}$ 表示 $t - i$ 时刻14个预报因子的观测值, ${X_{t - i}} = \left[ {x_1^{t - i}, x_2^{t - i}, \cdots , x_{14}^{t - i}} \right]$ , $i \in \left[ {1, 240} \right]$ , 因此输入样本维度为 $\left[ {None, 240, 14} \right]$ , $None$ 表示数据集样本数量; ${H_{t - i}}$ 表示 $t - i$ 时刻LSTM cell的输出值, ${H_{t - i}} = [ h_1^{t - i}, h_2^{t - i}, \cdots , h_n^{t - i} ]$ , $i \in \left[ {1, 240} \right]$ , 因此LSTM层的数据输出维度为 $[ None, $ $ 240, n ]$ , 其中, $n$ 表示LSTM基本节点中Sigmoid层与tanh层的输出维度, 也就是LSTM cell的输出维度, 需要人为设定, 下面将针对LSTM cell的实际输出维度进行探讨. Flatten表示压缩, 将LSTM层的输出数据从三维 $\left[ {None, 240, n} \right]$ 压缩至二维 $\left[ {None, 240 \times n} \right]$ , 然后将 $\left[ {None, 240 \times n} \right]$ 的二维数据送入dense全连接层, dense层包括360个神经元, 从而输出未来6个小时每分钟的 $RVR$ 值, 因此dense层的数据输出 $Y$ 维度为 $[ None, $ $ 360]$ .

LSTM的遗忘门、输入门和输出门都是通过图5中LSTM cell实现, LSTM cell具体算法流程如下:

输入: 上一个状态的信息, 假设输入门表示为 ${i_t}$ , 遗忘门表示为 ${f_t}$ 和输出门表示为 ${o_t}$ , 下标 $t$ 表示时刻, 使用 ${C_t}$ 表示LSTM cell在 $t$ 时刻的单元状态^[15];

步骤1. 接收输入信息. 通过当前 $t$ 时刻输入数据 ${X_t}$ 、上一时刻LSTM cell输出值 ${H_{t - 1}}$ 与上一时刻单元状态 $ {C_{t - 1}} $ , 计算输入门的值 ${i_t}$ , 输入门决定了将多少当前时刻输入数据 ${X_t}$ 的信息保存到单元状态 ${C_t}$ ;

步骤2. 遗忘状态信息. 遗忘门用于控制上一个时刻单元状态 $ {C_{t - 1}} $ 的哪些信息保留到当前时刻的单元状态 ${C_t}$ 中;

步骤3. 更新状态信息. 通过输入门决定当前时刻单元状态哪些信息需要被保留, 结合遗忘门新的需要添加的信息, 对当前时刻的单元状态进行更新, 得到新的当前时刻单元状态 $ {C_t} $ ;

步骤4. 输出新的信息. 输出门主要是通过Sigmoid层决定要输出细胞状态的相关信息, 然后将输出门的输出 ${o_t}$ 与tanh处理后的记忆单元状态 $ {C_t} $ 进行乘积, 得到最终当前层的输出信息 ${H_t}$ ;

输出: 当前LSTM单元的状态信息 $ {C_t} $ 及输出 ${H_t}$ .

预测模型网络结构确定之后, 为充分发挥LSTM网络的非线性映射能力, 将它们的cell输出维度 $n$ 分别从1递增到1 000, 并逐个进行实验, 寻找最适合本研究的LSTM cell输出维度组合. 基于LSTM的跑道视程预测模型的构建过程如图6所示.

为了避免随机初始权重和偏置对预测结果的影响, 分别将每种LSTM输出维度组合对应的预测模型进行100次训练和测试, 保存其效果最好时的网络参数.

通过实验发现, 随着LSTM层输出维度的增加, 预测模型效果先急剧上升, 然后渐趋平缓, 特别地, 当LSTM层1的输出维度大于490、LSTM层2的输出维度大于420、LSTM层3的输出维度大于360时, 继续增加输出维度给预测模型带来的效果提升几乎可以忽略不计. 综合考虑计算代价增量与效果提升幅度后认为: LSTM层1、LSTM层2与LSTM层3的输出维度数分别取490、420与360时最适合本研究.

其他相关的实验参数设置如下: 随机初始化权重和偏置, 损失函数为训练集的均方误差, 损失函数的优化算法采用RMSProp优化器, ${\rm dropout}$ 比率为0.2, 终止条件为训练集迭代次数达到1万次或者均方误差小于1E–5.

该网络采用基于TensorFlow的Keras API实现, 并采用4块NVIDIA TiTAN V GPU进行训练.

3.2 预测试验结果分析

AWOS观测设备分别位于两条跑道的4个跑道端点及2个中点, 2个跑道中点的AWOS观测设备只对少量气象要素进行监测, 缺少与 $RVR$ 相关性较强的预报因子(降水量、气压、相对湿度、温度等), 因此无法进行跑道视程预测.

将两条跑道4个跑道端点RWY23L、RWY05R、RWY23R、RWY05的AWOS观测数据经过数据预处理(缺省值处理、归一化、样本均衡)后, 按照6:2:2比例进行随机抽样, 划分成训练集、验证集和测试集, 送入第3.1节构建的LSTM跑道视程预测模型进行训练, 4个跑道端点预测模型的训练及验证 $Loss$ 曲线如图7.

通过图7可以看出, 随着迭代次数的增加, 4个跑道端点的 $Loss$ 值都在下降, 训练集下降比较平滑, 最后趋于稳定, 验证集下降过程起伏较大.

将测试集送入训练后的预测模型, 对4个跑道端点的跑道视程实际观测值与预测值进行比较, 分别计算拟合度及均方根误差. 拟合度(goodness of fit)是指预测值对观测值的拟合程度^[23], 一般使用变量 ${R^2}$ 表示, ${R^2}$ 值越接近1, 说明拟合程度越好, 拟合度 ${R^2}$ 计算方法: 设 $y$ 为待拟合值, 其均值为 $\bar y$ , 拟合值为 $\hat y$ , 记总平方和SST:

$ {\textit{SST}} = \mathop \sum \limits_{i = 1}^n {\left( {{y_i} - \bar y} \right)^2} $

(9)

回归平方和 ${\textit{SSR}}$ :

$ {\textit{SSR}} = \mathop \sum \limits_{i = 1}^n {\left( {{{\hat y}_i} - \bar y} \right)^2} $

(10)

残差平方和 ${\textit{SSE}}$ :

$ {\textit{SSE}} = \mathop \sum \limits_{i = 1}^n {\left( {{y_i} - {{\hat y}_i}} \right)^2} $

(11)

则 ${\textit{SST}} = {\textit{SSR}} + {\textit{SSE}}$ , 拟合度 ${R^2}$ :

$ {R^2} = \frac{{{\textit{SSR}}}}{{{\textit{SST}}}} = 1 - \frac{{{\textit{SSE}}}}{{{\textit{SST}}}} $

(12)

均方根误差(root mean square error, RMSE)是反映估计量与被估计量之间差异程度的一种度量^[24], 均方根误差越小越好. 均方根误差 ${\textit{RMSE}}$ :

$ {\textit{RMSE}} = \sqrt {E{{\left( {\hat y - y} \right)}^2}} = \sqrt {\frac{{{\textit{SSE}}}}{n}} $

(13)

未来6小时0–359分钟的预测模型拟合度 ${R^2}$ 及均方根误差 ${\textit{RMSE}}$ 变化过程如图8所示.

图8可见, 跑道视程预测模型在0–2小时内平均拟合度能够达到72%, 随着时间的增加, 预测模型的拟合度 ${R^2}$ 逐渐减小, 最后降至50%以下, 并且均方根误差 ${\textit{RMSE}}$ 逐渐增大, 最后增至438.471以上, 这说明跑道预测模型预测较近时间点的 $RVR$ 值具有较高的拟合度, 较低的均方误差, 预测得比较准确, 而预测未来较远时间点的 $RVR$ 值偏差会越来越大, 这也符合直观认知, 跑道视程预测比较适合0–2小时临近预报.

4 小结与讨论

跑道视程的时序分布特征等分析结果表明影响咸阳机场低跑道视程的天气主要是大雾. 由于大雾的局地特性很强, 其预报目前在气象领域依然是业务难点. 虽然近年来大雾预报由传统的经验或者统计预报向数值模式或者大雾模式预报转变, 但数值释用和雾模式预报准确性仍有待提高, 难以在实际业务预报中直接使用^[25].

考虑到每个预测时间前4小时的多维气象要素数据包含着各种气象要素的变化趋势, 例如降水增大, 未来跑道视程数据就会相应的降低, 湿度增大、温度降低、风速较小, 一般会伴随着大雾的发生(大雾的机理比较复杂, 湿度增大、温度降低、风速较小只是其中3个较为显著的气象条件), 未来跑道视程也会相应的降低. 本文基于长短时记忆网络的多维时间序列预测方法, 采用多维气象要素进行跑道视程预测, 旨在拟合出多维气象要素与跑道视程之间的映射关系.

实验表明采用长短时记忆网络, 利用风速、温度、湿度和跑道视距等预报因子建立一种机场跑道视程预测模型, 对测试集预测的0–2小时拟合度在58%–88%之间, 拟合度结果表明本文搭建的LSTM预测模型对跑道视程具有较高的预测能力, 具有推广价值和发展前景, 其结果可被航空气象保障人员参考应用LSTM的优越性和推广前景.

未来研究中将要改进的方面:

(1)低跑道视程天气的出现与季节、晨昏时间信息有关, 之后的研究工作中预报因子的选取考虑季节、晨昏等时间信息.

(2)冬季出现较低跑道视程时, 边界层内常出现大气层结中性弱不稳定、逆温以及大湿度区分布的垂直结构. 为了尽可能地描述大气垂直结构对低跑道视程天气的影响, 将增加探空观测的多层次的位势高度、温度、露点温度、风向、风速等资料作为预报因子^[25].

(3)随着人工智能技术的发展, 越来越多优秀的预测技术逐渐成熟, 采用最新的预测算法建模, 进行比较, 选取较优的预测模型为跑道视程的预测提供指导, 更好的保障航空器的安全起降.

(4)虽然0–2小时跑道视距预测具有很高的拟合度. 然而, 预测模型有几个部分任然需要进行改进, 如跟踪谷值^[26], 跑道视程谷值是航空管制员重点关注的, 需要根据跑道视程谷值判断飞机是否能够起降.