在早期对校园用户的移动性研究中多数是基于校园用户的上网日志, 研究者主要关注的是用户的上网习惯及无线网络的使用情况, 如用户的在线时长、用户的在线频率、系统当前的在线人数等. 现在越来越多的研究人员开始关注用户在无线网络下的轨迹变化规律. 例如文献[1]中作者使用无向加权的单模网络统计两个用户WiFi接入点时间轨迹矢量变化. 学生作为一个重要群体, 面临各种各样的问题, 有学业上的焦虑问题, 恋爱状态问题, 人际交往的问题^[2]. 有时学生不愿意说出来, 需要老师和学校多加注意, 及时关注心理状况. 从人际交往学和心理学分析, 良好的交际行为营造出的轻松舒适的氛围, 能够促进学生学习进步. 所以, 老师可以通过无线数据状态, 科学判断学生的社交状态, 依据判断结果, 发现有疑似孤僻的学生, 则需要排查和教育辅导. 从而为高校的学生日常教育提供据支撑.

目前, 已经有部分学者对此类问题进行研究, 文献[3]中作者使用Hausdorff距离进行时空轨迹相似度测量, 但是这种距离方式只能从点数据集合上判断相似度, 对移动物体整体度量分析效果不佳. 文献[4]使用校园卡数据进行轨迹模式挖掘, 但是校园卡使用地点有限, 时间上有间隔, 时效性较差. 文献[5]采用K-means对时空数据进行聚类, K-means 算法最终得到的可能是局部优化, 在非凸数据集或者类别规模太大的数据上聚类效果不好. 以上方法因为在相似性度量时对时间维度的依赖程度不同, 所以不同程度地影响聚类效果. 还有, 聚类算法的核心是相似度度量公式的使用, 除常用的Minkowski距离、向量内积、曼哈顿距离公式, 还有文献[6]改进版的MinKovDM, 实际场景中要根据语义结构复杂度和数据性质选取合适的公式进行轨迹匹配. 文献[7]提出最短时间距离子序列模型, 运用连续因子求空间相似性, 采用并行滑动时间进行时间相似性度量. 文献[8]中阐述DBSCAN和K-mans 算法在轨迹数据中的优缺点以及对移动对象聚类效果进行分类对比, 为本文的写作提供思路.

针对上述问题, 为了减少轨迹间偏差和兼容移动对象的移动模式, 更好地匹配轨迹模式, 增强度量方法的时间鲁棒性, 采用Hausdorff距离和Frechet距离相结合的距离公式, 不仅从整体上提升相似性度量效果, 而且能够保持轨迹整体形状. 因为DBSCAN算法适合任意形状, 对异常点有较好的鲁棒性, 相对于其他算法更适合查找异常点, 所以采用DBSCAN进行聚类.聚类之后为了更加清楚的判断聚类效果, 采用FineBI软件进行可视化展示.

1 模型方法 1.1 WiFi数据的处理

WiFi是一个高频无线电信号, 通过一个无线路由器可以发送出去. 其电波覆盖的有效范围可以通过设备连接. WiFi定位, 也就是通过移动终端和无线网络接入的信号交互来实现对移动终端的精准定位.无线AP (wireless access point) 是WiFi技术的一种, 利用无线技术实现网络数据的传输. 目前, 高校图书馆、食堂、宿舍、教学楼都安装了一定数量的AP设备, 基本实现了全覆盖. 本文所使用的原始数据根据RESTful接口定时获取的. RESTful接口是HTTP接口的实现方式之一. 接入控制器收集到数据后, 每一种数据资源都存入一条唯一的URL中. 因此使用RESTful接口的GET方法可以从AC获取用户使用无线网络的数据.智能手机在WiFi功能打开的状态下, 如果检测到已经连接过的AP, 会自动连接. 而且, 无线AP具有漫游功能, 保证学生移动过程中跨AP连接WiFi信号的连续性. 需要的原始数据如表1.

1.2 轨迹数据的时空距离

基于距离的相似度度量方法有很多, 包括欧氏距离和余弦距离、Hausdorff距离、Minkowski距离、Chebyshev 距离. Hausdorff距离是用来测量离散点的邻接度, 而运动轨迹是矢量空间中有序的序列点集, 即使两个序列有很小的Hausdorff距离, 也并不能表示轨迹间相似度高.

本文加入空间和时间维度, 更加合理地计算相似度. 通过对比分析, 同时使用Frechet距离公式, 以函数的形式定义曲线的距离, 从序列整体全局到局部细节分级进行度量, 避免Hausdorf距离分析只从点数据集合距离上判断各轨迹间相近度的缺陷, 整体态势越相近, 相似度越高.

计算方法如下:

定义1. 轨迹点, 带时间的轨迹点 $P$ =( $t$ , $d$ , $loc$ ), 其中 $t$ 表示用户停留在该轨迹点的时间点, $d$ 表示用户停留在该轨迹的时间长, $loc$ 表示用户停留的轨迹点位置.

定义 2. 一条轨迹 $Tr$ 定义为按时序组成的一组坐标点序列, 该序列由定义1的轨迹点组成. 设 $Tr = $ $ {p_1} \to {p_2} \to {p_3} \cdots \to {p_n}$ , 其中 ${p_{1,t}}$ $ < $ ${p_{i + 1,t}}$ , 按时间先后排序.

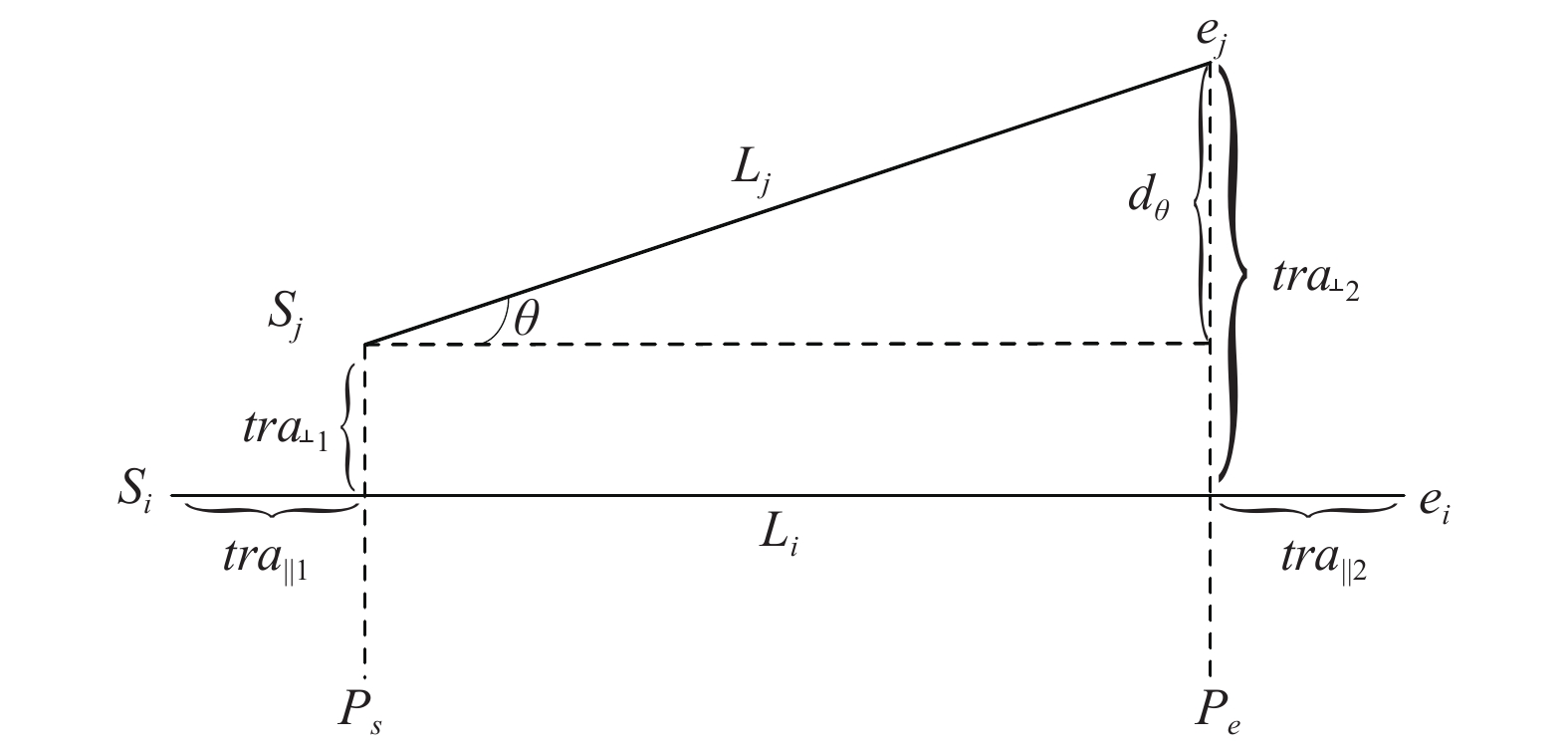
设有两条轨迹L_i和L_j, s_i、e_i、s_j、e_j分别表示L_i和L_j的开始点和结束点, 由L_j两端点向L_i两端点做垂直投影, 得到p_s和p_e, 空间距离如图1所示.

${L_i}$ 和 ${L_j}$ 垂直距离如下:

$ {d_ \bot }\left( {{L_i}, {L_j}} \right) = \frac{{tra_{{ \bot _1}}^2 + tra_{{ \bot _2}}^2}}{{tr{a_{{ \bot _1}}} + tr{a_{ \bot 2}}}} $

(1)

${L_i}$ 和 ${L_j}$ 平行距离:

$ {d_\parallel }\left( {{L_i}, {L_j}} \right) = MIN\left( {tr{a_{\parallel 1}}, tr{a_{\parallel 2}}} \right) $

(2)

角度距离:

$ {d_\theta }\left( {{L_i}, {L_j}} \right) = \left\{ {\begin{array}{*{20}{l}} {{L_j} \times \sin \theta ,\; {{\text{0}}^ \circ } \leqslant \theta \leqslant {{90}^ \circ }} \\ {{L_j}{\text{, }}\;{{90}^ \circ } \leqslant \theta \leqslant {{180}^ \circ }} \end{array}} \right. $

(3)

时间距离的计算:

$ DT = \left| {{t_i}} \right. - \left. {{t_j}} \right| $

(4)

综上:

$ DS = {d_ \bot }\left( {{L_i}, {L_j}} \right) + {d_1}\left( {{L_i}, {L_j}} \right) + {d_\theta }\left( {{L_i}, {L_j}} \right) $

(5)

考虑到时间距离和空间距离之间有数量级之间的差别, 使用z-score函数进行标准化. 例如对变量h进行标准化.

1)绝对值偏差的平均值的计算:

$ {S_h} = \frac{1}{n}\left( {\left| {{x_{1h}} - {m_h}} \right| + \left| {{x_{2h}} - {m_h}} \right| + \cdots + \left| {{x_{rh}} - {m_h}} \right|} \right) $

(6)

其中, ${x_{1h}}$ , ${x_{2h}}$ , …, ${x_{nh}}$ , 为 $h$ 的n个度量值, ${m_h}$ 为 $h$ 的均值.

$ {m_{{h}}} = \frac{1}{n}\left( {{x_{1h}} + {x_{2h}} + \cdots + {x_{{{nh}}}}} \right) $

(7)

2)标准度量值的计算:

$ {Z_{ih}} = \left( {{x_{ih}} - {m_h}} \right)/{s_h} $

(8)

用z-score函数对空间距离和时间距离标准化后, 表示为 $DS'$ 和 $DT'$ , 通过设置权重 $w\;(0 \leqslant \omega \leqslant 1)$ , 调整敏感度, 轨迹间时空距离定义为:

$ DST = w \times DS' + (1 - w)DT' $

(9)

定义3. 根据文献[9]定义两条轨迹Frechet距离表示为:

$ {\delta }_{df}(P, Q)=\underset{\text{coupling}{C}\left({p}_{i}, {q}_{j}\right)\in C}{\mathrm{min}\mathrm{max}|{p}_{i}}-{p}_{j}| $

(10)

假设 $P = ({p_1}, {p_2}, \cdots , {p_n})$ 为轨迹 $T{r_P}$ 采样点, $ Q = $ $ ({q_1}, {q_2}, \cdots , {q_n}) $ 为轨迹 $T{r_Q}$ 的采样点. $C = ({C_1}, {C_2}, \cdots , {C_n})$ 为两轨迹 $P$ 、 $Q$ 下标相同采样点的耦合距离集合; 根据式(9)得: ${C_R} = ({p_i}, {p_j})$ , $r$ =1, 2, …, $k$ , $i$ ∈{1, 2, …, $m$ }, $j$ ∈{1, 2, …, $n$ }.

利用式(10)递归计算两轨迹曲线P、Q间关键特征点的距离, 还不能判断两轨迹的相似度. 假设轨迹P、Q的至高点的最小离散Frechet距离为 $d_F^1\left( P, Q \right)$ , 两轨迹至低点的最小离散Frechet距离为 $d_F^2 \left(P, Q \right)$ , 那么离散的Frechet距离如式(11)所示:

$ dist = \left| {d_F^1} \right.(P, Q) - \left. {d_F^2(P, Q)} \right| $

(11)

1.3 基于Frechet的 DBSCAN时空聚类算法

DBSCAN算法, 作为最具有代表性的基于密度的聚类算法, 可以将高密度数据进行聚类, 最好是在存在“噪声”的目标对象里寻找所有可能的形状的簇^[10], 这样的聚类结果可筛选出异常轨迹.在传统的算法基础上, 增加时间和空间维度, 能够更加有效的提升聚类效果. 参数 $ Eps $ 反映了不同轨迹聚成一个类需满足的最低相似程度范围, 而 $ MinPts $ 刻画了不同轨迹聚成一个类需满足的最少数量. 如图2所示.

核心概念:

核心对象: 倘若目标的半径 $ Eps $ 内拥有多于 $ MinPts $ 的其他对象, 那么该目标就是核心对象.

边界点: 边界点不是核心对象, 但是位于其他核心对象的 $ Eps $ 半径内.

噪音点: 既不是核心点也不是边界点的任何点.

直接密度可达: 在核心对象 $p$ 的领域, 有一对象 $m$ , 那么称对象 $m$ 从对象 $p$ 出发是密度可达的. 如图2中 $p$ → $m$ .

密度可达: 集合B中存在一个对象串, ${p_1}$ , ${p_2}$ , ${p_3}$ $, \cdots $ , ${p_n}$ , 设 ${p_1} = p$ , ${p_n} = n$ , 若对象链中任意的 ${p_{i + 1}}$ 是从 ${p_i}$ 出发关于 $ Eps $ 和 $ MinPts $ 直接密度可达的, 那么对象 $n$ 是从对象 $p$ 出发的密度可达点. 如图2中 $p$ → $n$ .

密度相连: 若集合B存在对象o, 使得对象 $m$ , $n$ 都是从对象 $o$ 出发的密度可达点, 则对象 $m$ , $n$ 是从 $o$ 出发的密度相连的点. 如图2中 $m$ 和 $n$ 点.

应用到实际的轨迹聚类的算法中, 算法的时间复杂度主要在邻域的计算中, 可以通过使用索引的方法降低时间复杂度, 因此加入路网思想.

根据路网的思想, 首先根据定义好的n×n的网格空间, 在每一格空间进行序列的标注, 统计每条轨迹经过的网格. 计算轨迹段的领域时, 先以该轨迹中心点所在的网格为中心, 向5×5的区域扩展, 只判断所在25宫格区域内的轨迹, 减少搜索时间.

下面对DBSCAN算法的具体步骤介绍如下:

(1)由轨迹 $Tr$ 中任意一个未被访问的 $p$ 轨迹点作为核心点开始, 在 $Tr$ 中以宫格法搜索 $\varepsilon $ 邻域的轨迹点q, 即 ${{{N}}_\varepsilon }({{p}}) = \{ {{q}} \in Tr\left| {dist({{p}}, {{q}}) \leqslant {{Eps}}} \right.\}$ , $dist(p, q)$ 可由式(11)得到. 如果 $\varepsilon $ 领域里有足够的点| ${{{N}}_\varepsilon }({{p}})$ | $ \geqslant $ MinPts, 则认为这是一个新的簇C, 否则认为该轨迹点为边界点或噪声点.

(2)对 $p$ 点进行扩充, 寻找从该点出发的所有密度相连的轨迹点, 遍历每一个密度相连的轨迹点领域内所有核心点, 寻找和这些核心点密度相连的点, 直到没有可扩充的点为止.

(3)找到除 $p$ 以外尚未处理的核心点, 重复第一步, 对该核心点进行扩充直到轨迹数据集中没有新的核心点为止.

伪代码如下:

算法1. 改进的DBSCAN 算法

输入: 轨迹数据集 $\scriptstyle Tr$ , 半径 $\scriptstyle Eps$ , 最少轨迹数量 $\scriptstyle MinPts$

输出: 所有到达密度要求的轨迹簇

(1)起初将轨迹数据集 $\scriptstyle Tr$ 中的所有轨迹点对象标记为未处理状态

(2) for 数据集 $\scriptstyle Tr$ 中每个坐标点对象 $\scriptstyle p$ do

(3) if p已经归入某个簇或标记为噪声 then

(4)　continue;

(5) else

(6) 用宫格法检查坐标点对象 $\scriptstyle p$ 的 $\scriptstyle Eps$ 邻域 $\scriptstyle {{{N}}_\varepsilon }({{p}})$ ;

(7) if N_ε(p)包含的对象小于 $\scriptstyle MinPts$ then

(8) 标记对象 $\scriptstyle p$ 为边界点或噪声点

(9) else

(10)标记 $\scriptstyle p$ 为核心点, 建立新簇C, 并将 $p$ 邻域内所有点加入C

(11) for $\scriptstyle {{{N}}_\varepsilon }({{p}})$ 中所有尚未处理的轨迹点对象 $\scriptstyle q$ do

(12)检查其 $\scriptstyle Eps$ 邻域 $\scriptstyle {{{N}}_\varepsilon }(q)$ , 若 $\scriptstyle {{{N}}_\varepsilon }(q)$ 包含至少 $\scriptstyle MinPts$ 个对象, 则将 $\scriptstyle {{{N}}_\varepsilon }(q)$ 中未归入任何一个簇的坐标点对象加入C;

(13)　　　　　　　　　 end for

(14)　　　　　　 end if

(15)　　　 end if

(16) end for

1.4 特征轨迹提取

轨迹的运动特征指一些能够反映运动物体特征的指标. 比如轨迹速率、方向角和角速度等数据的均值、最值、中位值等^[11]. 下面对聚类后的簇进行特征轨迹提取.

主要思想: 用一条垂直于类别中所有线段的平均向量(轨迹本质是一种向量, 向量的长度为线段的长度, 求出所有的向量和, 再单位化, 得到的结果即为平均向量)的直线扫描各条子轨迹, 计算该线段在轨迹开始点和结束点分别有多少个交点, 将交点个数与设置的 $ Leastlns $ 比较, 如果小于该值则继续扫描, 否则计算所有交点的中心点并存储在向量中, 最后生成的轨迹点向量为特征轨迹.

假设每一个簇内所有轨迹段的向量集合 ${\boldsymbol{w}}$ ={ ${{\boldsymbol{w}}_{{1}}}{{, }} $ $ {{\boldsymbol{w}}_{{2}}}{{, }} \cdots {{, }}{{\boldsymbol{w}}_{{n}}}$ }, 设 $\left| {\boldsymbol{w}} \right|$ 表示集合内所有向量的和的长度.

步骤如下:

(1)对一个簇中所有向量求平均向量如下:

$ {\boldsymbol{w}} = \frac{{{{\boldsymbol{w}}_{{1}}}{{ + }}{{\boldsymbol{w}}_{{2}}}{{ + }} \cdots {{ + }}{{\boldsymbol{w}}_{{n}}}}}{{|{\boldsymbol{w}}|}} $

(12)

(2)把整个簇内的向量按平均向量旋转, 向量旋转的示例图如图3所示.

旋转后的向量公式:

$ \left[ {\begin{array}{*{20}{l}} {x'} \\ {y'} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos \theta }&{\sin \theta } \\ { - \sin \theta }&{\cos \theta } \end{array}} \right]\left[ {\begin{array}{*{20}{l}} x \\ y \end{array}} \right] $

(13)

(3)使用垂直于x轴的sweep line沿x轴平扫, 如果与这条直线相交的向量大于等于设置的最小值 $ Leastlns $ , 则计算这些相交点的y坐标的平均值, 形成点(x_i, ${\bar y_i}$ ), 该点计算方法由式(14)所示, 重复上述过程, 直到sweep line 的右边再无向量的起始或结束点.

$ \left( {x_1^\prime , \overline {y_1^\prime } } \right) = \left( {x_1^\prime , \frac{{y_{{l_1}}^\prime + y_{{l_2}}^\prime + \cdots + y_{l_n^{}}^\prime }}{n}} \right) $

(14)

(4)把步骤(3)生成的点旋转回原来的角度, 连接成一条轨迹, 这条轨迹就是特征轨迹, 如图4所示.

(5)对所有的轨迹簇重复上述4个步骤.

1.5 相似度度量

轨迹序列也是一种带时间空间属性的序列, 下面对提取出的特征轨迹进行相似性度量.

最长公共子序列(LCSS)算法是常用的从轨迹序列角度研究轨迹相似度的算法. 轨迹序列的子序列是指, 不改变该序列的顺序, 从序列中去掉某些元素获得新的序列, 该序列在两个序列中以相同的顺序出现, 不一定要连续^[12].

公共子序列: 比如给定的序列X和Y, 序列Z是X的子序列, 同时也是Y的序列, 则Z是X和Y的公共子序列.

LCSS是最长的公共子序列, 最长公共子序列的长度越长, 给定的两个序列相似度越高.相似性计算公式:

$ {\textit{Sim}}\left( {T{r_a}, T{r_b}} \right) = \frac{{\dfrac{{{k_\theta }}}{{{k_i}}} + \dfrac{{{k_\theta }}}{{{k_j}}}}}{2} $

(15)

其中, ${k_\theta }$ 表示最长公共子序列中行为记录总数, ${k_i}, {k_j}$ 表示轨迹序列行为总数.

改进的算法可以更好的体现出轨迹之间的重叠程度, 通过增加的相似度指数直观的判断轨迹相似性.

2 实验结果及分析 2.1 数据集介绍和实验设置

采集8周无线数据作为数据源, 根据原始数据参数处理成轨迹数据.

采集时间为2020.9.1–2020.10.31, AP数量: 318个, 学生数量: 13 568名.

改进的DBSCAN算法参数设置: ${\textit{Eps}}$ =1 km, $ MinPts $ =10.

2.2 数据筛选和预处理

提取实验数据集中的用户移动轨迹的信息, 形成定义1的基于用户轨迹的向量数据, 从而根据轨迹向量聚类之后提取特征轨迹进行相似值计算. 但是, 由于本校无线用户群体大, 终端多样性等特征, 还有Frechet计算方法对噪声敏感^[13], 为了降低向量相似性的计算的复杂度, 减小聚类结果的偏差. 进行了二次去噪的过程, 对筛选规则做了定义, 并使用基于使用频率和在线时长的方法对用户进行了过滤.

2.3 聚类结果分析

新提出的算法考虑了时间空间因素, 还有采用Frechet距离测量, 比传统的DBSCAN算法运行时间长. 虽然提高了聚类效果的准确性, 聚类开销变大, 但是运行时间的增长在可接受的范围内.

下面选取某一天上午9点到12点部分同学数据. 在保护隐私的条件下进行实验.

通过在运行时间, 特征轨迹的相似性对比效果两个方面进行分析, 验证本文所提出的改进的算法的优越性, 同时发现不足之处, 为后续的研究提供方向.

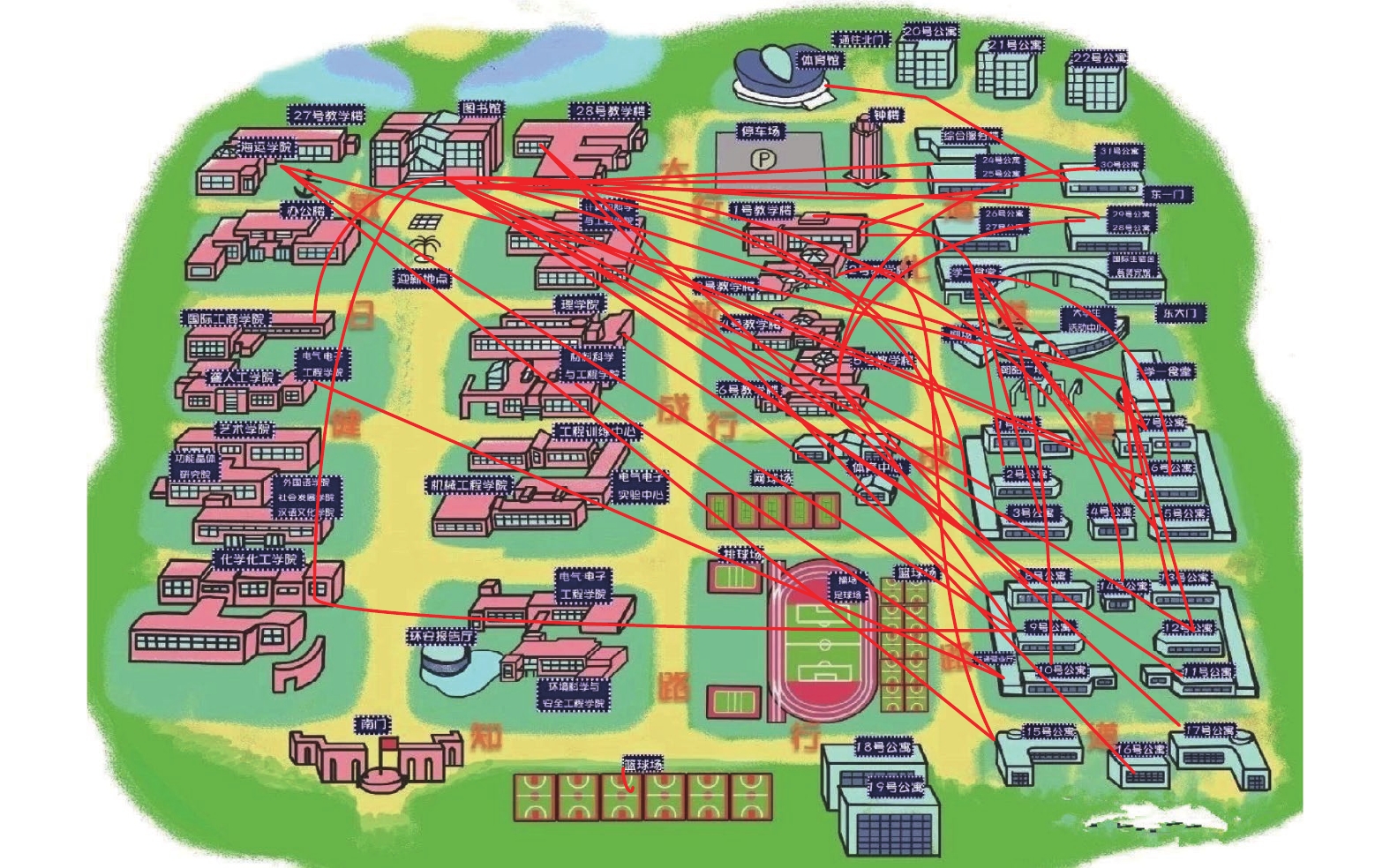
FinBI可以实现Windows系统类似的图形化系统界面^[14]来设计ETL转换过程, 所以用FinBI展示, 轨迹粗细表示人数多少. 如图5所示.

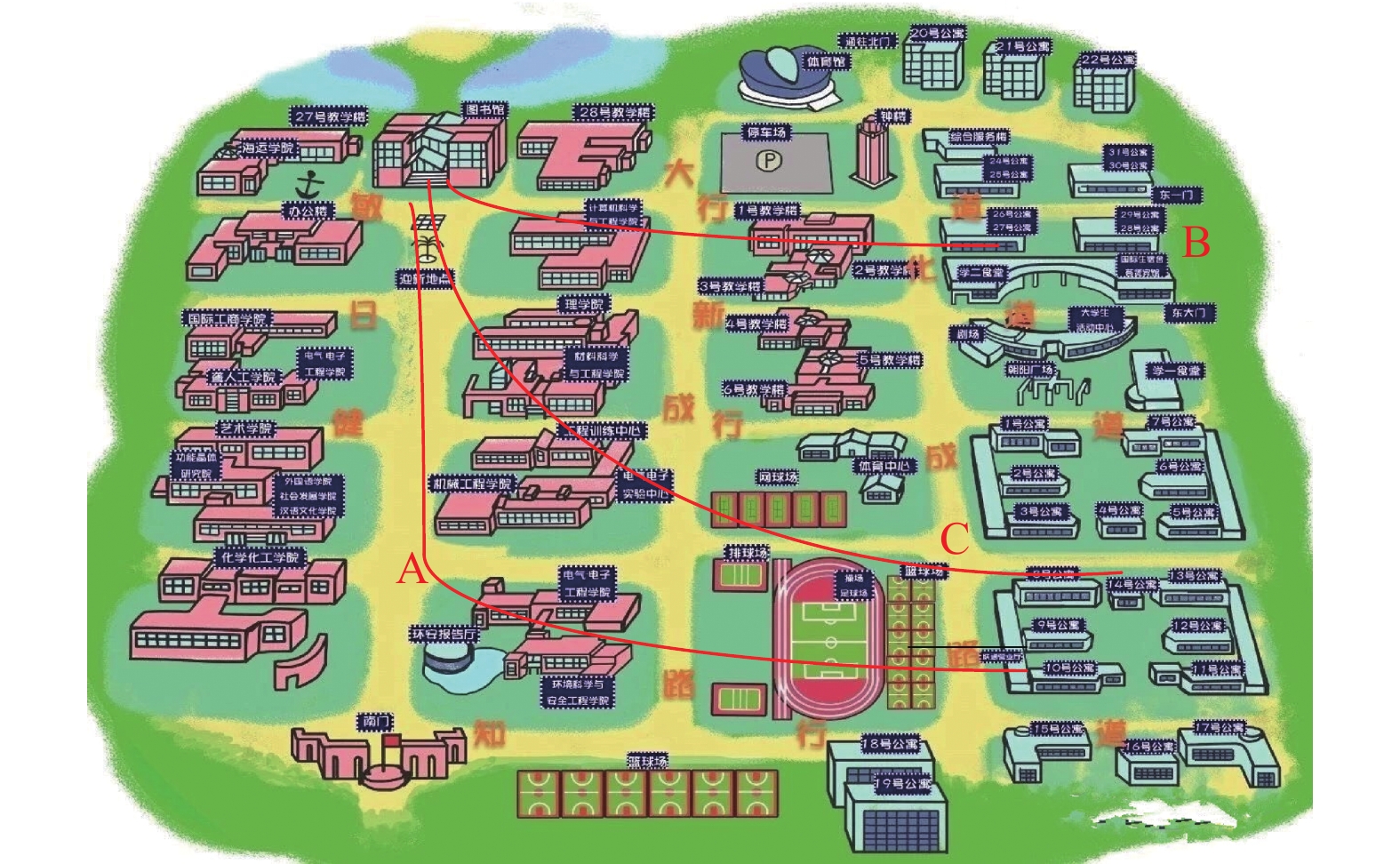
之后根据第1.4节中方法进行轨迹提取, 如图6.

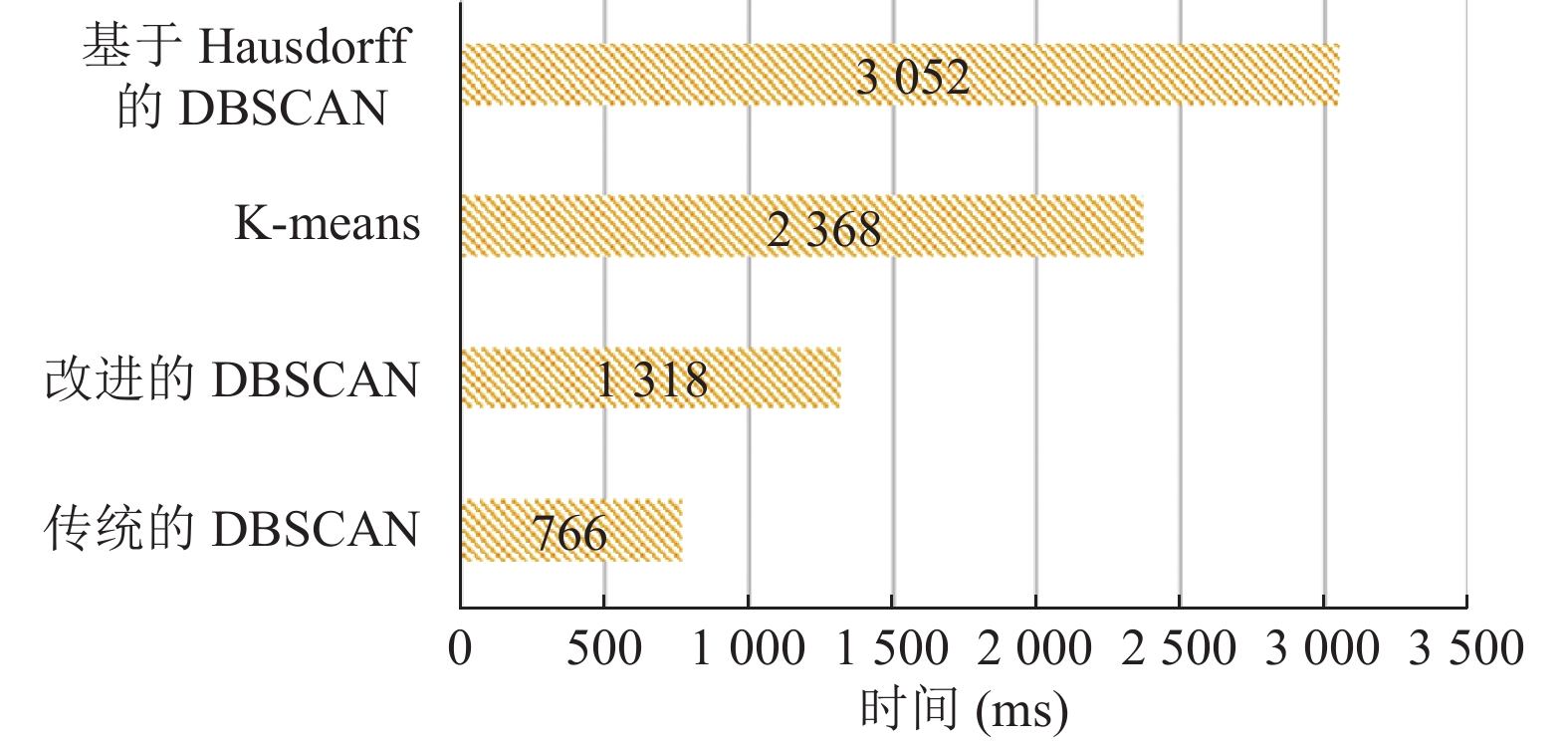
对整体数据集通过20次实验求取运行时间平均值和其他3种常见的模型对比, 如图7. 和传统的DBSCAN算法比较, 时间变长是因为增加了时间和空间的复杂度, 但是提升了相似度度量的效果, 所以增长的时间在可接受的范围内. 同时验证了Hausdoff在轨迹距离测量的效果不如Frechet距离. DBSCAN算法同K-means算法比较, 前者更适合时空轨迹这种形状不规则序列之间的聚类应用.

2.4 用户相似性分析

学生无线用户可以根据在网络信息中心注册的信息, 判断学生专业、年级、宿舍信息. 根据实验结果图可以得出, 本次数据大多为1–5号公寓楼学生. 开学前两个月, 同学们学习积极性比较高, 去往图书馆、学院楼、教学楼同学较多, 符合学生活动特点.

同公寓的学生大部分是同专业、同班级, 行为趋同性更高, 算法聚类可视化结果也表明了算法的正确性. 但是有部分同学行为轨迹差异大, 会选择较远的路线绕行.

提取出特征轨迹, 将改进的相似性度量方法和STD (最短时间距离模型, 根据模型中时间单位进行轨迹提取)、OWD (单向距离法, 基于两条轨迹围成的面积大小判断相似性. 面积越大, 说明轨迹之间距离较远, 相似度就低; 相反, 若围成的面积为0, 则说明两条轨迹重合, 相似度最高)、MBR (最小边界矩形法, 在设定的图形内通过求最小外接矩形和设定密度阈值进行聚类)进行实验对比, 见表2.

$Sim$ 值根据式(15)得出, 比值越高, 相似度越高. 前两列比值用来评价相似值区分度, 指数越高区分度越明显. 经过实验可以得出, 轨迹a和轨迹c相似度更高, OWD的相似性效果最差, STD和MBR实验结果比较相近, LCSS能够更有效的区分轨迹间差别. 在轨迹时空相似性的应用上效果更好. 相似性值低表示和其他同学共同轨迹较少, 有可能经常一个人进行各项活动, 或者是不善交际或者交友障碍, 所以较孤僻. 采取该类学生多日的轨迹数据进行聚类分析, 如果轨迹相似性总是较低, 辅导员可以进行排查寻访了解学生心理动态.

3 结束语

为了准确地分析校园无线网络数据中隐藏的社交关系亲密度, 本文提出了改进DBSCAN时空聚类算法, 运用LCSS算法进行轨迹间相似性度量. 该方法基于校园WiFi的数据特点和特有的应用场所, 结合时间空间信息, 整理出轨迹数据, 通过改进的DBSCAN时空算法进行聚类, 在聚类结果簇中提取出特征轨迹, 计算特征轨迹间相似值, 进一步推测学生之间的社交关系, 若发现可能孤僻的学生, 老师需要进行排查和教育辅导.聚类算法还可以应用在停留活动区域人流量分析、出行距离统计分析、无线网络吞吐量和在线时长聚类分析, 为制定人性化、智能化决策提供数据支撑. 最后, 运用高校的真实数据进行实验验证, 实验结果表明, 改进的DBSCAN算法能够提升聚类效果, 相似性度量效果更好, 在校园无线网络的实际环境中有较好的效果, 但是在DBSCAN算法中增加时间和空间的维度, 运行时间还是不太理想, 将在以后的研究中改进和完善.