在过去的10年里, 随着数字加密货币的普及, 区块链技术引起了学术界和工业界的极大关注. 此后, 区块链技术的发展已经超越了加密货币的范畴, 支持许多现有的商业和工业流程. 此外, 它还能够创造新的商业模式, 影响各行各业如金融、医疗保健、制造业和物流[1, 2].
区块链的技术特点使其有着广阔的应用前景, 但也面临可扩展性不足的瓶颈, 存在扩容需求[3, 4]. 现有的扩容技术主要包括分片方案[5]、DAG[6]、扩块[7, 8]、侧链技术[9]、状态通道[10]等. 其中分片方案是目前扩容技术中最为可行的方案, 它利用“分而治之”的思想, 将区块链的存储和负载分散到并行分片上. 目前分片分为网络分片、交易分片和状态分片, 网络分片是将全网节点划分到不同分片中, 是交易分片和状态分片的基础[11]; 交易分片是将全网交易划分到不同的分片中进行验证和打包, 全网多个分片通过并行对交易进行验证和打包可以在一定程度上提升公链的性能, 但由于每个分片都存储全部的账本信息, 就会造成资源瓶颈等问题; 状态分片是将系统的存储区域分开, 每个分片只负责本分片的数据, 不用存储完整的区块链状态, 缓解了节点的存储和处理压力, 可以有效提升区块链整体的性能, 可以从本质上解决公链可扩展性的问题, 是目前最理想但是难度也最大的分片方案. 在分片方案中, 网络中不可避免会存在跨分片交易[12]的问题, 而在状态分片中, 又由于各分片只维护本分片的状态信息, 这就使得状态分片下的跨分片交易更加的复杂, 对于跨分片交易的处理是状态分片下最大的难题之一.
针对在状态分片下处理跨分片交易的难题, 文献[13] ChainSpace方案利用智能合约进行分片, 通过“SMART’s PBFT”[14]协议来保证跨分片交易的安全性, 但是该论文对交易的假设是基于乐观并发控制, 对于回滚和悲观并发并未作出讨论. 文献[15] Omniledger方案中提出利用客户端驱动整个过程, 可以避免分片间通信, 避免分片间一致性开销, 但是加入了客户端便不能完全保证区块链系统的安全性, 无法从本质上解决状态一致性带来的问题. 文献[16]提出MRPV方案, 利用多轮验证的方式提高交易验证效率, 文献[17]在MRPV此基础上提出了一种解决跨分片交易回滚问题的方案, 但是此方案并未考虑分片状态, 并且由于轮数增加还带来了较高时延问题. 故本文针对以上分析, 提出一种利用状态归约并结合分片内多轮验证机制, 来处理跨分片交易的方案SRMR (state reduction and multi-round).
本文贡献如下: (1) 本文利用状态归约模型, 将跨分片交易转化成一种不跨分片的处理方案, 通过这种转化, 减少验证跨分片交易的可能性. 但经过分析, 推导出完全依赖归约模型存在上层分片交易负载过大的问题; (2) 为了防止交易堆积, 提出激励机制方案并将状态归约与多轮验证相结合, 提出了一种合理平衡归约与多轮验证的策略以减轻上层交易负载量. 此外, 该方案综合利用节点的能力, 并通过连续多轮的验证, 力保跨分片交易的顺利完成, 降低跨分片交易回滚率; (3)通过公式推导以及实验验证, 该方案具有可行性, 并可以有效地降低跨分片交易产生的时延问题, 提升系统的性能.
1 问题描述与分析 1.1 问题描述采用分片技术解决性能问题, 从宏观上来讲, 并未降低原来的工作量, 而是将原来的工作量分配到了各个分片当中, 通过增加原来系统的并行能力来提升整体的性能. 此外, 分片的引入从总工作量上来讲, 在原来的基础上还增加了跨分片交易验证的工作量. 尤其对于状态分片来讲, 其最具有挑战性的问题是跨分片交易的问题, 因特定分片只存储部分状态, 而不是完整的区块链状态, 这就导致了跨分片交易验证的复杂性. 为了提高系统运行效率, 不同分片间维护各自的账本, 分片内可以高效地处理交易, 但是对于不同分片之间如何低成本且高效地处理交易, 是目前亟需解决的问题. 甚至考虑一种极端情况: 在系统内的交易全部都是跨分片交易的情况下, 分片系统的性能是远远低于未分片前系统的性能. 现有的解决方案有同步和异步方案, 同步方案存在着难以应付连续状态改变的问题, 异步方案存在着自身原子性故障的问题. 因此, 在设计分片系统的过程中, 一种可行且高效的跨分片验证和交易处理策略至关重要.
区块链中应用最广泛的两种模型分别是基于账户的模型与UTXO (unspent transaction outputs, 未花费的交易输出)模型. 基于账户的模型虽然具有易用的优点, 但是该模型安全性差, 在一个分布式环境下只有一个地址存储数据, 有强一致性的要求, 这就会导致维护困难, 并且它还存在读写脏数据的问题, 对于同一个数据, 同一时刻不同用户分别在读和写, 还会带来数据失效性的问题. 相比较而言, UTXO模型以交易记录为中心, 记录每笔交易以及交易的流通地址, 其并发度好、安全性高、可溯源, 不存在读写脏数据的问题, 另外, UTXO的防攻击性也比账户模型更好. 因此综合考虑, 本文选择UTXO模型处理跨分片交易.
在UTXO模型中, 一笔交易的输入地址可能来自于不同分片, 在交易验证时, 验证者需要验证每笔输入尚未被消费, 并确保完成这笔交易后, 所有的输入都已不可再花费. 对所有交易的输入均验证成功后, 可以通过智能合约运算, 输出到其他分片中, 这就是跨分片交易, 其结构如图1所示. 假设一笔交易Tx有4个输入, 其中A1和A2的输入地址均映射到分片1, A3的输入地址映射到分片2, A4的输入地址映射到分片3, 该笔交易向分片n输出, 在交易验证时, 需要验证这3笔输入地址映射的分片, 3个分片验证成功后, 根据输出地址An将交易发送到分片n中, 处理完成一笔跨分片交易.
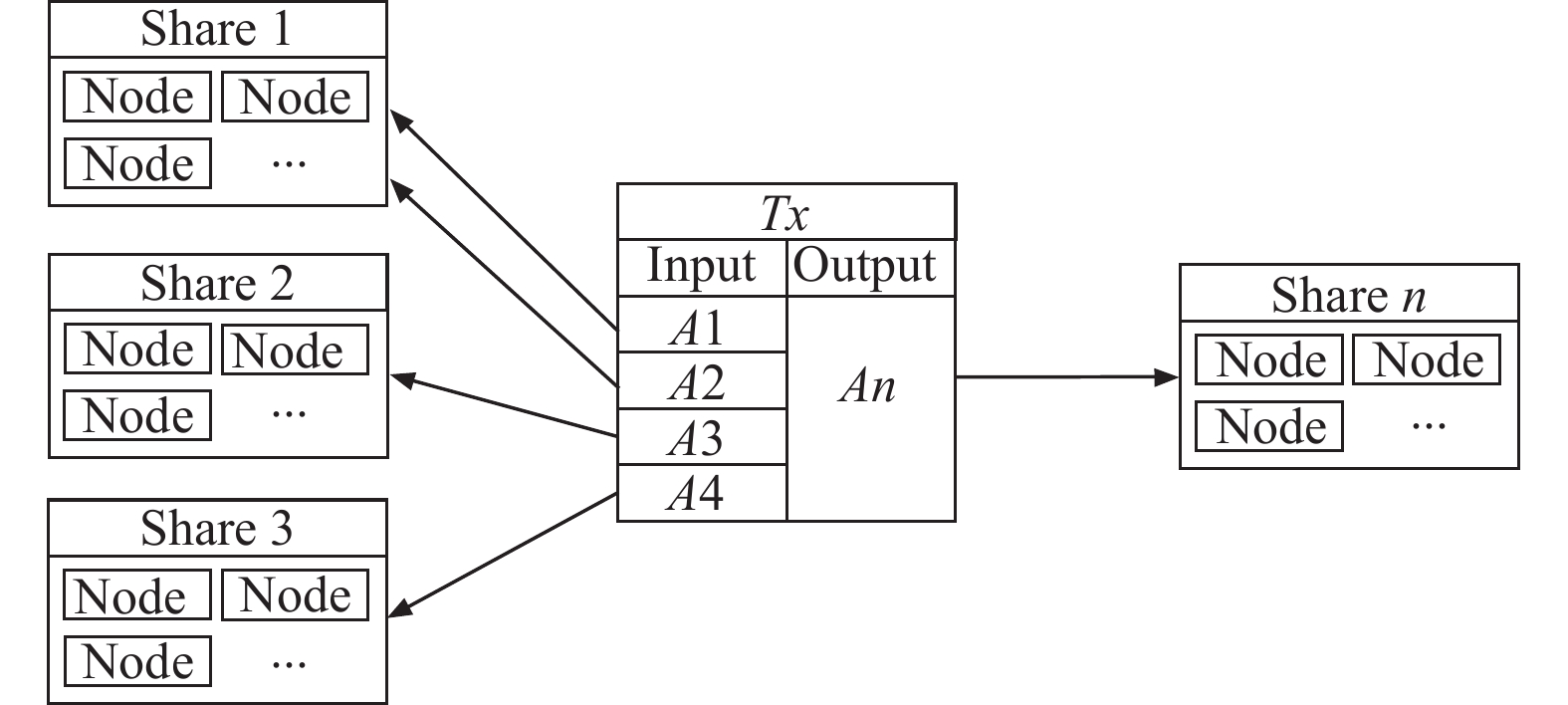
|
图 1 跨分片交易结构图 |
1.2 跨分片交易概率分析
在基于UTXO的模型中, 假设区块链系统中分片规模为n, 一笔交易的输入数为m, 根据分片的随机分配算法, 每笔交易的输入账户都是等概率分配在不同分片中, 那么可以得出单个分片间跨分片的概率P如式(1)所示.
| $ P = 1 - \left( \begin{gathered} n \hfill \\ 1 \hfill \\ \end{gathered} \right){\left( {\frac{1}{n}} \right)^m} $ | (1) |
根据公式可以计算在交易输入数为m的情况下, 跨分片交易P的概率如表1所示.
由表1可以看出, 跨分片交易概率随着分片规模n和分片个数m增加而增加, 当分片规模n为4时, 输入个数m大于8, 跨分片概率无限接近1; 当分片规模n为16时, 输入个数m为2时, 跨分片交易概率已经超过93%, 输入个数m为16时, 跨分片交易的概率为1, 必然存在跨分片交易. 由此可见, 在分片系统中, 出现跨分片交易的概率会非常高. 因此如何降低分片间跨分片交易、保证跨分片交易高效处理, 对区块链系统性能的至关重要.
| 表 1 输入数量对跨分片交易概率的影响 |
2 利用状态归约处理跨分片交易方案 2.1 状态归约模型与节点划分策略 2.1.1 状态归约模型
根据表1得出的数据, 在分片环境下, 存在跨分片交易的概率非常大, 为了降低跨分片交易的概率, 根据满二叉树结构, 本文提出了状态归约模型. 利用状态归约模型解决状态分片下跨分片交易验证的思想是利用状态归约模型将跨分片交易转变成不跨分片交易, 并完成状态同步, 状态归约模型如图2所示.
将分片按照满二叉树形式划分, 满二叉树的叶子结点代表真实存在的分片, 称为单分片; 非叶子结点为归约模型构造出的分片, 将其称为合成分片. 系统中有Si个单分片, 本文Si设置为16, 分别标注为Si1至Si16. 树的高度是logSi+1, 即高度为5, 那么按照高度由下至上将分片分为0至4五个等级.
分片模型构造完成后, 将节点分配到各个单分片中. 节点根据自身性能选择是否同步其兄弟结点状态向上归约, 节点向上归约策略在第2.2.2节叙述.
节点划分结束后, 再进行交易划分. 针对跨分片交易输入地址映射的分片, 将交易向上归约, 让上级分片对交易进行处理, 如: 输入地址映射到Si7、Si8分片, 那么将交易最终归约到C4分片中验证; 输入地址映射到Si1、Si3、Si7分片, 那么将交易最终归约到A1分片中验证. 除此之外, 更高级别分片内的节点, 除了可以验证仅在本级别验证的交易外, 还可以验证更低级别分片内的交易, 例如: 4级分片内的节点除了拥有验证该级分片中交易的权力, 还具有验证下一级(3级分片)甚至是单分片(0级分片)间交易的权力. 通过这种模型, 就将跨分片交易转换为一种不跨分片交易, 验证跨分片交易就转换为验证单个分片内交易.
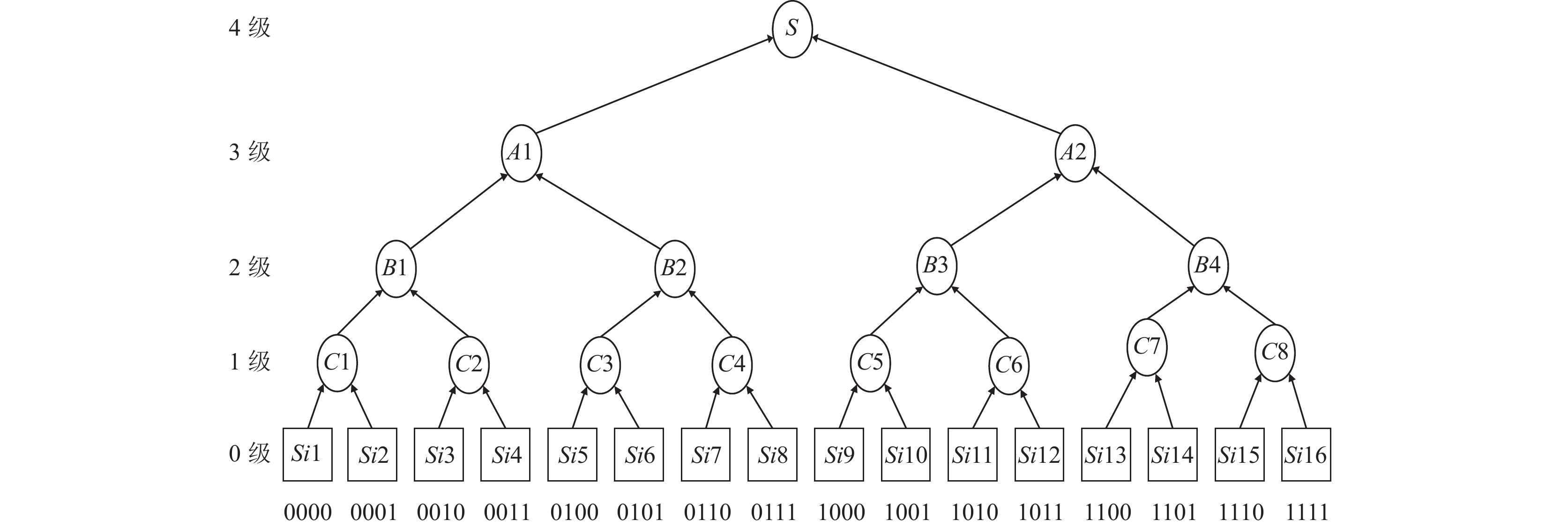
|
图 2 状态归约模型 |
2.1.2 节点划分策略
为了在状态分片下, 充分利用各个节点能力, 本文将节点进行划分. 将节点集合分成全局待选择节点序列、片内待同步节点队列, 分片内已同步节点队列和分片内验证节点集. 节点划分如图3所示.
(1)根据网络中的节点随机分配算法, 将全局待选择节点分配到每一个单分片中, 此时, 新加入的节点处于待同步状态, 具有网络中最小的状态.
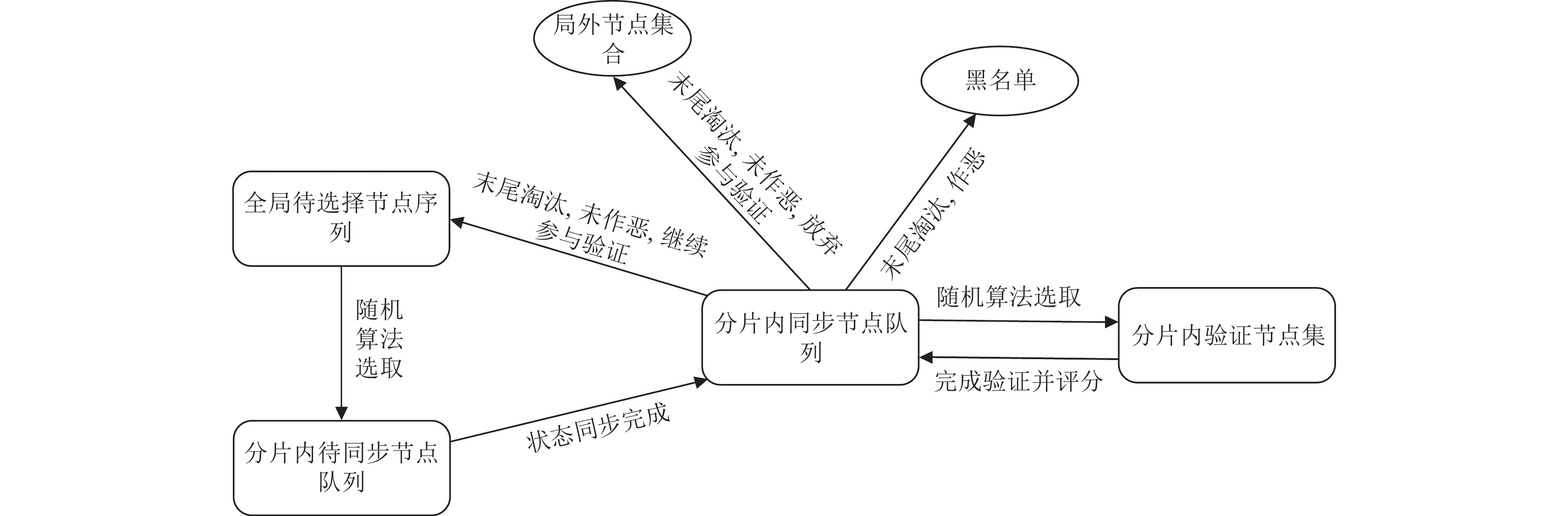
|
图 3 状态同步节点划分 |
(2)当分片内待同步节点队列中的节点完成状态同步后, 待同步节点进入已同步节点队列, 此时, 已同步节点集具有单分片内全部状态信息, 并且已同步节点可以根据自身性能等因素选择是否要同步其相邻的兄弟节点状态, 若选择不同步, 便通过随机算法选取部分已同步状态节点作为当前分片内的验证节点, 若选择同步, 便开始同步其兄弟分片中节点状态, 这样就同时具有该分片及其兄弟节点的全部节点状态, 这种节点就进入下一级别, 即其父结点之中, 具有更高的状态能力, 同理, 在这些更高级别的节点中, 同样根据随机算法选取部分节点作为这一级别的验证节点.
(3)当验证节点完成交易验证之后, 可以对其利用评分机制进行评分, 得分高的进入分片内同步节点队列中, 得分低的进行淘汰, 若得分低的原因并不是有恶意行为, 并且节点仍愿意继续参与验证, 那么节点进入全局待选择节点序列, 若末尾节点淘汰的原因不是有恶意行为, 但是不愿意继续参加验证, 则将其加入到局外节点集合, 之后还有机会继续加入全局待选择节点序列进行验证, 若淘汰的原因是因为节点作恶, 那么将节点加入黑名单, 之后不再参与共识验证. 通过这样设定流程可以避免因长时间不更新验证节点, 从而导致部分验证节点有机会作恶, 进而验证失效的问题.
由此可确定, 越上层分片内的节点, 具有越高的状态能力, 具有更详细的账本信息, 其中二叉树根节点具有网络中全部的账本信息, 也因此将最上层合成分片内的节点称为全状态节点.
2.2 基于状态归约模型的跨分片概率首先, 将跨分片交易输入地址映射的分片进行分类, K1={{Si1, Si2}, {Si3, Si4}, {Si5, Si6}, {Si7, Si8}, {Si9, Si10}, {Si11, Si12}, {Si13, Si14}, {Si15, Si16}}; K2={{C1, C2}, {C3, C4}, {C5, C6}, {C7, C8}}; K3={{B1, B2}, {B3, B4}}; K4={{A1, A2}}.
根据状态归约模型, 来计算利用状态归约模型解决跨分片交易问题时, 需要每一层节点验证交易的概率. 当一笔交易输入个数为m(m≥2, 当m=1时不存在跨分片交易), 分片规模为k, 准备归约到l级分片上, 计算当跨分片交易输入地址映射到K1集合, 即两个异或结果为0x0001的分片, 交易可归约到一级分片内节点验证的概率P(merge-one)如式(2)所示.
| $ P\left( {merge{\textit{-}}one} \right) = \left( {\frac{k}{{{2^l}}}} \right) \cdot \left[ {{{\left( {\frac{1}{{k/{2^l}}}} \right)}^m} - {2^l} \cdot {{\left( {\frac{1}{k}} \right)}^m}} \right] $ | (2) |
当跨分片交易输入地址映射到K2集合中元素对应的分片集, 以A1状态下的分片集合为例, 输入来自的分片集合为{{Si1, Si3}, {Si1, Si4}, {Si2, Si3}, {Si2, Si4}, {Si1, Si2, Si3}, {Si1, Si2, Si4}, {Si1, Si3, Si4}, {Si2, Si3, Si4}, {Si1, Si2, Si3,Si4}}, 计算交易可归约到二级节点验证的概率P(merge-two) (排除在1级节点中可验证的交易)如式(3)所示.
| $ \begin{split} P(merge{\textit{-}}two)=&\left(\frac{k}{{2}^{l}}\right)\bigg[{\left(\frac{1}{k/{2}^{l}}\right)}^{m}\\ & -{2}^{l}\cdot {\left(\frac{1}{k}\right)}^{m}-\frac{1}{{2}^{l-1}}\cdot P(merge{\textit{-}}one)\bigg] \end{split} $ | (3) |
当跨分配交易输入地址来自于K3集合中元素对应的分片集, 计算交易归约到3级节点验证的概率P(merge-three) (排除在1、2级中可验证的交易)如式(4)所示.
| $ \begin{split} &P(merge{\textit{-}}three)=\left(\frac{k}{{2}^{l}}\right)\bigg[{\left(\frac{1}{k/{2}^{l}}\right)}^{m}-{2}^{l}\cdot {\left(\frac{1}{k}\right)}^{m}\\ &-\frac{1}{{2}^{l-1}}\cdot P(merge{\textit{-}}one)-\frac{1}{{2}^{l-2}}\cdot P(merge{\textit{-}}two)\bigg] \end{split} $ | (4) |
以此类推, 求跨分片交易归约的某一级节点验证的概率, 便可依次减去上一级归约的概率. 根据上述公式计算当分片规模为16, 在不同输入m情况下, 归约到1到4级合成分片验证交易的概率P如表2所示.
| 表 2 在输入m不同时, 归约到各级合成分片验证的概率 |
根据表2分析可知, 当输入个数大于等于6时, 归约到1、2级合成分片验证的概率小于0.1%; 当输入个数大于等于8, 只能归约到3级合成分片验证的概率小于1%; 当输入个数大于12, 只能归约到3级合成分片验证的概率小于0.1%; 当输入个数等于6时, 只能归约到4级合成分片验证的概率超过96%, 并且随着m增加, 输入个数越多, 只能归约到3级节点验证的概率越高, 无限趋近于1.
虽然状态归约可以解决跨分片交易的难题, 但是存在一个明显的缺点是分片级数越高, 处理交易的量级越大, 便会出现父级分片处理压力汇集的问题. 通过对表2的分析, 对跨分片交易的处理大概率都汇集到全状态节点来处理, 对系统来讲, 分片的作用变低, 并行度也就变低, 这与分片的“分而治之”背道而驰.
2.3 利用激励机制对状态归约模型优化方案为了减轻上级合约分片处理跨分片交易的负载压力, 本文提出一种激励机制模型, 如图4所示.
(1) 我们可以鼓励用户不进行跨分片交易, 对跨分片的交易收取更高的gas费用, 这样用户就可以尽可能多地进行分片内交易, 以获得快速确认并支付更少的交易费用.
(2) 对归约模型的每一级设置不同的gas费用. 级别越高, gas费用越高, 验证等待时间越低. 用户可以在归约模型中选择在哪一层级的分片上提交交易进行验证.
由于归约过程中会存在性能方面的损耗, 可以确定, 叶子结点归约到上一级父亲结点后, 假设每个叶子结点处理事务的能力为d, 那么其父亲结点处理事务的能力D将远远小于2d(D<<2d), 令向上归约结点损耗集合Q={q, u, v, z}, 则D=(2×每一个叶子结点能力–Q集合中的元素). 因此可以推导出除0级结点外, 每一级父结点处理事务的能力D={Q, U, V, Z}={2d–q, 2×(2d–q)–u, 4×(2d–q)–2u–v, 8×(2d–q)–4u–2v–z}. 而对于gas费用的设置, 根据级别l, 设置在每一级分片用户的价格Price按照Price=2l+1–1进行规定. 让用户支付的每一级别的价格大于上一级价格的2倍, 但结点处理事务的能力却无法达到下一级结点的2倍. 级别高的分片验证时延短, 但是用户提交交易验证价格高; 级别低的分片验证时延长, 但交易验证价格低. 通过上述模式, 设计如图4所示的激励机制模型, 可以缓解交易在上层分片堆积的问题, 又可以确保每一级分片都有交易验证处理.
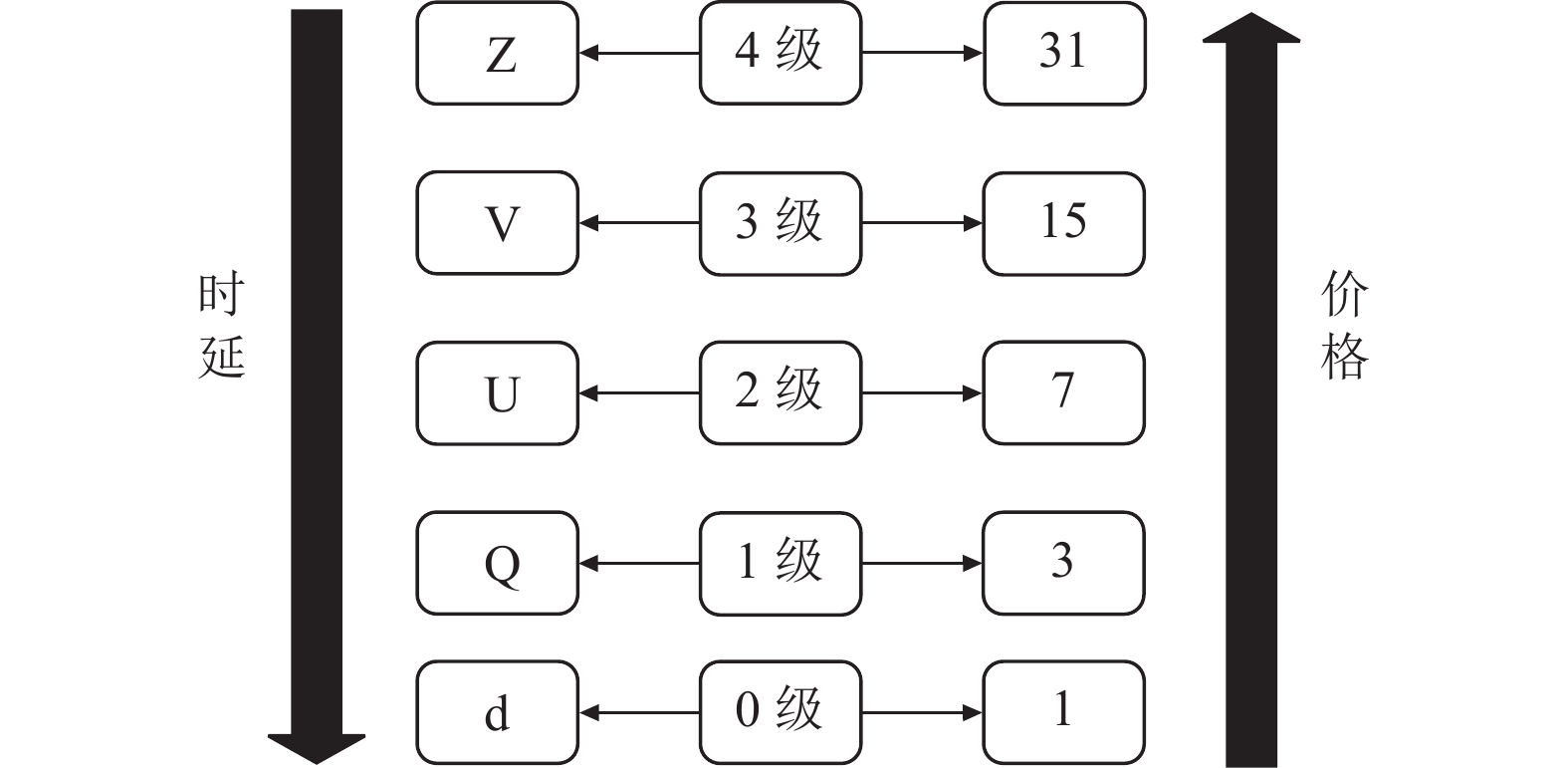
|
图 4 激励机制模型 |
3 SRMR方案设计
通过第2.3节激励机制模型, 可以让用户对于交易提交具有自主选择权, 可以避免交易都堆积到上层分片处理, 导致上层合成分片交易超过负载的问题. 如若用户提交交易所在的分片仍存在跨分片交易, 于是对系统进行平衡处理, 从系统负载能力、共识验证效率等角度分析这笔交易是否继续向上归约, 如果不继续归约且仍存在跨分片交易, 那么便提出将状态归约结合多轮共识方案, 通过对跨分片交易进行多轮次的验证, 来提升跨分片交易验证通过的概率.
3.1 SRMR方案验证流程多轮验证方案MRPV (multi-round PBFT verifi-cation)[16]根据“分而治之”的原理提出. 多轮验证方案的主要思想为当一笔交易根据映射规则被分配到一个既定的分片后, 由此分片中的所有节点对分片中的交易进行PBFT共识验证. 如果共识验证成功, 则将交易打包进区块. 若出现交易在分片内因拜占庭节点过多使交易验证超时未能有效验证交易, 那么对此交易进行新一轮共识验证[16].
多轮共识方案验证跨分片交易的中心思想是当一笔跨分片交易被发送到多个输入分片后, 由每个分片独立进行验证处理, 每个分片内交易验证成功后, 通过智能合约来传递信息, 确认无误后打包交易到区块.
利用状态归约处理跨分片交易多轮验证方案SRMR (state reduction and multi-round)思想是当用户提交交易到某一级后, 若仍存在跨分片交易, 这笔跨分片交易会被发送到对应的输入分片, 在每个分片内单独进行多轮验证. 如图5所示, 假设用户提交的一笔跨分片交易被发送到Si1、Si2、Si3分片中, 通过状态归约模型, 用户根据自身选择将交易提交到1级合成分片C1中, C1分片中有Si1与Si2全部的账本信息, 而C1与Si3还处于两个单独的分片, 利用多轮共识方案对C1和Si3开始独立进行验证处理.

|
图 5 用户提交跨分片交易模型 |
SRMR方案具体流程如图6所示.
(1) 分配节点到网络. 将网络中全局待选择节点序列根据VRF随机分配算法, 随机分配到各个分片中, 让每个分片节点进入待同步节点队列.
(2) 将节点进行状态同步. 在分片内的待同步节点队列进行状态同步, 同步完成的节点再判断是否继续同步兄弟结点, 最高同步到Lmax级别(Lmax为满二叉树的高度). 此时, 整棵二叉树中, 叶子结点(单分片)中有待同步节点和同步节点, 非叶子结点(合成分片)中有同步其子结点状态的同步节点. 以此递归, 完成在二叉树各级分片中节点的分配.
(3) 分配交易到分片中. 用户根据激励机制选择要提交到哪一级分片处理交易, 若提交到那一级别的交易仍存在跨分片交易, 根据输入地址映射的分片, 将交易Tx[i]继续分配到对应的0级单分片中. 系统根据整体性能的平衡判断, 是否进行归约到上一级处理验证交易, 在二叉树各级分片中完成交易分配.

|
图 6 SRMR方案流程图 |
(4)多轮共识验证交易. 各个分片内共识节点对交易集合中的交易进行PBFT共识, 共识成功则将交易打包到区块, 若因分片内共识节点中拜占庭节点比例较高导致共识失效, 那么将验证交易轮数round加1, 每进行一轮验证, 需要利用评分机制对共识节点进行评分, 评分高的节点可以进入该级别的同步节点队列, 评分低的根据末位淘汰的原则分配到全局待选择节点中进行重新轮换选择. 若交易验证次数超过轮数上限Rmax还未达成共识, 那么便放弃这笔交易.
3.2 参与共识节点验证概率在状态分片下, 对于验证跨分片交易需要确定参与共识验证节点的个数. 将网络中的节点利用VRF算法随机选取分配到各个分片内, 设置网络中节点总数为N, 网络节点中拜占庭节点比例为Pn, 选取单一分片内节点数为Ns, 分片内参与共识验证的节点数为Nsv, 令Xi表示分片内拜占庭节点数, Xj表示参与共识验证节点中拜占庭节点的数量, 分片内的节点分配可认为是从网络中N个总节点中选择Ns个节点, 令Xi表示选择的Ns个节点中拜占庭节点的数量, 则Xi服从超几何分布, 记为Xi~Hi(Ns, N×Pn, N); 共识组内的节点分配可认为是从分片内Ns个节点中选择Nsv个共识节点, 令Xj表示选择的Nsv个节点中拜占庭节点的数量, 则Xj同样服从超几何分布, 记为Xj~Hj(Nsv, Ns×Ps, Ns). 并且可知, 共识组中拜占庭节点数量与分片内拜占庭节点数量存在依赖条件, 利用二重求和可推导出式(5).
| $ P(Failure{\text{ }}of{\text{ }}consensus) = \sum\limits_{Xj = \frac{{Nsv}}{3}}^{X{{j}} = \min \{ Xi, Nsv\} } {\left( {\sum\limits_{Xi = \frac{{Nsv}}{3}}^{Xi = Ns} {\frac{{\left( \begin{gathered} N - N \cdot Pn \hfill \\ Ns - Xi \hfill \\ \end{gathered} \right)\left( \begin{gathered} N \cdot Pn \hfill \\ Xi \hfill \\ \end{gathered} \right)}}{{\left( \begin{gathered} N \hfill \\ Ns \hfill \\ \end{gathered} \right)}} \cdot \frac{{\left( \begin{gathered} Ns - Ns \cdot Ps \hfill \\ Nsv - Xj \hfill \\ \end{gathered} \right)\left( \begin{gathered} Ns \cdot Ps \hfill \\ Xj \hfill \\ \end{gathered} \right)}}{{\left( \begin{gathered} Ns \hfill \\ Nsv \hfill \\ \end{gathered} \right)}}} } \right)} $ | (5) |
假设当网络中节点总数N为4 000, 网络节点中拜占庭节点比例Pn为1/3时, 分片内同步节点与验证总数Nk为2 000, 设置分片数Ks为16, 单个分片内节点数Ns=Nk/Ks, 即Ns选取为125, 根据式(5), 计算分片内参与共识验证节点数Nsv在不同拜占庭比例Ps的情况下导致分片内共识失效的概率P(Failure of consensus). 计算结果如图7所示. 可以看出随着Nsv增加, 共识失效概率以3为周期震荡型降低, Nsv的节点数量可按3i+1来固定范围(i取正整数), 使得共识失效概率最低. 其中由于网络中最小带宽取决于系统中验证节点数量Nsv, 若Nsv设置过大, 会使网络中通信量过大从而造成网络负担加重, 若Nsv设置过小, 虽然通信量较低, 但是容易产生合谋攻击, 并导致严重的中心化以及安全性问题. 因此, 从通信量和网络带宽的角度考虑, 将Nsv设置在10到20之间进行计算. Nsv可取值为10、13、16、19, 分片内共识失效的概率为0.441、0.448、0.453、0.457.
3.3 多轮共识方案轮数选择对于一笔跨分片交易, 为了避免合谋攻击的情况以及在某一时刻单个分片内输入交易不足, 下一时刻输入交易满足条件的情况, 在此规定, 一笔交易验证通过至少需要2轮验证才可通过, 因此将轮数下限选择为2.
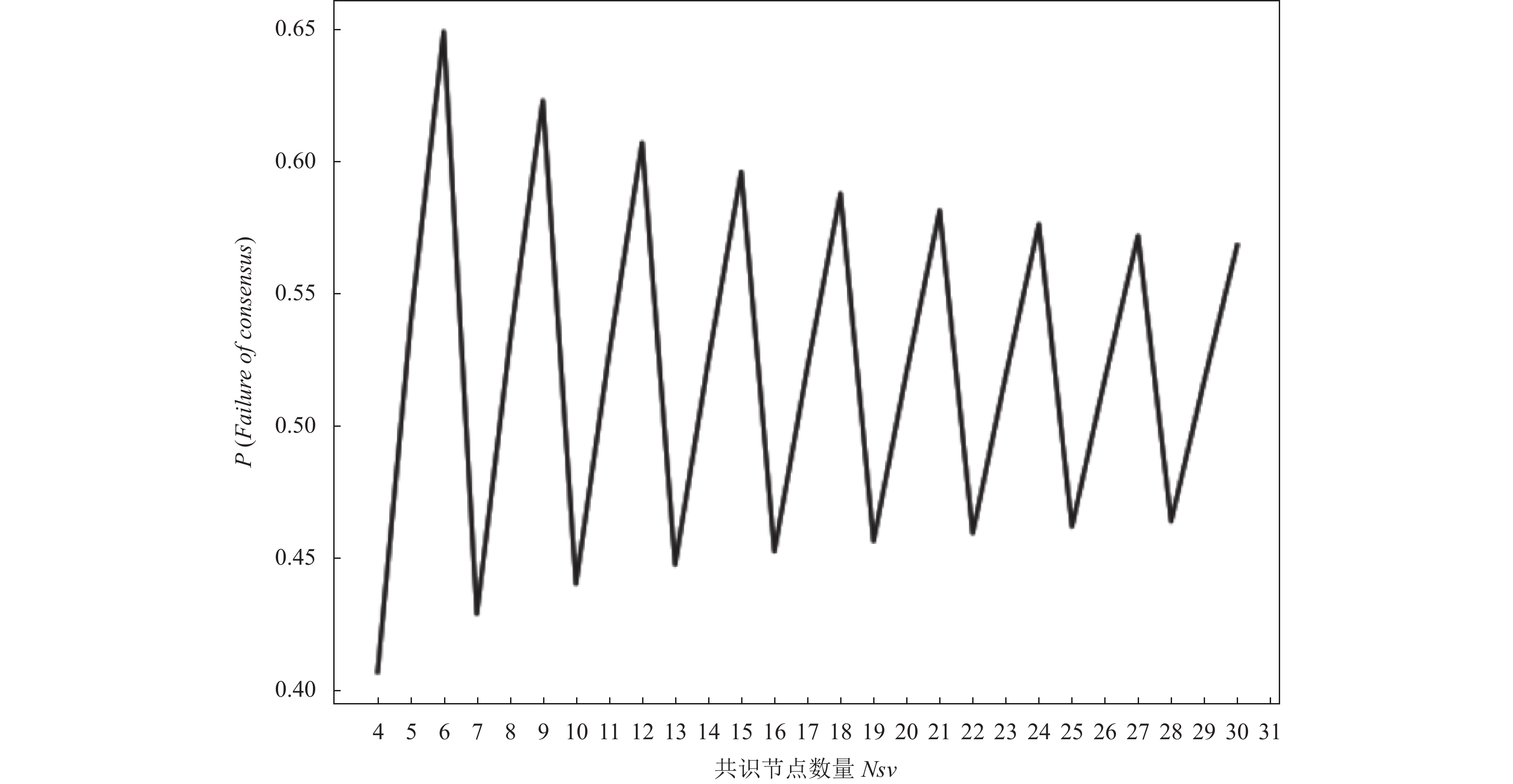
|
图 7 在不同共识验证的节点数Nsv下导致分片共识失效的概率P |
3.3.1 多轮轮数上限
对于需要多轮验证的跨分片交易, 即如图5所示的跨分片交易模型, 为了防止对某一分片中的交易连续进行多轮次的验证仍未通过导致性能损耗, 需要确定轮数上限Rmax, 即最大共识次数. 根据第3.2节对验证节点的选取可知, Nsv的值可为10、13、16、19, 并可计算出对应的失效概率P(Failure of consensus). 假定交易在r轮验证成功, 即r–1轮验证失败, 可以推导交易验证成功概率P(Success of consensus), 如式(6)所示.
| $ \begin{split} & P(Success\; of\text{ }consensus)\\ & {\text=\displaystyle \sum _{1}^{{r}}\left(1-P\left(Failure\text{ }of\text{ }consensus\right)\right)}\\ & \cdot {\left(P\left(Failure\text{ }of\text{ }consensus\right)\right)}^{r-1} \end{split}$ | (6) |
根据式(6)可计算出在不同拜占庭比例Pn和不同共识验证节点Nsv的条件下, 跨分片交易验证成功的概率大于1–10−8时轮数上限Rmax. 计算结果如表3所示.
| 表 3 在不同Pn和Nsv的条件下, 轮数上限Rmax的选择 |
当一笔交易连续经过Rmax轮共识后仍无法验证成功, 为保证系统整体性能便放弃这笔交易.
3.3.2 归约轮数选取本节针对于图6中判断是否归约策略进行细化, 计算向上归约的轮数下限Rmin.
当一笔需要多轮验证的跨分片交易输入地址发送到来自同一父级下相邻的结点, 记该集合为Q, 并且在Q集合下这两个分片下进行多轮验证均经过Rmin轮仍未验证成功, 那么这两个分片下的交易被判定为有向上一级归约的能力. 规定当跨分片验证成功概率大于99%时, Q集合中的分片均未共识成功, 那么Q集合中的分片具有向上归约的能力. 根据式(6)计算出在不同拜占庭比例Pn和不同共识验证节点Nsv的条件下, 跨分片交易验证成功的概率大于99.9%时, 符合归约条件的轮数下限Rmin. 计算结果如表4所示.
3.4 平衡多轮共识与归约策略针对空闲分片中的共识节点闲置太久, 浪费资源, 长时间得不到交易的进行验证, 或者单个分片验证跨分片交易过多, 导致单个分片负载过多, 或者单个分片共识节点不够, 无法进行交易验证, 导致交易长时间无法验证, 交易处理时延过长的问题. 根据状态归约模型处理跨分片交易的多轮共识方案, 提出了判断该笔验证的交易是否需要向上继续归约的这个解决方案. 该方案的处理流程图如图8所示.
| 表 4 在不同Pn和Nsv的条件下, 符合归约条件的轮数下限 |

|
图 8 归约处理流程图 |
当一笔跨分片交易输入地址被发送到多个分片后, 设置这笔交易的输入地址发送到各个单分片集合TotalSet中, 用户将这笔跨分片交易提交到某一Grade级分片之后, 若Grade>0, 则设置Grade级别下的单分片集合为SingleSet, 若Grade=0, 即用户提交到单分片中, 那么SingleSet集合为空. 这笔跨分片交易的输入地址映射到SingleSet集合的分片外的其他单分片, 设置这个集合为OtherSet, OtherSet=TotalSet–SingleSet. 这样, 当一笔交易Tx[i]被发送到Grade级分片后, 这笔交易需要满足以下条件才可进行归约.
(1) 系统开始判断是否提交到最高等级Lmax, 并且这笔交易验证的轮次是否大于Rmin
(2) 判断OtherSet集合中的是否存在验证这笔交易的分片的兄弟结点元素. 判断这个条件的原因在于, 当OtherSet集合中的两个元素是来自同一父级下的兄弟结点, 才有向上一父级分片归约判断的条件, 否则某一父级的分片下, 只有一个孩子结点, 便无需向上归约抢占资源, 只需要在单个分片内多轮验证即可.
(3) 判断向上归约的上级合成分片中节点状态是否可用. 上级节点状态是否可用的前提在于, 上层同步节点数量是否足够. 在状态同步下每个分片可用节点数是不一样的, 因为归约模型上层节点不属于分配型的, 属于激励型的, 底层分片中的节点是否向上归约是个不确定的情况, 因此可能存在上层分片在某个时刻没有足够的有效节点导致无法工作. 设合成分片中同步节点数量阈值为Nt, 某一合成分片内同步节点数量可查, 针对阈值Nt的选定, 考虑两种情况. 首先, 分片内共识节点完成一轮验证后, 需要进行节点轮换, 通过评分机制将完成一轮验证的节点进行打分, 分数低的淘汰, 由于多轮验证方案要求每一轮都需要轮换掉一个分值低的共识节点, 那么便需要一个同步节点被选取为共识节点, 总共进行R轮验证, 取轮数上限Rmax(第3.3.1节所求), 即首先确保可以达到Rmax个同步节点; 其次, 最坏的一种情况是, 分片内一笔交易共识失败, 那么选取共识节点Nsv中达到1/3评分低的节点, 将1/3×Nsv个验证节点替换掉, 同时需要1/3×Nsv个同步节点通过随机算法选取进入分片内验证节点集, 那么便需要分片内同步节点数大于1/3×Nsv+C(C>0, 且C为正整数). 通过上述策略分析可推导出阈值Nt的公式如式(7)所示. 那么系统判断, 当上层同步节点数大于Nt的值后, 并可以向上归约, 否则拒绝归约.
| $ Nt = R_{\rm{max}} + \frac{1}{3} \cdot Nsv + C $ | (7) |
(4) 判断上级分片内交易是否到达分片的负载. 在以上条件均满足的情况下, 确定上层的分片的负载情况, 可通过这一时隙交易完成后, 要向上归约到分片m中未验证的交易数Count(unTxm)来确定该分片负载情况. 本文假设每笔交易的大小大致相同, 根据每一层分片数Kp, 可以计算出每一层未验证交易总数为Count(unTxKp), 从而可推导出在每一层中各个分片负载均衡时, 单个分片平均未验证交易数Avg(unTx), 如式(8)所示. 这样, 利用这一时隙交易验证完成后, 各个分片Count(unTxm)与单个分片平均未验证的交易数为Avg(unTx)的比值, 可以计算出分片m的负载值Shardm. 若Shardm≤1, 说明分片m中的未确认交易数小于等于该层各分片未确认交易数平均值, 那么可以将交易归约到上层m分片中验证; 若Shardm>1, 说明分片m中的未确认交易数大于该层各分片未确认交易数平均值, 那么不可以将交易归约到上层m分片中验证, 这笔交易在这一时隙下不具有向上归约的条件.
| $ \text{A}vg(unTx)=\frac{Count(unT{x}_{Kp})}{Kp}=\frac{{\displaystyle \sum _{m=1}^{Kp}Count(unT{x}_{m})}}{Kp} $ | (8) |
为验证本文提出的利用状态归约模型的多轮验证方案的可行性, 首先通过对方案本身进行时延的计算, 按层递进, 对比本方案中各个步骤所消耗的时延; 其次, 对比MRPV方案与SRMR方案对降低跨分片交易回滚概率的影响.
4.1 实验设置为了可以更加高效的对本方案的可行性进行分析, 首先实验之前需要对参数进行如下设置.
(1) 设置系统中总节点数N=4000, 单分片内Ns=125, 分片数K=16, 分片内参与共识节点Nsv=19. 根据第3.3.1节关于轮数上限Rmax的分析, 选取跨分片交易验证成功概率高于1–10−8的轮数上限Rmax, 以及根据第3.3.2节关于符合归约条件下限Rmin, 选取跨分片交易验证成功的概率大于99.9%时, 符合归约条件的轮数下限Rmin
(2) 构造状态归约模型, 让1级合成分片中任意构造一个分片同步节点数目少于Nt, 另选一个分片让其负载值Shardm>1, 即通过这两种情况的设置让一个分片状态不可用, 让一个分片验证交易超过负载, 这两个分片将不会被系统设置为可向上归约的分片. 设置其他分片均为正常可用分片, 同级分片间性能相当, 越往上级性能越好, 负载越高, 但负载差异在分片可控范围内.
(3) 对P2P测试网络中的节点要求通信状况良好, 在有限的延迟内接收消息.
实验选用Linux作为开发平台, 以Go语言作为开发语言, 以Goland和Docker作为研发工具, 实验数据利用Python进行绘制.
4.2 时延测试交易时延是指一笔交易从发送到区块链网络, 到被系统中共识节点确认的时间. 处理交易的时延是确定区块链系统性能好坏的一个重要指标, 较低的时延可以让交易得到更快的确认. 设置一笔跨分片交易, 让其根据输入地址映射到各个分片中.
本次实验通过设置3个方案进行对比, 分别是方案1: 只在单分片内多轮验证、方案2: 结合归约模型进行多轮验证(未结合平衡多轮共识与归约策略)、方案3: SRMR (结合平衡多轮共识与归约策略). 实验测试了在拜占庭比例Pn=1/4的情况下, 跨分片交易涉及2、4、6、8、10、12、14、16个输入对象映射的分片数目下的8组对照实验. 实验结果如图9所示, 根据运行结果分析, 随着映射的分片数目越多, 这3种验证情况的时延都会增加, 但是结合归约模型多轮验证方案的时延明显低于单分片多轮验证方案, 并且SRMR方案比仅结合归约模型多轮验证方案还低一些.

|
图 9 不同方案下跨分片交易时延对比 |
分析方案一增长速度逐渐加快的原因在于, 当交易只在单分片内进行多轮验证, 很大程度存在着某一个分片验证轮次较高, 其他分片内交易等待导致时延突增; 在分片数目为2–8之间, 方案2、3差距不大的原因在于, 分片数目小于8的情况下, 系统判定向上归约的可能性不大, 不符合向上归约的要求; 分片数为16时, 方案2、3差距不大的原因在于, 默认用户对于这笔交易提交到了最高等级, 即系统判定不需要向上归约, 产生时延的主要原因在于对交易进行多轮验证以及最高层分片负载较大, 交易验证需要等待较长时间导致的.
4.3 跨分片交易回滚概率测试跨分片交易回滚是指, 某一输入对象映射的分片内的交易被验证为无效, 那么该笔交易其他分片已锁定的资源也必须回滚, 保证后续交易可正常使用.
本实验设置两个方案对比, 分别是MRPV方案与SRMR方案. MRPV方案未区分节点能力, 即MRPV方案中分片内节点数均为验证节点数, 因此根据本文SRMR设置对比实验时, 设置MRPV方案中节点数为125 (即与SRMR方案中分片内节点数Ns相同), 对比在拜占庭比例Pn=1/4的情况下, 当不同输入对象映射到不同分片数时, 交易到达验证最高轮数Rmax后仍存在回滚概率的情况. 实验结果如图10所示. 根据结果显示, MRPV随着输入分片数目增多, 跨分片概率逐渐增加, SRMR方案随着输入分片数量增加跨分片回滚概率明显低于MRPV分案, 甚至跨分片回滚概率逐渐趋于平稳.

|
图 10 不同方案下跨分片交易回滚概率对比 |
对上述运行结果进行分析, 由于SRMR方案相较于MRPV方案, 在同一输入分片数目的情况下, 在一定程度上通过归约模型减少了实际验证跨分片交易输入分片数量, 并且越向上层归约的节点性能越好, 验证通过的概率甚至更大.
两种实验方案表明, SRMR方案利用归约模型, 综合利用节点能力进行多轮验证, 不但可以有效降低时延, 还对多轮进行优化, 进一步降低了跨分片交易的回滚概率, 保证了系统可行性, 改善了系统的性能.
5 总结与展望本文针对状态分片下处理跨分片交易的难题, 提出了一种利用状态归约处理跨分片交易的多轮验证方案SRMR, 本方案通过归约模型, 利用满二叉树的结构, 将分片内的节点根据自身性能选择是否向上归约, 并分析在此模型下各层处理跨分片交易的概率; 随后, 本文分析出仅用归约模型的方案所产生的弊端, 并提出一种结合了激励机制和多轮验证的归约模型方案, 均衡了上层交易负载的问题, 最后推算出轮数的合理取值, 并提出了一种合理平衡归约与多轮验证的策略. 在该模型中, 我们综合利用节点的能力, 在降低了时延的同时, 进一步降低了跨分片交易回滚率. 本文对于后续针对跨分片交易的研究有一定的参考价值, 接下来的工作是利用SRMR方案, 可以继续针对状态分片下抗合谋攻击问题作出进一步研究, 此外, 本文未探索交易打包上链的方式, 可以后续对SRMR方案的打包上链方式进行探究.
| [1] |
Liu ZY, Luong NC, Wang WB, et al. A survey on blockchain: A game theoretical perspective. IEEE Access, 2019, 7: 47615-47643. DOI:10.1109/ACCESS.2019.2909924 |
| [2] |
Al-Jaroodi J, Mohamed N. Blockchain in industries: A survey. IEEE Access, 2019, 7: 36500-36515. DOI:10.1109/ACCESS.2019.2903554 |
| [3] |
潘晨, 刘志强, 刘振, 等. 区块链可扩展性研究: 问题与方法. 计算机研究与发展, 2018, 55(10): 2099-2110. DOI:10.7544/issn1000-1239.2018.20180440 |
| [4] |
袁勇, 王飞跃. 区块链技术发展现状与展望. 自动化学报, 2016, 42(4): 481-494. DOI:10.16383/j.aas.2016.c160158 |
| [5] |
Luu L, Narayanan V, Zheng CD, et al. A secure sharding protocol for open blockchains. Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security. New York: ACM, 2016.
|
| [6] |
高政风, 郑继来, 汤舒扬, 等. 基于DAG的分布式账本共识机制研究. 软件学报, 2020, 31(4): 1124-1142. DOI:10.13328/j.cnki.jos.005982 |
| [7] |
喻辉, 张宗洋, 刘建伟. 比特币区块链扩容技术研究. 计算机研究与发展, 2017, 54(10): 2390-2403. DOI:10.7544/issn1000-1239.2017.20170416 |
| [8] |
Javarone MA, Wright CS. From bitcoin to bitcoin cash: A network analysis. arXiv: 1804.02350, 2018.
|
| [9] |
Li M, Tang H, Hussein AR, et al. A sidechain-based decentralized authentication scheme via optimized two-way peg protocol for smart community. IEEE Open Journal of the Communications Society, 2020, 1: 282-292. DOI:10.1109/OJCOMS.2020.2972742 |
| [10] |
Poon J, Dryja T. The bitcoin lightning network: Scalable off-chain instant payments. https://lightning.network/lightning-network-paper.pdf. (2016-01-14).
|
| [11] |
Wang JP, Wang H. Monoxide: Scale out blockchains with asynchronous consensus zones. 16th USENIX Symposium on Networked Systems Design and Implementation. Boston: USENIX Association, 2019. 95–112.
|
| [12] |
Zamani M, Movahedi M, Raykova M. RapidChain: Scaling blockchain via full sharding. Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security. New York: ACM, 2018. 931–948.
|
| [13] |
Al-Bassam M, Sonnino A, Bano S, et al. Chainspace: A sharded smart contracts platform. arXiv: 1708.03778, 2017.
|
| [14] |
Sousa J, Bessani A. From Byzantine consensus to BFT state machine replication: A latency-optimal transformation. 2012 9th European Dependable Computing Conference. Sibiu: IEEE, 2012. 37–48.
|
| [15] |
Kokoris-Kogias E, Jovanovic P, Gasser L, et al. OmniLedger: A secure, scale-out, decentralized ledger via sharding. IEEE Symposium on Security and Privacy (SP). San Francisco: IEEE, 2018. 583–598.
|
| [16] |
王夫森. 采用多轮PBFT验证的分片规模和有效性研究[硕士学位论文]. 大连: 大连海事大学, 2020.
|
| [17] |
白兵, 李志淮, 李敏. 降低跨分片交易回滚概率的多轮验证方案. 计算机工程与应用, 2022, 58(2): 129–136.
|
 2022, Vol. 31
2022, Vol. 31



