路面病害中, 坑槽对高速公路车辆的安全驾驶威胁最大^[1]. 目前自动化提取路面坑槽病害的方法大体分为两类: 一是图像检测法^[2], 该方法通过道路图像的灰度信息识别坑槽面积, 但易受环境影响; 二是三维激光扫描法^[3-5], 该方法采用高精度、高密度的激光采集路面高程点云数据, 构建路面三维模型, 通过分析路面高程变化确定路面坑槽位置坑槽轮廓、面积等, 可以较好的提取路面病害.

基于路面激光点云数据的坑槽提取方法, 文献[6]提出一种剖面线自适应曲线拟合的坑槽提取方法, 该方法采用最小二乘曲线拟合方法拟合道路断面的剖面线, 通过剖面线的曲率判别坑槽边界点, 易损失部分边界点; 文献[7]提出了一种基于点云剖面特征描述的路面坑槽提取方法, 该方法对道路断面的剖面线进行拟合, 计算剖面的积分不变量和微分特性并根据坑槽的积分不变性及微分特性识别坑槽, 需要手动确定圆的半径及选择合适的判别坑槽积分不变量的阈值.

法向量是点云的重要几何属性之一, 可以精准地描绘模型表面, 可用于点云边界提取^{[8, 9]}, 特征提取, 表面重建等. 当前坑槽提取方法中, 未见利用法向量提取路面坑槽的方法, 本文从点云法向量出发, 提出一种基于法向量距离的路面坑槽提取方法, 可准确识别并提取坑槽轮廓, 面积和深度信息.

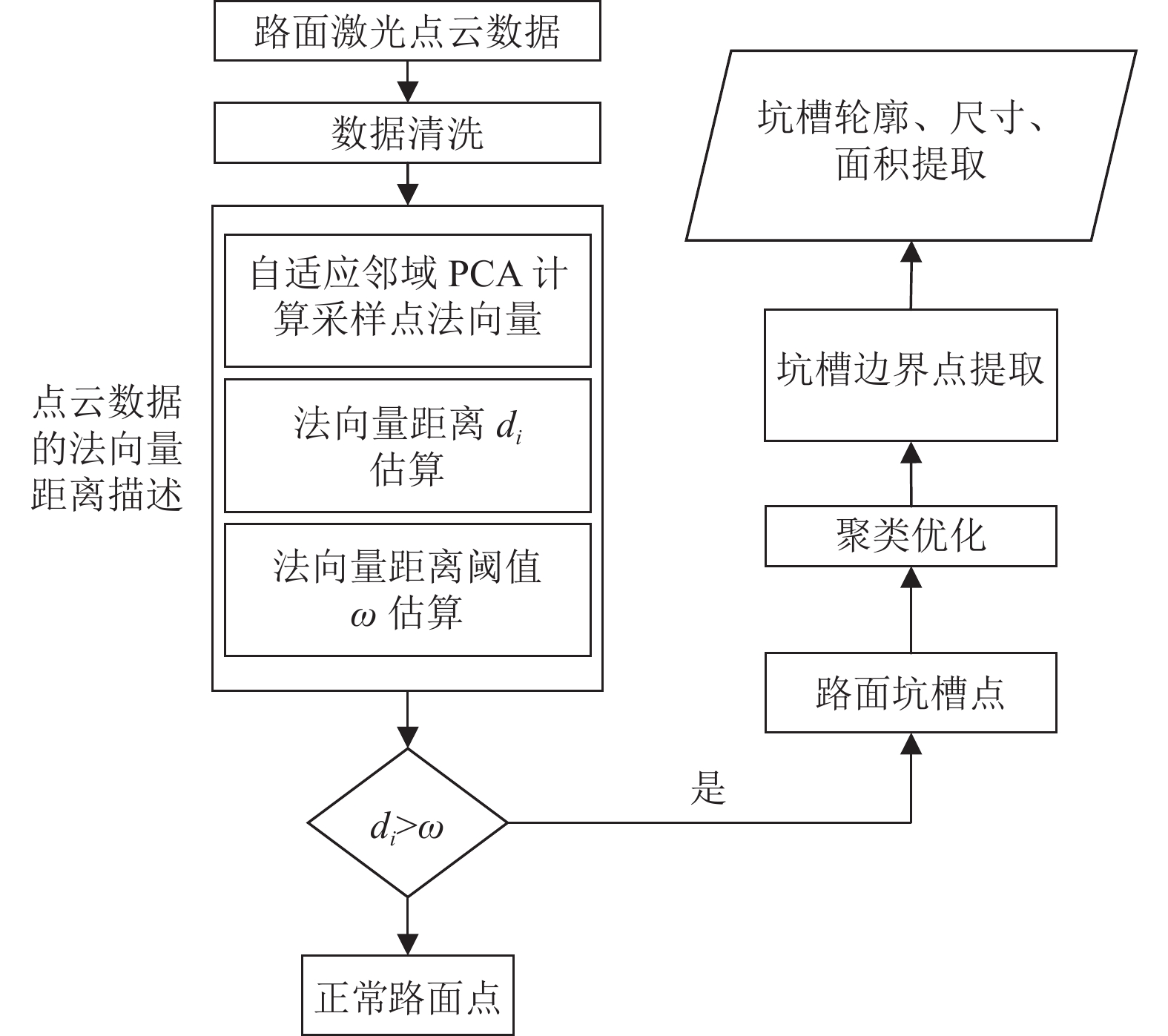
1 路面坑槽提取方法流程

针对路面高程激光点云数据, 本文应用法向量距离对路面点云数据的曲率进行描述, 以曲率为约束提取路面点云数据中的坑槽部分(高曲率部分). 整体流程图如图1所示.

2 路面高程点云预处理

利用车载三维激光采集路面高程数据时, 受仪器、环境、测量方式等因素影响, 路面高程点云数据中不可避免存在异常点, 异常点使得路面高程点云模型中的几何特征变得不明显, 影响数字高程模型的建立, 路面病害的提取.

2.1 路面坐标系建立

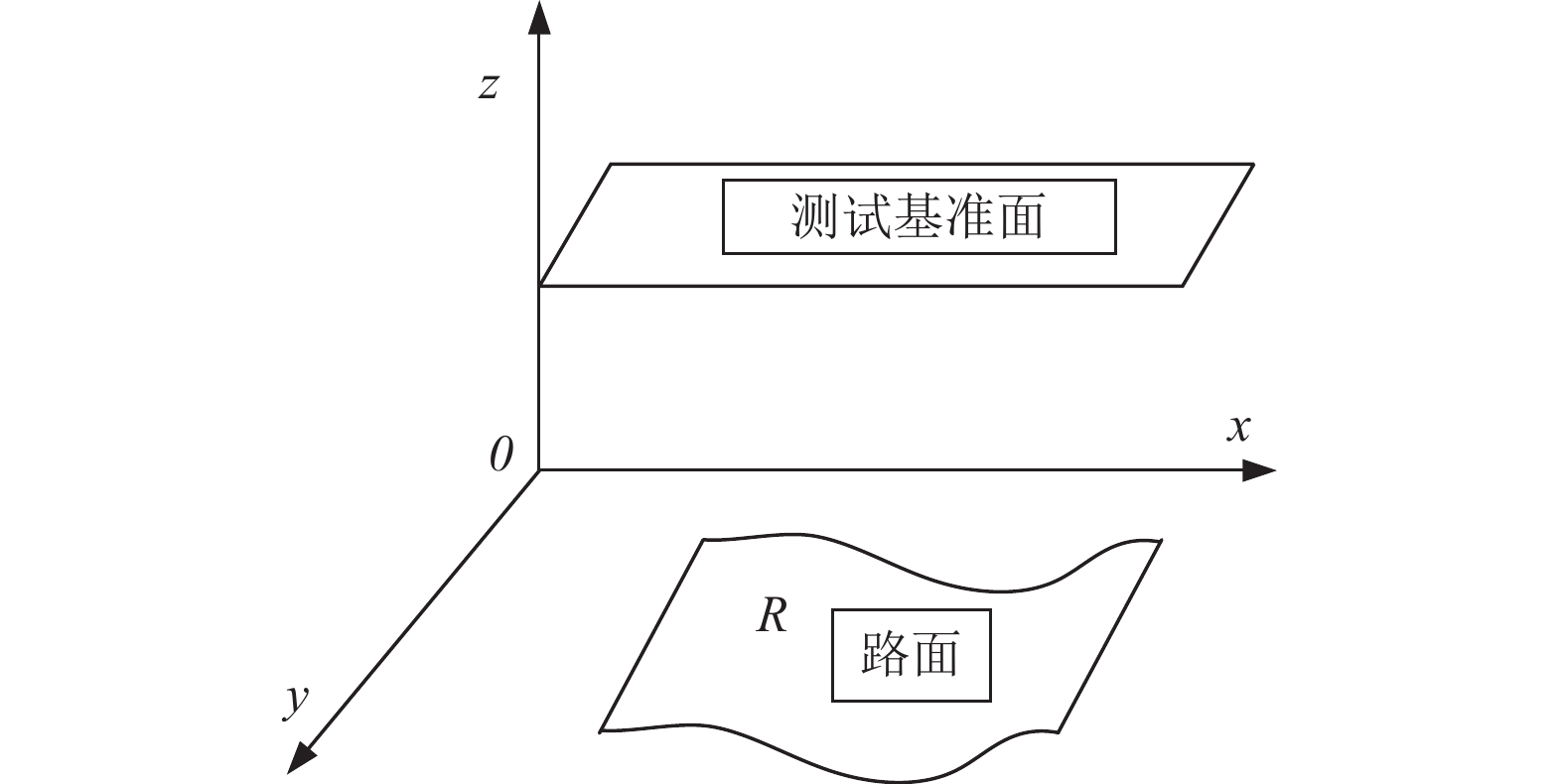
为了方便计算路面采样点的法向量, 必须将路面数据融合到一个统一的坐标系中. 本文建立以路面里程为x, 横断面为y, 各点高程为z的三维坐标系来完成三维重构. 图2给出了所建立的三维坐标系模型图.

在该坐标系下, 路面可以表示为一个连续的三维函数, 即:

$ R = f(x, y, {\textit{z}}) $

(1)

为了求得R的数学描述, 首先选择一个平行于路面的平面为基准测试平面, 假设基准测试平面方程为:

$ {\textit{z}} = D $

(2)

其中, D表示基准测试平面和xoy平面间的距离. 为分析方便, 令D=0. 即基准测试平面和平面重合. 设路面上各点到该基准面的距离为z, 则三维路面实体R可表示为以下各点的集合:

$ R = \left\{ {\begin{array}{*{20}{c}} {\left( {{x_1}, {y_1}, {{\textit{z}}_{11}}} \right)}&{\left( {{x_2}, {y_1}, {{\textit{z}}_{12}}} \right)}& \cdots &{\left( {{x_i}, {y_1}, {{\textit{z}}_{i1}}} \right)} \\ {\left( {{x_1}, {y_2}, {{\textit{z}}_{12}}} \right)}&{\left( {{x_2}, {y_2}, {{\textit{z}}_{22}}} \right)}& \cdots &{\left( {{x_i}, {y_2}, {{\textit{z}}_{i2}}} \right)} \\ \vdots & \vdots & \ddots &{}\vdots \\ {\left( {{x_1}, {y_j}, {{\textit{z}}_{1j}}} \right)}&{\left( {{x_2}, {y_j}, {{\textit{z}}_{2j}}} \right)}& \cdots &{\left( {{x_i}, {y_j}, {{\textit{z}}_{ij}}} \right)} \end{array}} \right\} $

(3)

式(3)中, 对于y坐标相同的各点代表路面R的一个纵断面, 如式(4)所示, 对于x坐标相同的各点可代表路面R的一个横断面, 如式(5)所示:

$ {L_j} = \left\{ {\left( {{x_1}, {y_j}, {{\textit{z}}_{1j}}} \right){\text{ }}\left( {{x_2}, {y_j}, {{\textit{z}}_{i2}}} \right){\text{ }} \cdots {\text{ }}\left( {{x_i}, {y_j}, {{\textit{z}}_{ij}}} \right)} \right\} $

(4)

$ {T_i} = \left\{ \begin{gathered} \left( {{x_i}, {y_{i1}}, {{\textit{z}}_{i1}}} \right) \hfill \\ \left( {{x_i}, {y_{i2}}, {{\textit{z}}_{i2}}} \right){\text{ }} \hfill \\ \qquad \vdots {\text{ }} \hfill \\ \left( {{x_i}, {y_{ij}}, {{\textit{z}}_{ij}}} \right) \hfill \\ \end{gathered} \right\} $

(5)

2.2 数据清洗

本文使用的路面点云数据来自长安大学激光检测车. 该车行驶在某一车道时, 周期性的对所在车道的道路横断面高程信息进行采集. 在低温、寒冷环境下, 车载激光测距设备获得的部分路面数据异常, 表现为整个横断面的高程数据与相邻数个正常横断面高程的差值较大, 如图3中x轴上区间[3000, 5000]所示; 此外, 受路面环境(其他车辆、水渍、路面孔洞等), 道路横断面内的点云数据存在漂移点、孤立点等噪点. 针对异常纵断面, 选用临近4个正常横断面高程数据, 采用牛顿插值法^[10]估计该横断面高程. 针对单个横断面内部的噪声点, 采用一维高斯滤波器对路面横断面节点进行高程平滑处理, 其中高斯函数为:

$ f(x) = \frac{1}{{\sigma \sqrt {2\pi } }}{{\rm e}^{ - {{(x - \mu )}^2}/{\sigma ^2}}} $

(6)

其中, $ x $ 为随机变量; $ \sigma $ 为尺度参数, 即 $ x $ 的标准差; $ \mu $ 为 $ x $ 的均值.

由于计算平均值时, 中心点就是原点, 所以 $ \mu $ =0; 本文选择大小为3, 标准差 $ \sigma = 1 $ 的模板, 利用式(6)计算横断面内相邻节点权重, 得到某节点平滑去噪高程值:

$ {{\textit{z}}}_{i, j}={\omega }_{1}\cdot{{\textit{z}}}_{i, j-1}+{\omega }_{2}\cdot{{\textit{z}}}_{i, j}+{\omega }_{3}\cdot{{\textit{z}}}_{i, j+1} $

(7)

其中, $ {{\textit{z}}_{i, j - 1}} $ , $ {{\textit{z}}_{i, j}} $ , $ {{\textit{z}}_{i, j + 1}} $ 分别代表横断面 $ {T_i} $ 内相邻3点的高程值, $ {\omega _1} $ , $ {\omega _2} $ , $ {\omega _3} $ 分别代表各点的权重, 其中 $ {\omega _1} = {\omega _3} = $ 0.2420, $ {\omega _2} = $ 0.3989.

3 路面高程点云的法向量距离描述

王晓辉等在文献[11]中首次提出法向量距离概念. 法向量距离是指采样点到其局部二次曲面的切平面的法向距离, 此算子可以用来描述采样点所在局部邻域曲率的大小. 采样点所在局部邻域的曲率越大, 其法向量距离越大; 采样点所在位置的曲率越小, 其法向量距离越小.

路面坑槽边缘和坑槽底部的曲率值较大, 表现为尖锐特征, 其法向量距离较大; 平坦路面曲率值较小, 表现为平缓特征, 其法向量距离就越小. 通过法向量距离对路面进行描述, 设置合适的法向量距离阈值便可以对坑槽边缘等尖锐特征部位进行提取.

法向量距离的计算依赖法向量的精确估计. 法向量估计一般采用主成分分析法(principal components analysis, PCA)^[12], 由于其在估计法向量时采用邻域范围大小是固定的, 导致其在尖锐特征处的法向量过于平滑. 宣伟等^[13]提出自适应最优邻域的PCA点云法向量估计方法, 该方法在计算尖锐特征的点云法向量具有较高的估计精度. 本文选择该方法估计路面点云中每个采样点的法向量. 由于路面点云的横向、纵向采样间距不一致 , 本文选择k-d树^[14]构建路面点云的拓扑关系, 以提高构建邻域的速度.

3.1 法向量计算

法向量的计算包括两步: 第1步介绍PCA方法计算法向量, 第2步为PCA方法的最优邻域范围选择.

给定路面点云数据集合, 集合中任意采样点的k邻域表示为 $ {N_k}({p_i}) $ . 求取采样点 $ {p_i} $ 的法向量可通过构建其局部邻域协方差矩阵 $ C $ 并进行特征值分解实现; 构建点云采样点 $ {p_i} $ 的协方差矩阵如式(8)所示:

$ C = {\left[ {\begin{array}{*{20}{c}} {{p_1} - \bar p} \\ \vdots \\ {{p_k} - \bar p} \end{array}} \right]^{\text{T}}}\left[ {\begin{array}{*{20}{c}} {{p_1} - \bar p} \\ \vdots \\ {{p_k} - \bar p} \end{array}} \right],\overline{p}=\dfrac{1}{k}\displaystyle\sum _{{p}_{j}\in {N}_{k}\left({p}_{i}\right)}{p}_{j} $

(8)

其中, 矩阵 $ C $ 表示了点集 $ {N_k}({p_i}) $ 的点的分布情况, 即邻域点与质心点 $ p $ 的偏离程度, $ {p_j} $ 为 $ k $ 邻域点集中的点, $ \bar p $ 为采样点及其 $ k $ 邻域所构成集合的质心.

对称半正定矩阵 $ C $ 有半3个非负实数特征值, 记为 $ {\lambda _1} $ , $ {\lambda _2} $ , $ {\lambda _3} $ ; 假设他们的大小关系为 $ {\lambda _1} \geqslant {\lambda _2} \geqslant {\lambda _3} \geqslant 0 $ , 其对应特征向量分别为 $ {v_1} $ , $ {v_2} $ , $ {v_3} $ .

采用矩阵 $ C $ 的特征值的维度特性构建点云局部邻域维度特征模型如式(9)所示, 建立局部邻域熵函数如式(10)所示:

$ \left\{ {\begin{split}& {L_\lambda } = \frac{{\sqrt {{\lambda _1}} - \sqrt {{\lambda _2}} }}{{\sqrt {{\lambda _1}} }}\\ & {P_\lambda } = \frac{{\sqrt {{\lambda _2}} - \sqrt {{\lambda _3}} }}{{\sqrt {{\lambda _1}} }} \\ &{S_\lambda } = \frac{{\sqrt {{\lambda _3}} }}{{\sqrt {{\lambda _1}} }} \hfill \end{split} } \right.$

(9)

其中, 局部邻域的维度特征 $ {L_\lambda } $ 、 $ {P_\lambda } $ 和 $ {S_\lambda } $ 分别表示局部邻域为一维线型的、二维平面的以及三维曲面的特征.

$ {E_\eta } = - {\eta _1}\ln \left( {{\eta _1}} \right) - {\eta _2}\ln \left( {{\eta _2}} \right) - {\eta _3}\ln \left( {{\eta _3}} \right) $

(10)

其中, ${\eta _i} = \dfrac{{{\lambda _i}}}{{\displaystyle\sum {\lambda _i}}}$ , $ {\lambda _i} $ 为式(8)中得到路面点云数据采样点局部邻域协方差矩阵的特征值.

利用PCA方法计算法向量时其最优邻域范围的确定方法如下:

(1) 设置邻域的区间 $ [{k_{\min }}, {k_{\max }}] $ , 设置邻域递增步长为 $ d $ , 初始化邻域大小为 $ k = {k_{\min }} $ ;

(2) 利用式(8)方法计算采样点的 $ {p_i} $ 的局部协方差的特征向量与特征值, 计算对应的局部邻域维度特征的熵函数并保存;

(3) 更新邻域大小为 $ k = k + d $ ; 直至 $ k > {k_{\max }} $ ;

(4) 选择局部邻域维度特征的熵函数最小时对应的 $ k $ 值即为最优 $ k $ 邻域.

选择如上方法得到最优 $ k $ 邻域, 并通过式(8)求出最小特征值 $ {\lambda _3} $ 对应的特征向量 $ {v_3} $ 即可作为采样点 $ {p_i} $ 的法向量 $ {n_i} $ , 记为 $ {n_i} = {v_3} $ .

3.2 法向量距离计算及阈值选择

定义路面点云采样点 $ {p_i} $ 的邻域点集对应的待重建曲面为 $ S $ , 采用局部邻域拟合平面近似作为采样点在曲面 $ S $ 上投影点处的切平面, 则采样点 $ {p_i} $ 到曲面 $ S $ 上切平面的间距为:

$ {d}_{i}=\left|({p}_{j}-{p}_{i})\cdot{n}_{i}\right| , {p_j} \in {N_k}({p_i}) $

(11)

其中, $ {d_i} $ 为采样点 $ {p_i} $ 到邻域对应曲面的切平面的距离的绝对值, 即法向量距离; $ {p_j} $ 为其邻域内距 $ {p_i} $ 最近的点.

分析原始点云数据, 在一个道路横断面中, 路面正常部分点的数量远大于坑槽部分点的个数, 以该横断面的法向量距离均值为基准, 取经验值作为法向量距离阈值; 选择法向量距离大于该横断面法向量距离阈值的采样点, 即可对路面坑槽部位进行提取.

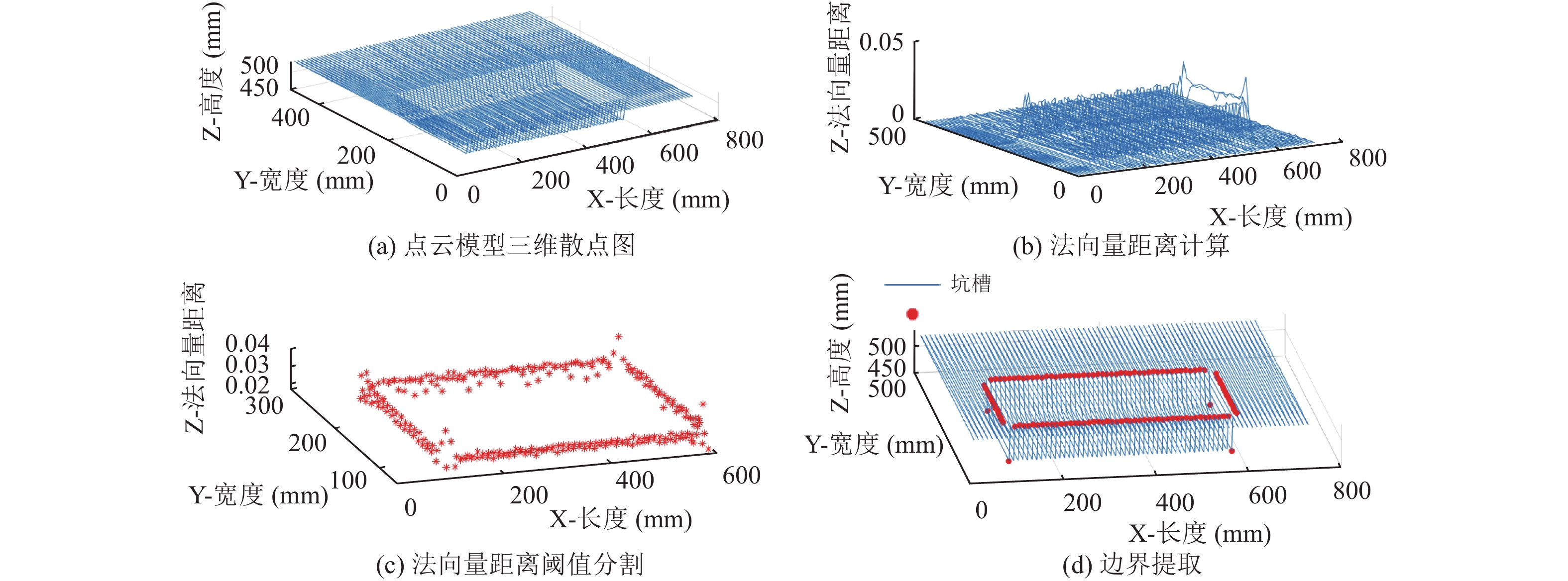
路面点云的法向量距离描述如图4所示, 图中X轴代表道路纵断面方向, Y轴为道路横断面方向. 图4(a)为坑槽的原始点云数据, 其中矩形坑槽的4个角的曲率最大. 意味着其法向量距离最大; 矩形的边缘的曲率比其邻域内平缓部分大, 意味着其法向量距离较大. 图4(b)为采用法向量距离对路面点云采样点的曲率表征的结果, 对于该坑槽及其邻域的法向量距离大小关系: 坑槽4个角的法向量距离大于坑槽边界法向量距离大于其他平缓部分的法向量距离; 对图4(b)中的每个道路横断面, 选用该横断面法向量距离平均值的1.5倍作为阈值, 用该阈值分割坑槽边界得到结果如图4(c)所示.

4 路面坑槽边界点提取及面积计算

通过法向量距离阈值提取的路面坑槽包括路面坑槽的边界点及其内部点; 将同一坑槽的点聚为整体, 提取坑槽边界点形成一个完整的坑槽轮廓, 同时进行去噪优化处理, 拟合坑槽轮廓并对其尺寸、面积信息进行提取.

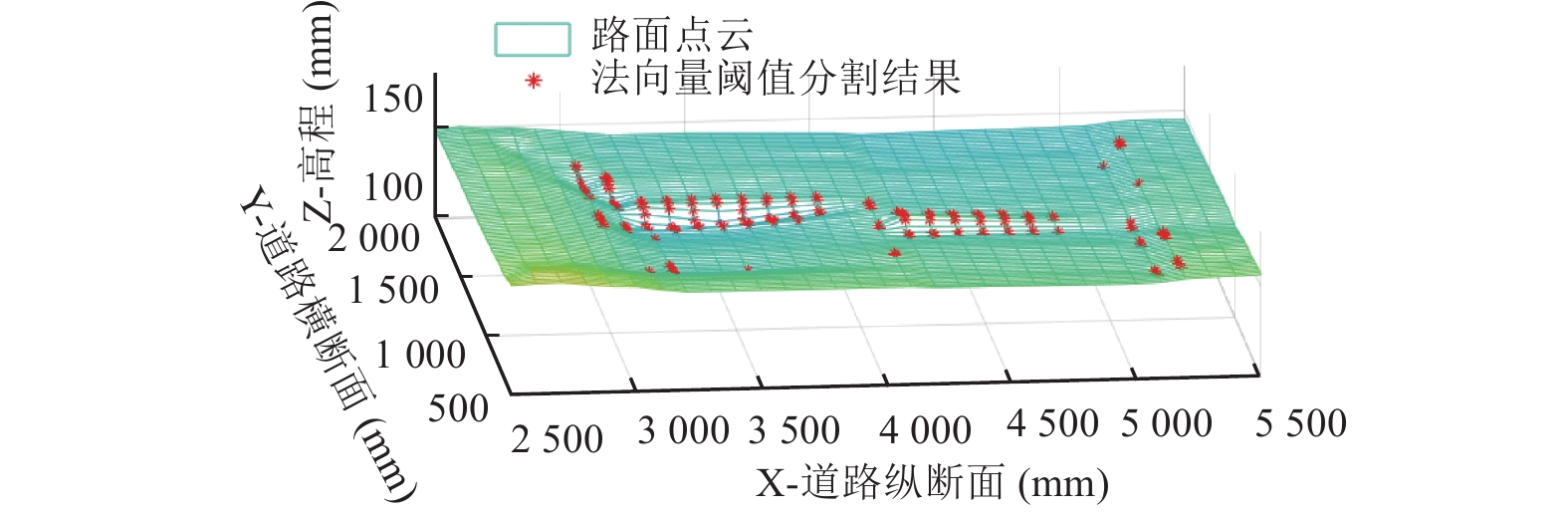
4.1 坑槽聚类及边界提取

通过上述操作可得到坑槽点云及少量的噪声点, 路面坑槽提取结果如图5所示. 图5为真实路面点云数据的网格模型, 其中有两个坑槽及少量噪点, 图中*为利用法向量距离阈值提取的路面坑槽点; 提取得到的路面坑槽点中包括部分孤立点(如X轴上[5000, 5500]所示), 其为受噪声影响部分. 将坑槽点云投影到xoy平面, 采用Mean-Shift聚类算法^[15]对坑槽点云进行聚类, 聚类得到点集数量即为路面坑槽个数, 聚类结果为多个点集, 每个点集代表路面上一个的坑槽; 噪点经过聚类之后, 表现为点个数较小的集合, 通过删除聚类结果中点个数过小的集合, 即可完成对噪点的去除.

本文通过法向量距离判断坑槽, 得到路面坑槽的点集, 其中包括坑槽边界点与其内部尖锐点; 计算路面坑槽轮廓与面积的前提是得到坑槽边界点.

为了提取坑槽边界, 将坑槽点的集合投影到xoy平面, 然后坑槽边界点提取可转换为平面点集的边界点提取问题; 选择Alpha-Shapes算法^{[16, 17]}提取从坑槽点集中提取其边界点的集合. 提取方法如下:

(1) 给定规模为 $ n $ 坑槽点集合 ${\textit S_1}$ , 通过集合中的 $ n $ 个点可组成 ${\rm C}_n^2$ 条线段; 过 ${\textit S_1}$ 中任意两点 $ {p_1} $ , $ {p_2} $ 共有 ${\rm C}_n^2$ 种组合;

(2) 过 $ {p_1} $ , $ {p_2} $ 绘制半径为r的圆, 如果圆内没有其他点, 则 $ {p_1} $ 、 $ {p_2} $ 为为边界点, 其连线 $ {p_1}{p_2} $ 为边界线段;

(3) 遍历集合中的 ${\rm C}_n^2$ 种组合直到终止, 否则执行步骤(2).

4.2 坑槽边界优化及面积计算

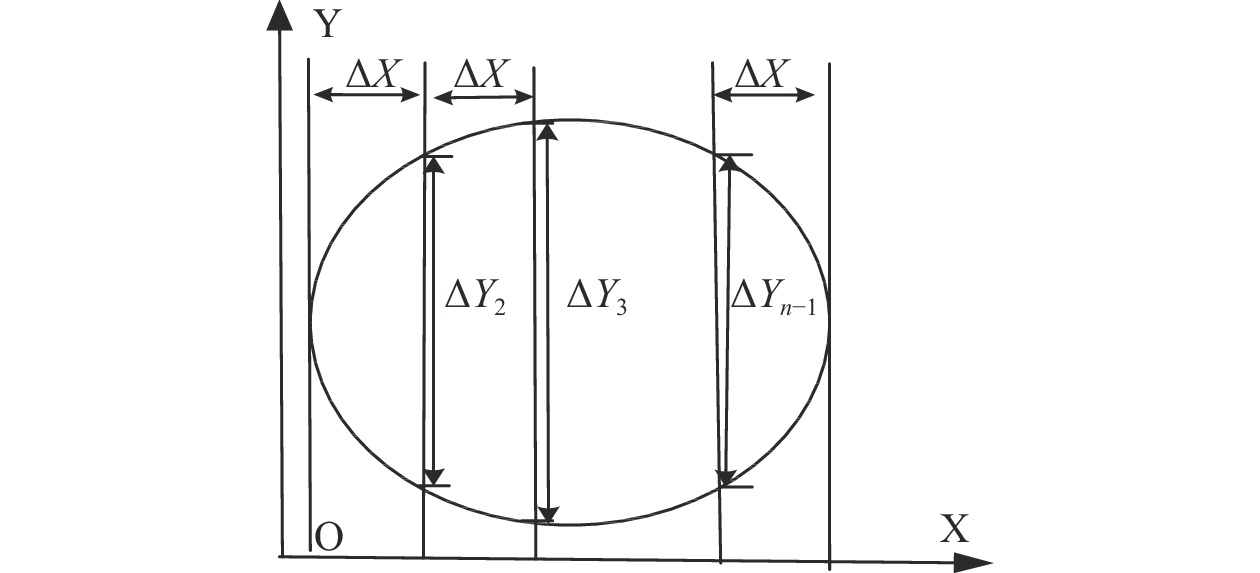
为了计算得到的边界点使边界线平滑, 更加接近坑槽实际形状, 并且方便后续的面积计算, 本文参考文献[8]中方法拟合坑槽边界. 对于第4.1节中得到的坑槽点集, 基于欧式距离将相邻的坑槽边界点建立一个元胞数组, 对于每个元胞数组, 采用三次样条插值进行边界拟合处理, 据此得到坑槽边界点集B; 参考文献[5]的积分思想, 将坑槽边界集合B映射到xoy平面, 则闭合曲线围成的面积即为坑槽面积, 如图6所示. 将该坑槽区域沿x轴方向分为n个宽度相同的梯形, 则积分计算其面积为:

$ S=\sum _{i=1}^{n}\text{Δ}{S}_{i}=\frac{1}{2}\sum _{i=1}^{n}\text{Δ}X\left({Y}_{i}+{Y}_{i-1}\right) $

(12)

坑槽深度的计算采用文献[5]中的等高线法思想并据此设计方法: 给定坑槽邻域内正常路面的点云数据, 计算坑槽内部点与坑槽邻域内正常路面点的高程差, 并选择其最大值作为坑槽深度. 长度、宽度的计算根据《沥青路面坑槽修补施工工艺》中“圆坑方补, 斜坑方补”原则, 计算坑槽边界点在x轴、y轴投影的极差作为长度、宽度.

5 实验结果与分析 5.1 实验设计与数据分析

为了验证本文算法在提取路面坑槽尺寸信息的准确性, 本文进行了两组实验: 第1组实验利用标准模型在室内环境下模拟路面坑槽, 采集数据作为研究对象并利用本文方法验证; 第2组实验利用长安大学激光检测车采集的路面真实坑槽的点云数据作为研究对象, 并采用本文方法进行验证.

第1组实验的模型包括两种: 长方体模型及圆柱体模型, 一共3组. 该模型的点云数据横纵采样间隔均为1 cm, 采用测距精度为1 mm的激光测距仪器采集其高程信息; 第2组实验中该检测车以低速通过校内某一路段并采集该路段的路面高程点云数据; 每次对一个道路横断面高程数据进行采集, 横断面内采样间隔(横向采样间距) 1 cm, 横断面间的采样间隔(纵向采样间距) 1 cm.

5.2 实验结果分析

本文实验进行在CPU为 i7-7700K@4.2 GHz, 内存为32 GB, 显卡为1080Ti的PC机上, 通过Python配合Open3D, VS2017配合Pcl 1.9.1 实现点云格式的转换, 通过Matlab配合vlfeat-0.9.21点云工具箱实现了本文算法.

以坑槽尺寸及面积为指标验证提取质量, 对于规则形状的坑槽模型, 本文提取结果与其标准尺寸的对比结果见表1中序号为1–3的坑槽; 对于真实路面坑槽, 本文提取结果与人工测量结果见表1中序号为4–9的坑槽.

对于序号1–3的规则坑槽模型, 本文提取结果在深度上的绝对误差为0.1–0.2 cm, 相对误差为1.1%–4.0%, 相对误差平均值为2.7%; 对于序号为6–9的路面真实坑槽, 本文提取结果在深度上的绝对误差为0.1–0.2 cm. 相对误差4.0%–6.7%, 相对误差平均值为4.7%. 对于规则坑槽模型及路面真实坑槽的深度, 本文方法提取结果较为准确.

本文方法对规则坑槽模型及路面真实坑槽均可准确提取其面积. 对于室内坑槽模型, 本文方法提取该坑槽面积的相对误差小于7%, 对于真实坑槽模型, 相对误差小于6%. JC510-2018《公路技术状况评定标准》中定义面积大于1 000 cm²的坑槽为重度坑槽, 小于等于1 000 cm²的坑槽为轻度坑槽. 本文对轻度坑槽的面积提取的相对误差的均值小于6%, 对重度坑槽的提取结果的相对误差的均值小于3%. 本文方法对重度坑槽具有较好的提取结果.

本文所使用路面点云数据的横向、纵向采样间距一致, 均为1 cm, 故将对槽长度、宽度一起分析. 对于坑槽模型, 本文对长度、宽度提取结果的绝对误差为0.5–1 cm, 相对误差小于等于5%, 相对误差的平均值为3.28%; 对于路面真实坑槽, 本文对其长度、宽度提取结果的绝对误差为1.0–2.0 cm, 相对误差小于6.5%, 相对误差的平均值为3.65%.

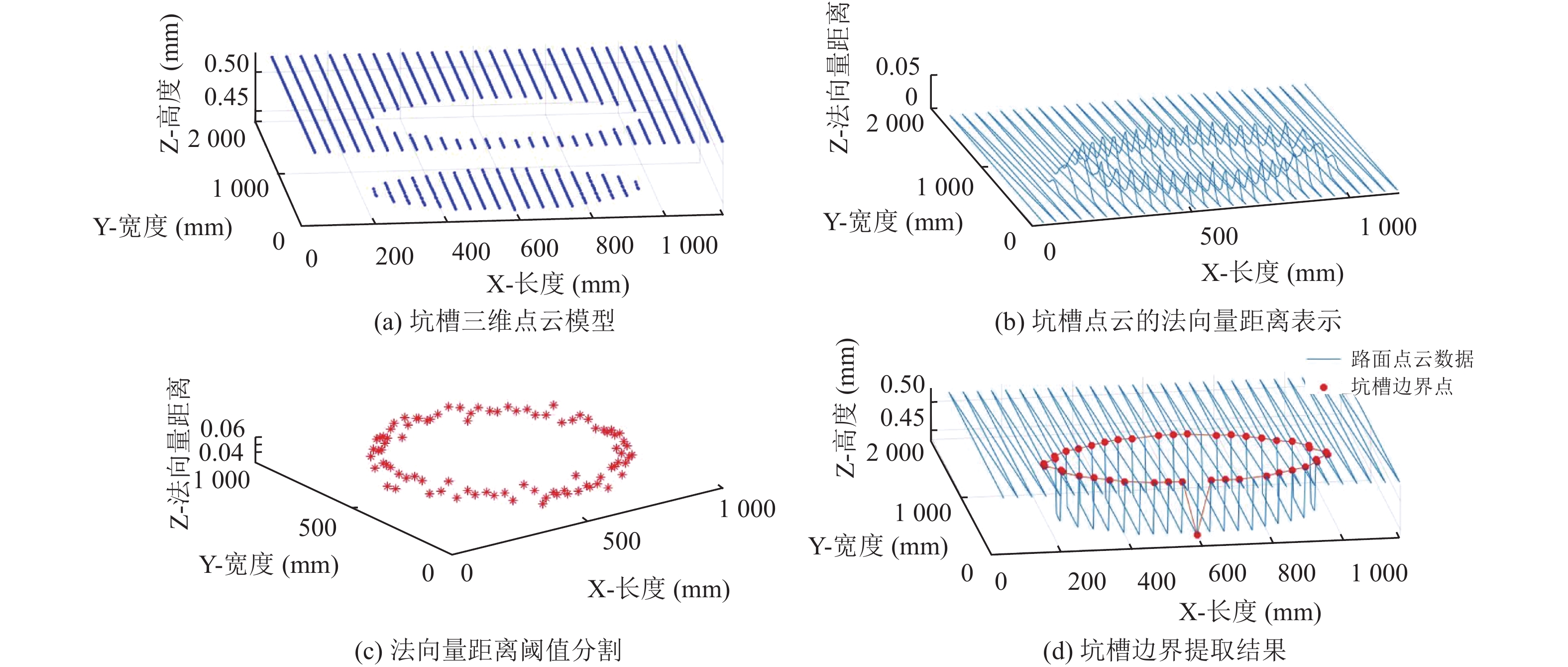
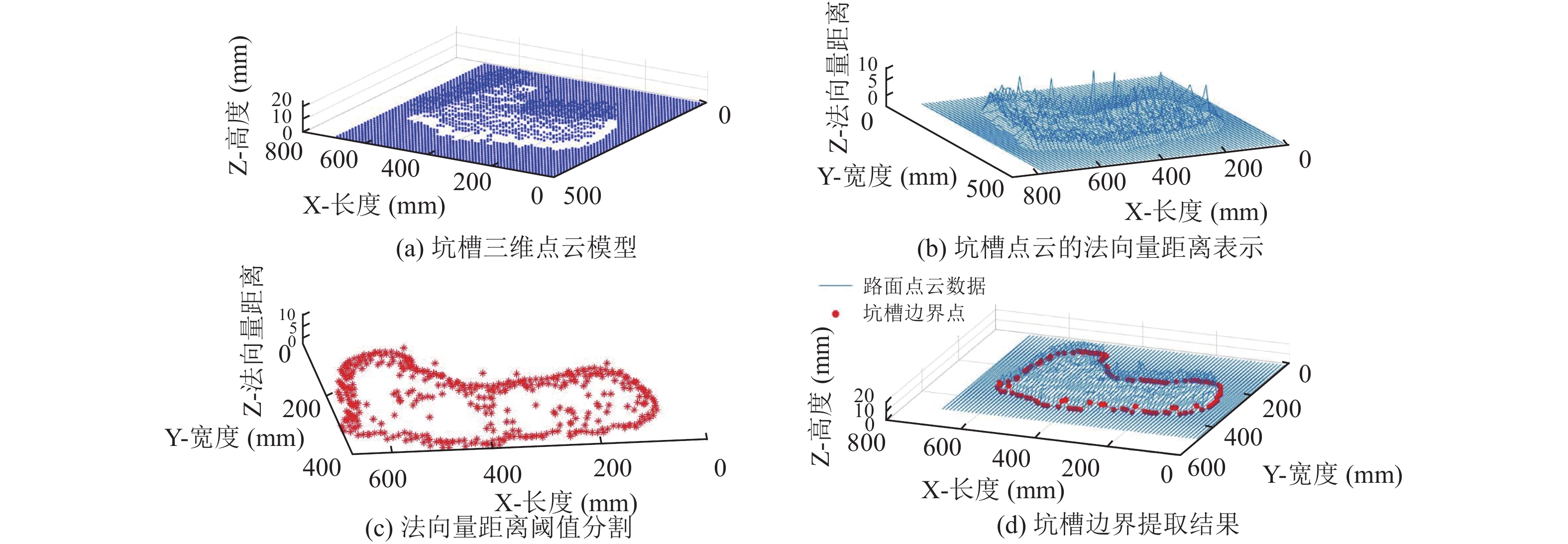
对于表1中序号1, 3的规则形状的坑槽模型与序号8的真实路面坑槽, 采用本文方法的提取过程分别如图7、图8、图9所示; 图7(a)、图8(a)、图9(a)为坑槽的原始高程点云模型; 图7(b)、图8(b)、图9(b)为对坑槽点云数据中的每个采样点采用法向量距离进行描述的结果; 图7(c)、图8(c)、图9(c)为以法向量距离阈值为限制提取的高曲率部分, 其中法向量距离阈值均选择采样点所在道路横断面法向量距离平均值的1.5倍; 图7(d)、图8(d)、图9(d)中圆点为采用Alpha-Shapes算法提取的坑槽边界点.

图7、图8分别为圆柱体模型、长方体模型, 其边界点提取结果分别如如图7(d)、图8(d)所示, 本文方法提取得到的坑槽边界点与坑槽原始点云数据中的边界点几乎完全重合; 图9为对真实路面坑槽的提取过程. 图9(c)中坑槽轮廓内存在分布不均匀的散点, 该散点为坑槽内部的高曲率部分. 与图9(c)对比, 图7(c)与图8(c)只提取到了坑槽边界, 没有提取到坑槽内部点, 这是因为图7对应的是圆柱体模型、图8对应的是长方体模型, 该模型表面平滑, 表面部分的曲率较小, 其法向量距离也就较小, 在以法向量距离阈值为约束后, 该部分点云数据就被筛除.

对于路面真实坑槽中的规则坑槽以及不规则坑槽, 其轮廓提取结果如图10与图11所示.

图10(a)为坑槽图像, 其边界线为凸多变形; 图11(a)为坑槽图像, 其边界线为凹凸状多边形. 本文方法提取坑槽轮廓如图10(b)与图11(b)所示, 本文方法提取的坑槽轮廓与坑槽图像中的轮廓具有较高的相似性, 较好地体现了坑槽的轮廓形状, 对于坑槽轮廓的部分细节亦可以准确提取.

分析上述结果, 对于规则坑槽模型、路面真实坑槽都能准确提取坑槽点以及坑槽边界点; 且对于规则形状及不规则形状的路面坑槽提取, 本文方法具有较好的适应性.

6 结论与展望

本文以路面高程点云为研究对象, 针对路面病害中的坑槽, 充分挖掘路面坑槽点云边界点的三维特征, 提出了一种基于法向量距离的路面坑槽提取方法. 该方法以自适邻域的PCA方法估计路面点云采样点的法向量; 通过计算采样点到其局部二次曲面的切平面的法向距离(法向量距离)对路面曲率进行描述; 通过阈值分割自动提取坑槽: 以Alpha-Shapes算法实现了坑槽边界点的准确提取, 解决了不同类型坑槽边界的准确提取问题. 实验结果表明, 本文方法对于规则坑槽模型、路面真实坑槽的尺寸、面积信息的提取结果与人工测量结果具有较高的一致性. 对于较小坑槽或模型的提取, 易受点云采样间隔的影响; 考虑到真实环境下数据采集的问题, 搭载激光检测设备的车辆高速行驶在路上, 减小沿着车辆行驶方向的采样间隔的难度很大, 且经点云信息提取的坑槽轮廓与路面坑槽的真实轮廓存在一定范围内的差别, 后期将从坑槽图像信息与点云信息融合的角度出发作进一步研究.