2. 安徽省高性能计算重点实验室, 合肥 230036
2. Key Laboratory of High Performance Computing of Anhui Province, Hefei 230036, China
随着实时计算需求的迅速增长, 对于分布式流计算框架的要求越来越高[1], 如何提高框架的效率已经成为学术界和工业界的研究热点. 在流计算框架的应用场景中, 反压问题[2]是已知的难点之一, 该问题轻则导致数据丢失, 重则导致系统崩溃, 亟需好的解决方法.
目前, 常见的流计算框架(如Flink[3]、Spark Streaming[4]和Storm[5])都有应对反压问题的解决机制. Storm框架默认的反压机制是在输入的Tuple无法被及时处理时直接丢掉后续的Tuple, 以此触发限流控制, 并向上传递以限制数据源的发送速率, 该机制属于被动响应, 在处理突发性大数据流时, 压力最终集中在数据源处, 数据源的发送速率降低使得系统延迟增加. Flink框架在旧版本的TCP滑动窗口机制上提出了Credit机制, 该机制解决了多个子任务共享TCP连接时由于单一子任务产生反压, 阻塞整条TCP连接的问题, 但该机制在单任务出现反压问题时仍需将压力向上游传递, 限制上游速率, 增加了系统的延迟. Spark Streaming是基于微批次的流计算框架, 框架内设置了rate参数来控制数据批次的发送速率, 通过下游节点向上游反馈rate值, 上游根据rate值动态调节数据的发送速率, 避免产生反压问题, 但Spark Streaming由于其微批次的设计, 在实时性上差于Storm和Flink框架, 同样在遇到突发性大数据流时, 也是通过限制数据源的发送速率将压力集中在数据源, 严重影响任务处理的实时性.
上述这些机制在处理反压问题时, 都是快速地向上游和数据源传递减速信息, 将压力向上游传递, 限制上游数据的发送速率, 这也导致了系统的吞吐量降低、延迟增加. 通过研究, 大部分反压问题是由系统内节点处理能力差异、链路带宽差异和数据分布不均所导致, 压力往往集中在局部区域, 系统内其他区域的负载压力很小, 上述机制没有很好地利用到这些轻载区域. 本文提出了一种基于数据迁移策略的反压解决方法, 目的是通过其他轻载节点分散压力来解决局部反压问题, 在维持数据源的高发送速率前提下降低系统的延迟.
1 相关工作 1.1 调度策略研究现状调度策略是分布式系统扮演着重要的角色, 系统的性能很大程度取决于调度策略的合理性. 分布式系统调度算法一直是分布式系统研究领域的一个热点问题[6].
Lopes等人[7]从3个维度出发, 并进一步对每个维度进行细分, 对分布式系统中的调度策略分类讨论和描述. Gautam等人[8]针对Hadoop分布式系统, 从多个角度(任务优先级、资源类型、网络异构性等)对调度策略分类, 详细地分析了各策略的优势和劣势. Hammoud等人[9]主要考虑数据局部性的问题, 通过研究网络对系统和任务的影响, 对MapReduce中的Reduce任务调度进行优化, 使得数据优先在本地处理, 提高了系统性能. Arslan等人[10]主要考虑文件读写代价的问题, 通过研究CPU负载对任务的影响, 同样对MapReduce中Reduce任务进行了优化. 刘梦青等人[11]基于分布式流计算系统Storm将动态的计算资源看作信息素, 将资源调度问题转化为最佳路径寻找算法并通过蚁群算法求解, 效果优于Storm的默认调度策略. 刘粟等人[12]同样针对 Storm 系统, 主要考虑任务调度中的流计算任务拓扑图, 通过拓扑中组件并行度进行分配排序, 并将上下游直接连接的子任务部署到相同的计算节点以减少网络传输次数, 提高系统的处理性能.
1.2 反压问题研究现状在分布式流计算框架中, 流计算过程被抽象成一个有向图, 有向图中的节点(部分框架称这些节点为算子)代表对数据的操作, 有向边代表数据流方向[2]. 在数据流的处理过程中, 当上游数据流的输入速率比向下游发送数据流速率快时, 某个算子或多个算子所处的节点将无法及时地将数据发送出去, 此时数据积压在缓冲区并逐渐耗尽缓冲区资源, 该数据层面上的压力将会逐层向数据源方向传递, 这种与数据流方向相反的数据压力称为反压(backpressure, BP).
反压问题存在于许多常见的场景, 如节假日抢购火车票、购物网站的促销活动、热点新闻的发布等, 反压所带来的问题是非常严重的, 其耗尽缓冲区资源, 轻则丢失数据, 重则系统崩溃. 反压问题的原因可分为3大类: 第1种是流量峰值, 数据量在短暂的时间内达到峰值, 此时数据源流入的数据量高于框架承受能力造成系统级反压; 第2种是数据分布不均匀, 由于输入数据的分布不均匀, 经由Map操作和Shuffle操作, 导致下游不同算子计算任务负载不均衡, 此时将造成局部反压; 第3种是计算的拓扑结构, 当某个算子是分支结构或者出现性能问题, 该算子不能及时地向下游输出数据流, 流入数据量保持不变, 导致数据堆积在算子的缓冲区, 此时将造成该算子的反压.
目前, 针对反压问题的解决方法并不丰富, 都依托了具体的框架中进行部署测试. 针对Strom框架, 熊安萍等人[2]提出一种能够灵活调节Topology中各环节数据负载的反压机制, 该机制采用可变队列, 并根据当前Tuple负载动态地调整队列大小, 该反压机制可以避免反压过程中的数据流震荡、提高性能和稳定性. 针对Flink框架, Hanif等人[13]提出了一种反压机制, 该机制使用阈值检查反压位置并通过动态调度缓解反压. 针对 Spark框架, Chen等人[14]提出了Governor控制机制, 该机制增加了将检查点成本考虑到反压机制中的控制器, 从而减少了由于检查点的干扰而造成的吞吐量损失.
本文旨在解决数据分布不均匀导致的局部反压问题, 分布式系统目前大多采用MapReduce方法, 在这个过程中, 相同的数据将交由同一算子节点进行处理, 当输入数据分布不均匀时, 下游的处理节点将要处理的数据量也是有很大差异的. 由此, 整个系统处理任务的耗时取决于处理时间最长的支路, 而其他支路将会处在资源空闲的状态, 这样, 整个系统的资源利用率并没有达到理想的状态. 为了让系统达到理想的状态, 可以采取静态分配的方法, 通过预处理得到不同节点的计算能力、缓冲能力、网络带宽以及数据的分布规律带入模型, 得到不同节点的数据处理能力, 手动将占比大的数据分配给处理能力较强的节点, 这样能更大限度地发挥系统的利用率. 但是静态方法依然存在弊端, 比如无法获知下游节点的处理能力和无法获知数据的分布情况等, 为了弥补静态方法的不足, 本文提出了一种基于数据迁移的方法, 动态地解决了局部反压问题.
2 方法设计本文的算法设计如图1所示, 首先确定系统是否存在反压节点, 然后锁定反压节点所在的网络拓扑支路, 通过数据迁移策略算法找到轻载支路, 并将重载支路要处理的数据迁移到该轻载支路处理, 分散重载支路的压力, 在反压问题解决后, 将系统恢复成原有的调度策略继续运行.

|
图 1 数据迁移调度方法概述 |
本文算法的关注点有二: 第一点是如何判断反压节点和锁定重载支路之后如何对其他支路进行打分并排序得到压力最小的轻载支路, 第二点是如何将重载支路的数据迁移轻载支路, 同时数据迁移后, 要保证整个任务的计算结果准确. 算法的具体步骤如算法1.
算法1. 数据迁移策略算法
步骤1. 确定分布式流计算任务, 定义此次任务的网络拓扑信息和每个节点的资源信息, 分配每个节点的任务, 生成模拟数据, 设定压力阈值, 运行任务.
步骤2.
步骤3.
步骤4.
步骤5. 每间隔一段时间检测反压列表中各节点的压力情况, 如存在节点压力低于预设恢复阈值, 则停止数据迁移策略, 并恢复默认的数据调度策略; 如重载支路未缓解, 数据迁移策略继续运行, 并返回步骤2, 继续监测系统.
步骤6. 恢复默认策略, 返回步骤2, 继续监测系统.
2.1 反压节点的识别和支路的打分机制反压节点的识别参考了Cicotti等人[15]的研究工作, 节点是否能处理施加任务或数据的4个指标是: CPU, 内存, I/O和网络带宽. 相比于王成章等人[16]的工作, 本文方法比较全面考虑了影响反压问题的可能因素(内存、CPU性能、I/O速度和网络带宽), 并用简洁的公式进行量化. 由于本实验是在模拟环境NS-3网络仿真器下运行, 本实验使用定长异步队列模拟了CPU和内存的效果, 通过对每个节点中队列的使用率以及输入输出的速率差异时别节点的压力情况. 当队列的使用率超过80%, 且该节点上游数据的输入速率高于向下游发送的输出速率时, 将该节点定义为反压节点, 并将该节点所在支路定义为重载支路.
对各支路进行打分的目的是快速计算出各个支路的资源使用情况, 再据此做出调度策略. 因此本实验考虑3个如下指标:
| $ Q_{{\rm{Branch}}[i]}=\max _{{\rm{N o d e}}[j] \in {\rm{B r a n c h}}[i]} Q_{{\rm{N o d e}}[j]} $ | (1) |
支路I/O速率差异Δ的计算方法如下:
| $ \varDelta_{ {{\rm{Branch}} }[i]}=\frac{{\textit{Sum}}_{\text {支路输入 }}-{\textit{Sum}}_{\text {支路输出 }}}{ { Time }} $ | (2) |
支路网络带宽的计算方法如下:
| $ B_{{{\rm{Branch}} }[i]}=\min _{{\rm{E d g e}}[j] \in {\rm{B r a n c h}}[i]} Q_{{\rm{N o d e}}[j]}$ | (3) |
这3个指标可以综合地代表CPU性能、内存使用率、I/O性能和网络带宽4种指标的效果. 式(1)是将该支路各节点的队列使用率的最大值作为支路队列使用率的代表; 式(2)是通过支路输入数据总量减去支路输出数据总量再除以间隔时间作为支路I/O速率差异的代表; 式(3)则是将该支路各连接的网络带宽最小值作为支路网络带宽的代表, 主要关注链路中的瓶颈. 通过这3个指标即可得到支路的压力大小P(pressure):
| $P_{{{\rm{Branch}} }[i]}=\frac{\alpha \times Q_{{\rm{Branch}}[i]}+(1-\alpha) \times \Delta_{ {{\rm{Branch}} }[i]}}{\left(B_{{\rm{Branch} }[i]}\right)^{\beta}}$ | (4) |
其中,
式(4)中
数据迁移策略依赖于分布式系统的MapReduce框架, 基于MapReduce框架的分布式系统在处理任务时, 会将一个任务拆分成多个关联的子任务进行处理, 并抽象出有向图的拓扑结构. 如图2所示, 通过定义Map、Shufflue和Reduce等操作, 将一个WordCount任务拆分, 子任务通过并行处理改善效率. 在拓扑图中, 通过子任务划分层次关系, 同层处理相同的子任务, 上游子任务的输出传递给下游子任务作为输入, 最终完成整个任务. 在实际计算机节点中, 单个子任务可能占据一个计算机节点, 也可能多个子任务占据一个计算机节点, 并通过系统的进程和线程机制区分子任务后计算.
在实际应用中, 由于分布式系统中节点性能差异和输入数据分布差异会导致部分节点的数据负载过重, 数据迁移策略是将重载节点要处理的数据发送给轻载节点, 以此缓解重载节点的负载压力, 同时在迁移数据过程中要考虑子任务的类型以保证迁移后计算结果的正确性. 相比于文献[17-20]提出的方法, 本文方法主要是解决反压问题, 一般情况下不改变系统中的节点并行度和拓扑结构, 在我们的设计和实现中迁移操作的粒度更细, 开销更小. 已有的其他相关工作主要是针对整个系统进行负载均衡, 需要改变节点并行度甚至系统拓扑结构, 因此两类方法有不一样的前提要求.

|
图 2 WordCount任务拓扑图 |
在不同类型的操作中, 通常Reduce操作是计算子任务中影响最大的操作, 也是计算耗时最长的操作. 数据迁移策略的针对点是Reduce操作的类型, Reduce操作类型是根据任务定义的, 如累积加和、取平均值、取极值、统计特定量、去重等. 不同的类型具有不同的特性, 其中结合律特性决定了其计算操作(如加法、减法、乘法、矩阵乘法等操作元)处理的次序是否影响最终结果, 交换律特性决定了其数据计算的次序是否影响最终结果. 对于数据迁移策略, 由于数据将会出现分段分节点处理, 算子和数据的计算次序都将会被打乱, 为了使计算结果准确无误, Reduce操作的类型通常需要同时满足结合律和交换律.
对于累积加和、取极值等同时满足结合律和交换律的计算方法, 无需特别处理, 直接应用迁移调度策略即可; 但是对于取平均值、统计特定量、去重等计算方法, 它们并不直接满足结合律和交换律, 此时需要记录额外信息使得计算结果准确无误. 以取平均值为例, 见式(5).
| $ { average }=\frac{\displaystyle\sum\nolimits_{i=1}^n a_{i}}{n} $ | (5) |
由于取平均值计算不满足结合律和交换律, 则有式(6), 其中,
| $ { average } \neq \dfrac{\frac{\displaystyle\sum\nolimits_{i=1}^{j} a_{i}}{j}+\dfrac{\displaystyle\sum\nolimits_{i=j}^{j^{\prime}} a_{i}}{j^{\prime}}+\cdots+\dfrac{\displaystyle\sum\nolimits_{i=j^{n}}^{n} a_{i}}{n-j^{\prime \prime}}}{n^{\prime}} $ | (6) |
通过记录额外信息, 则可以使得该计算方法仍然保证结果的准确无误. 在取平均值的过程中, 记录每个子任务的数据长度l, 在汇总数据的时候将所有的额外信息添加进来, 即可得到正确的结果, 以取平均值为例, 见式(7).
| $ { average }=\frac{\displaystyle\sum\nolimits_{i=1}^{ {\rm{sizeof} }\left( { {\rm{part}} }_{i}\right)} {ave} r_{ {\rm{part} }_{i}} \times l_{i}}{n} $ | (7) |
由此, 通过对不同计算方法的分析, 记录额外的数据信息, 如偏移量、长度等等, 通过在输出节点的额外处理, 即可使得不满足结合律和交换律的计算方法, 经过数据迁移策略的计算后仍然保证计算结果的准确性.
3 实验结果与分析 3.1 实验环境与配置本文实验为模拟仿真实验, 实验所用的环境是NS-3网络仿真器[21]. NS-3仿真器具有良好的体系结构, 易于搭建网络中各种实体模型, 同时其自带的Callback机制以及Tracing机制可以将网络行为清晰地展示出来, 便于使用者进行研究分析.
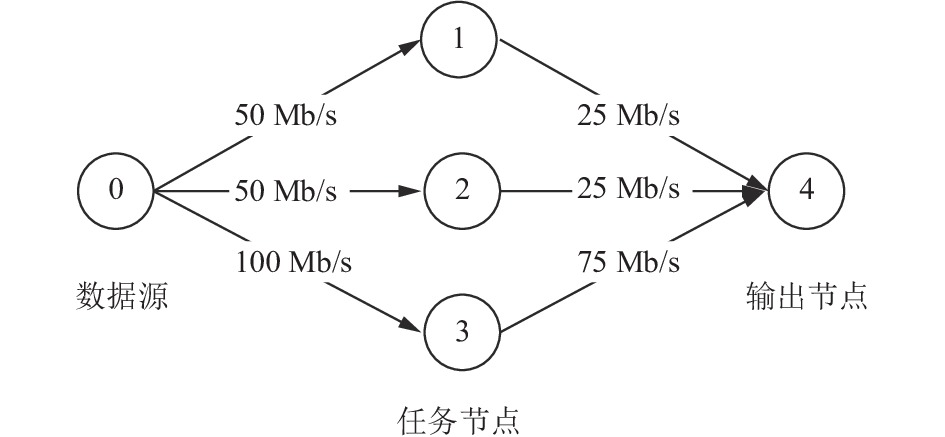
本文实验首先建立了网络拓扑, 如图3, 网络中共有5个节点, 6条信道, 不同信道的带宽和延迟都有所不同. 由于NS-3不支持CPU和内存的模拟, 本实验采用了异步定长队列作为二者的模拟.
|
图 3 模拟网络拓扑图 |
如图4所示, 每个节点都维护一个私有的队列, 网络中传输进来的数据先由生产者线程压入队列, 然后再由一个消费者线程取出队列头的元素进行处理并向下游发送. 当数据充满定长队列时, 节点向上游发送停止信号, 避免后续数据的丢失; 当队列占有量下降到50%再向上游反馈恢复信号.

|
图 4 网络节点结构图 |
在NS-3仿真平台上实现了Flink框架的Credit反压机制, 并以此作为实验参照. 如图5, 每隔一段时间, 下游的节点向上游节点反馈其定长队列所剩余的数据空间大小, 上游节点根据反馈回来的credit值判断是否继续传输数据.

|
图 5 Credit机制 |
实验采用流量统计作为测试用例, 流量统计与常见的词统计类似, 其中数据流是以数据包的形式向下游发出, 每个数据包大小为1 MB并拥有一个标识符用来指明它将被3个支路中哪一路进行处理, 数据源节点根据该标识符进行指定分发. 在常见的反压场景中, 输入数据通常具备两个特点: 突发性和不均匀性. 其中突发性是指在流量速率会突然地增加或减少, 不均匀性是指具有相同标识符的数据堆积不利于并行处理. 本实验的源数据通过控制发送速率来满足突发性, 通过控制数据包的分布来满足不均匀性. 以1 GB的流量总值为例, 图6展示源数据在处理时各节点负载分布情况, 其中每个区域展示了随时间变化各节点的负载变化情况. 从负载分布中可以看出, 节点接收的数据会在某段时间内突发性的增加和减少, 并且数据的分布不均导致了不同节点在相同时间段接收到的数据量差异很大, 这将使系统产生反压问题. 需要注意的是, 该负载分布模型是在不受限的网络拓扑中生成的, 是理想的不产生反压问题的情况下各节点的负载情况, 但实际上数据发送会在收到下游节点反馈的停止信号时停止, 直到接收到恢复信号再继续模拟生成, 负载也会据此变化.
最后本实验的测试实例共有4个, 流量总值分别是500 MB、1 GB、2 GB和5 GB. 实验结果以两个指标作为对比参考, 其一为延迟时间, 其二为完成通量占比. 延迟时间是整个任务从开始到结束的整体时间比较, 可以从整体上比较数据迁移策略的性能; 完成通量占比是当前处理的数据量占总数据量的比例, 它可以清晰地看出随着时间变化系统处理的性能差异以及吞吐量的变化趋势, 展示出反压问题出现时系统的反应速率.

|
图 6 各节点负载分布 |
3.2 实验结果与分析
实验首先对压力评分公式中的
表2展示了本文方法和Credit机制对在4个不同负载下的延迟时间对比. 当总体流量较小时, 整体处理时间较短, 数据迁移策略的启动和恢复都需要时间, 此时本文方法与Credit机制在延迟上相差不大; 当总体流量继续增大时, 本文方法的效果逐渐明显并产生了稳定影响, 平均能将延迟时间提高15%左右.
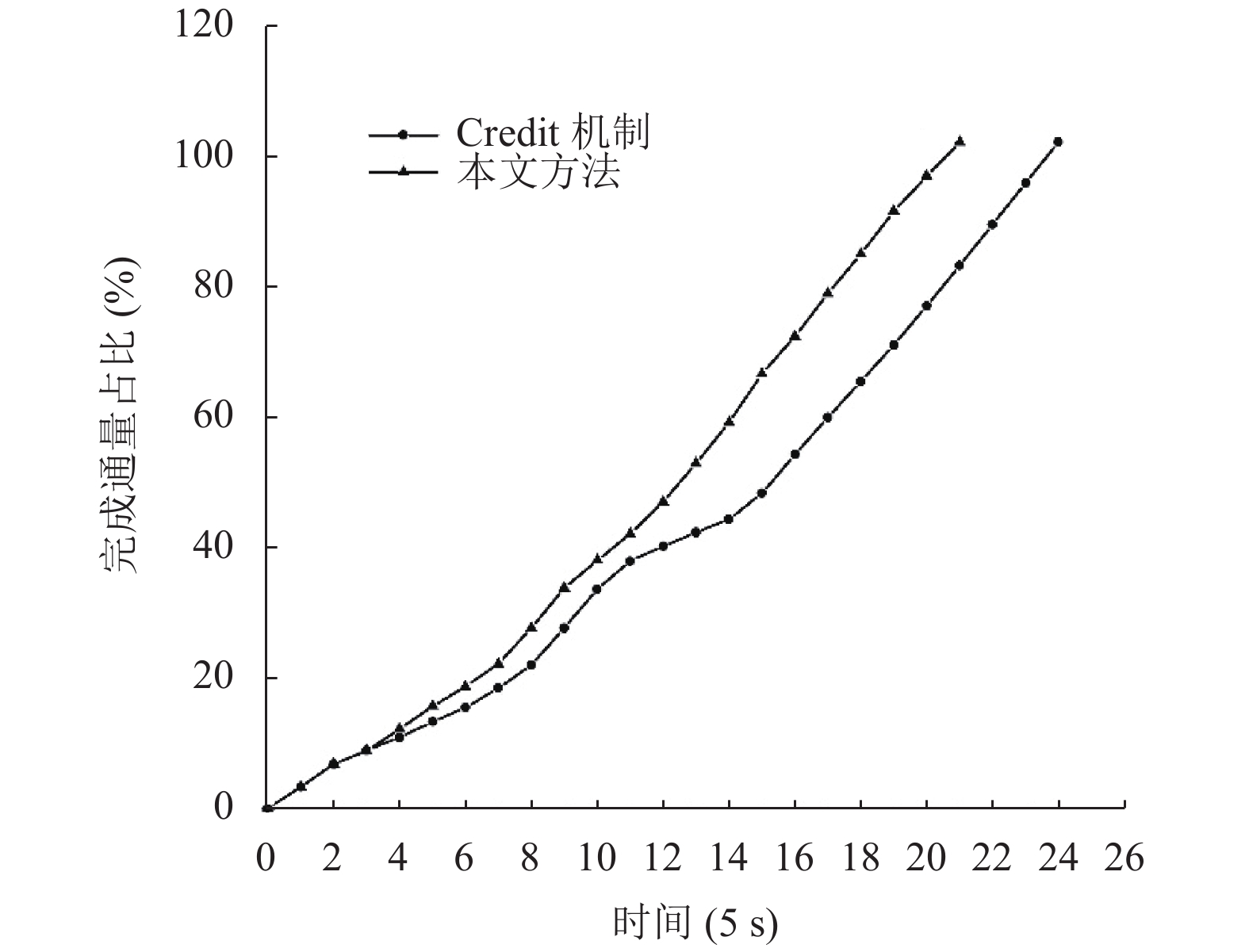
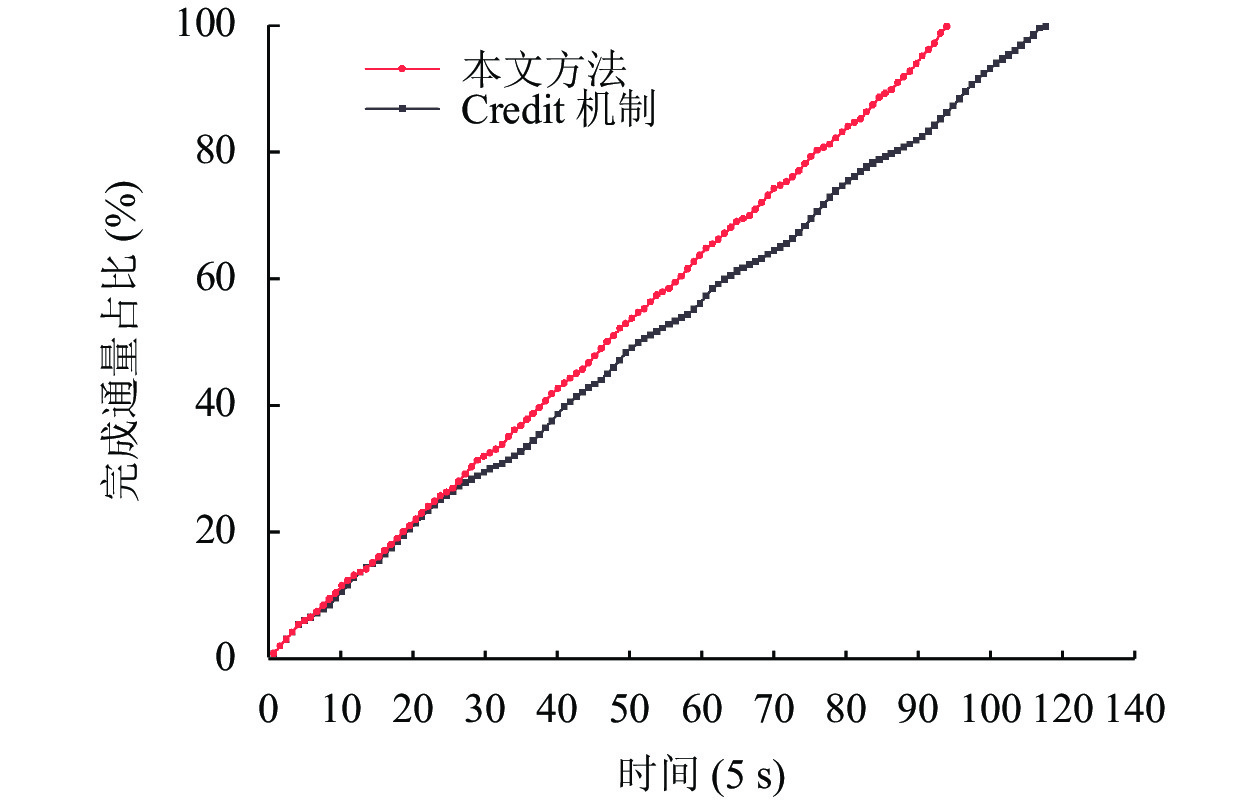
通过累积统计每5 s内系统的流量输出与流量总值的对比, 得到完成通量占比变化. 图7、图8分别展示了在1 GB流量和5 GB流量下Credit机制和本文方法在不同时间段的完成通量占比变化情况, 其中折线的斜率变化代表了系统的吞吐量变化. 在吞吐量的角度上看, 当反压问题刚出现时, 两种方法都出现了斜率趋于平缓即吞吐量下降的情况, 但是本文方法更快速地分散压力, 使得吞吐量增加, 折线更快地拉升, 表明本文方法在出现反压问题时能更快地处理压力. 在完成通量占比的角度上看, 随着时间变化, 本文方法的完成通量占比始终高于Credit机制, 更早地达到100%完成, 这表明本文方法降低了反压问题产生的延迟, 提高了系统性能.
| 表 1 延迟时间对比表(s) |
| 表 2 延迟时间对比表(s) |
|
图 7 流量为1 GB时完成通量占比 |
4 结论与展望
本文对分布式流计算系统中存在的反压问题进行分析, 基于系统中轻载节点分散重载节点压力的思路, 提出了一种基于数据迁移策略的反压问题解决方法. 实验结果表明, 本文提出的方法可以有效地降低系统的延迟并提高系统性能, 更高效地解决了系统中的反压问题. 下一步的工作重点是对带有Map和Reduce操作的任务以及多任务系统进行优化, 并将方法实现在实际的分布式流计算框架中进行验证.
|
图 8 流量为5 GB时完成通量占比 |
| [1] |
崔星灿, 禹晓辉, 刘洋, 等. 分布式流处理技术综述. 计算机研究与发展, 2015, 52(2): 318-332. DOI:10.7544/issn1000-1239.2015.20140268 |
| [2] |
熊安萍, 朱恒伟, 罗宇豪. Storm流式计算框架反压机制研究. 计算机工程与应用, 2018, 54(1): 102-106, 139. DOI:10.3778/j.issn.1002-8331.1701-0177 |
| [3] |
Chintapalli S, Dagit D, Evans B, et al. Benchmarking streaming computation engines: Storm, flink and spark streaming. 2016 IEEE International Parallel and Distributed Processing Symposium Workshops (IPDPSW). Chicago: IEEE, 2016. 1789–1792.
|
| [4] |
Zaharia M, Chowdhury M, Das T, et al. Resilient distributed datasets: A fault-tolerant abstraction for in-memory cluster computing. Proceedings of the 9th USENIX Symposium on Networked Systems Design and Implementation. San Jose: USENIX Association, 2012. 2.
|
| [5] |
Evans R. Apache storm, a hands on tutorial. 2015 IEEE International Conference on Cloud Engineering. Tempe: IEEE, 2015. 2.
|
| [6] |
胡亚辉, 朱宗卫, 刘黄河, 等. 面向任务调度优化的分布式系统信息管理框架. 计算机系统应用, 2019, 28(11): 54-62. DOI:10.15888/j.cnki.csa.007166 |
| [7] |
Lopes RV, Menascé D. A taxonomy of job scheduling on distributed computing systems. IEEE Transactions on Parallel and Distributed Systems, 2016, 27(12): 3412-3428. DOI:10.1109/TPDS.2016.2537821 |
| [8] |
Gautam JV, Prajapati HB, Dabhi VK, et al. A survey on job scheduling algorithms in big data processing. 2015 IEEE International Conference on Electrical, Computer and Communication Technologies (ICECCT). Coimbatore: IEEE, 2015. 1–11.
|
| [9] |
Hammoud M, Sakr MF. Locality-aware reduce task scheduling for MapReduce. Proceedings of the IEEE 3rd International Conference on Cloud Computing Technology and Science. Athens: IEEE, 2011. 570–576.
|
| [10] |
Arslan E, Shekhar M, Kosar T. Locality and network-aware reduce task scheduling for data-intensive applications. 2014 5th International Workshop on Data-intensive Computing in the Clouds. New Orleans: IEEE, 2014. 17–24.
|
| [11] |
刘梦青, 王少辉. 基于蚁群算法的Storm集群资源感知任务调度. 计算机技术与发展, 2017, 27(9): 92-96, 100. DOI:10.3969/j.issn.1673-629X.2017.09.020 |
| [12] |
刘粟, 于炯, 鲁亮, 等. Storm环境下基于拓扑结构的任务调度策略. 计算机应用, 2018, 38(12): 3481-3489. DOI:10.11772/j.issn.1001-9081.2018040741 |
| [13] |
Hanif M, Yoon H, Lee C. A backpressure mitigation scheme in distributed stream processing engines. 2020 International Conference on Information Networking (ICOIN). Barcelona: IEEE, 2020. 713–716.
|
| [14] |
Chen X, Vigfusson Y, Blough DM, et al. GOVERNOR: Smoother stream processing through smarter backpressure. 2017 IEEE International Conference on Autonomic Computing (ICAC). Columbus: IEEE, 2017. 145–154.
|
| [15] |
Cicotti P, Taufer M, Chien AA. DGmonitor: A performance monitoring tool for sandbox-based desktop grid platforms. The Journal of Supercomputing, 2005, 34(2): 113-133. DOI:10.1007/s11227-005-2336-y |
| [16] |
王成章, 林学练, 谭静芳. 流式处理系统的动态数据分配技术. 计算机工程与科学, 2014, 36(10): 1846-1853. DOI:10.3969/j.issn.1007-130X.2014.10.002 |
| [17] |
鲁亮, 于炯, 卞琛, 等. 大数据流式计算框架Storm的任务迁移策略. 计算机研究与发展, 2018, 55(1): 71-92. DOI:10.7544/issn1000-1239.2018.20160812 |
| [18] |
陆佳炜, 吴涵, 陈烘, 等. 一种基于动态拓扑的流计算性能优化方法及其在Storm中的实现. 电子学报, 2020, 48(5): 878-890. DOI:10.3969/j.issn.0372-2112.2020.05.007 |
| [19] |
Xu JL, Chen ZH, Tang J, et al. T-Storm: Traffic-aware online scheduling in storm. 2014 IEEE 34th International Conference on Distributed Computing Systems. Madrid: IEEE, 2014. 535–544.
|
| [20] |
Peng BY, Hosseini M, Hong ZH, et al. R-Storm: Resource-aware scheduling in storm. Proceedings of the 16th Annual MIDDLEWARE Conference. New York: ACM, 2015. 149–161.
|
| [21] |
茹新宇, 刘渊, 陈伟. 新网络仿真器NS3的研究综述. 微型机与应用, 2017, 36(20): 14-16. |
 2022, Vol. 31
2022, Vol. 31


