智能交通系统(intelligent transportation system, ITS)将人工智能、计算机技术等运用于道路交通领域, 通过实时数据分析和预测, 进行道路规划[1]. 准确的短时交通流预测不仅能为出行者提供合理的道路规划, 提高道路利用率, 同时还能将有限的交通资源进行合理地安排, 减少交通事故的发生[2].
目前, 交通流预测模型中最常见的模型就是统计模型和机器学习模型. 其中统计模型中典型的代表是差分自回归移动平均(autoregressive integrated moving average, ARIMA)模型. 文献[3]用ARIMA模型在周期性交通流数据下进行短时交通流预测; 文献[4]指出ARIMA模型适合于线性的数据预测, 对于非线性强度较高的交通流预测有一定的局限性. 鉴于此情况, 适合非线性的机器学习被广泛地应用到交通流预测中. 支持向量机(support vector machine, SVM)是传统机器学习中最常见的模型. 文献[5]利用SVM模型预测异常状态下的交通流, 证明了SVM模型能够提高预测精度. 但是, 研究表明机器学习难以捕捉交通流序列长期记忆的特点, 从而影响机器学习预测精度.
近些年, 随着人工智能的发展, 深度学习已经成为当前研究的热点, 被广泛地应用于交通流预测领域. 文献[6, 7]将长短时记忆网络(long-short term memory networks, LSTM)应用于交通流预测, 通过LSTM对交通流数据中的特征进行提取, 从而更好地表示交通流数据的非线性, 达到更好的预测结果. 为了提高交通流预测模型的准确性和泛化性, 文献[8]提出了基于模糊分析的LSTM交通流预测. 文献[9]利用卷积神经网络(convolutional neural network, CNN)与LSTM相结合的深度结构, 构建二者相结合的复合模型, 通过捕获交通网络的时空相关性进行有效的预测. 文献[10]在CNN-LSTM模型基础上加入了注意力机制(attention mechanism), 利用注意力机制重新分配权重的特点, 进而提高了预测精度. 在交通流时间序列中, 考虑前向和后向数据的变化规律有助于提高模型的拟合精度, 文献[11]利用双向长短时记忆网络(bi-directional long-short term memory, BiLSTM)模型对高速公路交通流进行预测, 结果表明BiLSTM模型预测精度优于LSTM模型预测精度. 文献[12]为了充分发挥CNN对空间特征的选择提取能力, 同时利用BiLSTM提取时间特征, 构建CNN-BiLSTM复合模型, 通过实验证明该模型的预测值与真实值更贴合, 证明了BiLSTM挖掘数据特征能力比LSTM更强, 对于复杂的回归问题具有较好的拟合性能. 深度学习模型结构复杂, 层数较多, 容易陷入局部最优的情况, 从而影响预测精度, 很难满足短时交通流预测.
为了解决上述问题, 2018年宽度学习系统(broad learning system, BLS)的提出被广泛应用于各类预测领域, 从理论上证明了BLS在时间序列的预测上具有良好的函数逼近能力, 且通过实验证明了BLS在回归性能上表现优异[13]. 文献[14]利用KNN筛选出时空相关性高的K个路段, 将选取的路段交通流输入到BLS网络中进行预测, 预测效果都显著的提高.
ITS中短时车流量的数据均会存在一定量的噪声, 为实现数据的准确预测, 可在数据处理时采用信号分解的方式. 文献[15]通过多种分解算法对交通流数据进行分解, 以此降低数据中的噪声对预测结果的影响, 接着使用K均值聚类将分量进行聚类, 之后通过BiLSTM对交通流进一步的预测. 结果表明, 经变分模态分解算法(variational mode decomposition, VMD)分解后的预测精度更高.
虽然上述方法都取得了较好的预测结果, 但都没解决深度学习带来局部最优的问题.本文的创新点是在交通领域首次引入BLS与深度学习结合, 通过其得到全局最优解, 解决深度学习易陷入局部最优从而影响预测精度的缺点. 同时考虑到交通流数据的噪声干扰, 引入了VMD进行降噪处理. 基于此, 本文提出基于VMD-BiLSTM-BLS模型的短时交通流预测. 为了证明本文模型预测的准确性和可应用性, 选取了美国加利福尼亚州交通局PeMS (performance measurement system)交通数据库实测的交通流数据进行实验. 通过对比基线模型、消融模型以及现有模型, 结果表明: 本文模型在预测精度方面显著提升. 另外值得指出的是, 本文提出的深度学习和宽度学习相结合的预测模型不但可以应用于交通领域, 其在金融、气象、海洋等需要大量时间序列分析预测等领域也有广泛的应用前景.
2 模型的构建 2.1 VMD模型2014年Dragomiretskiy等[16]提出了变分模态分解, 解决了经验模态分解中存在的端点效应和模态分量混叠的问题. 具体分解步骤如下:
Step 1. 首先通过式(1)–式(2)构建变分约束问题.
| $ \mathop {\min }\limits_{\{ {u_k}, {\omega _k}\} } \left\{ \sum\limits_k {{\text{||}}{\partial _t}} [\delta (t) + j/\pi t)\times {u_k}(t)]{{\rm{e}}^{ - j{\omega _k}t}}||_2^2\right\} \;\; $ | (1) |
| $ {\rm{s.t.}}\sum\limits_{k = 1}^K {{u_k}} = f\;\; $ | (2) |
其中, K为分解的模态个数,
Step 2. 通过式(3)转变约束变分问题.
| $ \begin{split} L(\{{u}_{k}\}, \{{\omega }_{k}\}, \lambda )=&\alpha {\displaystyle \sum _{k}\left|\right|{\partial }_{t}[(\delta (t)+j/\pi t})\times {u}_{k}(t)]{\rm{e}}^{-j{\omega }_{k}t}|{|}_{2}^{2}\\ & +\left|\right|f(t)-{\displaystyle \sum _{k}{u}_{k}}|{|}_{2}^{2}\text{\hspace{0.17em}}+ < \lambda (t), f(t)-{\displaystyle \sum _{k}{u}_{k}(t)} > \end{split} $ | (3) |
其中,
Step 3. 搜寻增广Lagrange函数的鞍点, 交替寻优迭代后的
| $ \hat u_k^{n + 1} = \frac{{\hat f(\omega ) - \displaystyle\sum\limits_{i \ne k} {{{\hat u}_i}(\omega ) + \hat \lambda (\omega )/2} }}{{1 + 2\alpha {{(\omega - {\omega _k})}^2}}} $ | (4) |
| $ \omega _k^{n + 1} = \frac{{\int\limits_0^\infty {\omega |\hat u_k^{n + 1}} (\omega ){|^2}d\omega }}{{\int\limits_0^\infty {|\hat u_k^{n + 1}} (\omega ){|^2}d\omega }} $ | (5) |
| $ {\hat \lambda ^{n + 1}}(\omega ) = {\hat \lambda ^n}(\omega ) + \gamma (\hat f(\omega ) - \sum\limits_k {\hat u_k^{n + 1}} (\omega )) $ | (6) |
其中,
LSTM网络在循环神经网的基础上增加了输入门、输出门和遗忘门, 通过这3个门, LSTM模型解决了循环神经网络中长序列依赖的问题. LSTM数学原理运算公式如式(7)–式(11)所示.
| $ {f_t} = \sigma ({W_{xf}}{x_t} + {W_{hf}}{h_{t - 1}} + {b_f}) $ | (7) |
| $ {i_t} = \sigma ({W_{xi}}{x_t} + {W_{hi}}{h_{t - 1}} + {b_i}) $ | (8) |
| $ {o_t} = \sigma ({W_{xo}}{x_t} + {W_{ho}}{h_{t - 1}} + {b_o}) $ | (9) |
| $ {c_t} = {f_t} \otimes {c_{t - 1}} + {i_t} \otimes \tanh ({W_{xc}}{x_t} + {W_{hc}}{h_{t - 1}} + {b_c}) $ | (10) |
| $ {h_t} = {o_t} \otimes \tanh ({c_t}) $ | (11) |
其中,
BiLSTM是由前向LSTM和后向LSTM构成, 进行双向训练, 既保留了LSTM能够处理长时间序列的特点, 又考虑到了前后数据变换的影响, 提高了特征提取的全局性, 对于复杂的回归问题具有较好的拟合性能. BiLSTM的结构图如图1所示.
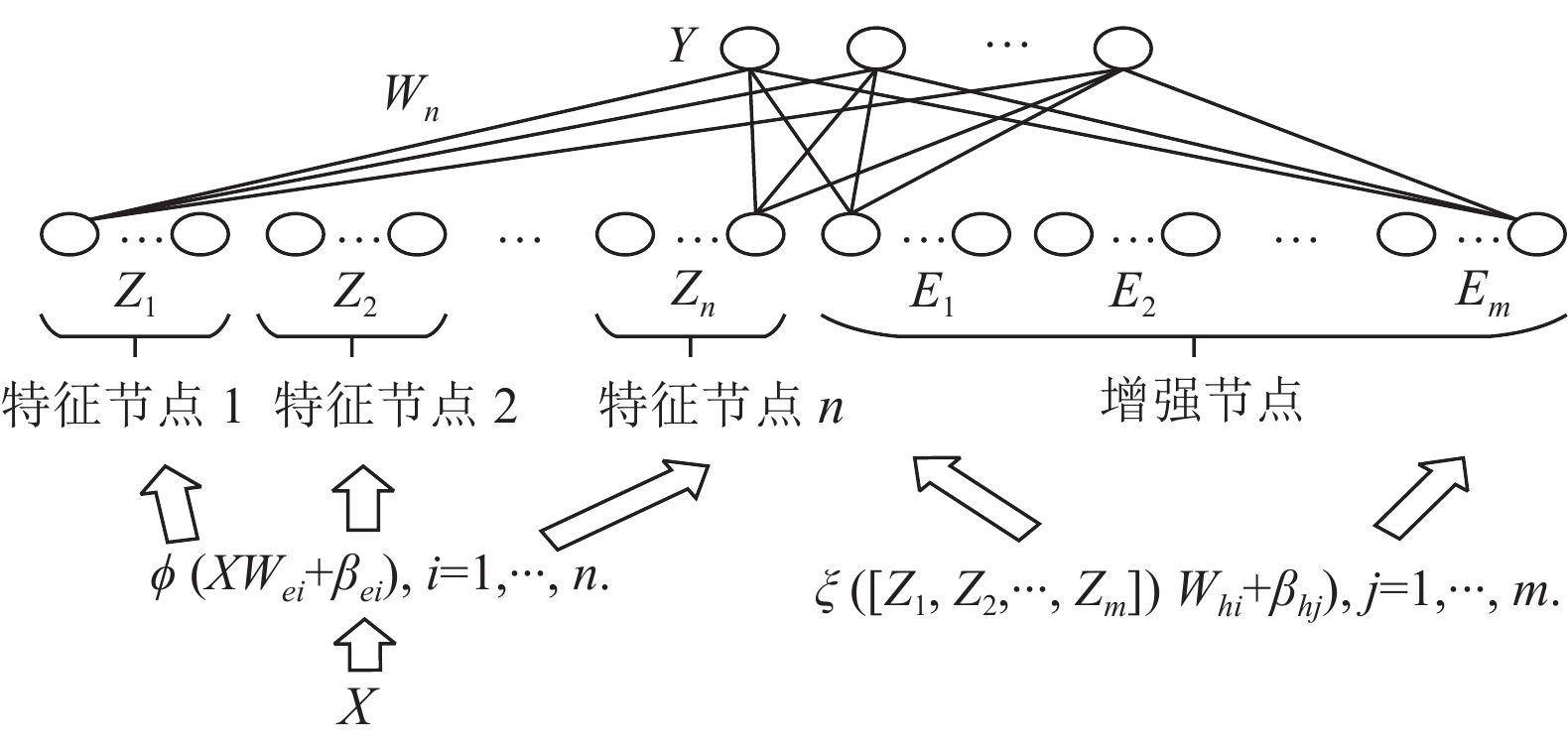
2.3 BLS原理及结构在随机向量函数链接神经网络的基础上提出BLS, 消除了局部最优的缺点. 图2为BLS结构系统图. 流程步骤如下.

|
图 1 BiLSTM结构图 |
|
图 2 BLS结构系统图 |
Step 1. 假设输入的数据为
Step 2. 将特征节点经过激活函数非线性变换, 得到
Step 3. 将特征节点组与增强节点组进行拼接作为系统的实际输入, 则系统的输出式如式(14)所示.
| $ {Z_i} = \phi (X{W_{ei}} + {\beta _{ei}}),\; i = 1, 2, \cdots, n $ | (12) |
| $ {E_m} = \xi ({Z_n}{W_{hm}} + {\beta _{hm}}) $ | (13) |
| $ Y = H{W^n} = [{Z_n}|{E_m}]{W^n} $ | (14) |
其中,
通过上述分析, 本文集聚了深度学习和宽度学习系统的优势, 并引入了VMD模块进行降噪处理, 提出了VMD-BiLSTM-BLS组合预测模型, 模型结构如图3所示.

|
图 3 VMD-BiLSTM-BLS模型结构图 |
由图3可以看出, 本文模型由车流量序列预处理、网络训练预测、预测输出3个模块构成. 具体步骤如下:
步骤1. 车流量序列预处理. 由于每天会出现上下班高峰期, 车流量原始序列可能存在奇异值, 为了减少奇异值对数据造成不必要的影响及加快梯度下降, 本文首先将原始序列进行归一化处理, 其归一化公式如式(15)所示. 接着为了减少噪声对该模型预测结果的影响, 将归一化之后的序列进行VMD分解, 得到多个不同频率下的子序列.
| $ {X_{\rm{scaled}}} = \frac{{X - {X_{\min }}}}{{{X_{\max }} - {X_{\min }}}} $ | (15) |
其中,
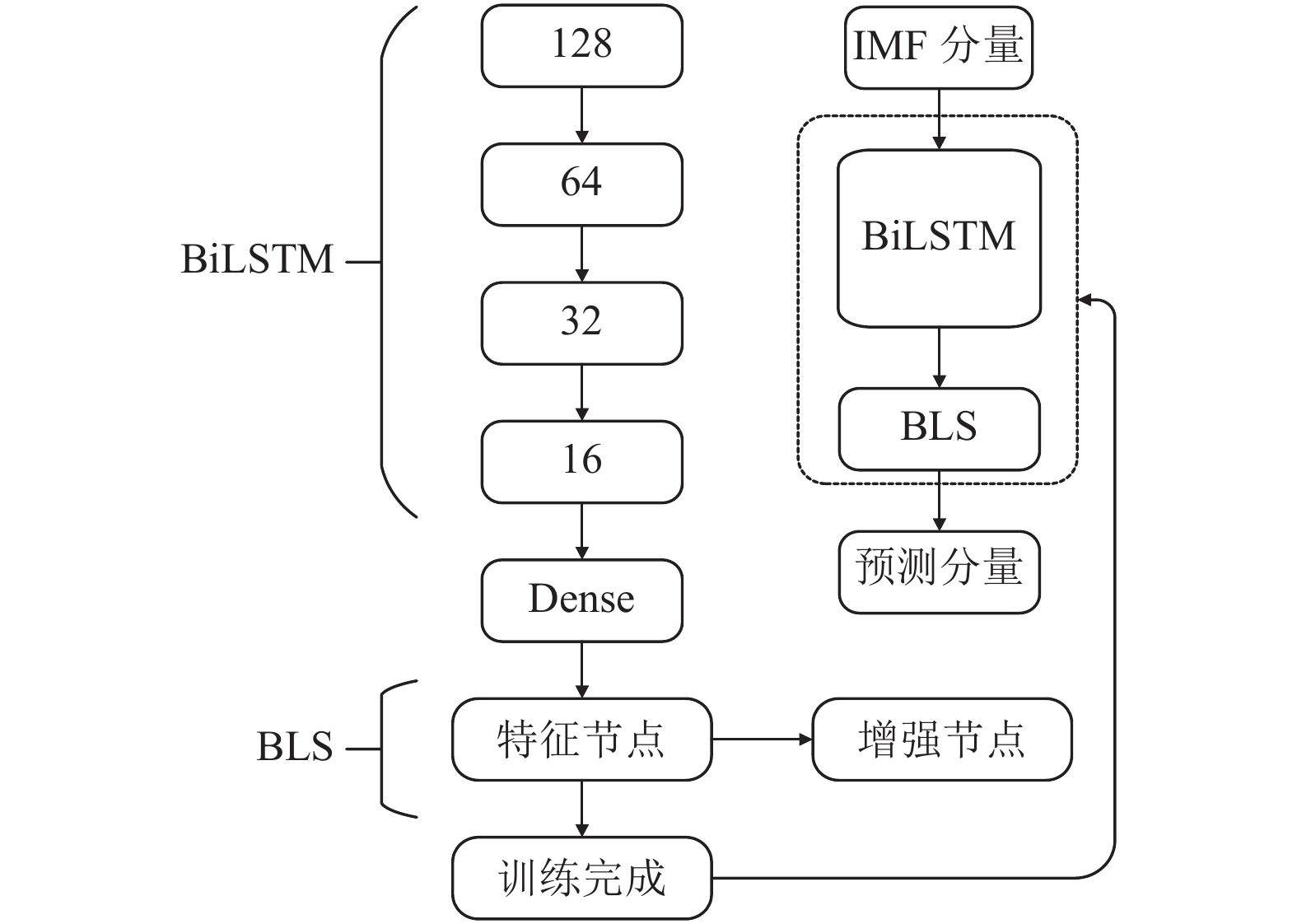
步骤2. 网络训练预测. 该模块是本文的创新模块, 首先将预处理后的数据输入到BiLSTM进行训练, 接着将全连接层的输出作为前
|
图 4 BiLSTM-BLS连接图 |
进一步, 求解
| $ \mathop {\min }\limits_{{W^n}} f({W^n}) = \mathop {\min }\limits_{{W^n}} ||H{W^n} - Y||_F^2 $ | (16) |
其中,
| $ H = [{Z^n}|{E^m}] = ({h_1}, {h_2}, \cdots, {h_l}) $ | (17) |
式(16)是一个最小二乘问题, 是关于
| $ {W^n} = {H^ + }Y $ | (18) |
其中,
| $ \mathop {\min }\limits_{{W^n}} f({W^n}) = \mathop {\min }\limits_{{W^n}} ||H{W^n} - Y||_F^2 + C||{W^n}||_F^2 $ | (19) |
式(19)为一个岭回归问题.
| $\left\{ {\begin{split} &{W^n} = {H^{\rm{T}}}{(CI + H{H^{\rm{T}}})^{ - 1}}Y, K < L\\ &{W^n} = {(CI + {H^{\rm{T}}}H)^{ - 1}}{H^{\rm{T}}}Y, K \geqslant L \end{split} } \right.$ | (20) |
步骤3. 预测输出. 首先将每个IMF预测结果进行加权求和, 再进行反归一处理, 最终输出预测结果.
3 实例分析 3.1 数据来源本文车流量数据来源于美国加利福尼亚州交通局PeMS交通数据库实测的交通流数据, 本文选用的交通流数据是从2016年1月4日至2016年2月16日内工作日的1车道点每5分钟统计一次的交通流, 共7 776组数据.
3.2 模型参数设置和评价指标根据本文数据集的特点, 将27天7 776组数据, 前90%作为训练集, 后10%作为测试集. 为了提升数据的平稳性, 设置时间滑动窗口为6. 利用VMD把原始序列分解为5个子序列, 将子序列转换为三维的张量输入给BiLSTM网络, 为了防止过拟合在每层的BiLSTM后加上Dropout机制. 再通过全连接层, 将其输出作为BLS层的特征节点, 特征节点经过激活函数非线性变换生成增强节点, 更新权重及其偏置. 本实验是基于深度学习框架Keras实现的, 通过多次重复实验, 选取了最优情况的数值. 具体的参数见表1. 其中Alpha为惩罚因子, K为分解的模态数, Tol为收敛准则容忍度, N1为每个映射特征节点个数, N2为映射特征个数, N3为增强节点个数, C为正则化参数.
| 表 1 VMD-BiLSTM-BLS模型参数表 |
在实验中, 选用了均方根误差(root mean square error, RMSE)、平均绝对误差(mean absolute error, MAE)以及决定系数
| $ {\textit{RMSE}} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{({y_i} - {{\hat y}_i})}^2}} } $ | (21) |
| $ MAE = \frac{1}{n}\sum\limits_{i = 1}^n {|{y_i} - {{\hat y}_i}|} $ | (22) |
| $ {R^2}\_score\;{\text{ = }}1{{ - }}\frac{{\displaystyle\sum\limits_{i = 1}^n {{{({y_i} - {{\hat y}_i})}^2}} }}{{\displaystyle\sum\limits_{i = 1}^n {{{({y_i} - {{\overline y }_i})}^2}} }}\; $ | (23) |
其中,
将原始序列进行VMD分解, 得到5组频率尺度不同的子序列, 图5是交通流数据分解图. IMF0为趋势分量, 反映了交通流序列的总体变化趋势. IMF1–IMF4为波动分量, 反映了曲线的随机波动细节. 分解的序列与原始序列相比, 平稳性和平滑性方面表现更好, 相似的细节信息更集中, 更加容易拟合.

|
图 5 交通流数据分解图 |
4.2 结果对比分析
(1)与基线模型对比分析
由于基线模型比较经典, 此外交通流数据存在一定的周期性, 基线模型在具有周期性的数据上预测效果还是有较好表现. 为了验证本文所提模型的预测能力, 首先将本文模型分别与基线模型ARIMA[3]、SVM[5]进行对比, 评价指标结果如表2所示. 各个模型的参数都是通过多次实验采用拟合效果最好的数值.
| 表 2 基线模型与本文模型评价指标对比表 |
从表2可以看出, ARIMA、SVM模型的RMSE都大于15, MAE都大于11, 而VMD-BiLSTM-BLS模型的RMSE、MAE均没超2, 且
(2)与消融模型对比分析
其次, 将本文模型与消融模型BiLSTM-BLS、VMD-BiLSTM[15]进行对比分析, 其中VMD-BiLSTM也是最新的模型. 评价指标结果见表3.
| 表 3 消融模型与本文模型评价指标对比表 |
通过表3可以看出, 本文模型与BiLSTM-BLS、VMD-BiLSTM相比, RMSE分别下降了8.287 7、4.050 4, MAE分别下降了5.999 9、3.6186, 且
(3)与现有模型对比分析
最后, 为了验证本文模型本文模型预测精度有所提升, 分别与现有模型BiLSTM[11]、当前研究较热的CNN-BiLSTM[12]模型以及最新模型, 含有注意力机制(attention mechanism)的CNN-LSTM[10]模型进行对比分析, 评价结果如表4所示.
从表4可以看出, 本文模型的3个评价指标明显优于现有模型BiLSTM, 其中CNN-BiLSTM模型与BiLSTM模型相比, RMSE下降了1.009 5,MAE下降了0.865 4, 这是由于CNN-LSTM不仅提取了时间特征, 还挖掘了空间特征, 可以提升预测精度. 在此基础上加上注意力机制的模型, 预测精度再次提升, 这是由于注意力机制进行权重新分配, 提高了预测精度. 本文模型与CNN-LSTM-Attention相比, RMSE、MAE分别下降了5.784 6、4.991 1,
| 表 4 现有模型与本文模型评价指标对比表 |
(4)可视化对比分析
为了更加直观地验证本文模型的有效性, 选取测试集中最后一天的交通流原始序列进行拟合分析, 图6–图10分别给出了本文模型与其他模型的预测结果对比图.
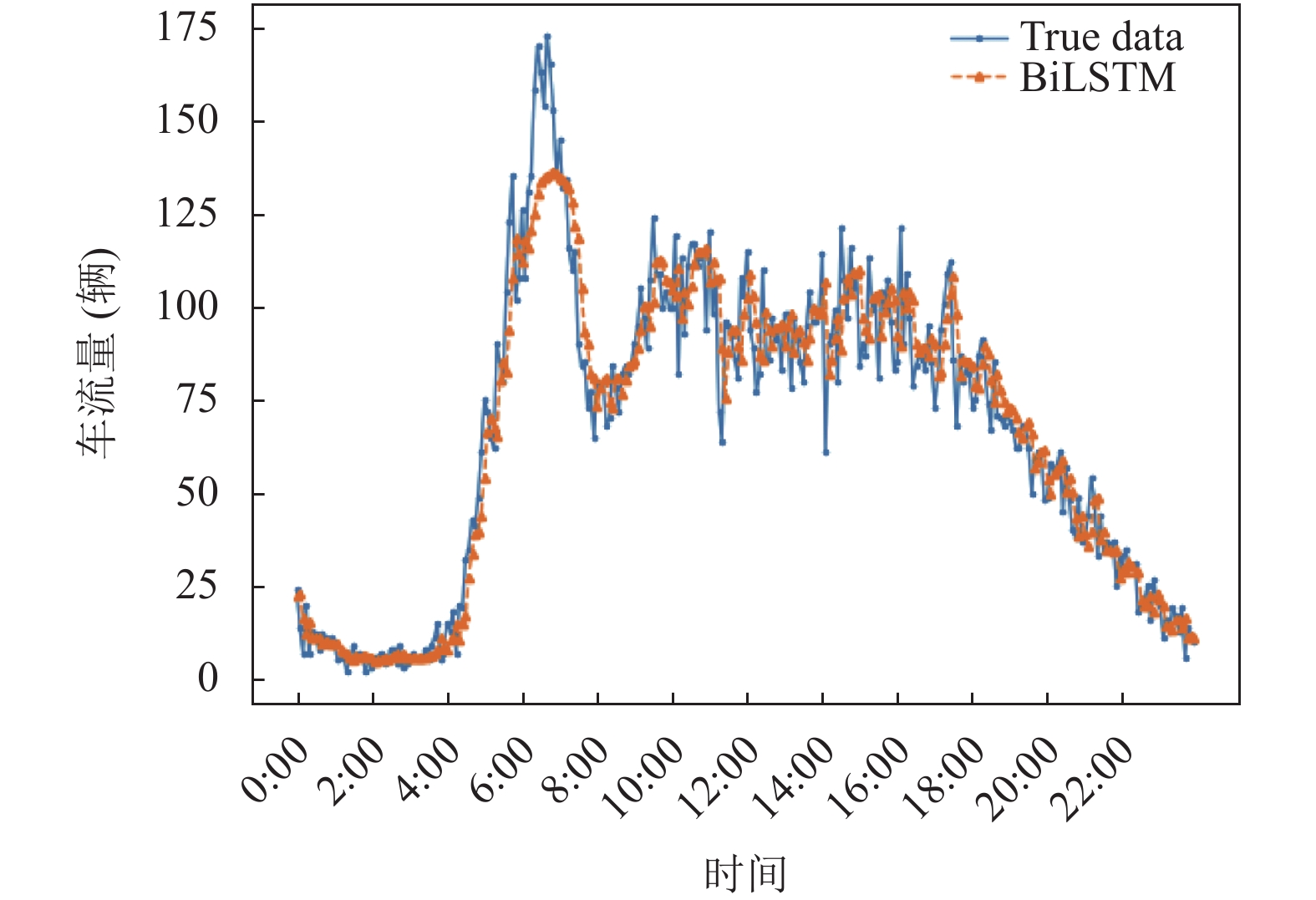
|
图 6 BiLSTM模型预测值与真实值对比图 |
从图6、图7中可以直观的看出VMD-BiLSTM模型相对于BiLSTM模型拟合效果有所提高, 这是由于原始序列经过VMD分解之后, 得到不同频率的子序列, 降低了噪声对原始数据造成不良的影响, 使得拟合程度增强. 从图6和图8可以看出, 在上班高峰期的时候BiLSTM模型拟合效果不如BiLSTM-BLS模型, 从而验证了BLS解决了局部最优的问题, 提高了预测的准确性. 分析图7和图8, 可以明显地看到, 不管是VMD-BiLSTM模型还是BiLSTM-BLS模型在波峰和波谷的时候拟合效果并不是很理想, 但是从图9可以看出VMD-BiLSTM-BLS模型明显改善了波峰和波谷不准确性的问题. 通过对图9和图10进行对比, 可以看到在8点到15点的时候, VMD-BiLSTM-BLS模型拟合效果要比现有模型中较火的CNN-BiLSTM模型明显提高.
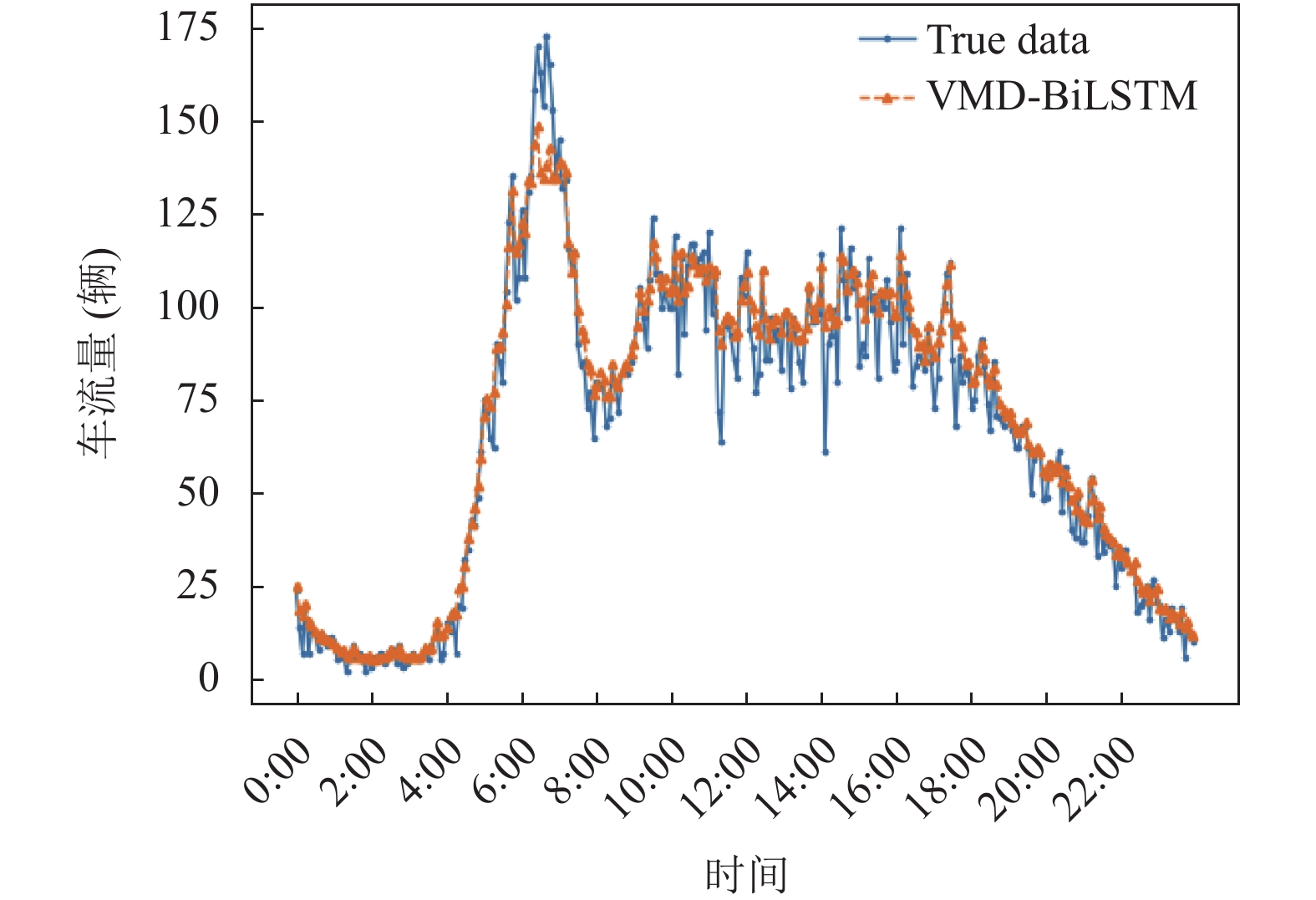
|
图 7 VMD-BiLSTM模型预测值与真实值对比图 |

|
图 8 BiLSTM-BLS模型预测值与真实值对比图 |
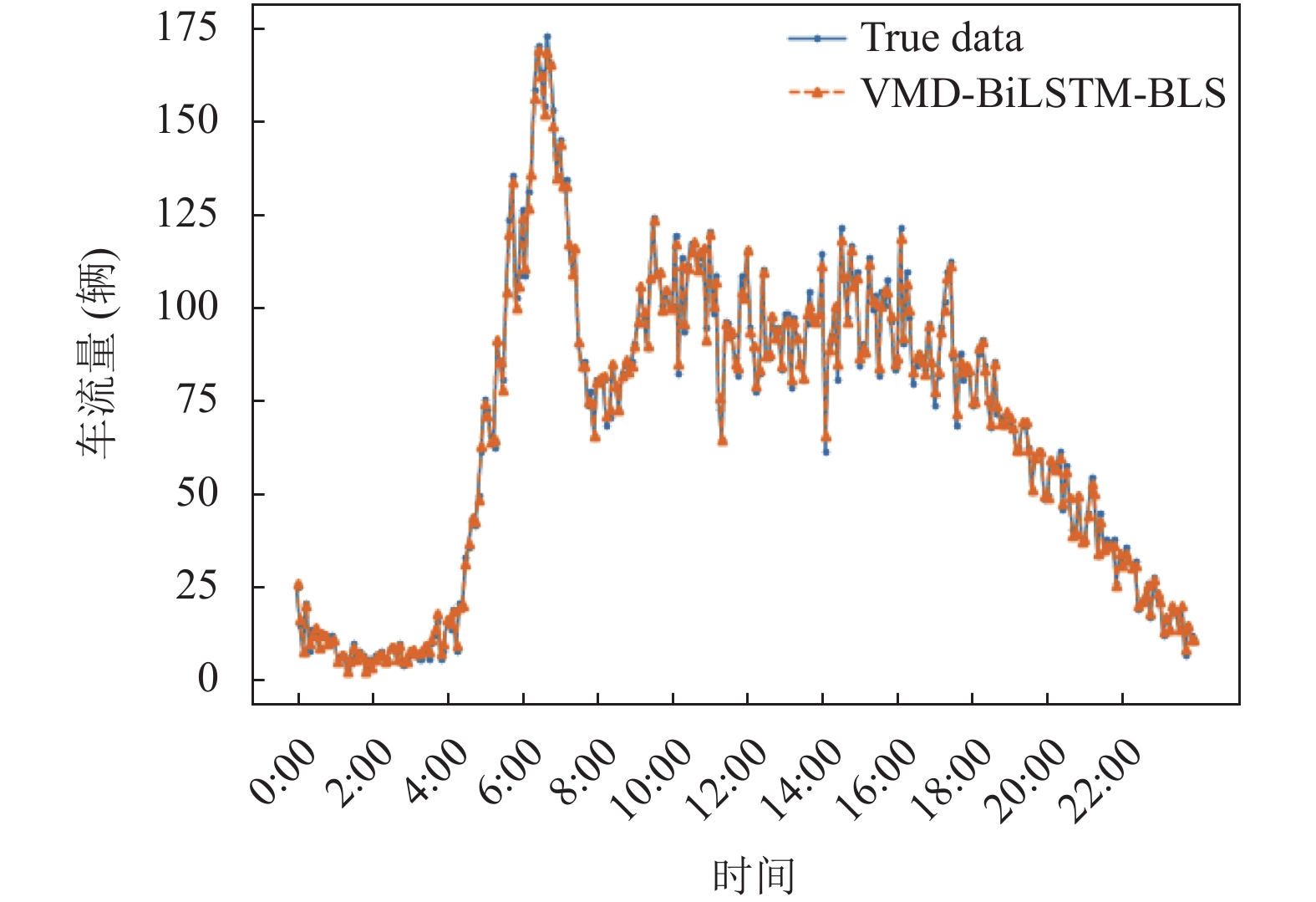
|
图 9 VMD-BiLSTM-BLS模型预测值与真实值对比图 |
通过以上实验的对比结果来看, 本文所提出的VMD-BiLSTM-BLS模型在评价指标RMSE、MAE、

|
图 10 CNN-BiLSTM模型预测值与真实值对比图 |
5 结论
准确的短时交通流预测会给人们的出行带来极大的便利, 不仅提出合理的出行意见, 而且减少了事故率. 准确的短时交通流预测是构建智慧交通的关键, 所以准确的掌握短时交通流的发展趋势, 建立健全的预测系统, 有利于交通部门做出合理的疏导安排.
本文所提出的短时交通流预测模型, 是将深度学习与宽度学习进行结合, 改善了现有模型预测不准确的问题. 将本文提出的模型与基线模型、消融模型以及现有模型进行对比, 实验结果表明本文所提出的短时交通流预测模型在RMSE、MAE、
| [1] |
Zhao JH, Ni SJ, Yang LH, et al. Multiband cooperation for 5G HetNets: A promising network paradigm. IEEE Vehicular Technology Magazine, 2019, 14(4): 85-93. DOI:10.1109/MVT.2019.2935793 |
| [2] |
Huang W, Jia WW, Guo JH, et al. Real-time prediction of seasonal heteroscedasticity in vehicular traffic flow series. IEEE Transactions on Intelligent Transportation Systems, 2018, 19(10): 3170-3180. DOI:10.1109/TITS.2017.2774289 |
| [3] |
祁伟, 李晔, 汪作新. 季节性ARiMA模型在稀疏交通流下的预测方法. 公路交通科技, 2014, 31(4): 130-135. DOI:10.3969/j.issn.1002-0268.2014.04.022 |
| [4] |
Niu K, Zhang HY, Zhou T, et al. A novel spatio-temporal model for city-scale traffic speed prediction. IEEE Access, 2019, 7: 30050-30057. DOI:10.1109/ACCESS.2019.2902185 |
| [5] |
Chen L, Li QR, Tian XY, et al. Paratactic spatial-temporal two dimension data fusion based on support vector machines for traffic flow prediction of abnormal state. Advanced Materials Research, 2012, 532–533: 1225–1229.
|
| [6] |
Chen XW. Research on short-term traffic flow forecasting model based on LSTM. World Scientific Research Journal, 2020, 6(5): 191-200. DOI:10.6911/WSRJ.202005_6(5).0021 |
| [7] |
马焱棋, 林群, 赵昱程, 等. 基于深度学习LSTM对交通流状态的预测. 数学的实践与认识, 2021, 51(4): 47-56. |
| [8] |
赵刚, 王梦灵. 基于模糊分析的LSTM交通流量预测. 计算机工程与设计, 2021, 42(4): 1103-1108. DOI:10.16208/j.issn1000-7024.2021.04.029 |
| [9] |
Yu HY, Wu ZH, Wang SQ, et al. Spatiotemporal recurrent convolutional networks for traffic prediction in transportation networks. Sensors, 2017, 17(7): 1501. DOI:10.3390/s17071501 |
| [10] |
王庆荣, 田可可, 朱昌锋, 等. 融合多因素的短时交通流预测研究. 计算机工程与应用, 2021: 1–12. http://kns.cnki.net/kcms/detail/11.2127.TP.20210806.0837.006.html. (2021-08-06)[2021-08-23].
|
| [11] |
张维, 袁绍欣, 陶建军, 等. 基于多元因素的Bi-LSTM高速公路交通流预测. 计算机系统应用, 2021, 30(6): 184-190. DOI:10.15888/j.cnki.csa.007969 |
| [12] |
Li T, Ni AN, Zhang CQ, et al. Short-term traffic congestion prediction with Conv-BiLSTM considering spatio-temporal features. IET Intelligent Transport Systems, 2020, 14(14): 1978-1986. DOI:10.1049/iet-its.2020.0406 |
| [13] |
Chen CLP, Liu ZL, Feng S. Universal approximation capability of broad learning system and Its structural variations. IEEE Transactions on Neural Networks and Learning Systems, 2019, 30(4): 1191-1204. DOI:10.1109/TNNLS.2018.2866622 |
| [14] |
罗向龙, 郭凰, 廖聪, 等. 时空相关的短时交通流宽度学习预测模型. 计算机工程与应用, 2021: 1–6. http://kns.cnki.net/kcms/detail/11.2127.TP.20210316.1912.023.html. (2021-03-17)[2021-04-20].
|
| [15] |
Huang HC, Chen JY, Huo XT, et al. Effect of multi-scale decomposition on performance of neural networks in short-term traffic flow prediction. IEEE Access, 2021, 9: 50994-51004. DOI:10.1109/ACCESS.2021.3068652 |
| [16] |
Dragomiretskiy K, Zosso D. Variational mode decomposition. IEEE Transactions on Signal Processing, 2014, 62(3): 531-544. DOI:10.1109/TSP.2013.2288675 |
 2022, Vol. 31
2022, Vol. 31



