随着互联网的快速发展, 在线社交网络在全世界普及, 社交网络的运营商收集了大量用户数据, 如果通过简单的匿名化处理将用户数据提供给第三方(研究人员、市场营销等)使用, 就会出现隐私泄漏的风险[1, 2]. 因此, 社交网络的隐私安全越来越受到人们的关注, 运营商需要在发布数据之前, 对用户数据进行匿名化处理, 确保用户隐私不会泄漏[3]; 同时尽可能地保留社交网络的结构特性, 从而保证数据的实用性[4, 5].
基于图结构变换的匿名方法[6], 能够有效地解决社交网络中用户的隐私保护问题. Backstrom等人[7]指出使用无意义的唯一标识符替换用户的身份作匿名化处理, 并不能防止用户隐私泄漏. Hay等人[8]发现利用节点周围的结构信息仍然能够在匿名图中重新识别该节点, 这种结构信息与节点及其邻居节点的度有关. Liu等人[9]基于k匿名性, 提出了k度匿名化模型, 这种匿名保护能够有效抵御以节点度数为背景知识的隐私攻击, 使得每个节点被重新识别的概率不大于
针对k度匿名化问题, Liu等人[9]基于动态规划思想生成匿名度序列, 根据该序列通过添加边的方式去构建图, 由于构图操作并不能保证一定成图, 所以需要构图测试, 这会增加算法运行时间; 而且构图操作的随机过程导致原图结构信息的损失. Lu等人[10]提出了一种贪心匿名化算法, 在给原图添加边的同时进行度序列的匿名化, 直接在原图上进行加边能够避免度序列的构图测试, 但是同步匿名化需要添加较多的边来实现图匿名化.
Chester等人[11, 12]提出了加点的匿名化策略, 基于动态规划思想生成匿名度序列, 通过新节点与原图节点连边满足节点匿名要求, 然而加点太多导致原图结构信息的损失. Ma等人[13]结合加边且可加点的匿名化策略提出匿名化算法, 利用贪心法生成匿名度序列, 并基于社区结构进行加边, 这种匿名化方式能较好地保留图的某些结构特性, 但添加的边或节点数较多. 吴童[14]结合加边且可加点的匿名化策略提出了改进算法, 利用Liu等人[9]提出的动态规划匿名分组算法生成匿名度序列, 根据该序列贪心加边; 若加边不能完成匿名化, 则进行加点完成图匿名化. 由于未充分利用原图中的点进行加边, 导致添加的节点数较多. Rajabzadeh等人[15]利用Ma等人[13]提出的贪心分组算法和基于模块度的社区发现算法[16]确定每个社区内节点的匿名化代价, 然后通过遗传算法决定每个社区内的节点之间如何连边, 从而实现图的度匿名化. 本文的主要贡献包括:
(1) 结合加边且可加点的策略, 改进了匿名化方式, 分两个阶段进行加边, 这种匿名方式能有效减少添加的边或节点.
(2) 在加边操作中, 考虑节点度、社区结构和节点距离等因素选择目标节点进行连边, 这种操作能够有效保留原图的某些结构特性.
(3) 在多个真实数据集上进行了大量实验, 实验结果验证了新算法的有效性.
2 预备知识本文将社交网络建模为无向图
给定无向图
设图
图匿名问题可描述如下: 给定无向图
新算法包括如下子算法: 匿名分组算法、加边算法、加点算法、层次社区发现算法. 新算法思想是利用贪心匿名分组算法生成匿名度序列, 基于层次社区结构加边, 优先满足匿名代价大于平均匿名代价的节点的匿名要求; 然后再次利用贪心匿名分组算法得到匿名度序列, 通过同样的加边操作满足未匿名节点的匿名要求; 若加边不能完成匿名化, 则通过加点实现图匿名化.
3.1 匿名分组算法本文采用Liu等人[9]提出的贪心匿名分组算法, 首先形成一个包含前
| $ {C_{{\text{merge}}}} = ({{\boldsymbol{d}}_G}({v_1}) - {{\boldsymbol{d}}_G}({v_{k + \, 1}})) + Cost({{\boldsymbol{d}}_G}[{v_{k + \, 2}}, {v_{2k + \, 1}}]) $ | (1) |
| $ {C_{{\text{new}}}} = Cost({{\boldsymbol{d}}_G}[{v_{k + \, 1}}, {v_{2k}}]) $ | (2) |
当
| $ Cost({{\boldsymbol{d}}_G}[{v_i}, {v_j}]) = \sum\nolimits_{l = i}^j {({{\boldsymbol{d}}_G}({v_i}) - {{\boldsymbol{d}}_G}({v_l}))} $ | (3) |
通过该算法得到匿名度序列, 每个组中至少有
加边算法包括两个阶段: 优先加边和普通加边. 优先加边阶段尽量满足匿名代价大于平均匿名代价的节点的匿名要求, 按照匿名代价降序遍历节点, 基于层次社区结构选择目标节点进行连边, 每次加边操作更新匿名代价序列. 在加边操作中, 从当前节点所在的社区开始遍历, 考虑两类节点: 1)节点度比当前节点度小; 2)节点度比当前节点度大且匿名代价大于0. 将符合条件的节点标识为目标节点, 并优先选择与当前节点距离近的目标节点进行连边. 若标记的目标节点数仍不能满足当前节点的匿名要求, 则向高级别社区遍历, 找到足够多的目标节点进行连边.
算法 1. 优先加边算法
输入: 图
输出: 图G'
1. initialize
2. FOR
3.
4. FOR
5.
6. IF
7. IF
8.
9. ELSE IF
10.
11. END IF
12. END IF
13. END FOR
14. IF
15. BREAK//目标节点数满足当前节点匿名要求
16. END IF
17. END FOR
18. sort
19. WHILE
20.
21.
22.
23. END WHILE
24. END FOR
25. RETURN
再次通过贪心匿名分组得到匿名度序列, 普通加边阶段根据该序列尽量满足所有节点的匿名要求. 采用与优先加边阶段同样的加边操作, 仅考虑匿名代价大于0的节点, 并优先选择与当前节点距离近的目标节点进行连边.
算法 2. 普通加边算法
输入: 图
输出: 图G'', 匿名代价序列
1. initialize
2. FOR
3.
4. FOR
5. FOR
6. IF
7.
8. END IF
9. END FOR
10.
11. END FOR
12. RETURN
在层次化社区树中, 社区级别越高则社区规模越大, 整个图为最高级别的社区, 如图1所示. 采用Louvain算法[16]获得层次化社区结构, 这是一种基于模块度优化[17]的启发式算法. 第1步, 每个节点都属于一个独立的社区, 通过社区之间的节点移动, 使得社区划分的模块度最大化; 第2步, 根据当前划分的每个社区聚合成单个节点, 节点之间的边权重为其代表的两个社区之间的边权重之和; 重复这两个步骤, 直到模块度大小不再变化. igraph软件包[18]提供了该算法的实现函数community_multilevel. 当传入参数
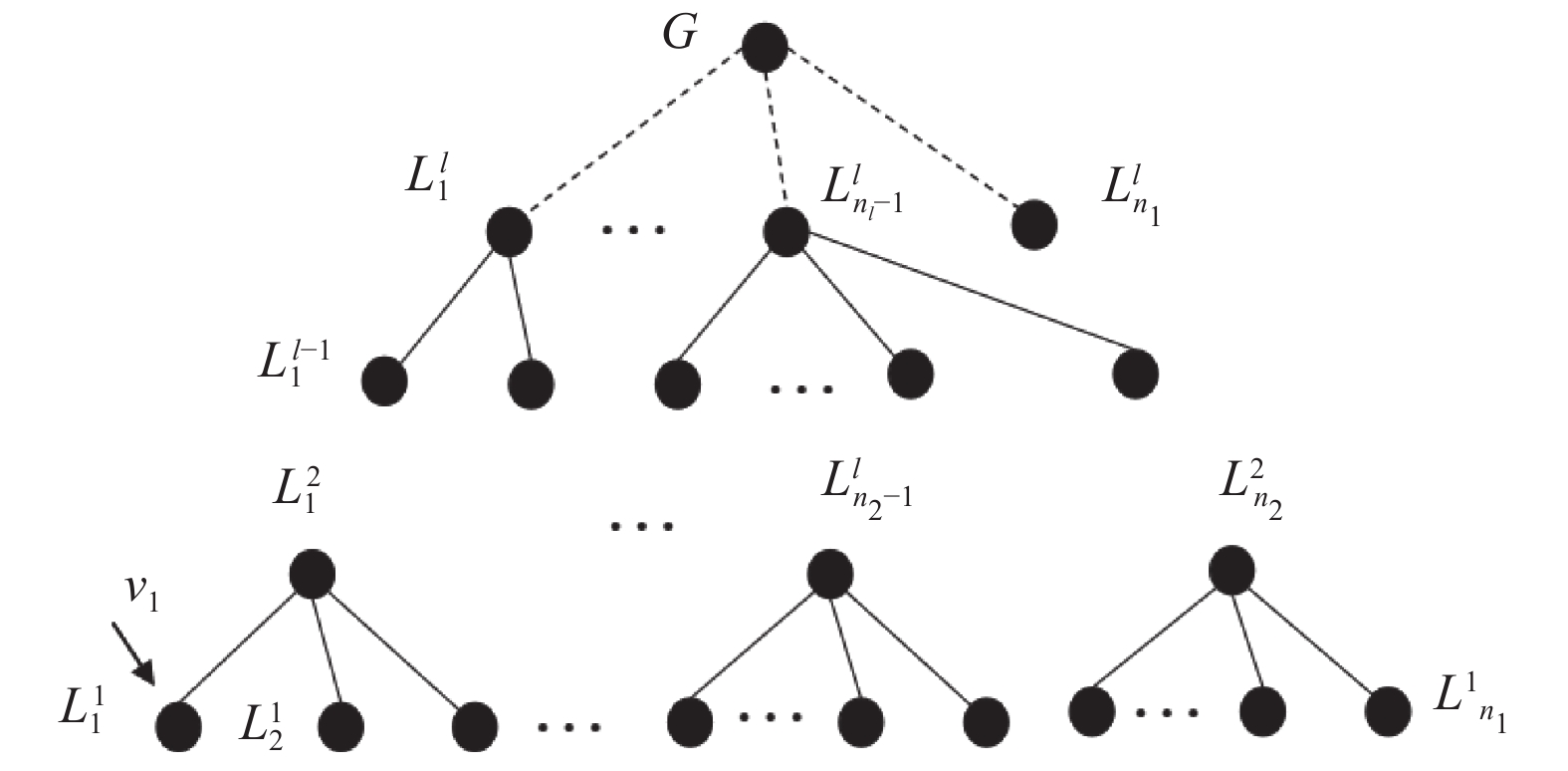
|
图 1 层次化社区树 |
算法 3. 层次社区发现算法
输入: 层次社区
输出: 包含
1. initialize
2. FOR
3. FOR
4. IF
5.
6. BREAK
7. END IF
8. END FOR
9. END FOR
10.
11. RETURN
图匿名化算法整合如下算法: 匿名分组算法、层次社区发现算法、加边算法和加点算法, 原图经过加边和加点操作生成满足k度匿名化的图.
算法 4.
输入: 图
输出: 匿名图
1.
2.
3.
4.
5.
6. IF
7.
8. END IF
9.
10. RETURN
对于一些特殊情况, 新算法仅通过加边无法满足节点匿名化要求. 所以, 通过Chester等人[11, 12]提出的加点算法, 将原图中未匿名的节点依次与新节点相连来满足节点的匿名化要求; 同时, 新节点也需要进行匿名化处理, 并最终实现图的匿名化. 新节点个数
| $ m = (1 + \max (mc, k)\boldsymbolod 2) + \max (mc, k) $ | (4) |
Liu等人[9]提出的贪心匿名分组算法的时间复杂度为
实验环境为Windows 10专业版, 运行环境采用PyCharm 2020 (Python语言), PC机主频3.6 GHz, 内存8 GB. 新算法命名为KDVEM21, 在5个真实数据集上进行实验, 同5个经典算法比较, 对比算法仅包含加边或加点的多项式时间复杂度算法: 包括Priority算法[9]、FKDA算法[10]、V_ADD算法[11, 12]、KDVEM15算法[13]和KDVEM18算法[14], 分别从匿名效果和匿名代价两个方面评估算法的性能, 并对实验结果进行分析.
4.1 数据集描述本文实验数据采用斯坦福大学提供的公开数据集(SNAP), 表1给出了数据集的详细介绍, 实验数据集都是无向的、简单的、无标记的.
4.2 评价方法徐恪等人[20]概述了典型的社交网络拓扑参数, Ji等人[21]讨论了图数据匿名化的研究演变和匿名度量的有效性, Zhao等人[22]指出组合多个度量指标作为隐私度量更具可比性, 赵蕙等人[23]认为社交网络匿名化度量方法的多样和复杂, 匿名算法研究者难以找到合适的方法评估自己的创新研究. 因此, 实验采用典型的3个图的结构特性作为匿名效果的度量指标.
(1) 平均路径长度(average path length)
平均路径长度计算公式如下,
| $ \overline P = \frac{{\displaystyle\sum\limits_{\left( {u, v} \right) \in CP} {{\textit{SPL}}(u, v)} }}{{|CP|}} $ | (5) |
(2) 传递系数(transitivity)
传递系数, 也称为全局聚类系数, 计算公式如下,
| $ T = \frac{\Delta }{ \wedge } $ | (6) |
(3) 平均聚类系数(average clustering coeffiient)
在社交网络中, 聚类系数的体现是一个人的两个好友彼此也是好友的概率, 计算公式如下:
| $ {C_i} = \frac{{2|{E_{xy}}|}}{{{d_i}({d_i} - 1)}}, {0 \leqslant {C_i} \leqslant 1} $ | (7) |
其中,
| $ \overline C = \frac{1}{n}\sum\limits_{i = 1}^n {{C_i}} , {0 \leqslant \overline C \leqslant 1} $ | (8) |
| 表 1 数据集描述 |
4.3 结果分析
实验参数

|
图 2 ca-GrQc数据集上匿名图的结构特性 |
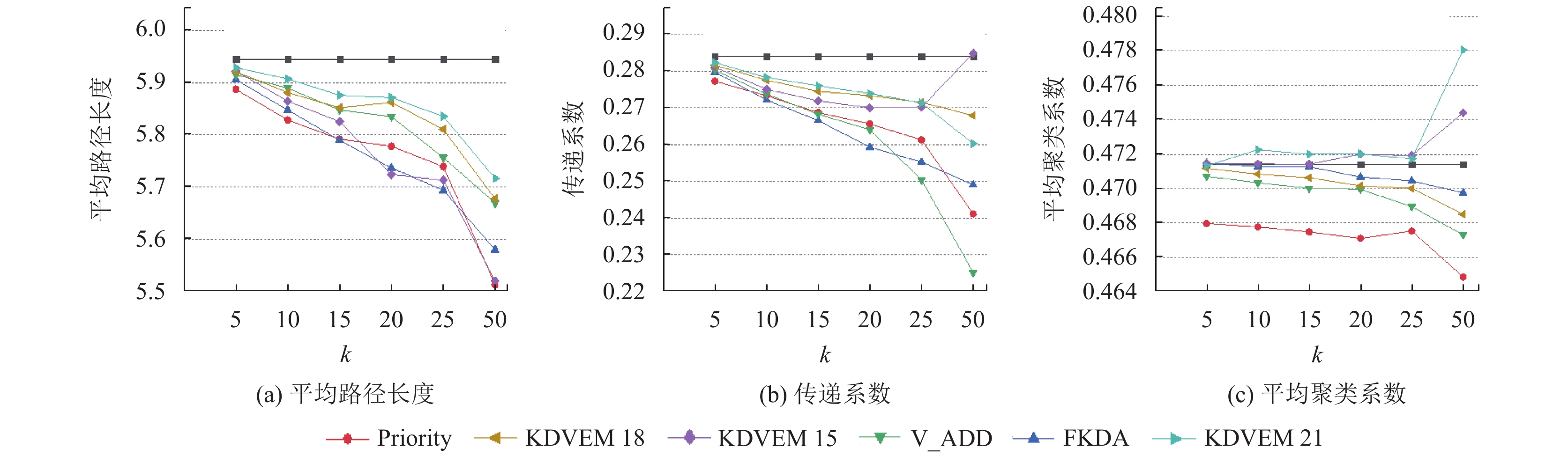
|
图 3 ca-HepTh数据集上匿名图的结构特性 |
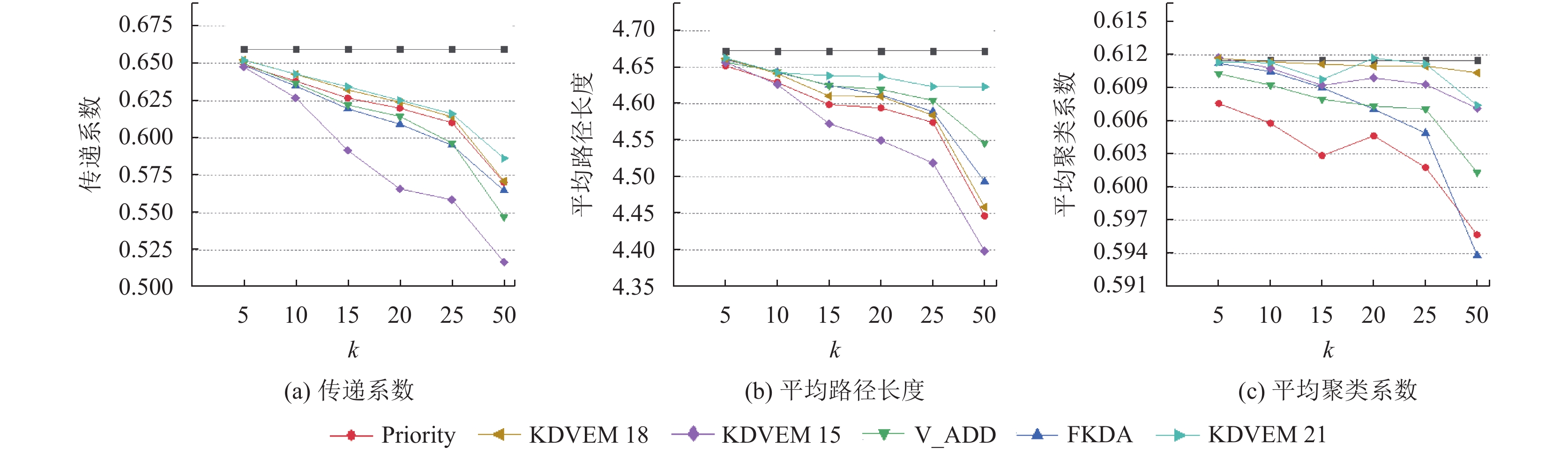
|
图 4 ca-HepPh数据集上匿名图的结构特性 |

|
图 5 ca-AstroPh数据集上匿名图的结构特性 |

|
图 6 ca-CondMat数据集上匿名图的结构特性 |
为了直观地对比算法性能, 采用平均变化量的百分比形式作为实验结果, 如表2所示, 数值越小说明匿名图与原图的结构特性差异越小. 计算公式如式(9), 其中,
| 表 2 匿名图的结构特性 |
| $ R = \frac{1}{{\left| k \right|}}\sum\limits_{i \in k} {{{\left| {\frac{{\vartriangle m}}{{{m_0}}}} \right|}_i}} \times 100 $ | (9) |
Rajabzadeh等人[15]认为3个度量指标具有同等的重要性, 取3个度量指标的平均值作为算法的综合评价. 随着参数
Zhang等人[24]通过对比添加边和节点来评估算法的匿名代价, 如表3、表4所示. KDVEM21算法采用两阶段加边操作, 充分利用原图的节点进行加边, 减少了添加的节点. 对比加边且可加点类算法, KDVEM21算法添加的边或节点更少.
| 表 3 ca-HepPh数据集上边和节点数的变化量 |
| 表 4 ca-AstroPh数据集上边和节点数的变化量 |
5 总结与展望
社交网络匿名化是复杂网络领域中一个重要的研究方向. 解决社交网络匿名化问题需要平衡用户隐私保护和图数据实用性二者的关系. 本文利用经典算法的优势提出了改进算法, KDVEM21算法采用加边且可加点的匿名化策略, 分两个阶段进行加边, 并结合节点特性和社区结构对加边操作进行了优化. 在5个真实网络上测试KDVEM21算法的有效性, 实验结果表明, 对比5个经典算法, 大多数情况下, KDVEM21算法能更好地保留图的几种典型的结构特性(平均路径长度、平均聚类系数和传递系数), 并且对比加边且可加点类算法, 添加边或节点更少; 但新算法的时间复杂度并不具备优势. 未来工作: 对算法时间复杂度进行优化; 探索算法在其它图结构特性度量下的匿名效果; 减少图匿名化的代价.
| [1] |
Sahoo SR, Gupta BB. Security issues and challenges in online social networks (OSNs) based on user perspective. In: Gupta BB, Agrawal DP, Wang HX, eds. Computer and Cyber Security. Boca Raton: Auerbach Publications, 2018. 591–606.
|
| [2] |
Beigi G, Liu H. A survey on privacy in social media: Identification, mitigation, and applications. ACM/IMS Transactions on Data Science, 2020, 1(1): 7. |
| [3] |
Kiranmayi M, Maheswari N. A review on privacy preservation of social networks using graphs. Journal of Applied Security Research, 2021, 16(2): 190-223. |
| [4] |
Casas-Roma J, Herrera-Joancomartí J, Torra V. k-Degree anonymity and edge selection: Improving data utility in large networks
. Knowledge and Information Systems, 2017, 50(2): 447-474. DOI:10.1007/s10115-016-0947-7 |
| [5] |
Casas-Roma J. DUEF-GA: Data utility and privacy evaluation framework for graph anonymization. International Journal of Information Security, 2020, 19(4): 465-478. DOI:10.1007/s10207-019-00469-4 |
| [6] |
Casas-Roma J, Herrera-Joancomartí J, Torra V. A survey of graph-modification techniques for privacy-preserving on networks. Artificial Intelligence Review, 2017, 47(3): 341-366. |
| [7] |
Backstrom L, Dwork C, Kleinberg J. Wherefore art thou R3579X?: Anonymized social networks, hidden patterns, and structural steganography. Proceedings of the 16th International Conference on World Wide Web. Alberta: ACM, 2007. 181–190.
|
| [8] |
Hay M, Miklau G, Jensen D, et al. Resisting structural re-identification in anonymized social networks. Proceedings of the VLDB Endowment, 2008, 1(1): 102-114. |
| [9] |
Liu K, Terzi E. Towards identity anonymization on graphs. Proceedings of the 2008 ACM SIGMOD International Conference on Management of Data. Vancouver: ACM, 2008. 93–106.
|
| [10] |
Lu XS, Song Y, Bressan S. Fast identity anonymization on graphs. Proceedings of the 23rd International Conference on Database and Expert Systems Applications. Vienna: Springer, 2012. 281–295.
|
| [11] |
Chester S, Kapron BM, Ramesh G, et al. k-Anonymization of social networks by vertex addition
. ADBIS, 2011, 789(2): 107-116. |
| [12] |
Chester S, Kapron BM, Ramesh G, et al. Why Waldo befriended the dummy? k-Anonymization of social networks with pseudo-nodes. Social Network Analysis and Mining, 2013, 3(3): 381-399. DOI:10.1007/s13278-012-0084-6 |
| [13] |
Ma TH, Zhang YL, Cao J, et al. KDVEM: A k-degree anonymity with vertex and edge modification algorithm
. Computing, 2015, 97(12): 1165-1184. |
| [14] |
吴童. k度匿名图构造算法的研究[硕士学位论文]. 上海: 华东师范大学, 2018.
|
| [15] |
Rajabzadeh S, Shahsafi P, Khoramnejadi M. A graph modification approach for k-anonymity in social networks using the genetic algorithm
. Social Network Analysis and Mining, 2020, 10(1): 38. DOI:10.1007/s13278-020-00655-6 |
| [16] |
Blondel VD, Guillaume JL, Lambiotte R, et al. Fast unfolding of communities in large networks. Journal of Statistical Mechanics: Theory and Experiment, 2008, 2008: P10008. |
| [17] |
Newman MEJ, Girvan M. Finding and evaluating community structure in networks. Physical Review E, 2004, 69(2): 026113. DOI:10.1103/PhysRevE.69.026113 |
| [18] |
Csárdi G, Nepusz T. The igraph software package for complex network research. InterJournal Complex Systems, 2006, 1695(5): 1-9. |
| [19] |
Kleene SC. Representation of events in nerve nets and finite automata. Automata Studies, 1956, 34: 3–41.
|
| [20] |
徐恪, 张赛, 陈昊, 等. 在线社会网络的测量与分析. 计算机学报, 2014, 37(1): 165-188. |
| [21] |
Ji SL, Mittal P, Beyah R. Graph data anonymization, de-anonymization attacks, and de-anonymizability quantification: A survey. IEEE Communications Surveys & Tutorials, 2017, 19(2): 1305-1326. |
| [22] |
Zhao YC, Wagner I. Using metrics suites to improve the measurement of privacy in graphs. IEEE Transactions on Dependable and Secure Computing, 2020, 19(1): 259–274.
|
| [23] |
赵蕙, 王良民, 申屠浩, 等. 网络匿名度量研究综述. 软件学报, 2021, 32(1): 218-245. DOI:10.13328/j.cnki.jos.006103 |
| [24] |
Zhang YL, Ma TH, Cao J, et al. K-anonymisation of social network by vertex and edge modification. International Journal of Embedded Systems, 2016, 8(2–3): 206–216.
|
 2022, Vol. 31
2022, Vol. 31


