2. 闽江学院 计算机与控制工程学院, 福州 350108;
3. 福建师范大学 数字福建环境监测物联网实验室, 福州 350117
2. College of Computer and Control Engineering, Minjiang University, Fuzhou 350108, China;
3. Digital Fujian Internet-of-Thing Laboratory of Environmental Monitoring, Fujian Normal University, Fuzhou 350117, China
脑机接口(brain computer interface, BCI)技术是一种建立在大脑和外部设备之间、且不依赖于外围神经系统与肌肉组织的新型人机交互方式[1]. BCI技术可以实现大脑与外部电子设备的直接通信与控制, 主要涉及认知神经科学、信号处理和模式识别等多学科交叉. 常见的BCI技术包括无创BCI[2]和有创BCI, 其中无创BCI可应用于常人, 不用面对伦理道德问题. 脑电信号是常用的无创BCI技术手段之一, 基于脑电信号(electroencephalogram, EEG)的BCI主要包含P300[3], 稳态视觉电位[4]和运动想象[5] 3个类别.
运动想象(motor imagery, MI)是指人在进行运动想象(如想象左手、右手、舌、双脚的运动)时所产生的大脑运动感知节律变化, 主要由mu节律和beta节律组成[6]. 如人在进行单侧肢体的想象运动时, 大脑皮层同侧感觉区中的mu和beta节律幅值会增加, 发生事件相关同步(event-related synchronization, ERS)现象; 同时, 大脑皮层对侧运动感觉区中的mu和beta节律幅值会减少, 发生事件相关去同步(event-related desynchronization, ERD)现象[7]. 基于EEG的运动想象脑机接口(motor imagery brain computer interface, MI-BCI)系统可以对这些不同的ERD/ERS模式进行分类, 其目的在于准确的辨认出受试者的肢体运动意图[8]. 但由于MI-BCI过程中采集到的EEG信号信噪比低、空间分辨率低、非线性、非平稳性和随机性强等特点, 导致现有的脑电识别技术对EEG信号的解码正确率较低.
近年来, 深度学习方法在图像识别[9]、语音识别[10]等领域体现出其巨大的优势. 目前, 众多研究者已经将深度神经网络(deep neural network, DNN)应用到MI-BCI过程中 EEG信号的模式识别中. 胡章芳等人[11]提出了一种短时傅里叶变换(short-time Fourier transform, STFT)和卷积神经网络(convolutional neural network, ConvNet)相结合的方法进行MI-BCI过程中EEG信号的识别分类, 该方法在BCI竞赛数据集上获得了86.5%的平均分类正确率, 优于其他传统识别分类方法. Tabar等人[12]结合卷积神经网络与堆叠自动编码器(stacked autoencoder, SAE)对MI-BCI过程中EEG信号进行模式识别研究, 该方法首先采用短时傅里叶变换进行EEG信号的时频域特征预提取, 接着通过SAE对ConvNet提取到的特征进行最终分类. 该方法在2008年BCI竞赛数据集2b上获得了不错的分类性能, Kappa值达到 0.547, 比竞赛第一名的算法高出9%. 褚亚奇等人[13]提出一种基于时空特征学习卷积神经网络(TSCNN)的运动想象脑电解码方法, 该方法对公共数据集的平均解码精度达到80.09%, 显著提升了运动想象脑电解码的可靠性. Dai等人[14]提出一种将卷积神经网络(CNN)结构与变分自编码器(VAE)相结合的MI-BCI过程中EEG信号分类框架, 该框架平均Kappa值为0.564, 优于文献中最好的BCI竞赛IV数据集2b的分类方法, 提高了3%的识别准确率. Dai等人[15]提出了一种混合尺度CNN架构和数据增强方法(HS-CNN)用于脑电运动图像分类, 该方法在两个常用数据集上的平均分类准确率分别达到91.57%和87.6%, 优于几种最新的脑电运动图像分类方法.
在采用深度神经网络进行MI-BCI过程中EEG信号的模式识别中, 传统的训练方法是使用trial-wise方法: 即将整个试验(trial)信号作为输入样本, 以每个trial的标签作为目标的训练策略. 但传统的trial-wise策略具有两大不足之处: 一是样本量太少, 不适合用于深度神经网络; 二是单个trial的时间域过长, 特征维度太高, 导致分类效果不好. 为此, Schirrmeister等人[16]设计了一种cropped训练策略, 该策略通过滑动时间窗口(sliding time windows)对每个trial进行裁剪, 既增加了训练样本量, 又避免了数据特征维度太高对结果的影响. 但是由于单纯的cropped训练策略未考虑到EEG信号具有时变性, 单纯的cropped训练策略无法提取和学习到各个切分后crops之间的关联性特征, 导致效果不佳. Schirrmeister等人[16]设计的cropped训练策略采用的是非重叠时间的cropped切分方式, 即各个crops之间没有重叠部分, 并且原文中并未进行trial-wise和cropped的方式对比. 对此, 本文提出一种新型的重叠时间切片的训练策略, 并且详细对比了几种划分方式的结果. 重叠时间切片的训练策略采用带有重叠时间的滑动时间窗口对原始输入进行切分, 并在计算最后的分类标签时, 采用多数投票制确定样本的预测标签. 带有重叠的时间滑动窗口可保证切分后的样本之间保留其重叠部分的信息, 可通过神经网络提取和学习到切分后样本之间的关联性特征. 除此之外, 保留样本间的重叠信息可以使可学习到的特征更加丰富, 可以更加适应较深层的网络.
本文的其余部分结构如下: 第2节介绍基于深度神经网络模型的运动想象EEG模式识别中常见的5种模型. 第3节首先介绍用于运动想象EEG信号的trial-wise和cropped训练策略, 以及本文提出的重叠时间切片的训练策略. 第4节为实验的结果与分析, 包括实验框架、3种开源MI实验数据集, 以及各种策略在各种模型的对比结果.
本文的主要贡献:
(1)提出了一种改进的重叠时间切片的训练策略, 该训练策略可有效弥补一般训练策略带来的训练样本不足、特征维度太高和未能解决EEG信号具有时变性的缺陷, 有效提升了EEG信号的分类准确率.
(2)在3种不同公共数据集上对比了3种不同训练策略的性能和效率. 本文提出的重叠时间切片训练策略对公共数据集的分类准确率相比于先前两种训练策略有较显著的提升.
2 基于深度神经网络模型的运动想象EEG模式识别 2.1 Deep ConvNetDeep ConvNet架构的灵感来自于Krizhevsky等人[17]提出的且在计算机视觉领域取得成功的一种架构. 该架构的出发点是想要找到一个能够提取广泛特征并且不限于特定特征类型的神经网络模型[18]. 设计这种通用体系的目的是揭露这种通用的ConvNet是否可以仅靠少量的专业知识就可以取得具有竞争力的准确率.
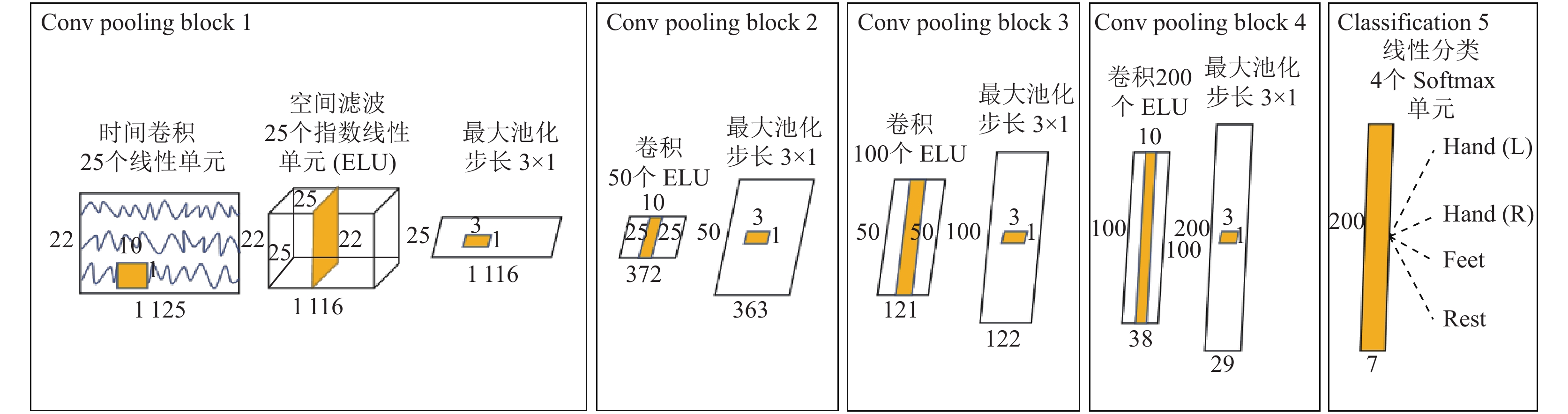
Deep ConvNet具有4个卷积最大池化块(convolution-max-pooling blocks), 其中第1个特殊的块用于处理输入的EEG信号, 然后是3个标准的卷积最大池化块和一个Softmax分类层. Deep ConvNet的体系结构如图1.
Deep ConvNet的一些设计策略:
(1)为了更好的处理大量输入通道, 第1个卷积块采取分步卷积, 分为两层: 在第1层中, 每个滤波器随时间进行卷积. 在第2层中, 每个滤波器对先前进行时间卷积后的电极对执行权重的空间滤波.
(2)使用指数线性单元(exponential linear units, ELU)[19]作为激活函数. 公式为:
| $ f(x) = \left\{ \begin{gathered} x,\; x \gt 0 \hfill \\ {e^x} - 1,\; x \leqslant 0 \hfill \\ \end{gathered} \right. $ | (1) |
(3)在每个卷积层的输出使用批标准化和归一化. 对每一批训练样本, 将网络的中间输出标准化为零均值和单位方差, 这可以使在训练过程中的层间的输入保持近似的正态分布, 有助于优化.
(4)在训练更新中采用dropout. 除第一个卷积层外, 以0.5的概率随机地将之后的卷积层的输入设置为零.
|
图 1 Deep ConvNet体系结构 |
2.2 Shallow ConvNet
Shallow ConvNet是一种比较浅的神经网络结构, 其受到滤波器组共空间模式(filter bank common spatial patterns, FBCSP)的启发, 是专门为解码频带功率特征而量身定制的. 这里首先介绍FBCSP解码试验标签的一些步骤:
(1)带通滤波: 应用不同的带通滤波器将原始EEG信号分离为不同的频带.
(2)划分时间: 将连续的EEG信号分为3部分.
(3) CSP特征计算: 在每个频带上, 将CSP算法应用于提取空间滤波器. CSP的目的是提取空间滤波器, 以通过空间滤波后的试验信号的功率来区分试验.
(4)空间滤波: 将步骤(3)中计算出的空间滤波器应用于EEG信号.
(5)特征构造: 特征向量由滤波后的信号构成, 具体来说, 特征向量是试验信号的每个频带使用不同空间滤波器空间滤波后的对数方差.
(6)分类: 基于特征向量训练一个分类器以预测每个试验标签.
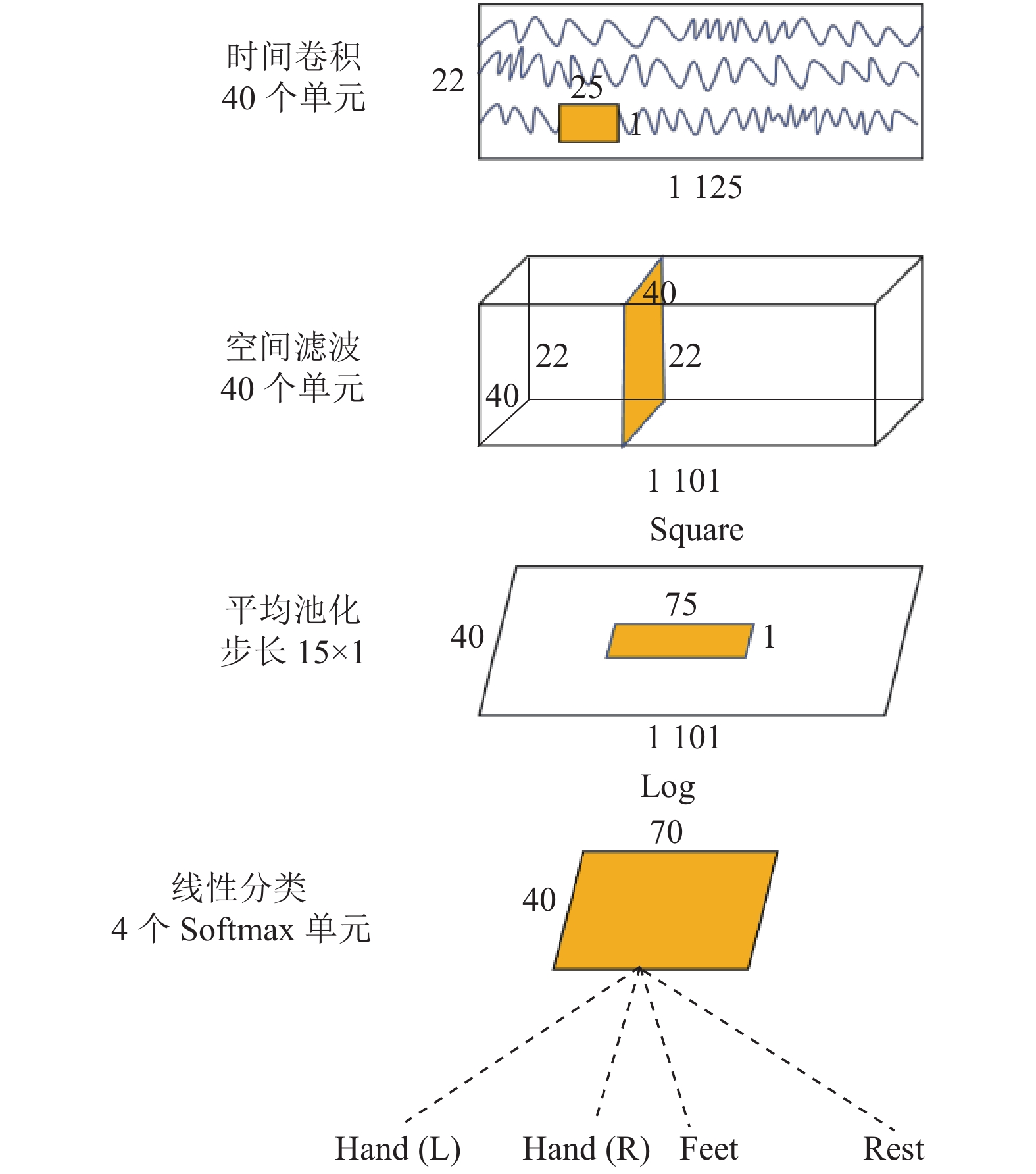
Shallow ConvNet的前两层执行时间卷积和空间滤波. 这类似于FBCSP中的带通滤波和CSP空间滤波步骤. 与Deep ConvNet相比, Shallow ConvNet的时间卷积具有更大的卷积核(25 vs. 10), 从而允许在该层进行更大范围的转换. 在Shallow ConvNet的时间卷积和空间滤波后, 使用了平方非线性函数(square)、均值池化层和对数激活函数(log), 这些步骤组合在一起类似于FBCSP中的试验的对数方差计算. 与FBCSP相比, Shallow ConvNet将所有计算步骤嵌入到单个网络中, 因此可以共同优化所有步骤. Shallow ConvNet的体系结构如图2所示.
|
图 2 Shallow ConvNet体系结构 |
2.3 Hybrid ConvNet
Hybrid ConvNet是一种融合Deep ConvNet和Shallow ConvNet的混合ConvNet模型. Hybrid ConvNet希望从Shallow ConvNet中提取到更具体特征, 以及从Deep ConvNet中提取到更通用的特征. Hybrid ConvNet用Deep ConvNet和Shallow ConvNet的60个和40个滤波器ELU层替换了两个ConvNet的4个滤波器Softmax分类层. 将生成的100个特征图连接起来, 并用作新的Softmax分类层的输入. Hybrid ConvNet不使用任何Deep或Shallow ConvNet预先训练好的参数, 而是对整个Hybrid ConvNet进行重新训练.
2.4 EEGNetEEGNet是由Lawhern等人[20]提出的基于CNN的模型, 是一种紧凑的脑电分析卷积神经网络, 专为常规EEG信号识别任务而设计. EEGNet可以应用于多种不同的BCI范式, 不但可采用非常有限的数据进行训练, 而且可以产生神经生理学上可解释的特征.
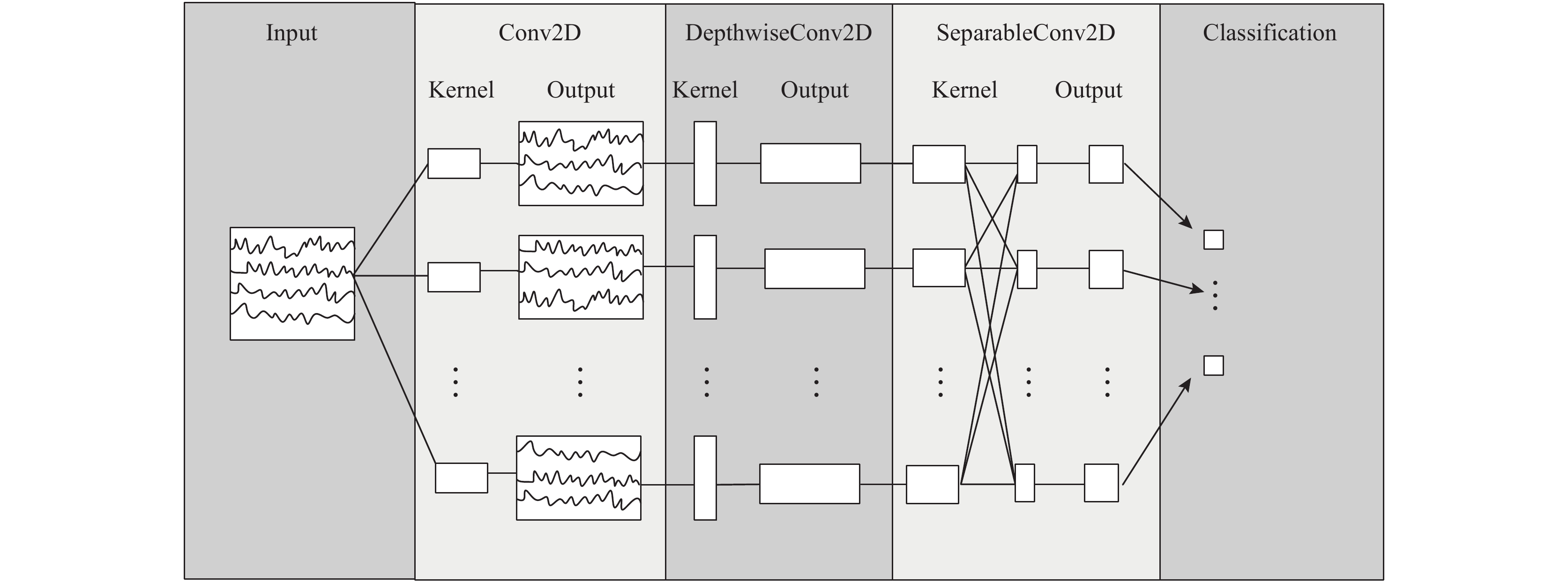
EEGNet保留了Shallow ConvNet中的时间和空间卷积层. EEGNet引入了深度卷积和可分离卷积, 来代替Shallow ConvNet中的简单卷积, 以减少训练参数的数量. EEGNet还使用了ELU激活函数代替Shallow ConvNet的平方激活函数. EEGNet的总体结构如图3所示, 对于一个22×1125的输入样本, 在Conv2D层使用8个大小为(1, 64)的卷积核, 使用线性激活函数, 输出大小为(8, 22, 1 125), 在DepthwiseConv2D层使用16个大小为(22, 1)的卷积核, 使用ELU激活函数, 输出大小为(16, 1, 1 125), 接着是一个平均池化层Average-Pool2D, 卷积核为(1, 4), 输出大小为(16, 1, 281), 在 SeparableConv2D层, 使用16个大小为(1, 16)的卷积核, 使用ELU激活函数, 输出大小为(16, 1, 281), 接着一个AveragePool2D层, 卷积核为(1, 4), 输出大小为(16, 1, 35), 然后展平成大小为560的一维数组, 最后一个全连接层有2 240卷积核, 使用Softmax激活函数, 输出大小为4的一维数组.
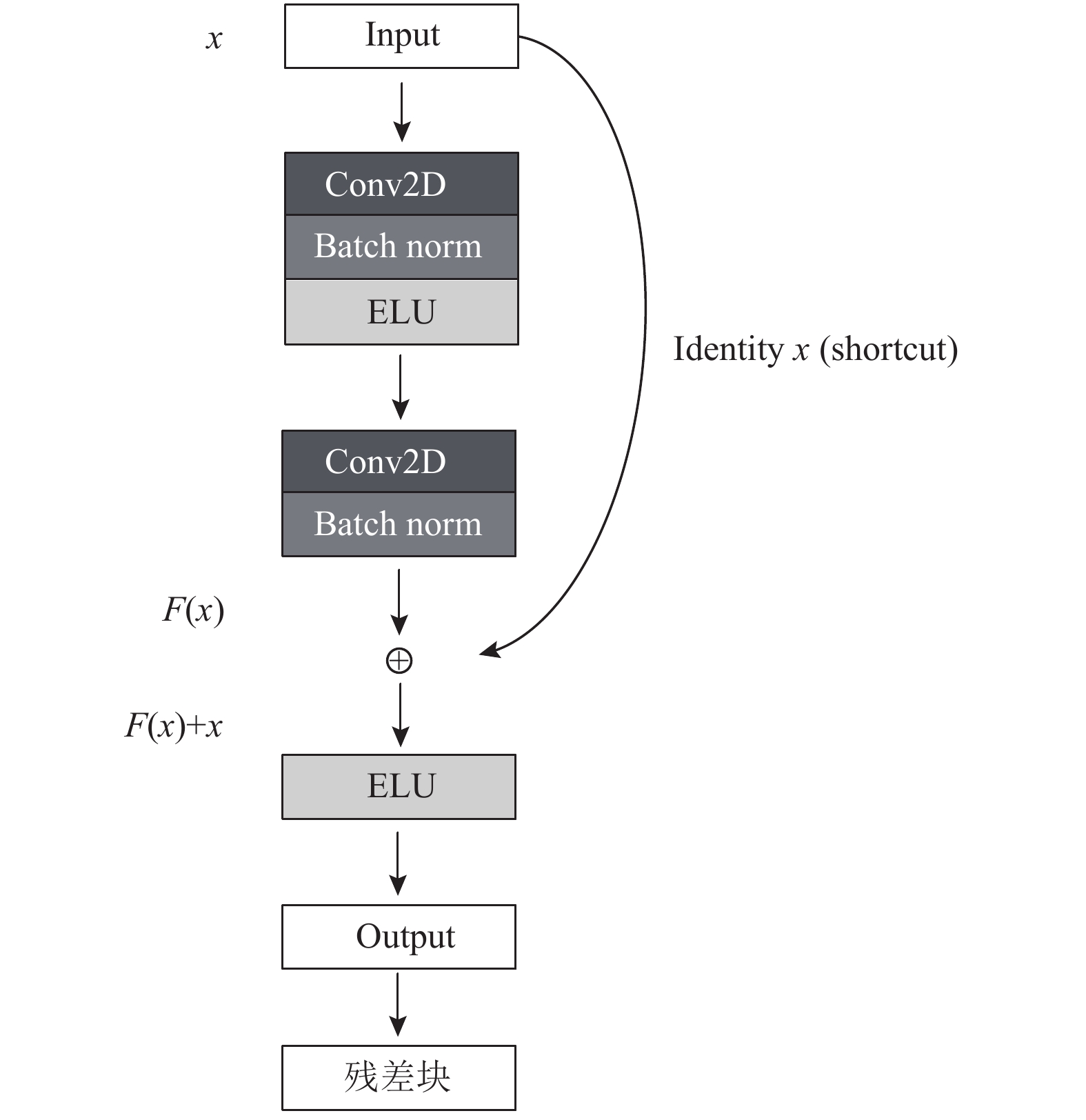
2.5 EEGResNet残差网络(residual network, ResNet)是由He等人[21]提出的一种卷积神经网络结构, 获得了2015年ImageNet大规模视觉识别竞赛的第一名. ResNet通常具有大量的层数, 将ResNet应用于EEG解码旨在研究这种具有更多层数的网络是否也能在EEG解码中获得良好的性能. 在ResNet的一个残差块结构中, 记输入为x, 其期望学习到的潜在映射记为
EEGResNet模型在第1块仍然是先进行时间卷积和空间滤波, 接着是14个残差块, 平均池化和最后的Softmax分类层. EEGResNet的体系结构如表1.
|
图 3 EEGNet总体结构 |
3 运动想象EEG信号单个trial重叠时间切片策略 3.1 Trial-wise策略的训练方法
通常, 为了训练一个ConvNet模型, 需要对ConvNet模型中所有参数(包括所有权重和偏置)进行联合训练. 在有监督分类问题中, 构建ConvNet模型的目的是计算从输入数据到其对应的真实类别标签的一个函数:
| $ f({X}^{i};\theta ):{R}^{E\cdot T}\to {R}^{K} $ | (2) |
其中,
| $ p({l_k}|f({X^i};\theta )) = \frac{{\exp ({f_k}({X^i};\theta ))}}{{\displaystyle\sum\nolimits_{m = 1}^K {\exp ({f_m}({X^i};\theta ))} }} $ | (3) |
其中,
| $ \theta = \arg \mathop {\min }\limits_\theta \sum\nolimits_{i = 1}^N {loss({y^i}, p({l_k}|{f_k}({X^i};\theta )))} $ | (4) |
其中,
| $ \begin{split} & loss({y^i}, p({l_k}|{f_k}({X^i};\theta ))) = \hfill \\ & \sum\nolimits_{k = 1}^K { - \log (p({l_k}|{f_k}({X^i};\theta ))) \cdot \delta ({y^i} = {l_k})} \hfill \end{split} $ | (5) |
其中,
|
图 4 残差块 |
| 表 1 EEGResNet体系结构 |
3.2 Cropped策略的训练方法
Cropped策略的训练使用裁剪方法, 即在原始输入试验中使用滑动窗口, 使输入深度神经网络模型中的训练样本比trail-wise策略更多, 更适合于深度神经网络模型的训练. 对于原始输入试验样本
| $ {C^i} = \left\{ {X_{1,\cdots,E, t,\cdots,t + T'}^i|t \in 1,\cdots,T - T'} \right\} $ | (6) |
其中, X1,…,E表示来自E个电极的输入矩阵, 所有
Cropped策略通过裁剪增加了训练集的大小, 为了减少其带来的计算负担, 将相邻的crops解码在一起, 并重用网络中的中间卷积输出. 该方法同时输入多个crops并在深度神经网络模型的一次正向传播过程中计算所有crops的预测值. 该方法会导致一个新的超参数: 同时处理的crops数量. 同时处理的crops越多, 网络获得的加速效果就越大.
在cropped训练策略中使用了新的损失函数, 其在trial-wise的损失函数的基础上添加了两个相邻crop的预测的交叉熵. 对于每个crop:
| $ \begin{split} & loss({y^i}, p({l_k}|{f_k}(X_{t,\cdots,t + T'}^i;\theta ))) \hfill \\ & =\sum\nolimits_{k = 1}^K { - \log (p({l_k}|{f_k}(X_{t,\cdots,t + T'}^i;\theta )))} \cdot \delta ({y^i} = {l_k}) \hfill \\ &\quad +\sum\nolimits_{k = 1}^K { - \log (p({l_k}|{f_k}(X_{t,\cdots,t + T'}^i;\theta )))} \hfill \\ &\quad \cdot p({l_k}|{f_k}(X_{t + 1,\cdots,t + {{T'}} + 1}^i;\theta )) \hfill \end{split} $ | (7) |
运动想象属于长时间、持续的过程, 根据经典运动想象刺激范式, 在整个4 s的信号采集过程中, 受试者都将持续保持运动想象. 虽然反映运动想象数据可能集中在部分采样区间中, 但由于不同受试者对于运动想象的反应时间、持续时间不同, 这样的区间却因为个体差异性而各不相同. 因此, 无法使用统一的方式从不同被试者的运动想象集中区间中提取有效特征. 实际上, 由于卷积神经网络的特性, 误差反向传播将会对不同区间的权重进行调整, 随着训练的进行那些蕴含运动想象特征的权重越来越高, 而不蕴含运动想象特征的权重将越来越低. 因此, 本文选择采用重叠切片的方式, 让蕴含和不蕴含运动想象特征的区间进行组合, 保证蕴含运动想象区间的部分以更多样性的组合形式输入至卷积神经网络中, 从而保证了采用卷积神经网络进行运动想象分类时的鲁棒性.
重叠时间切片(overlapped)策略同样使用滑动窗口对原始试验进行切分. 与cropped策略不同的是, 重叠时间切片策略通过
| $ O_{\alpha , \beta }^i = \left\{ {X_{1,\cdots,E, t,\cdots,t + \alpha }^i|t = 1, 1 + \beta, \cdots, 1 + n\beta } \right\} $ | (8) |
其中,
对于每个切分后的
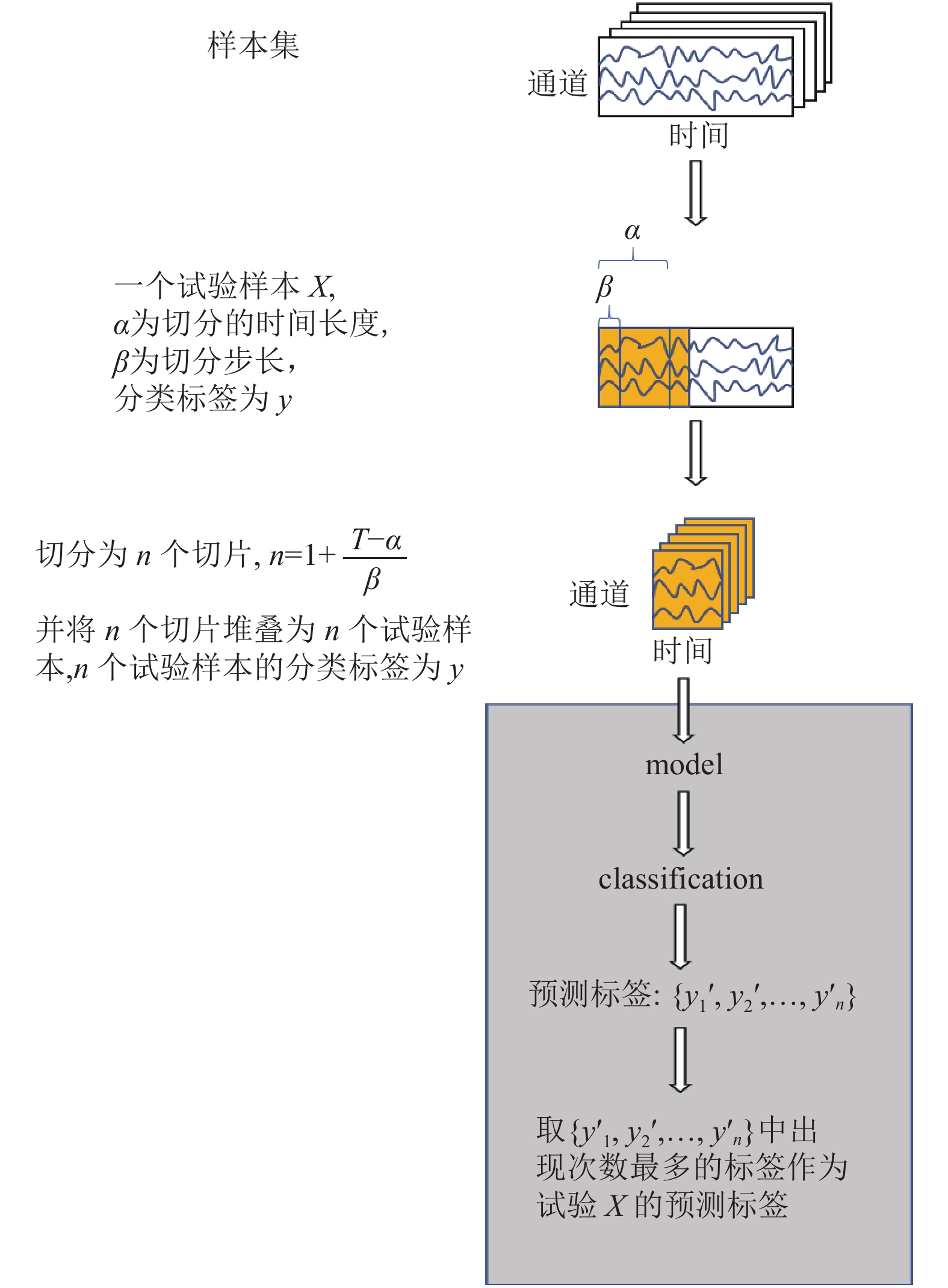
|
图 5 重叠时间切片切分策略 |
在重叠时间切片策略中, 对于每个切片
| $ \begin{split} & loss({y^i}, p({l_k}|{f_k}(O_{\alpha , \beta }^i;\theta ))) \hfill \\ & =\sum\nolimits_{k = 1}^K { - \log (p({l_k}|{f_k}(O_{\alpha , \beta }^i;\theta )))} \cdot \delta ({y^i} = {l_k}) \hfill \end{split} $ | (9) |
在预测样本标签时, 采用多数投票制, 即对于来自同一个原始试验的切片, 统计这些切片的预测值, 将这些切片中出现最多次数的预测标签作为这个样本本次预测的预测标签. 该策略的其余超参数与trial-wise策略的超参数保持一致.
4 实验与结果分析 4.1 实验初始化本文实验选用2008年BCI Competition IV Dataset 1、2a和2b三个公开数据集.
Dataset 1数据集包含来自7位健康受试者执行运动想象的EEG数据. 标签类型为2种, 其中类别1表示受试者在执行左、右手或者脚的运动想象, 类别0表示受试者无控制意图. 该数据集测量了每个受试者的59个在感觉运动区域上最密集的通道信号. 信号以1 000 Hz为采样频率, 并在0.05–200 Hz之间进行带通滤波. Dataset 2a数据集包含来自9个受试者执行运动想象的EEG数据. 运动想象类型为4种, 包括左手、右手、双脚和舌头. 信号以250 Hz为采样频率, 并在0.5–100 Hz之间进行带通滤波. 放大器的灵敏度设置为100 µV, 并使用了50 Hz陷波滤波器抑制线路噪声.
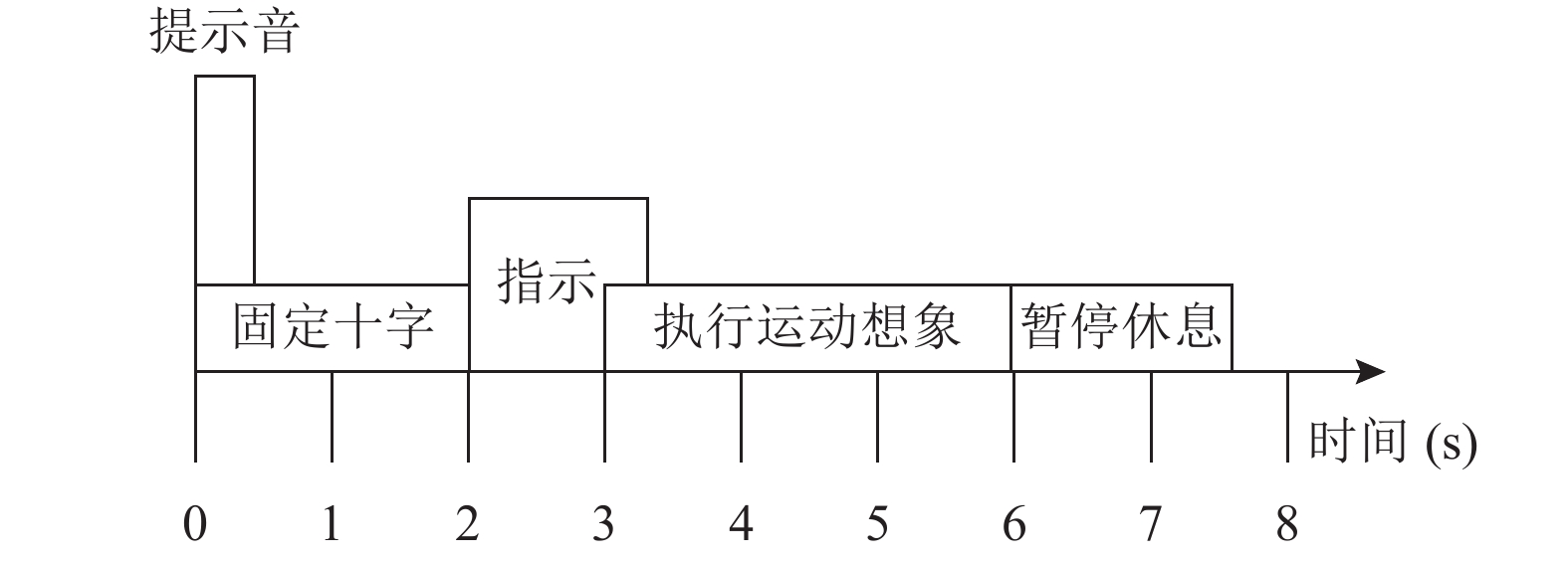
Dataset 2a数据集的EEG信号采集过程如图6所示. 每个受试者坐在计算机屏幕前的舒适扶手椅上. 在实验开始时, 屏幕上出现十字注视叉, 并发出简短的提示音, 2 s后, 屏幕上出现持续1.25 s的指向左、右、上或下(分别对应于4种运动想象类别)的箭头, 随后受试者执行箭头对应的运动想象并持续到实验开始后的第6 s. 训练数据集包含每个受试者的288次试验样本, 测试数据集同样包含每个受试者的288次试验样本.
|
图 6 Dataset 2a数据采集实验 |
Dataset 2b数据集包含来自9个右利手的受试者执行运动想象的EEG数据. 运动想象类型为2种, 包括左手和右手. 信号以250 Hz为采样频率, 并在0.5–100 Hz之间进行带通滤波. 放大器的灵敏度设置为100 µV, 并使用了50 Hz陷波滤波器以抑制线路噪声. 每位受试者的脑电数据集都包括5个 Session, 前2个Session为无视觉反馈的脑电想象数据, 后3个Session为包含视觉反馈的脑电想象数据.
Dataset 2b数据集的采集工作分为无视觉反馈和有视觉反馈实验. 无视觉反馈实验过程如图7所示, 在实验开始时, 屏幕上出现十字注视叉, 并发出简短的提示音, 2 s后, 屏幕上出现持续1.25 s的指向左或右(分别对应于左手或右手运动)的箭头, 随后受试者执行箭头对应的运动想象并持续到实验开始后的第6 s.
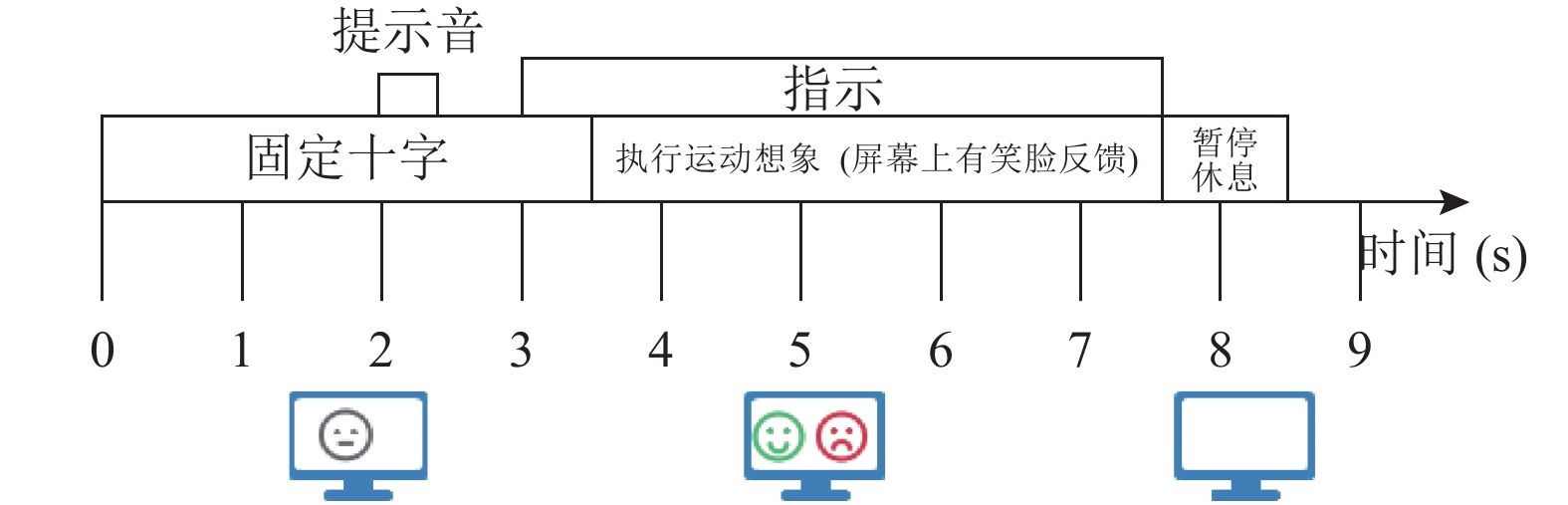
有视觉反馈实验过程如图8所示, 在实验开始时, 屏幕上显示灰色的笑脸, 2 s后发出简短的提示音, 3 s时屏幕上出现持续1.25 s的指向左或右(分别对应于左手或右手运动)的箭头, 随后受试者执行箭头对应的运动想象将笑脸向左或向右移动, 如果移动方向正确, 屏幕中的灰色笑脸就会变为笑脸, 反之, 变成哭脸.

|
图 7 Dataset 2b无视觉反馈数据采集实验 |
|
图 8 Dataset 2b有视觉反馈数据采集实验 |
本文实验的硬件配置为CPU: Intel(R) Core(TM) i5-10210U 1.60 GHz, GPU: NVIDIA GeForce MX350.
本文采用开源的ConvNet模型EEG信号识别框架进行EEG信号识别(
基于本文介绍的trial-wise、cropped和设计的重叠时间切片(overlapped)策略, 将这3种训练方法应用于本文介绍的5种深度神经网络模型: Deep ConvNet、Shallow ConvNet、Hybrid ConvNet、EEGNet和EEGResNet上. 由于Dataset 1数据集的单个trial持续时间较短, 在Dataset 1数据集上采用trial-wise、cropped和overlapped三种策略训练2种深度神经网络模型: Shallow ConvNet和EEGNet, 得到所有受试者的测试集上的识别准确率如表2所示. 其中, 实验的overlapped训练方法中的
由表2可以看出, 在Dataset 1数据集上, overlapped训练策略在Shallow ConvNet和EEGNet上的分类准确率均高于cropped训练策略的分类准确率, 分别提升了5.4%和6.9%. 在EEGNet模型上的分类准确率高于trial-wise训练策略的, 在Shallow ConvNet模型上的分类准确率与trail-wise的相差不大.
| 表 2 Trial-wise、cropped和overlapped (100, 20)方法在Dataset 1数据集上的识别准确率比较(%) |
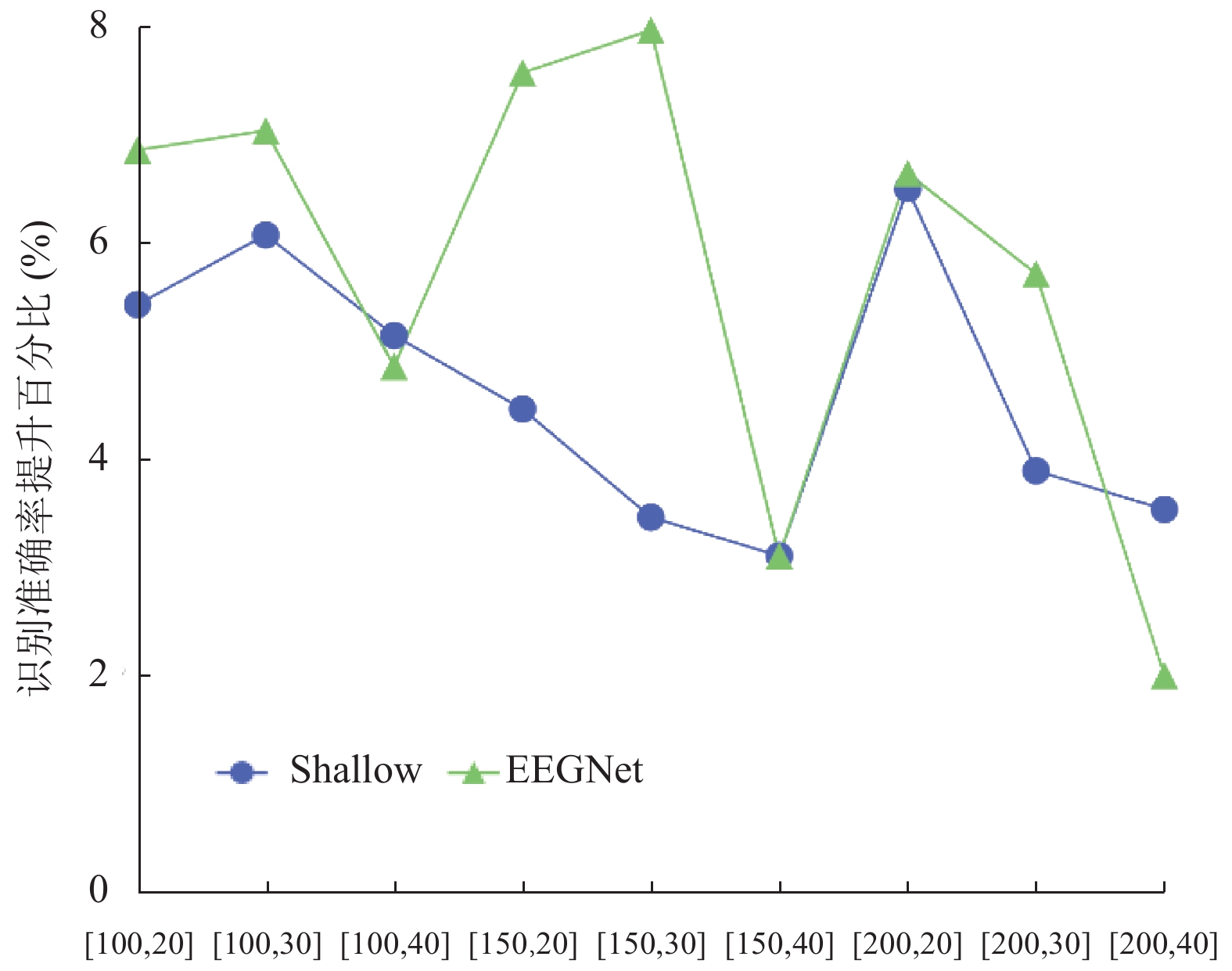
对于Dataset 1数据集, 实验将
9组不同参数组合的overlapped策略应用于2种不同模型的识别准确率的提升百分比如图9所示.
|
图 9 在Dataset 1上9组参数组合的overlapped策略的识别准确率提升百分比的比较 |
从图9可以看出, overlapped训练策略的9种参数组合在Shallow ConvNet和EEGNet两种模型的识别准确率均有提升. Shallow ConvNet在
基于本文介绍的trial-wise、cropped和设计的重叠时间切片(overlapped)策略, 将这3种训练方法应用于本文介绍的5种深度神经网络模型: Deep ConvNet、Shallow ConvNet、Hybrid ConvNet、EEGNet和EEG-ResNet上, 并计算出其在Dataset 2a数据集所有受试者的测试集上的识别准确率如表3所示. 其中, 实验的overlapped训练方法中的
由表3可以看出, 在Dataset 2a数据集上, 对于Shallow ConvNet和EEGNet这两种浅层模型, overlapped训练策略与trial-wise训练策略的分类准确率相差不大, 但都优于cropped训练策略. 对于Deep ConvNet、Hybrid ConvNet和EEGResNet 3种模型, overlapped训练策略的分类准确率均高于trial-wise和cropped训练策略的分类准确率.
本文还通过设置不同的
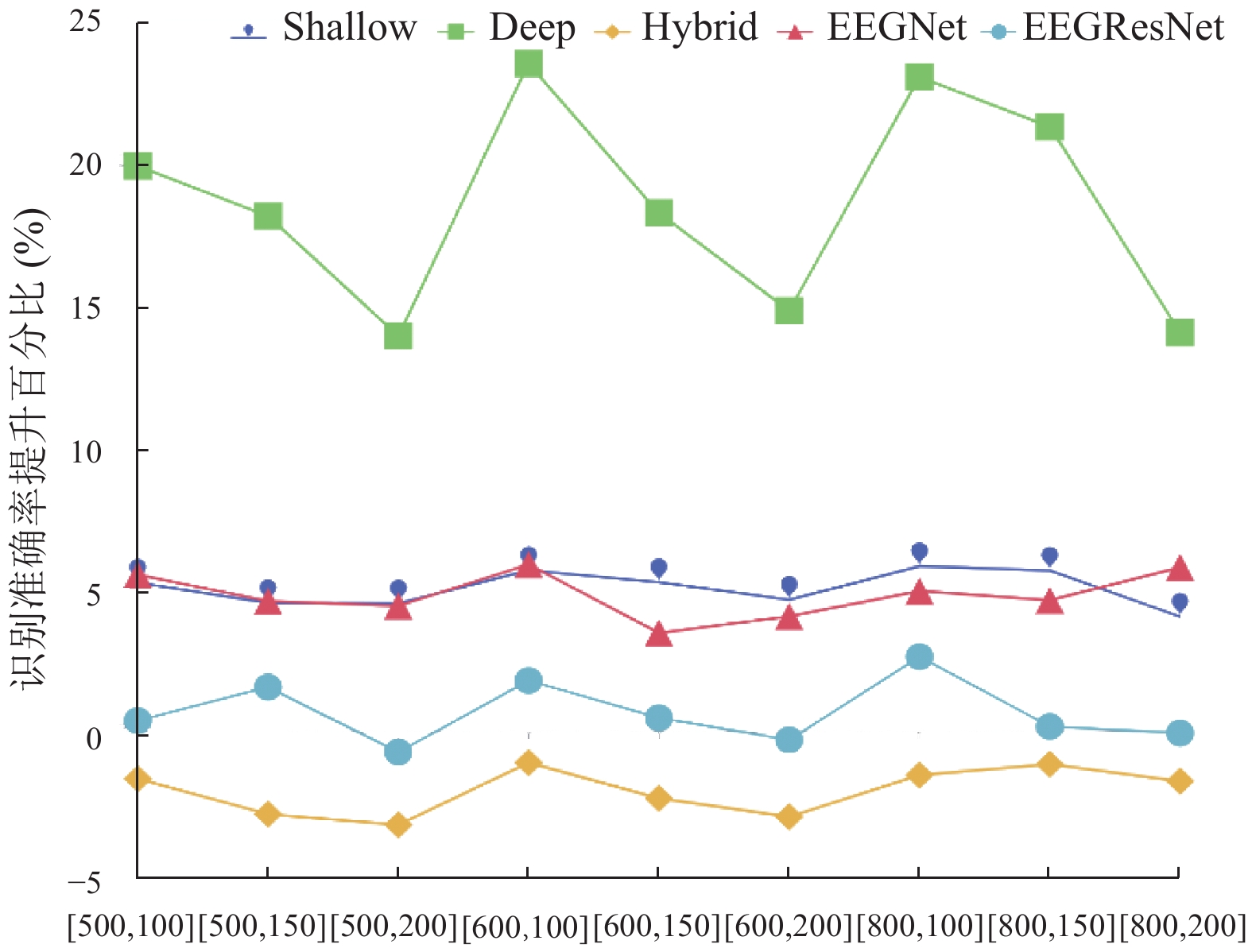
相比于cropped策略, 9组不同参数组合的overlapped策略应用于5种不同模型的识别准确率的提升百分比如图10所示.
| 表 3 Trial-wise、cropped和overlapped (500, 100)方法在Dataset 2a数据集上的识别准确率比较(%) |
|
图 10 在Dataset 2a上9组参数组合的overlapped策略的识别准确率提升百分比的比较 |
从图10可以看出, 除Hybrid ConvNet和EEGResNet在
同样, 在Dataset 2b数据集上采用cropped和overlapped两种策略训练5种深度神经网络模型, 得到所有受试者的测试集上的识别准确率如表4所示. 其中, 实验的overlapped训练方法中的
由表4可以看出, 在Dataset 2b数据集上, trial-wise训练策略在Shallow ConvNet、Deep ConvNet和EEGNet 3种模型上取得更好的分类准确率, cropped训练策略在EEGResNet模型上取得更好的分类准确率, overlapped训练策略在Hybrid ConvNet模型上取得更好的分类准确率.
从表2、表3和表4中的实验结果可以看出, 虽然overlapped方法不能同时比trial-wise和cropped方法显著提升识别准确率. 但是, 采用student-test方式进行假设检验, 在Dataset 2a和Dataset 2b数据集上的5种不同模型, oiverlapped方法总能比trial-wise或cropped方法显著提升识别准确率(p<0.05或p<0.01). 实际上, 针对EEG信号的预处理过程, 在不同数据集和不同卷积神经网络模型下, trial-wsie方法由于样本量较少, 更适合于简单模型或数据集(如Dataset 1数据集和Shallow ConvNet模型). Cropped方法能够弥补样本不足和特征维度较高的缺点, 因此更适合复杂的模型或数据量较大的情况(如Dataset 2a/2b数据集和Hybrid ConvNet/EEGResNet模型). 不同于二者都有适应自己情况的数据集和模型, 通过实验结果可以看出, overlapped方法能够同时满足数据量较小/较大、模型较简单/复杂的情况, 其对于运动想象识别率的鲁棒性较高. 在实际基于运动想象的脑机接口应用中, 采用overlapped方法能够极大的降低对于数据集和模型的依赖性, 保证运动想象识别准确率的稳定性.
| 表 4 Trial-wise、cropped和overlapped (500, 100)方法在Dataset 2b数据集上的识别准确率比较(%) |
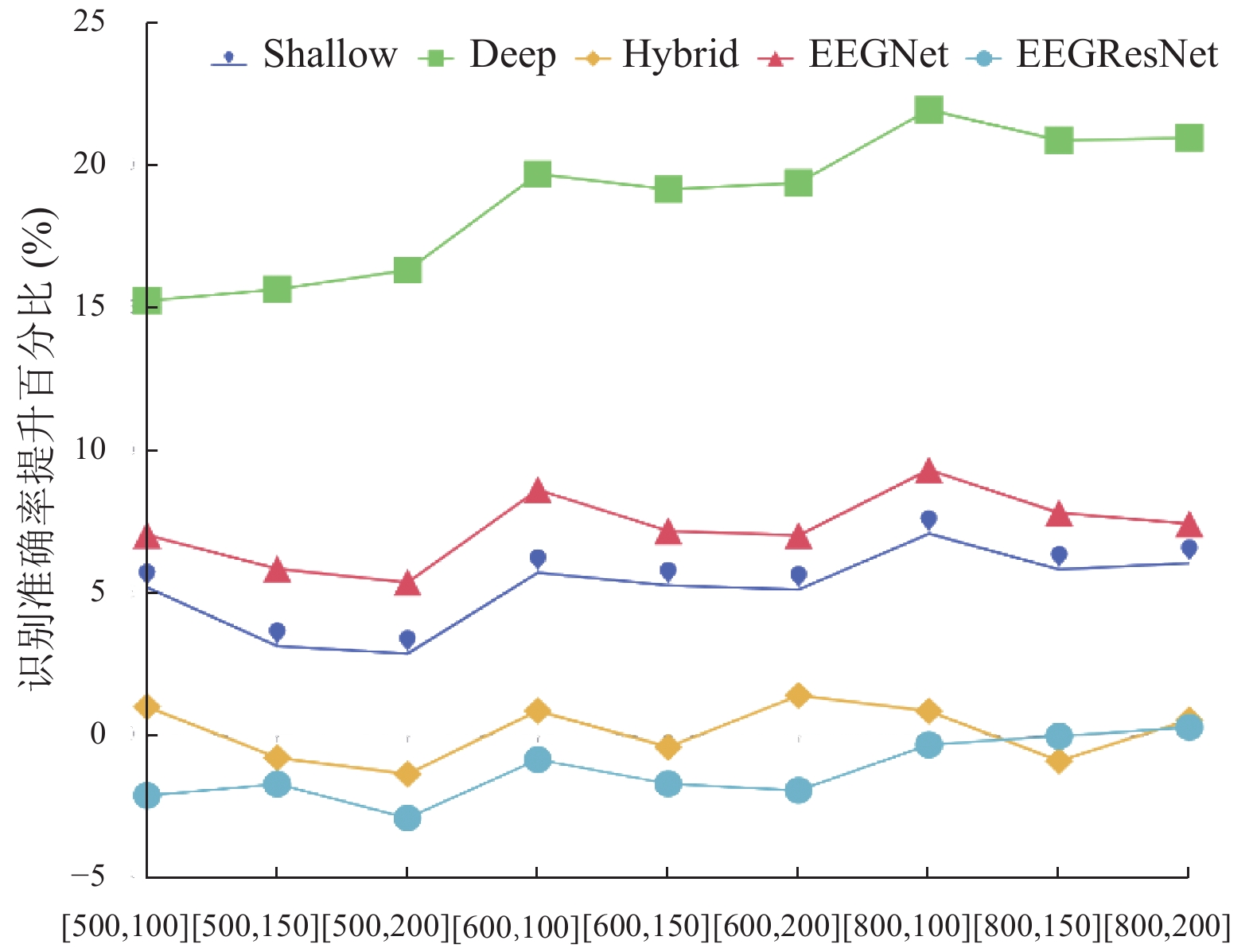
在Dataset 2b数据集上, 同样将
|
图 11 在Dataset 2b上9组参数组合的overlapped策略的识别准确率提升百分比的比较 |
从图11可以看出, overlapped训练策略在Shallow ConvNet、Deep ConvNet和EEGNet 3种模型的识别准确率提升百分比较高. 随着
综合以上在3个数据集上应用3种不同训练策略的实验结果分析, 由于Dataset 1、2a和2b数据集中每个样本的电极数分别为64、22和3, 在使用相同的采样率时, Dataset 2b数据集的数据量要远小于Dataset 1和2a的, 因此, 对于Dataset 1和2a数据集, 在遇到简单模型(如Shallow ConvNet模型)时, trial-wise和overlapped训练策略的识别性能相差不大, 当遇到更复杂的模型时, overlapped训练策略可提供的海量样本量的优势得以体现出来. 对于Dataset 2b数据集, 其数据量本身不大, 所以在简单模型上应用trial-wise训练策略的效果更好, 对于复杂模型, 由于数据量的限制, overlapped训练策略较cropped训练策略的优势不大.
实际上, 由于大数据时代的到来, 迁移学习形成的海量样本集, 促使我们使用更复杂的模型完成MI的分类工作, 如Hybrid ConvNet和EEGResNet, 此时采用overlapped训练策略能够保证较高的鲁棒性, 并且避免trial-wise训练策略带来的过拟合问题.
4.5 时间复杂度对比本文实验还记录了每个模型在应用不同训练策略时每次迭代所花费的时间, 以探究overlapped策略在获得更好的分类性能的同时, 其时间复杂度与cropped策略的时间复杂度的对比情况.
以Dataset 2a数据集的Subject 1的数据为例, 5种不同模型在应用cropped策略和应用overlapped的9种参数组合(与第4.3节中的参数组合相同)情况下, 平均每轮训练迭代所花费的时间如表5所示.
由表5可以看出,
| 表 5 Cropped与overlapped策略应用于5种模型的平均每轮训练迭代所花费的时间对比 (s) |
5 结论与展望
本文提出了一种新型的重叠时间切片的训练策略以改进深度神经网络在运动想象EEG信号模式识别中的性能.
首先, 本文设计了重叠时间切片的训练策略并设计了全新的损失函数和预测标签方法. 其次, 在Competition IV Dataset 1、2a和2b数据集上分别建立使用trial-wise、cropped和overlapped策略的5种深度神经网络模型, 其实验结果表明, overlapped策略较cropped策略拥有更好的识别性能. 对于使用的5种模型, 在Dataset 1、2a和2b数据集上最高分类准确率分别达到91.3%、77.3%和86.4%. 最后, 通过调整over-lapped策略的
今后的工作要通过优化深度神经网络结构以提升训练效率, 并将重叠时间切片策略与其他优化策略相结合, 如随机选取重叠切片, 将不同组合的重叠切片输入到网络中进行训练, 进一步提升运动想象EEG信号识别性能.
| [1] |
Wolpaw JR, Birbaumer N, Heetderks WJ, et al. Brain-computer interface technology: A review of the 1st international meeting. IEEE Transactions on Rehabilitation Engineering, 2000, 8(2): 164-173. DOI:10.1109/TRE.2000.847807 |
| [2] |
Shende PM, Jabade VS. Literature review of brain computer interface (BCI) using electroencephalogram signal. 2015 International Conference on Pervasive Computing (ICPC). Pune: IEEE, 2015. 1–5.
|
| [3] |
Oralhan Z. A new paradigm for region-based P300 speller in brain computer interface. IEEE Access, 2019, 7: 106618-106627. DOI:10.1109/ACCESS.2019.2933049 |
| [4] |
Wang M, Li RJ, Zhang RF, et al. A wearable SSVEP-based BCI system for quadcopter control using head-mounted device. IEEE Access, 2018, 6: 26789-26798. DOI:10.1109/ACCESS.2018.2825378 |
| [5] |
Shu XK, Chen SG, Meng JJ, et al. Tactile stimulation improves sensorimotor rhythm-based BCI performance in stroke patients. IEEE Transactions on Biomedical Engineering, 2019, 66(7): 1987-1995. DOI:10.1109/TBME.2018.2882075 |
| [6] |
Xiao D, Mu ZD, Hu JF. Classification of motor imagery EEG signals based on energy entropy. 2009 International Symposium on Intelligent Ubiquitous Computing and Education. Chengdu: IEEE, 2009. 61–64.
|
| [7] |
Huang DD, Qian K, Oxenham S, et al. Event-related desynchronization/synchronization-based brain-computer interface towards volitional cursor control in a 2D center-out paradigm. 2011 IEEE Symposium on Computational Intelligence, Cognitive Algorithms, Mind, and Brain (CCMB). Paris: IEEE, 2011. 1–8.
|
| [8] |
Ang KK, Chin ZY, Wang CC, et al. Filter bank common spatial pattern algorithm on BCI Competition IV datasets 2a and 2b. Frontiers in Neuroscience, 2012, 6: 39. |
| [9] |
张顺, 龚怡宏, 王进军. 深度卷积神经网络的发展及其在计算机视觉领域的应用. 计算机学报, 2019, 42(3): 453-482. |
| [10] |
韩文静, 李海峰, 阮华斌, 等. 语音情感识别研究进展综述. 软件学报, 2014, 25(1): 37-50. DOI:10.13328/j.cnki.jos.004497 |
| [11] |
胡章芳, 张力, 黄丽嘉, 等. 基于时频域的卷积神经网络运动想象脑电信号识别方法. 计算机应用, 2019, 39(8): 2480-2483. DOI:10.11772/j.issn.1001-9081.2018122553 |
| [12] |
Tabar YR, Halici U. A novel deep learning approach for classification of EEG motor imagery signals. Journal of Neural Engineering, 2017, 14(1): 016003. DOI:10.1088/1741-2560/14/1/016003 |
| [13] |
褚亚奇, 朱波, 赵新刚, 等. 基于时空特征学习卷积神经网络的运动想象脑电解码方法. 生物医学工程学杂志, 2021, 38(1): 1-9. |
| [14] |
Dai MX, Zheng DZ, Na R, et al. EEG classification of motor imagery using a novel deep learning framework. Sensors, 2019, 19(3): 551. DOI:10.3390/s19030551 |
| [15] |
Dai GH, Zhou J, Huang JH, et al. HS-CNN: A CNN with hybrid convolution scale for EEG motor imagery classification. Journal of Neural Engineering, 2020, 17(1): 016025. DOI:10.1088/1741-2552/ab405f |
| [16] |
Schirrmeister RT, Springenberg JT, Fiederer LDJ, et al. Deep learning with convolutional neural networks for EEG decoding and visualization. Human Brain Mapping, 2017, 38(11): 5391-5420. DOI:10.1002/hbm.23730 |
| [17] |
Krizhevsky A, Sutskever I, Hinton GE. ImageNet classification with deep convolutional neural networks. Proceedings of the 25th International Conference on Neural Information Processing Systems. Lake Tahoe: ACM, 2012. 1097–1105.
|
| [18] |
Hertel L, Barth E, Käster T, et al. Deep convolutional neural networks as generic feature extractors. 2015 International Joint Conference on Neural Networks. Killarney: IEEE, 2015. 1–4.
|
| [19] |
Clevert DA, Unterthiner T, Hochreiter S. Fast and accurate deep network learning by exponential linear units (ELUs). arXiv: 1511.07289, 2015.
|
| [20] |
Lawhern VJ, Solon AJ, Waytowich NR, et al. EEGNet: A compact convolutional neural network for EEG-based brain-computer interfaces. Journal of Neural Engineering, 2018, 15(5): 056013. DOI:10.1088/1741-2552/aace8c |
| [21] |
He KM, Zhang XY, Ren SQ, et al. Deep residual learning for image recognition. Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016. 770–778.
|
 2022, Vol. 31
2022, Vol. 31


