近年来, 许多研究人员将深度学习模型应用于推荐系统领域, 缓解了传统推荐系统的一些局限性, 提升了推荐性能[1]. 深度学习源于对人工神经网络的研究, 通过构造一个多层、非线性、层间互联的网络结构, 利用网络结构逼近一个复杂的多元函数作为训练目标, 并从许多未标记的训练数据集中学习数据集的原始特征[2]. 实际上, 微软、谷歌、阿里等公司已经提出了许多种不同的基于深度学习的推荐算法, 并且都在真实数据集上取得了很好的效果. 推荐系统也因此成为了人工智能和机器学习研究的一个分支, 被广泛应用到音乐、电影、社交网络等一系列推荐场景中.
推荐系统的一大基本问题是对用户兴趣的精准捕捉, 然而多数推荐模型不能有效地对用户动态变化的偏好进行建模, 只是单纯地对用户长期形成的兴趣偏好进行了建模, 或是仅仅捕捉了用户在短期内的兴趣偏好. 但实际上, 用户的兴趣会随时间推移而发生兴趣漂移等情况, 因此分别捕捉用户的长期与短期偏好才能够更好地刻画用户兴趣, 为用户提供更加精准的推荐.
在长短期偏好推荐方面, Rendle等人[3]提出一种结合矩阵分解和马尔可夫链的算法, 分别通过两种方法了解用户的总体喜好, 以及建模用户顺序行为; Song等人[4]使用深度语义结构化模型提取用户和项目的静态特征外, 同时利用循环神经网络建立了用户偏好随时序变化的动态模型; Lv等人[5]的序列深度匹配(sequential deep matching, SDM)模型通过多头自我注意模块对短期会话行为进行建模, 通过门控融合模块有效结合长期偏好和当前购物需求.
本文针对用户兴趣随时间发生兴趣漂移等问题, 提出一种融合隐语义模型与门控循环单元的推荐模型(RA_LST), 通过分别捕捉用户的长期与短期偏好, 以更好地刻画用户兴趣, 为用户提供更加精准的推荐. 其中, 用户的长期偏好是指随时间推移不会发生较大改变的用户喜好, 需要根据较长的时间序列来学习捕捉; 用户的短期偏好则是指会在短期内发生较大变化的用户喜好, 需要更加灵活的学习捕捉.
1 长短期兴趣捕捉针对用户长期兴趣与短期兴趣的捕捉, 存在许多比较经典的推荐模型. 其中, 用户长期形成的兴趣可以用矩阵分解等方法来建模[6], 而用户短期内的偏好则多用循环神经网络这一序列推荐模型来进行预测[7]. 本文提出的算法则采用隐语义模型和门控循环单元来分别捕捉用户的长短期偏好.
1.1 隐语义模型隐语义模型(latent factor model, LFM)是在推荐系统中普遍应用的一种模型[8], 它先对所有物品进行分类, 再根据用户兴趣分类向用户推荐该分类中的物品. 对于分类, LFM可以基于用户的行为进行自动聚类, 并且分类的粒度可控. 该模型的目标是求出用户与物品隐语义矩阵与, 分别表示用户对不同维度特征的偏好程度、物品在不同维度特征方面的特征强度, 两矩阵相乘即可表示用户对该物品的喜好程度[9], 用公式表示为式(1), 其中
| $ {\hat r_{ui}} = P_u^T{Q_i} = \sum\limits_{f = 1}^F {{P_{uf}}{Q_{fi}}} $ | (1) |
而用户与物品隐语义矩阵Pu、Qi由实际评分矩阵rui(稀疏矩阵)通过矩阵分解得来, 并且希望估计评分矩阵
| $ J = \sum\nolimits_{{r_{ui}} \ne 0} {{{({r_{ui}} - {{\hat r}_{ui}})}^2} + } \lambda \left(\sum {P_{uf}^2 + \sum {Q_{fi}^2} } \right) $ | (2) |
通过梯度下降的方法对式(2)进行求解, 即对损失函数求偏导以确定最快的下降方向, 公式如式(3)、式(4)所示.
| $ \frac{{\partial J}}{{\partial P_{uf}^{(t)}}} = \sum\nolimits_{i,{r_{ui}} \ne 0} { - 2({r_{ui}} - {{\hat r}_{ui}})Q_{fi}^{(t)} + 2\lambda P_{uf}^{(t)}} $ | (3) |
| $ \frac{{\partial J}}{{\partial Q_{fi}^{(t)}}} = \sum\nolimits_{u,{r_{ui}} \ne 0} { - 2({r_{ui}} - {{\hat r}_{ui}})P_{uf}^{(t)} + 2\lambda Q_{fi}^{(t)}} $ | (4) |
然后通过迭代计算更新、优化参数, 也可以使用随机梯度下降(stochastic gradient descent, SGD)方法, 比传统的梯度下降方法需要更少的迭代次数就可以收敛. 最后得到估计评分矩阵
门控循环单元(gated recurrent unit, GRU)是针对标准的循环神经网络(recurrent neural network, RNN)在长期依赖性问题上存在的梯度消失和梯度爆炸问题而提出的改进的循环神经网络[10], 同长短期记忆(long-short time memory, LSTM)一并成为了实际应用中有效的序列模型.
GRU不仅继承了RNN的优势, 通过将神经元某时刻的输出作为输入再次输入到神经元, 从而保持数据信息间的依赖关系, 能够很好地处理序列信息; 而且作为LSTM的简化模型, GRU构造更加精简, 在不影响训练效果的前提下加快了训练速度, 在训练数据大的情况下能节省很多时间.
如图1所示, GRU的输入输出结构与标准的RNN相同, 有一个当前输入Xt和上一节点传递下来的隐状态ht–1,
GRU的内部首先由上一节点传递下来的隐状态ht–1和当前输入Xt获得两个门控状态: 重置门控r和更新门控z, 其中, σ为Sigmoid函数.
| $ r = \sigma \left({W_r}\begin{array}{*{20}{c}} {{X_t}} \\ {{h_{t - 1}}} \end{array}\right), {\textit{z}} = \sigma \left({W_{\textit{z}}}\begin{array}{*{20}{c}} {{X_t}} \\ {{h_{t - 1}}} \end{array}\right) $ | (5) |

|
图 1 GRU输入输出结构原理图&内部结构原理图 |
接着使用重置门控来“重置”数据, 得到包含当前节点信息的h′.
| $ {h_{t - 1}}' = {h_{t - 1}} \cdot r, {h'} = \tanh \left(W\begin{array}{*{20}{c}} {{X_t}} \\ {{h_{t - 1}}'} \end{array}\right) $ | (6) |
再使用更新门控来“更新记忆”, 对原本的隐状态ht–1选择性遗忘, 对包含当前节点信息的h′选择性记忆.
| $ {h_t} = (1 - {\textit{z}}) \cdot {h_{t - 1}} + {\textit{z}} \cdot {h'} $ | (7) |
由于GRU的每个隐藏单元都拥有独立的重置门和更新门, 因此能够在不同的时间尺度上捕获依赖关系, 可以通过使用频繁激活的重置门来捕捉短期依赖关系, 通过使用活跃的更新门来捕捉长期依赖关系[11].
2 融合隐语义模型与门控循环单元的推荐算法本文提出一种融合隐语义模型LFM与门控循环单元GRU的神经协同过滤算法(RA_LST), 通过结合长期与短期行为来捕捉用户的动态偏好. 其中, 长期偏好属于用户的本质属性, 或者说是群体属性, 是指随时间推移不会发生较大改变的用户喜好. 例如男性与女性、不同年龄阶层对电影类型的喜好度区分: 低龄用户大多喜爱动画类型的电影, 而科幻类型的电影会更受男性用户的偏爱. 这一类用户属性需要根据较长的时间序列来学习捕捉. 而短期偏好则属于用户的阶段性属性, 是指会在短期内发生较大变化的用户喜好, 例如在某个时间段内或是某个时间节点处, 用户对特定演员或是特定属性电影的阶段性喜爱. 这一类属性会在短时间内出现与消失, 因此需要更加灵活的学习捕捉.
本文分别通过两个相应的模型组件来对用户行为进行建模: 使用LFM模块获取长期偏好, 使用GRU模块获取短期偏好, 再通过随机梯度下降(stochastic gradient descent, SGD)优化算法融合LFM与GRU. 模型的整体结构如图2所示.

|
图 2 融合隐语义模型与门控循环单元的推荐模型 |
2.1 基于FM的用户长期偏好捕捉
本文采用基于隐语义模型LFM的推荐算法来对用户与电影之间的长期状态进行建模预测. 该模型通过将用户历史交互/未交互矩阵分解为两个低维度矩阵: 用户潜在因子矩阵和项目潜在因子矩阵, 使其分别作为用户/项目特征, 结果基于用户行为统计自动聚类, 无需关心分类的角度, 分类粒度也可以通过设置最终分类数来控制, 分类数越大, 粒度越细.
图3所示为基于隐语义模型的推荐算法整体结构. 模型首先采用均值为0, 方差为1的高斯分布随机值来初始化用户与项目潜在因子矩阵P和Q. 接着, 在LFM层采用随机梯度优化算法迭代计算更新参数, 并且在每次迭代中都重新选择用户的负样本. 最终, 将训练好的用户隐因子向量与项目隐因子向量相乘, 获得用户对负例项目的预测喜爱度, 并对其降序排列取前N项进行推荐.
2.2 基于GRU的用户短期偏好捕捉本文采用基于门控循环单元GRU的推荐算法来对用户与电影之间的短期状态进行建模预测. 该模型的核心是GRU层, 输出是对项目的预测偏好, 即每个项目在用户下一次交互中的可能性. 当使用多个GRU层时, 前一层的隐藏状态是下一层的输入.
基于门控循环单元的推荐算法的整体结构如图4所示. 首先, 对实际项目进行one-hot编码, 令输入向量的长度等于所有项目的个数, 对于用户交互过的项目置为1, 未交互过的项目置为0. 接着, 在嵌入层使用tanh激活函数对输入向量进行嵌入处理, 令其编码程度更小, 更便于在低维空间优化模型. 之后通过GRU层获得预测结果, 在输出层输出预测评分.

|
图 3 基于隐语义模型的推荐算法整体结构 |

|
图 4 基于门控循环单元的推荐算法整体结构 |
在GRU层对数据集进行批量训练时, 每个用户交互过的项目数量不同, 甚至差距很大: 有些用户只有个位数的交互项目, 而其它用户可能有上千个交互项目. 而且在做序列推荐时, 我们的目标是捕捉交互项随时间的发展特征, 因此不能将其分解成片段, 这样就失去了序列预测的意义. 综合以上, 本算法使用基于会话序列推荐的循环神经网络建模方法GRU4Rec (gated recurrent unit for recurrent), 并行小批量来进行训练[12]: 该方法首先将N个用户的交互项组合成一个并行序列, 第一次将用户s在ts时刻的交互项输入到GRU中, GRU预测用户s在ts+1时刻的交互项. 第2次将用户s在ts+1时刻的交互项输入到GRU中, GRU预测用户s在ts+2时刻的交互项, 以此类推. 由于每个用户的交互项序列长短不一, 当一个序列训练结束后, 补充新的序列到并行序列当中, 同时重置为该新序列的隐藏状态, 这样最大限度地提高了训练效率. 图5给出了GRU4Rec批量训练的示意图. 其中, is,t表示用户s按时间排序的第t个交互项目.

|
图 5 GRU4Rec批量训练的示意图 |
2.3 长短期偏好的融合算法
在分别通过GRU4Rec模型与LFM模型获得用户的长短期偏好预测之后, 本算法(RA_LST)采用随机梯度下降优化算法SGD来对两部分结果进行融合, 以提高推荐效果. SGD的目标是要找到一组合适的附加参数, 使得预测值与真实值之间的差距最小.
具体来说, 分别假设GRU4Rec模型与LFM模型获得的用户预测评分为x1与x2, 然后为它们分配和为1的不同权重, 即定义最终预测评分为:
| $ {h_\theta }(x) = \theta {x_1} + (1 - \theta ){x_2} $ | (8) |
目标函数J(θ)定义为式(9), 其中, y是真实值.
| $ J(\theta ) = \frac{1}{m}\sum\limits_{i = 1}^m {{{[{h_\theta }(x) - y]}^2}} $ | (9) |
然后对目标函数求梯度, 即对其每个分量求偏导:
| $\begin{split} gradient &= \frac{\partial }{{\partial \theta }}J(\theta ) = \frac{\partial }{{\partial \theta }}\frac{1}{2}{[\theta {x_1} + (1 - \theta ){x_2} - y]^2} \\ &= [\theta {x_1} + (1 - \theta ){x_2} - y]({x_1} - {x_2}) \end{split}$ | (10) |
再通过求出的梯度与学习率更新参数θ:
| $ {\theta ^{t + 1}} = {\theta ^t} - \alpha \cdot gradient $ | (11) |
将更新后的θ继续带入下一用户数据进行迭代, 直至所有用户数据迭代结束, 最终所得θ对应的预测评分hθ(x)即为最终预测评分.
3 实验分析 3.1 实验数据集实验基于公开数据集MovieLens与Netflix进行. 其中, MovieLens是一个被广泛应用于评估推荐算法的电影评分数据集, 本实验使用的1M版本中包含6 000多名用户对4 000多部电影的100万条评分数据, 其中每个用户至少对20部电影做出了评级. 而Netflix同样作为电影评价数据集, 其中包含48万用户对1.7万部电影超过100万条评价数据. 两数据集均采用1–5分的评分制, 且评分信息均带有时间戳, 因此适用于本例等基于时间序列, 考虑用户对项目的交互顺序的推荐算法评估.
另外, 本实验拟采用一种广泛应用的留一法(leave-one-out)来划分训练集与测试集[13]. 具体做法是先按照时间顺序对所有交互进行排序, 然后将最后10%的项, 即用户最新交互的项作为测试集, 并将剩余的90%交互数据用于训练模型.
3.2 实验评估指标实验采用归一化折损累积增益(normalized discounted cumulative gain, NDCG)和均方根误差 (root mean square error, RMSE)作为评价指标, RMSE衡量的是预测值与真实值之间的偏差, NDCG则评价推荐列表与用户真实交互列表的差距. 简单来说, RMSE评估推荐值的误差, NDCG评估排名列表的质量.
RMSE常用作模型预测结果的衡量指标, 计算公式为式(12), 是在均方误差(mean square error, MSE)的基础上做开根号计算. 其中,yi表示的是用户真实评价值,
| $ {\textit{RMSE}} = \sqrt {\frac{1}{m}} \sum\limits_{i = 1}^m {{{({y_i} - {{\hat y}_i})}^2}} $ | (12) |
归一化折损累积增益指标通常用来衡量和评价搜索算法与推荐算法, 其思想是关联度越高的结果位置越靠前, 对最终指标得分影响越大, 也即NDCG值越大, 推荐系统的整体推荐效果越佳. 计算过程如下: 首先, 表示列表中每一个项目的相关性分数为Gain.
| $ Gain = r(i) $ | (13) |
接着对K个项目的相关性分数进行累加, 得到累积增益CG.
| $ CG@K = \sum\limits_i^K {r(i)} $ | (14) |
为了考虑序列因素, 让排名越靠前的项目越能影响结果, 为排名靠前项目赋予更高的增益, 而对排名靠后项目进行折损, 计算得折损累积增益DCG.
| $ DCG@K = \sum\limits_i^K {\frac{{{2^{r(i)}} - 1}}{{{{\log }_2}(i + 1)}}} $ | (15) |
最后, 对列表长度不一的用户指标进行归一化, 使用折损累积增益DCG除以理想状态下最大DCG值IDCG(ideal discounted cumulative gain), 即可得到归一化折损累积增益NDCG.
| $ NDCG@K = \frac{{DCG@K}}{{IDCG}},\; IDCG = \sum\limits_{i = 1}^{|REL|} {\frac{{{2^{r(i)}} - 1}}{{{{\log }_2}(i + 1)}}} $ | (16) |
为了评估融合后模型(RA_LST)的性能, 将其与LFM、GRU4Rec分别在MovieLens、Netflix数据集上进行对比实验. 实验在Python 3.8环境下进行, LFM与GRU4Rec模型的学习率分别设置为0.02、0.001. 最终的实验结果如表1所示.
| 表 1 各模型在各数据集上的评估指标 |
从表1可以看出, 在不同的数据集中, 本文提出模型RA_LST的NDCG比融合前的独立模型都要高, 表示该模型通过兼顾用户长短期偏好, 有效地提高了预测的准确性. 另外, 在不同的数据集中, 本文提出模型RA_LST的RMSE比融合前的独立模型都要低, 也表示该模型通过兼顾用户长短期偏好, 有效地降低了预测误差.
图6、图7所示的是隐语义模型(LFM)、门控循环单元(GRU)以及本文提出的融合模型(RA_LST)在MoviesLens数据集上的性能随迭代次数(epoch)变化对比图. 其中, RA_LST的学习率设置为0.01. 从图中可以看出, 本文提出的融合模型的NDCG值和RMSE值, 在不同的训练批次下都较原有算法有了明显的提升. 其中, NDCG值较GRU平均提升了0.015, RMSE值较LFM平均降低了0.116.
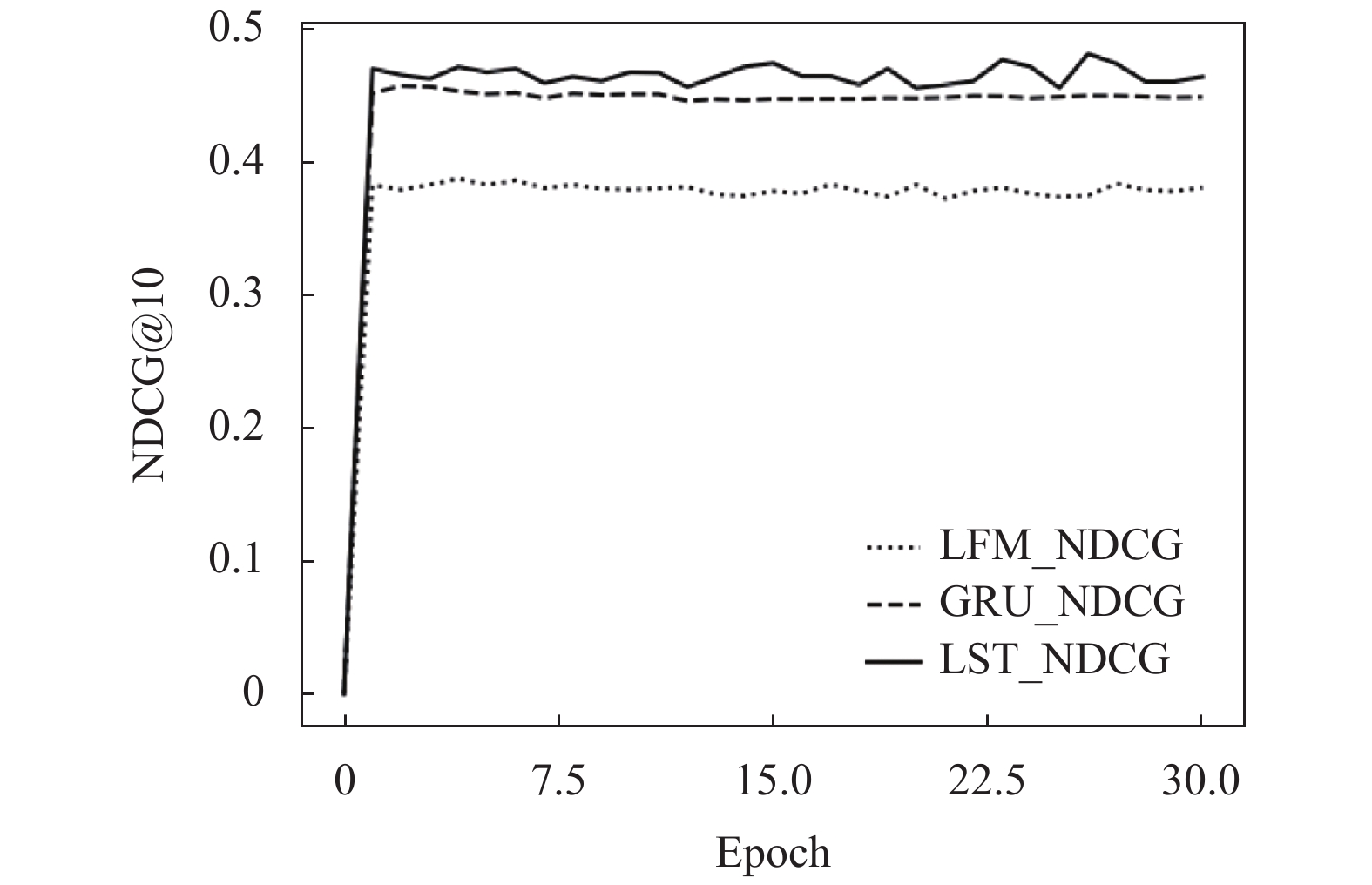
|
图 6 不同模型的NDCG值对比图 |

|
图 7 不同模型的RMSE值对比图 |
4 结语
本文针对传统推荐系统缺乏对时间因素的考虑的问题, 提出了一种兼顾用户长短期偏好的推荐算法, 该算法分别使用门控循环单元与隐因子模型来捕捉用户的短期与长期兴趣, 并通过SGD优化算法融合两部分结果, 以构建更完善的用户画像, 进而提高推荐性能. 在MovieLens与Netflix数据集上的评估指标RMSE与NDCG都表明, 该算法能够有效提高预测的准确性.
| [1] |
李丹, 高茜. 基于深度学习推荐系统的研究与展望. 齐鲁工业大学学报, 2020, 34(6): 29-38. |
| [2] |
Mu RH. A survey of recommender systems based on deep learning. IEEE Access, 2018, 6: 69009-69022. DOI:10.1109/ACCESS.2018.2880197 |
| [3] |
Rendle S, Freudenthaler C, Schmidt-Thieme L. Factorizing personalized markov chains for next-basket recommendation. Proceedings of the 19th International Conference on World Wide Web. Raleigh North: Association for Computing Machinery, 2010. 811–820.
|
| [4] |
Song Y, Elkahky AM, He XD. Multi-rate deep learning for temporal recommendation. Proceedings of the 39th International ACM SIGIR Conference on Research and Development in Information Retrieval. Pisa: Association for Computing Machinery, 2016. 909–912.
|
| [5] |
Lv FY, Jin TW, Yu CL, et al. SDM: Sequential deep matching model for online large-scale recommender system. Proceedings of the 28th ACM International Conference on Information and Knowledge Management. Beijing: Association for Computing Machinery, 2019. 2635–2643.
|
| [6] |
程龙, 李涵. 基于矩阵分解的推荐算法研究综述. 北京信息科技大学学报, 2021, 36(2): 38-45, 51. |
| [7] |
Chakrabarti N, Das S. Neural networks and collaborative filtering. Proceedings of 2019 IEEE International Conference on System, Computation, Automation and Networking (ICSCAN). Pondicherry: IEEE, 2019. 1–4.
|
| [8] |
Han JY, Zheng L, Huang H, et al. Deep latent factor model with hierarchical similarity measure for recommender systems. Information Sciences, 2019, 503: 521-532. DOI:10.1016/j.ins.2019.07.024 |
| [9] |
Jenatton R, Le Roux N, Bordes A, et al. A latent factor model for highly multi-relational data. Proceedings of the 25th International Conference on Neural Information Processing Systems, Volume 2. Lake Tahoe: Curran Associates Inc., 2012. 3167–3175.
|
| [10] |
Bengio Y, Simard P, Frasconi P. Learning long-term dependencies with gradient descent is difficult. IEEE Transactions on Neural Networks, 1994, 5(2): 157-166. DOI:10.1109/72.279181 |
| [11] |
Cho K, van Merriënboer B, Gulcehre C, et al. Learning phrase representations using RNN encoder-decoder for statistical machine translation. Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP). Doha: Association for Computational Linguistics, 2014. 1724–1734.
|
| [12] |
Hidasi B, Karatzoglou A, Baltrunas L, et al. Session-based recommendations with recurrent neural networks. arXiv: 1511.06939, 2015.
|
| [13] |
He XN, Liao LZ, Zhang HW, et al. Neural collaborative filtering. Proceedings of the 26th International Conference on World Wide Web. Perth: International World Wide Web Conferences Steering Committee, 2017. 173–182.
|
 2022, Vol. 31
2022, Vol. 31


