2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
随着计算机科学的发展, 不同特色的程序语言不断涌现, 由于Fortran更接近数学语言, 执行效率较高, 有着较低的开发成本, 因此在数值计算、科学和工程技术领域, Fortran依旧占据主流地位; 大量的数值计算工程软件, 开发语言同样仍以Fortran为主. 但在气候、流体力学等多个领域的模拟过程中, 随着计算规模的扩大以及对于计算精度的更高要求, 程序计算所需的时间也在不断延长, 部分大型程序需要几天甚至几十天才能完成计算. 传统的优化方式是将Fortran程序与MPI进行结合, 通过实现粗粒度的并行来提高计算效率. 近些年来, 随着高性能计算机的迅速发展, 通过GPU和CPU的异构计算平台[1]来实现细粒度的并行这一课题成为了学术界和工业界的研究热点. 基于Fortran所开发的科学计算软件及程序, 通过异构并行来实现性能的巨大提升, 在工程上有着急切的需求. 在异构计算平台上, 以用于GPU编程的CUDA C语法为主流的行业标准, AMD平台使用的ROCm语法也参照CUDA C规范. 但是从Fortran到CUDA C的移植过程, 不仅要求开发人员对Fortran与CUDA C均有较高的熟悉度, 而且在复杂的文件和模块中检索相关变量的信息并编写相应CUDA函数往往有着巨大的工程量, 如果完全通过人工完成, 不仅效率低下、极易出错, 且后期难以维护和调试. 因此从Fortran 到CUDA C的自动转码工具, 有着极大的需求.
现如今仅有一些将C语言转换为CUDA的工具, 加拿大多伦多大学的Han等人设计了一种基于指令的CUDA编程语言hiCUDA[2], 西安交大的Li等人实现了一种源到源自动并行化工具GPU-S2S[3], 孙香玉提出了一种面向 CUDA 的源到源并行化架构 STS-CUDA[4], 三者都是用于实现C语言到CUDA的自动转换, 但对于大型计算程序来说, 需要人工检索程序中大量变量的相关信息, 再对内存的分配拷贝释放等诸多操作插入编译指导语句. 通过这种方式来进行转化所需的工作量同样是十分巨大的. 荷兰埃因霍芬理工大学的Nugteren等人设计了自动转换编译器Bones[5], Bones是一个概念性的验证而非工业性的编译器, 其侧重点在于对特定结构的程序进行转换以及自动优化, 对于实际程序中的复杂情况不能很好的支持. 除此之外, 部分学者设计了与CUDA转化相关的编译器[6-8], 取得了不错的效果. 而从Fortran向CUDA C的转化工具, 仅美国国家海洋和大气管理局地球系统研究实验室开发了一种名为F2C-ACC的编译器[9], 但作者并未给出具体实现细节以及实际效果.
2 应用技术简介 2.1 正则表达式正则表达式是对字符串进行逻辑过滤的一种逻辑操作[10]. 将某类字符抽象为一些特定的字符, 通过某些特定字符的组合来描述字符串匹配的模式.
正则表达式具有强大的灵活性与功能性, 仅需非常简便的代码就可以实现复杂的字符串操作. 通过正则表达式, 可以实现如下功能: (1)匹配. 判断目标字符串是否与描述的模式相匹配; (2)获取. 从字符串中提取需要的特定信息; (3)编辑. 对字符串的子集进行切割、替换等操作.
2.2 shell脚本shell 脚本是一种为 shell 编写的脚本程序, 能够轻易的处理文件与目录之类的对象. 通过结合正则表达式以及sed、grep、awk等命令可以在短时间内完成一个功能强大又好用的脚本, 如下代码实现了获取使用操作符“( )”的变量名的功能:
cat filename.F90 |\
grep -oi "[a-z_]\+\w*[ ]*([^()]*)" | grep -vi "float" |\
awk -F "[(]" '{print $1"("}'|\
sed -e "s/[A-Z]/\l&/g" -e "s/=//" -e "s/ //g" |\
sort | uniq > result
如果采用C语言编写实现上述功能, 可能需要几十行甚至上百行的代码, 由此可见shell脚本在字符串处理方面的强大功能.
3 转换算法的设计 3.1 转换难点分析Fortran与CUDA C在语法规范、内存分配等方面均有较大的差异, 直接从Fortran转换为CUDA C有着较大的难度. 而C语言与Fortran无论是从结构方面还是语法的角度都比较相似, 同时在CUDA C程序中, 运行在主机端的代码仍然采用C语言进行编写, C语言很好的建立了从Fortran到CUDA C的桥梁. 因此将Fortran程序转换为CUDA C的过程分为如下两部分: (1) Fortran语言到C语言的转换; (2)从C语言转化为CUDA C. 结合Fortran与CUDA C两种语言的特点, 转换过程需要解决如下问题:
(1) 数组的处理. Fortran中数组下标可以采用形如A(index1:index2)形式来自定义起始下标与终止下标, 若采用默认定义, 则起始下标为1[11]; 而在C语言中所有数组下标均从0开始, 且不支持自定义的方式来访问元素. 对于多维数组, Fortran采用列优先的方式进行存储, 而C语言为行优先. 因此如何完成下标映射将成为转换过程中的一大难点. 对于动态分配的数组, 定义中的维度用“:”来进行, 需要额外检索allocate语句来获取对应的数组维度. Fortran对数组的访问也更加灵活, 如对于维度相同的一维数组A、B, 则可以直接通过A(:)=B(:)来完成对应元素的赋值. 因此对于使用“:”作为维度的相关语句需要进行较为复杂的处理.
(2) 引用外部模块. Fortran90采用module将一系列的数据与函数封装起来, 任何程序都可以通过use语句来引用该module中的内容; 而在C语言中引用其他变量通过include或者extern关键字来实现. 因此转换过程中, 文件的检索范围不仅限于本模块, 还需要包含引用的所有外部模块. 同时为了将转换后的CUDA C程序与原有的Fortran程序链接起来, 对变量的名称需要根据编译器进行额外的处理, 因此如何将引用的外部模块转换为同时兼容C程序、Fortran程序的形式将是一大难点.
(3) CUDA函数的处理. 在异构计算平台上, CPU用于控制计算过程和实施存储策略, 而具体的计算过程则由GPU进行[12]. 而在GPU上不能直接访问CPU端的内存, 因此GPU计算所需的数据以及计算得到的结果必须显式地与CPU进行数据的传输. 除此之外, 在GPU端执行的代码需针对并行做相应的修改. 因此针对计算过程中的大量变量, 如何自动生成函数实现内存的分配、拷贝以及释放将是转换过程中的一大挑战.
针对以上难点, 本文进行了相关算法设计和实现.
3.2 算法设计与实现 3.2.1 Fortran语言到C语言的转换在Fortran到C语言的转换过程中, 一方面需要完成相关语法、关键字等内容的转换, 另一方面对于每个变量, 需要从本文件或外部模块中检索来建立一张变量信息表, 表中需包含文件名称、变量名称、变量类型、维度等转换中必要的信息. 转换流程如图1所示.

|
图 1 Fortran到C的转换流程图 |
(1) 规范代码行
处理源文件中的注释与跨行. 为保证程序的可读性, 源程序的注释不删除, 将“!”所注释的内容均修改为C的“//”形式; 删除跨行符“&”并合并多行为一行, 删除文件中的空行.
(2) 提取变量信息
1) 数组型变量
首先检索源文件中的变量定义语句, 获取所有的内部数组变量名称. 根据下标运算符“( )”提取所有可能的数组变量, 去除关键字、函数名以及内部数组变量, 得到所有外部数组类型的变量名称.
通过对源文件进行检索, 截取数组变量的定义或allocate语句的相关信息, 建立内部数组变量与相应维度、类型的映射关系. 同理, 根据use语句提取源文件引用的module名称, 在相应文件中查找并建立外部数组变量信息表.
2) 基本数据类型变量
由于直接从源文件筛选可能的变量名不仅效率低下, 而且准确率较低, 因此从引用的模块中提取出所有的变量定义(不含数组类型变量), 依次进行过滤, 仅保留在源文件中使用的子集, 从而建立外部变量与相应类型的映射关系.
(3) 引用模块转换
对源文件中引用的每一个模块, 生成相应的头文件, 该文件中对使用到的相关变量进行声明. 对于非数组型变量直接将其转换为C语言的形式. 对于数组型变量, 由于C程序数组的处理与Fortran存在较大差异, 如C程序数组维度仅能通过常量定义, 起始下标为0, 不支持自定义下标等, 因此将其声明为同类型的指针变量, 通过一维数组的方式进行访问.
(4) 结构转换
1) 关键字以及语句的转换
将Fortran中的关键字与语句均转换为C语言中对应的形式, 包括但不限于表1的内容. 注释在C程序中无需使用的语句, 最大限度保证程序的可读性.
2) 数组下标索引的转换
对于Fortran中定义的数组, 如real(8) dimension(index1) :: A, 则数组A的维度大小为index1, 由于C语言中起始下标默认为0, 当通过下标来进行元素的访问时需要减去相应的偏移量, 如A(i)应转换为A[i–1]. 更一般的, 对于Fortran中自定义下标的数组, 如: real(8) dimension(index1:index2) ::B, 则数组B的维度大小为index2–index1+1, 相应的访问B(i)应转换为B[i–index1].
对于多维数组, 如Fortran中定义数组real(8), dimension (dimx, dimy) :: D, 由于行列优先的不同, 对应C程序的数组定义为: double D[dimy][dimx] , 相应下标访问D(i, j)对应C程序中的D[j–1][i–1]; 根据上文所述, 将多维数组均视为一维数组进行相关运算, 下标访问需进一步转换为D[(j – 1)*dimy+(i–1)].
| 表 1 Fortran与C关键字及语句对照表 |
3) 数组名称的转换
代码的前后处理在CPU上进行, 一般使用原有代码, 这就需要实现C和Fortran的混合编程, 主要是实现数组或变量的互相访问. 以ifort编译器下的文件param.F90中定义的外部数组变量b为例, 将数组名称b转换为param_mp_b_, 所有外部数组变量均要做相应的替换.
Fortran到C的整体转换算法如算法1所示.
算法1. Fortran到C的转换
1. 输入Fortran文件
2. 预处理
3. 匹配call语句, 提取函数名称
4. 匹配use语句, 提取引用模块名称
5. for file in 源文件, 引用模块文件
6. 匹配变量define语句、allocate语句
7. 存储变量名称、所在文件、类型、维度等信息
8. end for
9. for var in 变量信息表
10. if var in引用模块文件
11. //以ifort编译器为例
12. 替换变量名称: var → filename_mp_var_
13. end if
14. end for
15. 转换Fortran关键字、语句为C形式
16. 创建头文件
17. 输出C文件
3.2.2 C语言到CUDA C的转换CUDA C语法规定用__global__修饰符所修饰的函数为核函数, 核函数运行在设备端, 而运行在主机端的代码与C语言是完全兼容的. 因此从C语言到CUDA C的转换仅需考虑在设备端运行的部分代码即可, 这部分代码所涉及的数据以及得出的结果均需要在主机与设备内存间显式的进行复制[13], 即需要额外生成对应的拷贝函数. 除此之外, 由于核函数只能在主机端调用, 设备端执行[14], 因此主机端需要显式的进行核函数的调用, 并传递运行时所需参数, 核函数的内容需结合多线程并行的特点做出相应的调整. 转换流程如图2所示.

|
图 2 C到CUDA C的转换流程图 |
(1) 内存拷贝函数的生成
1) 确定拷贝对象
核函数中参与运算的所有数组变量均需要在设备端显式的进行内存的分配. 通过查找上文建立的变量信息表确定类型与维度, 声明同类型空指针, 分别利用cudaMalloc、cudaFree进行GPU内存的分配与释放. 如参与运算的某一数组定义为real, dimension(m, d):: a, 则需生成如下CUDA C语句:
double param_mp_a_[d][m];//转换后C形式的定义
double *d_a=NULL;//同类型指针声明
//GPU内存的分配
CHECK(cudaMalloc(&d_a, d*m*sizeof(double)));
CHECK(cudaFree(d_a));//GPU内存的释放
其中内存分配与释放语句中的CHECK为宏定义, 用于接收cudaError并输出提示信息, 保证程序的健壮性.
2) 生成拷贝函数
以所有外部数组变量为全集, 检索源文件中赋值运算符“=”, 出现在运算符左侧的所有变量将其从设备端拷贝到主机端, 相应拷贝函数封装为test_DtoH(), 出现在运算符右侧的变量将其从主机端拷贝到设备端, 相应拷贝函数封装为test_HtoD(). 如对于c(j, i)=c(j, i)+a(j, k)*b(k, i), 则应有如下函数被生成:
extern "C" void test_DtoH(){//从GPU到CPU的内存拷贝
CHECK(cudaMemcpy(param_mp_c_, d_c,
n*m*sizeof(double), cudaMemcpyDeviceToHost));
}
(2) 核函数的转换
1) 核函数范围的确定
一般情况下, 建议用户将核函数部分放在一个单独的Fortran文件中, 使用subroutine或者function来将其封装, 在主程序中通过call语句来对其进行调用.
同时, 我们允许手动指定核函数的范围, 在对应的代码块加入如下指导语句:
#pragma test kernel begin
kernel code
#pragma test kernel end
二者之间的代码被认为是一个完整的名为test的核函数.
2) 形参列表的确立
核函数中所用到的变量均需要作为形参列表的一部分来进行传递, 具体分类如下: ① 对于基本数据类型: 整型、实型、字符型、逻辑型, 直接将其转换为C中所对应的类型, 作为参数来进行传递. ② 对于数组型变量, 将其均视为一维数组, 相应类型的指针作为形参来进行传递. ③ parameter关键字定义的常量采用在头文件中宏定义的方式进行处理, 无需进行参数的传递.
3) 函数体的转换
GPU上的计算以kernel函数为主, 科学计算软件中主要的计算代码是do循环计算(模板计算), 图3给出了模板计算的kernel函数生成. 首先是插入了线程号计算代码, 然后根据线程号将循环计算任务分配给相应的线程. 由于控制循环的变量被修改, 因此原先由循环变量控制的数组下标也要做出相应的修改. 在Fortran程序中由数组下标i控制的循环, 在循环展开后i的含义变为CUDA C程序中的线程号. 多维情况与一维情况类似, 不再赘述.

|
图 3 循环展开格式 |
C到CUDA C的整体转换算法如算法2所示.
算法2. C到CUDA C的转换
1. 输入C文件
2. for var in变量信息表
3. if var in 引用模块文件
4. 声明设备端相应变量, 创建cudaMalloc函数
5. if var match 赋值语句左侧
6. 创建GPU到CPU的cudaMemcpy函数
7. else if var match 赋值语句右侧
8. 创建CPU到GPU的cudaMemcpy函数
9. end if
10. 创建cudaFree函数
11. end if
12. end for
13. 确立形参列表, 生成核函数
14. 转换核函数函数体
15. 输出CUDA C文件
4 实验验证本文实验环境如表2所示.
| 表 2 实验环境配置 |
4.1 矩阵乘法的异构代码自动生成
稠密矩阵的乘法是典型的计算密集型问题, 且具有较好的并行性. 以计算矩阵乘法:
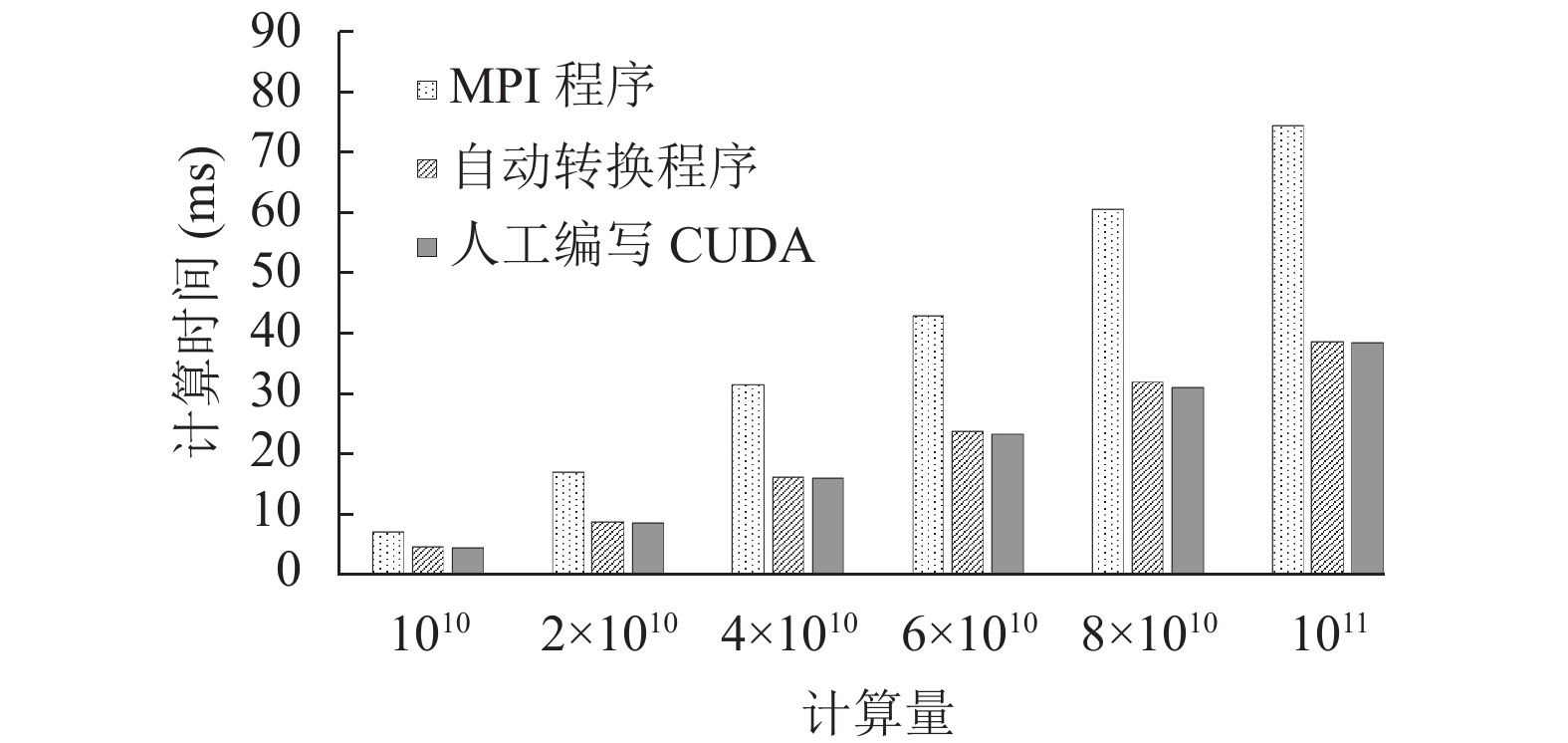
转换后程序的性能表现如图4所示, 其中横坐标是矩阵规模(m×d×n), 纵坐标是计算时间. 点状柱是原MPI程序在1个节点(2颗CPU)下的计算时间, 条纹柱与灰柱分别对应使用本文算法转换完成和手动实现的CUDA C代码在同1张GPU卡上的计算时间. 从计算结果中可以得出, 由本文算法自动转换得到的CUDA C矩阵乘法在性能上与人工编写的CUDA C矩阵乘法相当, 较原MPI程序平均加速了1.83倍. GPU+CPU的异构计算较原CPU并行能够取得更好的加速效果.
4.2 海洋环流模式LICOM的异构代码生成LICOM 是由中科院大气物理研究所LASG 国家重点实验室发展的全球海洋环流模式. 它是中国科学院地球系统模式CAS-ESM 的重要组成部分[15].
|
图 4 矩阵乘法性能对比 |
源程序采用Fortran语言编写, 核心计算程序普遍引用了多个模块, 大量的数组变量通过allocate语句来分配内存, 以readyt为例, 核函数部分计算变量累计86个, 其中数组型变量共52个, 引用自14个模块中数组变量共40个, 采用本文算法进行代码自动转换, 生成的文件结构及功能如图5所示.

|
图 5 readyt转换文件结构及功能说明 |
实验证明: 对于复杂的大型程序, 本文提出的转换算法仍能够自动检索核函数所需变量, 从对应文件中提取变量的相关信息, 自动生成内存分配、拷贝、释放等一系列的函数, 结合现有的变量信息表以及转化完成的代码进行调试, 手动修改少量代码后即可编译通过, 转化代码的正确率高达80%以上, 初步完成了LICOM3 CUDA C异构代码的开发.
进一步分析转换算法的输出结果, 探究转换过程中出错的主要原因: (1)计算中含有冒号的数组索引未能进行相应的展开; (2) readyt内部定义的部分数组变量在实际的CUDA C程序中仍需进行额外的处理. 若针对上述两点预先对Fortran程序进行简单的修改, 则转换正确率可达90%以上.
经过测试, Fortran程序中readyt函数平均耗时72.32 s, 转换完成的CUDA C程序中该函数平均耗时1.29 s, 加速了56.06倍.
5 结论展望本文在深入分析Fortran语言以及CUDA C相关特征的基础上, 使用正则表达式和shell语言, 实现了一套逻辑清晰、功能强大的Fortran到CUDA C的转换方法. 经过测试, 该方法转换正确率高达80%以上, 转换后的代码性能与人工编写的CUDA C代码相当, 能够有效节省大型程序的移植时间. 本文的实现存在一定的局限性, 对于较复杂的软件代码得到的转换结果仍需开发人员手动进行调试, 且实现的代码还需要进行深度优化.
| [1] |
Li Y, Dai ZT. Design and implementation of hardware accelerator for recommendation system based on heterogeneous computing platform. Proceedings of the 3rd International Conference on Mechatronics Engineering and Information Technology (ICMEIT 2019). Dalian: Wuhan Zhicheng Times Culture Development Co. Ltd., 2019. 966–971.
|
| [2] |
Han TD, Abdelrahman TS. hiCUDA: High-level GPGPU programming. IEEE Transactions on Parallel and Distributed Systems, 2011, 22(1): 78-90. DOI:10.1109/TPDS.2010.62 |
| [3] |
Li D, Cao HJ, Dong XS, et al. GPU-S2S: A compiler for source-to-source translation on GPU. Proceedings of the 3rd International Symposium on Parallel Architectures, Algorithms and Programming. Dalian: IEEE, 2010. 144–148.
|
| [4] |
孙香玉. 面向CUDA的循环语句源到源并行化研究[硕士学位论文]. 兰州: 西北师范大学, 2014.
|
| [5] |
Nugteren C, Corporaal H. Bones: An automatic skeleton-based C-to-CUDA compiler for GPUs. ACM Transactions on Architecture and Code Optimization, 2015, 11(4): 35. |
| [6] |
Yu CL, Royuela S, Quiñones E. OpenMP to CUDA graphs: A compiler-based transformation to enhance the programmability of NVIDIA devices. Proceedings of the 23th International Workshop on Software and Compilers for Embedded Systems. St. Goar: ACM, 2020. 42–47.
|
| [7] |
Lee S, Min SJ, Eigenmann R. OpenMP to GPGPU: A compiler framework for automatic translation and optimization. ACM SIGPLAN Notices, 2009, 44(4): 101-110. DOI:10.1145/1594835.1504194 |
| [8] |
Stauber T, Sommerlad P. Parsing CUDA for Transformation to SYCL in an IDE. Proceedings of the International Workshop on OpenCL. Boston: ACM, 2019. 20.
|
| [9] |
Govett MW, Middlecoff J, Henderson T. Running the NIM next-generation weather model on GPUs. Proceedings of the 10th IEEE/ACM International Conference on Cluster, Cloud and Grid Computing. Melbourne: IEEE, 2010. 792–796.
|
| [10] |
高阳阳, 徐烈伟, 俞剑, 等. 一种新型动态可重构的正则表达式匹配引擎设计. 复旦学报(自然科学版), 2019, 58(6): 706-718. |
| [11] |
段红英. Fortran程序CUDA并行化总结. 物联网技术, 2015, 5(11): 92-93. DOI:10.3969/j.issn.2095-1302.2015.11.033 |
| [12] |
Brodtkorb AR, Hagen TR, Sætra ML. Graphics processing unit (GPU) programming strategies and trends in GPU computing. Journal of Parallel and Distributed Computing, 2013, 73(1): 4-13. DOI:10.1016/j.jpdc.2012.04.003 |
| [13] |
韩雪. 面向CPU_GPU异构系统的通用计算模型研究[硕士学位论文]. 沈阳: 东北大学, 2015.
|
| [14] |
王泽寰, 王鹏. GPU并行计算编程技术介绍. 科研信息化技术与应用, 2013, 4(1): 81-87. |
| [15] |
王文浩, 姜金荣, 王玉柱, 等. 海洋模式LICOM的MIC并行优化. 科研信息化技术与应用, 2015, 6(3): 60-67. |
 2022, Vol. 31
2022, Vol. 31


