信息社会产生的大量数据急需强有力的数据分析工具, 将数据转换成有用的信息、知识, 因此, 数据挖掘技术[1]应运而生. 高校体测数据的关联规则挖掘能直接反映项目集中数据的潜在关联, 对帮助学生提高体能素质具有重要的意义.
张崇林等[2]通过体质测试数据处理方法分析, 认为体质测试数据适合进行关联规则数据挖掘, 并且通过关联规则数据挖掘, 发现了原知识体系利用BMI和体脂率评价肥胖的矛盾现象, 可知Apriori算法利用逐层迭代搜索的方法挖掘数据间的关联关系, 是目前关联规则应用最广、最经典的算法. 赵常红等[3]运用关联规则的Apriori算法并设置支持度、置信度, 分析男、女生的不同体测数据, 各测试指标等级数量分布情况及其之间的关联性, 但是忽略了算法的运行效率. 刘辛等[4]提出一种基于数组的Apriori算法, 减少了候选频繁集冗余, 提高了Apriori算法效率, 找出了各体测项目间的关联关系, 但是忽略了遍历数据库的次数对运行效率的影响. 崔亮等[5]提出一种基于动态散列和事务压缩的关联规则挖掘算法, 通过估计产生候选项集的大小来动态选择是否使用hash技术, 并且利用事物压缩技术删除不包含频繁项集的事务, 从而提高算法运行效率.
由上述文献可知关联规则Apriori算法可应用于高校体测数据场景, 其弊端在于数据量增加到一定程度时算法效率低下[6]. 与崔亮等[5]提出的方法不同, 本文提出的基于事务压缩和hash技术的改进Apriori算法, 无需估计产生候选项集的大小, 是根据体测数据特征有限并且长度一致的特点, 先使用散列技术压缩要考察的候选项集, 再结合事务压缩技术减少遍历数据集的事务项数和长度, 将这两种算法优势完美结合, 从而大大提高算法的运行效率, 并且有效得到体测数据间的关联, 能较好地预测影响学生体能素质的因素, 从而辅助指导学生的体能训练.
1 基于事物压缩和hash技术的Apriori关联规则算法关联规则是描述数据事务特征属性间的规律, 通过某些属性来预测其他属性的关联. 在体测数据中, 设项集itemset={item_1, item_2, …, item_n}是高校学生体测数据特征属性的集合, n是属性的个数[7]. 一条学生体测数据是一个事务T, 一个事务T是一个项集, 每个事务均与一个唯一标识符Tid相联系, 体测数据中学籍号是唯一的标识符Tid[8]. 不同学生的体测数据组成了事务集D, 它构成了关联规则发现的事务数据库.
用支持度和置信度衡量关联规则的标准, 例如形如
| $ \begin{split} {\textit{Support}}(A \Rightarrow B) &= P(A \cup B) \\ & = \frac{{{\textit{Support}}\_count(A \cup B)}}{{{\textit{Total}}\_count}} \end{split} $ | (1) |
其中, Support_count(A∪B)表示A和B同时存在的事务个数, Total_count表示所有事务的个数.
| $ \begin{split} {\textit{Confidence}}(A \Rightarrow B) &= \frac{{{\textit{Support}}(A \cup B)}}{{{\textit{Support}}(A)}} \\ & = \frac{{{\textit{Support}}\_count(A \cup B)}}{{{\textit{Support}}\_count(A)}} \end{split} $ | (2) |
其中, Support_count(A)表示A存在的事务数.
如果
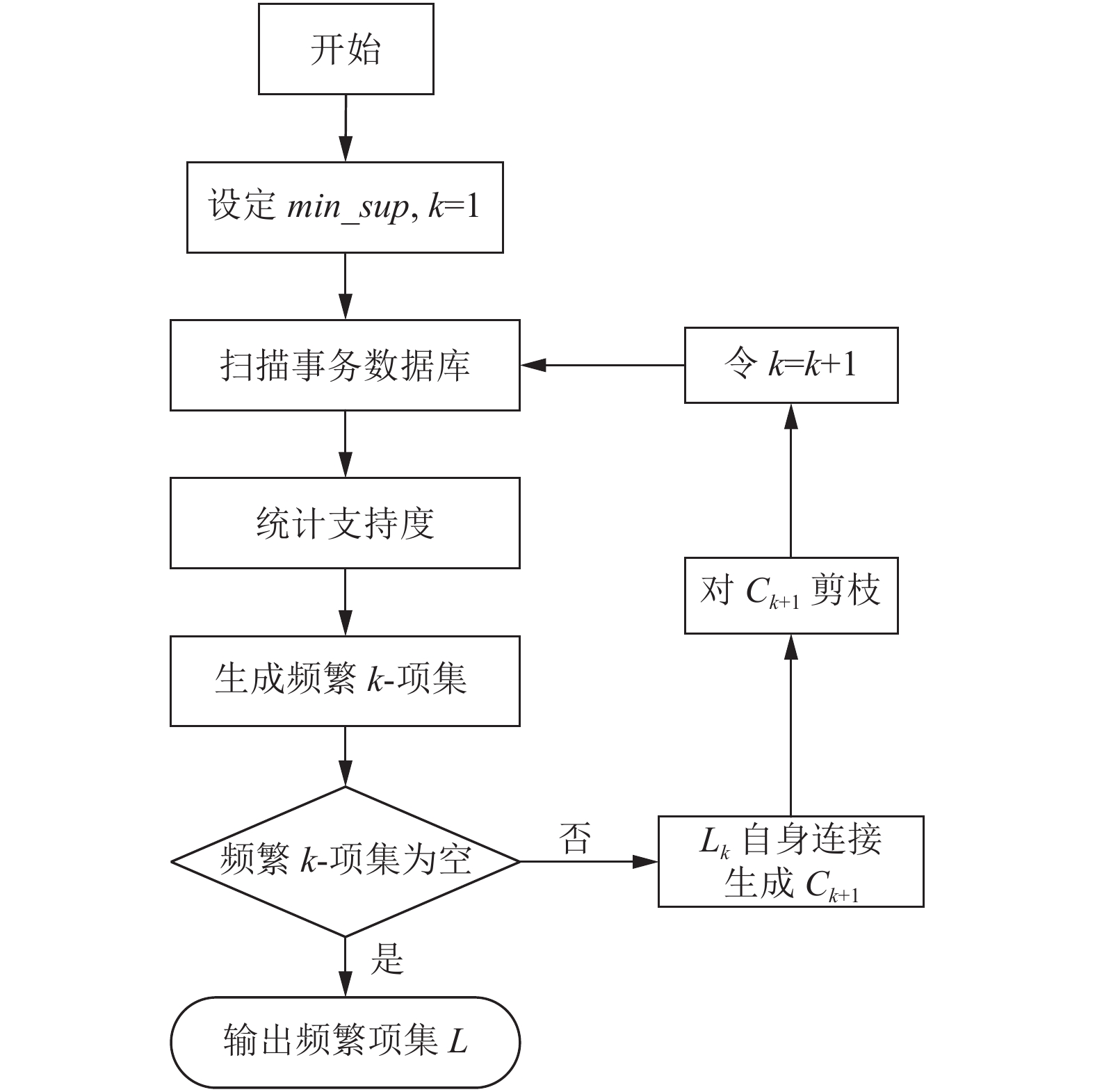
Apriori算法是利用k-项集来产生(k+1)-项集迭代的方法[9], 其操作流程如图1, 设定最小支持度min_sup和最小置信度min_conf, 扫描整个数据库, 统计长度为1的每一项的个数, 筛选满足最小支持度的项, 得到频繁1-项集L1; 由L1自身连接生成候选2-项集C2, 得到的C2进行剪枝操作, 统计长度为2的每一项的个数, 删除不满足最小支持度的项, 得到频繁2-项集L2, 如此迭代下去, 直到不能再找到频繁k-项集[10], 最终得到频繁项集L={L1, L2, …, Lk}.
Apriori算法的弊端在于数据量增加到一定程度时算法效率低下, 具体表现在以下3个方面:
1)在Lk–1与自身连接生成Ck过程中, 可能需要产生大量候选项集. 例如, 假设Lk–1中有m个k-项集, 则在进行自身连接需要进行比较的时间复杂度为O(k×m2).
2)在对Ck剪枝的过程中, 判断Ck中任意一个k项候选集的(k–1)-项候子集是否为Lk–1的子集, 最快只需要扫描一次得出结果, 最慢需要k–1次, 所以平均时间为|Ck|×|Lk–1|×k/2.
3)在筛选满足最小支持度的候选项集过程中, 对Ck中的每个项进行计数, 需要扫描数据库|Ck|次.
1.2 基于散列技术的Apriori算法散列技术又名hash技术[11], 基于散列技术的Apriori算法的优势主要体现在能将生成的Ck进行压缩, 大大缩小了Ck占用空间. 首先, 扫描数据库所有的事务得到C1, 筛选满足最小支持度的候选项集得到L1; 然后利用散列技术来改进产生频繁2-项集的方法, 具体如下: 将每条事务生成其所有的2-项集并且运用散列技术构造散列函数把它散列到相应的散列表中, 即分配到不同的桶中并计数, 而且相同的数据项被分配到同一存储空间, 且对应着同一计数器, 只需计数加一即可, 且降低了所需的存储空间. 同样的生成频繁k-项集也是用相同的方法, 并且在散列表中可以筛选出容器计数小于支持度阈值的k-项集, 因此可以很好的对要检测的k-项集执行压缩操作.
散列技术的缺点是其运行效率依赖于事务的平均长度, 也就是说如果数据集的特征少, 平均长度短, 其运行效率就高, 反之运行效果差. 而Apriori方法运行效率不依赖于数据集特征的长度和数量, 所以一定程度上弥补hash技术的缺点, 两者互补可以大大增加算法的运行效率.
|
图 1 经典Apriori算法流程 |
1.3 基于事务压缩技术的Apriori算法
基于事务压缩技术的Apriori算法的优势主要体现在将进一步迭代扫描的数据库进行压缩, 进而影响扫描事务库的次数, 增加算法的运行效率[12]. 该技术的改进是根据经典Apriori算法的性质, 即如果一个事务不包含任何的频繁k-项集, 则其也不包含任何的频繁(k+1)-项集. 因此在生成Lj(j>k)时, 遇到上述事务时, 可以加上标记或删除, 扫描数据库时不需要再扫描该事务, 减少扫描事务库的次数.
1.4 基于散列技术和事务压缩相结合的改进根据以上了解可知, 基于散列技术的改进和基于事务压缩技术作用于Apriori算法过程中的不同部分, 基于散列技术的改进体现在减少候选项集的规模, 并更进一步减少数据库扫描的次数, 而事务压缩技术能够逐渐减小数据库中事务的长度和规模, 都主要作用在Apriori算法的剪枝部分[13], 并且两者会促进对方的效果, 而不产生负面影响.
改进算法流程如算法1所示, 根据高校体测数据的特征有限和并且长度一致的特点, 利用散列技术遍历一次事务集, 即可生成频繁项集L1, L2, L3, 再利用事务压缩技术由L3生成L4, 如此迭代下去, 直到不能再找到频繁k-项集. 因为迭代生成候选项时可能性太多, 数据量大时占用内存太大, 所以不继续使用hash技术继续生成L4, 而改用事务压缩技术, 有效地避免hash技术的短板.
算法1. 改进Apriori算法
输入: 数据库D, 最小支持度min_sup, 最小置信度min_conf
过程:
1)扫描数据库, 利用散列技术生成频繁1-项集L1, 频繁2-项集L2, 频繁3-项集L3;
2)通过频繁项集Lk–1自身连接生成Ck候选项集, 再进行剪枝;
3)利用事务压缩技术减少扫描事务集的次数, 删除不满足最小支持度的项集, 生成频繁k-项集Lk;
4)对k>3, 重复执行步骤2)和3), 判断频繁k-项集的长度, 如果为0, 则跳出循环, 得到最终结果频繁项集L, 否则返回步骤2);
5)筛选出满足min_sup和min_conf的频繁项集即强关联规则, 结束.
输出: 强关联规则
2 实验过程及分析 2.1 数据准备以我校2016级7 709名大学生第一学年的体测成绩为实验对象, 从数据库中提取与体测成绩有关的数据, 如: 学籍号、性别、身高、体重、肺活量、50 m、立定跳远、1 000 m (男生)、800 m (女生)、引体向上(男生)、仰卧起坐(女生)共11个属性, 表1是以学籍号为主键的体测成绩.
2.2 数据清洗及转换实验数据来源于我校体测中心, 所以得到的数据较为规范, 但是数据中存在部分学生体测成绩缺项, 又考虑到部分特殊学生免测的情况, 所以要对原始数据先进行预处理, 经过数据清洗、数据转换和数据消减, 实现算法在高校学生体测中的应用.
| 表 1 学生2016年的体测成绩 |
数据清洗的实际操作主要有:
(1)针对缺项数据, 如果缺项数据较多则删除该学生的体测成绩[12]; 如果缺项较少, 则可以通过求该项目成绩的平均值、众数或者中位数填充;
(2)针对免考学生的数据, 由于各项成绩为缺项, 可以直接删除, 使得清洗后的数据标准、干净且连续.
数据转换将不同标准的连续型数据转换成标准相同的离散型数据, 便于后续的统一处理. 虽然体测项目间的评判标准不同, 但是都可以划分为A、B、C、D四个等级, 即优秀、良好、及格、不及格, 其次, 为了方便统计以及提高数据挖掘的效率, 用数字1和2分别代替性别的男和女, 用小写字母开头代替各项目的名称, 如: 肺活量用fhl代替.
数据转换结果如表2所示, 经过数据清洗及转换得到的标准数据最终有7 337条.
| 表 2 数据转换结果 |
2.3 数据消减
数据消减是在保持数据库的完整性的情况下, 从上述数据集中获得精简的数据集, 能够保证不影响最终的算法结果. 男生和女生体测项目和评价标准有所不同, 所以本文将在数据挖掘时对男生和女生的体测成绩数据分别进行处理. 数据消减就是针对数据库中筛选出的男生、女生的体测数据, 消除与体测项目属性无关的项, 例如学籍号, 性别.
2.4 实验验证试验环境为Intel(R) Core(TM) i5-5200U 2.20 GHz处理器, 4 GB内存, 操作系统为Windows 10, 算法在Python 3.8下实现.
设定min_conf = 0.9, 设置不同的最小支持度, 利用Apriori算法以及本文提出的事务压缩和hash结合的算法得到的结果如表3所示, 在相同的最小支持度下得到的关联规则数目相同, 表示改进后的算法确保了Apriori算法的准确性, 由此可以得到改进算法的可靠性; 随着最小支持度的增加, 改进后的算法执行效率大大提高. 改进后的算法在保证挖掘精度的同时提高算法效率.
| 表 3 两种算法比较 |
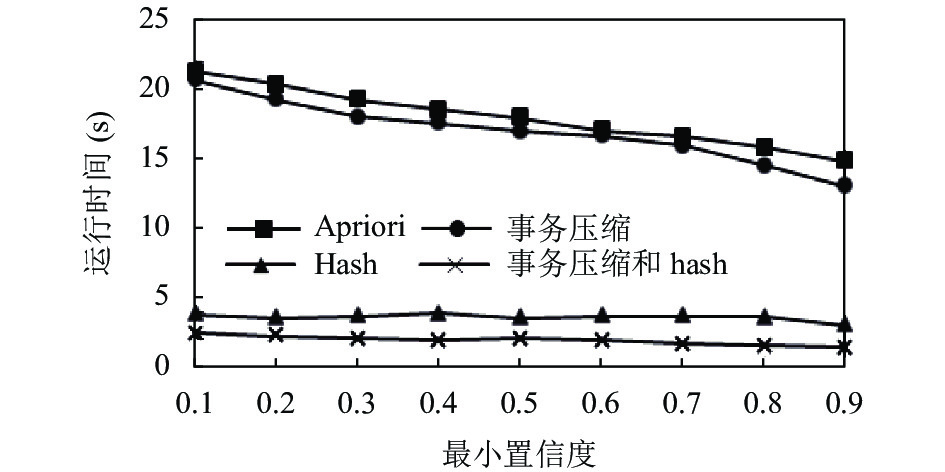
为了能直观地反映出改进后的算法运行效率更高, 在设置不同最小置信度、最小支持度情况下, 将得出的实现数据进行分析对比, 结果如图2和图3所示. 图中结果可知, 本文提出的改进算法效率明显优于经典Apriori算法、基于hash的Apriori算法以及基于事物压缩的Apriori算法. Apriori算法和基于事物压缩的Apriori算法随着支持度和置信度的增加执行效率比较接近, 其中基于事物压缩的Apriori算法效率稍高; 基于hash改进算法相较于Apriori算法和基于事物压缩的Apriori算法本身具有一定的优越性, 本文将hash技术与事务压缩技术相结合得到了更好的效果.
2.5 结果分析原始的体测数据经过数据预处理后得到2 266条女生体测数据和5 071条男生体测数据, 设置最小置信度min_conf = 0.9, 最小支持度min_sup = 0.3, 将这两类数据分别用文中提到的4种算法进行关联规则挖掘, 将各运行效率进行比较, 如表4所示, 可以看出本文提出的基于事物压缩和hash结合的算法执行效率更高, 与经典Apriori算法执行效率相比, 女生体测数据算法执行效率提高了86.12%, 男生提高了90.63%; 与基于事物压缩的Apriori算法相比, 女生体测数据算法执行效率提高了80.57%, 男生提高了89.32%; 与基于hash的Apriori算法相比, 女生体测数据算法执行效率提高了48.1%, 男生提高了55.69%; 可见, 该4种算法应用于男生的体测数据的执行效率比女生更高, 说明数据集量越大改善效果越明显.

|
图 2 不同支持度性能对比 |
|
图 3 不同置信度性能对比 |
| 表 4 4种算法执行效率比较 (s) |
表5和表6分别是男生和女生体测成绩的关联规则挖掘结果, 由表5可以看出挖掘出的男生第一条关联规则50 m:C
现在数据挖掘技术已经非常成熟, 然而数据挖掘和体能分析结合的应用却很少, 本文通过对比4种算法实现的结果和执行效率, 表明改进后的算法在高校学生体测中的应用具有一定的可靠性和有效性, 对于比较大的数据集效率改善更明显. 并且将本文所提出的算法, 与经典Apriori算法相比, 可知执行效率提高了85%以上, 并且挖掘出体测成绩间的潜在关联, 分析身体素质的不足之处, 对学生重视体育锻炼, 辅导老师安排学生的训练计划具有指导性的意义.
| 表 5 关联规则 (男生) |
| 表 6 关联规则 (女生) |
| [1] |
Casado R, Younas M. Emerging trends and technologies in big data processing. Concurrency and Computation: Practice and Experience, 2015, 27(8): 2078-2091. DOI:10.1002/cpe.3398 |
| [2] |
张崇林, 虞丽娟, 吴卫兵. 关联规则数据挖掘技术在体质测试分析中的应用. 上海体育学院学报, 2012, 36(2): 42-44. DOI:10.3969/j.issn.1000-5498.2012.02.010 |
| [3] |
赵常红, 王琳, 冯刚, 等. 民族院校大学生体质测试数据的分析与应用——以西北民族大学为例. 兰州文理学院学报(自然科学版), 2017, 31(3): 108-112. |
| [4] |
刘辛, 杨素锦. 基于数组的Apriori算法在体质测试数据分析中的应用. 山东理工大学学报(自然科学版), 2011, 25(5): 55-58. DOI:10.3969/j.issn.1672-6197.2011.05.016 |
| [5] |
崔亮, 郭静, 吴玲达. 一种基于动态散列和事务压缩的关联规则挖掘算法. 计算机科学, 2015, 42(9): 41-44. DOI:10.11896/j.issn.1002-137X.2015.9.009 |
| [6] |
Chen Z, Cai SB, Song QL, et al. An improved Apriori algorithm based on pruning optimization and transaction reduction. 2011 2nd International Conference on Artificial Intelligence, Management Science and Electronic Commerce. Deng Feng: IEEE, 2011. 1908–1911.
|
| [7] |
纪文璐, 王海龙, 苏贵斌, 等. 基于关联规则算法的推荐方法研究综述. 计算机工程与应用, 2020, 56(22): 33-41. DOI:10.3778/j.issn.1002-8331.2006-0158 |
| [8] |
杜永兴, 高迪, 李宝山, 等. 改进Apriori算法在荒漠草原的应用. 计算机工程与设计, 2019, 40(7): 2082-2086, 2093. DOI:10.16208/j.issn1000-7024.2019.07.046 |
| [9] |
Jin R, Lin ZJ, Xue CM, et al. An improved association-mining research for exploring Chinese herbal property theory: Based on data of the Shennong’s Classic of Materia Medica. Journal of Integrative Medicine, 2013, 11(5): 352-365. DOI:10.3736/jintegrmed2013051 |
| [10] |
Zhang CS, Li Y. Extension of local association rules mining algorithm based on Apriori algorithm. 2014 5th IEEE International Conference on Software Engineering and Service Science. Beijing: IEEE, 2014. 340–343.
|
| [11] |
彭永供, 王靓明, 朱敏, 等. 基于散列技术的高效剪枝关联规则挖掘算法. 南昌大学学报(理科版), 2009, 33(5): 494–498.
|
| [12] |
孙金华, 谢彦麒. 基于事务压缩的关联规则挖掘算法改进. 微计算机信息, 2010, 26(27): 223-225. DOI:10.3969/j.issn.2095-6835.2010.27.090 |
| [13] |
Wang P, An CH, Wang L. An improved algorithm for Mining Association Rule in relational database. 2014 International Conference on Machine Learning and Cybernetics. Lanzhou: IEEE, 2014. 247–252.
|
 2022, Vol. 31
2022, Vol. 31


