1 引言

随着计算机网络技术的进步和信息时代的到来, 几乎每个人都有一部智能手机, 我们在日常生活中经常用它来拍照, 记录一些图像信息, 并在互联网上共享和传输数字图像. 虽然电脑和智能手机使我们能够方便地传输图像信息, 但通过互联网传输重要或秘密的图像, 如商业企业或军方使用的图像, 可能会带来一定的危险. 攻击者或间谍可以通过监视互联网来检测和捕获有价值的图像, 因此在考量如何保证秘密图像传输的安全性时, 需要采用相应的图像保护机制.

加密^{[1, 2]}和信息隐藏^{[3, 4]}是目前最常见的图像保护技术. 加密后的图像是类噪声的, 使攻击者看不到任何秘密信息, 但类噪声图像很容易被攻击者怀疑含有秘密信息, 从而破坏甚至破解原始的秘密图像, 造成原秘密图像的破坏和泄露. 信息隐藏可以弥补加密的不足. 它能将秘密图像嵌入到可理解的载体图像中, 使攻击者不会怀疑秘密信息的存在, 从而有效地规避攻击. 但仅用信息隐藏算法太过单一. 如果是重要的秘密图像, 无法达到军事等领域需要的权限分享, 多方协作要求. 所以结合信息隐藏的秘密共享方案可以解决这个问题.

Shamir^[5]首先提出了基于多项式的秘密共享(SS)方案, 通过构造一个t–1次多项式来产生n个秘密共享从而对秘密信息进行加密. 当收集t个或多个共享时, 可以通过拉格朗日插值重构多项式来解密. 受到Shamir工作的启发, Thien等人^[6]把多项式应用在图像领域进行秘密共享. 但在灰度图像中, 每个像素具有256个可能值, 并且256不是质数, 因此他们采用小于256的最大质数251作为p. 所有大于250的像素值将被模块251截断, 从而导致有损恢复. 另外, 为了消除相邻像素之间的相关性, 他们的方案需要在共享前对原始图像的像素进行置乱, 导致了影响效率的辅助加密.

由于模块化方法仅需O(k)运算^[7]即可恢复每个秘密像素, 因此基于中国剩余定理(CRT)的图像秘密共享具有计算量小的优点, 这在考虑大量图像像素时非常重要. Asmuth等人^[7]以及Mignotte^[8]分别于1983年提出了基于CRT的(t, n)门限秘密共享. 基于CRT^{[9, 10]}的秘密图像共享方法也有很多, 但是这些研究主要集中在灰度图像上, 而我们日常生活中使用的图像大多是彩色的. 为了具有实用价值, 我们需要将秘密共享方案有效地应用到彩色图像中.

彩色图像秘密共享是通过处理彩色图像, 实现共享的方案. 传统的彩色图像秘密共享方案是分别共享和恢复R、G和B色平面^[11-13]. 闫伟齐等人^[14]首先将CRT引入图像秘密共享, 它可能会有少量的信息泄漏和恢复损失. Ulutas等人^[15]提出了一种基于文献[7]方案的CRT图像秘密共享, 将像素值分成两部分间隔. 但他们没有给出精确的参数限制, 当随机数太小时, 可能达不到(t, n)阈值. Hu等人^[16]提出了一种基于混沌映射的CRT图像秘密共享, 涉及辅助加密. Chuang等人^[17]对Ulutas等人^[15]提出的基于CRT的图像秘密共享进行了扩展, 设计了一个(t, n)门限图像秘密共享, 只共享最重要的7位, 以满足CRT的限制. 它们独立地存储和传输秘密图像像素的最低有效位(LSB), 或者直接丢弃它们. 因此, 它们的缺点是恢复的秘密图像有损且传输成本高. 近期的彩色图像秘密共享方案中, Wu等人^[18]解决了像素扩展问题, 但恢复的图像是二值秘密图像与彩色影子图像的叠加图像, 对于各种应用场景不具有普适性, 且需要多次重建, 并不能做到直接恢复出无损的秘密图像. Wang等人^[19]运用的秘密图像是彩色图像. 但恢复的还是彩色秘密图像与彩色影子图像的叠加图像, 且PSNR值低. Prasetyo等人^[20]的彩色影子图像有轮廓, 即影子图像有相关性, 像素并非均匀分布. 且若要无损恢复彩色秘密图像需要多次异或叠加, 复杂度较高. Mhala等人^[21]恢复的彩色秘密图像是类噪声的, 并非无损恢复. Blesswin等人^[22]没有显示彩色影子图像, 且RGB三通道的灰度影子图像较黑, 说明像素值较低, 模数较低, 并非均匀分布, 无法保证安全性, 不能满足基于CRT的秘密共享对于模数的控制.

本文在CRT的基础上, 提出了一种(t, n)门限的无损高效彩色图像秘密共享信息隐藏算法, 该方案将基于中国剩余定理(CRT)的秘密共享与DCT信息隐藏技术进行结合, 保障了传输彩色秘密图像的安全性. 在生成端, 利用DCT信息隐藏算法将彩色秘密图像通过CRT生成的彩色秘密影子图像, 嵌入至用户提供的彩色载体图像中, 并分发. 在恢复端提取出影子图像, 使用CRT恢复彩色秘密图像. 实验结果表明, 本文提出的算法能无损恢复秘密图像, 影子图像像素值近似均匀分布, 也不产生像素扩展, 与其它方案相比本文方案具有较高效率.

2 预备知识 2.1 秘密共享

在密码学中, 秘密共享是将秘密信息分成众多子秘密, 形成共享份, 使用达到阈值的子秘密共享份就可以还原该秘密信息. 秘密共享技术具体形式如下:

绝大多数涉密需要保护的通信系统, 它的安全性皆是由主密钥决定的. 如若出现主密钥被破坏或在传输过程中丢失的情况, 该系统将不再安全.

密码学中提出了一种解决办法: 秘密共享技术. 该技术可以达到减小风险, 分散权力, 容许攻击的目的. 通过将一个主密钥s分割成n份 $ {s_1}, {s_2}, \cdots , {s_n} $ , 获取满足门限值t的份额通过秘密共享算法即可恢复秘密s, 而获取不满足门限值t的份额时, 无法恢复秘密s.

2.2 基于中国剩余定理的秘密共享方案

本方案基于中国剩余定理(CRT), 提出了一个(t, n) 秘密共享方案, 由秘密s通过CRT相关公式计算得到y. 再与n个递增的模数 $ {m_1}, {m_2}, \cdots , {m_n} $ 通过取模运算得到 $ \left( {{m_i}, {y_i}} \right) $ 即是共享份, 在实际方案中只需要保存 $ {y_i} $ .

2.2.1 参数选取

参数的选择满足以下要求.

(1) $q > s$ .

(2) ${\rm gcd} ({{m}_1},{{m}_j}) = 1,\forall i,j,i \ne j$ .

(3) ${\rm gcd} (q,{{m}_i}) = 1,i = 1,2, \cdots, n$ .

(4) $N = \displaystyle\prod\nolimits_{i = 1}^t{m_i} > q \displaystyle\prod\nolimits_{i = 1}^{t - 1}{m_{n - j + 1}}$ .

2.2.2 秘密共享与恢复

参数A经由随机选取, 范围是 $0 \leqslant A \leqslant \left\lfloor N/ q \right\rfloor - 1$ . 根据公式 $ y = s + Aq $ , 求得用于计算共享份的参数y, 该参数满足 $y \lt q + Aq = \left( {A + 1} \right)q \leqslant \left\lfloor N /q \right\rfloor \cdot q \leqslant N$ . 由 $ {y_i} \equiv y\boldsymbolod $ $ {m_i}\left( {i = 1, 2, \cdots , n} \right) $ . $ \left( {{m_i}, {y_i}} \right) $ 是共享份额, 因为模数公开, 所以将其中的 $ {y_i} $ 作为子共享, 分发给用户. 达到门限值的t个用户 $ {i_1}, {i_2}, \cdots , {i_t} $ 提供自己的子共享, 根据 $\{ ( {{m_{{i_j}}}, {y_{{i_j}}}} ) $ $ |i = 1, 2, \cdots , t \}$ 建立方程组.

$ \left\{ {\begin{array}{*{20}{l}} {{y_{{i_1}}} \equiv y\;{\rm{mod}}\;{m_{{i_1}}}}\\ {{y_{{i_2}}} \equiv y\;{\rm{mod}}\;{m_{{i_2}}}}\\ \qquad\vdots\\ {{y_{{i_t}}} \equiv y\;{\rm{mod}}\;{m_{{i_t}}}} \end{array}} \right.$

(1)

可以求得:

$ y\equiv {y}^{\prime }\;\mathrm{mod}\;{N}^{\prime } $

(2)

其中, $ y' \equiv \displaystyle\sum\nolimits_{j = 1}^t {{y_{{i_j}}}{M_{{i_j}}}} {M_{{i_j}}}^{ - 1} $ , $ {M_i} = {M \mathord{\left/ {\vphantom {M {{m_i}}}} \right. } {{m_i}}} $ . 同时 $ {M_i}{M_i}^{ - 1} \equiv $ $ 1(\boldsymbolod {m_i}) $ . $ {M_i}^{ - 1} $ 是 $ {M_i} $ 的逆元. 本文使用基于费马小定理的逆元求解法. 只需进行模幂运算就可以快速求解, 即 $ {M_i}^{ - 1} \equiv {M_i}^{{m_i} - 2}(\boldsymbolod {m_i}) $ .

最后根据 $ N' \equiv \displaystyle\sum\nolimits_{j = 1}^t {{m_{{i_j}}} \geqslant N} $ , 得到 $ y \equiv y'\boldsymbolod N' $ , 由 $ y\boldsymbolod q $ 解得秘密s.

2.2.3 (t, n)门限确定依据

因为由t个成员的共享计算得到的模满足条件 $y＜N\leqslant N{'}$ , 所以 $ y = y' $ 是唯一的. 再由 $ y' - Aq $ 即得秘密s.

若仅有t–1个参与者提供自己的共享份 $ \left( {{m_i}, {y_i}} \right) $ , 则只能求得 $ y'' \equiv y\boldsymbolod N'' $ . 其中 $ N'' = \displaystyle\prod\nolimits_{j = 1}^{t - 1} {{m_{{i_j}}}} $ , 得 $N{'}{'}＜N/q$ , $N/N{'}{'}＞q$ . 令 $ y = y'' + \alpha N'' $ , 其中 $0\leqslant \alpha ＜y/N{'}{'}＜N/N{'}{'}$ . 由于 $N/N{'}{'}＞q$ , $ (N'', q) = 1 $ , 当 $ \alpha $ 在[0, q–1] 变化时, $y{'}{'}+\alpha N{'}{'}＜N$ , 都是y的可能取值. 因此t–1个参与者无法确定y.

2.3 DCT信息隐藏算法嵌入参数选择

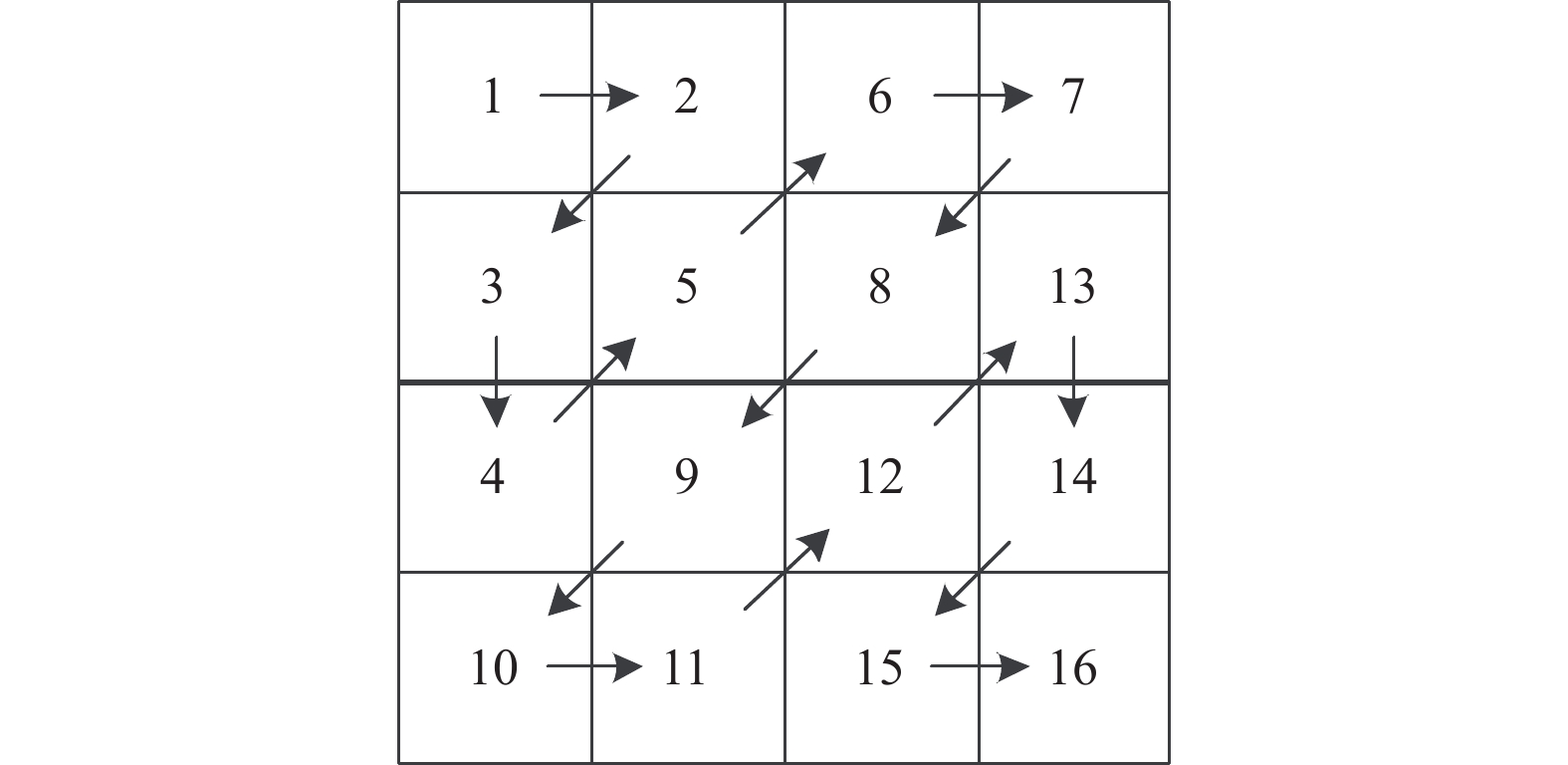
本文方案中待嵌入的数据是彩色秘密共享的RGB三通道灰度图与超过255像素边界值产生的倍数与余数图像. 将以上的图像进行分块处理, 分为4 × 4的像素块. 以Zigzag的顺序^[23], 如图1所示, 在二维DCT变换操作后, 进行像素扫描. 从低频到高频, 对DCT系数进行排列, 将系数间存在的相关性作为信息隐藏的依据. 本方案在恢复端将无损恢复彩色秘密图像, 非中高频范围的选取会导致无法无损恢复的情况.

2.4 DCT信息隐藏算法

本文选择第12个系数, 即中高频系数进行嵌入, 所以, 规则如下:

$ \left\{ \begin{gathered} K{12_i} \geqslant 0,\;\;\;\;{W_i} = 1 \hfill \\ K{12_i} \lt 0,\;\;\;\;{W_i} = 0 \hfill \\ \end{gathered} \right. $

(3)

根据 $ {W_i}{\text{ = }}0 $ 取值, 有如下两种情况, 其中, k是水印嵌入强度.

${W_i}{\text{ = }}0 $ 时, 满足 $ K{12_i} \leqslant - k $ :

$ K{12_i} = \left\{ \begin{gathered} - K{12_i},\;\;\;\;\;\;\;K{12_i} \gt k \hfill \\ - k,\;\;\;\;\;\;\;\;\;\;\;\;\;\;k \geqslant K{12_i} \geqslant - k \hfill \\ K{12_i},\;\;\;\;\;\;\;\;\;K{12_i} \lt - k \hfill \\ \end{gathered} \right. $

(4)

$ {W_i}{\text{ = }}1 $ 时, 满足 $K{12_i}\geqslant k$ :

$ K{12_i} = \left\{ \begin{gathered} K{12_i},\;\;\;\;\;\;\;K{12_i} \gt k \hfill \\ k,\;\;\;\;\;\;\;\;\;\;\;\;\;\;k \geqslant K{12_i} \geqslant - k \hfill \\ K{12_i},\;\;\;\;\;\;\;\;K{12_i} \lt - k \hfill \\ \end{gathered} \right. $

(5)

按照 $ K{12_i} $ 的正负, 将 $ {W_i} $ 提取:

$ {W_i} = \left\{ \begin{gathered} 1,\;\;\;\;\;\;\;K{12_i} \geqslant 0 \hfill \\ 0,\;\;\;\;\;\;\;K{12_i} \lt 0 \hfill \\ \end{gathered} \right. $

(6)

3 无损(t, n)门限彩色图像秘密共享信息隐藏算法

本文设计的方案, 包括以下几个重要的过程: 首先, 生成彩色共享影子图像, 再运用DCT信息隐藏算法生成含彩色影子图像的彩色载体图像. 最后, 不少于门限值t个用户提取彩色影子图像, 并通过CRT恢复彩色秘密图像. 流程图如图2.

3.1 参数测试

公布互素、递增的模数 $A \in \left[ {0, \left\lfloor N /q \right\rfloor - 1} \right]$ . 素数q满足 $A \in \left[ {0, \left\lfloor N /q \right\rfloor - 1} \right]$ 且与模数互素. 本方案中的秘密图像是64×64的彩色秘密图像. 彩色秘密图像中的每个像素值域为[0, 255], 所以选取 $A \in \left[ {0, \left\lfloor N/ q \right\rfloor - 1} \right]$ 满足算法要求, 即大于255. 随机取 $A \in \left[ {0, \left\lfloor N/ q \right\rfloor - 1} \right]$ . 由公式 $ y = s + Aq $ 得y, 带入公式 $ {y_i} \equiv y\boldsymbolod {m_i} $ . 只要分别保存RGB三通道生成的5个64×64的 $ {y_i} $ . 即5份可视灰度秘密共享影子图像, 影子图像大小与原图一致, 不会出现部分多项式秘密共享出现的像素扩展现象. 再将RGB三通道分别生成的5份可视的灰度秘密共享影子图像通过cat函数组合成彩色秘密共享影子图像. 由于选取的模数 $ {m_i} $ ＞255, 且选取的素数q＞255, 所以生成的 $ {y_i} $ 可能会超过灰度图像能够保存的最大像素值255. 根据像素(pixel)、倍数(multiple)和余数(remainder)的英文首字母列出以下公式: p=255×m+r, 因此本文将超过255像素值的倍数与余数分别保存成图像.

3.2 生成含彩色影子图像的彩色载体图像

将n份彩色秘密共享影子图像中含有的RGB三通道灰度秘密共享影子图像与伴随它们存在的3份倍数图像、余数图像运用DCT信息隐藏算法, 将它们的像素连在一起存成一个大字符串进行DCT嵌入. 嵌入n张用户提供的载体图像中.

3.3 不少于门限值t个用户提取彩色影子图像

提取时不需要获得整个字符串, 只需要知道字符串的长度, 便可以实现秘密信息的盲提取. 根据(t, n)门限, 需要进行t次提取, 可完整提取出嵌入的字符串, 再将它们分割, 分别存成RGB三通道灰度影子图像、倍数图像、余数图像. 并将RGB三通道灰度影子图像通过cat函数还原成t份RGB彩色影子图像.

3.4 恢复彩色秘密图像

在恢复端读取整型的RGB三通道灰度影子图像与伴随它们存在的3份倍数和余数图像通过公式p=255×m + r对应相加, 并将p存成双精度型的矩阵进行秘密共享恢复操作. t个用户拿出自己的秘密共享份额, 根据CRT建立方程组, 对RGB三通道运算, 分别解得s, 存成矩阵, 并利用cat函数还原彩色秘密图像. 在本文的实验结果部分将给出参数论证例子及效果展示.

3.5 算法实现创新工作

算法实现创新工作在于: 解决了基于CRT的秘密共享算法在彩色图像应用实现上出现的像素溢出问题, 将超过255像素值的共享数据根据上文分别存成倍数图像与余数图像, 并开创性的结合信息隐藏算法, 将共享影子图像、倍数图像、余数图像全都嵌入到彩色图像中, 从而使该算法全部在彩色图像上进行操作, 实现了彩色秘密图像的无损恢复.

4 实验结果及分析

为了更好的展示基于CRT的彩色高效无损门限秘密图像信息隐藏算法, 对基于(3, 5)门限的方案进行验证. 最后, 综合学界相关论文的诸多参数与其他方案进行比较.

4.1 参数测试

本方案选取互素模数 $ {m_1} = 283 $ , $ {m_2} = 293 $ , $ {m_3} = 307 $ , $ {m_4} = 311 $ , $ {m_5} = 313 $ . 素数 $ q = 257 $ .

$ \begin{split} N =& \prod\nolimits_1^3 {{m_i}} = 25456133 \gt q \times {m_4} \times {m_5} \\ =& 257 \times 311 \times 313 = 25017151 \\ \end{split} $

(7)

$ A \in \left[ {0, \left\lfloor {{\raise0.7ex\hbox{$N$} \mathord{\left/ {\vphantom {N q}}\right.}\lower0.7ex\hbox{$q$}}} \right\rfloor - 1} \right] $ , 代入即[0, 99050] 内, 取A=22548. 彩色秘密图像的第64 × 64个像素中红色通道的像素值作为证明对象. 选取红色通道的最后一个像素255为秘密. 由:

$ \begin{split} y = s + Aq = 255 + 22548 \times 257 = 361467 \\ \end{split} $

(8)

代入公式 $ {y_i} \equiv y\boldsymbolod {m_i} $ , 得出 $ {y_i} $ . 如式(9)所示:

$ \left\{ \begin{gathered} {y_1} \equiv y\boldsymbolod {m_1} \equiv 5795051\boldsymbolod 283 \equiv 100 \hfill \\ {y_2} \equiv y\boldsymbolod {m_2} \equiv 5795051\boldsymbolod 293 \equiv 137 \hfill \\ {y_3} \equiv y\boldsymbolod {m_3} \equiv 5795051\boldsymbolod 307 \equiv 159 \hfill \\ {y_4} \equiv y\boldsymbolod {m_4} \equiv 5795051\boldsymbolod 311 \equiv 228 \hfill \\ {y_5} \equiv y\boldsymbolod {m_5} \equiv 5795051\boldsymbolod 313 \equiv 209 \hfill \\ \end{gathered} \right. $

(9)

遍历彩色图片红绿蓝三通道所有像素, 计算得到 $ y_i$ . 在恢复端, 取(283, 100)、(307, 159)、(311, 228). 参数 $M=m_1\times m_3\times m_4=27019991$ . 计算 $M_i=M/m_i$ . 还需计算 $m_i^{-1}$ , $ m_i^{-1} $ 是 $m_i$ 的逆元, 公式表示为:

$ M_iM_i^{-1}\equiv 1\;({\rm{mod}}\;m_i)$

(10)

综合求得参数:

$ \begin{split} y \equiv &\left( {\sum\nolimits_1^t {{y_i}{M_i}{M_i}^{ - 1}} } \right)\boldsymbolod M \equiv ( 100 \times 95477 \times 275 \\ & + 159 \times 88013 \times 291 + 228 \times 86881 \times 25 ) \\ & \boldsymbolod 27019991 \equiv 5795091 \\ \end{split} $

(11)

最后一步得:

$ \begin{gathered} s \equiv y\boldsymbolod q \equiv 5795091\boldsymbolod 257 \equiv 255 \end{gathered} $

(12)

证明彩色图像红色信道的秘密共享生成与恢复过程正确. 恢复彩色秘密图像需要遍历计算红色信道的每一个像素值. 同理计算绿色与蓝色信道的每一个像素值. 最后用cat函数生成彩色图片即可得到子秘密彩色图像.

4.2 (3, 5)门限无损高效彩色图像秘密共享信息隐藏方案实验结果

首先运行算法程序, 由彩色秘密图像共享生成彩色秘密共享影子图像, 如图3所示.

彩色秘密共享影子图像是类噪声的无意义图像, 无法获得任何秘密信息. 下文将讨论影子图像的无相关性并用直方图进行分析.

通过DCT信息隐藏算法, 将彩色秘密共享图像中的RGB三通道灰度图与其相应的余数图像嵌到用户提供的彩色载体图像中, 本实验使2048×2048的Lena图与其直方图展示效果, 如图4所示.

通过图4中直方图可以看出嵌入信息的载体图像在像素值分布上与原图基本一致, 从而认证从视觉角度看, 嵌入秘密共享影子图像与余数图像的载体图像与原载体图像没有区别. 同时当PSNR值大于33时^[24], 肉眼无法识别不同之处并获取秘密图像信息. 由表1体现本方案中信息隐藏的效果优于其他方案, 说明嵌入的秘密信息安全. 峰值信噪比, 即PSNR值越大, 嵌入的秘密信息越不容易被识别, 隐藏性越好. 平均结构相似性, 即MSSIM值越接近1, 嵌入秘密的载体图像与原载体图像越相似, 隐藏程度越好. 见表1.

从嵌入秘密的载体图像中提取出5份彩色秘密共享影子图像的RGB三通道图片与之相应的余数图片, 并组合存成双精度浮点型矩阵, 再利用CRT进行还原. 最后无损恢复原彩色秘密图像.

通过比较图5中提取的秘密共享影子图像的直方图可以看出像素值均匀分布, 证明影子图像是类噪声的, 没有轮廓, 无法获得任何信息, 安全性好.

将嵌入的图像像素首尾相连存为一个字符串, 再转成二进制, 通过BER (误比特率)函数, 比较原图像与回复后图像的比特流, 若值为0, 说明无误比特, 即证明本方案无损恢复秘密图像. 见表2.

如表2所示, 通过BER函数比较恢复前后秘密图像完全一致, 本文方案无损的恢复了秘密图像.

4.3 与相关成果的对比分析

本方案在同等512×512的图像下做多次实验, 取平均值, 并与现今一些方案进行了效率对比, 体现出本方案效率的提升.

从表3中可以看出本方案比文献[27]的传统算法效率高.

同时由图6中可以体现出基于中国剩余定理的秘密共享方案在像素值越大, 门限要求越高的大计算量条件下优于基于多项式的秘密共享算法.

由表4可以看出与其他方案对比, 本文提出的方案满足以下条件: 不需要辅助加密, 可以无损恢复秘密图像, 具有(t, n)门限以及高效性.

5 结束语

本文利用基于中国剩余定理(CRT)的门限秘密共享技术, 设计了一个基于CRT的无损高效门限彩色图像秘密共享信息隐藏算法. 以(3, 5)门限彩色图像秘密共享信息隐藏算法为例论证. 实验结果表明本文设计的秘密共享信息隐藏算法在全彩色图像操作环境上, 能无损恢复秘密图像, 从而达到在系统中安全传输秘密图像, 实现权力共享的机制. 诸多指标优于学界其他方案. 下一步将探究更多的秘密共享算法并进行改进, 在彩色图像上进行实验, 进一步提升性能.