随着轮胎行业的竞争愈演愈烈, 提高生产效率, 降低生产成本是企业发展的必经之路, 因此引进计算机开环控制系统对简化胎面生产过程、缩短研发周期、提高胎面质量具有重要意义. 其中, 胎面缠绕仿真是计算机开环控制轮胎胎面缠绕生产的核心, 由于目前的缠绕仿真软件内置的算法使用直线与圆弧对缠绕过程中的曲线进行仿形, 仿真结果与实际缠绕结果偏差较大, 得到的仿形结果很难应用到生产中去, 故目前生产中的轮胎胎面缠绕多根据工程师的生产经验来调整, 因此以设计一种能够精准拟合缠绕过程中的曲线、精确控制胶条位置的算法用于缠绕仿真软件具有重要意义[1].
2018年, 杨瑞林提出了轮胎胎面缠绕机组及缠绕控制方法. 在胎面缠绕生产线上, 经过冷却装置降温后的胶条有可能发生微小的形变, 通过在轮胎缠绕机上安装带有按压轮的气缸, 对胶条进行再次处理即可保证胶条质量与形状稳定, 提高轮胎胎面对称性, 延长轮胎的使用寿命[2].
2020年, 天津赛象科技股份有限公司介绍了一种工程机械子午线轮胎成型机组胎面缠绕机的数学模型及其结构, 设计了一套新算法, 该算法通过预先计算缠绕机头的运行轨迹函数来确定胶条的准确位置. 该算法通过分析工程机械子午线轮胎外型参数, 根据空气动力学原理, 计算最大充型体积. 根据最大充型体积得到截面数据设立方程, 通过变分学中的等周问题计算出曲线轨迹方程, 计算曲线轨迹方程的斜率来控制缠绕机头轴线和缠绕曲线法线的夹角, 再根据轮胎具体参数得出缠绕机头运行轨迹函数, 从而控制缠绕过程[3].
2020年张鹏[4]运用B样条曲线对轮胎胎面进行仿形, 得到较为精确的仿形结果并且运用到生产中去, 但B样条曲线存在无法拟合除抛物线外的二次曲线、对曲线控制不灵活且缠绕效率较低的问题, 故在此基础上选用NURBS曲线对轮胎胎面缠绕算法进行改进.
NURBS曲线是近些年计算机用来处理几何图形、设计以及数据交换的工业标准曲线. 相比于B样条曲线[5-7], NURBS曲线解决了B样条曲线无法拟合除抛物线外的二次曲线问题, 同时通过增加权重因子来灵活的控制各控制点对曲线整体形状的影响, 可以更好的拟合不同情况下的曲线, 因此本文提出运用NURBS曲线对胎面轮廓线和胶条轮廓线进行精准仿形, 使用基于粒子群优化的仿生学算法确定胶条起点从而合理排布胶条位置的算法, 并选取胎面工艺参数对算法进行验证.
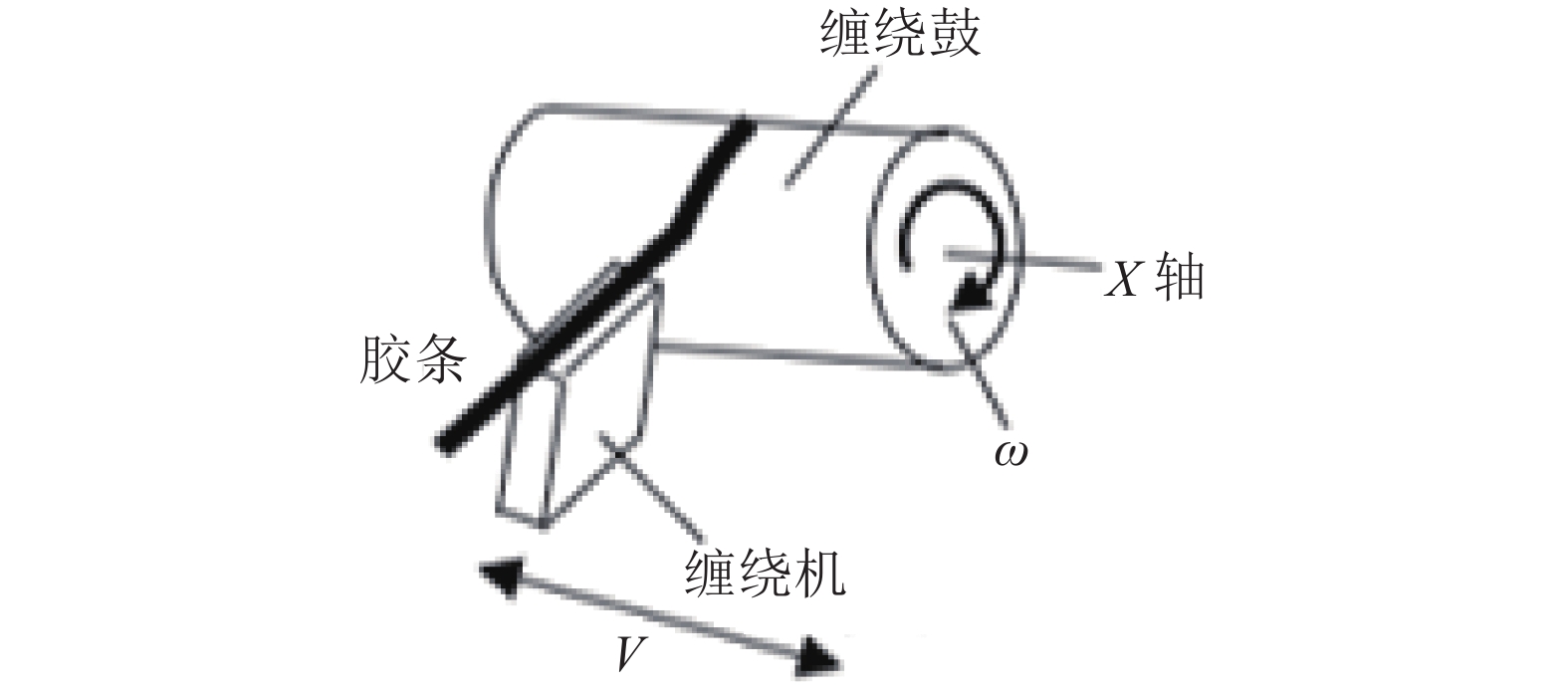
1 轮胎胎面缠绕仿真原理轮胎胎面由缠绕系统联动控制缠绕机与缠绕鼓, 将胶条缠绕贴合到轮胎胎胚上而成, 缠绕鼓承载轮胎胎胚做角速度为ω的自转运动, 缠绕机沿x轴移动将胶条贴到轮胎胎胚上, 缠绕原理如图1所示[8].
|
图 1 缠绕原理图 |
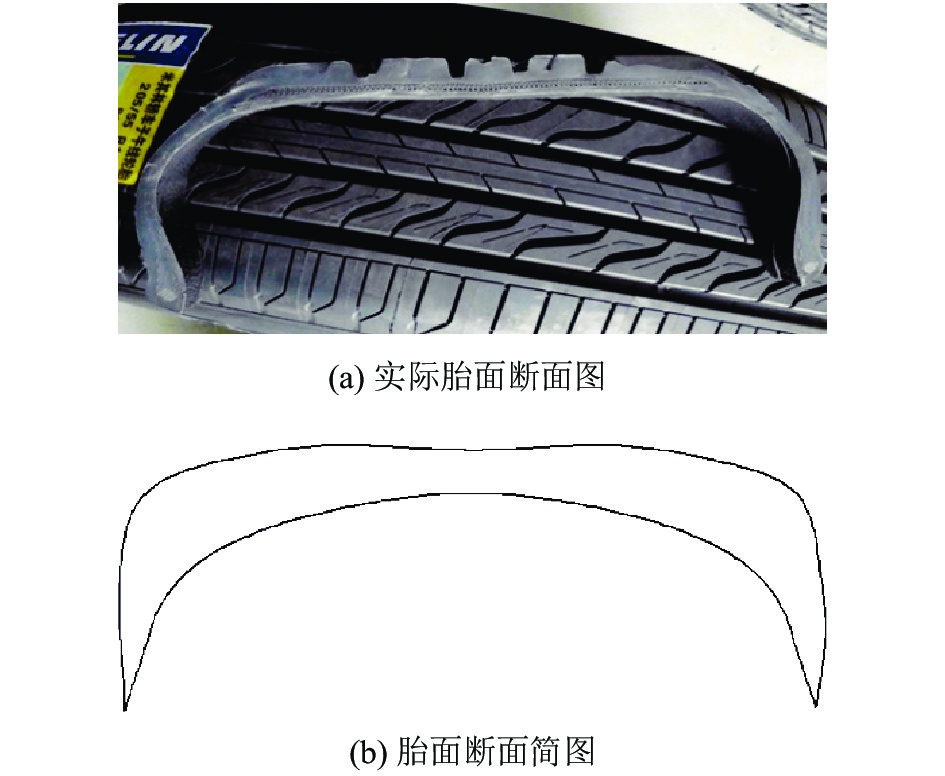
轮胎胎面断面图如图2所示.
|
图 2 轮胎胎面断面图 |
2 NURBS曲线
给定控制点Pi, 整数p, 单调不减的节点矢量u, 即可确定一条p次的NURBS曲线, 其数学表达式为:
| $ C(u) = \sum\limits_{i = 0}^n {\frac{{\mathop N\nolimits_{i, {p}} (u)\mathop \omega \nolimits_i }}{{\displaystyle\sum\limits_{j = 0}^n {\mathop N\nolimits_{j, {p}} (u)\mathop \omega \nolimits_i } }}\mathop P\nolimits_i } $ | (1) |
式中, C(u)为曲线上位置向量; ωi为权因子;
取胎面截面数据点进行NURBS曲线拟合时, NURBS曲线的权因子ωi取1, 此时NURBS曲线的求导公式为:
| $ d(x) = \sum\limits_{i = 0}^{n - 1} {\mathop N\nolimits_{i + 1, 2} (u)\frac{{3(\mathop x\nolimits_{i + 1} - \mathop x\nolimits_i )}}{{\mathop u\nolimits_{i + 4} - \mathop u\nolimits_{i + 1} }}} $ | (2) |
| $ d(y) = \sum\limits_{i = 0}^{n - 1} {\mathop N\nolimits_{i + 1, 2} (u)\frac{{3(\mathop y\nolimits_{i + 1} - \mathop y\nolimits_i )}}{{\mathop u\nolimits_{i + 4} - \mathop u\nolimits_{i + 1} }}} $ | (3) |
式中, ui为节点矢量值.
此时, NURBS曲线上任一点(xa, ya)的法线方程为:
| $ \mathop y\nolimits_{} = - \left( {\frac{{d(\mathop x\nolimits_a )}}{{d(\mathop y\nolimits_a )}}} \right)x + \mathop y\nolimits_a $ | (4) |
(1) NURBS曲线拟合
计算出轮胎胎面轮廓线和胶条轮廓线上的数据点后, 采用全局插值法拟合出上述曲线[9-11]. 全局插值法通过向心参数化计算各数据的参数值uk, 并采用取平均值的方法计算出节点矢量U, 建立式(5)所示线性方程组, 求解该方程组得出NURBS曲线的控制点从而拟合出NURBS曲线.
| $ \mathop Q\nolimits_k = C(\mathop {\bar u}\nolimits_k ) = \sum\limits_{i = 0}^n {\mathop N\nolimits_{i, {p}} (\mathop {\bar u}\nolimits_k )\mathop P\nolimits_i } $ | (5) |
式中, Pi为未知的曲线控制点.
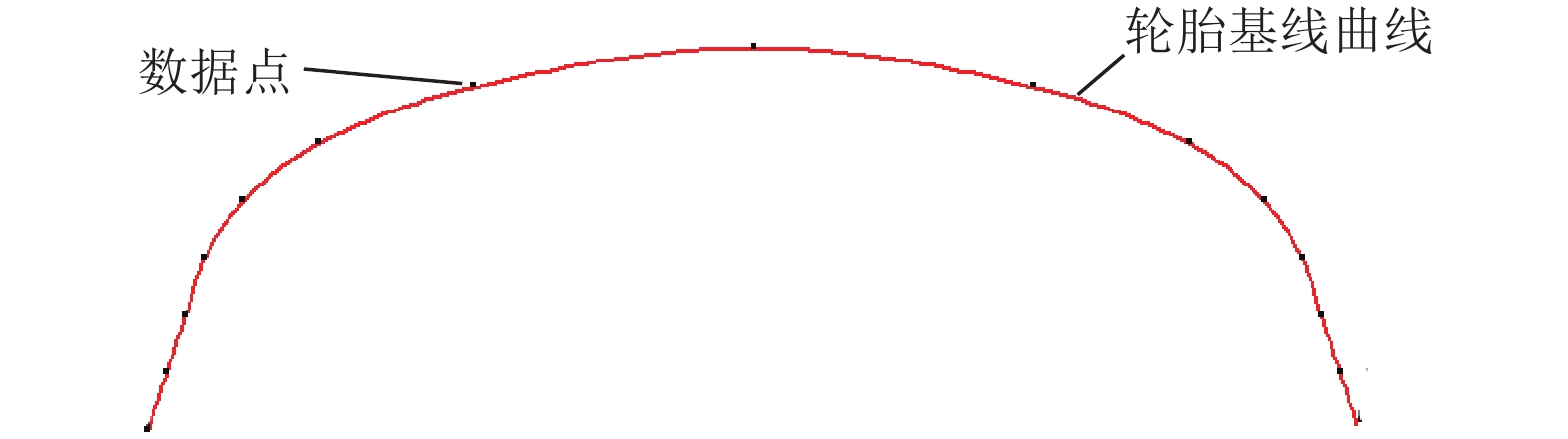
以拟合轮胎基线为例, 仿真效果如图3所示.
|
图 3 轮胎基线拟合图 |
(2) NURBS曲线拼接算法
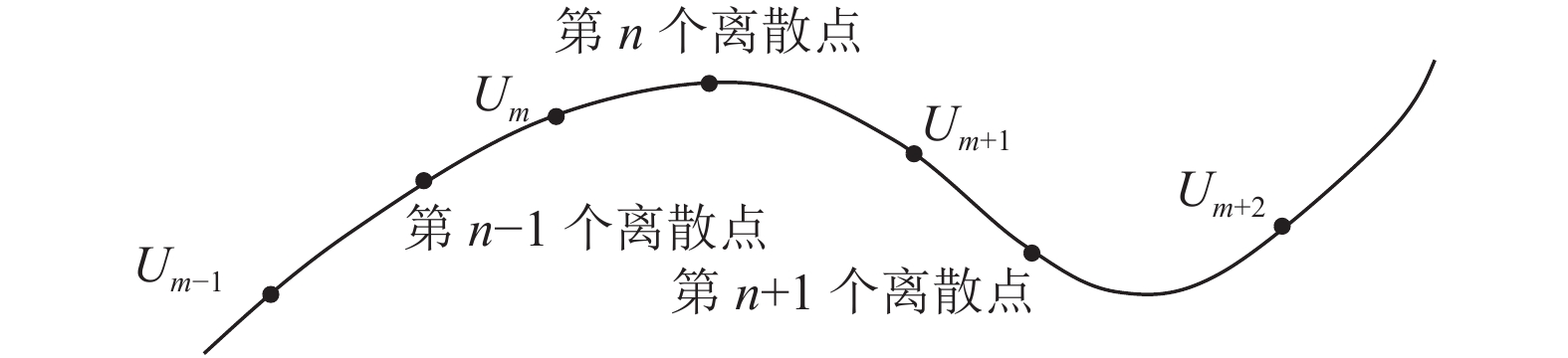
胶条下底曲线是由前一根胶条部分上底曲线和部分轮胎基线拼接获得, 现有的NURBS曲线拼接算法需要处理连接点的连续性问题, 计算较为繁杂, 因此提出了一种基于等弧长原则离散NURBS曲线算法的NURBS曲线拼接算法, 该算法首先将两端曲线等弧长离散成一系列离散点, 随后将离散点拟合为一条NURBS曲线, 计算示意图如图4所示. 算法步骤如下:
步骤1. 计算NURBS曲线离散段弧长, 需要先使用式(6)计算曲线总弧长L:
| $ \begin{split} {L} &= \sum\limits_{j = 0}^{n - 1} \mathop l\nolimits_j = \sum\limits_{j = 0}^{n - 1} \int \sqrt {\mathop {[\mathop {C'}\nolimits_x (u)]}\nolimits^2 + \mathop {[\mathop {C'}\nolimits_y (u)]}\nolimits^2 } du \\ &= \int_0^1 {\sqrt {\mathop {[\mathop {C'}\nolimits_x (u)]}\nolimits^2 + \mathop {[\mathop {C'}\nolimits_y (u)]}\nolimits^2 } du} \end{split} $ | (6) |
式中, L为总弧长; lj为节点矢量u∈(uj, uj+1)段对应弧长.
得到总弧长L之后, 按照指定的离散点个数N, 将NURBS曲线划分为每段弧长为Ln=L/N的曲线段.
步骤2. 根据曲线离散段弧长得出每一个离散点的节点矢量值u所在范围. 在上述步骤1可以得到节点矢量每个区间对应的弧长lj, 第n+1个离散点对应的弧长为Σla, 通过迭代计算, 当Σla大于Σlm小于Σlm+1时, 说明第n+1个离散点的节点矢量在(um, um+1)范围内.
步骤3. 确定离散点的节点矢量所在区间, 计算离散点的节点矢量u值.
| $ {\int }_{{u}_{m+1}}^{u}\sqrt{\left(\right[{C}_{x}^{\text{'}}\left(u\right){]}^{2}+\left[{C}_{y}^{\text{'}}\right(u\left){]}^{2}\right)}du={L}_{n}-{\sum }_{j=0}^{m}{l}_{j} $ | (7) |
|
图 4 NURBS曲线离散节点u求解示意图 |
步骤4. 将得出的节点矢量u值带入NURBS曲线公式(1)得出离散点坐标.
步骤5. 利用全局插值拟合算法将离散点拟合为一条NURBS曲线.
以拟合第二根胶条下底为例, 该算法的仿真结果如图5所示. 从图中可以看出, 将两段曲线离散后可拟合为一条较好曲线.

|
图 5 拟合第二根胶条下底曲线 |
(3) 基于PSO算法的NURBS曲线求交
粒子群优化算法(PSO)是基于群体智能理论的优化算法[12,13]. 使用PSO算法计算曲线交点相比于迭代法和遗传算法求交点规则简单, 不需要“交叉”和“变异”操作, 编程简单, 计算效率高. PSO算法从随机解出发, 通过迭代寻找最优解. 初始时(k=0), 随机地确定每个粒子的位置和速度, 随后按下列公式对粒子的速度和位置进行更新:
| $ \left\{ \begin{split} &{V}_{i}^{k+1}=\omega {V}_{i}^{k}+{c}_{1}\cdot rand\left(\right)\cdot \left({P}_{i}^{k}-{X}_{i}^{k}\right)+{c}_{2}\cdot rand\left(\right)\cdot \left({P}_{g}^{l}-{X}_{i}^{k}\right) \\ &{X}_{i}^{k+1}={X}_{i}^{k}+{V}_{i}^{k+1} \end{split}\right.$ |
式中,
合理排布胶条的核心是确定胶条的起点位置, 通过观察可知, 胶条的起点位置始终是前一根胶条的上底曲线与胎面分层曲线的交点. 本文选用基于PSO算法求此交点, 取两条NURBS曲线C1(u)和C2(v)上点
| $ f({{\displaystyle X}}_{i}^{k})=f({{\displaystyle u}}_{i}^{k}\text{, }{{\displaystyle v}}_{i}^{k})=\Vert {{\displaystyle C}}_{1}\left({{\displaystyle u}}_{i}^{k}\right)-{{\displaystyle C}}_{2}\left({{\displaystyle v}}_{i}^{k}\right)\Vert $ | (8) |
当迭代次数达到最大且满足筛选条件时, 所得出的全局最优位置看作两条曲线的交点.
3 基于NURBS和PSO的胎面缠绕仿真算法基于NURBS和PSO的胎面缠绕仿真算法实现流程如图6所示.

|
图 6 算法实现流程 |
(1)绘制胎面轮廓曲线
胎面轮廓曲线由轮胎基线和理想胎面曲线组成. 其中轮胎基线由测量的轮胎基线数据点结合全局插值拟合算法拟合得出; 理想胎面曲线根据输入的工艺参数设计算法计算得出.
理想胎面曲线的工艺参数为基线上不同弧长处到理想胎面曲线的高度. 计算理想胎面曲线分为两步:
① 计算理想胎面曲线的数据点. 首先利用式(6)和式(7)求出工艺参数表上各弧长处对应的基线上的节点矢量值并得到坐标值. 其次使用式(5)计算出各点对应的法线方程, 最后使用直线上两点的距离公式计算出相应的理想胎面曲线数据点.
② 利用得出的理想胎面曲线的数据点, 通过全局插值法求出控制点, 得出理想胎面曲线, 理想胎面曲线仿真结果如图7所示.

|
图 7 理想胎面曲线仿真图 |
(2) 分层设置
在实际的缠绕过程中, 理想胎面曲线太高时, 在缠绕过程中胶条会出现胶条堆叠现象, 胶条堆叠会使胶条与轮胎胎胚粘连部分太少造成胶条脱空. 因此需要设置分层曲线, 其中分层数目根据工艺要求, 且通过每一层缠绕后的胎面曲线即为下一层的缠绕基线, 以分两层为例如图8所示.

|
图 8 分层实例示意图 |
分层时从第一跟胶条起始点缠绕开始, 保存每一根胶条上底和分层曲线的交点之间的曲线如P1P2. 将曲线上所有的上底型值点坐标进行记录保存, 第一场缠绕结束后, 将所有记录的型值点通过NURBS曲线反求控制点的方法, 求得分层后的曲线方程, 以该方程与最终的理想胎面方程为基准, 即可完成全部缠绕过程.
(3) 绘制胶条
绘制胶条首先要确定胶条的起点. 第一根胶条的起点是轮胎基线的起点, 计算后续胶条的起点采用基于PSO的NURBS曲线算法求交前一根胶条上底曲线与分层曲线的交点. 当交点个数较多时, 设置筛选条件选出合适的交点做为胶条起点.
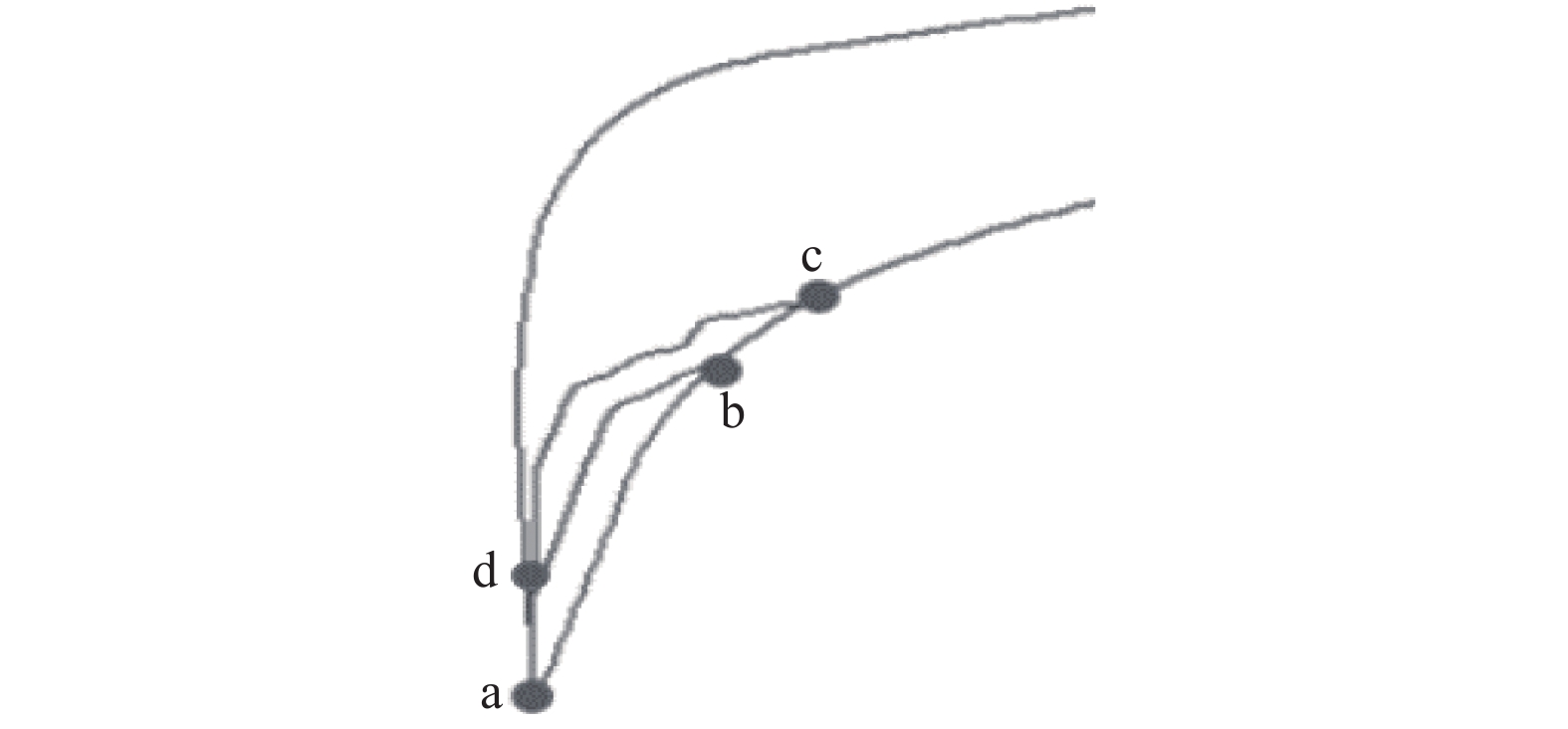
其次绘制胶条下底曲线. 计算示意图如图9所示, d点为第二根胶条的起点, b点为前一根胶条上底曲线终点, 当db弧段长度小于胶条下底弧长时, 截取基线上bc弧长, dbc弧长即为胶条下底. 利用NURBS曲线拼接算法拟合出胶条下底, 最后根据胶条工艺参数值计算得到胶条上底曲线.
|
图 9 后续胶条曲线计算示意图 |
4 实例分析
为测试本文提出算法的有效性和可行性, 选取某型号胎面工艺参数和胶条工艺参数对算法进行测试, 胶条型号如图10所示. 通过缠绕后胎面与理想胎面曲线对比, 判断算法准确性, 通过左右胎肩高度对比, 判断胎面对称性.

|
图 10 胶条截面 |
(1)实例1
如表1、表2所示, 给定的进给胶条速度为16 m/min, 给定的胶条胶料密度为0.94 g/cm3.
| 表 1 轮胎基线坐标值 |
| 表 2 理想胎面曲线工艺参数表 |
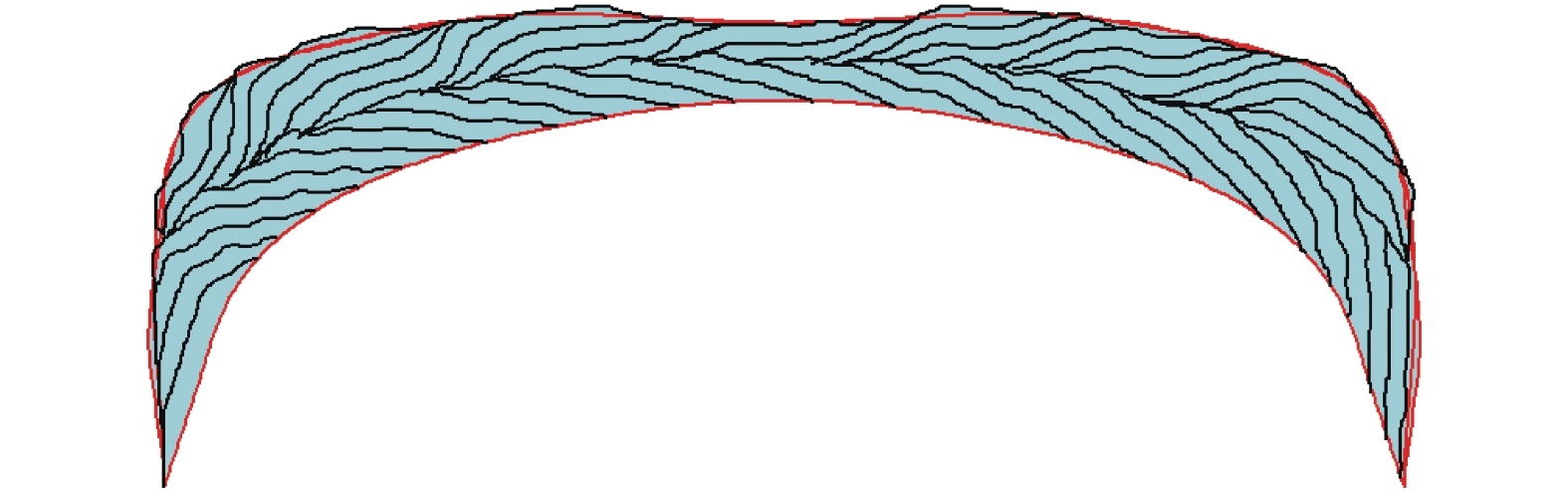
基于本文提出的算法, 采用上述工艺参数, 得到的胎面缠绕仿真结果如图11所示.
|
图 11 缠绕仿真结果图 |
缠绕完成后的胎面效果如图11所示, 红色轮廓为理想胎面曲线, 黑色边界即为实际缠绕胎面. 根据胎面所用胶条总长度和胶条截面面积计算出轮胎的总重量为37.71 kg, 在HG/T 4958-2016行业标准与国内某合作企业要求37.31±0.56 kg的范围内. 缠绕完成后, 根据计算胎肩两侧的高度分别为左侧141.1 mm, 右侧为141.5 mm, 右胎肩高度比左胎肩高度高0.2%, 对称性满足要求. 生产时长根据胎面缠绕所需胶条的总长度以及进给胶条速度计算得到大约为10 min.
(2)实例2
如表3、表4所示, 给定的进给胶条速度为16 m/min, 给定的胶条胶料密度为0.94 g/cm3.
| 表 3 轮胎基线坐标值 |
| 表 4 理想胎面曲线工艺参数表 |
基于本文提出的算法, 采用上述工艺参数, 得到的胎面缠绕仿真结果如图12所示.

|
图 12 缠绕仿真结果图 |
缠绕完成后的胎面效果如图12所示, 红色轮廓为理想胎面曲线, 黑色边界即为实际缠绕胎面. 根据胎面所用胶条总长度和胶条截面面积计算出轮胎的总重量为30.10 kg, 在HG/T 4958-2016行业标准与国内某合作企业要求30.00±0.31 kg的范围内. 缠绕完成后, 根据计算胎肩两侧的高度分别为左侧53.9 mm, 右侧为54.1 mm, 右胎肩高度比左胎肩高度高0.3%, 对称性满足要求. 生产时长根据胎面缠绕所需胶条的总长度以及进给胶条速度计算得到大约为8 min.
5 结论针对计算开环控制的胎面缠绕生产系统中配置的胎面缠绕系统算法性能差的问题, 本文提出了一种基于NURBS曲线的胎面缠绕仿真算法. 该算法对胎面缠绕过程中的曲线仿形效果较好, 其中基于PSO的NURBS曲线求交算法能快速稳定的计算出合理的胶条起点, 具有编程简单、计算效率高的优点. 相比与以往的胎面缠绕, 本算法不再侧重于缠绕精度的问题, 而在保证缠绕精度的基础上大幅提高了缠绕的效率. 通过两次实例实验结果图表明, 缠绕后的胎面形状较好, 满足胎面的对称性要求, 轮胎重量符合行业要求, 生产总时长大幅降低, 能有效的提高生产效率.
| [1] |
陈卫勇, 李红卫, 刘超, 等. 冠带条缠绕方式对轮胎均匀性的影响分析. 轮胎工业, 2021, 41(2): 109-114. |
| [2] |
杨瑞林. 胎面仿形缠绕集群控制系统. 橡塑技术与装备, 2012, 38(4): 44-47. |
| [3] |
牛荦. 工程机械子午线轮胎成型机组胎面缠绕机的研究. 橡胶科技, 2020, 18(11): 647-650. |
| [4] |
张鹏. 基于B样条曲线的轮胎胎面缠绕仿真系统设计[硕士学位论文]. 青岛: 青岛大学, 2020.
|
| [5] |
范磊亭, 尹炳鹏, 赵尊梅, 等. 轮胎成型机冠带条缠绕张力控制研究. 橡塑技术与装备, 2020, 46(7): 1-4. |
| [6] |
张鹏, 沈精虎, 彭婷. 基于B样条曲线的轮胎胎面缠绕算法. 传感器与微系统, 2019, 38(11): 151-153, 156. |
| [7] |
张麒, 赵华. 八绳单独缠绕系统在轮胎式集装箱起重机上的应用. 起重运输机械, 2019(1): 151-153. DOI:10.3969/j.issn.1001-0785.2019.01.022 |
| [8] |
王娟娟, 平雪良, 周忠良, 等. 采用NURBS曲线的钢球减速器的型线设计研究. 机械科学与技术, 2021, 40(12): 1849-1855. DOI:10.13433/j.cnki.1003-8728.20200258 |
| [9] |
吴婷, 邹海. B样条曲线全局插值优化算法及其实现. 陕西理工学院学报(自然科学版), 2015, 31(3): 71-74. |
| [10] |
陈确林, 赖籍红, 何大志. 一种新型冠带条缠绕方法在子午线轮胎制造中的应用. 中国橡胶, 2018, 34(12): 49-51. DOI:10.3969/j.issn.1009-5640.2018.12.013 |
| [11] |
聂瑞涛, 邓杰, 郑捍东, 等. 一种在轮胎成型机上缠绕冠带条的装置. 中国: CN200810188290.1, 2008.
|
| [12] |
帅茂杭,熊国江,胡晓,等. 基于改进多目标骨干粒子群算法的电力系统环境经济调度. 控制与决策, 2022, 37(4): 997-1004. DOI:10.13195/j.kzyjc.2020.1440 |
| [13] |
张浩科, 高静, 赵智龙, 等. 人工神经网络结合粒子群优化算法优化不同产地广藿香挥发油提取工艺. 中国中医药信息杂志, 2021, 28(5): 83-87. |
 2022, Vol. 31
2022, Vol. 31


