随着科技的高速发展, 可靠的数学模型在解决现实问题中起着重要的作用. 预测模型作为目前使用较多的分析方法, 可以通过对海量的历史数据不断学习, 确定数据特征之间的关系, 进而科学的预测某一变量的未来走势. 即根据学习到的对象特征预测其他的特征值. 这种方法在各个领域引起了广泛的关注, 许多国家也已致力于对预测模型的研究.

现阶段预测模型广泛应用于医疗、交通、工业、军事、农业、商业等现实生活中的方方面面, 极大地提高了生产生活的效率. 常见的预测模型有时间序列预测模型、灰色预测模型、神经网络预测模型、回归预测模型等. 如刘学刚等人使用以ARIMA(差分自回归移动平均模型)为代表的时间序列预测模型实现了对上海市大连路交通流的静态预测^[1], 但这种模型结构单一, 局限在于需要保证时序数据的稳定性且具有很强的空间依懒性, 本质上只能获取线性变化的关系. Zeng等人使用灰色预测模型对粮食生产情况进行了预测^[2], 这种算法具有容易运算, 所需变量个数少的优点, 但仅仅适用于数据量呈指数增长的预测. Zeng等人结合粒子群和BP神经网络实现了对校园交通流量的预测^[3], 这种组合的网络模型依赖于给定的数据集样本, 没有很好的泛化能力; KTBoost预测模型作为回归预测模型中的新算法, 是由Sigrist于2019年提出的一种增强算法^[4], 它创新性的将回归树^[5,6]和RKHS函数^[7]结合, 与原始的回归树、核提升算法相比, KTBoost预测模型的预测精度有了显著提升. 同时, 将其与SVR^[8-10]、XGBoost^[11]、随机森林^[12-14]等传统的回归预测模型对比, KTBoost预测模型的预测精度更高.

基于此, 为了获取KTBoost算法更精准的预测结果, 本文利用OGWO算法所具有的可寻找最优解的特性, 对KTBoost算法中的超参数进行调节, 并以交通流预测^[15-18]为应用场景, 以各模型的决定系数值作为衡量标准进行对比实验. 实验结果证明相比于其他模型, OGWO-KTBoost模型的预测精度更好, 拟合效果更佳.

1 优化GWO算法的KTBoost预测模型 1.1 GWO算法及其改进

澳大利亚的学者们通过观察狼群的行为, 提出了灰狼优化算法(grey wolf optimizer, GWO)^[19], 因为此算法具有设置参数较少, 易操作和实现等诸多优点, 引起了广泛的讨论, 在众多领域得到了应用^[20]. 其搜索代理群从高到低分别是α、β、δ和ω即分别代表算法中较好的3个解和剩余的其他解^[21]. 狼群主要通过3大行为完成对猎物的猎杀, 分别是追踪、狩猎和攻击.

GWO对追踪行为定义如下:

$ \overrightarrow D {\text{ = }}\left| {\overrightarrow C \cdot \overrightarrow {{X_p}} (t) - \overrightarrow X (t)} \right|\; $

(1)

其中, t表示更新次数, 表示狼群和猎物所处的位置, 为式中的系数向量, 表示狩猎者和被捕者之间的间隔和方位.

$ \overrightarrow X (t + 1) = \overrightarrow {{X_p}} (t) - \overrightarrow A \cdot \overrightarrow D $

(2)

其中, $ \overrightarrow X (t + 1) $ 表示对狼群的位置进行更新.

$ \overrightarrow A = 2\overrightarrow a \cdot \overrightarrow {{{\mathbf{r}}_1}} {\text{ - }}\overrightarrow a $

(3)

其中, 代表[0, 1]之间的随机数, $ \overrightarrow A $ 为收敛因子. 收敛因子为线性递减函数, 初始值为2, 之后随自变量的增加减小到0^[22].

$ \overrightarrow C = 2 \cdot \overrightarrow {{{\mathbf{r}}_2}} $

(4)

其中, 代表[0, 1]之间的随机数.

$ \overrightarrow {{D_\alpha }} = \left| {\overrightarrow {{C_1}} \cdot \overrightarrow {{X_\alpha }} - \overrightarrow X } \right| $

(5)

$ \overrightarrow {{D_\beta }} = \left| {\overrightarrow {{C_2}} \cdot \overrightarrow {{X_\beta }} - \overrightarrow X } \right| $

(6)

$ \overrightarrow {{D_\delta }} = \left| {\overrightarrow {{C_3}} \cdot \overrightarrow {{X_\delta }} - \overrightarrow X } \right| $

(7)

其中, $ \overrightarrow {{C_1}} $ , $ \overrightarrow {{C_2}} $ , $ \overrightarrow {{C_3}} $ 分别是[0.2]之间的随机向量 $ \overrightarrow {{D_α}} $ , $ \overrightarrow {{D_β}} $ , $ \overrightarrow {{D_δ}} $ 分别表示α、β、δ个体狼跟踪猎物的位置向量.

$ \overrightarrow {{X_1}} = \overrightarrow {{X_\alpha }} - {A_1} \cdot \overrightarrow {{D_\alpha }} $

(8)

$ \overrightarrow {{X_2}} = \overrightarrow {{X_\beta }} - {A_2} \cdot \overrightarrow {{D_\beta }} $

(9)

$ \overrightarrow {{X_3}} = \overrightarrow {{X_\delta }} - {A_3} \cdot \overrightarrow {{D_\delta }} $

(10)

其中, $ \overrightarrow {{X_1}} $ , $ \overrightarrow {{X_2}} $ , $ \overrightarrow {{X_3}} $ 分别表示ω狼群受到α、β、δ狼的影响后更新的位置向量.

$ \overrightarrow X (t + 1){\text{ = }}\frac{{\overrightarrow {{X_1}} + \overrightarrow {{X_2}} + \overrightarrow {{X_3}} }}{3} $

(11)

其中, $ \overrightarrow X (t + 1) $ 表示狼群参考α、β、δ的位置向量后更新的最终位置^[23].

$ \left| {\overrightarrow A } \right| > 1 $

(12)

$ \left| {\overrightarrow A } \right| < 1 $

(13)

由以上公式可知, 狼群主要通过与α、β、δ狼的距离确定狼群的位置, 因此如果收敛因子 $ \overrightarrow A $ 的绝对值大于1, 狼群将分散开寻找猎物, 进行大范围的查找; 收敛因子 $ \overrightarrow A $ 的绝对值小于1表示狼群局部搜索, 对猎物进行围堵.

研究发现在有效的迭代范围内随着迭代次数的增加, $ \overrightarrow \alpha $ 随之减小, 之后决定系数将不再变化, 即此时的 $ \overrightarrow \alpha $ 变化已无法影响到决定系数的变化. 所以为了进一步对灰狼优化算法的勘探和搜索能力进行改进, 本文对GWO算法进行优化, 在此采取的方法是对收敛因子 $ \overrightarrow \alpha $ 和 $ \overrightarrow A $ 进行调节: 依据反正切函数是单调递增函数的特性, 将反正切函数用于收敛因子的公式中, 改进公式如下所示:

$ a = \left\{ {\begin{array}{*{20}{l}} 2,&{i = 0} \\ {2.53 \cdot \arctan (\max (sub{a_i}, sub{a_{i - 1}})) + random},&{i > 0} \end{array}} \right. $

(14)

其中, i表示收敛因子的迭代次数, 为了避免陷入局部最优值, 本文设置random的初始值为0.01, 当i%3=0时, random值为1.

1.2 OGWO-KTBoost模型

KTBoost模型以回归树和RKHS函数作为基学习器, 将内核和树结合, 获得一种新的增强算法, 其中RKHS岭回归采用高斯核. 相比于经典的树与核, 不同类型基学习器的互补既具有树的学习不连续函数的优势, 又具有RKHS函数适合学习平滑函数的特点, 泛化误差更小, 可以实现接近最优的测试误差. KTBoost默认依赖所有特征, 先采用梯度下降法^[24,25]并行学习回归树和惩罚PKHS回归函数, 每次增强迭代时, 从回归树和惩罚PKHS回归函数中选择其中一个作为基学习器, 添加到集成中, 以结构风险最小化学习规格, 相比于其他算法, KTBoost具有更高的泛化能力和非线性建模精度, 其优势在小样本数据和有噪数据中表现明显.

尽管KTBoost模型优势突出, 但底层思想还是通过对多个弱学习器的集成, 使之成为一个强学习器, 从而建立最终的预测模型. 因此, 同Boosting模型类似, KTBoost模型的超参数对预测精度影响较大, 而灰狼优化算法具有较强的参数寻优能力, 利用灰狼优化算法可以选择KTBoost模型中超参数的最佳值, 因此, 本文采用优化后的灰狼优化算法(OGWO)优化KTBoost模型中弱学习器的个数n_estimators和弱学习器的最大深度max_depth这两个重要参数, 从而提出了OGWO-KTBoost模型, 其算法步骤如下所示:

(1) 构建OGWO算法, 对狼群数目N、最大迭代次数Max_iteration等相关参数进行初始化.

(2) 根据OGWO算法初始化KTBoost训练模型, 并通过计算获取结果.

(3) OGWO算法根据优化后的超参数, 在下一次迭代时重新设置超参数并训练模型.

1.3 特征工程

原始数据集中为零的数据已提前通过取缺失点前后数据均值的方式进行了数据修复. 本文主要对每一个传感器的时间戳进行操作, 从时间戳中提取出week, day, hour和minute的时间特征, 与历史的车辆数量结合起来作为预测因子构建OGWO-KTBoost模型进行学习.

2 实验与结果分析 2.1 数据来源及其环境设置

本文中的实验数据均来自经过实测的交通数据集PeMs数据集, 其数据的时间始于2014年5月1日, 结束于2014年6月30日, 共计61天数据, 包含24个传感器, 每隔5分钟获取一次检测器数据, 即每个传感器含有17568组数据, 数据量大且全面. 将数据集中70%的数据用于模型的训练, 20%的数据用于在验证中调节参数, 剩余数据用于测试模型效果.

所有实验都在配置为RAM 16.0 GB, Intel(R) Core(TM) i5-10210U CPU @ 1.60 GHz 2.11 GHz的处理器, 64位操作系统的笔记本上完成的, 仿真软件采用PyCharm 3.0.

2.2 模型处理和参数调优

在回归预测问题中, 判断模型好坏的标准有残留标准误差(RSE)、均方根误差(RMSE)、决定系数(R²_score)等, 其中是一个归一化的度量标准, 它既能体现出预测值和真实值之间的差值, 也能体现出真实值之间的差值. 总而言之, 通过决定系数可以体现出拟合效果的好坏, 所以本文中所有实验都将R²_score的结果作为判断模型优劣的依据, 其结果保留小数点后5位. 评价公式如下所示:

$ {R^2} = 1 - \dfrac{{\displaystyle\sum\nolimits_i {{{({{\hat y}^{(i)}} - {y^{(i)}})}^2}} }}{{\displaystyle\sum\nolimits_i {{{(\bar y - {y^{(i)}})}^2}} }} $

(15)

其中, y⁽ⁱ⁾、 $\bar y $ 、 $\hat y^{(i)}$ 表示真实值、平均值、预测值. GWO算法中当种群规模过大会影响收敛速度, 但全局解整体朝向稳定的进化方向, 即使出现极个别最优解, 也影响较小; 规模过小易出现局部最优解, 但收敛速度快, 因此需要不断调整默认参数-灰狼数量SearchAgents_no以确定最佳值.

如表1所示, 为了呈现改进算法的效果, 在OGWO-KTBoost模型上运行, 通过控制变量法确保除灰狼数量之外的其他参数全部相同, 经实验验证, 当灰狼数量赋值30时效果最好.

灰狼优化算法主要通过调节a值完成勘探和开发的平衡, 分别将未改进的和改进后的a值在基于灰狼优化算法的KTBoost模型上运行. 在对传统的GWO-KTBoost模型运行后发现, 当迭代次数达到6后, 模型的决定系数基本保持在0.78左右, 后续a值的变化将不再影响决定系数, 即后续的迭代皆为无效迭代, 通过对参数a的改进, R²_score在原有的基础上有了一定的提升, 达到了0.82650. 具体的a值对比结果如表2所示.

2.3 多模型对比

为了更直观的体现出本文提出的OGWO-KTBoost预测模型性能的优势, 基于上述数据集和评价指标, 将OGWO-KTBoost与现有模型RBF、RFR、KTBoost、OGWO-RBF, OGWO-RFR分别进行对比分析不同

模型的参数设置如下: RBF神经网络的隐藏层神经元核函数为Gaussian函数, 基函数中心采用前人已经验证过的成熟算法K-means算法进行训练, 权值参数采用梯度下降法. OGWO-RBF模型中除原有的默认参数外, 运用OGWO优化RBF模型中的c和gamma. RFR模型中的分类器个数(n_estimators)为10, 最大特征数目(max_features)设置为auto, 最大深度(max_depth)默认为2, 采用五折交叉验证法. OGWO-RFR模型中除RFR模型中的默认参数外, 运用OGWO优化RFR模型中的分类器的个数n_estimators和最大特征数目max_features. KTBoost模型的默认参数如下: Alpha为1, n_neighbors为5, n_components为100, 分类器个数(n_estimators)取值500, 最大特征数(max_features)取值15. 各个模型的预测结果图如图1–图6.

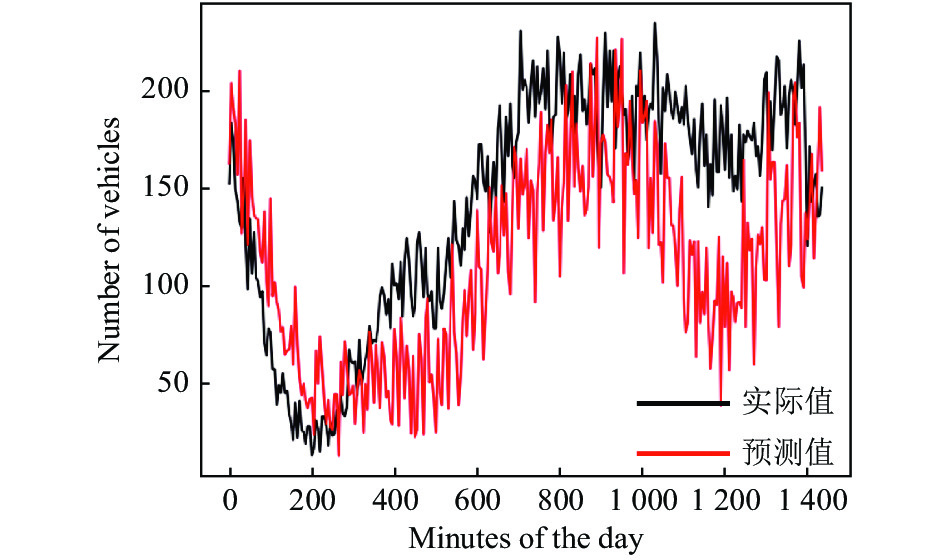
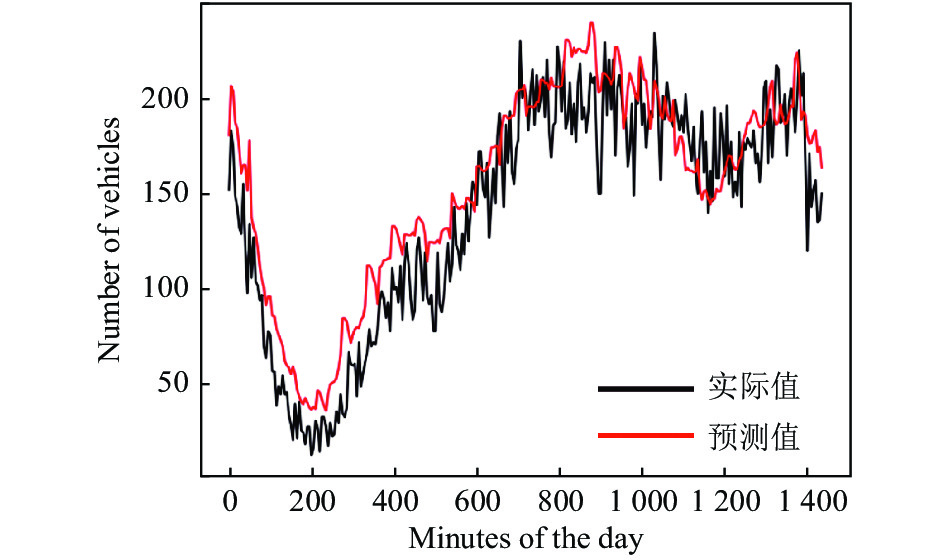
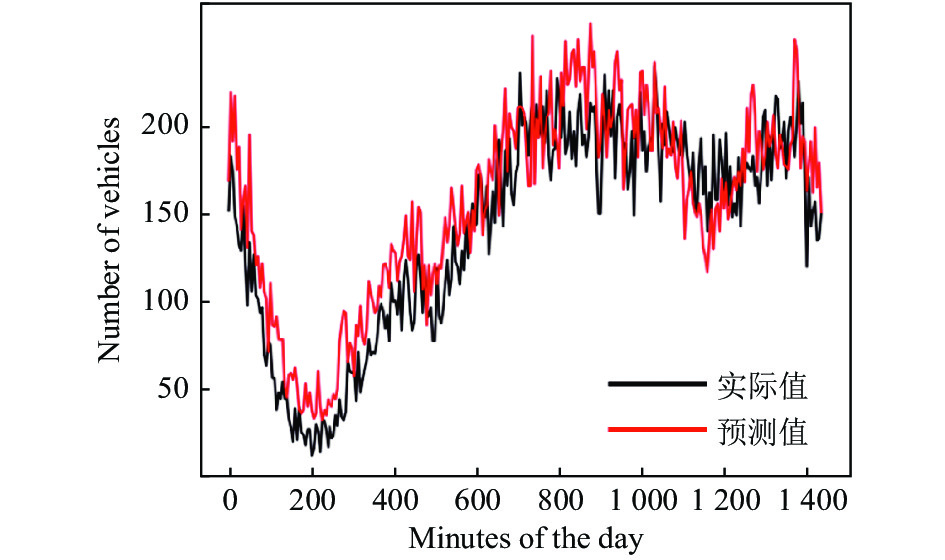
为了清晰的呈现出预测效果, 在此通过实验预测其中一天的车流量. 如图1–图6所示, 以一天中的分钟值为横坐标, 实时车流量为纵坐标, 黑色折线表示实际的车流量走势, 红色折线为模型的拟合效果. 其中RBF模型的预测效果最差, 出现了欠拟合现象; RFR模型预测效果不佳, 尤其在300分钟后预测结果明显小于实际结果; KTBoost模型基本捕捉到了交通流预测的特征; OGWO-RBF模型的前期预测效果差, 后期结果良好; OGWO-RFR模型基本满足预测要求, 拟合效果良好. 而OGWO-KTBoost模型的拟合精度更佳, 预测效果最好. 各模型的预测数据如表3所示.

如表3所示, 预测最差的是RBF神经网络, 基本不能满足预测要求, 预测最好的是OGWO-KTBoost模型. KTBoost模型虽然与预期目标有所差距, 但与RBF模型、RFR模型相比, 可以看出它在预测方面具有显著优势. 通过将OGWO-RBF模型与RBF模型的决定系数进行对比, 可明显看出OGWO-RBF模型的决定系数已有了大幅度提升, 从而侧面证明了OGWO算法适用于对模型的优化.

3 结论

本文提出了一种新的预测模型, 首先针对传统灰狼优化算法中存在的无效迭代问题, 通过对参数a进行改进, 提高了灰狼优化算法在有效迭代范围内的寻优速度. 利用改进后的算法优化KTBoost模型的弱学习器的个数n_estimators 和避免过拟合参数max_depth, 得到了OGWO-KTBoost预测模型. 然后将该模型放在交通流预测的场景中, 采用PeMs数据集进行实验, 实验结果表明, OGWO-KTBoost模型预测精度约为0.8265, 已达到预期目标值. 同时将该模型与RBF、RFR、KTBoost、OGWO-RBF, OGWO-RFR模型进行了对比, 由实验结果知OGWO-KTBoost预测模型优于其他预测模型, 实际预测精度最佳.