基于双种群两阶段变异策略的差分进化算法

引用本文

王丽颖, 帅真浩. 基于双种群两阶段变异策略的差分进化算法. 计算机系统应用, 2022, 31(4): 288-295.http://www.c-s-a.org.cn/1003-3254/8461.html

Wang LY, Shuai ZH. Differential Evolution Algorithm Based on Two-stage Mutation Strategy of Two-population. Computer Systems and Applications, 2022, 31(4): 288-295(in Chinese).http://www.c-s-a.org.cn/1003-3254/8461.html

基于双种群两阶段变异策略的差分进化算法

王丽颖, 帅真浩

大连海事大学信息科学与技术学院, 大连 116033

收稿日期：2021-07-02; 修改日期：2021-07-30; 采用时间：2021-08-31; csa 在线出版时间：2022-03-22

通讯作者：王丽颖, E-mail: 1962438611@qq.com.

摘要：针对差分进化算法差分策略优化问题上的不足, 解决DE/best/1策略全局探测能力差, DE/rand/1局部搜索能力弱而带来的鲁棒性降低及陷入局部最优等问题, 本文在差分策略上进行改进, 并且加入邻域分治思想提高进化效率, 提出一种基于双种群两阶段变异策略的差分进化算法(TPSDE). 第一个阶段利用DE/best/1的优势对邻域向量划分完成的子种群区域进行局部优化, 第二个阶段借鉴DE/rand/1的思想实现全局优化, 最终两阶段向量加权得到最终变异个体使得算法避免了过早收敛和搜索停滞等问题的出现. 6个测试函数的仿真实验结果表明TPSDE在收敛速度、优化精度和鲁棒性方面都得到了明显改善.

关键词: 差分进化算法双种群两阶段变异策略局部优化全局优化自适应进化算法

Differential Evolution Algorithm Based on Two-stage Mutation Strategy of Two-population

WANG Li-Ying, SHUAI Zhen-Hao

School of Information Science and Technology, Dalian Maritime University, Dalian 116033, China

Abstract: The differential evolution algorithm is limited in the optimization of the differential strategy, the DE/best/1 strategy has a poor global detection ability, and the weak local search ability of the DE/rand/1 strategy leads to the reduction in robustness and local optimal problems. In this study, the differential strategy is improved and the idea of neighborhood divide and conquer is added to improve the evolutionary efficiency. A differential evolution algorithm (TPSDE) based on two-stage mutation strategy with two populations is proposed. In the first stage, the advantages of the DE/best/1 strategy are employed to locally optimize the subpopulation area with completed neighborhood vector partition. In the second stage, the idea of the DE/rand/1 strategy is borrowed to achieve global optimization. Finally, the final variant individuals are obtained by weighting the vectors of the two stages, which avoids problems such as premature convergence and search stagnation. The simulation results of six test functions show that the TPSDE has significantly improved the convergence speed, optimization accuracy, and robustness.

Key words: differential evolution algorithm double populations two-stage mutation strategy local optimization global optimization adaptive evolutionary algorithm

差分进化算法(DE)是美国学者Storn^[1]于1995年以技术报告的形式提出的基于种群优化理论的算法, 通过变异、交叉和选择父代之间的差异向量来优化, 与常见的进化计算技术^[2-4]类似, 进化计算使用逐代优化过程, 然后使用并行处理在引导随机搜索中选择该群体, 以实现期望的目的. 近年来, 许多改进变异策略的DE的变体都得到了很好的改进. 其在约束优化计算^[5], 聚类优化计算^[6], 非线性优化控制^[7], 神经网络优化^[8], 滤波器设计^[9], 阵列天线方向图综合^{[10, 11]}及其它方面^[12-14]得到广泛应用.

1 差分策略

自DE概念化以来, 研究主要围绕着种群重构问题, 差分策略问题以及控制参数问题3个方面进行改进, 本文则主要针对差分策略问题进行改进. 为了更加有效的解决实际问题, 国内外许多学者对DE算法在差分策略上进行了大量的改进. Das等人^[15]和Zhang等人^[16]在2009年对每个种群成员采用邻域的概念, 并在DE中采用DE/target-to-best/1突变方案. Zhang等人^[16]在2009年提出了一种具有可选的外部存档和自适应更新控制参数的差分变异策略DE/current-to-best^p, 其可选的归档操作利用历史数据来提供有关进展方向的信息. Mallipeddi等人^[17]在2010年提出了一种不同的突变策略池以及每个控制参数的值池在整个进化过程中共存, 并竞争产生后代解的EPSDE策略. Islam等人^[18]在2012年提出了一种新的具有二项交叉和自适应控制参数的变异策略. Piotrowski^[19]在2013年提出了一种基于全局邻域和局部邻域的模因变异算子. Liao等人^[20]在2014年利用基于环拓扑的突变策略提高DE的性能, 以更快地收敛到全局解. Aldabbagh等人^[21]同年提出了DE的一种将标准变异方案DE/current-to-rand/1替换为DE/current-to-rand方案的新变体DE-bea, 其新突变方案称为细菌突变方案. Yu等人^[22]在2015年提出了一种DE变体, 当种群聚集在局部最优时, 他们考虑自适应控制参数. Mohamed^[23]在2015年提出了一种基于凸组合向量的三角形突变方法. 他随机选取3个向量, 计算出最佳和最差向量的差值, 并将其与基本变异规则相结合. Cui等人^[24]在2016年发了一种MPADE算法, 该算法根据适应度值将种群分为3部分, 并在其上应用3种变异策略进行开发或探索, 进而设计一种参数调整的自适应技术. Sun等人^[25]在2017年将依靠邻域关系的DE算法变异算子称为NDE池的种群拓扑用于定义多个社区关系, 为每个单独的邻里关系是自适应地选择.

差分策略可以被表示为DE/x/y, 其中, x表示当前被变异的向量的状态, 是随机的, 最佳的或者其他; y表示在变异过程中所采用的差分向量的个数. 多种变异策略中DE/best/1和DE/rand/1的应用最为广泛. 其中, DE/best/1策略的局部搜索能力强, 但是与此同时, 存在全局探测能力较差的特点; 而DE/rand/1策略全局探测能力强, 但是拥有局部搜索能力弱的缺点. 为了解决这一问题,本文基于差分突变的灵感提出了一种不需要作为参考的可行解的方法, 即结合两个著名的DE变体: DE/rand/1和DE/best/1, 提出了一种新的变异策略. 结合外部存档的思想, 同时将分治法的思想引入种群初始化, 提出DE/best_b^p-rand_w/2策略和DE/best_w^p-rand_b/2策略相结合的双种群两阶段变异策略(TPSDE), TPSDE大致可以划分为两个阶段, 分别是初始化后每i个邻域内的局部搜索阶段, 以及在整个集合内的搜索阶段. 首先, TPSDE第一阶段是在初始化后, 经过一轮训练, 个体按照适应度大小排序完成后, 将整个种群进行区域划分为子种群P₁和子种群P₂, 其中P₁种群个体适应度普遍比P₂更高, 然后分别按照不同的变异策略进行局部搜索. 这种做法使得算法在进化过程的初期, 两个子种群的内部进化可以让结构往好的方向发展, 更好的提高算法的收敛速度找到最优解; 但是, 在种群进化后期, 算法经过多次迭代之后, 由于个体间差异过小, 从而导致后期种群向全局最优解的进化停滞, 收敛速度较慢. 因此, 为了增加个体多样性, 同时需要第二个阶段勘测整个种群范围来提高全局搜索寻优能力. 其相对于其他的变异策略主要的优势在于可以很好的平衡收敛性能的提高和种群多样性保持之间的关系.

2 差分进化过程

DE是一种低空间复杂度, 高可拓展性并且在解决非线性、多模态和不可分离性等各种具有挑战性问题时表现更高效的优化进化算法. DE 算法有两个阶段, 分别是初始化和进化. 在第一阶段, 种群是随机生成的, 是一次性的过程; 在第二阶段, 即进化, 生成的种群会经历突变、交叉和选择过程, 这些过程在DE的搜索过程中重复进行, 直到满足终止标准, 最终在 D 维实参数空间中搜索全局最优点. 终止条件可以通过如下来判断: 根据目标函数的复杂性所对应固定次数的迭代 G_max值; 群体的最佳适应度在连续迭代中没有明显变化; 取得了预先指定的目标函数值.

算法的基本流程为: 首先随机初始化一个随机设定的NP维实值参数向量的总体. 每个向量, 也称为基因组或者染色体, 形成多维优化问题的候选解. 我们将用G=0, 1,…, G_max来表示DE中的后代. 从中随机选取两个解向量作差, 用一个标量F来定标, 定标后的差加到第3个向量上进而产生一个新的解即变异个体 $ {v_{i,g}} $ . 然后这个新的解与预先设定的初始解 $ {x_{i,g}} $ 根据交叉原则进行操作, 在保证变异个体一定对交叉后的解产生一些影响即有基因传给下一代的同时, 按照一定的概率决定生成的个体 $ {u_{i,g}} $ 继承的基因来自于哪个个体. 交叉操作完成后, 为了在随后的世代中保持种群大小不变, 算法的下一步需要进行选择, 需要将 $ {x_{i,g}} $ 和 $ {u_{i,g}}$ 进行一对一的锦标赛选择, 如果的 $ {u_{i,g}}$ 适应度值优于 $ {x_{i,g}} $ 的适应度值, 则 $ {u_{i,g}} $ 取代 $ {x_{i,g}} $ 继续进行进化活动, 算法通过不断地迭代计算, 保留适应度值更高的个体, 即保留更优解取代局部最优解, 直到向全局最优解逼近. 下面为标准差分进化算法步骤:

(1)种群初始化, 初始化是在 DE 中寻找位于D维参数空间中的实数全局最优解的第一个过程. 对于问题的每个参数, 可能存在一定的范围, 参数的值应该被限制在这个范围内. 初始种群即在G= 0 时, 应通过在受规定的最小和最大边界约束的搜索空间内均匀随机化个体来尽可能覆盖此范围. 参数向量个体表示为:

$ {X_{i,g}} = \left[ {x_{i,g}^1,x_{i,g}^2, \cdots ,x_{i,g}^D} \right],\begin{array}{*{20}{c}} {}&{i = 1,2, \cdots ,NP} \end{array} $

(1)

$ {x_{i,g}} $ 表示的是第g代的第i个解, 即目标个体, 随机产生NP个初始解, 每个解均有D维向量. 式(2)为在可行域内随机产生的初始种群.

$ x_{i,g}^0 = {x_{\min,j}} + rand(0,1)({x_{\max,j}} - {x_{\min,j}}) $

(2)

其中, ${x_{\max,j}},{x_{\min,j}}$ 分别是个体中第j个分量的上下限; rand(0, 1)为[0, 1]区间的一个随机数.

(2)变异操作. 生物学上, “突变”是指染色体基因特征的突然变化. 然而, 在进化计算范式的背景下, 突变也被视为随机元素的变化或扰动. 变异操作即将目标向量x_i,g通过差分变异操作后与自身重组形成变异向量v_i,g+1的过程, 其最大优势之一是变异步长的大小和方向都会自动适应目标函数值. 这个过程一般需要3个个体, 而这3个目标向量索引的选取是从范围[1, NP]中随机选择的互斥整数r₁、r₂和r₃, 将任何两个向量差值都按标量F进行缩放, 然后再将缩放后的差值添加到第3个向量中. 如图1所示. 两个应用最广泛的变异策略DE/best/1的第3个个体 $ {x_{r1,g}}$ 是种群中的最优个体; 而DE/rand/1策略的 ${x_{r1,g}} $ 是种群中的随机个体, 然后将 $ ({x_{r2,g}} - {x_{r3,g}}) $ 乘上F后与 $ {x_{r1,g}} $ 求和而产生变异个体 $ {V_{i,g + 1}} $ . 具体如式(3)表示.

$ {v_{i,g + 1}} = {x_{r1,g}} + F({x_{r2,g}} - {x_{r3,g}}) $

(3)

其中, F是变异因子, 位于[0, 1]之间, 一般取值0.5. g表示进化的代数, i表示第i个染色体, 即第i个个体, r₁, r₂, r₃表示索引, 即随机第r_i个个体.

(3)交叉操作. 通过交换部分变异向量 $ {v_{i,g}} $ 和目标向量 $ {x_{i,g}} $ 维度产生中间向量 ${U_{i,g}}$ 来提高种群的多样性, 使用下面交叉策略进行交叉. 染色体i=1, 2, 3,…,N; 基因j=1, 2, …,D; CR是交叉因子是[0, 1]内随机数, 一般取值0.5. j_rand是1到D随机数, 以保证变异向量至少有一维信息被保存在交叉向量里. j取随机数保证了交叉过程中一定会有变异后个体 ${v_{i,(g + 1)}}$ 的基因, 而r1, r4的取值小于等于CR, 因此交叉后代 $ {u_{i,(g + 1)}}$ 的基因来自于变异后的染色体 $ {v_{i,(g + 1)}}$ , 而r2, r3的大于CR, 因此交叉后代 $ {u_{i,(g + 1)}}$ 的基因来自于亲本的染色体 $ {x_{i,g}} $ .

${u_{ji,g + 1}} = \left\{ {\begin{array}{*{20}{l}} {{v_{ji,g + 1}}},&{{\rm{if}}\;rand(0,1) \leqslant CR\;{\rm{or}}\;j = j_{rand}}\\ {{x_{ji,g}}},&\rm{otherwise} \end{array}} \right.$

(4)

(4)选择操作. 选择所的生成的下一代个体是 ${x_{i,g}} $ 还是 ${u_{i,g}}$ , 即最优解是初始解还是经过一系列操作之后形成的新解. 需要将这组新解根据适应度和原来那组解进行一对一的锦标赛选择, 式(5)为差分进化算法适应度计算方法. 对于求最小值问题, 如果目标函数值比原来那组解小则将它们替换掉, 否则保留原来解. f(x)为目标函数值, 而对于应用在神经架构搜索中的差分进化算法的选择方法是根据适应度函数进行选择.

${x_{i,g + 1}} = \left\{ {\begin{array}{*{20}{l}} {{u_{i,g + 1}}},&{{\rm{if}}\;f({u_{i,g + 1}}) \leqslant f({x_{i,g}})}\\ {{x_{i,g}}},&\rm{otherwise} \end{array}}, \right.\;i = 1,2, \cdots, N$

(5)

(5)适应度函数的计算. 适应度指的是个体在种群生存的优势程度度量, 用于区分个体的“好与坏”, 通过比较适应度值的大小. 对于求函数最优解问题时, 标准差分进化算法需要将这组解和原来那组解根据适应度值的大小进行一对一的锦标赛选择, 判断从上面得到的进化之后的解是否可以作为下一代的解, 适应度函数即用来计算适应度值的函数.

3 改进差分策略的差分进化算法

本文通过重新构建子种群网络, 并按照各自合适的变异策略进行变异, 同时结合局部和全局同时进化的方法, 取代使用单一变异策略, 从而提高了种群的全局搜索寻优能力和局部搜索寻优能力, 进而避免了过早收敛和搜索停滞等问题的出现, 提升算法的收敛速度和求解精度. TPSDE首先随机初始化固定长度的种群, 经过一轮训练后得到种群的适应值大小, 然后进行变异交叉的操作. 为了进行下面的变异操作, TPSDE提出了向量之间的邻域结构, 向量的邻域是它所连接的其他参数向量的集合. 该邻域是根据种群成员的适应度顺序确定的. 例如, ${\vec X_{6,g}}$ 和 ${\vec X_{8,g}}$ 是 ${\vec X_{7,g}}$ 的两个邻域向量. 因为邻域大小必须小于种群大小, 所以每个向量都有一个半径为k的邻域, 其中k是从0到(NP–1)的非零正整数, 取 $k = \left\lfloor {(NP - 1)/2} \right\rfloor $ , $i = \left\lfloor {(NP - 1)/2} \right\rfloor $ , 领域向量被表示为:

${\vec X_{i - k,g}}, \cdots, {\vec X_{i,g}}, \cdots, {\vec X_{i + k,g}}$

(6)

同时, 他们适应度的大小为:

$f({\vec X_{i - k,g}}) > \cdots> f({\vec X_{i,g}}) > \cdots >f({\vec X_{i + k,g}})$

(7)

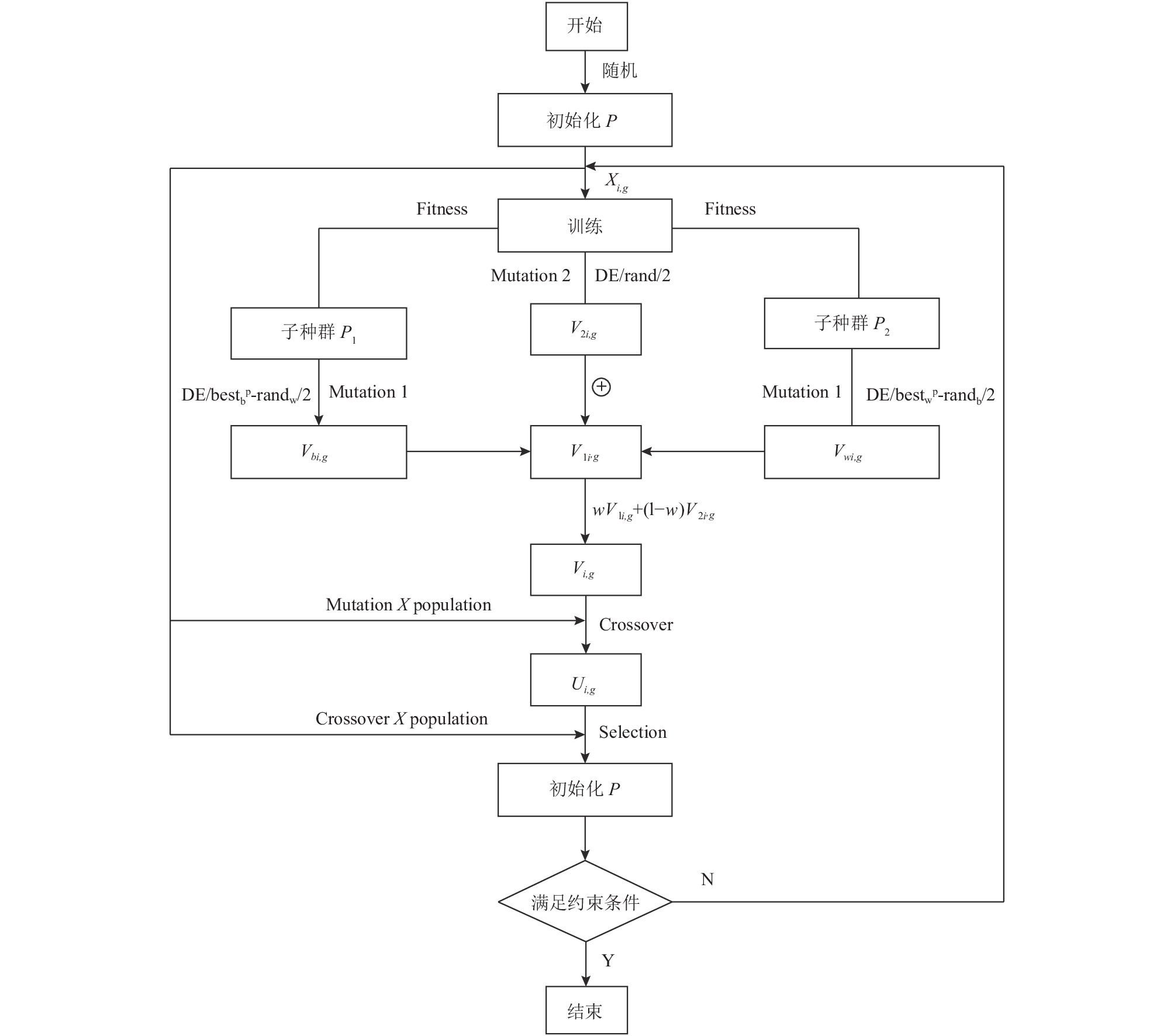
图 1 TPSDE基本流程图

局部优化过程针对不同子种群运用不同的变异策略. 结合DE/best/1和DE/rand/1策略的优点做出改进应用于不同的进化阶段, 仿真实验结果表示这比整个进化过程中仅采用一种变异策略表现出了更加优越的性能. 基于此, 本文提出DE/best_b^p-rand_w/2策略和DE/best_w^p-rand_b/2策略相结合的变异策略使两个子种群协同进化, 这种策略下较好个体的数量会随着阶段的发展逐级增加, 不仅不断增强子种群P₁的全局搜索寻优能力; 而且子种群P₂的局部搜索寻优能力同时得到提高. 从而避免了其因个体间差异过小, 种群个体多样性的缺失, 从而导致的搜索停滞问题. 双种群变异策略具体如下.

对于子种群P₁的进化如式(8). ${v_{bi,g}}$ 表示子种群P₁第g代的第i个个体变异后所产生的新个体; ${x_{bi,g}}$ 表示子种群P₁的第g代的第i个个体; F是变异因子; ${{x}}_{{\rm{best}}, g}^p$ 表示子种群P₁的前p%个最好的个体, 其中p是优秀因子; ${\tilde x_{wr2,g}}$ 表示在子种群P₂中随机选择的个体. 变异过程需要借助两个个体, 一个是 ${{x}}_{{\rm{best}}, g}^p$ , 另一个 ${\tilde x_{wr2,g}}$ ; $(x_{{\rm{best}},g}^p - {x_{bi,g}})$ 代表了群体中的个体都向适应度最高的方向学习, 这样可以起到加速收敛的作用; 为了起到扩大群体的多样性的作用从而避免陷入局部最优的情况, $({x_{br1,g}} - {\tilde x_{wr2,g}})$ 来加入适应度较低的解的特点.

$ {V_{bi,g}} = {x_{bi,g}} + F(x_{{\rm{best}},g}^p - {x_{bi,g}}) + F({x_{br1,g}} - {\tilde x_{wr2,g}}) $

(8)

对于子种群P₂的进化过程如式(9). ${v_{wi,g}}$ 表示子种群P₂第g代的第i个个体变异后所产生的新个体; ${x_{wi,g}}$ 表示子种群P₂的第g代的第i个个体; F是变异因子; ${{x}}_{{\rm{best}}, g}^p$ 表示子种群P₂的前p%个最好的个体, 其中p是优秀因子; ${\tilde x_{br2,g}}$ 表示在子种群P₁中随机选择的个体.

$ {V_{wi,g}} = {x_{wi,g}} + F(x_{{\rm{best}},g}^p - {x_{wi,g}}) + F({x_{wr1,g}} - {\tilde x_{br2,g}})$

(9)

第一阶段产生的变异子向量V_1i,g表示为:

${V_{1i,g}} = \omega {V_{bi,g}} + (1 - \omega ){V_{wi,g}}$

(10)

第一阶段局部搜索所产生的变异子向量V_1i,g需要和全局变异子向量V_2i,g协同优化得到最终的变异向量V_i,g, 全局优化采用的是DE/rand/2策略, 那么第二阶段全局变异子向量V_2i,g表示为:

${V_{2i,g}} = {x_{i,g}} + F({x_{bi,g}} - {x_{i,g}}) + F({x_{r1,g}} - {x_{r2,g}})$

(11)

于是, 最终形成的变异个体v_i,g为:

$ {V_{i,g}} = \omega {V_{1i,g}} + (1 - \omega ){V_{2i,g}} $

(12)

TPSDE引入了新的参数ω在DE中起着参数F的相同作用. 参数ω控制勘探和开采之间的平衡, 比如ω取较小的值时, 比如趋近于0, 有利于全局变量分量, 即更好的开采, 而取较大的值时, 比如趋近于1时, 有利于局部邻域分量, 即更好的勘探.

结合标准差分进化算法的框架以及双种群两阶段的变异策略, 局部与整体协同进化的思想, 提出基于双种群两阶段变异策略的差分进化算法(TPSDE), 具体实现流程如下所示.

Step 1. 种群初始化. 随机生成种群规模为NP的初始解集合.

Step 2. 第一阶段局部优化. 将初始化的种群进行一轮训练, 并且按照适应度从大到小排序, 并在k=(NP–1)/2处将其分成两个子种群区域, 即子种群(better)P₁和子种群(worse)P₂.

Step 3. 对于子种群P₁的个体, 采用DE/best_b^p-rand_w/2的变异策略进行差分进化得到向量V_bi,g.

Step 4. 对于子种群P₂的个体, 采用DE/best_w^p-rand_b/2的变异策略进行差分进化得到向量V_wi,g.

Step 5. 将子种群P₁, P₂变异后产生的V_bi,g和V_wi,g加权求和产生变异子向量V_1i,g.

Step 6. 第二阶段全局优化. 采用DE/rand/1的变异策略在全种群范围内搜索, 得到变异子向量V_2i,g.

Step 7. 将变异子向量V_1i,g和变异子向量V_2i,g按照同样的规则组合在一起得到最终的变异向量v_i,g.

Step 8. 按照式(4)交换部分变异向量v_i,g和目标向量x_i,g基因产生中间向量u_i,g.

Step 9. 算法初始化将产生的交叉向量u_i,g和目标向量x_i,g根据适应度的大小进行一对一的锦标赛选择, 保留适应度更高的个体作为新的种群P'.

Step 10. 种群初始化判断算法是否满足终止条件. 若满足, 则算法结束, 输出当前最优值为最终结果; 若不满足, 则令g=g+1, 并跳到Step 2. 图1即TPSDE的基本流程图.

4 实验设计与结果分析 4.1 实验仿真

为了验证TPSDE算法的有效性与先进性, 在实验过程中将标准Benchmark测试函数分别进行固定次数的仿真实验, 这里我进行30次实验之后进行统计, 同时对于函数的选取也是极具代表性, 选取的这些测试函数包括单峰函数以及多峰函数, 单模态以及多模态函数, 函数曲线是连续或者间断的以及有的具有多个局部最优解而有的函数没有局部最优解. 他们的函数名称、搜索范围, 维数以及理论上最优值如表1所示. 所有函数维数取D=30, 种群规模NP=50, F=0.5, CR=0.5, 4种算法独立运行30次后的误差平均值与标准方差的统计结果如表2所示.

表 1 测试函数及特征

表 2 各算法运行30次统计

函数	变异策略	最大值	最小值	平均值	标准差
f₁(x)	DE/best/1	0.0024589	0.0024560	0.0024562	3.3529E–012
	DE/rand/1	0.0027149	0.0024572	0.0025023	3.9697E–008
	TPSDE1	0.0026725	0.0024560	0.0024565	2.3656E–012
	TPSDE	0.0027058	0.0024560	0.0024579	1.2456E–015
f₂(x)	DE/best/1	7.5252E–013	7.5252E–014	7.1548E–018	4.0159E–028
	DE/rand/1	5.5852E–019	1.6989E–024	2.4852E–024	2.4561E–027
	TPSDE1	7.1512E–023	7.0415E–026	3.7815E–024	4.0048E–037
	TPSDE	0	0	0	0
f₃(x)	DE/best/1	0.564210	0.214545	0.348545	0.151525
	DE/rand/1	0.1505412	8.1541E–007	8.1711E–004	9.1452E–008
	TPSDE1	4.5151E–005	8.1447E–002	1.2545E–003	6.5454E–008
	TPSDE	0	0	0	0
f₄(x)	DE/best/1	5.7541E–012	2.8454E–016	8.1541E–013	2.1154E–023
	DE/rand/1	4.6154E–020	6.1514E–025	1.7264E–022	4.1541E–032
	TPSDE1	1.2541E–020	2.5484E–029	1.8412E–022	4.1541E–041
	TPSDE2	2.5141E–300	2.1414E–307	1.4548E–301	0
f₅(x)	DE/best/1	4.5115E–007	3.1411E–013	4.4485E–009	8.2151E–016
	DE/rand/1	0	0	0	0
	TPSDE1	0	0	0	0
	TPSDE	0	0	0	0
f₆(x)	DE/best/1	1.4254E–002	5.5414E–004	2.1514E–003	1.1541E–008
	DE/rand/1	2.1541E–001	4.1541E–003	6.1451E–002	2.1515E–004
	TPSDE1	1.5451E–001	0.1541E–005	0.5415E–001	0.1542E–006
	TPSDE	0	0	0	0

表 2 各算法运行30次统计

4.2 实验结果分析

将TPSDE算法与目前性能最优、应用范围最广的两种变异策略下的差分进化算法和我所提出算法的一种变体进行对比实验, 分别为DE/best/1, DE/rand/1和TPSDE1, 其中TPSDE1是TPSDE算法的变体, 是邻域向量划分的时候, i和k的取值均为一个随机整数, 即多种群的变异策略, 此时i的取值范围为[0, (NP–1)/2)∪((NP–1)/2, NP–1]范围内的随机整数, k为[1, (NP–1)/2)∪((NP–1)/2, NP–2]内随机生成的整数. 选择最小误差、取得固定误差值所需要的函数评价次数这两个指标进行结果分析, 具体如图2所示.

从表2可以看出, 无论是简单30维单模态Sphere函数还是多模态Rantrigin函数, 无论是单峰函数还是多峰函数, 从优化结果可以看出, 各个算法的最优值、最差值、平均值和标准差结果显示, TPSDE算法都具有的寻优能力明显优于其他算法, 能够持续有效地搜索函数全局最优点. 图2为每个测试函数经过多轮迭代之后的误差值统计图. 我们可以很明显的看出, TPSDE算法几乎在每个测试函数上相对于其他3种差分策略的算法都表现出了突出的优势. 当TPSDE算法和各种差分策略算法都能找到函数的最优点时, TPSDE算法表现出了较好的全局收敛性和健壮性, 其前期收敛速度快, 能够在最优极值点所在局部区域进行细致搜索, 能够快速的找到最优解所在的局部区域, 收敛曲线能够迅速地接近于最优点, 利用较短的时间就可以接近于最小误差值; 后期能够增加种群的多样性, 跳出局部最优解, 避免出现搜索停滞, 从他们接近于最小误差时的迭代次数可以看出, 对于Schaffer和Griewank测试函数图显示函数收敛到大概相同误差值时, DE/best/1算法使用的迭代次数最少; Rantrigin函数的收敛曲线图说明在前期TPSDE1变异策略能达到一个较好的效果, 而更多的情况, 比如Rosenbrock、Step和Sphere测试函数误差图显示, TPSDE算法使用最少的评估次数, 可以做到快速收敛到极值点附近, 而其他差分策略收敛速度较慢.

5 结论与展望

本文提出的基于双种群两阶段变异策略的差分进化算法, 通过将全局优化和双种群协同进化策略下的局部优化相结合, 在以最有效的方式搜索到最优解的同时, 增加了种群多样性, 防止了搜索停滞和陷入局部最优解现象的出现. 以上函数仿真实验结果表明TPSDE算法在迭代次数明显减少, 精度得到明显提高, 以及鲁棒性上都达到了更加优秀的效果. 另外, 在接下来的研究中, 由于差分进化算法的通用性强, 易与其他算法相结合, 诸如与人工免疫网络、神经架构搜索等相结合, 进行模型参数优化, 相信其在提高预测精度上会有较好的效果, 能够更好地解决现实中的问题.

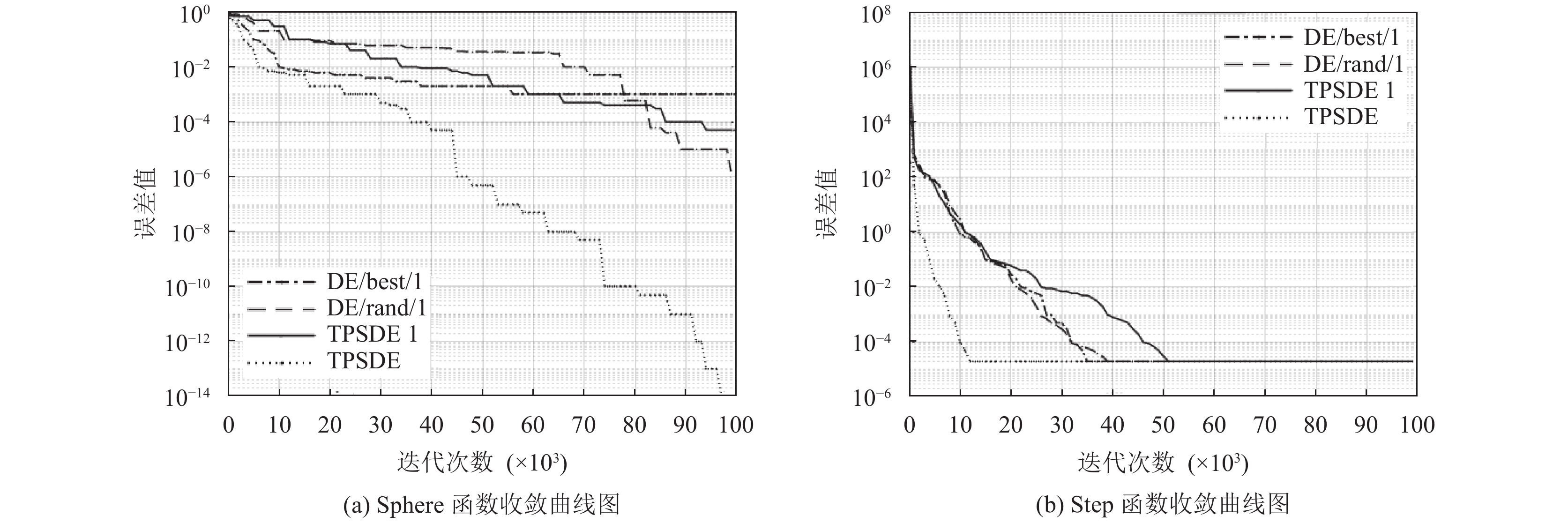
图 2 测试函数收敛图

参考文献

[1]	Storn R, Price K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. Journal of Global Optimization, 1997, 11(4): 341-359. DOI:10.1023/A:1008202821328
[2]	Angeline PJ, Saunders GM, Pollack JB. An evolutionary algorithm that constructs recurrent neural networks. IEEE Transactions on Neural Networks, 1994, 5(1): 54-65. DOI:10.1109/72.265960
[3]	徐斌, 陶莉莉, 程武山. 一种自适应多策略差分进化算法及其应用. 化工学报, 2016, 67(12): 5190-5198.
[4]	张贵军, 王文, 周晓根, 等. 基于动态策略的差分进化柔性车间优化调度. 计算机科学, 2018, 45(10): 240-245. DOI:10.11896/j.issn.1002-137X.2018.10.044
[5]	Kim HK, Chong JK, Park KY, et al. Differential evolution strategy for constrained global optimization and application to practical engineering problems. IEEE Transactions on Magnetics, 2007, 43(4): 1565-1568. DOI:10.1109/TMAG.2006.892100
[6]	Omran MGH, Engelbrecht AP. Self-adaptive differential evolution methods for unsupervised image classification. 2006 IEEE Conference on Cybernetics and Intelligent Systems. Bangkok: IEEE, 2006. 1–6.
[7]	Zhang RQ, Ding JX. Non-linear optimal control of manufacturing system based on modified differential evolution. The Proceedings of the Multiconference on Computational Engineering in Systems Applications. Beijing: IEEE, 2006. 1797–1803.
[8]	Dhahri H, Alimi AM. The modified differential evolution and the RBF (MDE-RBF) neural network for time series prediction. The 2006 IEEE International Joint Conference on Neural Network Proceedings. Vancouver: IEEE, 2006. 2938–2943.
[9]	Liang WL, Jiao YC, Zhang L. Sideband suppression in time-modulated linear array by modified differential evolution algorithm. 2015 IEEE International Conference on Communication Problem-solving. Guilin: IEEE, 2015. 399–401.
[10]	Massa A, Pastorino M, Randazzo A. Optimization of the directivity of a monopulse antenna with a subarray weighting by a hybrid differential evolution method. IEEE Antennas and Wireless Propagation Letters, 2006, 5: 155-158. DOI:10.1109/LAWP.2006.872435
[11]	Ulker ED, Haydar A. A hybrid algorithm based on differential evolution, particle swarm optimization and harmony search algorithms. 2013 Federated Conference on Computer Science and Information Systems. Krakow: IEEE, 2013. 417–420.
[12]	吴亮红, 王耀南, 袁小芳, 等. 自适应二次变异差分进化算法. 控制与决策, 2006, 21(8): 898-902. DOI:10.3321/j.issn:1001-0920.2006.08.012
[13]	Su CT, Lee CS. Network reconfiguration of distribution systems using improved mixed-integer hybrid differential evolution. IEEE Transactions on Power Delivery, 2003, 18(3): 1022-1027. DOI:10.1109/TPWRD.2003.813641
[14]	翟捷, 王春峰, 李光泉. 基于差分进化方法的投资组合管理模型. 天津大学学报, 2002, 35(3): 304-308.
[15]	Das S, Abraham A, Chakraborty UK, et al. Differential evolution using a neighborhood-based mutation operator. IEEE Transactions on Evolutionary Computation, 2009, 13(3): 526-553. DOI:10.1109/TEVC.2008.2009457
[16]	Zhang J, Member S, et al. JADE: Adaptive differential evolution with optional external archive. IEEE Transactions on Evolutionary Computation, 2009, 13(5): 945-958. DOI:10.1109/TEVC.2009.2014613
[17]	Mallipeddi R, Suganthan PN, Pan QK, et al. Differential evolution algorithm with ensemble of parameters and mutation strategies. Applied Soft Computing, 2011, 11(2): 1679-1696. DOI:10.1016/j.asoc.2010.04.024
[18]	Islam SM, Das S, Ghosh S, et al. An adaptive differential evolution algorithm with novel mutation and crossover strategies for global numerical optimization. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 2012, 42(2): 482-500. DOI:10.1109/TSMCB.2011.2167966
[19]	Piotrowski AP. Adaptive memetic differential evolution with global and local neighborhood-based mutation operators. Information Sciences, 2013, 241: 164-194. DOI:10.1016/j.ins.2013.03.060
[20]	Liao JL, Cai YQ, Chen YH, et al. Improving differential evolution with ring topology-based mutation operators. 2014 9th International Conference on P2P, Parallel, Grid, Cloud and Internet Computing. Guangdong: IEEE, 2014. 103–109.
[21]	Al-Dabbagh RD, Botzheim J, Al-Dabbagh MD. Comparative analysis of a modified differential evolution algorithm based on bacterial mutation scheme. 2014 IEEE Symposium on Differential Evolution (SDE). Orlando: IEEE, 2014. 1–8.
[22]	Yu XB, Cai M, Cao J. A novel mutation differential evolution for global optimization. Journal of Intelligent & Fuzzy Systems:Applications in Engineering and Technology, 2015, 28(3): 1047-1060.
[23]	Mohamed AW. An improved differential evolution algorithm with triangular mutation for global numerical optimization. Computers & Industrial Engineering, 2015, 85: 359-375. DOI:10.1016/j.cie.2015.04.012
[24]	Cui LZ. Adaptive differential evolution algorithm with novel mutation strategies in multiple sub-populations. Computers and Operations Research, 2016, 67: 155-173. DOI:10.1016/j.cor.2015.09.006
[25]	Sun G, Cai YQ. A novel neighborhood-dependent mutation operator for differential evolution. 2017 IEEE International Conference on Computational Science and Engineering (CSE) and IEEE International Conference on Embedded and Ubiquitous Computing (EUC). Guangzhou: IEEE, 2017. 837–841.