2. 西南交通大学 机械工程学院, 成都 610031;
3. 轨道交通运维技术与装备四川省重点实验室, 成都 610031;
4. 航空工业成都飞机工业(集团)有限责任公司, 成都 610073
2. School of Mechanical Engineering, Southwest Jiaotong University, Chengdu 610031, China;
3. Technology and Equipment of Rail Transit Operation and Maintenance Key Laboratory of Sichuan Province, Chengdu 610031, China;
4. AVIC Chengdu Aircraft Industrial (Group) Co. Ltd., Chengdu 610073, China
快递业务量自2010年的不足24亿件, 迅速攀升到2020年的833.6亿件. 剧增的快递业务量对配送效率提出了更高的要求, 使得各大快递企业不断导入新的技术和手段. 为了实现高效快捷的包裹配送, 超过60%的物流配送中心装备了分拣系统[1]. 采用自动导引车(automated guided vehicle, AGV)分拣的系统具有高度无人化、自动化、智能化等优势, 但多AGV分拣作为高度复杂的集成系统, 需要合理的集群调度方案和路径优化策略方能保证所有AGV得到高效利用, 并在尽可能短的时间内完成包裹的分拣. 多个AGV在分拣中心同时作业时, 需为每个AGV合理规划路径, 避免AGV间发生冲突、死锁等情况, 保持整个分拣系统的正常运行.
多AGV路径规划旨在为每个AGV规划一条合适的路线, 以便在AGV运行空间内将物品从起点移动到目的地. 研究多AGV路径规划问题对于快递包裹分拣效率的提升具有积极的理论和应用意义. 业界对于多AGV路径规划的需求包括以下3个方面: (1)随着包裹数量和土地成本的急剧升高, 仓储对于密集的多AGV转运系统需求日益增强, 因而对于在此环境下保持多AGV系统高效运行的技术理论存在迫切需求; (2)随着消费产业愈发成熟, 商品种类迅速增多, AGV面临的任务特点和任务要求也越发复杂. 除搬运到指定位置外, 还面临平稳、快速、大体积、超重搬运等多种搬运需求, 使得多AGV路径规划也面临新的挑战; (3)随着5G高速通信和轻量化深度学习技术的出现, AGV系统的搭建存在更多新的技术选择, 以远程检测和视觉导航为代表的新兴AGV技术使得多AGV路径规划面临新的约束和场景. 本文聚焦多AGV路径规划在无碰撞要求下的算法改进, 瞄准上述所提的需求(1).
针对多AGV路径规划, 其制定的线路须确保各台AGV不会发生碰撞和死锁等, 且需要实现最短行驶时间、最短距离长度或最少能量消耗等目标. 选择合适的路线对系统的性能有一定的影响, AGV分拣单件包裹的时间越长, 在给定时间周期内可以处理的分拣任务就越少. 因此, 国内外学者对多AGV路径规划问题进行了大量的研究, 主要的解决方法有精确算法、启发式算法、人工智能和仿真模拟等[2]. 在精确算法方面, Langevin等[3]采用动态规划实现对两台AGV调度与无冲突路径规划相结合的优化问题求解. Desaulniers等[4]提出了结合贪婪搜索、列生成和分支切割的精确算法, 可以解决最多4台AGV的情况. 但该算法存在一定的局限性, 其效率高度依赖于启发式算法的性能, 如果搜索启发式方法不能找到可行解, 则不能找到最优解. 与精确算法相比, 启发式方法的优势在于求解速度快, 适合解决大规模问题. 对于AGV路径规划, A*算法成为多数研究的首选方法, 譬如改进A*算法[5-7]、变步长双向A*算法[8]、时空冲突约束A*算法[9], 并且在诸多场景中得到了应用, 包括智能泊车[10]、自动驾驶[11]等. 关于A*算法的更多应用已由Foead等进行了总结[12]. 除此之外, 遗传算法[13]、人工蜂群算法[14]、迭代贪婪算法[15]、蚁群算法[16]等元启发式算法也相继被用于解决AGV路径规划. 随着人工智能技术的日益成熟, 部分学者也将人工智能算法用于解决多AGV路径规划问题, 并取得了一定的效果[17]. Srivastava等[18]提出了基于智能体的框架来克服冲突和死锁等问题, 该框架通过整合路径生成、旅程时间计算、碰撞识别和死锁识别等不同活动来控制AGV的运行. 刘辉等[19]提出了多智能体独立强化学习算法, 用于同时优化多AGV的任务调度和路径规划. 仿真模拟法可以更加直观地反应每个AGV的作业情况, Ashayeri等[20]介绍了交互式微型计算机自动物料搬运系统的GPSS仿真程序生成器. Um等[21]提出了基于多AGV的柔性制造系统仿真设计与分析方法. Kim等[22]提出了面向对象的仿真建模环境-AgvTalk, 为AGV系统的仿真提供灵活的建模能力.
现有多AGV路径规划研究大多是针对二维平面环境, 尽管存在时间窗模型等考虑时效约束的研究, 但是少有研究系统地从时空维度动态地解决路径规划问题. 即将基于时间的搜索与基于空间的搜索结合起来, 以实现算法计算时间开支最小与路径规划空间距离最短的均衡.
从这一角度出发, 本文首先根据物流分拣中心的场地特点选择合适的地图建模方法, 然后将时间维度导入A*算法, 将其改进为时空A*算法, 并将时空A*算法作为基于冲突搜索框架的下层规划器, 用于求解多AGV无冲突路径规划问题. 对上述两种算法的融合, 旨在优势互补为解决路径规划中的冲突问题提供新的求解思路. 最后, 通过仿真实验验证所提算法在不同冲突情况下的求解效果.
2 地图选择与单AGV路径规划 2.1 地图选择生成AGV无冲突路径方案首先需要构建地图模型. 只有在AGV工作环境已知的情况下才能利用有效的路径规划算法为AGV找到合适的行驶路线, 而环境信息的描述正是通过建立地图模型实现的. 环境信息描述的准确性和复杂程度受到地图建模方式的影响, 进而影响路径规划的决策效率和响应速度, 因此选择合适的地图建模方法是非常有必要的[23].
栅格地图法是将已知的工作环境划分为大小相同的固定栅格. 如图1所示, 栅格按照颜色的不同分为黑白两种, 黑色栅格表示障碍物, 白色栅格表示可通行区域. 若障碍物位置变化, 仅需调整栅格的占用情况. 栅格法构建地图时需要确定栅格尺寸, 栅格地图的精度与栅格尺寸密切相关, 尺寸越小精度越高. 若地图精度过高, 需要占用大量存储空间且计算时间过长, 但如果精度过低, 又会影响AGV移动和定位的准确性, 因此选择合适的栅格尺寸尤为重要. 一般来说, 以AGV车体的大小为基准设置栅格的尺寸, 即可满足地图的精度需求. 针对物流分拣中心布局规则、场地平坦、障碍物少等特征, 栅格地图法优势明显, 因此在后续的多AGV路径规划算法研究中采用栅格地图法建立地图模型.
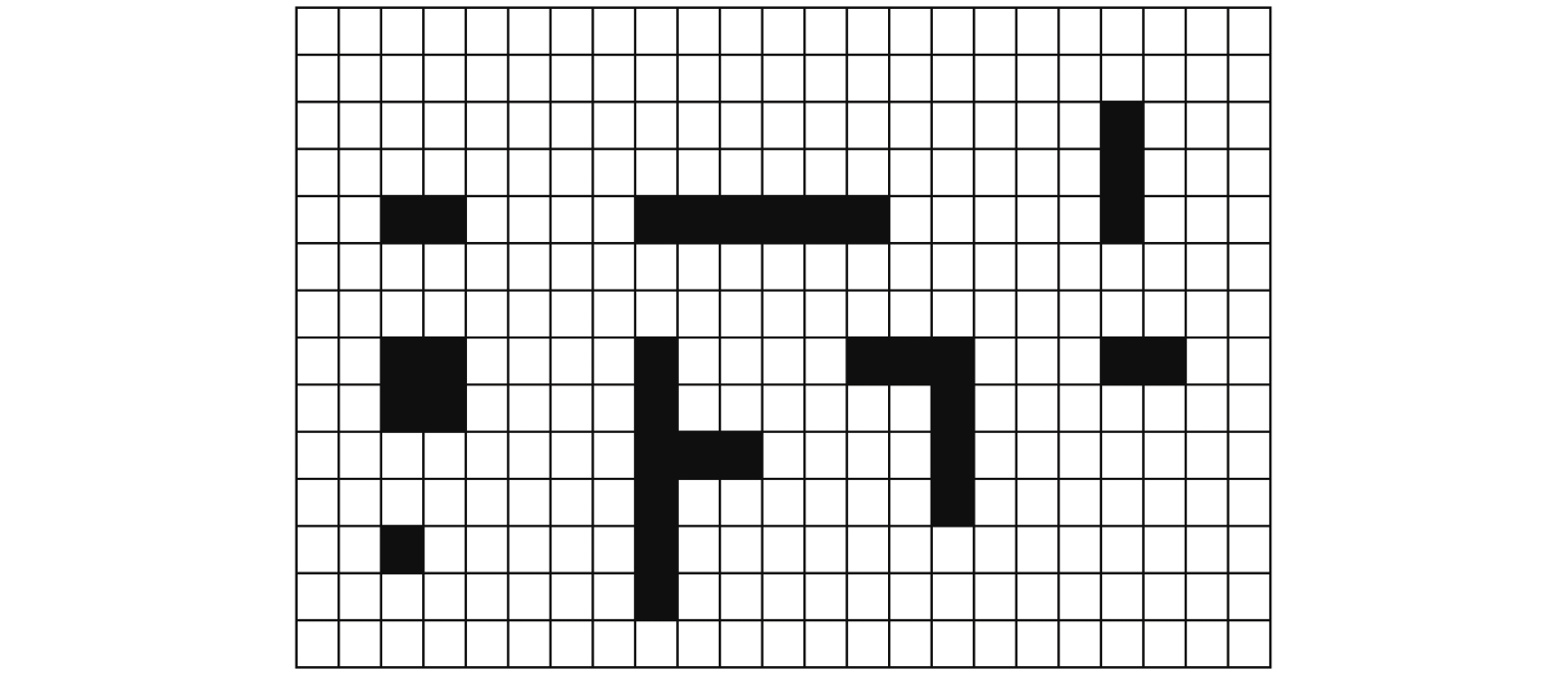
|
图 1 栅格地图法示意图 |
2.2 单台AGV路径规划
当分拣系统中仅有一台AGV工作时, 不存在路径冲突问题. 本文单AGV最优路径规划问题选用A*算法进行搜索. A*算法利用评价函数在每次搜索时都对所有可扩展点进行评估, 从而找到每次搜索的最佳扩展点, 直至找到目标节点. 使用评价函数的好处在于可以避免搜索过多无用的点, 算法的搜索效率得以提高. 评价函数如下:
| $ f(i)=g(i)+h(i) $ | (1) |
其中, f(i)表示从起点经由节点i到达终点的路径代价估计值; g(i)表示节点i距离起点的路径代价实际值; h(i)表示节点i距离终点的路径代价估计值. A*算法在每次搜索时, 选择拥有最小f(i)值的节点作为下一次搜索的节点.
分拣中心的AGV通常是水平方向或竖直方向行走, 不会出现斜着走的情况. 因此设置A*算法的搜索方向为四邻域, 即如图2所示的节点扩展方式. 以四邻域搜索方式扩展节点时, A*算法的启发函数使用曼哈顿距离, 其计算表达式如下:
| $ h(i)=D \times ({\rm{abs}}(x_{i}-x_{j})+{\rm{abs}}(y_{i}-y_{j})) $ | (2) |
式(2)中, D表示相邻两个节点的移动距离; xi和yi分别表示节点i的横纵坐标; xj和yj分别表示终点j的横纵坐标.

|
图 2 四邻域搜索方式 |
3 基于冲突搜索的多AGV路径规划算法
在实际的分拣场景中通常多辆AGV同时执行分拣任务, 此时, AGV间可能会发生冲突. 传统的A*算法只能解决单AGV路径规划问题, 而多AGV路径规划问题本质上就是各AGV相互协作, 在保证不发生碰撞的前提下完成被分配的任务, 因此需要改进传统的A*算法使之能够解决多AGV路径规划问题.
冲突搜索是由Sharon等[24]提出的多Agent路径规划(multi-agent pathfinding, MAPF)问题求解框架. 在本文中Agent即AGV. 该算法由上下两层搜索结构组成, 在上层搜索中, 使用二叉树寻找多个AGV间的冲突, 如果存在冲突, 则施加相应的约束用于下层搜索; 在下层搜索中, 将MAPF分解为多个单AGV, 运用单AGV路径规划算法分别为每个AGV规划路径. 本文在下层搜索中使用的单AGV路径规划算法为时空A*算法.
3.1 冲突类型在多AGV环境中, 不同的运行情况会引发不同的冲突类型. 本文主要考虑如图3所示的两种冲突. 当两辆AGV在同一路段上相向行驶时会发生图3(a)所示的相向冲突, 当两辆AGV位于十字路口处且行驶方向垂直时会发生图3(b)所示的节点冲突. 假设所有AGV的行驶速度始终保持匀速, 不会发生赶超等情况.

|
图 3 两种冲突类型 |
3.2 时空A*算法
当环境中只有一辆AGV时, AGV在静态的环境中不会发生冲突, 只需在二维空间地图中进行路径规划. 一旦环境中有多辆AGV时, 运行中的AGV会成为其它AGV的动态障碍物, 为此须在时间和空间两个维度上对车辆进行有序地控制. 为了解决物流分拣中心中的多AGV路径规划, 考虑在二维空间地图中加入时间维度, 进而拓展为三维时空地图.
A*算法在二维空间地图搜索时只需要记录拓展节点的位置信息, 在引入时间维度后, 不仅需要记录位置信息, 还需要记录在每个位置的时间信息. 对传统的A*算法进行改进, 将改进后的算法命名为时空A*算法. 在时空A*算法中将时间编码为图中的状态, 时间是线性推进的, 将图简化为时空树. 时空搜索树是在普通的搜索树中加入时间节点, 树每搜索一层, 时间也随之增加一个单位.
以图4所示的小规模地图为例, 当点A为AGV起点时, 时空A*算法搜索的时空树如图5所示.

|
图 4 小规模示例地图 |
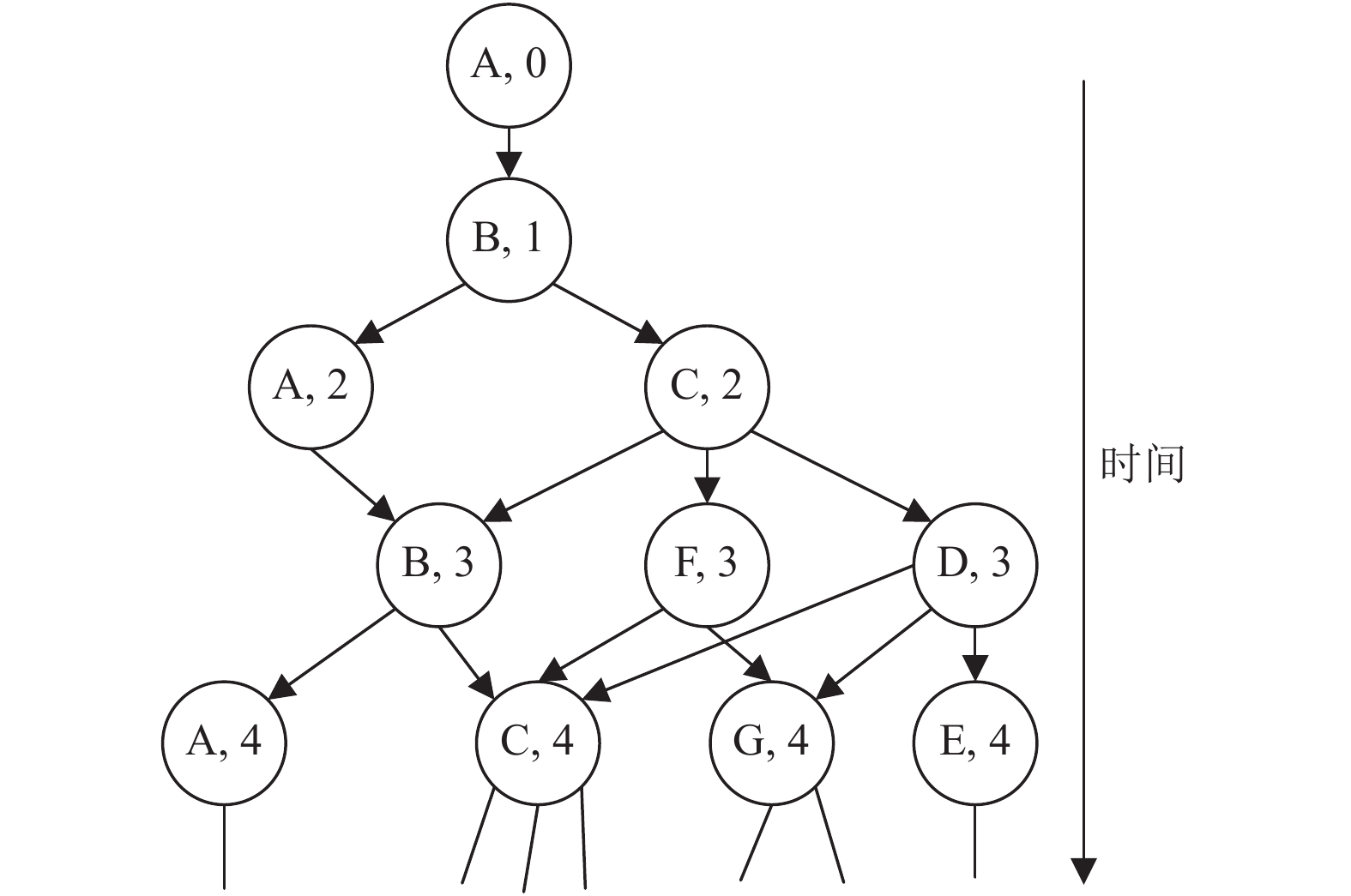
|
图 5 小规模示例地图时空树 |
树中每个分支点的字母表示节点位置, 数字表示到达该位置的时间点, 搜索的起始时间设置为0, 到达下一邻接点需要一个单位的时间. 从图4可以看到, A点的邻接点只有B点, 所以树的下一层只有位置B及对应的时间点1; B点的邻接点为A点和C点, 因此树的下一层包含位置A和位置C及对应的时间2; 由于本章采用四邻域方向, 因此C点的邻接点为B点、D点和F点, A点的邻接点为B点, 所以树的下一层包含位置B、位置D和位置F, 时间点为3; 以此类推, 直至找到目标节点. 本文提出算法的核心在于生成树的过程, 找到目标节点的方法与一般的广度优先搜索类似, 搜索以及产生路径流程如图6.

|
图 6 时空A*算法流程 |
3.3 基于冲突搜索
基于冲突搜索的核心思想是算法上层搜索路径间存在的冲突, 然后生成对应的约束, 下层找到满足这些约束的路径, 如果新生成的路径仍然存在冲突, 则通过添加新的约束来解决冲突. 可能发生的冲突分为点冲突和边冲突. 点冲突用元组<Ak, Aa, v, t>表示, 其中Ak和Aa分别表示第k辆和第a辆AGV, v表示位置点, t表示时间, 意为Ak和Aa会在t时刻同时占据v点. 当检测到点冲突时会分别为两辆AGV施加约束<Ak, v, t>和<Aa, v, t>. 边冲突用元组<Ak, Aa, v1, v2, t>表示, 意为Ak和Aa会在t时刻到t+1时刻之间交换位置, 也即是说Ak从v1点移动到v2点, Aa从v2点移动到v1点. 当检测到边冲突时会分别为两个AGV施加约束<Ak, v1, v2, t>和<Aa, v2, v1, t>.
搜索冲突和添加约束的过程在算法上层的约束树(constraint tree, CT)中进行. CT是二叉树, 树中的任一节点i都包括以下3条内容:
(1) i.constraint: 一组约束, 由所有被施加的约束构成, 每个约束都属于某一AGV.
(2) i.solution: 一个解决方案, 由多条路径组成的集合, 路径数即为AGV个数. 解决方案只有当每条路径满足所有约束时才可行, 这些路径是在下层搜索中找到的.
(3) i.cost: 当前解决方案i.solution的总成本, 即所有路径的成本总和.
约束树的根节点包含的约束集合为空, 因为根节点的策略是为对每辆AGV的路径进行无约束搜索, 显然根节点的解决方案中的每条路径都是忽略其它AGV的存在而找到的. 若节点i的i.solution有效, 则该节点即为目标节点. 若节点i的i.solution无效, 即i.solution中的路径存在冲突, 则需要从节点i分支出两个子节点, 并对两个子节点分别施加新的约束. 分支出两个子节点是为了检查两种可能性, 其目的是为了保证最优性. 两个子节点会根据新施加的约束生成各自的解决方案和路径总成本, 算法的上层对约束树进行最佳优先搜索, 根据路径总成本的大小对节点进行排序. 若两个子节点的解决方案均有效, 则返回拥有最小路径总成本的解决方案. 若两个子节点的解决方案均无效, 则对拥有最小路径总成本的节点进行下一步扩展, 直至找到有效的解决方案. 需要注意的是, 新扩展的子节点不需要保存父节点的所有约束, 只需要保存最新的约束, 然后通过其父节点遍历从当前节点到根节点的其它约束.
算法1. 基于冲突搜索的算法流程
输入: 环境地图, AGV数量, 每个AGV的起点和终点.
初始化根节点r的r.constraint为空集合;
调用下层搜索获得r.solution和r.cost;
将根节点r放入OPEN表中;
while OPEN表不为空 do
i←OPEN表中拥有最小i.cost的点;
ifi.solution无冲突 then
返回i.solution;
c←i.solution中的第一个冲突<Ak, Aa, v, t>;
for c中的每个AGV Ax do
P←创建一个新节点;
P.constraint←i.constraint+<Ax, v, t>;
P.solution←i.solution;
Ax调用下层搜索更新P.solution;
P.cost←计算P.solution的路径长度;
将P点放入OPEN表中;
end for
end while
在为约束树的节点添加新的约束后, 调用下层搜索. 下层搜索使用单AGV路径规划算法, 旨在为每个AGV规划出当前约束下成本最小的路径. 本文采用时空A*算法作为下层规划器. 当上层搜索检测到冲突并施加相应的约束后, 下层搜索只需要对与新添加的约束相关联的AGV重新规划路径, 其它AGV的路径无需重新规划, 因为它们没有被施加新的约束. 时空A*算法通过时空树进行搜索, 一旦为所有需要重新规划路径的AGV找到了满足约束的路径后, 所有路径会从时间和空间两个维度上进行相互验证, 从而判断当前的解决方案是否有效.
虽然在下层搜索中每条路径都是单独规划的, 但是为了尽量避免与其它已有路径发生冲突, 还引入了冲突规避表(conflict avoidance table, CAT). 该表保存了所有AGV的路径信息, 通过该表可以获取任意节点在任意时刻的AGV数量, 即CAT值. 时空A*算法在评价时空树中某一节点的两个邻接点时, 如果两个邻接点的评价函数值f(i)相同, 则选择CAT值小的点. 基于冲突搜索的算法框架伪代码如算法1所示.
4 多AGV无冲突路径规划仿真实验为验证基于冲突搜索的多AGV路径规划算法的有效性, 以规模为8个分拣台和35个投放口的分拣中心为仿真实例, 生成对应的栅格地图, 进行3组不同AGV数量和分拣任务的仿真实验. 所有的仿真实验在配置为AMD Ryzen 5-4600U with Radeon Graphics CPU @ 2.10 GHz, 16 GB的个人电脑上运行, 用Python语言实现.
栅格化后的地图环境如图7所示, 四周的黑色障碍物为墙壁, 墙壁内部为AGV的行驶区域, 被划分为18行27列, 共计486个栅格. 栅格的大小以AGV自身的大小为基准, 每个栅格大小相同且具有各自的位置坐标(x, y), 其中x表示栅格所在行数, y表示栅格所在列数. 从当前栅格到达下一栅格需要耗费一个单位的时间. 障碍物的大小不同其占据的栅格数也不同, 其中充电区占据9个栅格, 每个投放口占据1个栅格, 每个分拣台占据2个栅格.
4.1 相向冲突仿真实验本节仿真实验用于验证算法解决相向冲突的有效性, 该仿真实例中有2辆AGV同时分拣, 行驶路线如图8所示. AGV1的起点为坐标(10, 3)的栅格, 即红色圆圈所在位置, 终点为坐标(10, 14)的栅格, 即红色方框所在位置. AGV2的起点为坐标(10, 25)的栅格, 即绿色圆圈所在位置, 终点为坐标(10, 11)的栅格, 即绿色方框所在位置. 红色线段为AGV1的行驶路线, 绿色线段为AGV2的行驶路线. 从图中可以看出AGV1并没有从栅格(10, 13)直接到达终点栅格(10, 14), 而是从栅格(10, 13)到栅格(11, 13), 然后经过栅格(11, 14)才到达栅格(10, 14), 这样是为了避免在栅格(10, 14)与AGV2发生冲突. 二者路线从空间上存在交叉, 但是基于所提出的时空搜索框架, 二者在时间上并不会同时访问到任何一点, 因此避免了潜在的碰撞冲突.
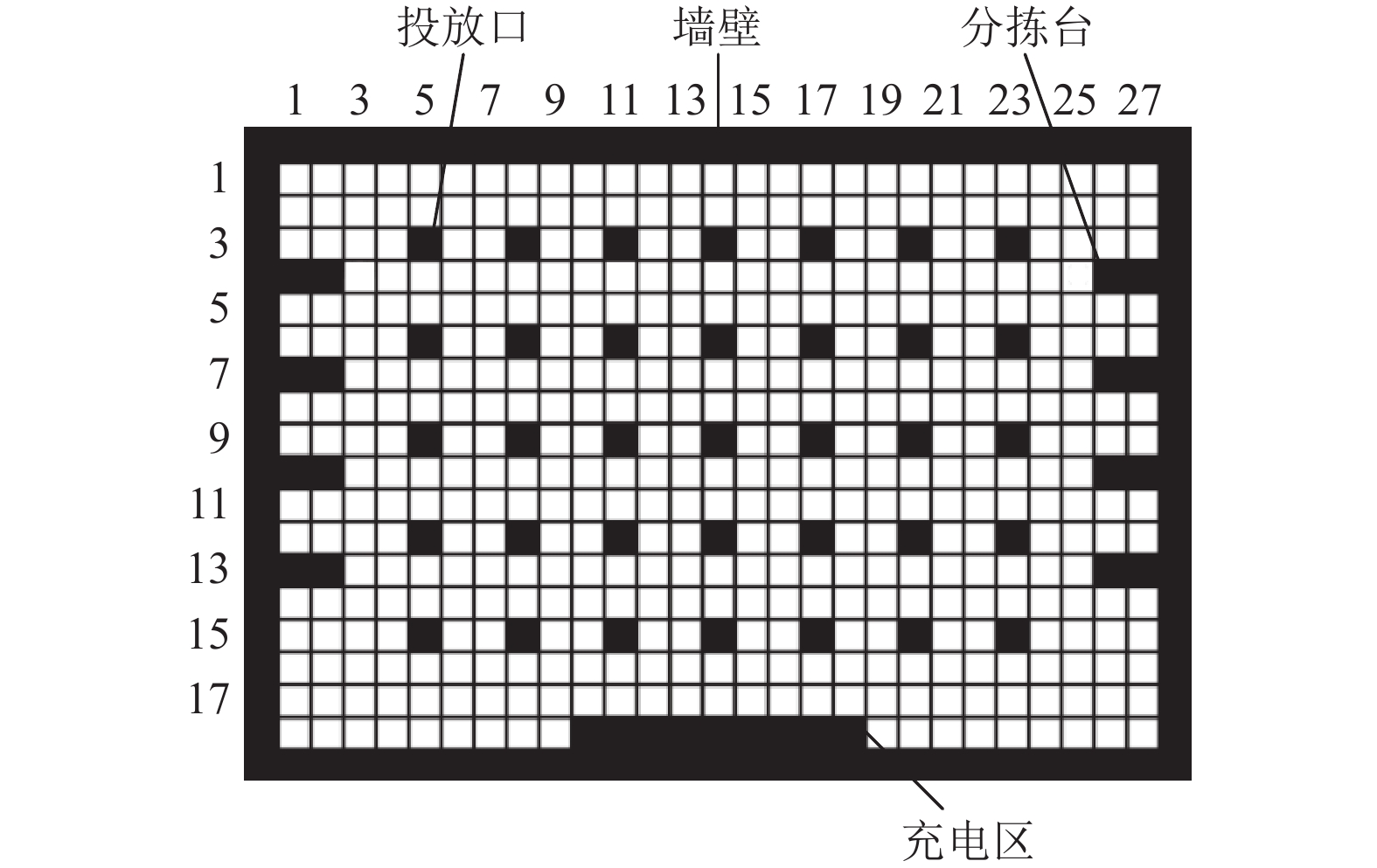
|
图 7 栅格地图 |

|
图 8 双AGV相向行驶路线图 |
图9为AGV1和AGV2按照图8所示的起点和终点相向行驶时的三维时空图, 时空图的x轴和y轴表示栅格的位置坐标, z轴表示时间t, 两条线段分别表示两辆AGV的行驶路径. 通过时空图可以清晰地看到AGV在不同时间点所在的栅格位置. 图9(a)为未使用基于冲突搜索算法进行规划时的时空图, 从图中可以看出两条线段在(10, 14, 11)有交叉, 交叉点用小黑点表示, 这表明当t=11时, 两辆AGV在栅格(10, 14)处发生了冲突. 图9(b)为使用基于冲突搜索算法规划后的时空图, 从图中可以看出两条线段不存在交叉, AGV2维持原有的路径, 而AGV1的路径发生了变化, 当t=11时, AGV1未到达栅格(10, 14), 而是到达了栅格(11, 13), 因此两辆AGV未发生冲突. 避免冲突的方式为算法的上层检测到冲突<A1, A2, (10, 14), 11>, 然后对AGV1施加新的约束<A1, (10, 14), 11>, 算法的下层根据AGV1新施加的约束重新为其规划路径. 由此可看出, 基于冲突搜索的多AGV路径规划算法可以有效解决时空角度的相向冲突.

|
图 9 双AGV相向行驶三维时空图 |
4.2 节点冲突仿真实验
本节仿真实验使用两辆沿着垂直方向行驶的AGV验证算法解决节点冲突的有效性, 使用基于冲突搜索算法规划的两辆AGV的行驶路线如图10所示. AGV1的起点位置和终点位置分别为栅格(7, 3)和栅格(7, 14), 分别用红色圆圈和红色方框表示. AGV2的起点位置和终点位置分别为栅格(17, 13)和栅格(4, 14), 分别用绿色圆圈和绿色方框表示. 红色线段表示AGV1的行驶路线, 绿色线段表示AGV2的行驶路线. 栅格(7, 12)处的字母P表示AGV1到达该栅格后停留了一个单位时间才前往栅格(7, 13), 这样可以避免两辆AGV在栅格(7, 13)发生节点冲突.

|
图 10 双AGV垂直方向行驶路线图 |
图11为AGV1和AGV2按照图10所示的起点和终点沿着垂直方向行驶时的三维时空图, 图11(a)为未使用基于冲突搜索算法进行规划时的时空图, 从图中可以看出两条线段在(7, 13, 10)处有交叉, 即当t=10时, 两辆AGV在栅格(7, 13)处发生了碰撞. 图11(b)为使用基于冲突搜索算法规划后的时空图, 从图中可以看出两条线段无交叉, 表示AGV2的绿色线段未发生变化, 而表示AGV1的红色线段在t=9后有所改变. AGV1的变化在于当t=10时, AGV1未到达栅格(7, 13), 而是继续停留在栅格(7, 12), 等待AGV2通过栅格(7, 13)后才离开, 因此两辆AGV未发生冲突. 与相向冲突的解决方式同理, 算法的上层检测到冲突<A1, A2, (7, 13), 10>, 然后给AGV1添加新的约束<A1, (7, 13), 10>, 为了满足AGV1的约束, 算法下层为其重新规划了满足约束的路径. 由此可以看出, 节点冲突在使用基于冲突搜索的多AGV路径规划算法后也可以得到有效解决.

|
图 11 双AGV垂直方向行驶三维时空图 |
4.3 多种冲突并存的仿真实验
本节仿真实验用于验证算法在多种冲突并存情形下的有效性, 仿真实例中共有8辆AGV同时运行, 每辆AGV的编号、起点栅格坐标、终点栅格坐标和被标识的颜色如表1所示.
| 表 1 各AGV对应信息表 |
图12和图13分别为使用基于冲突搜索算法前后8辆AGV的行驶路线图. 图12中每个AGV都从给定的起点出发前往对应的终点, 图中不同的颜色对应不同的AGV, 圆形表示AGV的起点, 方框表示AGV的终点, 红色六角星表示该处有冲突发生.
图12所示的8条行驶路线对应的三维时空图如图14 (a)所示. 图14 (a)中的8条路径在时空中存在5个交叉点, 对应了图12中的5个红色六角星, 表示发生了5次冲突. 结合这两张图可以看出, 当t=7时, AGV1和AGV2在栅格(10, 10)发生冲突, AGV7和AGV8在栅格(10, 16)发生冲突; 当t=11时, AGV3和AGV4在栅格(10, 16)发生冲突; 当t=15.5时, AGV6和AGV7在栅格(4, 18)和栅格(4, 19)中间发生冲突; 当t=20时, AGV5和AGV6在栅格(4, 14)发生冲突.
采用基于冲突搜索算法规划的8条路线如图13所示, 从图中可以看出使用算法规划后的路径成功避免了上述的5处冲突. 图13中的8条路径对应的三维时空图为图14(b). 从图14(b)中也可以看出任意两条路径在时空中均无黑色交叉点, 说明路径间无冲突. 结合两张图可以看出AGV2、AGV3、AGV5和AGV8的路径没有改动, 而AGV1、AGV4、AGV6和AGV7的路径为避免冲突发生了变化.

|
图 12 算法使用前的多AGV路线图 |

|
图 13 算法使用后的多AGV路线图 |
算法的上层检测到5处冲突<A1, A2, (10, 10), 7>、<A7, A8, (10, 16), 7>、<A3, A4, (7, 14), 11>、<A6, A7, [(4, 19), (4, 18)], 15.5>和<A5, A6, (4, 14), 20>后, 施加对应的5个约束<A1, (10, 10), 7>、<A7, (10, 16), 7>、<A4, (7, 14), 11>、算法的下层根据AGV1、AGV4、AGV6和AGV7新添加的约束为它们重新规划了路径, 因此这4个AGV的路径有所变化. 由此可以看出, 当多种冲突并存且AGV数量较多时, 基于冲突搜索算法也可以有效解决.

|
图 14 多AGV三维时空图 |
5 结论
本文从物流分拣中心场地的特性出发, 选择栅格地图法作为多AGV路径规划的地图建模方法. 采用四邻域搜索方式实现了单AGV路径规划. 为解决多AGV无冲突路径规划问题, 提出在传统A*算法中加入时间维度升级为时空A*算法, 进一步将其作为基于冲突搜索的多AGV路径规划算法的下层规划器. 通过仿真实验验证了所提出的基于冲突搜索的多AGV路径规划算法能够有效解决节点冲突、相向冲突和多种冲突并存的情况. 下一步研究的重点将聚焦在利用时空A*算法进行实际场景测试与系统开发上面, 同时也将与相关算法进行性能对比分析.
| [1] |
Reem K, Alan E, Alejandro T. Two-stage sort planning for express parcel delivery. IIE Transactions, 2021, 53(12): 1353-1368. |
| [2] |
Fazlollahtabar H, Saidi-Mehrabad M. Methodologies to optimize automated guided vehicle scheduling and routing problems: A review study. Journal of Intelligent & Robotic Systems, 2015, 77(3): 525-545. |
| [3] |
Langevin A, Lauzon D, Riopel D. Dispatching, routing, and scheduling of two automated guided vehicles in a flexible manufacturing system. International Journal of Flexible Manufacturing Systems, 1996, 8(3): 247-262. DOI:10.1007/BF00403127 |
| [4] |
Desaulniers G, Langevin A, Riopel D, et al. Dispatching and conflict-free routing of automated guided vehicles: An exact approach. International Journal of Flexible Manufacturing Systems, 2003, 15(4): 309-331. DOI:10.1023/B:FLEX.0000036032.41757.3d |
| [5] |
王保剑, 胡大裟, 蒋玉明. 改进A*算法在路径规划中的应用
. 计算机工程与应用, 2021, 57(12): 243-247. DOI:10.3778/j.issn.1002-8331.2008-0099 |
| [6] |
张金越, 侯至丞, 张弓, 等. 基于交通约束及多元启发函数的改进A*算法
. 组合机床与自动化加工技术, 2021(1): 53-56. |
| [7] |
李强, 于振中, 樊启高, 等. 基于改进A*算法在AGV路径规划中的应用
. 组合机床与自动化加工技术, 2019(5): 98-101. |
| [8] |
张阳伟,乔越,李成凤. 基于四叉树栅格环境的变步长双向A*算法. 控制工程, 2021, 28(10): 1960-1966. DOI:10.14107/j.cnki.kzgc.20200115. |
| [9] |
李鑫, 廖凯文, 陈薇, 等. 多自动导引车路径规划的时空冲突约束A*算法
. 计算机集成制造系统, 2021, 27(11): 3219-3226. |
| [10] |
张原, 陈宇轩, 魏璐璐. 基于改进A*算法的AGV智能泊车算法
. 计算机系统应用, 2019, 28(1): 216-221. DOI:10.15888/j.cnki.csa.006712 |
| [11] |
Min HT, Xiong XY, Wang PY, et al. Autonomous driving path planning algorithm based on improved A* algorithm in unstructured environment. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 2020, 235(2–3): 513–526.
|
| [12] |
Foead D, Ghifari A, Kusuma MB, et al. A systematic literature review of A* pathfinding. Procedia Computer Science, 2021, 179: 507-514. DOI:10.1016/j.procs.2021.01.034 |
| [13] |
Yang YS, Zhong MS, Dessouky Y, et al. An integrated scheduling method for AGV routing in automated container terminals. Computers & Industrial Engineering, 2018, 126: 482-493. |
| [14] |
Zou WQ, Pan QK, Meng T, et al. An effective discrete artificial bee colony algorithm for multi-AGVs dispatching problem in a matrix manufacturing workshop. Expert Systems with Applications, 2020, 161: 113675. DOI:10.1016/j.eswa.2020.113675 |
| [15] |
Zou WQ, Pan QK, Tasgetiren MF. An effective iterated greedy algorithm for solving a multi-compartment AGV scheduling problem in a matrix manufacturing workshop. Applied Soft Computing, 2021, 99: 106945. DOI:10.1016/j.asoc.2020.106945 |
| [16] |
叶杭璐, 何利力. 基于改进蚁群算法的智慧物流调度规划. 计算机系统应用, 2021, 30(1): 207-213. DOI:10.15888/j.cnki.csa.007802 |
| [17] |
陈学松, 杨宜民. 强化学习研究综述. 计算机应用研究, 2010, 27(8): 2834-2838, 2844. DOI:10.3969/j.issn.1001-3695.2010.08.006 |
| [18] |
Srivastava SC, Choudhary AK, Kumar S, et al. Development of an intelligent agent-based AGV controller for a flexible manufacturing system. The International Journal of Advanced Manufacturing Technology, 2008, 36(7): 780-797. |
| [19] |
刘辉, 肖克, 王京擘. 基于多智能体强化学习的多AGV路径规划方法. 自动化与仪表, 2020, 35(2): 84-89. |
| [20] |
Ashayeri J, Gelders LF. Interactive GPSS-PC program generator for automated material handling systems. The International Journal of Advanced Manufacturing Technology, 1987, 2(4): 63-77. DOI:10.1007/BF02601493 |
| [21] |
Um I, Cheon H, Lee H. The simulation design and analysis of a flexible manufacturing system with automated guided vehicle system. Journal of Manufacturing Systems, 2009, 28(4): 115-122. DOI:10.1016/j.jmsy.2010.06.001 |
| [22] |
Kim KS, Chung BD, Jae M. A design for a tandem AGVS with multi-load AGVs. The International Journal of Advanced Manufacturing Technology, 2003, 22(9): 744-752. |
| [23] |
Yu JJ, LaValle SM. Optimal Multirobot Path Planning on Graphs: Complete Algorithms and Effective Heuristics. IEEE Transactions on Robotics, 2016, 32(5): 1163-1177. DOI:10.1109/TRO.2016.2593448 |
| [24] |
Sharon G, Stern R, Felner A, et al. Conflict-based search for optimal multi-agent pathfinding. Artificial Intelligence, 2015, 219: 40-66. DOI:10.1016/j.artint.2014.11.006 |
 2022, Vol. 31
2022, Vol. 31



