脑胶质瘤(glioma)是中枢神经系统中最常见的原发性肿瘤^[1]. 成年人中, 脑胶质瘤占所有脑肿瘤的30%~40%, 占脑部恶性肿瘤的80%左右^[2]. 世界卫生组织(world health organization, WHO)中枢神经系统肿瘤分类将胶质瘤分为I~IV级, 其中I、II级为低级别脑胶质瘤(low grade glioma, LGG), III、IV级为高级别脑胶质瘤(high grade glioma, HGG). 我国脑胶质瘤发病率为每10万人有5~8人, 5年病死率在全身肿瘤中仅次于胰腺癌和肺癌^[3].

磁共振成像(magnetic resonance imaging, MRI)具有无辐射损伤、高对比度等多种特点, 使得它成为了非侵入式鉴别脑肿瘤的重要技术之一, 广泛应用于临床检测^[4]. 目前, MRI的4种成像技术常用于胶质瘤的临床诊断, 分别为平扫T1加权(T1-weighted MRI, T1)、对比增强T1加权(T1-weighted MRI with gadolinium enhancing contrast, T1c)、T2加权成像(T2-weighted MRI, T2)和液体衰减反转恢复的T2加权成像(T2-weighted MRI with fluid-attenuated inversion recovery, FLAIR). 不同成像模态能够提供各方面的信息来分析脑肿瘤信息, 临床上通常结合以上4种图像共同诊断脑肿瘤出血、坏死、水肿等病灶组织的信号强度、占位情况, 确定肿瘤病变的侵袭范围^[5]. 由于脑部MRI序列图像的数据量庞大, 人工分割不仅费时而且效率低下, 并且人工分割的结果受医生的专业知识和操作熟练度的影响, 可能会产生较大差异的结果. 因此, 脑肿瘤分割仍然是一项艰巨的任务^[6].

近年来, 对MRI影像中脑肿瘤病灶进行分割的研究是脑胶质瘤影像辅助诊断治疗的热点之一^[7]. 常见的脑肿瘤MRI图像分割方法主要分为以下几类方法: 基于阈值的分割方法^[8,9]、基于区域增长的分割方法^[10,11]、基于机器学习的分割方法^[12-14]、基于深度学习的分割方法等^[5,15,16]. 基于阈值的分割方法通过将图像的灰度值与阈值进行比较, 从而实现图像的分割. 但是这种方法需要人为的设置阈值, 容易产生过分割或欠分割. 基于区域生长的分割方法实现简单, 对灰度单一, 纹理清晰的图像分割结果较好, 但是容易受到局部噪声和不均灰度的影响导致过度分割. 基于机器学习的分割方法通过人工构造特征, 然后利用随机森林^[17]或支持向量机^[18]等分类器进行分类. Nabizadeh等^[19]通过提取统计特征、纹理特征和Gabor特征, 然后利用SVM对其进行分类, 得到最终的分割结果. 但是在特征提取阶段, 只在单个空间域或者频域上提取特征, 如果只考虑到单个领域的信息, 有可能会丢失其他领域中某种重要的信息.

目前, 深度学习已广泛应用于医学图像处理当中. Long等^[20]提出了全卷积神经网络(fully convolutional neural networks, FCNN), 通过利用卷积层替代了卷积神经网络(convolutional neural networks, CNN)中的全连接层, 实现从图像级分类到像素级分类的转化. Ronneberger等^[21]对FCN进行了网络结构改进提出了U-Net网络, 通过利用跳跃连接的方式将图像的深层信息和浅层信息相结合, 实现了对医学图像分割, 夺得了2019年脑肿瘤挑战赛冠军. Huang等^[22]利用DenseNet和注意力机制改进卷积神经网络, 获得了较好的结果. 虽然基于深度学习的分割方法能够获得较好的分割结果, 但是需要依赖大量的标记数据进行训练. 然而在医学图像的分割任务中, 对数据集进行人工标注不仅费用高昂而且需要大量的时间与精力, 并且对标注人员还要求具有相关的专业技术, 因此无法获得大量的标注数据.

半监督学习^[23]是介于传统监督学习和无监督学习之间的一种机器学习方法. 其思想是在标注样本数量较少的情况下, 通过利用大量的无标注样本对模型进行训练, 从而解决监督学习中训练样本不足的问题. 它的核心问题是先验假设的一致性, 其一是距离较近的样本较大可能具有相同的标签; 其二就是流形假设, 即假设数据分布在一个流形结构上, 邻近的样本拥有相似的输出值. 在标记样本很少的情况下, 通过在模型训练中引入无标记样本来避免传统监督学习在训练样本不足时出现性能退化的问题. 一方面解决了获取标记样本成本过高的问题, 另一方面能够取得与传统监督学习算法相近甚至更好的效果. 图半监督学习作为半监督学习中的一种分支, 通过将少量的标注样本和大量的无标注样本构造成图, 然后将图中的无标注样本进行标注. Zhou等^[24]利用拉普拉斯矩阵, 将无标注样本进行传播, 对其进行标注. Iscen等^[25]通过利用最小化信息熵获得置信度高的预测分布作为伪标签, 并作为标准交叉熵损失来训练目标.

综上, 针对脑肿瘤的分割任务, 本文提出了一种局部-全局自适应信息学习分割算法. 通过利用空间域和频域相结合的方法对4个模态分别提取特征, 得到增强特征用于表达脑部结构信息; 并将4个模态提取到的特征进行融合, 得到最终的融合特征; 采用 ALGIL算法, 可以用于标注数据较少的分割任务当中. 本文首先利用小波变换将图像从空间域变换到频域当中, 从低频和高频中提取统计特征和纹理特征; 通过从专家的粗略标注结果中随机选取标注数据, 利用随机森林算法生成最终的特征集并且获得特征权重; 利用ALGIL算法, 通过将随机森林算法得到的特征权重对图像进行加权构造相似性矩阵, 然后利用指数衰减函数自适应调整初始标注样本对算法的影响程度获得最终的分割结果. 实验结果表明该方法在减少标注数据的同时保证肿瘤分割的精度, 显著提高图像分割效率, 所产生的量化指标为脑胶质瘤核磁的早期临床诊断提供了依据.

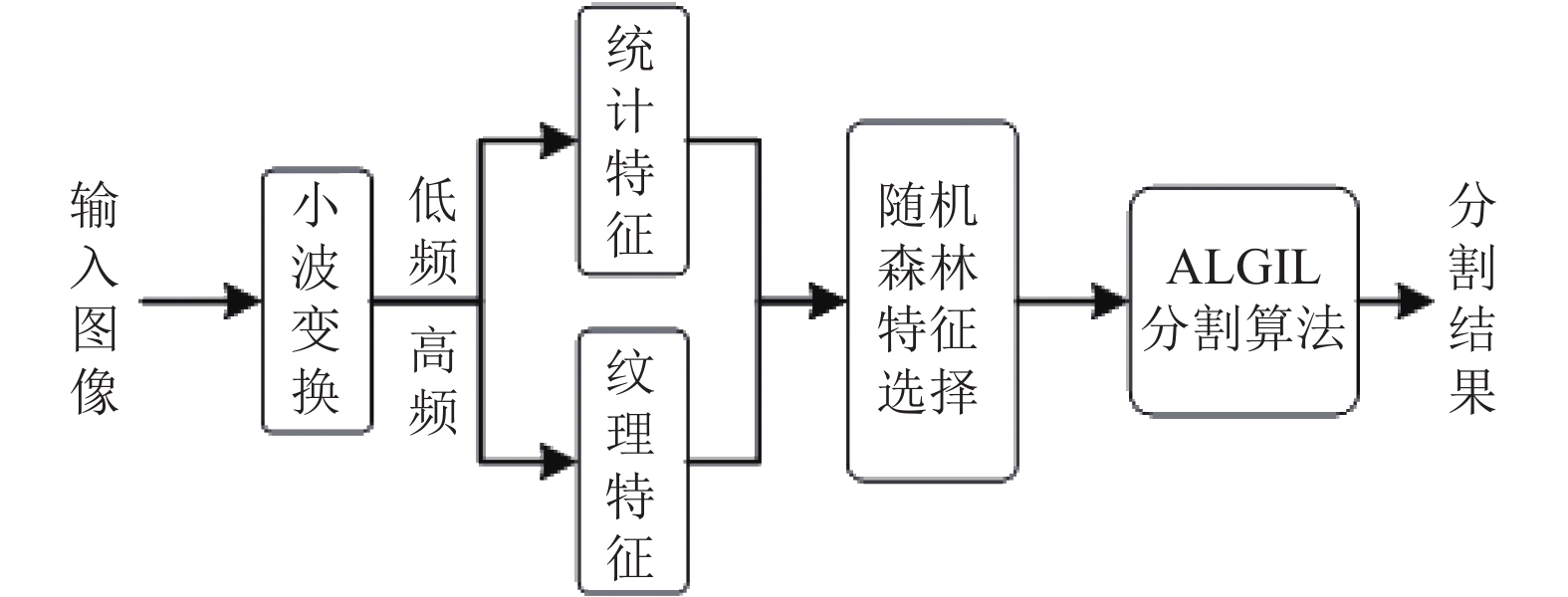
1 本文方法

为了解决上述的问题, 本文提出一种局部-全局自适应信息学习分割算法, 包括特征提取、特征选择以及ALGIL算法. 本文提出的方法的流程如图1所示.

如图1所示, 首先利用小波变换将图像从空间域转化到频域, 将图像分解为1个低频子带和3个高频子带; 然后从低频子带中提取统计特征, 从3个高频子带中提取纹理特征, 将提取到的特征进行融合; 接着利用随机森林算法对提取到的特征进行选择, 得到最终的特征子集和特征权重; 最后利用ALGIL算法, 利用特征权重对图像进行加权构造相似性矩阵, 并且使用指数衰减函数自适应调整初始标注数据对算法的影响程度, 得到肿瘤分割结果.

1.1 空间域和频域相结合的特征提取方法

基于影像组学的脑胶质瘤特征提取是进行脑胶质瘤分割的关键一步. 对于传统的特征提取方法来说, 仅考虑单个领域里的特征信息, 并没有考虑到不同领域直接是否存在着某种联系. 并且如果仅考虑单个元素, 会忽视元素和邻域元素之间的关系. 因此本文提出小波统计纹理特征(wavelet statistical texture feature)提取方法. 通过利用小波变换将图像从空间域变换到频域上, 然后用大小为5×5的窗口分别从低频和高频处提取相应的空间信息. 本文总共从MRI图像中提取了224个定量图像特征, 分别为小波统计特征(wavelet statistical features, WSF)和小波纹理特征(wavelet texture features, WTF).

小波变换^[26]具有多分辨率分析的特征, 能够将图像从空间域转换为频域, 并且可以在不同尺度下对图像进行分解和可视化. 离散小波变换的定义如下:

$ {W_{j, k}}(t){\text{ = }}{2^{\frac{{ - j}}{2}}}\partial ({2^{ - j}}t - k) $

(1)

其中, $ j, k \in Z $ , $ j $ 表示小波函数在频域上的伸缩, $ k $ 表示小波函数的平移, $ \partial (t) $ 表示小波函数. 在二维小波变换中, 图像由1个近似图像和3个细节图像表示, 分别代表图像的低频和高频信息. 图2(a)为经过二维离散小波变换的分解过程, 经过一次离散小波变换图像被分解为4个子带. LL代表经过两层离散小波分解后的低频部分, LH, HL, HH分别代表水平、垂直和对角方向的细节, 是图像的高频部分.

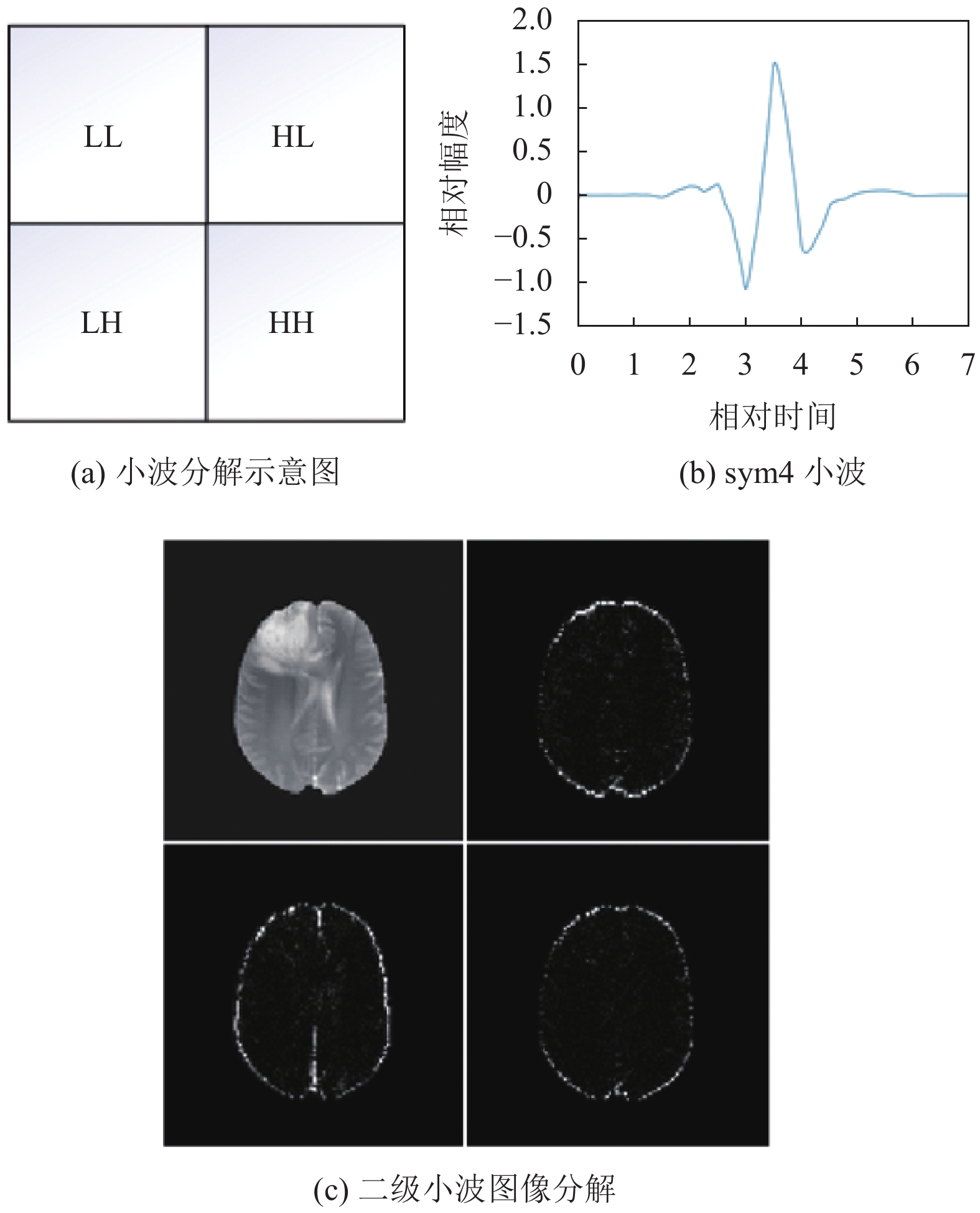
本文重构所采用的小波为Symlet小波, 该小波为双正交小波, 近似对称, 可以应用于离散小波变换. 通过实验, 本文采用sym4小波函数作为小波母函数, 对MRI图像进行分解, 小波母函数图形如图2(b)所示. 图2(c)表示为分解后的各个子带的图像. WSF从小波的低频子带中提取, WTF则从高频子带中提取.

1.1.1 小波变换的统计特征提取

在经过离散小波变换以后, 将图像分解为低频和高频两个部分, 强度特征能够直接反应图像的物理特性. 因此本文从4个模态的MRI图像的LL子带中提取小波统计特征, 分别为均值、最大值、最小值、中值、方差、标准差、偏度、峰度. 最后获得32维特征向量.

1.1.2 小波变换的纹理特征提取

小波纹理特征则通过高频子带借助灰度共生矩阵(gray level co-occurrence matrix, GLCM)得到的. GLCM通过计算像素相对距离( $ d = 1 $ )和4个不同的方向( $\theta = {0^\circ }, $ $ {45^\circ }, {90^\circ }, {135^\circ }$ ), 并且对原始图像灰度级量化成16级得到的. 计算出的12个Haralick纹理特征为: 对比度、相关性、能量、同质性、角二阶矩、方差、差异性、熵、自相关、共生和方差、共生和熵、共生差方差. 最后获得192维特征向量.

1.2 随机森林特征选择

特征之间的相关性和冗余性会降低分类的准确率, 并且特征过多将会提高分类器的复杂度, 造成过拟合, 降低分类器的泛化能力, 因此需要对特征集合进行选择和优化. 随机森林是一种集成的机器学习方法, 通过利用Bootstrap抽样技术生成不同的特征子集, 利用不同的特征子集训练生成不同的决策树. 对于每棵树给出最优的分类结果, 最终结果为k棵决策树中得票最多的选择.

由于利用Bootstrap抽样技术, 因此会有部分样本没有被选到, 这部分样本被称为“out of bag (OOB)”. 对于样本 $ ({x_n}, {y_n}) $ 中, OOB样本数量大约为 $ {(1 - 1/N)^N} $ . 因为OOB样本集能够用来当作测试集, OOB误差被用作验证随机森林的泛化误差, 公式如下:

$ {E_{\rm oob}}(G) = \frac{1}{N}\sum\nolimits_{n = 1}^N {err} ({y_n}, G_n^ - ({x_n})) $

(2)

其中, ${E}_{\rm oob}(G)$ 为加入噪声以后的OOB误差. 每个特征参数的最终重要度得分是所有树的平均值:

$ VI({x_j}) = \frac{{\displaystyle\sum\nolimits_{t = 1}^N {V{I^{(t)}}({x_j})} }}{N} $

(3)

其中, $ N $ 为决策树的数量. 通过最后得到的特征的重要性程度进行排序, 取重要性程度较高的部分特征作为最终的特征子集. 本文中最终从224维特征中选择了32维特征作为最终的特征子集.

1.3 局部-全局自适应信息学习分割算法

为了解决医学图像中标注信息过少的问题, 本文提出了一种自适应的局部-全局信息学习分割算法. 该算法基于特征加权的思想, 通过从随机森林获得的特征权重, 利用权重向量构造相似性矩阵, 并且引入指数衰减函数自适应调整标签对算法的影响程度. 该算法的过程如下:

假设样本集为 $ X = \left\{ {{x_1}, \cdots, {x_m}, {x_{m + 1}}, \cdots, {x_n}} \right\} \subset R $ , 样本标签为 $ L = \left\{ {1, \cdots, c} \right\} $ . 记有标签的数据为 $ {X_l}\left( {l < m} \right) $ , 无标签的数据为 $ {X_u}\left( {m + 1 < u \leqslant n} \right) $ . 定义一个one-hot矩阵 $ {Y_{nc}} $ 来标记初始信息, 如果样本 $ {x_i} $ 的标签为 $ {y_j} $ , 则 $ {Y_{ij}}{\text{ = }}1 $ , 否则 $ {Y_{ij}}{\text{ = }}0 $ ; 且未标注的样本 $ {Y_{ij}} $ 为零向量.

1)首先利用随机森林算法得到的特征的重要性程度, 然后利用 ${{\rm{e}}^{{x_j}}}/\displaystyle\sum\nolimits_{i = 1}^n {{{\rm{e}}^{{x_i}}}}$ 对权重向量进行归一化, 得到权重向量 $w, \displaystyle\sum\nolimits_{i = 1}^n {{w_i} = 1}$ . 利用高斯核函数与权重向量构造一个样本间的相似性矩阵 $ W $ , 当 $ i \ne j $ 时 $ {W_{ij}} = \exp $ $ \left( { - d{{\left( {{x_i}, {x_j}} \right)}^2}/2{\sigma ^2}} \right){w_i} $ , 并且令样本本身的值为0. 其中x_i, x_j为样本, $ \sigma $ 为常数.

2) 计算W的对角矩阵D, ${D_{ii}} = \displaystyle\sum\nolimits_{j = 1}^n {{W_{ij}}}$ , 即计算矩阵W的第i行之和. 然后建立矩阵 $ S = {D^{ - 1/2}}W{D^{ - 1/2}} $ .

3)初始化 $ F\left( 0 \right) = Y $ , 利用迭代对无标注的样本进行标注并更新, 迭代公式如下:

$ F\left( {t + 1} \right) = \left( {1 - \exp \left( { - ut} \right)} \right)QF\left( t \right) + \exp \left( { - ut} \right)Y $

(4)

其中, $ \exp \left( { - ut} \right) $ 为指数衰减函数, u为衰减权重, 本文设置为0.2, t为迭代次数. 为了自适应调整初始标签对模型的影响, 通过设置指数衰减函数, 在迭代初期, 为了使模型保持良好的准确率, 初始标签的权重较高; 随着迭代次数的增加, 模型趋于稳定, 初始标签的权重也随之减小.

4) $ {F^{\text{*}}} $ 代表式(4)在迭代一定次数后收敛的结果, 则 $ {x_i} $ 的标签为:

$ {y_i} = \mathop {\arg \max }\limits_{y \leqslant c} F_{_{ij}}^* $

(5)

2 实验与结果分析

本文构建了基于定量影像组学的肿瘤分割方法, 首先对数据集进行预处理; 然后通过空间域和频域相结合的方法提取图像的WSF和WTF特征, 利用随机森林选取最终的特征子集和特征权重; 最后利用ALGIL算法对肿瘤进行分类, 得到最终的分割结果. 在标注数据的选取方面, 由于精确的标注数据不仅费时, 而且需要消耗标注人员的大量精力, 而粗略的勾画对标注人员来说只需要少量的时间并且不需要太多的精力就能够完成. 因此本文在选取标注样本时, 在保证勾画的类别没有错误的前提下让专家对每个病例的2–3张MRI图像进行粗略勾画. 为了降低样本不平衡带来的影响, 在初始选取标注样本时对正常区域的选取比例变大, 增加正常区域的标注样本. 为了验证本文方法的有效性, 本文通过一系列的对比实验进行比较, 分别通过改变初始标记的样本个数以及改变模型的迭代次数. 此外, 本文还通过与其他方法进行比较来验证本文提出的性能.

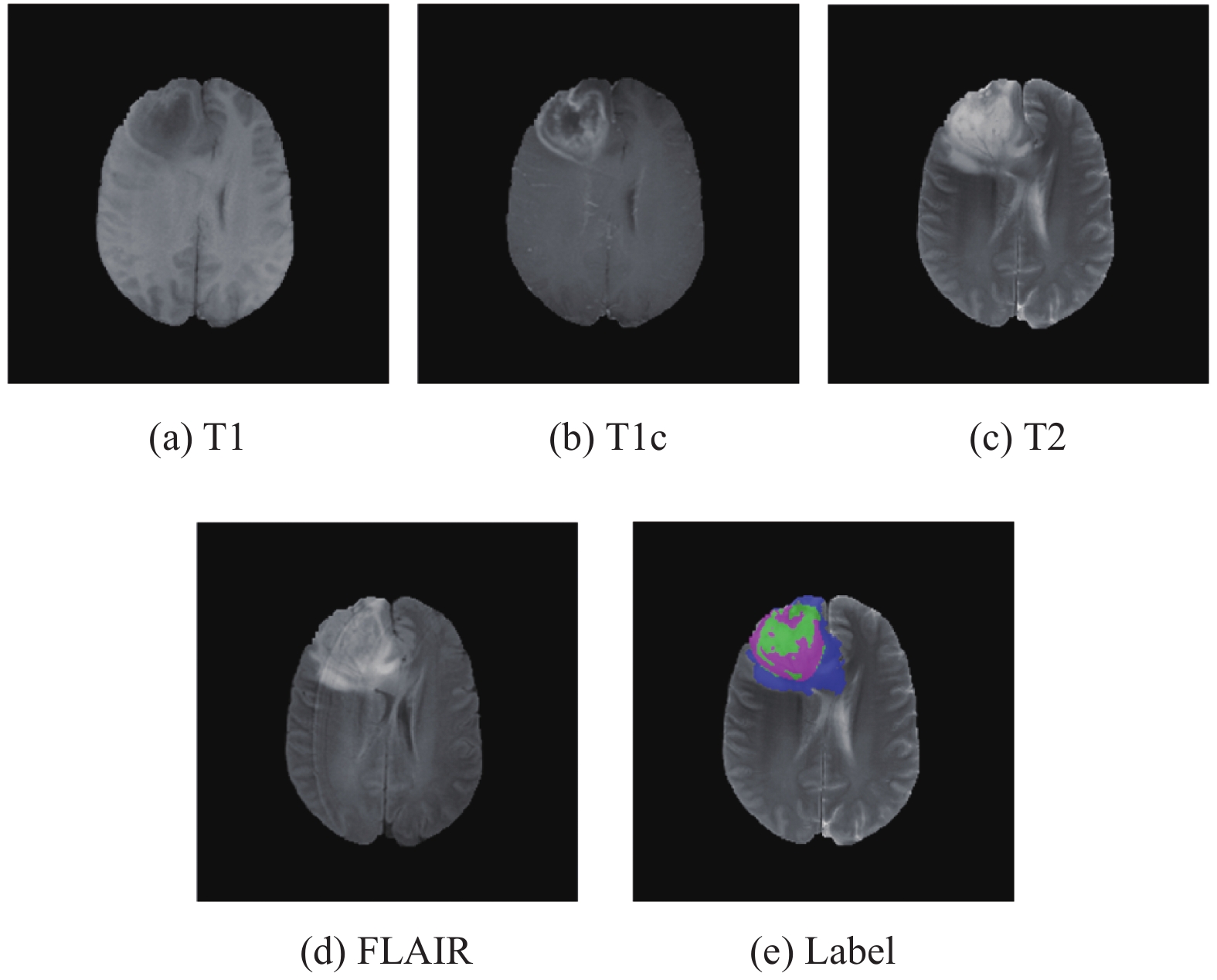
2.1 Brats数据集

本文实验使用的数据集来源于脑肿瘤公开数据集Brats2018, 该数据集由训练集、验证集和测试集组成. 其中, 训练集包含210例高级别肿瘤病例和75例低级别肿瘤病例, 并且提供了相应的分割结果. 每个病人影像分别由T1、T1c、T2和FLAIR四种序列以及专家手动标注的标签组成. 标签将脑胶质瘤划分为3个区域, 分别为: 整体肿瘤(whole tumor, WT)、肿瘤核心(tumor core, TC)和增强肿瘤核心(enhancing tumor core, ET). 图3为数据集中同一组图像的4种模态的MRI图像以及专家手动标注的标签图像, 其中蓝色部分为水肿区域、粉红色部分为肿瘤核心区域、绿色部分为增强肿瘤区域. 这些数据集是经过预处理后提供的, 即共同注册到相同的解剖模板, 内插到相同的分辨率(1 mm³)和颅骨剥离, 每个MRI序列的大小为240×240×155.

2.2 预处理与后处理

首先由于数据集中4个模态的序列对比度不同, 因此对每个模态的图像除黑色背景以外的区域归一化至 $ \left[ {0, 1} \right] $ , 具体归一化公式为:

$ {X_{\rm norm}} = \frac{{X - {X_{\min }}}}{{{X_{\max }} - {X_{\min }}}} $

(6)

其中, $ {X_{\max }} $ 为MRI图像的最大值, $ {X_{\min }} $ 为MRI图像的最小值. 并且为了得到更为光滑的分割结果, 采用形态学操作对最终的分割结果进行后处理.

2.3 评价指标

为了衡量本文分割方法的准确性, 本文采用Dice、Sensitivity、Hausdorff distance (HD)作为评价指标, 公式分别如下:

Dice相似系数(dice similarity coefficient, DSC)用于衡量两个样本之间的相似程度, 是一种几何相似度度量的指标, DSC值越大说明两个样本的相似性程度越高. 计算公式为:

$ Dice = \frac{{2TP}}{{TP + 2FP + FN}} $

(7)

灵敏度(Sensitivity)表示在所有阳性样本中预测出真阳性所占的比例, 计算公式为:

$ Sensitivity = \frac{{TP}}{{TP + FN}} $

(8)

豪斯多夫距离表示预测结果的边界与专家手动标注的标签边界之间的距离, 是分割误差最大的标志. 预测结果越好, $ {d_H}(A, B) $ 值越小, $ {d_H}(A, B) $ 的定义为:

$ {d_H}(A, B){\text{ = }}\max \left\{ {{{sup }_{a \in \partial A}}{d_m}(a, b), {{sup }_{b \in \partial B}}{d_m}(a, b)} \right\} $

(9)

2.4 初始标注样本对模型性能的影响

为了验证初始标注样本数量对模型性能的影响, 本文通过随机从专家粗略标记的标签中随机抽取样本数进行试验, 并且由于肿瘤与正常组织样本差异过大, 为了解决正常组织样本过多的问题, 本文在样本数量的设置上对正常组织样本的数量有所增加. 本文通过对3种肿瘤样本数量分别设置为10–200, 每次增加10个样本; 正常组织的样本数量设置为2500–5000, 每次增加250个样本. 不同标注样本数量对模型性能的实验结果如图4所示, 其中紫色方柱表示精度, 蓝色折线表示灵敏度. 图5为不同标注样本数量的分割结果对比图.

由图4可知, 模型性能的准确性在0.9以上, 但是不同的标注样本的数量对模型的精度有一定的影响. 因此本文根据实验结果选取肿瘤样本数量为150, 正常组织样本数量为3750.

由图5可以看出, 在初始标注样本数量较少时, 分割效果较差, 有很大一部分的肿瘤被标注成正常组织. 随着初始标注样本的增加, 分割结果越来越接近于专家手动标注的结果.

2.5 与目前先进方法进行比较

为验证本文所提出模型的有效性, 利用Brats2018数据集测试, 测试了该模型在各类分割区域的平均分割精度. 图6为本文分割模型对其中3名病例的4种模态的MRI图像脑肿瘤预测分割结果, 其中图6(a)–图6(d)为4种模态图像, 图6(e)为专家手动标注的标签图, 图6(f)为本文分割模型的预测分割结果.

由图6可见, 本文所提出的分割模型得到的分割结果与专家手动标注的结果相近, 并且对于难以精确分割的增强肿瘤区域, 分割结果也与专家标注的结果较为接近. 表明本文所提出的模型具有较高的稳定性和准确性.

本文分割模型在各个肿瘤区域的分割评价指标如表1所示. 本文所提出的分割模型在各肿瘤区域的分割效果都达到了令人满意的结果, Dice相似系数与灵敏度均高于0.8. 其中, 整体肿瘤的Dice相似系数与灵敏度均高于肿瘤核心与增强肿瘤核心, 说明自动分割结果与标注结果的内部相似性较高, 但HD95较高, 这可能是由于肿瘤浸润导致边缘模糊, 使分割结果与标注结果的形状相似性较差. 而相对于整体肿瘤和肿瘤核心, 对增强肿瘤核心的分割效果较差, 这可能是肿瘤的内部结构复杂, 有坏死、囊变或钙化等成分, 在增强MRI上呈低信号, 而肿瘤实性组织呈高信号, 出现信号不均从而导致增强肿瘤的分割效果较低.

本文分别对Brats2018数据集的分割结果进行定量评价, 由于本文方法需要对每个病例的2–3张肿瘤图像进行粗略标注, 因此本文仅在训练集上进行测试. 本文分别与Aboelenein^[27]提出的HTTU-Net、Gates ^[28]提出的MSCNN、Weninger^[29]提出的3D-Unet三种不同的模型进行比较. 表2为不同模型在不同类型的肿瘤的分割结果的平均指标.

从表2可以看出本文所提出的分割模型所得的脑胶质瘤分割结果在一定程度上优于其他模型. WT、TC和ET的Dice指标都优于其他模型, 分别为0.947、0.849和0.830. 而Sensitivity指标分别为0.921、0.803和0.815. 并且HD指标要优于其他模型, 分别为3.791、2.667和2.036.

本文方法的分割结果与真实数据之间平均Dice指标达到0.875, 平均Sensitivity指标达到0.846, 平均HD95指标达到2.831. 与其他模型相比, 本文方法具有更好的鲁棒性, 每种类型的平均指标相对稳定, 并且相对于其他模型来说, 本文所提出的分割模型为半监督学习的分割方法. 只需要少量的标注样本就能够达到其他监督学习的模型效果. 不仅节省了大量标注所需要的时间, 同时也节省了标注时所需的大量费用.

3 结论与展望

MRI脑肿瘤精确分割对准确的诊断和手术治疗方案具有重要意义. 但是肿瘤的大小、形状、位置和灰度值等特征变化大并且复杂, 而手动分割耗时且会受到主观差异的影响. 因此自动精确分割肿瘤是一项艰巨的任务.

在脑肿瘤分割任务方法中, 本文针对传统机器学习中提取特征单一化的缺陷, 并且针对监督学习中所需标记的样本数据量大, 而无监督学习中分割效果较差等缺陷, 提出了一种基于局部-全局自适应信息学习的分割算法. 本文所提出的方法将空间域和频域结合进行特征提取, 采用随机森林算法获取特征子集及特征权重, 最后通过局部-全局自适应信息学习分割算法对图像进行分割. 实验结果表明, 通过将空间域的图像转化到频域上, 能够更准确地提取图像中的有效信息. 此外本文提出的分割模型相较于普通的全监督学习方法, 在少量标注数据的条件下, 预测结果达到甚至超过全监督方法, 在内部结构更为复杂的TC和ET中分割结果也近似于专家的标注结果.

对于医学图像中标记样本稀缺的情况下, 本文方法利用半监督学习的思想, 仅用少量的标注数据就能够得到较为准确的分割结果. 不仅解决了监督学习中需要大量的标记样本的问题, 还确保了最终分割结果的精度不因为标记样本的减少而下降. 同时本文中也存在些许不足, 例如全连接测量整张图像的像素之间的距离而导致耗时较长; 在标记样本的选取中, 还需要专家对图像进行标注. 为来考虑利用稀疏矩阵的方法构造相似性矩阵, 提升模型的计算速度; 利用无监督聚类的思想对数据集进行初始聚类, 得到聚类中心, 选取置信度高的样本作为标注样本, 省去专家标注的步骤.