2. 河南大学 计算机与信息工程学院, 开封 475001
2. School of Computer and Information Engineering, Henan University, Kaifeng 475001, China
视频目标跟踪是指对图像序列中机动目标进行检测、提取、识别和跟踪, 以获得机动目标位置、速度、加速度、运动轨迹等运动参数, 从而对机动目标进行进一步处理与分析的过程[1]. 随着计算机运算能力和存储能力的迅速发展及大数据分析需求的逐渐增大, 视频跟踪技术在交通控制[2]、视频检索[3]、人机交互[4]等方面有了广泛应用. 早期的目标跟踪算法主要根据目标建模或对目标特征进行跟踪, 主要的方法有基于目标模型建模方法与基于搜索的方法[1]. 特征匹配法是常用的基于目标模型建模方法, 首先提取目标特征, 然后在后续帧中找到最相似的特征进行目标定位; 均值漂移(mean-shift)算法[5]是常用的基于搜索的方法, 该方法利用图像特征构造概率密度函数, 由梯度方向搜索局部最大值作为目标位置. 由于在新近的较有挑战的数据集例如VOT2018或者大规模数据集TrackingNet上, 传统跟踪算法达不到实际要求, 而深度学习因为其强大的特征提取能力以及端对端的训练模式慢慢受到了广泛关注. 近年来越来越多基于深度学习的跟踪方法被相关学者提出, Chao等[6]将深度学习网络及自适用相关滤波器结合, 提出了ECO (efficient convolution operators for tracking)算法, 该算法在速度和精度上都有较好的表现. Wang等[7]使用Transformer[8]深度学习跟踪器将不同时刻视频帧桥连起来, 传递了丰富的时序信息, 该算法在最新数据集上有很高的速度与精度.
在对视频中目标跟踪过程中不可避免会存在目标快速移动问题, 即对视频序列中机动目标进行跟踪时, 如果跟踪目标在前后两视频帧间位移超过20个像素点, 则被认为是快速移动[9]. 此时目标可能超出了搜索范围或移动到了搜索范围边界, 导致丢失目标的情况, 进而跟踪失败. 目标位置预测是解决机动目标快速移动问题的首要难点, 虽然卡尔曼滤波算法可以快速预测目标位置, 但是不能很好地解决机动目标运动过程中存在的非线性情况, 而粒子滤波算法具有解决非线性问题的特性, 对非线性运动过程有较好的预测效果. Nummiaro等[10]提出了基于颜色特征的粒子滤波跟踪(particle filter, PF)算法. PF首先在目标区域提取颜色特征, 然后散播粒子, 计算每个粒子的权重, 最后根据粒子位置及权重预测目标位置. PF提取目标区域颜色特征, 得到丰富的特征信息, 可以有效地对非刚性和快速移动目标进行跟踪, 而且在遮挡以及复杂环境情况下也有较好的鲁棒性. 然后对目标位置进行修正, 为了正确跟踪目标, 修正算法需要有较高的速率及准确率, 深度学习方法准确率高但运行时间过长. Bolme等[11]设计了MOSSE (minimum output of squared error )滤波器, 将计算由时域转换到频域, 提供了运算速度, 对信号相关性的求解保证了算法精度. MOSSE虽然运算速度快, 但不能直接对快速移动的机动目标进行跟踪. Henriques等[12]在MOSSE基础上引入循环矩阵及核函数, 提出CSK (circulant structure of tracking-by-detection with kernels)算法. 精度上相对于MOSSE有了很大提升, 但CSK特征选取比较单一, 而且对快速移动情况没有处理, 很难直接跟踪快速移动的机动目标. Henriques等[13]在CSK的基础上改变灰度特征提取为FHOG特征提取, 同时加入核方法, 提出了KCF (kernel correlation filter)及DCF (dual correlation filter)算法, KCF对应非线性核, DCF对应线性核. Li等[14]在KCF的基础上将单一特征选择扩展为多个特征选择, 并添加了尺度池, 提出了SAMF (scale adaptive with multiple features tracker)算法. SAMF算法虽然精度相对于KCF有些许提升但是速度比较慢, 所以这里选择KCF作为修正算法. 最后针对机动目标在视频中由于快速移动问题导致的形变、模糊问题, 融入零截距以及平均峰值相关能量. 实验结果表明, 新方法在公开数据集OTB100与UA-DETRAC上都有较高的识别率.
2 核相关滤波Danelljan等[15]将相关滤波器的求解转换为岭回归问题进行推导运算, 利用循环矩阵的特性将问题从时域变换到频域进行快速计算, 为了解决高维运算问题引入了核方法. KCF可以分为滤波器模型建立、目标搜索、模板更新3部分.
(1) 滤波器模型建立. 岭回归问题的目标函数为:
| $ f({\mathbf{z}}) = {{\mathbf{w}}^{\text{T}}}{\mathbf{z}} $ | (1) |
需要合适的目标函数使如下残差函数最小:
| $ \mathop {\min }\limits_{\mathbf{w}} \sum\limits_i {\left( {f\left( {{{\mathbf{a}}_i}} \right) - {b_i}} \right)} + \lambda {\left\| {\mathbf{w}} \right\|^2} $ | (2) |
其中,
| $ {\mathbf{w}} = {({{\mathbf{A}}^{\text{H}}}{\mathbf{A}} + \lambda {\mathbf{I}})^{ - 1}}{{\mathbf{A}}^{\text{H}}}{\mathbf{b}} $ | (3) |
其中, A表示样本向量
由于循环矩阵可以通过对角矩阵(
| $ {\mathbf{A}} = {\mathbf{F}}\;{\text{diag}}({\mathbf{\hat a}})\;{{\mathbf{F}}^{\text{H}}} $ | (4) |
式中, F表示与基础向量a无关的常数矩阵,
| $ {\mathbf{\hat w}} = {{{{{\mathbf{\hat a}}}^ * } \otimes {\mathbf{\hat b}}} \mathord{\left/ {\vphantom {{{{{\mathbf{\hat a}}}^ * } \otimes {\mathbf{\hat b}}} {{{{\mathbf{\hat a}}}^ * } \otimes {\mathbf{\hat a}} + \lambda {\mathbf{I}}}}} \right. } {{{{\mathbf{\hat a}}}^ * } \otimes {\mathbf{\hat a}} + \lambda {\mathbf{I}}}} $ | (5) |
其中,
考虑实际中存在非线性问题, 使用核技巧可以将非线性回归问题映射到对偶空间, 使最优化问题依旧是线性的. 假设映射函数为
| $ {\mathbf{w}} = \sum\limits_i {{\alpha _i}} \varphi ({{\mathbf{a}}_i}) $ | (6) |
原本对
| $ {\mathbf{\hat \alpha }} = {{{\mathbf{\hat b}}} \mathord{\left/ {\vphantom {{{\mathbf{\hat b}}} {{{{\mathbf{\hat k}}}^{aa}} + \lambda {\mathbf{I}}}}} \right. } {{{{\mathbf{\hat k}}}^{aa}} + \lambda {\mathbf{I}}}} $ | (7) |
式中, kaz表示核矩阵
(2) 目标搜索. 对响应函数求解得目标位置
| $ {\mathbf{\hat f}}({\mathbf{z}}) = {{\mathbf{\hat k}}^{{{az}}}} \otimes {\mathbf{\hat \alpha }} $ | (8) |
其中, kaz表示基础样本a以及循环移位后训练样本z的核相关运算[17,18].
(3) 模板更新. 更新策略如下:
| $ {\bf{\beta }} = \left( {1 - \mu } \right){{\mathbf{\beta }}_{i - 1}} + \mu {{\mathbf{\beta }}_i} $ | (9) |
式中,
PF可分为模型建立、粒子散播、位置估计3部分.
(1) 模型建立. 首先提取颜色特征来计算颜色直方图[19]
| $ p_{{y_i}}^{({\rm{u}})} = f\sum\limits_{i = 1}^L {k\left( {{{\left\| {{y_i} - {x_0}} \right\|} \mathord{\left/ {\vphantom {{\left\| {{y_i} - {x_0}} \right\|} a}} \right. } a}} \right)} \delta [h({y_i}) - u] $ | (10) |
式中,
| $ k\left( r \right) = \left\{ \begin{array}{l} 1 - {r^2},\;\;\;r < 1 \\ 0,\;\;\;\;\;\;\;\;\;\;\;\;{\text{otherwise}} \\ \end{array} \right. $ | (11) |
其中, r表示像素点与中心的距离. 然后利用颜色直方图计算巴氏系数[20,21]以及巴氏距离:
| $ \rho \left[ {{\mathbf{p}}, {\mathbf{q}}} \right] = \sqrt {{{\mathbf{p}}^{\rm{T}}}{\mathbf{q}}} $ | (12) |
| $ d = \sqrt {1 - \rho \left[ {{\mathbf{p}}, {\mathbf{q}}} \right]} $ | (13) |
(2) 粒子散播. 粒子散播动态模型如下:
| $ {{\mathbf{s}}_t} = {\mathbf{J}}{{\mathbf{s}}_{t - 1}} + {{\mathbf{w}}_{t - 1}} $ | (14) |
式中,
(3) 位置估计. 根据粒子权重及粒子位置集合
| $ E\left[ {{{\mathbf{s}}_t}} \right] = \sum\limits_{n = 1}^N {\pi _t^{\left( n \right)}} s_t^{\left( n \right)} $ | (15) |
其中,
| $ {\pi ^{\left( n \right)}} = {1 \mathord{\left/ {\vphantom {1 {\sqrt {2\pi \sigma } }}} \right. } {\sqrt {2\pi \sigma } }}{{\rm{e}}^{ - {{{d^2}} \mathord{\left/ {\vphantom {{{d^2}} {2{\sigma ^2}}}} \right. } {2{\sigma ^2}}}}} $ | (16) |
结合KCF精度高及PF对快速移动目标跟踪有较好的鲁棒性的优点, 并针对机动目标移动过程中产生的形变、模糊问题, 有机融合PF与KCF, 提出了基于位置一步预测的核相关目标跟踪算法(KCF-PF). KCF-PF在KCF与PF的基础上融入了零截距[22]以及平均峰值相关能量(
为解决形变问题, 首先根据目标区域的色调(H)矩阵求得色调直方图, 然后对其反向投影[24]得到概率(
| $ {\mathbf{prob}}(x, y) = {{his}}({\mathbf{H}}(x, y)) $ | (17) |
其中,
| $ {M_{{\text{00}}}}{\text{ = }}\sum\nolimits_x {\sum\nolimits_y {{\mathbf{prob}}(x, y)} } $ | (18) |
| $ s = k\sqrt {{{{M_{{\text{00}}}}} \mathord{\left/ {\vphantom {{{M_{{\text{00}}}}} {{\text{256}}}}} \right. } {{\text{256}}}}} $ | (19) |
式中, k表示一个大于1的常数,
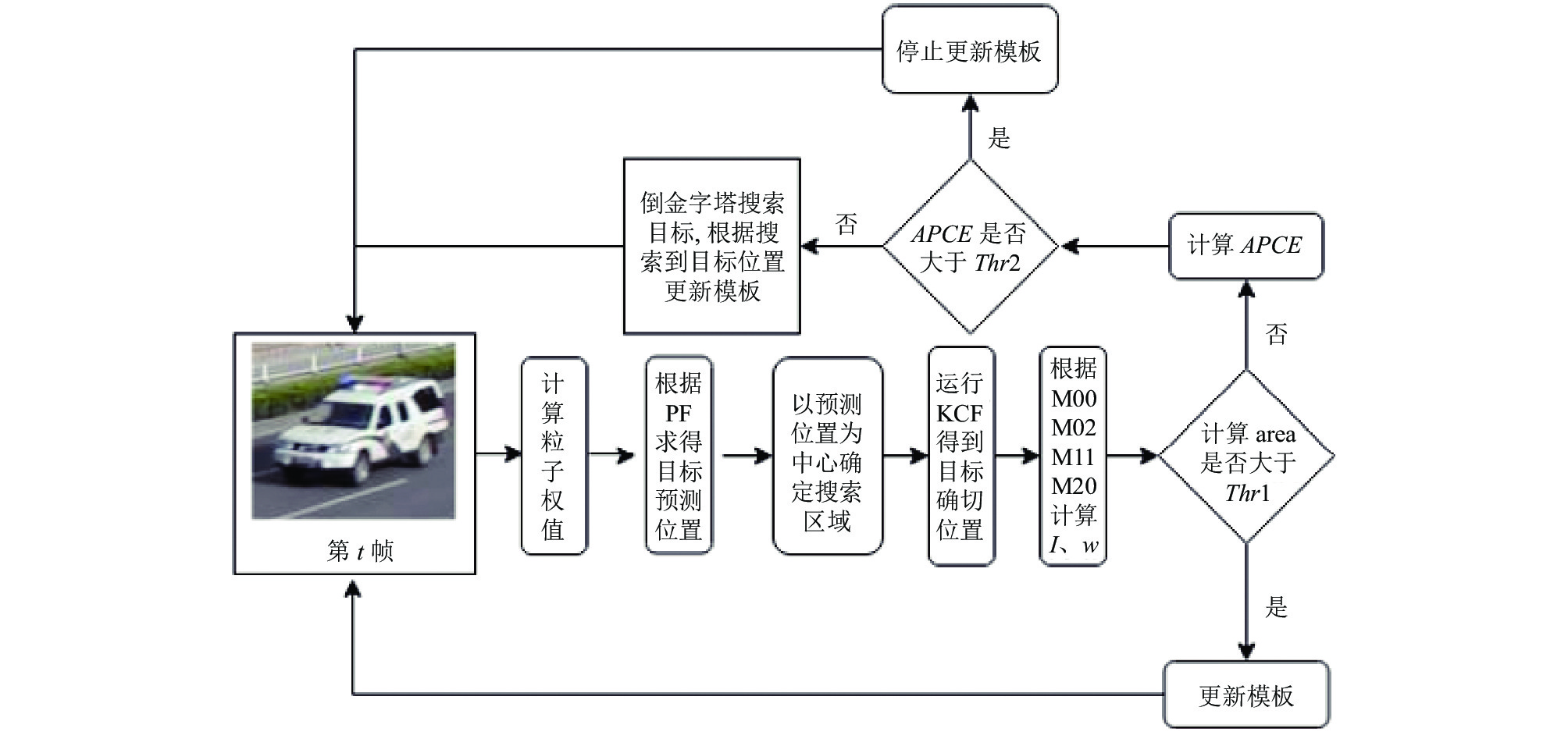
|
图 1 KCF-PF流程图 |
由于机动目标在快速运动过程中很容易出现模糊情况, 如果对此不进行处理, 会在每一帧更新的模板中加入背景扰动, 最终影响跟踪精度. 针对该问题, 首先利用
| $ APCE = {{\left| {{F_{\max }} - {F_{\min }}} \right|} \mathord{\left/ {\vphantom {{\left| {{F_{\max }} - {F_{\min }}} \right|} {mean\left( {\sum\nolimits_{w, h} {{{\left( {{F_{w, h}} - {F_{\min }}} \right)}^2}} } \right)}}} \right. } {mean\left( {\sum\nolimits_{w, h} {{{\left( {{F_{w, h}} - {F_{\min }}} \right)}^2}} } \right)}} $ | (20) |
其中,
然后
考虑到跟踪过程中时间与空间的连续性, 如果仅丢失一帧, 目标不会移动很远, 可以在上帧目标位置周围搜索, 但当连续帧丢失目标时, 目标可能位移到任何位置, 此时需要扩大搜索范围. 传统的遍历搜索方法花费时间长, 为减少重跟踪时长, 将视频帧划分成n个不重叠区域, 用倒金字塔搜索方式进行重跟踪. 倒金字塔搜索方式的迭代公式及步长计算公式如下:
| $ \left\{ \begin{gathered} Pos(x_k^{(i)}, {y^{(i)}}) = Pos(x_{k - 1}^{(i)}, {y^{(i)}}) + \textit{Step}{_i}(x_{\rm step}^{(i)}, 0){\text{ }} \hfill \\ Pos({x^{(i)}}, y_k^{(i)}) = Pos({x^{(i)}}, y_{k - 1}^{(i)}) + \textit{Step}{_i}(0, y_{\rm step}^{(i)}){\text{ }} \hfill \\ \end{gathered} \right. $ | (21) |
| $ \textit{Step}{_n}(x_{\rm step}^{(n)}, y_{\rm step}^{(n)}) = \tau \textit{Step}{_1}(x_{\rm step}^{(1)}, y_{\rm step}^{(1)}) $ | (22) |
其中, x、y表示横纵坐标, 式(21)中的上下两式分别表示沿着x、y方向的搜索迭代公式,
为了更好地解释倒金字塔跟踪方式, 假设只有3个分区, 分区图如图2所示.

|
图 2 倒金字塔搜索方式分区图 |
根据上次正确跟踪地目标位置为中心划分区域, 距离中心越远搜索步长越大, 第一分区是距离目标最近的搜索区域, 在第一分区进行搜索时步长最短. 第二分区步长是第一分区的二倍, 第三分区步长是第二分区的二倍, 公式如下所示:
| $ \left\{ {\begin{array}{*{20}{c}} {\textit{Step}{_2}(x_{\rm step}^{(2)}, y_{\rm step}^{(2)}) = 2\textit{Step}{_1}(x_{\rm step}^{(1)}, y_{\rm step}^{(1)})} \\ {\textit{Step}{_3}(x_{\rm step}^{(3)}, y_{\rm step}^{(3)}) = 4\textit{Step}{_1}(x_{\rm step}^{(1)}, y_{\rm step}^{(1)})} \end{array}} \right. $ | (23) |
为了对KCF-PF算法量化评价, 引入OTB数据集两个评价标准: 精确度(precision plot)以及成功率(success plot), 下面分别对两个评价标准进行简介.
(1) Precision plot: 跟踪过程中, 算法估计出的目标位置称为预测值, 人工标注目标位置为真实值, 两者的差值小于阈值的帧数占总帧数的百分比就是精确度. 一般选择20个像素点作为阈值, 给定的阈值不同, 求出的precision plot也不同.
(2) Success plot: 成功率的计算用到了覆盖率公式:
| $ Cov = {{Area\left( {{B_T} \cap {B_G}} \right)} \mathord{\left/ {\vphantom {{Area\left( {{B_T} \cap {B_G}} \right)} {Area\left( {{B_T} \cup {B_G}} \right)}}} \right. } {Area\left( {{B_T} \cup {B_G}} \right)}} $ | (24) |
其中,
为了更好地验证新方法的准确性, 设置了两组参数在不同的数据集上进行实验, 实验参数如表1所示.
| 表 1 实验参数 |
6.2 模板更新策略的阈值选定实验
Jogging中部分视频帧与

|
图 3 目标状态分析 |
对图3左边跑步女人分析, 第3帧没有遮挡及模糊情况, 此时
根据以上分析, 为了更好地运用历史信息并减少模糊、遮挡的影响, 得到新的模板更新策略如下:
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathbf{mel}} = \left( {1 - \mu } \right){\mathbf{me}}{{\mathbf{l}}_{T - 1}} + \mu {\mathbf{me}}{{\mathbf{l}}_T}},&{APCE \geqslant {\text{30}}} \\ {{\mathbf{mel}} = \left( {1 - 2\mu } \right){\mathbf{me}}{{\mathbf{l}}_{T - 1}} + \mu {\mathbf{me}}{{\mathbf{l}}_T} + \mu {\mathbf{me}}{{\mathbf{l}}_{T - 2}}}, &{{\text{30}} > APCE \geqslant {\text{20}}} \\ {{\mathbf{mel}} = {\mathbf{me}}{{\mathbf{l}}_{T - 1}}},&{APCE < {\text{20}}} \end{array}} \right. $ | (25) |
其中,
|
表 2 目标状态与
|
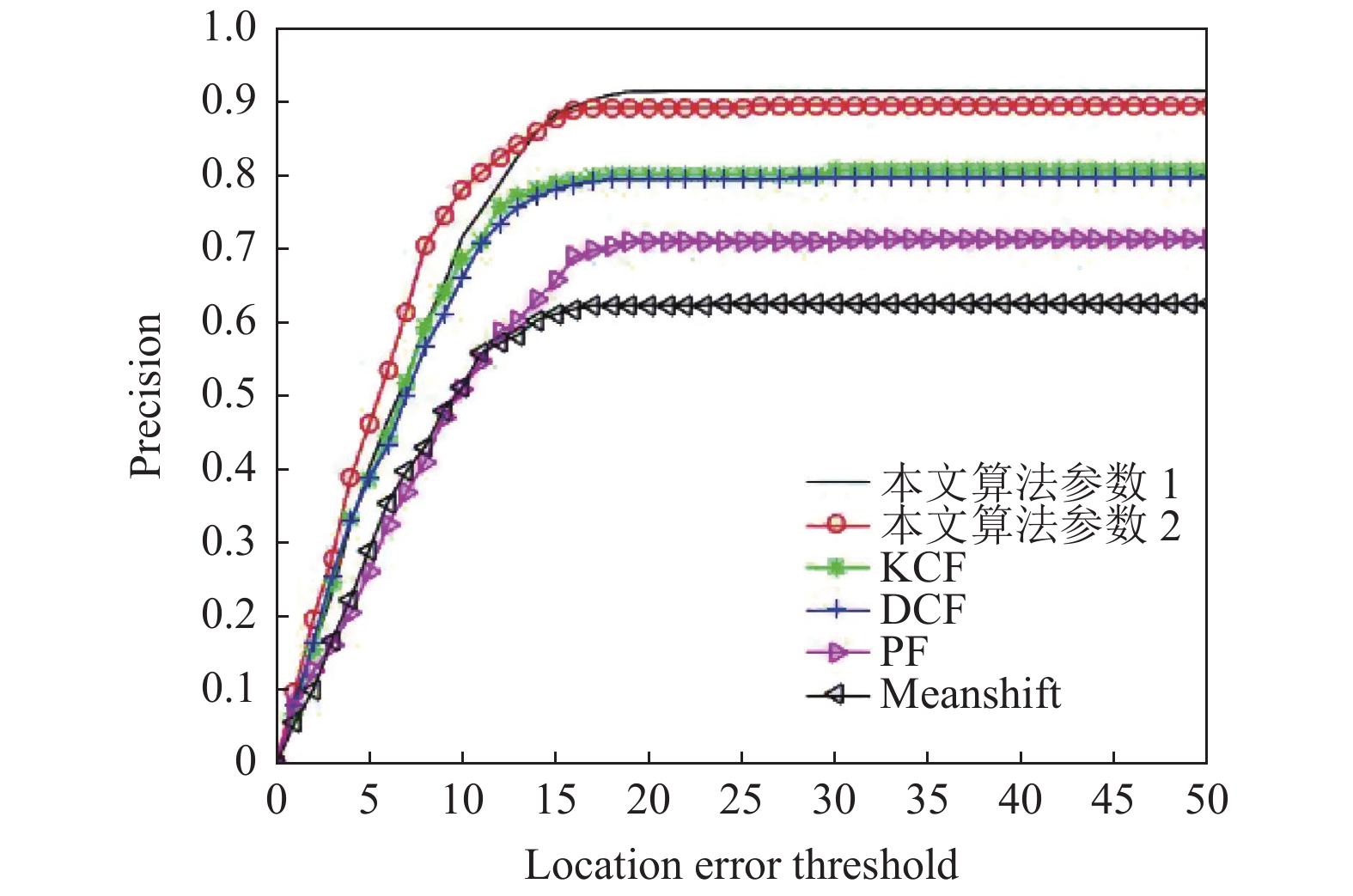
|
图 4 算法性能比较 |
6.3 性能分析
与Meanshift、PF、KCF、SAMF相比, KCF-PF在UA-DETRAC及OTB100数据集上有更高的识别率, 具体提升如表3和表4所示.
6.3.1 定性分析本节选取UA-DETRAC视频数据集中两个视频片段进行定性分析. 图5与图6为跟踪效果图, 其中红色框是KCF-PF, 黄色框是SAMF, 绿色框是KCF, 黑色框是PF, 蓝色框是Meanshift. 由图5与图6可以看出随着目标车辆的快速移动SAMF、KCF、PF、Meanshift都丢失了目标, 而KCF-PF可以对目标准确跟踪.
6.3.2 定量分析本节对UA-DETRAC以及OTB100数据集进行定量分析, 结果如图7所示. 其中图7(a)与图7(b) 是在10个有快速移动情况车辆行驶序列中进行算法对比的结果; 图7(c)与图7(d) 是在25个车辆行驶视频序列中进行算法对比的结果; 图7(e)与图7(f)是在OTB100数据集中算法对比的结果; 图7(g)与图7(h)是在混合了OTB100与UA-DETRAC数据集中算法比较的结果.
| 表 3 UA-DETRAC数据集的实验结果(%) |
| 表 4 混合OTB100与UA-DETRAC数据集的实验结果 |

|
图 5 由远及近车辆跟踪效果 |

|
图 6 侧拍车辆跟踪效果 |
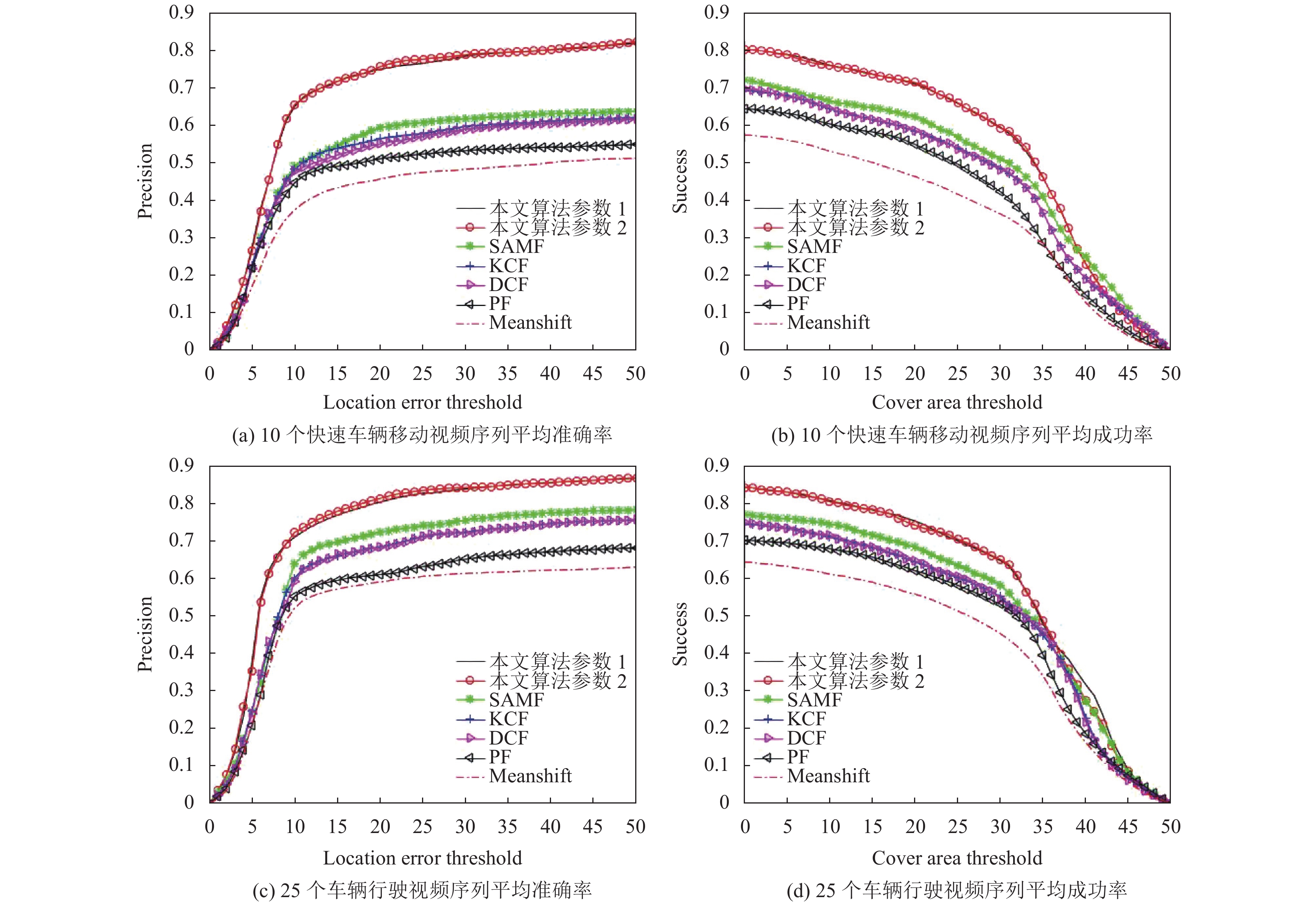
|
图 7 |

|
图 7 定量分析图 |
7 结语
视频机动目标快速移动问题一直是目标跟踪问题中的难点, 结合粒子滤波以及核相关滤波算法的优点, 提出首先由粒子滤波算法预测目标位置, 然后核相关滤波算法修正目标位置的新方法, 在一定程度上解决了快速移动问题. 针对形变问题加入了零截距, 实现了对快速移动形变机动目标的跟踪, 在原模板更新策略的基础上融入平均峰值相关能量, 更好的利用了历史信息. 实验结果表明, 新方法可以有效地跟踪快速移动的机动目标.
| [1] |
孟琭, 杨旭. 目标跟踪算法综述. 自动化学报, 2019, 45(7): 1244-1260. DOI:10.16383/j.aas.c180277 |
| [2] |
王海涛, 王荣耀, 王文皞, 等. 目标跟踪综述. 计算机测量与控制, 2020, 28(4): 1-6, 21. DOI:10.16526/j.cnki.11-4762/tp.2020.04.001 |
| [3] |
苏松志, 李绍滋, 陈淑媛, 等. 行人检测技术综述. 电子学报, 2012, 40(4): 814-820. DOI:10.3969/j.issn.0372-2112.2012.04.031 |
| [4] |
Shajideen SMS, Preetha VH. Hand gestures-virtual mouse for human computer interaction. Proceedings of 2018 International Conference on Smart Systems and Inventive Technology. Trivandrum: IEEE, 2018. 543–546.
|
| [5] |
Comaniciu D, Meer P. Mean shift: A robust approach toward feature space analysis. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(5): 603-619. DOI:10.1109/34.1000236 |
| [6] |
Chao M, Huang JB, Yang XK, et al. Hierarchical convolutional features for visual tracking. Proceedings of 2015 IEEE International Conference on Computer Vision. Santiago: IEEE, 2015. 3074–3082.
|
| [7] |
Wang N, Zhou WG, Wang J, et al. Transformer meets tracker: Exploiting temporal context for robust visual tracking. arXiv: 2103.11681v2, 2021.
|
| [8] |
Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need. Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach: NIPS, 2017. 6000–6010.
|
| [9] |
Wu Y, Lim J, Yang MH. Object tracking benchmark. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(9): 1834-1848. DOI:10.1109/TPAMI.2014.2388226 |
| [10] |
Nummiaro K, Koller-Meier E, Van Gool L. An adaptive color-based particle filter. Image and Vision Computing, 2003, 21(1): 99-110. DOI:10.1016/S0262-8856(02)00129-4 |
| [11] |
Bolme DS, Beveridge JR, Draper BA, et al. Visual object tracking using adaptive correlation filters. Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Francisco: IEEE, 2010. 2544–2550.
|
| [12] |
Henriques JF, Caseiro R, Martins P, et al. Exploiting the circulant structure of tracking-by-detection with kernels. Proceedings of the 12th European Conference on Computer Vision. Florence: Springer, 2012. 702–715.
|
| [13] |
Henriques JF, Caseiro R, Martins P, et al. High-speed tracking with kernelized correlation filters. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2015, 37(3): 583–596.
|
| [14] |
Li Y, Zhu JK. A scale adaptive kernel correlation filter tracker with feature integration. Proceedings of European Conference on Computer Vision. Zurich: Springer, 2014. 254–265.
|
| [15] |
Danelljan M, Khan FS, Felsberg M, et al. Adaptive color attributes for real-time visual tracking. Proceedings of 2014 IEEE Conference on Computer Vision and Pattern Recognition. Columbus: IEEE, 2014. 1090–1097.
|
| [16] |
Rifkin R, Yeo G, Poggio T. Regularized least-squares classification. Nato Science Series Sub Series III Computer and Systems Sciences, 2003, 190: 131-154. |
| [17] |
Galoogahi HK, Sim T, Lucey S. Multi-channel correlation filters. Proceedings of 2013 IEEE International Conference on Computer Vision. Sydney: IEEE, 2013. 3072–3079.
|
| [18] |
Boddeti VN, Kanade T, Kumar BVKV. Correlation filters for object alignment. Proceedings of 2013 IEEE Conference on Computer Vision and Pattern Recognition. Portland: IEEE, 2013. 2291–2298.
|
| [19] |
Zivkovic Z, Krose B. An EM-like algorithm for color-histogram-based object tracking. Proceedings of 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Washington, DC: IEEE, 2004. I–I.
|
| [20] |
Aherne FJ, Thacker NA, Rockett PI. The Bhattacharyya metric as an absolute similarity measure for frequency coded data. Kybernetika, 1998, 34(4): 363-368. |
| [21] |
Kailath T. The divergence and Bhattacharyya distance measures in signal selection. IEEE Transactions on Communication Technology, 1967, 15(1): 52-60. DOI:10.1109/TCOM.1967.1089532 |
| [22] |
Bradski GR. Real time face and object tracking as a component of a perceptual user interface. Proceedings of the 4th IEEE Workshop on Applications of Computer Vision. Princeton: IEEE, 1998. 214–219.
|
| [23] |
Mahalanobis A, Kumar BVKV, Casasent D. Minimum average correlation energy filters. Applied Optics, 1987, 26(17): 3633-3640. DOI:10.1364/AO.26.003633 |
| [24] |
Schiele B, Crowley JL. Recognition without correspondence using multidimensional receptive field histograms. International Journal of Computer Vision, 2000, 36(1): 31-50. DOI:10.1023/A:1008120406972 |
| [25] |
Bradski GR, Clara S. Computer vision face tracking for use in a perceptual user interface. Proceedings of the 4th IEEE Workshop on Applications of Computer Vision. Princeton: 1998. 98–113.
|
 2022, Vol. 31
2022, Vol. 31


