目标跟踪是计算机视觉领域的一个主流方向[1], 而长期目标跟踪因更接近实际应用而受到越来越多的关注[2]. 但对于长期目标跟踪算法中存在的形变、运动模糊、遮挡及目标短暂出视野等问题, 所以, 建立一个同时具有鲁棒性和良好运行速度的长期目标跟踪系统是有必要的.
相关性, 通常是指两种事物中存在的联系. 对于信号处理中的函数来说, 相关即判断两个函数在某时刻的相似程度. 在目标跟踪中, 相关滤波方法的本质就是在运动模型预测的下一帧目标位置中找到与给定目标产生最大响应的区域来作为下一帧中的目标位置. 相关滤波[3]由于其性能优越, 研究者一直对其进行研究. 2010年, 文献[4]首次将相关滤波用于目标跟踪, MOSSE算法也是“相关”思想在目标跟踪中应用的开端, 该算法的目的就是寻找一个能在目标位置响应最大的滤波器, 且使用傅里叶变换将相关运算转换到频域, 很大程度上提高了算法的运行速度. 文献[5]提出了CSK算法, 利用循环矩阵的特性达到了密集采样的目的, 增加了样本的可分性. 随后, 文献[6]提出KCF (kernelized correlation filter)算法, 它拓宽了已有算法所使用的特征范围, 选择了对方向敏感的方向梯度直方图特征, 提高了算法的精度. 同时文献[7]提出一种利用颜色特征的目标跟踪算法, 也获得不错的效果. 随着深度学习的发展, 文献[8]提出一种利用高级语义特征的ECO算法, 该算法同时压缩了训练样本空间, 在提升算法性能的同时加快了算法运行速度. 文献[9]提出的算法根据不同的应用场景采用不同的特征选择,使算法可以应对更多干扰因素.
在目标跟踪的过程中, 目标会因严重遮挡和出视野造成目标丢失, 为解决这一问题, 2011年, 文献[10]提出TLD算法, 是一种将目标检测和目标跟踪相结合的跟踪器, 实现在目标丢失后重新出现在视野时, 检测器可以再次捕捉到目标. 由于其使用特征点跟踪的模式, 跟踪的进度较低. 为提高精度, 文献[11]提出了LCT算法, 一种基于相关滤波和随机蕨分类器结合的长时目标跟踪器, 有效提高了算法的精度, 但检测范围存在局限性.
综上, 针对长期目标跟踪算法LCT出现的特征使用单一和重检分类器的局限性问题, 本文在将目标跟踪任务分解为目标的平移和尺度估计的基础上, 融合了改进的方向梯度直方图特征、颜色特征和局部二值模式特征, 提高跟踪器的鲁棒性; 用孪生网络实例搜索替代了LCT中用于目标重检的蕨分类器, 解决了蕨分类器存在的检测范围局限性的问题.
1 长期相关滤波算法长期相关滤波算法(long-term correlation tracking, LCT)是基于相关滤波器的跟踪算法, 它从单一框架中学习了两个回归模型. 一个是时间上下文回归器, 利用目标和周围时间相关性, 积极适应平移估计来解决重大变形和遮挡问题; 另一个是目标回归器, 仅模拟目标外观, 并建立外观金字塔以进行尺度估计. 目标回归器同时也作为判别回归模型, 用最大响应值评估跟踪结果置信度, 并使用阈值
LCT跟踪器将跟踪任务分解成位置估计和尺度估算两个子任务. 分别由两个相关滤波器
相关滤波器的获得方式, 是利用循环矩阵的性质对大小为M×N个像素的图像进行密集采样得到更多的循环样本即xm,n(m,n),训练岭回归分类器如式(1):
| $ \min \mathop \sum \limits_{m, n} {\left\| {\varphi ({x_{m, n}}) \cdot \omega - y(m, n)} \right\|^2} + \lambda {\left\| \omega \right\|^2} $ | (1) |
其中, φ(xm, n)是核空间映射函数; ω为所求滤波器; λ为正则化项参数.
最终计算求得ω的具体表达式为
| $ A = F(a) = \dfrac{{F(y)}}{{F(\varphi (x) \cdot \varphi (x))}} $ | (2) |
在新的图像帧中, 需要对每一个预估的目标框计算相应的输出值, 计算方式为:
| $ \hat y = {F^{ - 1}}(A \odot F(\varphi ({\textit{z}}) \cdot \varphi ({\hat x} ))) $ | (3) |
所得响应的最大值被认作新一帧中感兴趣区域的位置.
1.2 更新机制与目标重检在更新机制和目标重检测方面, LCT算法均使用设定阈值的方法来控制是否进行模型更新和目标重检.
当滤波器的响应值
| $ {{{\hat {{x}}}}^t} = (1 - \alpha ){\hat x^{t - 1}} + \alpha {x^t} $ | (4) |
| $ {\hat A^t} = (1 - \alpha ){\hat A^{t - 1}} + \alpha $ | (5) |
其中, t代表当前帧, α是学习速率.
当目标发生遮挡或出视野时, 算法会出现跟丢目标的情况. 这时为了保持跟踪器模型的准确性, 要停止目标模型更新. 为此, LCT算法通过判定跟踪框响应值与规定阈值大小来判定是否更新模型.
跟踪器在新一帧所得目标框的响应值记为该帧的置信度, 研究者经多次实验选定置信度阈值, 低于该值, 证明所得目标错误率较高, 需要再次检测. 此时暂停模型更新, 开始进行目标重检测. 选择将高置信度的每个跟踪结果调整为15×15大小, 以形成灰度特征向量来训练随机蕨分类器. 同时, 将重检器获得到的检测框位置作为这一帧图像确定的目标位置, 并继续进行跟踪.
2 优化的LCT算法 2.1 更新机制与目标重检选择合适的特征有助于跟踪器更好的学习目标的外观模型. HOG特征, 对几何方向敏感而对颜色变化不敏感. 为了得到一个性能优良的跟踪器, 本文将多种特征融合在一起, 即使用局部二值模式(LBP)特征、改进的方向梯度直方图(FHOG)特征以及颜色(CN)特征进行融合.
2.1.1 FHOG特征FHOG特征由Felzenszwalb等人[12]提出, 它在HOG (histogram of oriented gradient)特征的基础上利用每个cell的4个邻域进行归一化和截断处理, 由于方向敏感的划分方式和不敏感划分方式在不同目标类别上表现效果各异, 故选择对方向敏感的(18维)特征和对方向不敏感的(9维)特征, 但特征维度太大对特征在行列两方向上累加, 进行特征降维提取方式如图1所示.
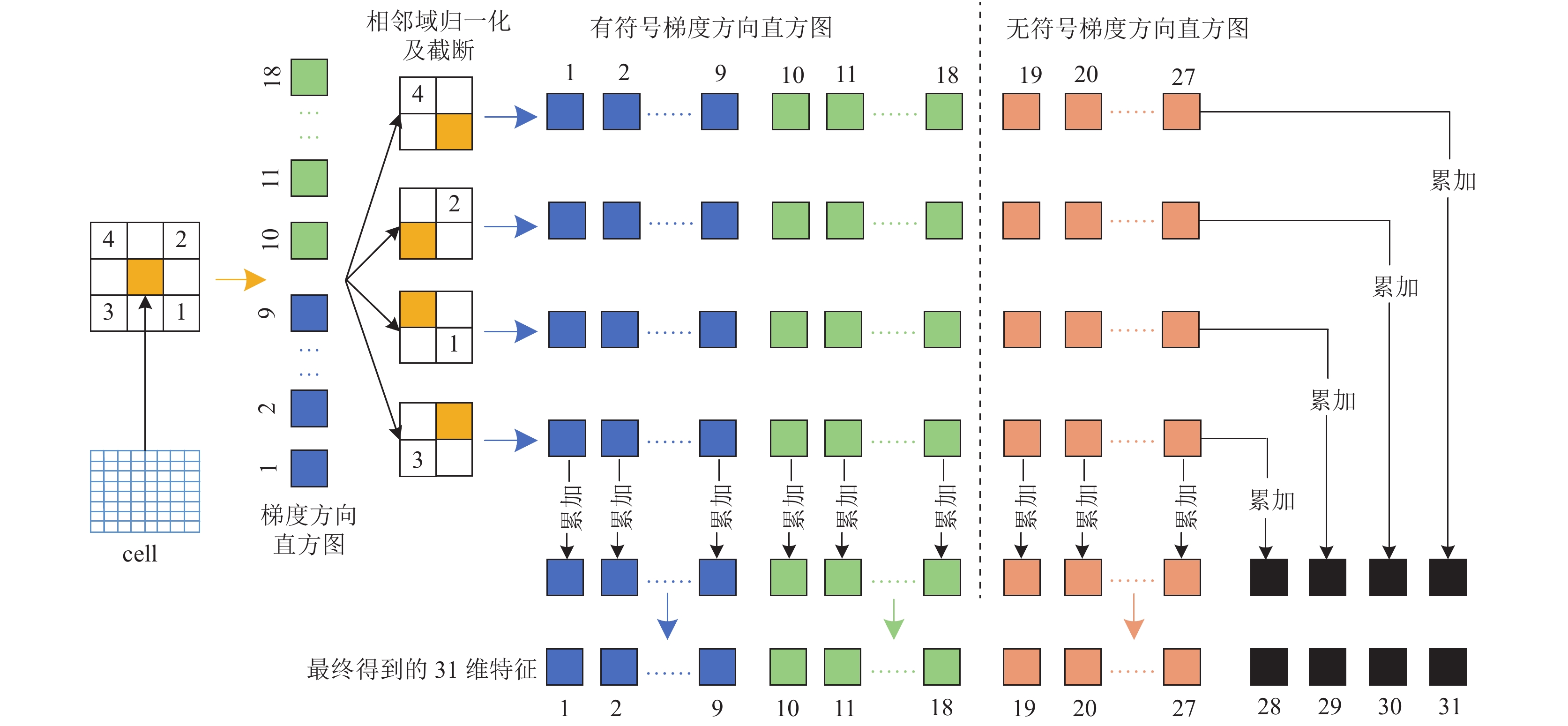
|
图 1 FHOG特征提取原理图 |
2.1.2 LBP特征
LBP (local binary pattern)是局部二值模式, 体现图像的局部纹理特征, 可以有效对抗旋转和灰度的变化. 提取方式为: 选中图像中的某一像素并将其作为阈值, 以其为中心建立3×3的窗口, 让每一小格像素值分别与阈值比较. 若此值大于或等于阈值, 则在LBP编码图中, 对应位置记为1, 反之记为0. 对产生8位二进制数十进制化, 得到LBP编码值. LBP特征是对目标外观模型的纹理特征的体现, 反映物体表面的变化. 它的提取示意图如图2所示.
2.1.3 CN特征CN (color names)特征是图像重要的特征之一, 但颜色特征对一些形变不敏感, 在一些判别性场景中应用广泛. CN颜色特征应对目标形变效果不佳, 适用于不涉及目标空间位置的情景. 相比其他特征, 颜色特征以低复杂度获得研究者的青睐. 该特征将传统的RGB空间的特征映射为11维度的CN特征, 在面对光照变化的干扰因素时可以较好地应对和处理, 从而保证跟踪效果的准确性.

|
图 2 LBP特征提取原理图 |
2.1.4 特征融合策略
对当前图像序列采用FHOG特征、LBP特征、CN特征3种特征根据各自权重实现融合. 首先用公式
| $ {f_{\rm hog}}({\textit{z}}) = \mathop F\nolimits^{ - 1} ({\hat \omega _{\rm hog}} \odot \hat {\textit{z}}) $ | (6) |
| $ {f_{\rm lbp}}({\textit{z}}) = \mathop F\nolimits^{ - 1} ({\hat \omega _{\rm lbp}} \odot \hat {\textit{z}}) $ | (7) |
| $ f{}_{\rm cn}({\textit{z}}) = \mathop F\nolimits^{ - 1} ({\hat \omega _{{\text{cn}}}} \odot \hat {\textit{z}}) $ | (8) |
其中,
| $ \alpha = \dfrac{{\max (\mathop f\nolimits_{\rm hog} ({\textit{z}}))}}{{\max (\mathop f_{\rm hog} ({\textit{z}})){\text{ + }}\max (\mathop f\nolimits_{{\text{lbp}}} ({\textit{z}})) + \max (\mathop f_{\rm cn} ({\textit{z}}))}} $ | (9) |
| $ \beta = \dfrac{{\max (\mathop f_{\rm lbp} ({\textit{z}}))}}{{\max (\mathop f_{\rm hog} ({\textit{z}})){\text{ + }}\max (\mathop f_{{\text{lbp}}} ({\textit{z}})) + \max (\mathop f_{\rm cn} ({\textit{z}}))}} $ | (10) |
| $ \gamma = \dfrac{{\max (\mathop f_{\rm cn} ({\textit{z}}))}}{{\max (\mathop f_{\rm hog} ({\textit{z}})){\text{ + }}\max (\mathop f_{{\text{lbp}}} ({\textit{z}})) + \max (\mathop f_{\rm cn} ({\textit{z}}))}} $ | (11) |
α、β、γ分别为FHOG特征、LBP特征、CN特征的融合权重. 最后, 根据所得的融合权重得到最终的响应如式(12):
| $ f({\textit{z}}) = \alpha f_{\rm hog} ({\textit{z}}) + \beta f_{{\text{lbp}}} ({\textit{z}}) + \gamma f_{\rm cn} ({\textit{z}}) $ | (12) |
本文提出使用基于深度学习的重检测器. 用全局孪生网络实例搜索SINT来改善随机蕨分类器对目标重检测范围的局限性, 从而提高重检测器的跟踪性能.
SINT网络模型如图3所示, 左右两边网络结构相同. 左边网络存储目标模板信息, 右边网络用于目标区域特征提取, 孪生网络的工作核心是学习一个匹配函数, 能够将每幅图像对应特征空间中的一个特征向量. 训练时, 度量距离即向量差异, 最终, 通过拟合此距离来表示与输入图像的相似度差异.
当SINT在外部视频中学习一个用于跟踪的通用匹配函数, 可以稳健地处理一个对象在视频序列中可能经历的常见外观变化. 学习到的函数可以不需要任何调整, 直接应用到新的跟踪视频中. 该视频中的目标对象是之前没有看到过的对象. 故本文利用ALOV数据集中训练好的SINT网络模型参数. 当重检模块被激活时, SINT简单的将第一帧中初始目标区域与新帧中的候选目标区域进行匹配, 并通过匹配函数, 返回最相似的区域. 候选框的选择采用半径采样策略, 即围绕前一帧的预测位置, 在不同半径的圆上均匀采样位置, 搜索半径设置为第一帧中初始框的较长轴. 将重检响应值与阈值
| $ \hat c = \mathop {\arg }\limits_{ c_i } \max v( x_{\rm obj} , \mathop c\nolimits_i ), \;\;i = 1, 2, \cdots , N $ | (13) |
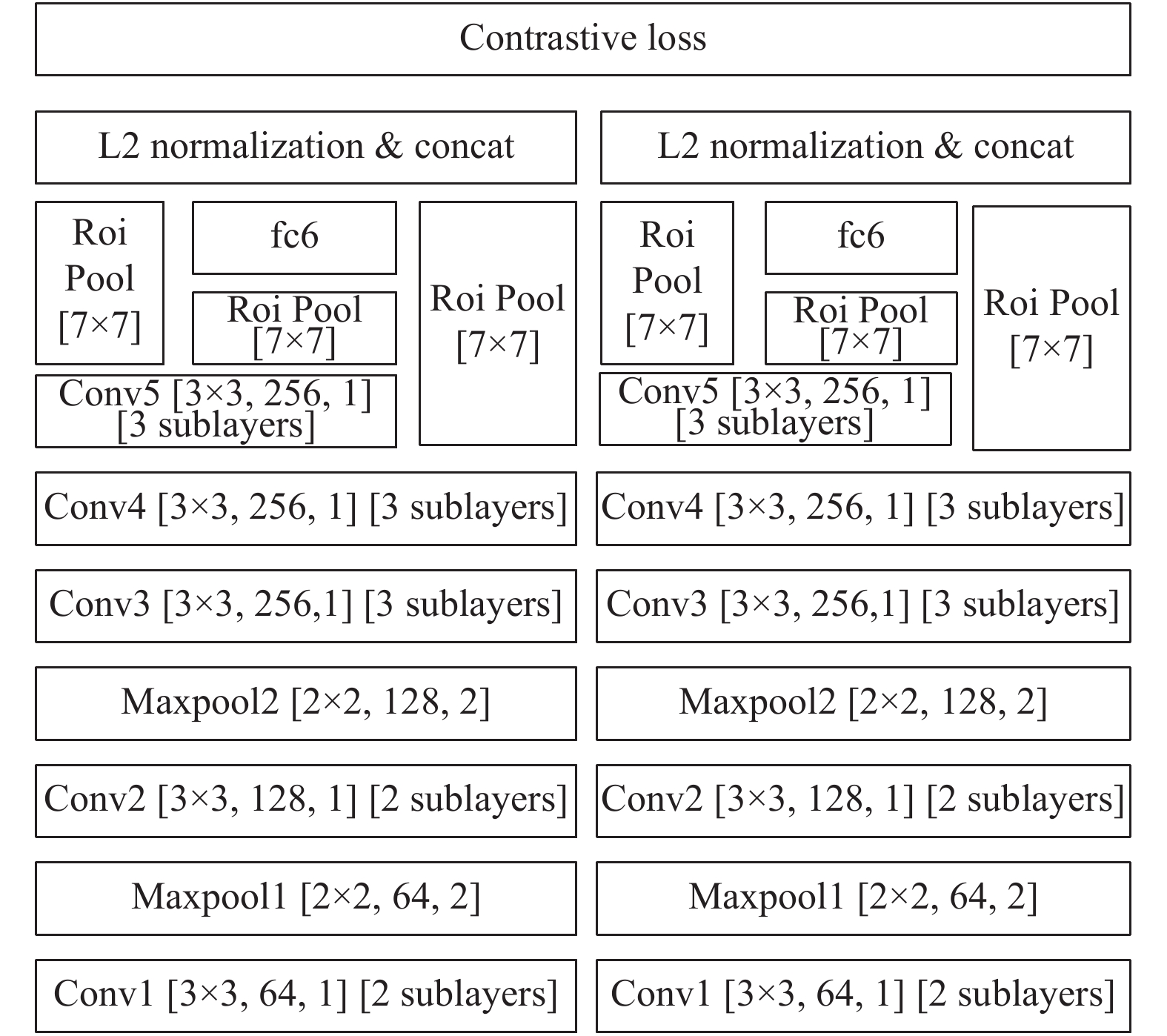
|
图 3 SINT模型的整体结构 |
2.3 改进的算法流程
改进的算法流程图如图4所示, 具体步骤描述如算法1.
算法1. 改进算法
输入: 初始目标中心点位置pos1与尺度s1.
输出: 输出目标估计状态中心点位置post与尺度st. 两个滤波器模型
Step 1. 根据pos1和s1, 从第1帧中裁剪搜索窗口并提取3种特征.
Step 2. 用
Step 3. 在新的目标中心点位置post周围构建目标金字塔, 然后用滤波器Rt和式
Step 4. 使用最优尺度下的响应值来确定跟踪结果的置信度, 若
Step 5. 使用孪生网络实例搜索SINT搜索目标的新位置, 若新位置post'的响应值大于
Step 6. 若
Step 7. 若序列结束, 则停止算法, 否则重复Step 3~Step 6.
3 实验结果与分析 3.1 实验环境及配置本文所提算法的核相关滤波器的参数设置和LCT算法设置一致. 对于重检器孪生网络, 训练时, 总共从ALOV数据集中采样了60000对帧, 使用ImageNet预先训练好的网络参数Siamese网络进行微调. 初始设定学习率为0.001、权重衰减为0.001. 学习率每隔两个周期下降10倍. 当验证损失不再减少时, 停止调优.
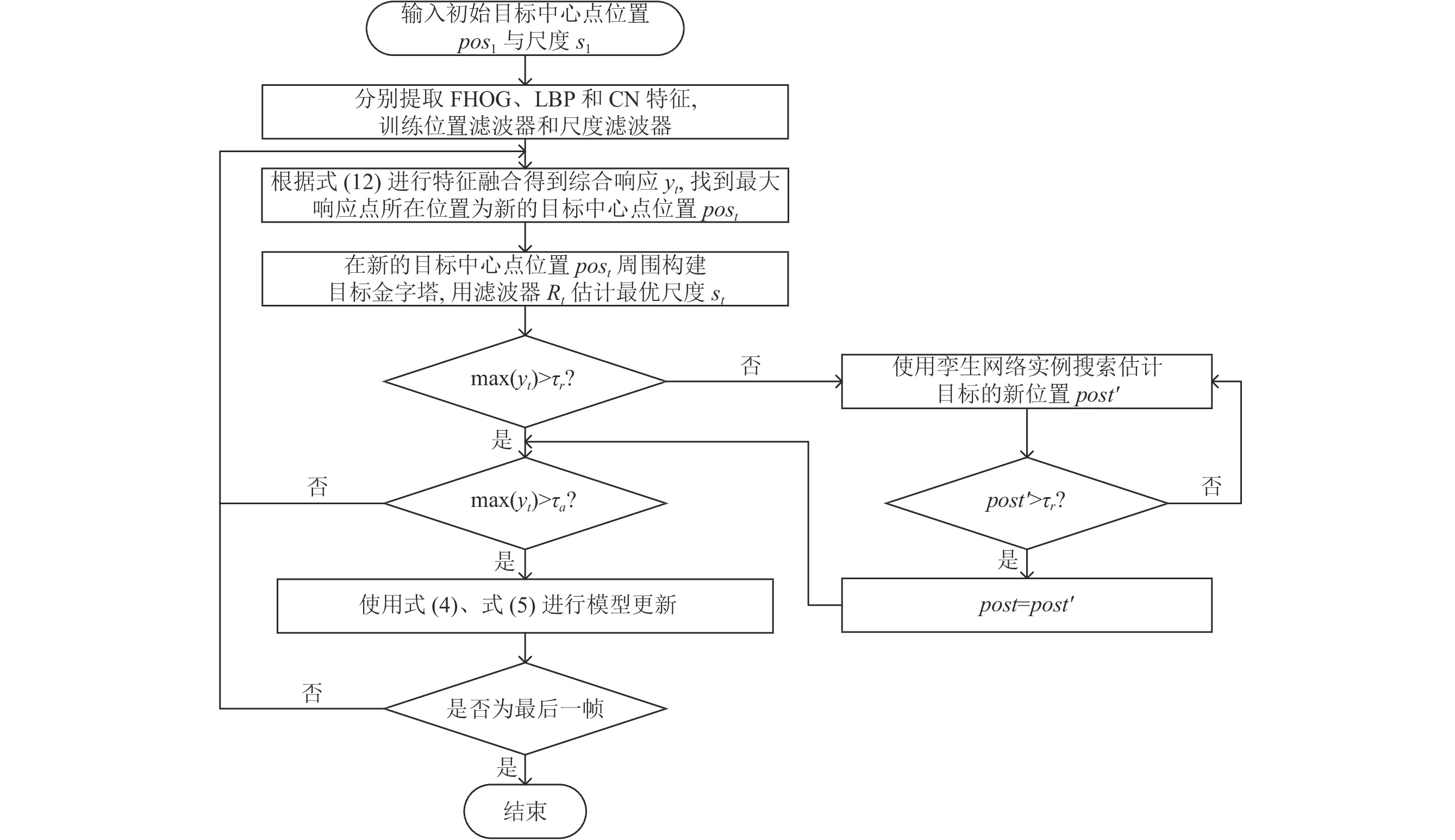
|
图 4 改进的算法流程图 |
算法的实验代码在LCT的开源的Matlab代码上进行改进. 将重检测模块用训练好的孪生网络实例搜索代替原有算法中的随机蕨分类器, 使用的软件平台为Matlab 2020a. 硬件配置为: NVIDIA GXT 1070 GPU, 8 GB内存, 使用Caffe深度学习框架.
3.2 评估指标本文选择重叠成功率(overlap success rate, OSR), 距离精度(distance precision, DP)和选择帧率(frame per second, FPS)评测算法且本文都选择采用一次性评估方式, 即只在视频序列第一帧进行初始化.
重叠成功率是指给定的标注框与算法得到的实际框之间的重叠率大于阈值的帧数与总帧数的比. 本文阈值选择0.5. 重叠得分定义如式(14):
| $ S = \dfrac{{\left| {{B_t} \cap \left. {{B_{\rm gt}}} \right|} \right.}}{{\left| {{B_t} \cup {B_{\rm gt}}} \right|}} $ | (14) |
其中,
中心位置误差CLE指的是实际框中心(xt, yt)与标注框中心(xgt, ygt)的欧氏距离.
| $ CLE = \sqrt {{{\left( {{{{x}}_t}, {y_t}} \right)}^2} + {{\left( {{x_{\rm gt}}, {y_{\rm gt}}} \right)}^2}} $ | (15) |
距离精度是指中心位置误差小于设定阈值的视频帧数占总帧数的比例. 本文阈值为20 pixels.
使用帧率来评估算法的运行速度.
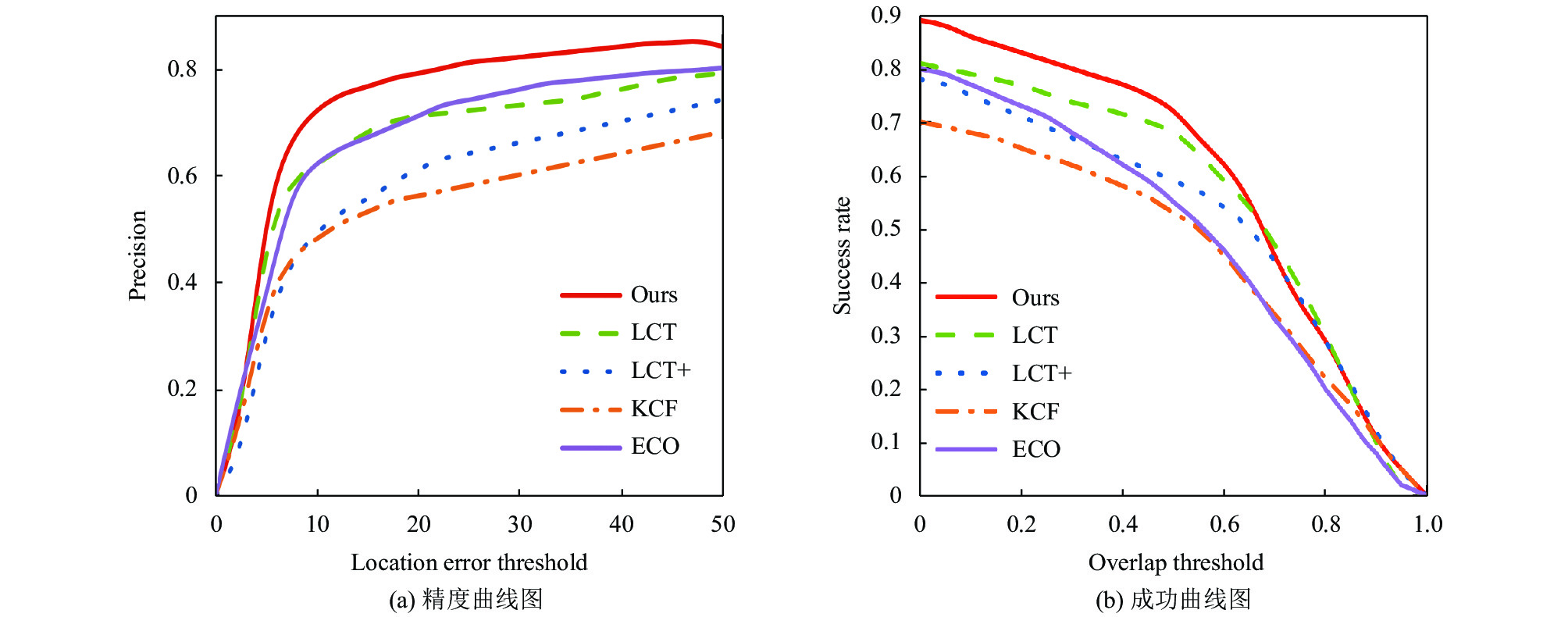
3.3 定性分析由于OTB100公开数据集涵盖了大量的具有挑战性情况的视频集, 包含遮挡、形变、运动模糊、光照变化、目标出视野等. 为了与其他算法进行对比, 将本文与4种跟踪算法进行对比, 它们分别是LCT、LCT+、KCF、ECO. 表1为实验所得数据, 图5为5种算法在OTB100数据集上得到的精度曲线图和成功率曲线图. 由表1可知, 本文算法精确度为80.7%, 重叠成功率为71.6%, 运行速率为16.5 fps, 与原始算法对比, 本文算法的距离精度和重叠成功率分别提高了13%和10.3%. 相较于深度学习的目标跟踪算法, 本文算法在与其性能相当的基础上, 运行速度为16.5 fps可以实现实时跟踪. 图6、图7、图8分别为遮挡、尺度变化和运动模糊情况下的结果对比图. 由对比得出, 与主流算法相比, 本文提出算法的抗干扰能力更强, 也更具鲁棒性.
3.4 定量分析从实验视频中选取5个跟踪成功的视频对本文算法与主流算法进行定性分析. 所选视频序列存在遮挡(OCC)、尺度变化(SV)、形变(DEF)、运动模糊(MB)等不同的挑战. 跟踪结果如图9所示.
| 表 1 在OTB100数据集上5种跟踪算法对比 |
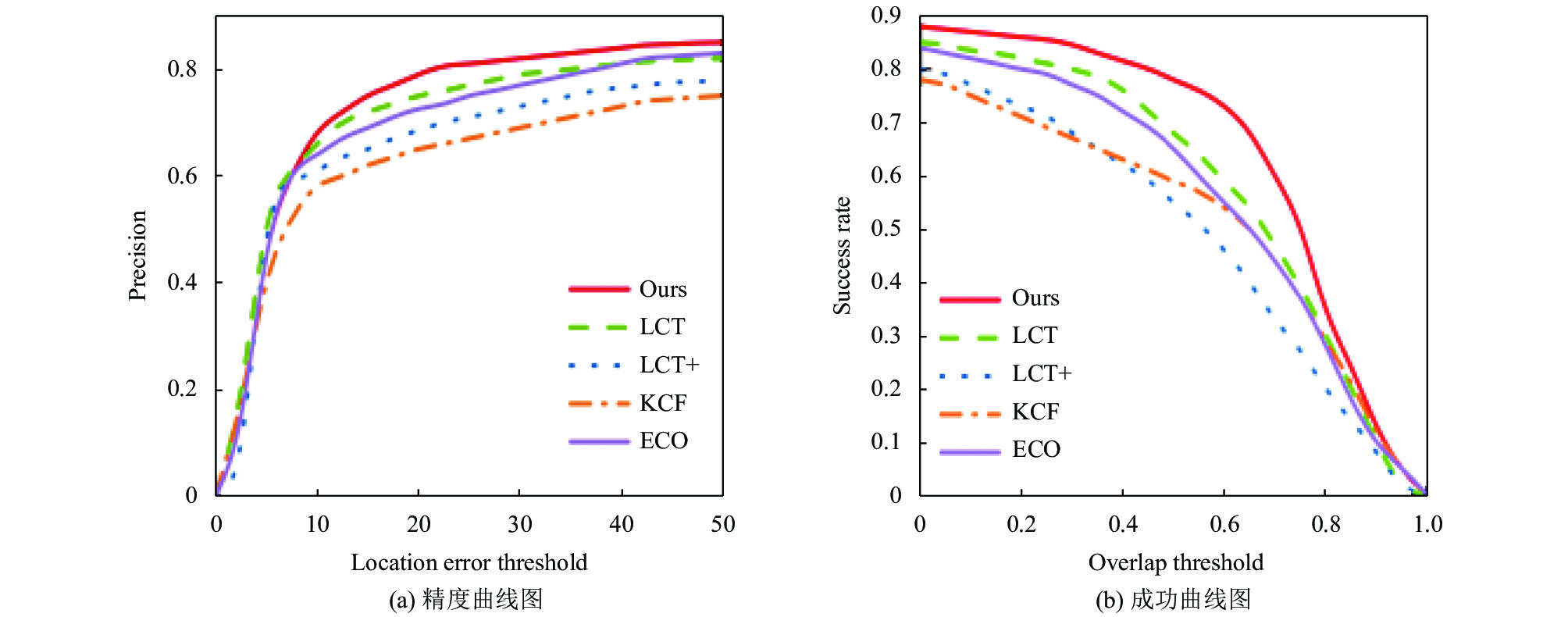
|
图 5 OTB100数据集的结果对比 |
|
图 6 OTB100的遮挡数据集结果对比 |
如图9所示, 在图9(a) Jogging和图9(e) Learning视频序列中, 所有算法在目标没有被遮挡时, 都能稳定的跟踪, 图9(a)序列在53帧及图9(e)序列262帧、334帧在目标发生严重遮挡时, 本文算法使用孪生网络重检器, 目标重现时, 可再次捕捉目标并继续跟踪. 而KCF算法和ECO算法在目标被严重遮挡后, 无法重新跟踪目标. 在图9(b) Bird2中, 目标多次发生平面内旋转、平面外旋转、形变、运动模糊等情况, 51帧目标发生平面内旋转之后, 发生了形变, 我们的算法可以继续跟踪目标而LCT算法和KCF出现了跟踪失败的情况, LCT+算法和ECO算法的跟踪框也发生了偏离. 第91帧到99帧, 目标由于平面内旋转再次发生形变, 而此时多个算法出现跟丢的情况, 只有本文算法可以稳定跟踪目标. 在图9(c) BlurCar1中, 第786帧出现严重的运动模糊状况, 跟踪算法都能继续跟踪目标, 而本文算法能更准确地跟踪目标. 本文算法在目标发生严重遮挡时, 由于目标周围的上下文仍可能保持不变, 所以时间上下文回归器Rc可以很好地应对目标严重遮挡, 依然稳定地跟踪目标.

|
图 7 OTB100的尺度变化数据集结果对比 |

|
图 8 OTB100的运动模糊数据集结果对比 |
4 结论
针对长期相关滤波跟踪算法特征单一、重检精度低, 提出了一种结合深度学习的多特征融合的长期目标跟踪算法. 在LCT算法的基础上, 使用FHOG特征、LBP特征、CN特征来训练位置滤波器Rc和尺度滤波器Rt, 当目标发生遮挡或出视野时, 采用选定阈值判断是否激活孪生网络重检器. 在目标位置构建目标金字塔及尺度滤波器Rt判断目标尺度并与相应阈值来判断是否更新目标模型. 本文的算法在OTB100数据集上进行了实验, 得到的结果表明, 与LCT算法相比, 本文算法在跟踪精度和覆盖成功率上都有所提高; 和一些相关算法对比, 本文算法的跟踪性能有所提升. 但在运行速率上有待提高.

|
图 9 不同算法在5个视频序列上的跟踪效果 |
| [1] |
黄凯奇, 陈晓棠, 康运锋, 等. 智能视频监控技术综述. 计算机学报, 2015, 38(6): 1093-1118. DOI:10.11897/SP.J.1016.2015.01093 |
| [2] |
尹宏鹏, 陈波, 柴毅, 等. 基于视觉的目标检测与跟踪综述. 自动化学报, 2016, 42(10): 1466-1489. |
| [3] |
Chen Z, Hong ZB, Tao DC. An experimental survey on correlation filter-based tracking. Computer Science, 2015, 53(6025): 68-83. |
| [4] |
Bolme DS, Beveridge JR, Draper BA, et al. Visual object tracking using adaptive correlation filters. 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Francisco: IEEE, 2010. 2544–2550.
|
| [5] |
Henriques JF, Caseiro R, Martins P, et al. Exploiting the circulant structure of tracking-by-detection with kernels. Proceedings of the 12th European Conference on Computer Vision. Florence: Springer, 2012. 702–715.
|
| [6] |
Henriques JF, Caseiro R, Martins P, et al. High-speed tracking with kernelized correlation filters. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(3): 583-596. DOI:10.1109/TPAMI.2014.2345390 |
| [7] |
Danelljan M, Khan FS, Felsberg M, et al. Adaptive color attributes for real-time visual tracking. 2014 IEEE Conference on Computer Vision and Pattern Recognition. Columbus: IEEE, 2014. 1090–1097.
|
| [8] |
Danelljan M, Bhat G, Khan FS, et al. ECO: Efficient convolution operators for tracking. 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Honolulu: IEEE, 2017. 6931–6939.
|
| [9] |
沈秋, 严小乐, 刘霖枫, 等. 基于自适应特征选择的多尺度相关滤波跟踪. 光学学报, 2017, 37(5): 0515001. |
| [10] |
Kalal Z, Mikolajczyk K, Matas J. Tracking-learning-detection. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(7): 1409-1422. DOI:10.1109/TPAMI.2011.239 |
| [11] |
Ma C, Yang XK, Zhang CY, et al. Long-term correlation tracking. 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Boston: IEEE, 2015. 5388–5396.
|
| [12] |
Felzenszwalb PF, Girshick RB, McAllester D, et al. Object detection with discriminatively trained part-based models. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(9): 1627-1645. DOI:10.1109/TPAMI.2009.167 |
 2022, Vol. 31
2022, Vol. 31



