计算句子相似度是自然语言处理领域研究的一个基础且重要的工作, 有着广泛的应用方向, 多用于智能问答、信息检索、语义分析和文本分类等场景.
目前对于句子相似度的研究停留在语义理解范围, 依托越来越庞大的数据库做大量的仿真, 做到让机器理解人类的语言, 但现有的句子相似度计算方法主要分为两大类: 基于统计的方法和基于深度学习的方法[1]. 典型的方法有莱文斯坦距离、BM25、TF-IDF、Word2Vec余弦相似度、Jaccard系数相似性计算等.
国内外各个学者对句子相似度的研究做了广泛的探索. Tian等[2] 提出一种基于同义词表的改进Word2Vec句子相似度算法, 通过构建同义词表和融合词向量来提高句子相似度计算的准确性; Wilson等[3]提出一种使用组合语义方法来测量文档相似性的有效方法, 该方法结合了多个语义计算; 文献[2, 3]的研究由于语义工具和应用逻辑的效率决定了应用程序的准确度和整体性能, 待进一步提升; Goz等[4]研究基于关键字的社交网络相似性的适用性; Ruan等[5]计算句子相似度是将Word2Vec方法和词嵌入相似度方法结合, 二者对于关键词词性信息稍欠考虑; 翟社平等[6]提出多特征的句子词形、词序及句长特征融合的相似度计算方法, 由于句子关键词存在一词多义, 只考虑了句子的字面特征, 将导致相似度匹配不准确.
句子由多个词组成也包含多种属性, 句长度、词出现的频率和词在句中的词性以及其在句中的顺序对句子语义的影响度不同, 需综合考虑到句子深层和表层所有因素[7]. 因此本文以句子的语序结构、词性信息和形态结构等特点为核心要素, 构建研究领域本体库, 通过给各属性分配权重, 提出一种基于句子的多属性融合相似度计算方法, 以提升句子相似度计算的合理性.
1 相似度概念 1.1 句子相似度文本相似度一般指文本在语义上的相似程度[8], 句子相似度指的是句子在语义上的相似程度, 用来评估句子之间符合程度. 如果两个句子之间符合程度高, 那两者一定有相似或相同的属性, 令
(1)
(2)
(3)
(4)
两个句子的相似度可以用向量余弦值的值来衡量, 称为余弦相似度[9]. 首先, 将两个句子数字化变成向量, 其次, 计算其夹角余弦

|
图 1 向量的余弦相似度 |
将句子S1和S2以向量
| $ {S}_{1}: \left({v}_{1}, {v}_{2}, {v}_{3}, \cdots, {v}_{n}\right) $ |
| $ {S}_{2}: \left({v}_{1}', {v}_{2}', {v}_{3}', \cdots, {v}_{n}'\right) $ |
则句子的余弦相似度计算公式为:
| $ \textit{SIM}\left( {{S_1}, {S_2}} \right) = \frac{{\displaystyle \sum \nolimits_{i = 1}^n {v_i} \times v_i'}}{{\sqrt {\displaystyle\sum \nolimits_{i = 1}^n v_i^2 \times \displaystyle\sum \nolimits_{i = 1}^n v_i^2} }} $ | (1) |
一个句子除包含的关键词外, 也不能忽略自身的一些属性, 比如词频、词序、词性和句长, 本文将4个属性进行加权融合得到句子相似度. 句子之间在词语形态上的相似度, 即出现共有关键词的频率为词频相似度; 句子之间共有关键词的相对位置关系的相似度为词序相似度; 句子之间共有关键词的词性的相似度为词性相似度; 两个句子的长度的关系为句长相似度.
传统方法对句子进行分词、去停等操作提取关键词进行表面特征的相似度比较, 这是不全面的, 中文自然语言不同于英文自然语言, 中文有着丰富且灵动的表达形式. 如词性方面, “退役士兵有什么需要?”与“退役士兵需要有什么?”, 此处的两个“需要”字面特征一致, 本质却不同, 名词和动词的词性不同导致句子所表达的意思有差别. 词性序列如表1所示.
| 表 1 句子关键词词性 |
本文将使用哈尔滨工业大学开发的在线语言技术平台(language technology platform, LTP)[10]进行分词并得到所需的句子属性信息. LTP处理后的结果如图2.
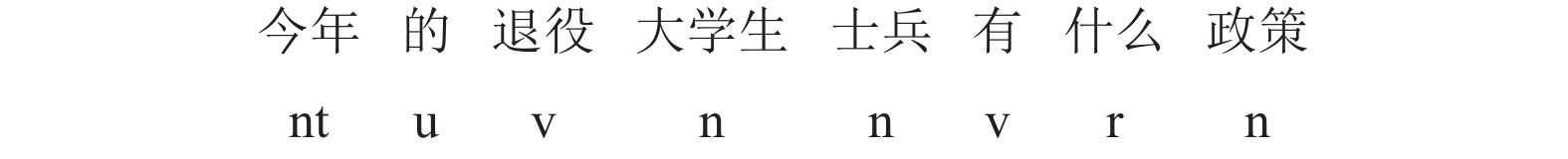
|
图 2 分词和词性标注的结果 |
2.1 词频相似度计算方法
改进基于向量空间模型TF-IDF (term frequency- inverted document frequency) 的词频计算方法[11]. TF-IDF简单结构没有考虑词语的语义信息, 无法处理一词多义与一义多词的情况.
采用词语逆频率方式计算加权算法TF-IWF (term frequency-inverse word frequency), 将句子
| $ \textit{WorSim}\left( {{S_1}, {S_2}} \right) = \frac{{\displaystyle \sum \nolimits_{i = 1}^n {f_i} \times f_i'}}{{\sqrt {\displaystyle\sum \nolimits_{i = 1}^n f_i^2 \times \displaystyle \sum \nolimits_{i = 1}^n f_i^2} }} $ | (2) |
句子中共有关键词需考虑其相对位置关系, 词序相似度是共有关键词在两个句子中的位置相似度, 词位置顺序不同导致句子意思不同. 句子
举例说明,
以句子
首先以两个句子所含相同关键词的逆序数作为衡量因素,
| $ RevOrdSim\left( {{S_1}, {S_2}} \right) = \left\{ {\begin{array}{*{20}{l}} {1 - \dfrac{{Ron\left( {{S_1}, {S_2}, s} \right)}}{{s - 1}},\;\; s > 1} \\ {0, \;\;s = 0} \\ {\dfrac{1}{2},\;\; s \leqslant 1} \end{array}} \right. $ | (3) |
得出句子
| $ \textit{RevOrdSim}\left( {{S_1}, {S_2}} \right) = \frac{1}{4} $ |
然后以两个句子所含相同关键词的向量距离[14] 作为衡量因素,
| $ \textit{VecOrdSim}\left( {{S_1}, {S_2}} \right)\left\{ {\begin{array}{*{20}{l}} {1 - \dfrac{{distance\left( {{S_1}, {S_2}} \right)}}{{maxDistance}},\;\; s > 1} \\ {0, \;\;s = 0} \\ {\dfrac{1}{2},\;\; s \leqslant 1} \end{array}} \right. $ | (4) |
得出句子
| $ \textit{VecOrdSim}\left( {{S_1}, {S_2}} \right) = \frac{2}{3} $ |
逆序数
| $ \textit{OrdSim}\left( {{S_1}, {S_2}} \right) = \frac{{Rev\left( {{S_1}, {S_2}} \right) + Vec\left( {{S_1}, {S_2}} \right)}}{2} = \frac{{11}}{{24}} $ | (5) |
词性相似度(nature similarity)指两个句子中共有关键词的词性相似度, 此相似度计算方法用来完善一词多义的情况[15], 定义为具有相同词性的共有关键词数与两个句子总关键词数和之比. 计算公式为:
| $ \textit{NatSim}\left( {{S_1}, {S_2}} \right) = \frac{{2 \times Ncs\left( {{S_1}, {S_2}} \right)}}{{Com\left( {{S_1}} \right) + Com\left( {{S_2}} \right)}} $ | (6) |
使用LTP分词后并将得到的关键词词性进行比较, 式子中
以词频、词序、词性为核心要素计算相似度时, 而要完整、准确的反映句子的信息也要考虑句长的存在.
两个句子长度的差的绝对值, 可以反映一定程度上的句子相似度, 其与绝对值的大小成反比, 值越小, 说明此种程度上的相似度越大. 假设句子
| $ \textit{LenSim}\left( {{S_1}, {S_2}} \right) = 1 - \frac{{abs\left( {Len\left( {{S_1}} \right) - Len\left( {{S_2}} \right)} \right)}}{{Len\left( {{S_1}} \right) + Len\left( {{S_2}} \right)}} $ | (7) |
式中, abs()
综合词频、词序、词性、句长4种属性, 融合4种相似度, 其计算流程如图3所示.

|
图 3 方法计算流程 |
首先输入句子
| $ \begin{split}& \textit{StrSim}\left( {{S_1},{S_2}} \right)= \\ &\alpha *\textit{WorSim}\left( {{S_1},{S_2}} \right) + \beta *\textit{OrdSim}\left( {{S_1},{S_2}} \right) \\ &+\gamma *\textit{NatSim}\left( {{S_1},{S_2}} \right) +\delta *\textit{LenSim}\left( {{S_1},{S_2}} \right) \end{split} $ | (8) |
式中,
本文采用层次分析法(AHP)[16]通常被用到处理复杂的决策问题, 准备采取决策的问题分成3个层次, 基于该方法计算出的各相似度的权重. 步骤如下:
(1)将问题条理化、层次化, 根据词频、词序、词性和句长相似度建立层次结构模型.
(2)根据经验赋予各相似度重要程度并构造判断矩阵, 词频与词序相似度重要程度高且一致, 相较而言, 词性和句长相似度重要程度低且一致, 并使用1~9及其倒数作为标度来确定
显然, 表2中的元素满足:
| $ {a_{ij}} > 0\text{; }{a_{ij}} = \frac{1}{{{a_{ij}}}}\text{; }{a_{ij}} = 1 $ |
根据层次分析法规则可得比较矩阵, 如表3所示.
| 表 2 重要程度 |
| 表 3 比较矩阵 |
(3)层次单排序并进行一致性检验, 根据表3可得判断矩阵A.
| $ A = \left[ {\begin{array}{*{20}{c}} 1&1&5&5 \\ 1&1&5&5 \\ {\dfrac{1}{5}}&{\dfrac{1}{5}}&1&1 \\ {\dfrac{1}{5}}&{\dfrac{1}{5}}&1&1 \end{array}} \right] $ |
计算该判断矩阵的最大特征值
| $ CI = \frac{{{\lambda _{\max}} - n}}{{n - 1}} $ | (9) |
其中, n为矩阵的维度, 得出CI=0, 表示完全一致. CI的值越小, 表示越一致, CI的值越大, 表示越不一致.
(4)使用Satty模拟1000次得到的RI表计算一致性比率, RI表如表4所示.
| 表 4 RI表 |
根据
本文算法实验中, 开发环境为Windows 10 X64, 开发工具为VSCode1.54.1, 开发语言为Python 3.6.4. 采用哈尔滨工业大学开发的在线语言技术平台(LTP)进行关键词分词并得出所需的句子的属性.
为验证方法的效果, 对本文提出的基于句子的多属性融合相似度计算方法和Jarcarrd、文献[14]方法, 设计对比试验, 以召回率(Recall)、准确率(Precision)、F-度量值(F-Measure)[17]对比不同算法的性能, F度量值综合涵盖召回率与准确率两个指标, 值越接近于100%, 说明准确率和召回率越均衡, 方法的效果越好, 相反, 如果F度量值越接近于0, 说明两个指标的均衡性越差, 方法效果欠缺.
(1)召回率(Recall)衡量相似度匹配的查全率.
| $ 召回率=\frac{正确检测到的相似句子数}{实际存在的相似句子数} $ | (10) |
(2)准确率(Precision)衡量相似度匹配的查准率.
| $ 准确率=\frac{正确检测到的相似句子数}{所有检测到的相似句子数} $ | (11) |
(3) F-度量值(F-Measure)是召回率与准确率的指标归一化平均值, 用于反映整体的指标.
| $ F-度量值=2\times \frac{准确率\times 召回率}{准确率+召回率} $ | (12) |
实验步骤如下:
实验所需数据为随机从国家与地方退役军人事务局等网站爬取的, 经过数据处理建立的问答库, 从中选取300条问答对作为初始数据集
| 表 5 句子相似度对比实验(%) |
Jaccard方法和文献[14]方法与本文方法的实验结果从表5可以看出, Jaccard方法具有较高准确率和较低召回率, 但该方法以句子的字面量为特征, 所以有一定限制在一词多义层面的相似度计算方面, 句子中包含的关键词相似, 但却忽略了关键词词性的不同. 文献[14]方法解决了一义多词问题, 比较而言, 其召回率比Jaccard方法高64.3%, 准确率却下降了26.2%, 显而易见, 两种方法均没有达到均衡稳定的效果. 本文方法相较于文献[14]方法准确率提高约20%, 且F-度量值更接近于100%, 明显优于使用Jaccard方法和文献[14]方法.
4 结论与展望本文提出的基于句子的多属性融合相似度计算方法, 综合考虑了句子的结构和包含的属性, 以词频、词序、词性和句长4种相似度加权融合计算, 对提高句子相似度计算的准确率有利, 且不会大范围出现召回率的降低, 其可靠性及可行性优于传统方法, 召回率、准确率不仅均衡且归一化F度量值较高, 达到87.12%, 拥有综合优势. 接下来, 将该方法应用于智能问答系统的句子匹配, 可适用普遍存在的句子语法情况, 进一步研究时, 将继续优化此方法的复杂度及问答效率.
| [1] |
李慧. 词语相似度算法研究综述. 现代情报, 2015, 35(4): 172–177.
|
| [2] |
Tian HN, Guo X. Research on improved sentence similarity calculation method based on Word2Vec and synonym table in interactive machine translation. 2021 5th International Conference on Robotics and Automation Sciences (ICRAS). Wuhan: IEEE, 2021. 255–261.
|
| [3] |
Wilson PK, Jeba JR. An efficient methodology for measuring sentence similarity using combinational semantics. 2021 7th International Conference on Advanced Computing and Communication Systems (ICACCS). Coimbatore: IEEE, 2021. 1872–1876.
|
| [4] |
Goz F, Kabasakal O, Mutlu A. Experimental analysis of keyword-based social network similarity approach for document classification. 2020 28th Signal Processing and Communications Applications Conference (SIU). Gaziantep: IEEE, 2020. 1–4.
|
| [5] |
Ruan HP, Li Y, Wang QL, et al. A research on sentence similarity for question answering system based on multi-feature fusion. 2016 IEEE/WIC/ACM International Conference on Web Intelligence. Omaha: IEEE, 2017. 507–510.
|
| [6] |
翟社平, 李兆兆, 段宏宇, 等. 多特征融合的句子语义相似度计算方法. 计算机工程与设计, 2019, 40(10): 2867–2873, 2884.
|
| [7] |
吴全娥, 熊海灵. 一种综合多特征的句子相似度计算方法. 计算机系统应用, 2010, 19(11): 110–114.
|
| [8] |
王寒茹, 张仰森. 文本相似度计算研究进展综述. 北京信息科技大学学报, 2019, 34(1): 68–74.
|
| [9] |
翟永杰, 吴童桐. 基于语义空间信息映射加强的零样本学习方法. 计算机应用与软件, 2020, 37(12): 113–118, 196.
|
| [10] |
郎君, 刘挺, 张会鹏, 等. LTP: 语言技术平台. 中国中文信息学会. 第三届学生计算语言学研讨会论文集. 沈阳: 中国中文信息学会, 沈阳航空工业学院, 2006. 64–68.
|
| [11] |
Pang SC, Yao JM, Liu T, et al. A text similarity measurement based on semantic fingerprint of characteristic phrases. Chinese Journal of Electronics, 2020, 29(2): 233–241.
|
| [12] |
张俊飞. 改进TF-IDF结合余弦定理计算中文语句相似度. 现代计算机, 2017, (32): 20–23, 27.
|
| [13] |
Abuobieda A, Osman AH. An adaptive normalized Google distance similarity measure for extractive text summarization. 2020 2nd International Conference on Computer and Information Sciences (ICCIS). 2020. 1–4.
|
| [14] |
周艳平, 李金鹏, 蔡素. 基于同义词词林的句子语义相似度方法及其在问答系统中的应用. 计算机应用与软件, 2019, 36(8): 65–68, 81.
|
| [15] |
吴浩, 艾山·吾买尔, 卡哈尔江·阿比的热西提, 等. 融合词性特征的中文句子相似度计算方法. 计算机工程与设计, 2020, 41(1): 150–155.
|
| [16] |
刘万里, 刘卫锋, 常娟. AHP中互反判断矩阵的区间权重确定方法. 统计与决策, 2021, 37(6): 33–37.
|
| [17] |
刘辉. 基于强类别特征的文本相似度计算及其性能评估. 软件工程, 2020, 23(10): 5–7, 4.
|
 2022, Vol. 31
2022, Vol. 31



