随着传统电网的各种弊端不断显现, 智能电网以其双向通信, 多元化梯度电价, 状态分析预警等优势^{[1, 2]}逐渐被各个国家重视^[3-5]起来.

在智能电网中, 部署了大量的传感器, 尤其是智能电表, 每隔15分钟发送电力数据给控制中心以供分析与调配^[6]. 然而大量的实时传输数据不仅会损耗海量资源同时还存在隐私泄露的问题^{[7, 8]}. 因此为了克服以上问题, 数据聚合技术被引入, 它可以节省计算资源, 同时允许控制中心收集聚合数据而不是单个数据的思想很好的保护用户的隐私且不影响数据的分析和电力供应的调整.

但是, 现有大多数聚合方案存在以下两个问题: 很多方案设计时采用代价很高的公钥同态加密技术, 这对资源受限的智能电表很不友好; 许多方案没有考虑错误容忍的问题, 但是智能电表是普通电子设备很有可能出现故障, 这样会导致整个系统无法正常运作.

基于上述问题, 本文提出了一个智能电网中高效的支持错误容忍的数据聚合方案, 该方案能抵抗由网关和控制中心发起的合谋攻击, 此外, 当智能电表故障时, 控制中心仍能正常恢复聚合数据.

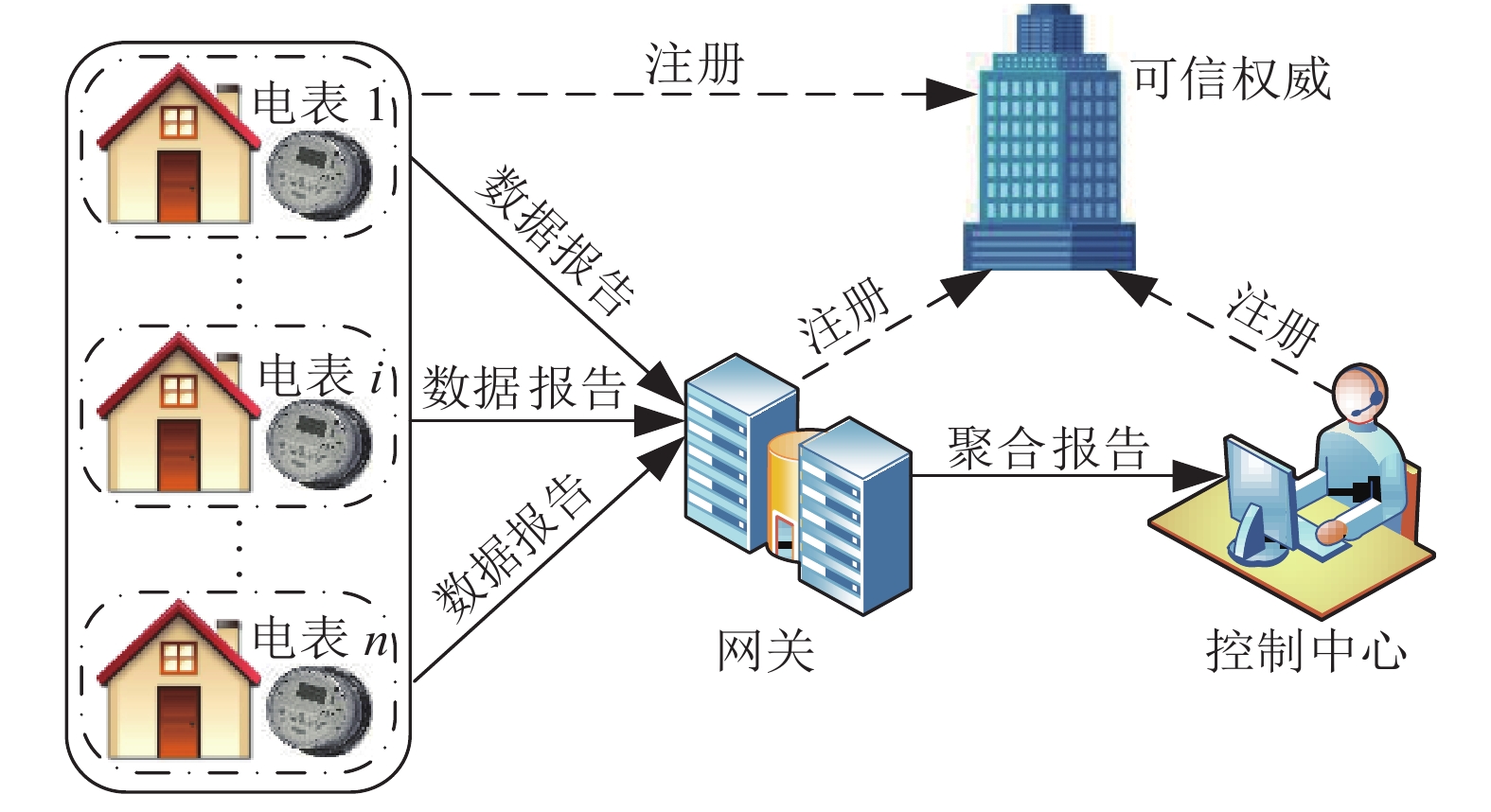
1 背景知识 1.1 系统模型

本文的系统模型如图1所示, 其中有4个实体: 可信中心TA, 控制中心CC, 网关GW和智能电表SM_i $ (i = 1, 2, \cdots , n)$ . GW负责其下n个 $\textit{SM}{_i}\;(n \gt 1)$ .

(1) TA: 表示完全可信的实体. TA产生系统参数, 并负责 $\textit{SM}{_i}$ , GW和CC的注册. 如果 $\textit{SM}{_i}$ 产生故障, TA生成虚拟密文.

(2) CC: 诚实且好奇的实体. 收到GW的聚合报告, CC检查报告的完整性, 解密和分析电力测量数据.

(3) GW: 诚实且好奇的实体, 负责检验和聚合 $\textit{SM}{_i}$ 的电力报告并传输聚合报告给CC.

(4) $\textit{SM}{_i}$ : 表示第i个智能电表, 是可信实体, $\textit{SM}{_i}$ 主要收集和加密电力测量数据, 然后传输电力报告给GW.

1.2 安全需求

(1)机密性: 方案中使用的密文不能被敌手攻破, 即敌手不能获得真正的明文消息, 只能得到无意义的字符串.

(2)可认证性: 敌手可能伪装成合法用户来破坏系统, 所以该方案应该对报告的来源进行身份认证.

(3)完整性: 在公开信道中传输的报告可能被敌手拦截篡改再重新发送, 这会给正常报告注入错误数据. 因此该方案应该能检测报告是否被篡改.

(4)错误容忍: 智能电表有可能发生故障, 当有故障发生时, 系统应该能继续正常运行.

(5)抵抗合谋攻击: GW和CC是半可信的实体, 他们联合起来好奇单个智能电表的电力数据. 在该方案中, 合谋攻击应该被抵抗.

(6)抵抗重放攻击: 攻击者将以前在公开信道中传输的报告重新传输, 扰乱系统运行. 在该方案中, 重放攻击应该被抵抗.

1.3 设计目标

(1)隐私保护: 除了TA, 其他任何实体不允许知道单个 $S{M_i}$ 的电力测量数据. 聚合的电力测量数据只允许CC获得, 用于分析和优化.

(2)高效性: 由于智能电表和网关等实体的计算和通信资源都是有限的, 所以在满足上述隐私保护的前提下, 尽可能使方案的计算和通信代价最小.

1.4 椭圆曲线密码学

椭圆曲线E由方程 ${y^2} = {x^3} + ax + b{\text{ mod }}p$ 所定义^[9], 该方程是基于有限域 ${F_p}$ 上的, 这里 $a, b \in {F_p}$ 且满足 $4{a^3} + $ $ 27{b^2} \ne 0$ . 所有E上的点和无穷远点O共同组成了加法循环群 ${\mathbb{G}}$ , 阶数是q, 生成元是P. 标量点乘定义为 $kP=P+P+\cdots +P\;(k次)$ , 这里 $k \in {\mathbb{Z}}_q^*$ .

椭圆曲线离散对数假设(ECDLA): 给定任意 $P,\;aP \in \mathbb{G}$ , ( $a, b \in Z_q^*$ ), 在多项式时间算法内很难算出 $a \in \mathbb{Z}_q^*$ .

1.5 对称同态加密

文献[10]首次提出对称同态加密技术, 然而文献[11]将其攻破, 根据其弱点, 现在本文改进该技术, 具体描述如下:

$KeyGen(\tau )$ : 输入安全参数 $\tau $ , 密钥生成算法输出对称同态加密密钥 $K = \{ s, d, \hat q, \hat p\} $ , 其中两个大素数 $ \hat p, \hat q $ 满足 $ \hat p \gg \hat q $ , $ s $ 是从 $ \mathbb{Z}_{\hat p}^* $ 随机选择的, 密文等级d是小的正整数. 计算公开参数 $ N = \hat p\hat q $ .

$Enc(K, m, r)$ : 输入明文 $m \in \mathbb{Z}_{\hat q}^*$ 和对称同态加密密钥 $K = \{ s, d, \hat q, \hat p\} $ , 加密算法选择随机数 $r \in {\{ 0, 1\} ^\tau }$ 满足 $|r| + $ $ |\hat q| \lt {\kern 1pt} {\kern 1pt} {\kern 1pt} |N|$ , 然后加密明文:

$ c = {s^d}(r\hat q + m)\boldsymbolod N $

$Dec(K, c)$ : 输入密文c和对称同态加密密钥 $K = $ $ \{ s, d, \hat q, \hat p\} $ , 解密算法计算:

$ m = ({s^{ - d}}c\boldsymbolod N)\boldsymbolod \hat q $

2 本文方案 2.1 系统建立

(1)基于非奇异椭圆曲线E, TA生成阶数为素数q的加法循环群 $ \mathbb{G} $ 和其生成元P.

(2) TA生成对称同态加密密钥 $K = \{ s, d, \hat q, \hat p\} $ . TA计算公开参数 $ N = \hat p\hat q $ .

(3) TA随机选取一组盲化因子 ${\xi _1}, {\xi _2}, \cdots , {\xi _n} \in \mathbb{Z}_N^*$ , 然后计算 $\xi = \displaystyle\sum\nolimits_{i = 1}^n {{\xi _i}}$ .

(4) TA选择安全哈希函数 $ {H_i}:{\{ 0, 1\} ^*} \to \mathbb{Z}_q^*(i = 1, 2) $ , 公布系统参数: $ \lt \mathbb{G}, q, P, N, {H_1}, {H_2} \gt $ .

2.2 注册

所有 $\textit{SM}{_i}\;(i = 1, 2, \cdots , n)$ , $ GW $ 和 $ CC $ 都需要在可信中心TA处进行注册, 并获得相应的密钥和盲化因子.

(1) $\textit{SM}{_i}$ 注册

① $\textit{SM}{_i}$ 随机选择 $ {s_i} \in \mathbb{Z}_q^* $ 作为自己的签名私钥, 选择随机数 $ {u_i} \in \mathbb{Z}_q^* $ , 计算对应公钥 ${S_i} = {s_i}P$ 和知识签名 ${U_i} = $ $ {u_i}P, {v_i} = {s_i}{H_1}\left( {I{D_i}, {S_i}, {U_i}} \right) + {u_i}$ , 然后发送 $\lt I{D_i}, {S_i}, {U_i}, {v_i} \gt$ 给TA.

② TA收到后, 检查 $ {v_i}P = {S_i}{H_1}\left( {I{D_i}, {S_i}, {U_i}} \right) + {U_i} $ 是否成立, 如果成立, 公布 $ \lt I{D_i}, {S_i}, {U_i}, {v_i} \gt $ , 并秘密发送 $ \lt {\xi _i}, K \gt $ 给 $S{M_i}$ .

(2) GW注册

① GW随机选择 $ {s_{GW}} \in \mathbb{Z}_q^* $ 作为自己的签名私钥, 选择随机数 $ {u_{GW}} \in \mathbb{Z}_q^* $ , 计算公钥 ${S_{GW}} = {s_{GW}}P$ 和知识签名 ${U_{GW}} = {u_{GW}}P, {v_{GW}} = {s_{GW}}{H_1}\left( {I{D_{GW}}, {S_{GW}}, {U_{GW}}} \right) + {u_{GW}}$ , 然后发送 $ \lt I{D_{GW}}, {S_{GW}}, {U_{GW}}, {v_{GW}} \gt $ 给TA.

② TA收到消息后, 检查下列等式 ${v_{GW}}P = {S_{GW}}{H_1} $ $ \left( {I{D_{GW}}, {S_{GW}}, {U_{GW}}} \right) + {U_{GW}}$ 是否成立, 如果成立, 公布 $ \lt I{D_{GW}}, {S_{GW}}, {U_{GW}}, {v_{GW}} \gt $ .

(3) CC注册

① CC随机选择 $ {s_{CC}} \in \mathbb{Z}_q^* $ 作为自己的签名私钥, 选择随机数 $ {u_{CC}} \in \mathbb{Z}_q^* $ , 计算对应公钥 ${S_{CC}} = {s_{CC}}P$ 和知识签名 ${U_{CC}} = {u_{CC}}P, {v_{CC}} = {s_{CC}}{H_1}\left( {I{D_{CC}}, {S_{CC}}, {U_{CC}}} \right) + {u_{CC}}$ , 然后发送 $ \lt I{D_{CC}}, {S_{CC}}, {U_{CC}}, {v_{CC}} \gt $ 给TA.

② TA收到消息后, 检查下列等式 ${v_{CC}}P = {S_{CC}}{H_1} $ $ \left( {I{D_{CC}}, {S_{CC}}, {U_{CC}}} \right) + {U_{CC}}$ 是否成立, 如果成立, 公布 $ \lt I{D_{CC}}, {S_{CC}}, {U_{CC}}, {v_{CC}} \gt $ , 并秘密发送 $ \lt \xi , K \gt $ 给CC.

2.3 报告产生

(1) $\textit{SM}{_i}$ 收集电力测量数据 ${m_i}$ , 随机选择 $ {r_i} $ 满足 $|{r_i}| + |\hat q| \lt {\kern 1pt} {\kern 1pt} |N|$ , 计算:

$ {C_i} = {s^d}({r_i}\hat q + {m_i} + {\xi _i})\boldsymbolod N $

(2) $\textit{SM}{_i}$ 随机选择 $ {e_i} \in \mathbb{Z}_q^* $ , 计算:

$ {E_i} = {e_i}P, {\sigma _i} = {s_i}{H_2}\left( {{C_i}, {S_i}, I{D_i}, {E_i}, {T_i}} \right) + {e_i} $

其中, ${T_i}$ 是当前时间戳. $\textit{SM}{_i}$ 发送 $ \lt {C_i}, I{D_i}, {E_i}, {\sigma _i}, {T_i} \gt $ 给GW.

2.4 报告聚合

(1)当收到所有 $\textit{SM}{_i}$ 的报告 $ \lt {C_i}, I{D_i}, {E_i}, {\sigma _i}, {T_i} \gt $ 后, GW首先检查时间戳 ${T_i}$ 的有效性, 然后为了加速验证^[12], GW随机选取一组小数 ${\theta _1}, {\theta _2}, \cdots , {\theta _n} \in [1, {2^n}]$ , 检查等式:

$ \left(\sum\nolimits_{i = 1}^n {{\theta _i}{\sigma _i}} \right)P = \sum\nolimits_{i = 1}^n {{\theta _i}{S_i}{H_2}({C_i}, {S_i}, I{D_i}, {E_i}, {T_i})} + \sum\nolimits_{i = 1}^n {{\theta _i}{E_i}} $

是否成立, 如果成立, 计算:

$ C = \sum\nolimits_{i = 1}^n {{C_i}} \boldsymbolod N $

(2) GW随机选择 $ {e_{GW}} \in \mathbb{Z}_q^* $ , 计算 ${E_{GW}} = {e_{GW}}P, {\sigma _{GW}} = $ $ {s_{GW}}{H_2}\left( {C, {S_{GW}}, I{D_{GW}}, {E_{GW}}, {T_{GW}}} \right) + {e_{GW}}$ 其中 ${T_{GW}}$ 是当前时间戳. 最后, GW发送报告 $ \lt C, I{D_{GW}}, {E_{GW}}, {\sigma _{GW}}, {T_{GW}} \gt $ 给CC.

2.5 报告阅读

(1)当收到GW的报告 $ \lt C, I{D_{GW}}, {E_{GW}}, {\sigma _{GW}}, {T_{GW}} \gt $ 后, CC首先检查时间戳 ${T_{GW}}$ 的有效性, 然后验证等式:

$ {\sigma _{GW}}P = {S_{GW}}{H_2}\left( {C, {S_{GW}}, I{D_{GW}}, {E_{GW}}, {T_{GW}}} \right) + {E_{GW}} $

(2)如果等式成立, CC解密聚合的电力报告:

$ \sum\nolimits_{i = 1}^n {{m_i}} = [({s^{ - d}}C - \xi )\boldsymbolod N]\boldsymbolod \hat q $

(3) CC分析该GW所管辖区域的电力数据并优化电力分配策略.

正确性:

$ \begin{split} & \left[\left({s^{ - d}}C - \xi \right)\boldsymbolod N\right]\boldsymbolod \hat q \hfill \\ & = \left[\left({s^{ - d}}\displaystyle\sum\nolimits_{i = 1}^n {{C_i}} - \xi \right)\boldsymbolod N\right]\boldsymbolod \hat q \hfill \\ & = \left[\left({s^{ - d}}\displaystyle\sum\nolimits_{i = 1}^n {({s^d}({r_i}\hat q + {m_i} + {\xi _i}))} - \xi \right)\boldsymbolod N\right]\boldsymbolod \hat q \hfill \\ & = \left[\left(\hat q\displaystyle\sum\nolimits_{i = 1}^n {{r_i}} + \displaystyle\sum\nolimits_{i = 1}^n {{m_i}} + \displaystyle\sum\nolimits_{i = 1}^n {{\xi _i}} - \xi \right)\boldsymbolod N\right]\boldsymbolod \hat q \hfill \\ & = \left(\hat q\displaystyle\sum\nolimits_{i = 1}^n {{r_i}} + \displaystyle\sum\nolimits_{i = 1}^n {{m_i}} \right)\boldsymbolod \hat q \hfill \\ & = \displaystyle\sum\nolimits_{i = 1}^n {{m_i}} \hfill \\ \end{split} $

本方案的具体流程如图2所示.

2.6 错误容忍

假如第1个到第 $t\;(t \lt n)$ 个 $\textit{SM}{_i}$ 是正常工作的, 第 $t + 1$ 个到第n个 $\textit{SM}{_i}$ 发生了故障, 无法发送电力报告给GW.

(1) GW像第2.4节一样先进行时间戳的检查和完整性的验证, 然后计算 $\hat C = \displaystyle\sum\nolimits_{i = 1}^t {{C_i}} \boldsymbolod N$ 并发送给CC, 同时告知TA故障的智能电表有哪些.

(2) TA收到后, 替所有故障的电表计算聚合虚拟密文 ${C_{TA}} = {s^d}\left({r_i}\hat q + 0 + \displaystyle\sum\nolimits_{i = t + 1}^n {{\xi _i}} \right)\boldsymbolod N$ , 发送它给CC.

(3) CC收到 $ \lt \hat C, {C_{TA}} \gt $ 后, 解密计算:

$ \sum\nolimits_{i = 1}^t {{m_i}} = [({s^{ - d}}(\hat C + {C_{TA}}) - \xi )\boldsymbolod N]\boldsymbolod \hat q $

3 安全分析与性能评价 3.1 安全需求分析

本小节将逐个分析第1.2节中所提出的安全需求.

(1)机密性: 方案中, 假如外部敌手获得了一个明文密文对 $({m_i}, {C_i})$ , 还存在5个未知数; 即使敌手获得 $\lambda $ 对 $({m_i}, {C_i})$ , 仍然存在 $2\lambda + 3$ 个未知数, 由于欠定非线性系统的求解是NP困难的^[10], 这样无法在多项式时间内破解该方程. 因此, 该方案能保证机密性.

(2)可认证性: ${\textit{SM}}{_i}$ 提前用自己的身份进行了注册, 后面发送报告时, GW在对签名验证的同时也对身份合法性进行认证. 因此, 该方案可以实现用户的认证.

(3)完整性: 利用Schnorr签名^[13], 密文报告被签名为 $({\sigma _i}, {E_i})$ , 基于ECDL假设, 没有密钥 ${s_i}$ 的敌手无法产生合法签名, 篡改的报告在检测时就会被拒绝. 所以, 方案可以保证报告的完整性.

(4)错误容忍: 在方案中, 如果某些智能电表 ${\textit{SM}}{_i}$ 发生故障无法发送报告, TA会替故障电表产生聚合的虚拟密文 $ {C_{TA}} $ 来保证CC可以顺利解密密文. 因此, 本方案可以支持错误容忍.

(5)抵抗合谋攻击: 如果GW和CC合谋想获得某一个 ${\textit{SM}}{_i}$ 的电力数据, 通过密钥K的解密, CC只能获得 ${m_i} + {\xi _i}$ , 电力数据 ${m_i}$ 被盲化因子 ${\xi _i}$ 所保护. 因此, 本方案可以抵抗合谋攻击.

(6)抵抗重放攻击: ${\textit{SM}}{_i}$ 和GW发送的报告中都包含时间戳 ${T_i}$ 或 ${T_{GW}}$ , GW和CC可以检查报告的新鲜度. 因此, 本方案可以抵抗重放攻击.

3.2 功能比较

本小节将所提方案与文献[14-16]进行功能对比. 如表1, 其中F1表示机密性; F2表示可认证性; F3表示完整性; F4表示错误容忍; F5表示抵抗合谋攻击; F6表示抵抗重放攻击. 从表1中可以看出, 文献[14]无法支持错误容忍功能, 文献[15]不能抵抗重放攻击, 文献[16]不能抵抗合谋攻击. 而我们所提出的方案可以满足所有在第1.2节中描述的安全需求.

3.3 计算代价比较

文献[14,16]基于双线性对, 它定义为 $e:{\mathbb{G}_1} \times $ $ {\mathbb{G}_1} \to {\mathbb{G}_T}$ , 这里 ${\mathbb{G}_1}$ 是加法循环群; ECC中循环群记作 $\mathbb{G}$ . 本文使用MIRACL Crypto SDK^[17]得到密码学操作的执行时间并列举在表2中, 其硬件设备为2.53 GHzi5CPU和4 GB内存的笔记本电脑, 操作系统是64位Windows 10.

对于文献[14]来说, 报告产生阶段的计算时间是 ${T_{E\text{-}P}} + 2{T_{e\text{-}p}} + {T_{m\text{-}E}} + {T_{mtp}} = 16.04{\kern 1pt} {\kern 1pt} {\rm{ms}}$ , 聚合阶段的时间是 $(n + 2){T_{BP}} + (n + 1){T_{mtp}} + {T_{m\text{-}E}} = (13.89n + 24.58)\; {\rm{ms}}$ , 阅读阶段的时间是 $2{T_{BP}} + {T_{mtp}} + {T_{D\text{-}P}} + 2{T_{e\text{-}p}} = 34.35{\kern 1pt} {\kern 1pt} {\rm{ms}}$ . 总的计算开销是 $(29.93n + 58.93)\; {\rm{ms}}$ .

对于文献[15]来说, 报告产生阶段的计算时间是 ${T_{e\text{-}{n^2}}} + {T_{E\text{-}P}} + {T_{e\text{-}G}} + {T_{e\text{-}n}} = 15.84{\kern 1pt} {\kern 1pt} {\rm{ms}}$ , 聚合阶段的时间是 $(n + 2){T_{e\text{-}n}} + n{T_{e\text{-}G}} = (2n + 1.16)\; {\rm{ms}}$ , 阅读阶段的时间是 ${T_{e\text{-}n}} + {T_{D\text{-}P}} = 10.47{\kern 1pt} {\kern 1pt} {\rm{ms}}$ . 总的开销是 $(17.84n + 11.63) \;{\rm{ms}}$ .

对于文献[16]来说, 报告产生阶段的计算时间是 $2{T_{e\text{-}T}} + {T_{e\text{-}G}} = 2.46{\kern 1pt} {\kern 1pt} {\rm{ms}}$ , 报告聚合阶段的计算时间是 $(n + 3){T_{e\text{-}G}} = (1.42n + 4.26)\; {\rm{ms}}$ , 报告阅读阶段的计算时间是 $3{T_{e\text{-}G}} + {T_{BP}} + {T_{\log }} = 15.21{\kern 1pt} {\kern 1pt} {\rm{ms}}$ . 总的计算开销是 $(3.88n + $ $ 19.47) \;{\rm{ms}}$ .

对于本方案来说, 报告产生阶段的计算时间是 ${T_{m\text{-}E}} + {T_{e\text{-}N}} = 0.6{\kern 1pt} {\kern 1pt} {\rm{ms}}$ , 报告聚合阶段的计算时间是 $(n + 2){T_{m\text{-}E}} = (0.38n + 0.76)\; {\rm{ms}}$ , 报告阅读阶段的时间是 $2{T_{m\text{-}E}} + {T_{e\text{-}N}} = 0.98{\kern 1pt} {\kern 1pt} {\rm{ms}}$ . 总的开销是 $(0.98n + 1.74) \;{\rm{ms}}$ .

图3展示了总体计算代价与智能电表数量之间的关系比较图, 从图中可以看出: 相比于文献[14–16], 所提方案的总体计算代价的增长是最缓慢的. 这很适合于计算资源有限的智能电表和网关.

3.4 通信代价比较

为了更清晰地比较通信代价, 本文做了如下设定: $|\mathbb{G}| $ = 160 bits; $|{\mathbb{G}_1}| $ = 512 bits; $|{\mathbb{G}_T}|$ = 1024 bits; $|\mathbb{Z}_q^*| = $ 160 bits; $|{\mathbb{Z}_n}| $ = 1024 bits; $|{\mathbb{Z}_{{n^2}}}| $ = 2048 bits; $|N| = 768 \; {\rm{bits}}$ ; 身份和时间戳的长度均为 $32 \; {\rm{bits}}$ . 表3比较了文献[14–16]与所提方案的通信代价.

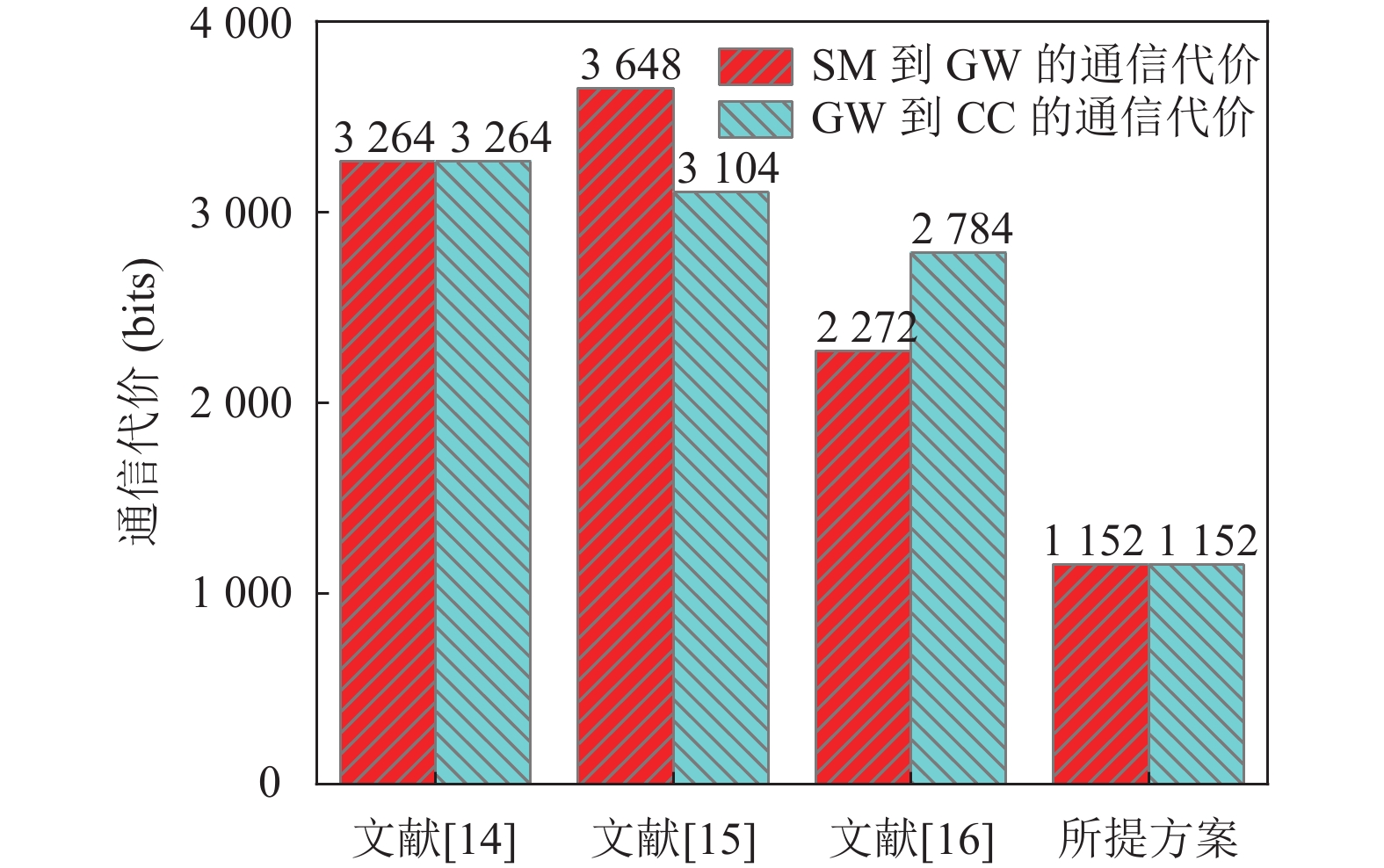
图4形象地展示了通信代价比较图. 从图中可以看出: 相比于文献[14–16], 所提方案的SM到GW之间的和GW到CC之间的通信代价是最低的, 十分契合通信资源有限的SM和GW.

4 结论

为了克服现有数据聚合方案的问题, 本文提出了一个智能电网中高效的支持错误容忍的数据聚合方案, 其利用改进的对称同态加密技术实现高效性, 同时利用椭圆曲线密码学技术满足了报告的完整性和可认证性. 另外该方案可以抵抗合谋攻击和重放攻击, 保护了用户的隐私信息. 当有智能电表发生故障无法发送报告时, 权威中心会帮忙产生聚合的虚拟密文以确保控制中心正常解密聚合数据. 最后, 本文满足所提的安全需求, 并且轻量级的计算代价和通信代价适用于资源有限的智能电表.