Spark是主流基于内存的大数据计算框架, 因其低延时, 高性能, 生态丰富被广泛使用[1]. 传统的机器学习系统正在迁移到Spark平台上, 利用并行计算和内存迭代等特点提升训练效率, 优化Spark框架执行效能可以节约用电成本, 降低碳排放[2-4]. 基于内存迭代计算不具有稳定性, 易发生数据丢失, 在多次迭代计算中, RDD数据丢失会导致高度冗余计算, Spark引入检查点机制避免因内存数据丢失导致的重复计算问题.Spark检查点备份过程是在作业计算完成后触发且需要根据检查点RDD血统依赖重新计算备份数据结果集, 具有较大计算开销. 在实际使用中, 为了避免检查点写入HDFS时的RDD重算过程, 一般在作业初次计算时将需要保存为检查点的RDD进行缓存, 在写入HDFS时从缓存中读取检查点RDD数据. 然而, 检查点缓存数据需要由编程人员手动清理, 而在Spark框架中检查点执行过程对编程人员是透明的, 过早清理检查点缓存数据可能无法避免检查点写入HDFS时的重复计算问题, 太迟清理检查点缓存数据影响内存使用, 所以检查点缓存数据清理策略就成为一个值得研究的问题. 为此, 本文建模推导出检查点缓存在大量检查点环境下不具有可扩展性, 并提出基于效用熵的检查点缓存并行清理(PCC)策略, 通过在效用最佳时间点自动清理失效检查点缓存数据, 达到避免重复计算效果, 同时优化内存占用和程序执行效能.
1 相关工作基于内存计算的缺点是数据易丢失且对内存资源要求较高, 高效容错机制可以提升作业恢复执行效率, 提高内存利用率[5]. 目前国内外学者针对并行计算框架容错效率优化研究做了大量工作.
针对检查点容错效率优化, 易会战等[6]提出基于异步缓存的异步检查点技术, 主要思想是将检查点备份过程分为两步, 第一步将需要备份的数据写入内存, 第二步通过帮助程序异步写入磁盘, 节省同步写入的时间开销. Ying等[7]针对Spark作业内检查点选择问题建模作业恢复模型, 提出关键RDD权重计算公式, 优先最大权重 RDD实现容错优化. Zhu等[8]提出分离Spark检查点选择和写入时机的策略, 选择作业间重用RDD作为待写入检查点, 当堆栈区老生代负载超过阈值, 将所有待写入的检查点写入HDFS, 降低垃圾全回收次数, 提高容错效率.
容错机制涉及多级存储, 针对缓存级别优化, Duan等[9]提出分布式缓存替换策略, 以计算代价、分区大小、使用次数等建立清理权值, 当内存不足时优先清理低权值分区, 实验证明有效提升内存利用率, 缺点是该策略无法感知分区数据是否使用完毕, 未使用的检查点缓存数据可能被清理. 刘恒等[10]提出考虑任务的Locality Level因素综合计算代价、分区大小、使用次数、RDD生命周期等参数建立分区清理权值, 优先清理低价值分区, 实验证明整体效率优于LRU策略, 但是由于检查点缓存被后台作业引用, 该策略无法收集相关权值参数. More等[11]提出利用闪存优势提升缓存性能, 但需要增加硬件设备, 有一定开销成本. 廖旺坚等[12]提出适当用基于DAG图重算代替缓存的策略优化内存消耗, 但是应用场景有限, 仅当RDD计算代价很小时该策略有效, 对检查点数据来说并无效果. 赵俊先等[13]立足单节点、大内存服务器环境, 针对内存不足频繁调用垃圾回收机制且大内存使得垃圾回收开销巨大问题, 拆分原本主要服务各节点间的数据传输序列化功能和缓存功能, 提出非序列化RDD存储结构减小序列化带来的计算开销, 利用堆下存储区域无垃圾回收特点降低垃圾回收开销, 提升缓存效率, 从而提升作业整体执行效率, 然而单节点环境影响Spark并行执行能力, 应用场景有限. 卞琛等[14]构建用户程序RDD结构树记录缓存引用待使用次数, 当树节点引用值为零时, 清理缓存RDD, 实验证明该策略有效提升缓存利用率. 但由于检查点缓存是Spark后台检查点作业引用, 结构树无法感知运行状态, 故尚不能对检查点缓存起到清理优化效果.
与以往工作不同, 本文重点在于通过优化Spark检查点缓存清理过程提升容错效率.
2 基于检查点缓存效用熵的并行清理策略 2.1 问题建模与分析本节抽象出来相关属性和定义, 分析检查点执行流程, 并推导出现有检查点缓存清理方法随着检查点数量增多, 其失效缓存清理时延和空间占用增大, 不具有可扩展性.
定义1. 作业检查点. 作业检查点
定义2. 作业检查点缓存. 作业检查点缓存
定义3. 内存资源槽. 内存资源槽
检查点执行流程. 设第i道作业中, 检查点集合为
定义4. 失效检查点缓存. 若
定义5. 失效检查点缓存清理时延. 第i个失效检查点缓存时延
| $ dela{y_i} = clean\_c{t_i} - write\_{t_i} $ | (1) |
推论1. 随着检查点数量增加, 失效检查点缓存清理时延增大.
证明: 设第一个检查点写入HDFS用时为
| $ {T_k} = \sum\nolimits_{i = k + 1}^{i = n} {{t_i}} + \sum\nolimits_{i = 1}^{i = k - 1} {{t_{mi}}} $ |
当有n+j个检查点时, 第k个失效检查点缓存清理时延为:
| $ T_k' = \sum\nolimits_{i = k + 1}^{i = n + j} {{t_i}} + \sum\nolimits_{i = 1}^{i = k - 1} {{t_{mi}}} $ |
通过作差比较:
证明完毕.
推论2. 随着检查点数量增加, 失效检查点缓存占用总空间增大.
证明: 设第一个检查点RDD大小为
当有k个检查点时, 最后一个检查点写入HDFS后, 失效检查点缓存占用空间为:
| $ {V_k} = \sum\nolimits_{i = 1}^{i = k} {si{\textit{z}}{e_i}} $ |
当有k+j个检查点时, 最后一个检查点写入HDFS后, 失效检查点缓存占用空间为:
| $ {V_{k + 1}} = \sum\nolimits_{i = 1}^{i = k + j} {si{\textit{z}}{e_i}} $ |
通过作差比较:
证明完毕.
2.2 最佳清理时间点计算本节提出检查点缓存效用熵定义, 量化检查点缓存效用和占用的内存资源槽匹配度, 利用效用最佳匹配原则计算最小化资源占用时的最佳清理时间点, 为算法设计与实现提供理论依据.
定义6. 检查点缓存累加和.检查点缓存累加和刻画在内存资源槽
| $ \textit{SUM}{_i} = \int_{write\_c{t_i}}^{clean\_c{t_i}} {si{\textit{z}}{e_i}dt} $ |
定义7. 检查点缓存效用熵.衡量检查点缓存和内存资源槽的匹配程度, 用检查点效用函数值
| $ \begin{split} & Fr(CA\_Checkpoin{t_i}) =\\ & \left\{\begin{array}{l} 0,\;\;clean\_ct_i \lt write\_t_i\\ Ft(CA\_Checkpoint_i), \;\; clean\_ct_i \geqslant write\_t_i \end{array}\right. \end{split}$ |
执行器m内检查点缓存效用熵记为:
| $ {Q_m} = \sum\nolimits_{job} {\sum\nolimits_{i = 1}^{i = k} {\frac{{Fr(CA\_Checkpoin{t_i})}}{{SU{M_i}}}} } $ |
检查点缓存效用熵越大, 说明检查点缓存与内存槽越匹配, 内存资源槽利用率越高, 故检查点缓存清理的优化目标函数为:
| $\left\{\begin{split} & \max ({Q_m}) \\ & {\rm s.t.}\;\;clean\_ct_i \gt write\_ct_i, si{\textit{z}}e_i \gt 0,\\ &\;\;\;\; Fr(CA\_Checkpoin{t_i}) \geqslant 0 \end{split}\right.$ |
定理1. 效用最佳匹配原则.在保证检查点缓存效用的前提下, 当且仅当
证明. 若不影响检查点缓存效用, 则检查点缓存数量k、缓存大小
由定义2、定义4可知,
证明完毕.
2.3 算法设计与实现上节基于效用熵概念, 通过效用最佳匹配原则证明给出避免检查点重复计算, 同时最小化其内存占用时长的检查点缓存清理时间点是检查点写入HDFS时刻, 本节结合Spark检查点实现原理和编程接口给出具体算法设计与实现步骤.
检查点缓存并行清理(PCC)算法初始化一个空的检查点对象集合, 通过插入后台监听代码片段捕获程序运行中设置的检查点对象, 对检查点对象集合中元素状态改变监听. 通过分析Spark检查点源码可知, 在检查点数据写入HDFS系统时, 检查点RDD的完成状态标志发生改变, 此刻立即清理该RDD占用的内存空间. 具体步骤如下:
(1)在主进程中启动后台监控程序, 建立RDD监听集合.
(2)依次扫描作业中所有检查点RDD, 并将其对象引用添加到监听集合中.
(3)监听RDD引用集合中检查点的状态, 检测集合中检查点完成状态是否发生改变.
(4)对集合中完成状态发生改变的RDD立即释放缓存空间, 并从该集合中删除该RDD引用.
(5)检测集合中剩余RDD的状态, 重复(3)(4), 直至集合为空.
(6)所有作业运行完毕, 后台监听程序退出.具体执行过程如算法1所示.
算法1. 检查点缓存并行清理算法
输入: 检查点RDD 对象 CheckPointRDD.
初始化: QUEUE ← new List<RDD>; // 初始化清理队列
作业线程:
1. WHILE( CheckPointRDD NOT IN QUEUE)
2. CheckPointRDD.cache();
3. CheckPointRDD.checkpoint();
4. QUEUE.append(CheckPointRDD);
5. END WHILE
监控线程:
6. WHILE TRUE
7. FOR qs IN QUEUE
8. IF qs.checkpointed() THEN
9. qs.unpersist(); //释放失效检查点缓存空间
10. QUEUE.pop(qs); //删除已经释放空间的RDD引用
11. END IF
12. END FOR
13. IF QUEUE.size() == 0 THEN
14. break;
15. END IF
16. END WHILE
算法1中检查点状态监听队列及时删除已经释放空间的检查点对象引用, 提高队列元素扫描速度, 避免出现内存泄露问题. 同时, 该算法通过后台监控线程响应检查点状态改变事件从而触发检查点清理动作, 其异步并行过程不影响作业线程执行.从整体执行过程看, 检查点缓存完成重算效用后, 此刻效用熵最大, 立即被清理出内存, 避免失效缓存占用和累积问题.
3 实验验证与分析 3.1 实验环境设置实验环境用14台节点服务器创建14个Spark计算节点的计算集群, 使用Cloudera Manager管理和监控集群, 启动参数按Spark默认配置, 服务器配置如表1所示.
| 表 1 节点服务器配置参数 |
3.2 检查点缓存清理时间点分析
实验设置检查点大小均为1 GB, 通过监听单道PageRank作业执行中每个检查点写入HDFS时刻, 每个检查点缓存清理时刻, 分析PCC策略在选择清理时机上的特点以及PCC策略缩短检查点缓存清理时延的效果.
|
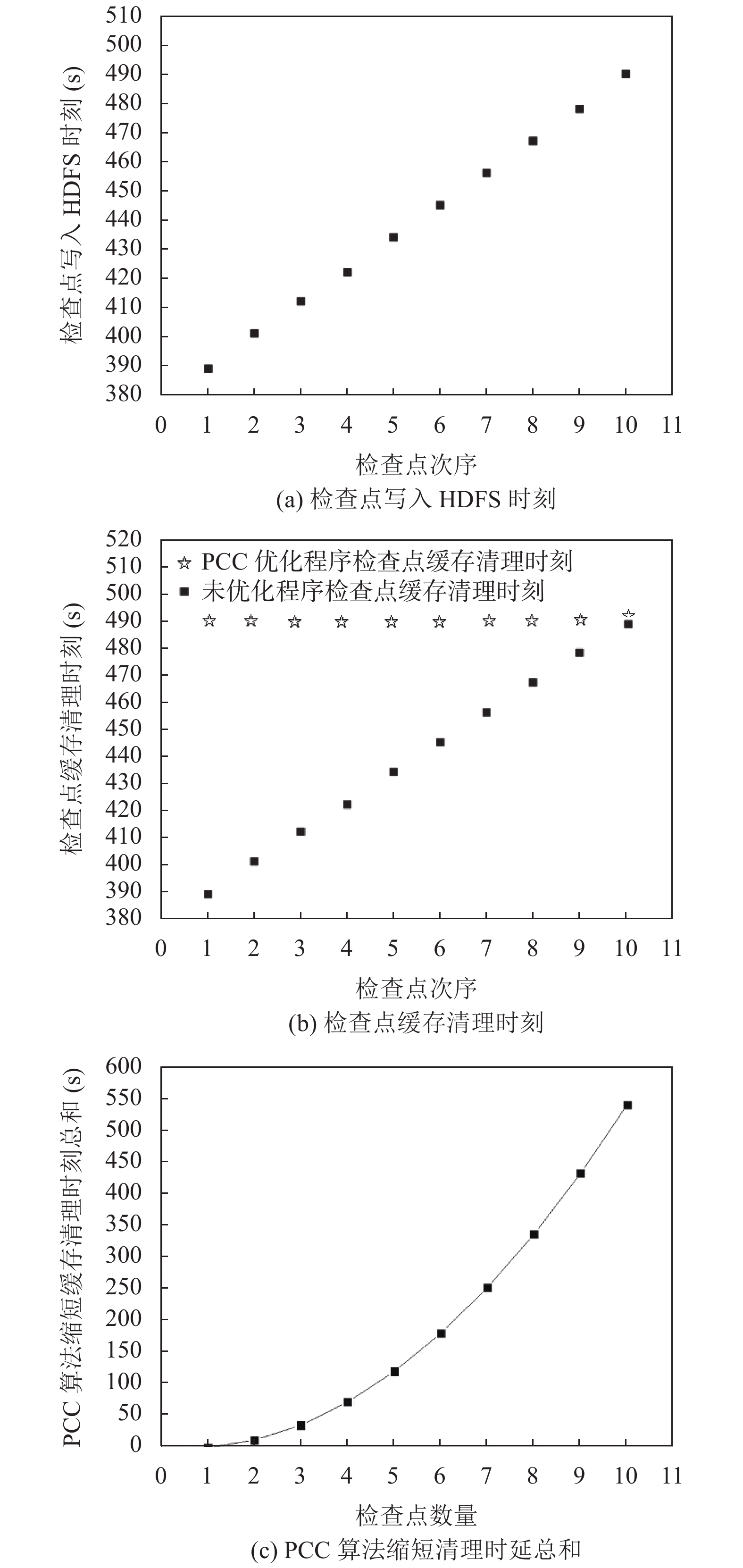
图 1 检查点写入HDFS时刻、缓存清理时刻和PCC算法缩短清理时延总和 |
如图1(a)所示, 检查点写入HDFS的时刻呈现分批次, 逐个写入的特点, 且次序大的检查点写入HDFS时刻晚于次序小的检查点. 对比图1(a)和图1(b), 通过基于PCC算法优化的程序, 检查点缓存清理时间是逐批次进行, 每当检查点写入HDFS后, 即时清理失效检查点缓存, 检查点缓存清理时延近似为0. 未优化的程序检查点缓存清理时间是在最终所有检查点写入HDFS完毕后开始清理. 对比基于PCC算法优化的程序和未优化的程序检查点缓存清理情况, 未优化的程序存在失效检查点缓存长时间占用情况, 且随着检查点个数增加, 未优化的程序累积失效检查点缓存增多, 失效检查点缓存数据清理时延增大, 验证了推论1, 推论2. 观察图1(c), 由于失效检查点缓存存在累积效应, 使用PCC算法优化后, 缓存清理时延总和随着检查点个数增多, 缩短明显.
3.3 失效检查点缓存空间占用分析实验采用基于公平调度的模式并行提交3个page-rank作业, 每个作业用(网页数量/亿, 迭代次数/次, 检查点个数/个)三元组表示, 作业一、二、三依次为(1.2, 10, 30)、(1.2, 15, 30)、(1.2, 30, 30), 测试在多作业并行执行环境下, 失效检查点缓存内存占用情况.
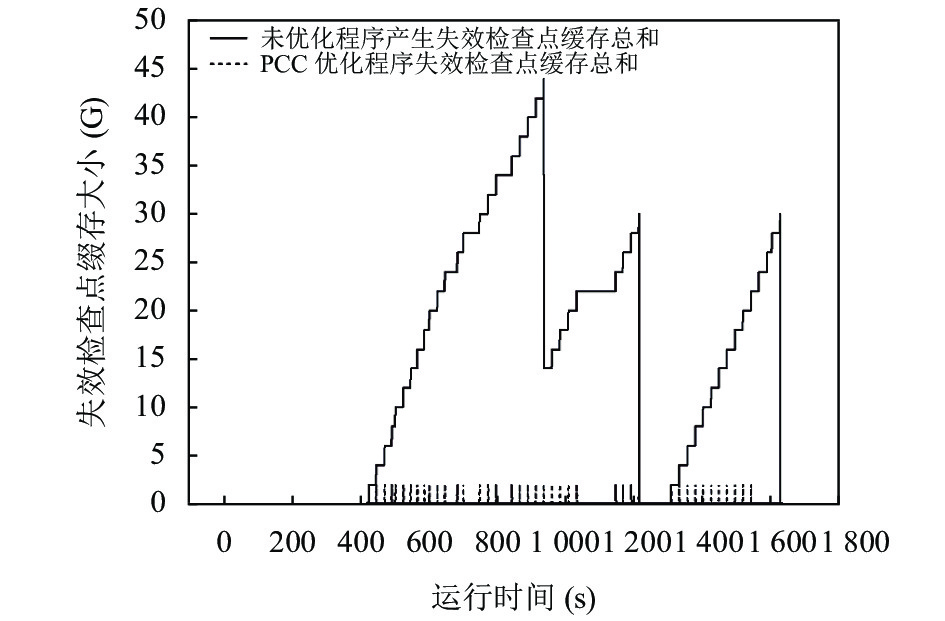
如图2所示, 3道作业先后分别出现失效检查点缓存占用情况. 且多作业环境下, 未优化程序失效缓存占用总和出现累积的负面效应. 观察PCC优化程序失效检查点缓存总和可知, 每当出现检查点缓存失效情况, PCC算法立即清理失效检查点缓存, 内存槽被释放, 有效避免失效检查点缓存累积, 提高内存利用率.
|
图 2 失效检查点缓存占用空间 |
3.4 程序执行效能分析
实验采用公平调度模式测试top-n任务, K-means任务和PageRank任务下3作业同时提交, 每个作业用三元组表示, 设置实验组如表2所示, 每个实验组内作业一为最短作业, 作业三为最长作业, A组、B组、C组、D组、E组实验依次增加计算规模和检查点个数, 测试在多作业并行执行环境下, 失效检查点缓存对长作业执行的影响.通过后台监控进程收集程序执行时间、GC时间等实验结果数据, 使用数显电表记录程序执行前后服务器用电量大小.
| 表 2 实验组设置 |
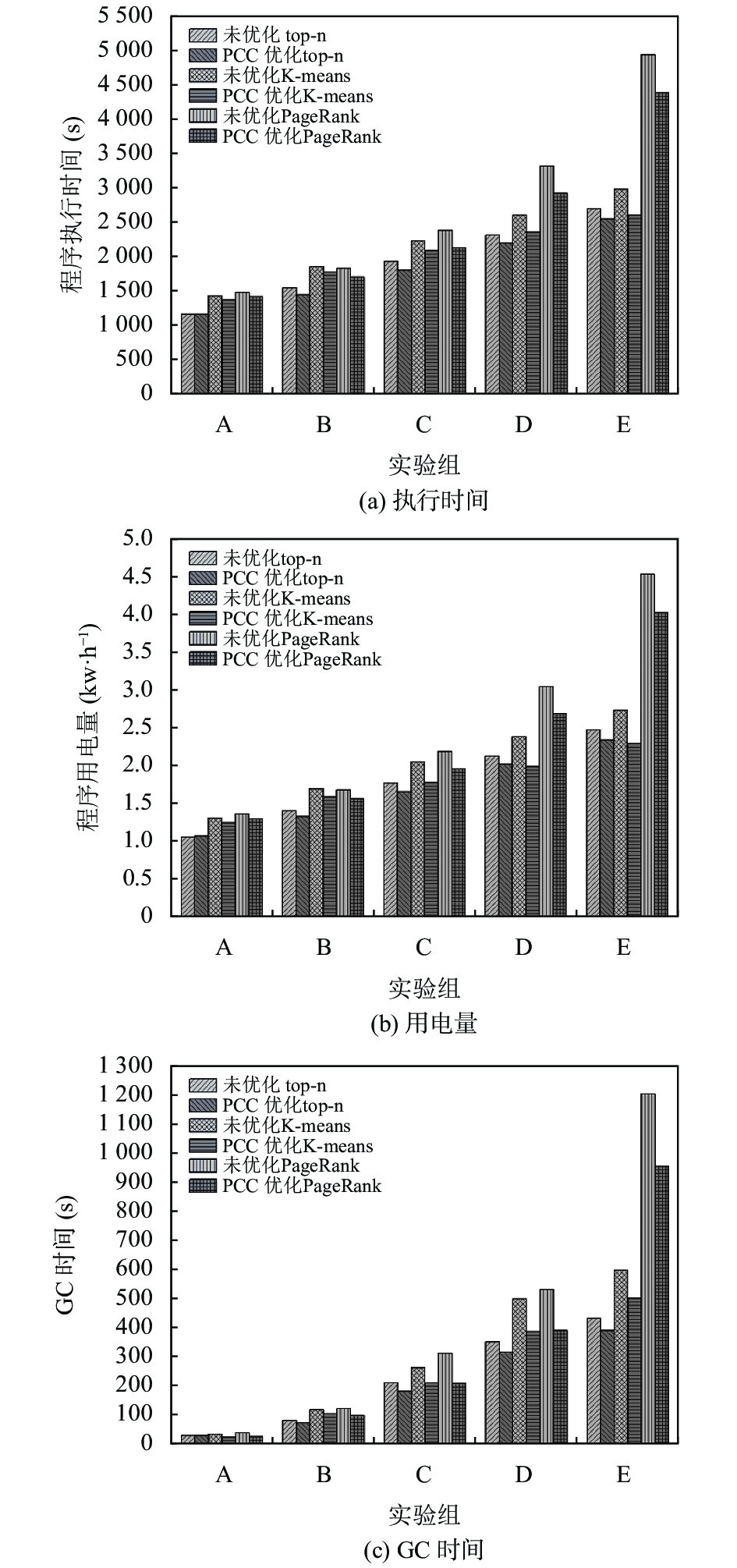
图3显示不同实验组中, 各任务下3道作业并行执行时, 使用PCC优化程序和未优化的程序对执行时间、用电量和GC时间的影响.
|
图 3 程序执行时间、用电量和GC时间 |
如图3所示, 随着最大迭代轮次和检查点数量的增加, 作业执行时间不断增加, GC时间、用电量也不断增加. A组中top-n作业检查点数量为1, PCC未表现出优化效果, K-means和PageRank作业检查点数量大于1, PCC开始表现出优化效果. 随着最大迭代轮次和检查点数量的增加, PCC优化3种任务的效果逐渐明显, 且3种任务均在E组出现最显著的优化效果, 其中top-n作业执行时长缩短6.3%, GC时间缩短9.3%, 用电量节约5.2%, K-means作业执行时长缩短9.7%, GC时间缩短17.1%, 用电量节约9%, PageRank的执行时长缩短10.1%, GC时间缩短19.5%, 用电量节约9.5%.
4 结论与展望针对编程人员清理缓存不及时可能引起的Spark作业检查点失效缓存长时间累积占用资源问题, 通过分析检查点执行流程, 推导出随着检查点数量增加, 失效检查点缓存存在累积现象, 影响内存利用率. 本文提出一种基于检查点缓存效用熵的并行清理策略, 保证检查点缓存效用前提下, 最小化资源占用. 实验结果表明, PCC策略即时自动清理失效检查点缓存数据, 避免失效检查点缓存累积, 有效提升内存利用率, 且随着计算规模和检查点数量增加, 程序执行时间、用电量和GC时间优化效果明显. 下一步研究方向是不同作业负载下缓存管理策略对程序执行性能影响.
| [1] |
Ahmed N, Barczak ALC, Susnjak T, et al. A comprehensive performance analysis of Apache Hadoop and Apache Spark for large scale data sets using HiBench. Journal of Big Data, 2020, 7(1): 110. DOI:10.1186/s40537-020-00388-5 |
| [2] |
Hajkacem MAB, N’Cir CEB, Essoussi N. A parallel text clustering method using Spark and hashing. Computing, 2021, 103(9): 2007–2031.
|
| [3] |
葛庆宝, 陶耀东, 高岑, 等. 基于关键阶段分析的Spark性能预测模型. 计算机系统应用, 2018, 27(8): 232–236.
|
| [4] |
Li HJ, Wei YJ, Xiong Y, et al. A frequency-aware and energy-saving strategy based on DVFS for Spark. The Journal of Supercomputing, 2021, 77(10): 11575–11596.
|
| [5] |
Spark Core Programming. https://www.tutorialspoint.com/apache_spark/apache_spark_rdd.htm. [2020-07-15].
|
| [6] |
易会战, 王锋, 左克, 等. 基于内存缓存的异步检查点容错技术. 计算机研究与发展, 2014, 51(6): 1229–1239.
|
| [7] |
Ying CT, Yu J, He JS. Towards fault tolerance optimization based on checkpoints of in-memory framework Spark. Journal of Ambient Intelligence and Humanized Computing, 2018, 49(4): 11–24.
|
| [8] |
Zhu W, Chen HP, Hu F. ASC: Improving spark driver performance with automatic spark checkpoint. 2016 18th International Conference on Advanced Communication Technology (ICACT). Pyeongchang: IEEE, 2016. 607–611.
|
| [9] |
Duan MX, Li KL, Tang Z, et al. Selection and replacement algorithms for memory performance improvement in Spark. Concurrency and Computation: Practice and Experience, 2016, 28(8): 2473–2486.
|
| [10] |
刘恒, 谭良. 并行计算框架Spark中一种新的RDD分区权重缓存替换算法. 小型微型计算机系统, 2018, 39(10): 2279–2284.
|
| [11] |
More A, Ganjewar P. Dynamic cache resizing in flashcache. Proceedings of the 3rd International Conference on Frontiers of Intelligent Computing: Theory and Applications (FICTA) 2014. Cham: Springer, 2015. 537–544.
|
| [12] |
廖旺坚, 黄永峰, 包从开. Spark并行计算框架的内存优化. 计算机工程与科学, 2018, 40(4): 587–593.
|
| [13] |
赵俊先, 喻剑. 基于RDD非序列化本地存储的Spark存储性能优化. 计算机科学, 2019, 46(5): 143–149.
|
| [14] |
卞琛, 于炯, 英昌甜, 等. 并行计算框架Spark的自适应缓存管理策略. 电子学报, 2017, 45(2): 278–284.
|
 2022, Vol. 31
2022, Vol. 31


