现代条件作战, 面临的将是高精度、远距离、高毁伤的火力战, 装备的受损将成倍增加, 如何保持部队持续作战能力是取得胜利的关键. 在第4次中东战争中, 以色列军队在开战之初有过半的坦克受到损伤, 但凭借其高效的战场抢修能力, 损伤的坦克在基本在一天内就能恢复战斗力, 进而获得了战争主动权. 在海湾战争中, 伊军虽有近万辆坦克和装甲装备, 但无法进行有效的战场抢修, 使其损坏率高达到66%, 最终溃不成军. 因此, 战场已经变成了交战双方战场抢修能力的竞争场, 而装备战场损伤等级评定又是战场抢修的前提与基础[1].
目前对装备战场损伤等级评估的研究方法包括贝叶斯推理[2-4]、案例推理[5]、神经网络[6,7]以及模糊集合理论[8,9]等. 传统的方法如贝叶斯推理、案例推理不能有效处理不确定性信息. 而置信规则推理方法能有效地处理各种类型的数据信息, 建立输入和输出之间的非线性模型. 相比于神经网络、模糊理论等方法, 置信规则库是一个“白盒系统”, 其推理过程与人类思考问题的方式类似, 具有良好的可解释性. 此外, 专家信息可参与也是此方法所特有的优势.
鉴于以上分析, 本文建立一种BRB-ER战损等级评定模型, 采用BRB表示装备战损等级评定过程中所需专家知识和相关信息, 利用局部粒子群算法对初始BRB进行优化学习, 得到更新后的BRB进行推理的过程. 最后, 通过实例验证了所提方法的有效性.
1 装备战损影响因素分析及评定等级划分 1.1 战场损伤影响因素分析分析实际情况下的装备战场受损因素, 主要包括: 威胁因素、装备因素、防护因素. 对装备战损影响因素进行细致分析, 是设计置信规则库前提属性的重要基础. 考虑到实际可以将3种影响因素细化为[10]:
(1) 威胁因素
① 威胁程度(
② 炸点与装备中心之间的距离(
③ 炸点到装备中心连线与地水平线夹角(
④ 弹着点相对于目标装备的位置(
(2) 装备因素(
装备因素主要是指装备的类型和名称, 不同种类和类型装备的损伤机理往往是不同的, 例如: 坦克、履带式步兵战车等装甲装备, 其自身防护能力较强, 战时受到破片、冲击波等损害威胁较低; 而牵引火炮等轮式装备, 其防护能力较差, 战时易受到破片、冲击波等威胁机理的作用发生破孔损伤; 此外, 电子类装备诸如雷达、通信设备等除了会受到破片、冲击波等传统威胁机理的破坏外, 还易受到电磁脉冲的影响. 在此, 我们可以通过编码的方式来表示不同类型的装备.
(3) 防护因素(
合理设置掩体对于降低装备损伤程度具有重要作用, 掩体防护主要包括半掩体、简易掩体和永固掩体3种. 不同掩体的防护能力是不同的, 可对其进行归一化.
1.2 战损等级的划分根据战损装备的功能丧失程度和可修复性, 结合维修保障资源配置情况, 以及修复损伤装备所需时间, 我军习惯上将装备战场损伤等级划分为4等6级, 如表1所示.
| 表 1 战场损伤等级划分表 |
2 BRB-ER战损等级评定模型 2.1 BRB专家系统
置信规则库[11]是一类模型的总称, 这类模型在传统IF-THEN规则的基础上引入了置信度和权重参数, 克服了传统规则库过于简单绝对的问题. 一个基本的BRB模型描述如下, 即:
| $ \begin{split} {R_k}:& \;{\rm{If}}\;{{x}_{\rm{1}}}\;{\rm{is}}\;A_1^k \wedge {{x}_{\rm{2}}}\;{\rm{is}}\;A_2^k \wedge \cdots \wedge {{x}_M}\;{\rm{is}}\;A_M^k,\\ & {\rm{Then}}\;\{ ({{D}_1},{\beta _{1,k}}),({{D}_2},{\beta _{2,k}}), \cdots ,({{D}_N},{\beta _{N,k}})\} \\ & {\rm{With\;a\;rule\;weight\;}}{\theta _k}\;{\rm{and\;attribute\;weight}}\;{\bar \delta _{\rm{1}}},{\bar \delta _{\rm{2}}}, \cdots ,{\bar \delta _M} \end{split} $ |
其中,
BRB中规则的推理包括两步, 首先是计算每条规则的激活权重, 然后根据激活权重将规则进行融合.
(1) 激活权重计算
一般而言, 当输入
| $ \alpha _i^j = \left\{ \begin{gathered} \frac{{A_i^{k + 1} - {x_i}}}{{A_i^{k + 1} - A_i^k}},\;\; A_i^k \leqslant {x_i} \leqslant A_i^{k + 1}\;{\text{and }}\;j = k \hfill \\[-1pt] \frac{{{x_i} - A_i^k}}{{A_i^{k + 1} - A_i^k}}, \;\;A_i^k \leqslant {x_i} \leqslant A_i^{k + 1}\;{\text{and }}\;j = k + 1\hfill \\[-1pt] 0,\;\;\;\;\;\;\;\;j \ne \left\{ \begin{gathered} k \hfill \\ k + 1 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \right. $ | (1) |
然后通过式(2)计算第
| $ {\omega _k} = \frac{{{\theta _k}\displaystyle\sum\limits_{i = 1}^M {\alpha _i^k} }}{{\displaystyle\sum\limits_{l = 1}^L {{\theta _k}\displaystyle\sum\limits_{i = 1}^M {\alpha _i^l} } }} $ | (2) |
(2) ER算法融合
通过ER算法对BRB中所有激活的规则进行融合推理, ER算法的解析公式如下:
| $ \begin{split} &{\hat \beta _j} = \frac{{\mu \times \left[ \displaystyle{\prod\limits_{k = 1}^L {({\omega _k}{\beta _{j, k}} + 1 - {\omega _k}\displaystyle\sum\limits_{i = 1}^N {{\beta _{i, k}})} } } \right]}}{{1 - \mu \times \left[ {\displaystyle\prod\limits_{k = 1}^L {(1 - {\omega _k})} } \right]}}\\ &\quad \quad-\frac{{\mu \times \left[ {\displaystyle\prod\limits_{k = 1}^L {(1 - {\omega _k}\displaystyle\sum\limits_{i = 1}^N {{\beta _{i, k}})} } } \right]}}{{1 - \mu \times \left[ {\displaystyle\prod\limits_{k = 1}^L {(1 - {\omega _k})} } \right]}} \end{split} $ | (3) |
| $ \begin{split} &\mu = \left[ {\sum\limits_{j = 1}^N {\prod\limits_{k = 1}^L {({\omega _k}{\beta _{j, k}} + 1 - {\omega _k}\sum\limits_{i = 1}^N {{\beta _{i, k}}} )} } } \right. \hfill \\ &\quad-{\left. {\left( {N - 1} \right)\prod\limits_{k = 1}^L {(1 - {\omega _k}\sum\limits_{i = 1}^N {{\beta _{i, k}}} )} } \right]^{ - 1}} \hfill \\ \end{split} $ | (4) |
其中,
选择最高置信度对应的输出等级作为最终的战损等级评估结果:
| $ {f_c}(x) = \arg \max ({\hat \beta _j}), j = 1, 2, \cdots , N $ | (5) |
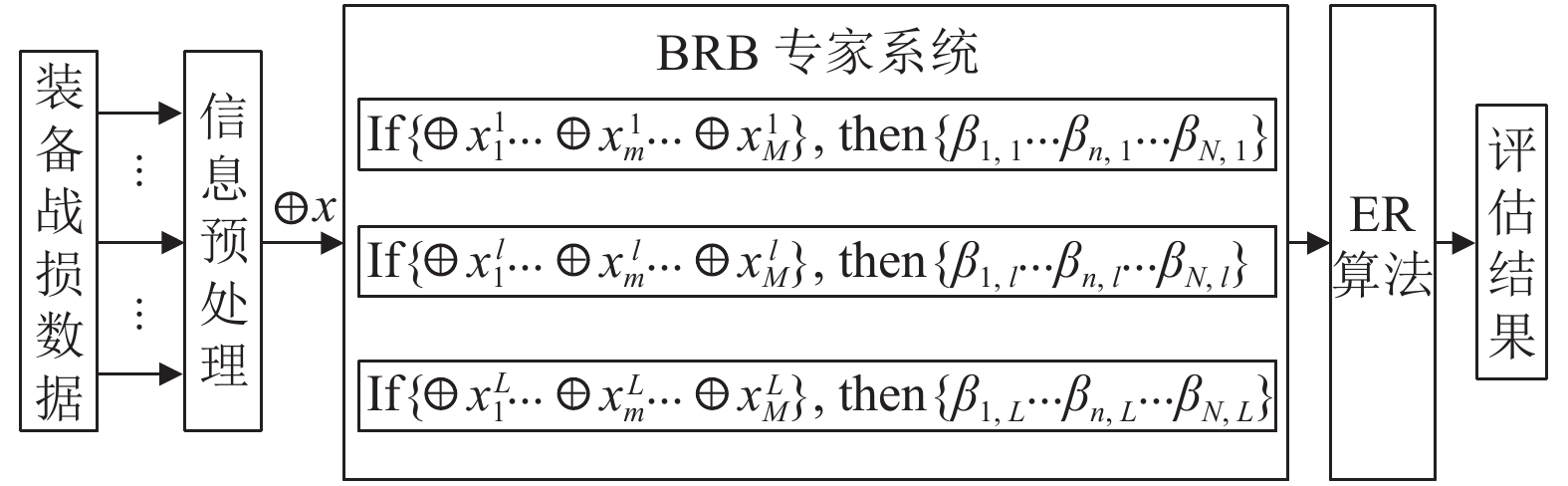
显然, 装备发生战斗损伤的3种影响因素与装备的受损程度(装备的损伤等级)之间存在一种非线性映射关系. 为此, 建立如图1所示的BRB-ER战损等级评定模型进行推理. 该模型主要包含两个部分: 第1部分是置信规则专家系统, 主要进行装备战损等级评定规则的建立; 第2部分是ER算法, 主要进行规则的推理合成. 当通过对装备战损数据进行预处理后, 利用BRB-ER模型的进行推理融合, 就能得到装备战损等级评估结果.
|
图 1 BRB-ER战损等级评定模型结构 |
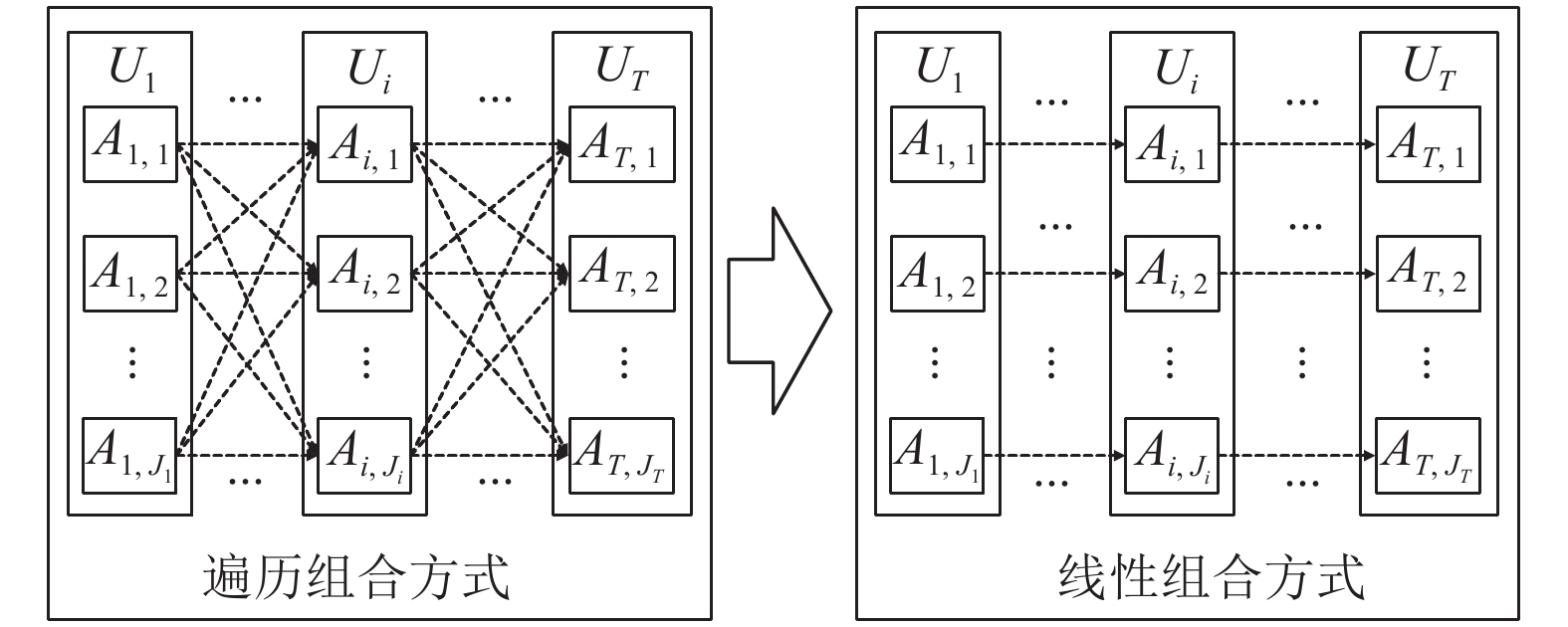
现有BRB的构建大多采用遍历组合的方式, 当前提属性个数较多时, 就容易造成“组合爆炸”问题. 如果构建的置信规则库共有M个前提属性, 并且第m个前提属性有
在构造初始BRB时, 系统的参数通常由人为随机给定, 造成主观性过大, 其战损评估的准确度可能会被降低. 因此, 本文提出了一种基于局部粒子群的BRB参数优化算法来提高战损等级评定精度.
|
图 2 构建规则库的不同组合方式 |
3.1 BRB-ER的参数优化模型
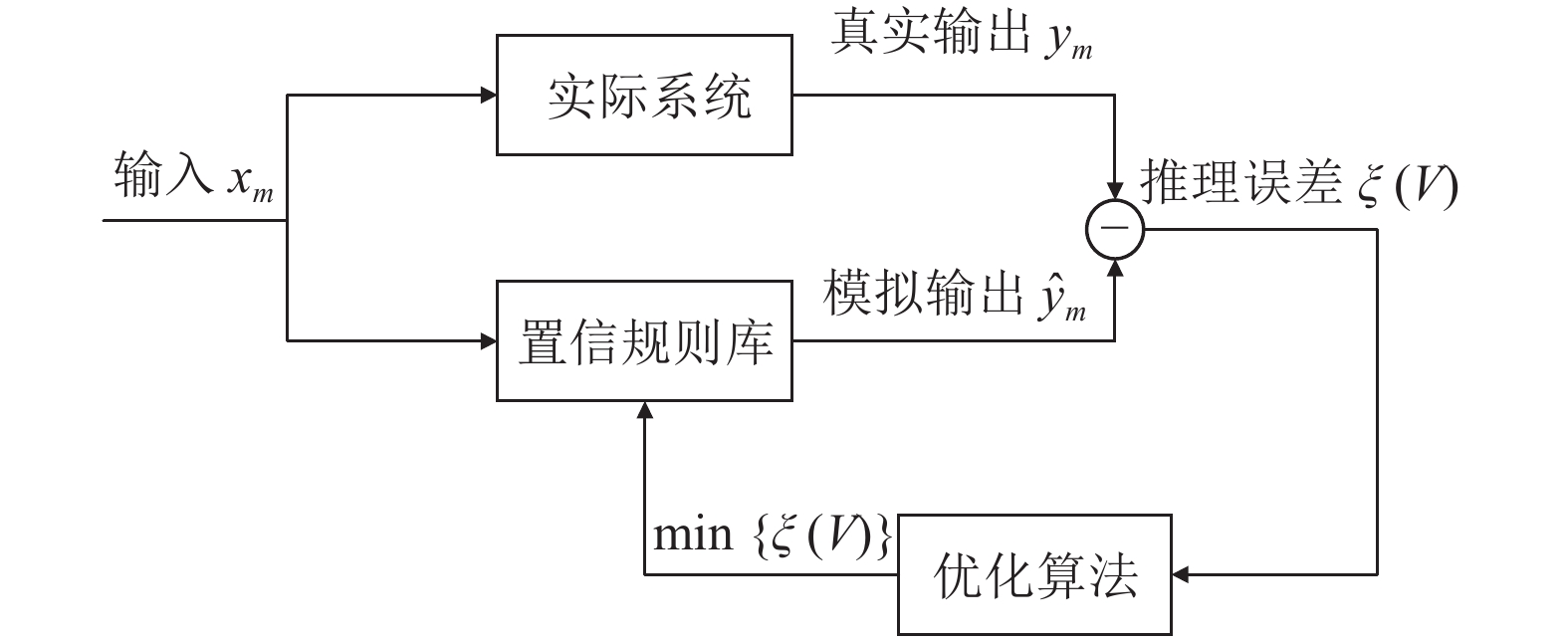
为了选取置信规则库的最优参数, Yang提出了对置信规则库参数优化的基本思想[11]. 其优化学习模型具体结构见图3.
对于BRB的参数优化模型, 其符号表达式如下:
| $ \begin{split} &{\text{ }}\min \{ \xi (V)\} \;\; {\rm{s.t.}} \;A(V) = 0, B(V) \geqslant 0 \hfill \\ \end{split} $ | (6) |
其中, V表示由
|
图 3 BRB系统参数优化模型 |
图3中,
| $ {E_i} = \left\{ \begin{gathered} 1,\begin{array}{*{20}{c}} {}&{{y_m} \ne {{\hat y}_m}} \end{array} \hfill \\ 0,\begin{array}{*{20}{c}} {}&{{y_m} = {{\hat y}_m}} \end{array} \hfill \\ \end{gathered} \right. $ | (7) |
则系统的推理误差可用均方误差(mean square error, MSE)表示, 即:
| $ \xi (V) = \textit{MSE}({A_{ij}}, \beta _j^k, {\theta _k}) = \frac{1}{n}\sum\limits_{i = 1}^n {{E_i}} $ | (8) |
BRB优化模型中各参数需满足如下约束条件:
(1) 标准化前提属性参考值, 对于第
| $ \left\{ \begin{gathered} l{b_i} \leqslant A_i^k \leqslant u{b_i}, \;i = 1, \cdots , M, \;k = 1, \cdots , K \hfill \\ A_i^k - A_i^{k + 1} \lt 0 \hfill \\ A_i^1 = l{b_i} \hfill \\ A_i^K = u{b_i} \hfill \\ \end{gathered} \right. $ | (9) |
其中,
(2) 任意一条规则中每个评价结果上的置信度需满足:
| $ \left\{ { \begin{array}{l} 0 \leqslant {\beta }_{j, k} \leqslant 1\\ {\displaystyle \sum _{j=1}^{N}{\beta }_{j, k} \leqslant 1}\end{array}\text{, }j=1, 2, \cdots , N\text{, }k=1, 2, \cdots , L } \right.$ | (10) |
(3) 规则权重的取值需要归一化, 即:
| $ 0 \leqslant {\theta }_{k} \leqslant 1\text{, }k=1, 2, \cdots , L $ | (11) |
在优化过程中, 首先给定初始参数, 根据优化模型, 利用训练数据对模型进行训练. 目前已有不少优化方法被提出, 诸如Matlab中的FMINCON函数[13]以及群智能算法, 包括差分进化算法[14]、布谷鸟算法[15]、粒子群算法[16]等. 粒子群算法需要调整的参数少, 原理简单, 容易实现, 本文通过局部粒子群算法求解BRB参数的最优值.
3.2 局部粒子群算法粒子群算法(particle swarm optimization, PSO)的基本概念源于对鸟群觅食行为的研究. PSO是一种基于迭代的优化算法, 每个粒子都有一个由被目标函数决定的适应度值. 在搜索开始前, 在解集范围内随机初始化每个粒子的速度和位置, 然后在每次迭代搜索中, 粒子根据个体极值
| $ \begin{split} {V_i}(t + 1) = \omega {V_i}(t) + {c_1}{r_1}({p_{{\text{best}}}} - {x_i}(t))+{c_2}{r_2}({g_{{\text{best}}}} - {x_i}(t)) \hfill \\ \end{split} $ | (12) |
| $ {x_i}(t + 1) = {x_i}(t) + {v_i}(t + 1) $ | (13) |
其中,
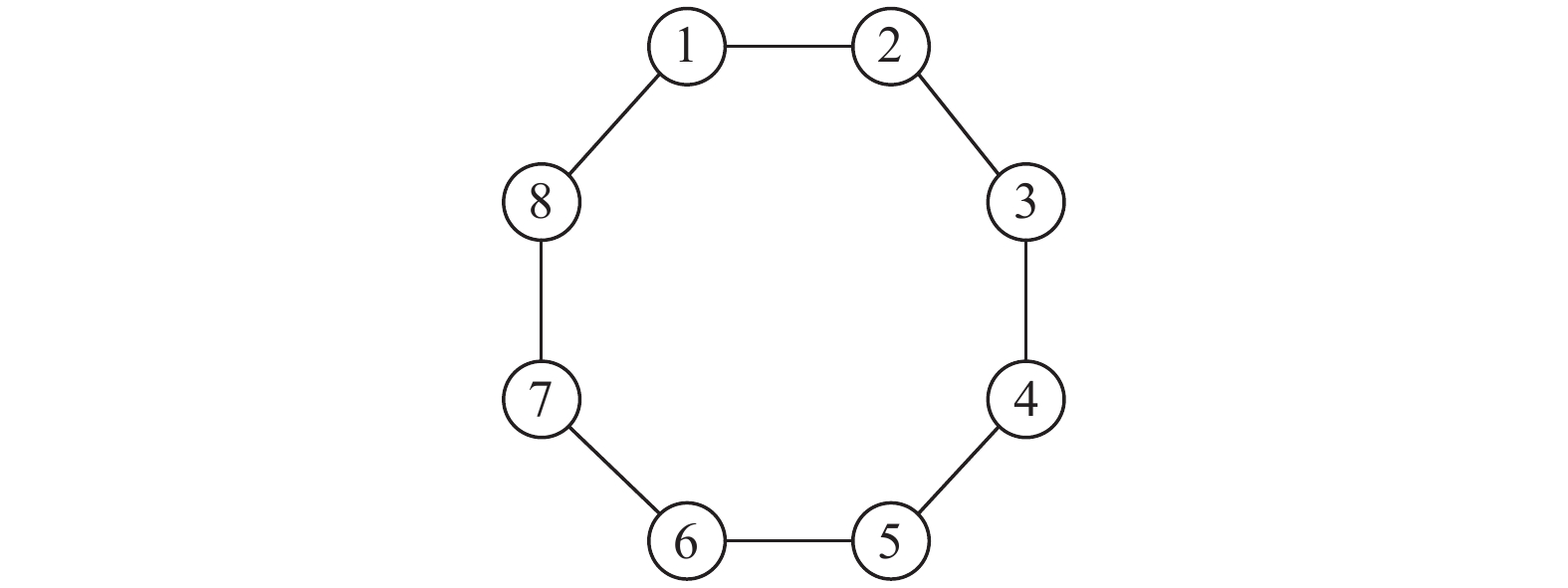
为克服粒子群算法易早熟收敛和陷入局部最优解等问题, 改变粒子速度更新公式, 即将影响粒子速度更新的全局极值
|
图 4 按环形编号取粒子邻域 |
|
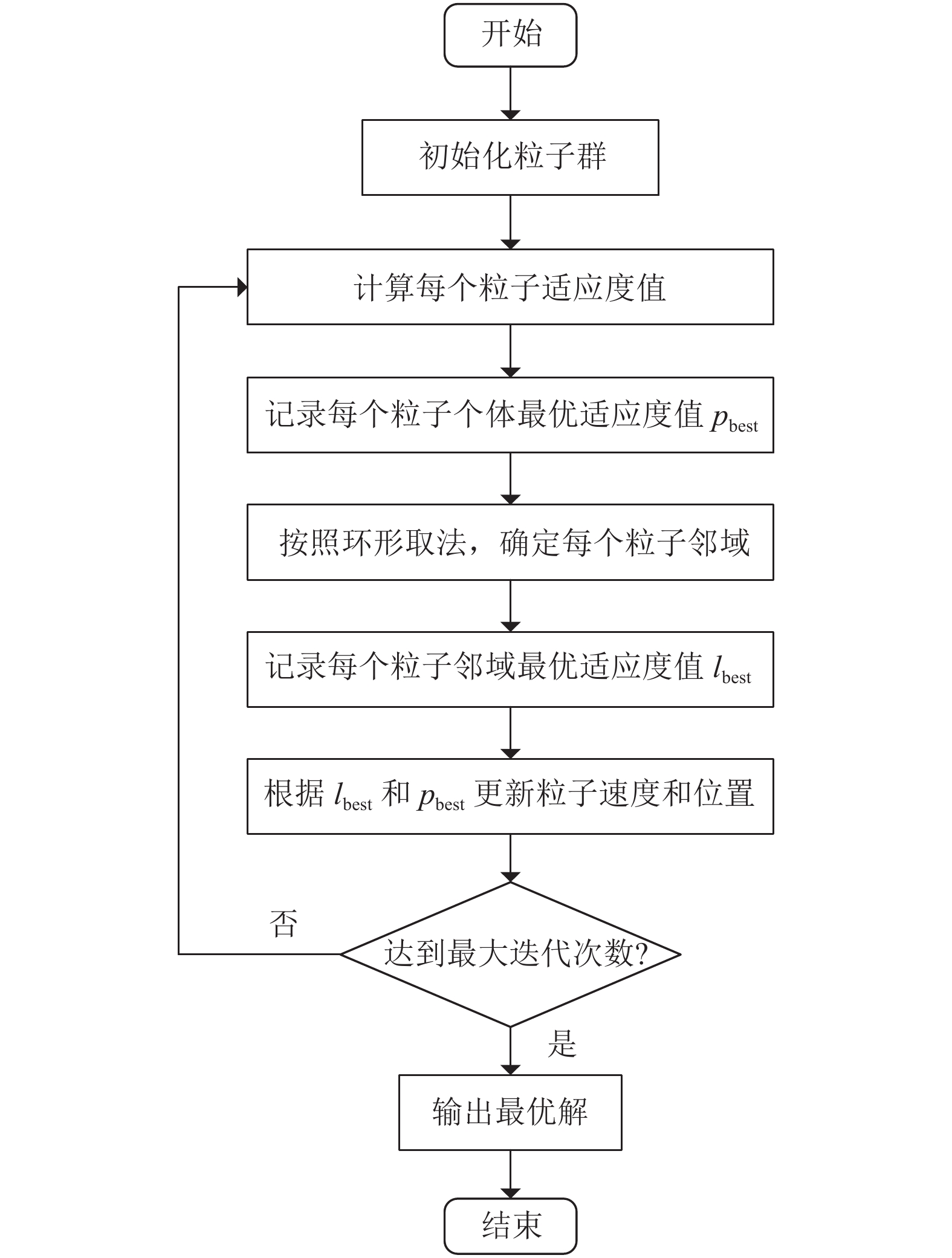
图 5 局部粒子群算法优化流程图 |
步骤1. 设置算法参数. 对BRB需要优化的参数
步骤2. 初始化粒子群. 在式(9)–式(11)的约束条件范围内, 随机初始化种群中各粒子的速度和位置.
步骤3. 计算适应度值. 对于每个粒子, 通过适应度函数来计算适应度值, 并记录个体最优解
步骤4. 更新粒子速度和位置. 将标准PSO更新速度和位置的公式中的
步骤5. 判断终止条件. 当达到了预设的最大迭代次数
如上文所述, 装备战损等级评估的过程受6个因素的影响, 所以本文建立的BRB-ER评估模型只考虑此6类因素. 由于目前的装备战损数据有限, 仅以122榴弹炮、152加农榴弹炮和130加农炮为例, 建立战损等级评定置信规则库. 对战场损伤模拟试验数据进行整理, 筛选出120组训练样本, 根据各威胁对装备的毁伤作用效果, 组织有关专家对装备的损伤情况进行了评分, 具体评分标准如表2所列.
| 表 2 装备损伤程度评分表 |
4.2 置信规则库建立
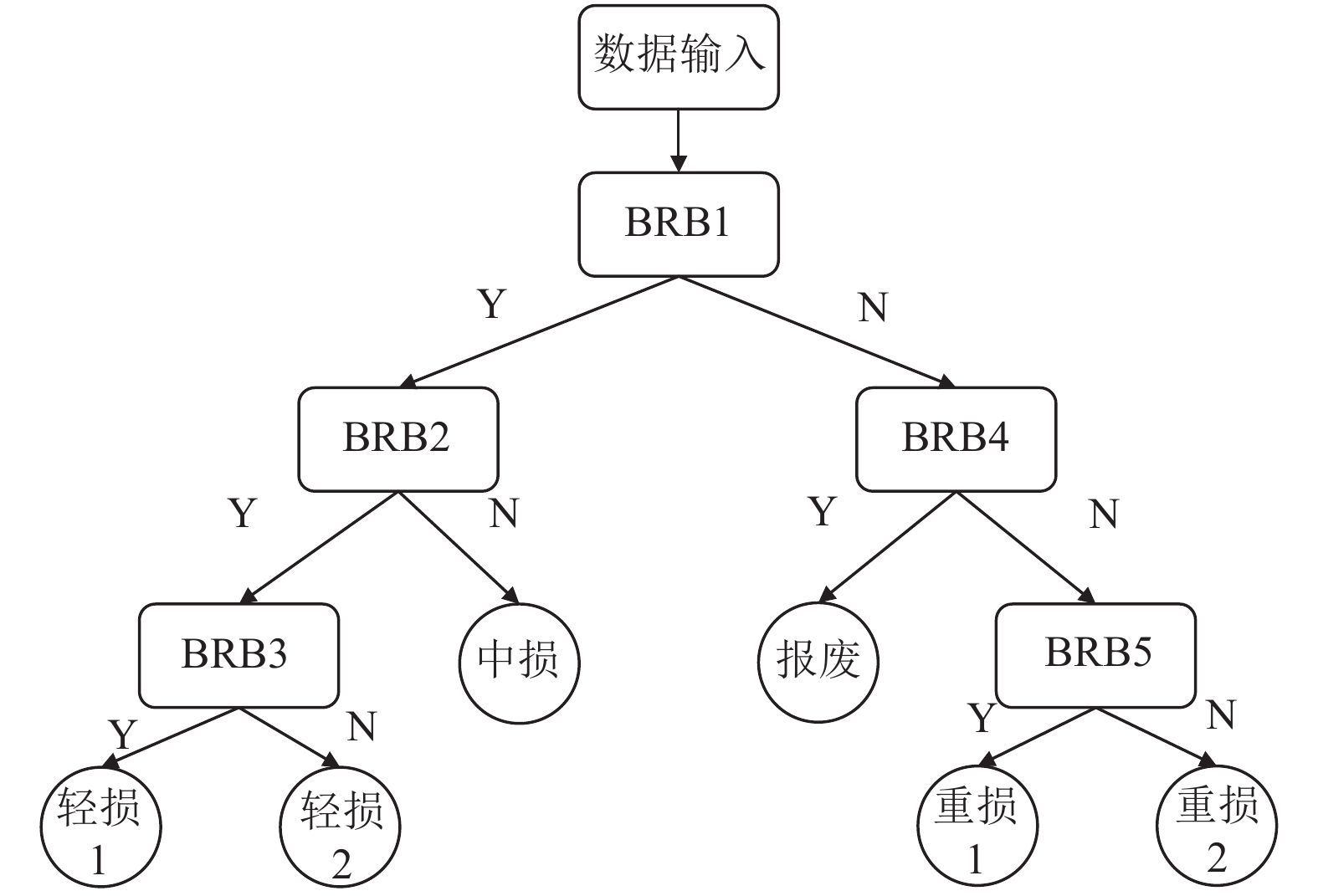
根据战场损伤等级划分标准, 可采用有向无环图来构建装备战损等级评定的众仓决策模型, 如图6所示. 可以看出, 需要建立5个BRB对装备战损数据进行分类, 每条规则仅设计两个评价等级, 其推理结果只做出是与否的置信决策. 每个BRB在训练的过程中互不影响, 可以采用并行的策略同时进行训练. 实验环境为: Intel(R) Core(TM) UHD i7-8550U CPU @ 1.80 GHz处理器、8 GB内存, Windows 10操作系统. 程序均在Matlab 2020a中实现.
随机选择100组样本作为训练数据, 设每个BRB的规则数均为4条, 在初始权重都相同的情况下, 等间隔输入规则参考值, 评价结果对应的置信度由专家给定, 得到初始置信规则库规则. 因篇幅原因, 初始置信规则库在此不罗列. 利用本文提到的基于LPSO优化方法, 选择粒子群种群个数为100, 最大迭代次数为50, 对参数进行训练后, 得到优化后5个BRB为表3至表7所示.
|
图 6 装备战损等级评定众仓决策模型图 |
| 表 3 置信规则库1 |
| 表 4 置信规则库2 |
| 表 5 置信规则库3 |
| 表 6 置信规则库4 |
| 表 7 置信规则库5 |
4.3 对比分析
将剩余的20组战损试验数据作为测试集, 利用本文提到的基于LPSO优化方法, 在相同的约束条件下与基于标准PSO参数优化方法作为比较对象, 分别对初始BRB进行参数优化训练, 得到测试结果如表8.
| 表 8 评估结果对比(%) |
根据结果可知, 初始BRB模型的评定准确度有所欠缺, 经过PSO优化后的BRB模型将评定结果的总体准确度提高到了90%. LPSO-BRB模型则是经过LPSO算法优化, 得到了准确度非常高的结果, 达到了96.7%, 充分说明了所提战损评定模型的有效性.
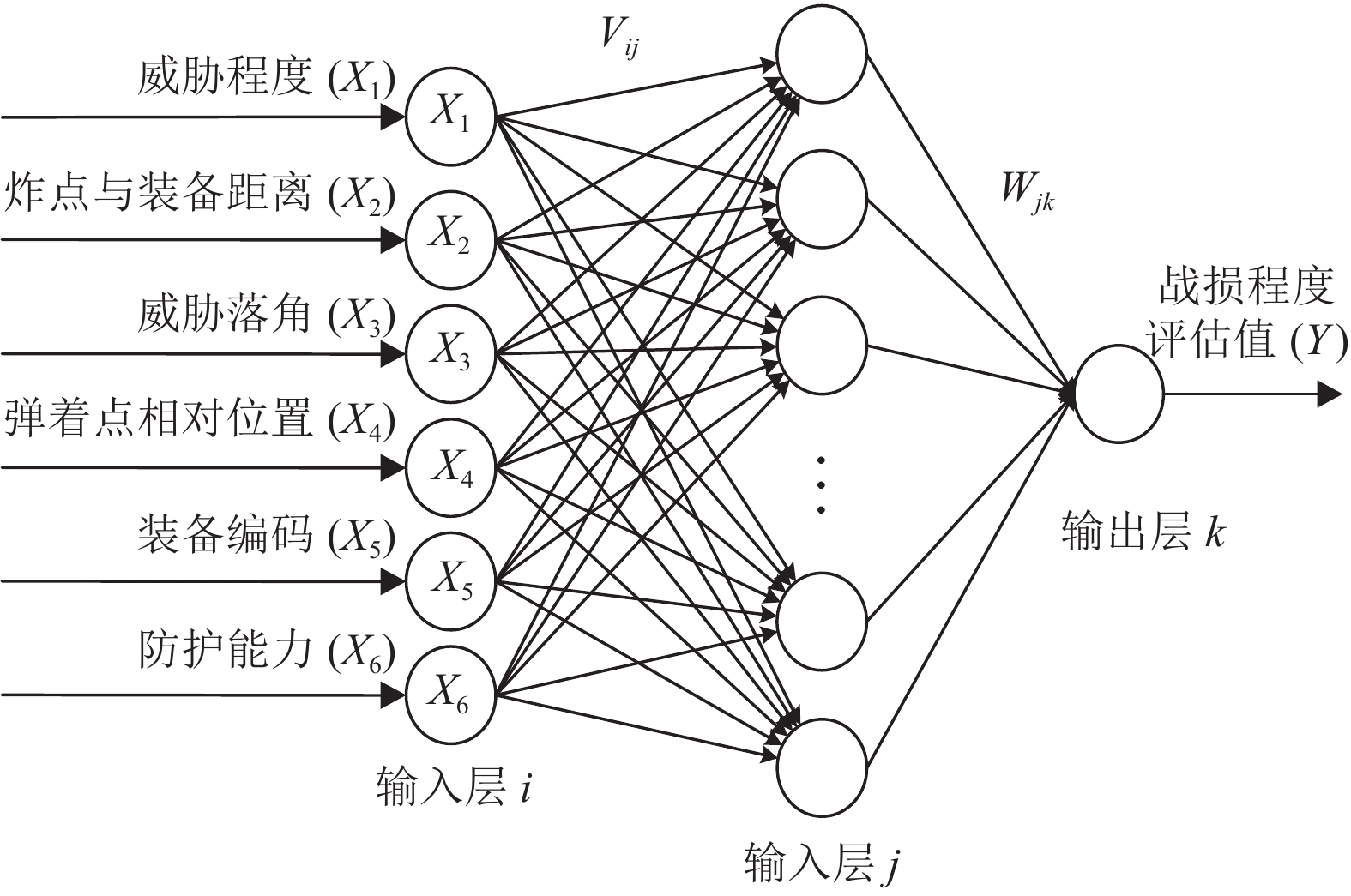
为体现本文方法有效性, 同样针对战损评定问题, 利用相同的装备战损数据将本文方法和BP神经网络方法以及支持向量机方法进行对比. 首先建立3层BP神经网络, 输入层包含6个节点, 每个节点表示一种战损影响因素, 隐含层节点数则根据经验公式选取为13, 输出层则为1个节点, 表示装备损伤程度的评估值, 根据评估值进而确定战损等级, 如图7所示. 将支持向量机应用于多分类问题, 一般使用LibSVM工具包[18]进行解决, 本文设置核函数为径向基函数(RBF核函数), 使用网格搜索法确定参数c=11.3137和g=0.125.
|
图 7 装备战损等级评定神经网络模型 |
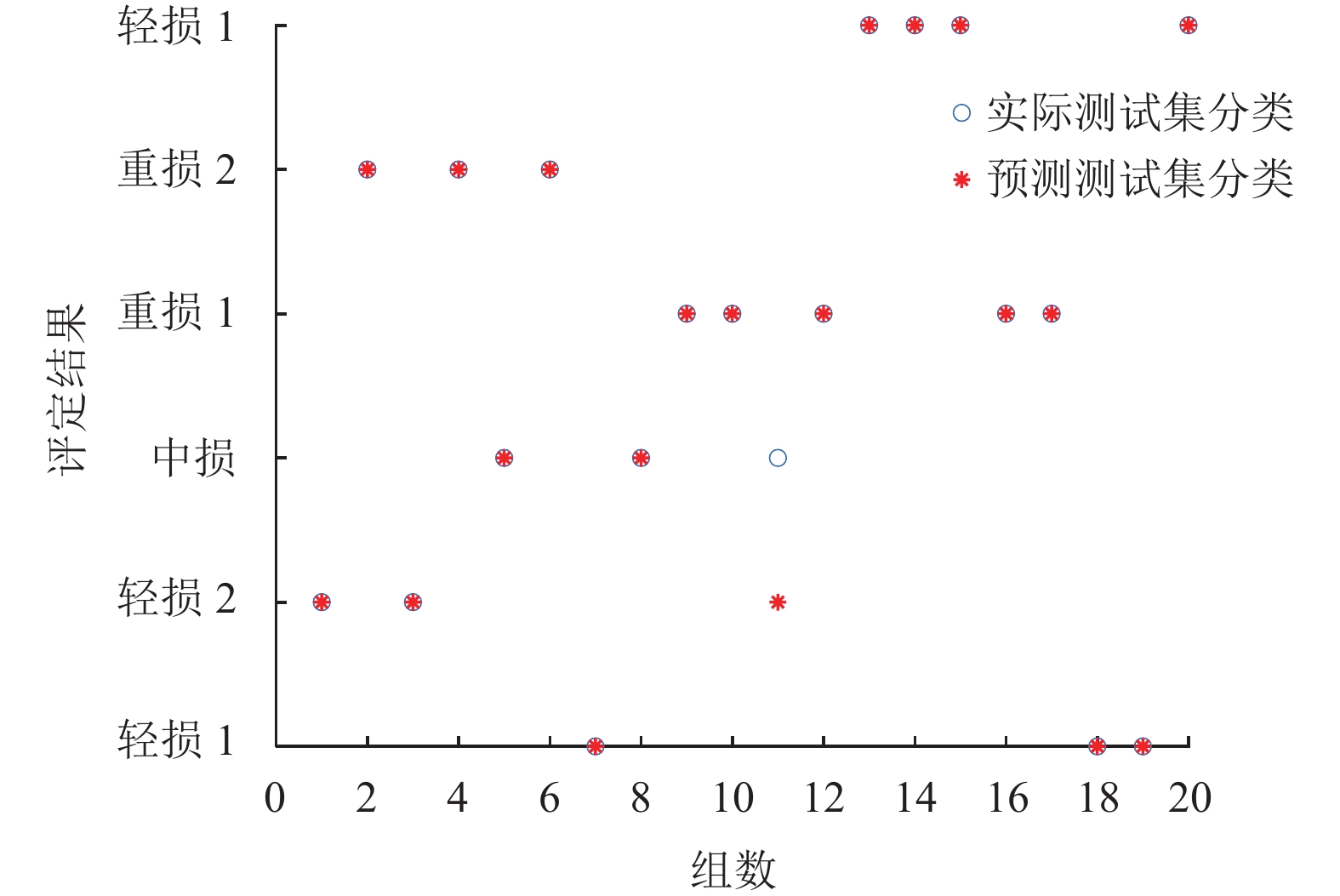
3种方法针对测试集的战损评定结果如图8–图10所示, 从图中可以看出BP神经网络方法有3个测试数据分类错误, 评定准确率为85%; 本文方法与支持向量机均只有一个测试数据分类错误, 评定准确率为95%.
|
图 8 优化的BRB的评定结果 |

|
图 9 BP神经网络的评定结果 |
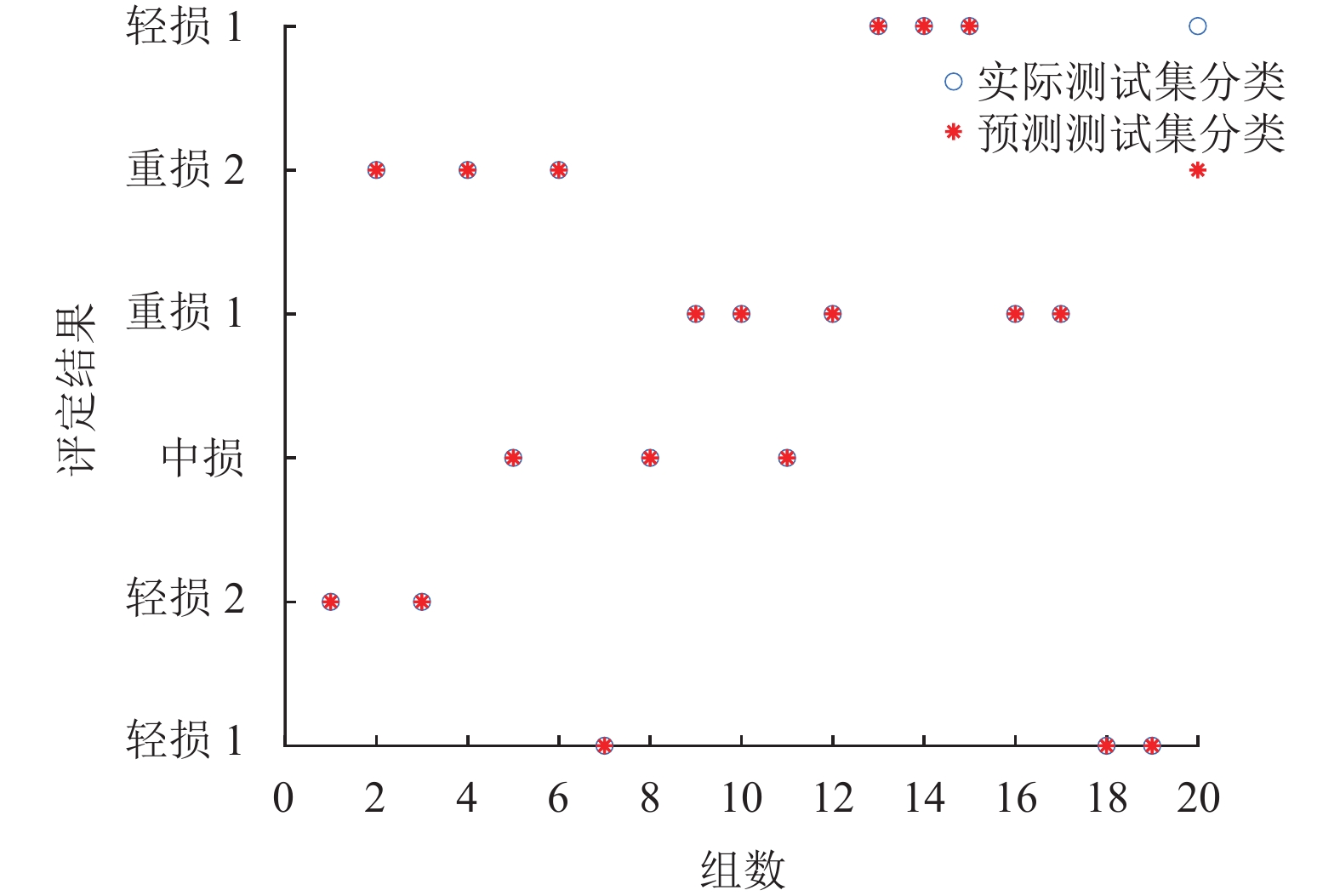
|
图 10 SVM的评定结果 |
记录3种方法对测试数据的累积误差和MSE, 分别见图11和图12. 从图中可以看出, 优化后的BRB评定的误差要明显低于BP神经网络和SVM, 可见在样本较少的情况下, 本文所提方法的战损等级评定性能更好, 具有更高的推理精度.
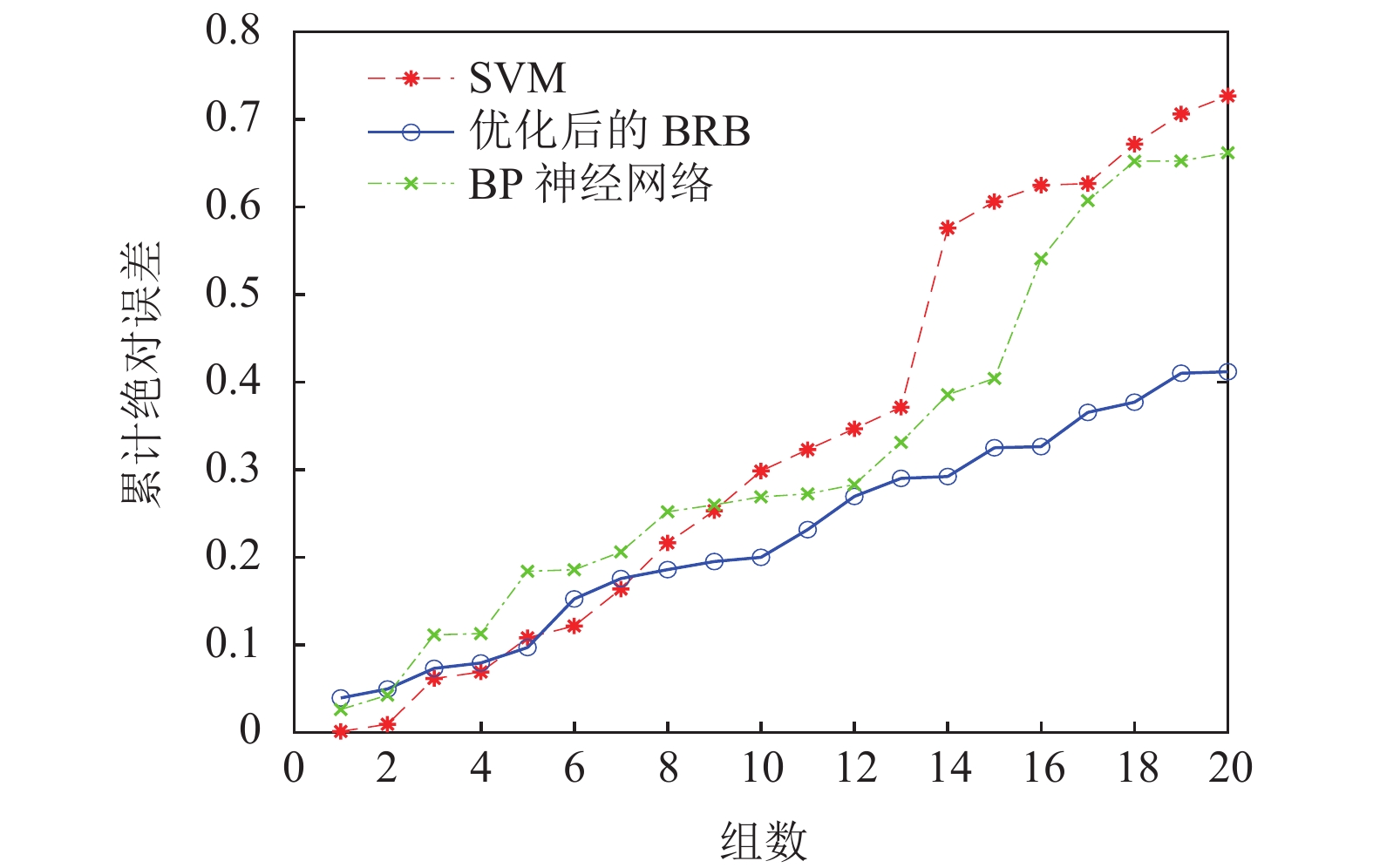
|
图 11 不同方法的累积误差对比 |
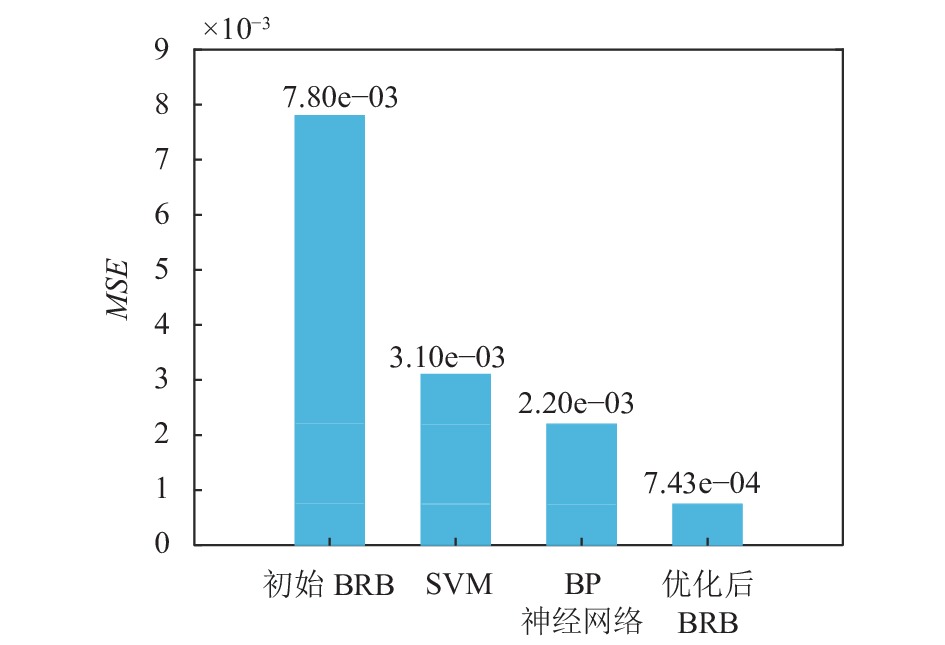
|
图 12 不同方法的MSE对比 |
5 结语
本文基于多源信息处理过程中的数据融合以及不确定性推理方法, 提出了一种新的装备战损等级评定方法. 该方法综合利用装备战损数据和专家知识建立置信规则库, 再通过证据推理算法对装备战损等级进行分类评估. 针对初始置信规则库推理精度差的问题, 利用局部粒子群算法对模型参数进行优化, 并建立二择众仓决策模型, 以此改进置信规则库推理性能. 最后, 根据某战损试验对该方法的有效性进行验证. 研究结果表明, 本文方法能够有效融合战损数据的定量信息和专家经验的定性知识, 且无需大量统计数据也能够对装备战损等级进行准确评估. 因此, 本文方法是一种有效的装备战损等级评定方法, 具有较大的应用价值和较强的适用性, 进而为战场态势分析和指挥决策提供可靠依据.
| [1] |
宋明昌, 石全, 尤志锋, 等. 多信息源条件下战损部件恢复能力评估方法. 系统工程与电子技术, 2020, 42(11): 2538-2545. DOI:10.3969/j.issn.1001-506X.2020.11.16 |
| [2] |
Xia C, Lin L, Dong L. Battle damage level prediction on fuzzy theory and Bayesian method. Proceedings of the 5th International Conference on Robotics, Automation and Mechatronics. Qingdao: IEEE, 2011. 295–298.
|
| [3] |
马晓明, 丁平, 晏卫东. 基于贝叶斯网络的舰船目标毁伤评估. 兵工自动化, 2016, 35(6): 72-75. DOI:10.7690/bgzdh.2016.06.017 |
| [4] |
韩城, 杨海燕, 马嘉呈. 基于贝叶斯网络的防空作战战损评估模型构建. 火力与指挥控制, 2018, 43(2): 36-40. DOI:10.3969/j.issn.1002-0640.2018.02.008 |
| [5] |
陈建海, 冯杰, 王志勇. 基于案例推理的装备战损评估专家系统. 舰船电子工程, 2009, 29(12): 45-48. DOI:10.3969/j.issn.1627-9730.2009.12.012 |
| [6] |
胡海峰, 王志明, 刘恒博. 一种快速评定通信设备战损等级的方法. 指挥控制与仿真, 2009, 31(3): 114-116. DOI:10.3969/j.issn.1673-3819.2009.03.032 |
| [7] |
Qi ZF, Liu QQ, Wang J, et al. Battle damage assessment based on an improved Kullback-Leibler divergence sparse autoencoder. Frontiers of Information Technology & Electronic Engineering, 2017, 18(12): 1991-2000. |
| [8] |
赵英俊, 宋文焦, 段楠楠, 等. 地空导弹装备战场损伤等级的综合指标评判. 火力与指挥控制, 2011, 36(1): 108-110, 117. DOI:10.3969/j.issn.1002-0640.2011.01.028 |
| [9] |
李军, 戚英华. 基于多目标多维模糊决策的装备战场损伤等级评定方法. 装甲兵工程学院学报, 2009, 23(3): 20-24. DOI:10.3969/j.issn.1672-1497.2009.03.005 |
| [10] |
石全, 王广彦, 胡起伟, 等. 装备战场损伤建模与仿真技术. 北京: 国防工业出版社, 2017.
|
| [11] |
Yang JB, Liu J, Wang J, et al. Belief rule-base inference methodology using the evidential reasoning approach-rimer. IEEE Transactions on Systems, Man, and Cybernetics-Part A: Systems and Humans, 2006, 36(2): 266-285. DOI:10.1109/TSMCA.2005.851270 |
| [12] |
Chang LL, Zhou ZJ, You Y, et al. Belief rule based expert system for classification problems with new rule activation and weight calculation procedures. Information Sciences, 2016, 336: 75-91. DOI:10.1016/j.ins.2015.12.009 |
| [13] |
鱼蒙, 黄健, 孔江涛. 输入信息不完整的置信规则库推理方法. 哈尔滨工业大学学报, 2019, 51(4): 51-59. DOI:10.11918/j.issn.0367-6234.201804076 |
| [14] |
王韩杰, 杨隆浩, 傅仰耿, 等. 专家干预下置信规则库参数训练的差分进化算法. 计算机科学, 2015, 42(5): 88-93. DOI:10.11896/j.issn.1002-137X.2015.5.018 |
| [15] |
李敏, 傅仰耿, 刘莞玲, 等. 置信规则库参数训练的布谷鸟搜索算法. 小型微型计算机系统, 2018, 39(6): 1149-1155. DOI:10.3969/j.issn.1000-1220.2018.06.006 |
| [16] |
苏群, 杨隆浩, 傅仰耿, 等. 基于变速粒子群优化的置信规则库参数训练方法. 计算机应用, 2014, 34(8): 2161-2165. DOI:10.11772/j.issn.1001-9081.2014.08.2161 |
| [17] |
杨英杰. 粒子群算法及其应用研究. 北京: 北京理工大学出版社, 2017.
|
| [18] |
Chen T, Ju SH, Ren F, et al. EEG emotion recognition model based on the LIBSVM classifier. Measurement, 2020, 164: 108047. DOI:10.1016/j.measurement.2020.108047 |
 2022, Vol. 31
2022, Vol. 31



