随着生产技术的发展与制造业内在需求的变化, 制造业正在向着智能制造的方式转变, 作为产品生产制造中重要一环, 车间调度问题得到了极大关注. 柔性作业车间调度问题(flexible job-shop scheduling problem, FJSP)作为经典作业车间调度问题(job-shop scheduling problem, JSP)的延伸被认为是NP-难问题, 相较于JSP具有更高灵活性与求解难度. 如今智能制造是制造业主要发展方向, 制造系统的高效运行是智能制造主要要求之一. FJSP具有工序排序与机器选择两个子问题, 其求解更具复杂性, 同时也更贴近实际车间生产制造情况, 为寻求高效求解方法, 对于FJSP的求解方法具有广泛的研究. 目前对FJSP的求解方法主要集中于元启发式算法. 张超勇等^[1]对遗传算法进行改进, 改变了染色体的表示方式, 结合多种策略生产高质量初始种群等多种操作, 在基准问题上进行验证; Li等^[2]将禁忌搜索算法策略嵌入到遗传算法中, 综合利用二者的寻优能力, 为更好平衡算法的勘探与开发, 通过与其他算法进行对比实验, 改进的混合算法具有显著改进; 仲于江等^[3]利用改进的粒子群算法对多目标FJSP进行研究, 利用小生境技术更新解集避免算法陷入局部最优, 并改进最优解的选择方式, 在算例与车间仿真实验中验证改进算法可行性.

随着计算机科学技术发展, 新式元启发式算法不断涌现, 如灰狼优化算法^[4], 人工蜂群算法^[5]等, 学者利用新兴的元启发式算法对FJSP进行进一步研究, Lu等^[6]设计了一种改进的多目标混合灰狼优化算法, 在算法中嵌入遗传算子增强全局搜索能力, 在多目标动态调度模型中与其他经典算法进行比较, 体现改进算法的优越性; Karthikeyan等^[7]针对有限资源约束下的多目标FJSP, 考虑3个最小化目标, 结合邻域结构的局部搜索方法, 提出一种混合萤火虫算法并将其离散化应用于多目标FJSP; 姜天华^[8]采用两段式编码方式将改进的灰狼优化算法应用于FJSP, 引入变邻域搜索方法与遗传算法中交叉和变异算子的方式提高算法勘探能力在基准与随机算例中与其他算法进行对比, 数据证明改进算法; 王玉芬等^[9]针对FJSP, 对人工蜂群算法进行改进, 在搜索阶段利用IPOX与多点交叉方法避免产生非法解, 通过增加侦察蜂的数量保持全局搜索能力, 且用贪婪策略保留较优解, 在算例上验证改进算法的有效性与收敛性; Li等^[10]针对FJSP, 提出了一种基于禁忌搜索的混合人工蜂群算法来求解, 并使用聚类分组轮盘赌的方式来初始化种群, 同时为提高种群质量, 在计算过程中引入交叉算子, 在基准算例上与其他算法进行比较并证明了算法有效性; 刘雪红等^[11]对候鸟算法做出改进, 使用精英分批策略提高算法性能, 使其应用于FJSP, 解决最小完工时间与最小批次数目的多目标FJSP. 综上, 学者基于元启发式算法解决FJSP进行了广泛研究.

鲸鱼优化算法(whale optimization algorithm, WOA)^[12]是一种基于种群的元启发式算法, 已应用于模型预测^[13], 参数优化等方面^[14], WOA具有独特的搜索机制, 其应用参数少, 算法整体稳定性高, 寻优能力较强^[15], 元启发式算法在解决车间调度问题方面具有一定优势, WOA作为元启发式算法的一种, 同样应用于在车间调度应用的方面, 闫旭等^[16]首先将WOA应用于车间调度问题, 利用量子计算方式改进的WOA求解JSP; 张斯琪等^[17]提出一种改进的WOA优化单目标的FJSP. 为进一步丰富FJSP的求解算法, 对FJSP求解进行深入研究, 本文首先利用非线性收敛因子与正余弦算法对WOA进行改进, 提出一种混合正余弦鲸鱼优化算法(sine cosine whale optimization algorithm, SCWOA), 并应用SCWOA求解以最小化最大完工时间的FJSP.

1 问题描述

FJSP是经典JSP的扩展, 其问题可以描述为: 假设在车间内n个工件 $({J_1}, {J_2}, \cdots,{J_n})$ 需在m台机器 $({M_1}, $ $ {M_2}, \cdots , {M_m})$ 上进行加工, 每个工件 ${J_i}$ 包含一个以上工序, 工序按预定顺序进行加工. 使用 ${O_{ij}}$ 表示工件 ${J_i}$ 的第j道工序, ${M_{ij}}$ 表示可加工工序的机器集合, 工序可在具备处理能力的机器上进行加工. 工序 ${O_{ij}}$ 在不同机器上的加工时间不同. FJSP的调度目标是为 ${O_{ij}}$ 选择机器进行加工, 同时对机器上各个待加工工件工序进行排列以确定加工时间, 平衡各性能指标以达到最好方案.

FJSP的目标是在一定的约束条件下对工件和机器按时间进行分配并安排加工次序, 使得加工性能指标达到最优.

本文评价目标是最大完工时间最小, 目标函数可表示为:

$ f=\min (\max (C)), \; 1 \leqslant j \leqslant n $

(1)

式中, ${C_j}$ 为工件最后完成时间, n为工件数.

2 基本算法描述 2.1 鲸鱼优化算法

WOA的设计源于鲸鱼群的捕食行为. 在鲸鱼群体中, 其捕食行为常常伴随着个体之间的合作, 鲸鱼群捕食行为中最特别之处是气泡网捕食行为, 即鲸鱼群在发现猎物之后, 会以螺旋路径逐渐包围猎物, 将猎物活动范围逐渐缩小, 最终捕食猎物^[12]. WOA从鲸鱼群独特的捕食行为中进行研究, 通过仿效鲸鱼群捕食的方式, 从搜索、包围、捕食猎物3个方面建立数学模型, 模拟算法寻优过程.

2.1.1 包围猎物阶段

WOA模仿鲸鱼群协同捕食方式, 会有多个鲸鱼个体对猎物进行包围捕猎, 算法在开始时设置一组随机解并计算解的适应度, 同时将适应度最高的解视作目标, 其余鲸鱼个体会向目标靠拢接近, 其位置更新方式可以表示为:

$ X(t + 1) = {X^*}(t) - A \cdot D $

(2)

$ D = \left| {C \cdot {X^ * }(t) - {X^ * }(t)} \right| $

(3)

式中, ${X^*}$ 为猎物位置, t为迭代次数, A, C为系数, 其计算方式为:

$ A = 2a \cdot r - a $

(4)

$ C = 2 \cdot r $

(5)

其中, $a$ 随迭代次数增加从2线性下降为0, $ r \in $ [–1, 1]的随机数.

2.1.2 气泡网捕食

鲸鱼群在进行捕食时会沿着圆形或“9”形的路径捕食猎物, 为模仿这种捕食方式, WOA设置两种方法进行模仿, 第1种为个体收缩环绕机制, 这一机制通过 $a$ 的线性降低来实现, 由式(4)可知, A的值也会随 $a$ 的减小而减小, 当a的值在 $\left[ { - 1, 1} \right]$ 时, 鲸鱼个体会对目标猎物进行收缩环绕行为. 第2种为鲸鱼个体螺旋形位置更新, WOA首先计算鲸鱼个体与捕猎目标之间距离, 然后在二者之间建立一个螺旋方程, 模拟鲸鱼个体的螺旋形运动方式^[17], 公式为:

$ X(t + 1) = {D'} \cdot {e^{bl}} \cdot \cos (2\pi l) + {X^ * }(t) $

(6)

$ {D'} = \left| {{X^ * }(t) - X(t)} \right| $

(7)

式中, ${D'}$ 为鲸鱼个体与猎物之间的距离, $b$ 为定义螺旋形状的常数, $l$ 为[−1, 1]之间的随机数. WOA通过这两种机制模拟整个鲸鱼群捕食路径, 为模拟同时发生的两种行为, 设置WOA分别以50%的几率进行收缩环绕机制或螺旋更新机制, 公式如下:

$ X(t + 1) = \left\{\begin{split}&{{X^{ * (t) - A \cdot D}}},&{{{p}} < 0.5} \\ &{{{D'} \cdot {{\rm{e}}^{bl}} \cdot \cos (2\pi l) + {X^ * }(t)}},&{{{p}} \geqslant {\text{0}}{\text{.5}}}\end{split} \right. $

(8)

其中, p为[0, 1]之间的随机数.

2.1.3 寻找猎物阶段

为进一步寻找猎物, WOA利用A的变化来进行探索, 即 $\left| A \right| < 1$ 时算法会进行精确搜索, 鲸鱼个体会向当前最优个体进行移动, 与开发阶段不同, 当A的随机值大于1或小于−1时, 鲸鱼个体会远离当前猎物并且根据一个随机鲸鱼个体来更新自己的位置, 位置更新公式如下:

$ X(t + 1) = {X_{\rm rand}} - A \cdot D $

(9)

$ D = \left| {C \cdot {X_{\rm rand}} - X} \right| $

(10)

其中, ${X_{\rm rand}}$ 为随机选取的鲸鱼个体的位置.

WOA从一组随机解开始. 在每次迭代中, 鲸鱼个体会根据随机选择的鲸鱼个体位置或当前最优个体位置更新自身的位置, 当 $\left| A \right| > 1$ 时, 鲸鱼群进行随机搜索, $\left| A \right| < 1$ 时, 每个鲸鱼个体会依据猎物位置更新本身所处位置, 以此来进行勘探与开发; 同时根据p的随机取值, 选择对数螺旋方式或收缩环绕方式靠近捕获猎物, WOA会在达到最大迭代次数时结束. 元启发式算法作为求解FJSP的有效手段, 其中WOA作为众多元启发式算法的一种, 本身具备较强的搜索能力, 在函数求解方面的稳定性与求解精度强于大部分元启发式算法, 但同时也具有元启发式算法共有的易陷入局部最优等的缺点^[18]. 因此本文在引入非线性收敛因子与正余弦算法策略对WOA进行改进, 并应用于FJSP的求解.

2.2 正余弦算法

正余弦算法(sine cosine algorithm, SCA)由Mirjalili在2016年提出^[19], SCA算法的主要思想是在算法寻优过程中综合使用正弦函数与余弦函数来进行勘探与开发, 通过正余弦函数的周期性变化实现勘探与开发. SCA算法首先随机创建一组初始解, 然后根据正余弦函数进行迭代更新位置, 寻找最优解, 其位置更新公式可以表示为:

$ {X_{t + 1}} = \left\{ {\begin{array}{*{20}{c}} {{X_t} + {r_1} \cdot \sin \left( {{r_2}} \right) \cdot \left| {{r_3}{P_t} - {X_t}} \right|,\;\;{r_4} < 0.5} \\ {{X_t} + {r_1} \cdot \cos \left( {{r_2}} \right) \cdot \left| {{r_3}{P_t} - {X_t}} \right|,\;\;{r_4} \geqslant 0.5} \end{array}} \right. $

(11)

其中, ${X_t}$ 是在第t次迭代时个体的位置, ${p_t}$ 表示在第t次迭代时适应度最高的个体所处位置, SCA控制参数包括 ${r_1}$ 、 ${r_2}$ 、 ${r_3}$ 、 ${r_4}$ , 其中 ${r_1}$ 的表示公式如下:

$ {r_1} = k - t\frac{k}{T} $

(12)

其中, k为常数, t为当前迭代次数, T为最大迭代次数; ${r_2} \in \left[ {0, 2\pi } \right]$ , ${r_3} \in \left[ {0, 2\pi } \right]$ , ${r_4} \in \left[ {0, 1} \right]$ , 均为随机数. 在SCA算法中, ${r_1}$ 确定个体下一次更新的运动方向; ${r_2}$ 确定个体的移动距离; ${r_3}$ 是当前最优个体位置的一个权重, 若 ${r_3} > 1$ 表示增大当前最优个体位置对其他个体改变的影响, 若 ${r_3} < 1$ 表示减弱当前最优个体位置对其他个体改变的影响; ${r_4}$ 代表随机选择正余弦函数. 在4个参数中, ${r_1}$ 的取值对SCA全局探索与局部开发之间的平衡影响较大, ${r_1} > 1$ 时, 函数 ${r_1}\sin ({r_2})$ 与 ${r_1}\cos ({r_2})$ 的值会大于1或小于−1, 此时个体会远离当前的最优个体, 算法会探索更加广阔的求解区域, 保证算法全局探索能力; 当 ${r_1} \leqslant 1$ 时, 函数 ${r_1}\sin ({r_2})$ 与 ${r_1}\cos ({r_2})$ 的值会处于−1到1之间, 此时个体会逐渐向当前最优个体移动, 算法会对区域内进行进一步精确搜索, 保证算法进行良好的局部开发. SCA在正弦余弦函数中利用自适应参数平滑实现从全局探索到局部开发, 能够将全局探索和局部开发有效结合起来.

3 混合正余弦鲸鱼优化算法 3.1 编码解码

基于FJSP的特性, 设置基于机器分配与工序排序的两段式向量进行编码, 分别对应FJSP的两个子问题, 对于一个鲸鱼个体向量 $X=({{{x}}}_{1}, {{{x}}}_{2},\cdots, {{{x}}}_{n})$ , 将其分为长度相等两段, 满足 $n = 2l$ ,l为FJSP总工序数, 第一段向量用于表示机器分配, 第二段向量表示工序排序, 并设置个体位置取值范围为 $\left[ { - \varepsilon , \varepsilon } \right]$ , $\varepsilon $ 为FJSP总工件数. 假设存在一个3个工件, 每工件含2道工序的调度问题, 则可表示为两段向量, 每段向量长度为6, 个体位置向量总长为12, 个体位置元素的取值介于[−3, 3]之间, 如图1所示是一段个体位置向量.

3.1.1 编码

首先对第一段机器分配向量进行编码, 参考文献[20]的编码方法, 通过式(13)将鲸鱼个体位置向量映射到当前可选机器集合的机器序号, 从而完成个体位置转换机器分配的过程.

$ u(j) = round\left(\frac{1}{{2\varepsilon }}(s(j) - 1) \cdot (x(j) + \varepsilon ) + 1\right) $

(13)

其中, $x(j)$ 为鲸鱼个体向量, $s(j)$ 为可选机器集合, $u(j)$ 为机器集合中的序号. 如图2为第一段机器分配向量的转换过程.

工序 ${O_{11}}$ 选择可选机器集合中的序号2机器即 ${M_3}$ , 工序 ${O_{12}}$ 选择可选机器集合中序号1机器即 ${M_1}$ .

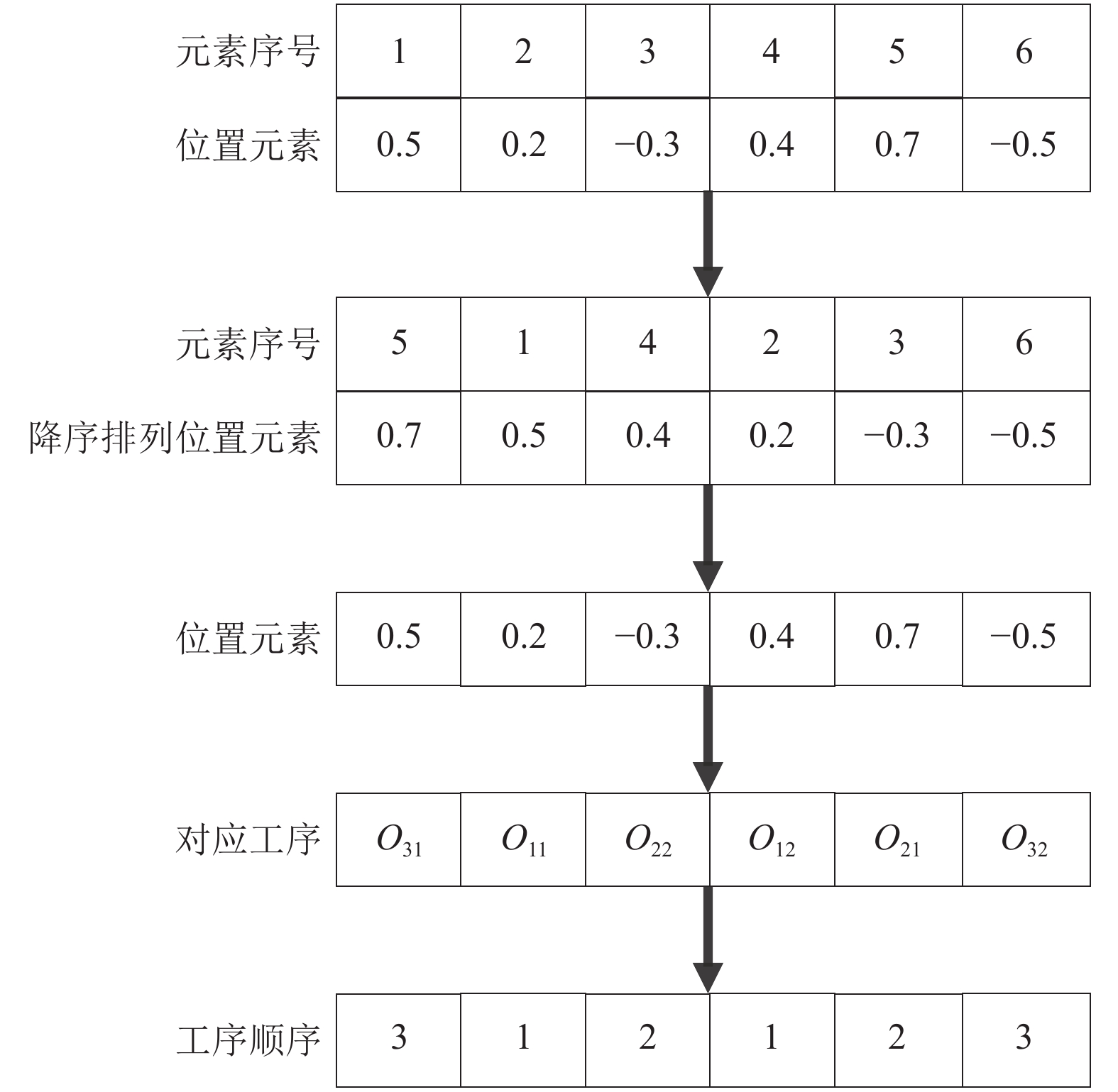
工序排序向量的编码采用文献[21]的最大位置值规则(largest position value, LPV)来实现, 首先按照位置元素值的大小进行降序排列, 之后依照这一排列顺序实现工序顺序的排列, 最后确定工序顺序. 如图3所示为第2段向量的转换过程.

3.1.2 解码

解码也包括机器分配与工序排序两部分, 机器分配向量向个体位置向量的转换是公式的逆转换, 即:

$ x(j) = \frac{{2\varepsilon }}{{s(j) - 1}}(u(j) - 1) - \varepsilon , {\text{ 1}} \leqslant j \leqslant l $

(14)

若发生特殊情况, 在可选集合中仅存在唯一一台机器, 即当 $s(j)$ 为1时, 此时 $x(j)$ 取值为 $\left[ { - \varepsilon , \varepsilon } \right]$ 之间的随机数.

工序排序向量的解码同样依据LPV规则, 工序排序向量 $\pi (j)$ 的转换根据式(15)实现.

$ x(\pi (j) + l) = \varepsilon - \frac{{2\varepsilon }}{{l - 1}}(j - 1), {\text{ }}1 \leqslant j \leqslant l $

(15)

3.2 非线性收敛因子

任何群智能优化算法在寻优的过程中都存在全局探索与局部开发两个阶段, 恰当平衡两个阶段, 可使算法在初期寻优中探索更大范围, 同时提升其后期对于局部范围的搜索精度, 提升算法求解的整体准确性. WOA的勘探与开发平衡主要由 $\left| A \right|$ 确定, 又由式(4)可知 $\left| A \right|$ 是由收敛因子 $a$ 的变化决定, 收敛因子 $a$ 的值较大时, $\left| A \right|$ >1, 算法会处于全局探索阶段, 反之 $\left| A \right|$ <1, 算法会处于局部开发阶段. 针对SCA, 其勘探与开发两阶段之间平衡主要取决于参数 ${r_1}$ .

然而无论是WOA收敛因子a还是SCA参数r₁都根据迭代次数由2线性递减至0, 为适应WOA与SCA的优化过程, 因此本文提出一种非线性收敛因子调整策略, 对WOA的收敛因子 $a$ 进行改进, 其改进公式如下:

$ {a'} = 2 \times \sin \left(\frac{\pi }{2} \times {\left(\frac{t}{T}\right)^\lambda } + \mu \right) $

(16)

其中, t为当前迭代次数, T为最大迭代次数, $\lambda $ , $\mu $ 都为常数. 此种改进使得 ${a'}$ , $r_1'$ 的值可以随着迭代过程进行非线性变化, 适应WOA与SCA的非线性优化过程.

如图4所示为WOA收敛因子与非线性收敛引子在迭代过程中的变化对比. 非线性收敛因子相比标准WOA的收敛因子, ${a'}$ , $r_1'$ 的值在其优化过程前期取值较大且递减速度较慢, 保证 $\left| A \right|$ 的取值较大, 进而使得算法前期全局搜索范围较大, 适用于全局搜索, 在后期取值较小且递减速度加快, $\left| A \right|$ 的取值较小, 算法在更小范围内进行搜索, 保证算法局部搜索精确性, 提高算法搜索精度, 同时可提高算法收敛速度.

3.3 正余弦算法策略

SCA利用正余弦函数的周期性变化实现寻优过程, 这种位置更新方式使得算法勘探时会探索更大区域, 局部开发时会在更小范围内进行精确搜索, 综合利用SCA的位置更新方式, 将其应用于WOA的位置更新与螺旋更新中, 对WOA进行改进, 提高WOA的整体寻优水平. 标准SCA参数 ${r_1}$ 作为平衡探索与开发的重要参数, 其迭代变化也与WOA中收敛因子类似, 呈线性变化, 这种线性变化无法充分发挥算法在探索、开发能力^[22]. 因此同样考虑对SCA参数 ${r_1}$ 引入非线性收敛因子策略, 对 ${r_1}$ 改进如式(17)所示, 增强SCA的全局探索能力与局部搜索能力.

$ r_{1}^{\prime}=2 \times \sin \left(\frac{\pi}{2} \times\left(\frac{t}{T}\right)^{\lambda}+\mu\right) $

(17)

3.3.1 改进鲸鱼个体位置更新方式

WOA全局探索能力依靠式(9)来实现, 即通过随机选择鲸鱼个体来确保算法的全局探索, 这种随机产生鲸鱼个体的方法只有同时满足 $p$ <0.5且 $\left| A \right|$ >1时, 算法才会采用式(9)进入全局探索阶段, 过多的条件限制使得WOA全局探索能力略显不足, 因此将SCA与WOA进行混合, 利用SCA的寻优方式, 结合SCA较强的全局探索能力, 首先对WOA的全局探索方式进行改进. 利用控制参数为指数函数递减的SCA较原算法具有更高的计算精度, 同时提高了算法的求解效率, 因此结合非线性收敛因子策略, 同时把式(11)引入WOA, 对式(10)进行改进如下:

$ {D_1} = \left\{ {\begin{array}{*{20}{c}} {r_1' \cdot \sin \left( {{r_2}} \right)\left| {C \cdot {X_{\rm rand}} - X} \right|, \;\;\;\theta < 0.5} \\ {r_1' \cdot \cos \left( {{r_2}} \right)\left| {C \cdot {X_{\rm rand}} - X} \right|, \;\;\;\theta \geqslant 0.5} \end{array}} \right. $

(18)

其中, $r_1'$ 以非线性递减的方式从2减小到0, $\theta $ 为[0, 1]之间的随机数. 在原WOA中, 当 $\left| A \right| \geqslant 1$ 时, 会随机选择一个鲸鱼个体, 以此为目标实行位置更新, 实行全局勘探. 现在, 当参数 ${a'} \geqslant 1$ 时, $\left| A \right| \geqslant 1$ , 随机使用正弦余弦函数, 可以产生更大的D, 结合式(9), 鲸鱼个体下次迭代的位置会处于更加广阔的范围, 使得鲸鱼个体可以访问更大的探索空间, 进而可使算法对更大的范围进行探索.

基于同样考虑, 把SCA策略引入WOA的局部开发过程中, 提升算法的局部开发能力, 对式(3)进行改进如下:

$ {D_2} = \left\{ {\begin{array}{*{20}{c}} {r_1' \cdot \sin \left( {{r_2}} \right)\left| {C \cdot {X^ * } - X} \right|, \;\;\;\theta < 0.5} \\ {r_1' \cdot \cos \left( {{r_2}} \right)\left| {C \cdot {X^ * } - X} \right|, \;\;\;\theta \geqslant 0.5} \end{array}} \right. $

(19)

其中, $r_1'$ 的值同样以非线性递减的方式从2减小到0. 在原WOA中, 当 $\left| A \right| < 1$ 时, 根据当前适应度最优的鲸鱼个体位置进行位置更新, 实现局部开发; 现在, 当参数 ${a'} < 1$ 时, $\left| A \right| < 1$ , 此时随机使用正弦余弦函数, 鲸鱼个体位置更新会在更小的范围内, 使得鲸鱼个体可以对局部范围进行精确探索, 进一步提高算法的局部开发能力, 提高算法的收敛精度.

3.3.2 改进鲸鱼个体螺旋更新方式

由式(6)可知, 在WOA中个体会一直以对数螺旋的轨迹方式进行位置更新, 这种螺旋更新位置的方式虽然可以加快整体收敛速度, 但是会导致群体内个体以较快速度聚合在一起, 进而导致整个种群丧失多样性, 最终增大陷入局部最优的几率. 因此, 为增强整个种群多样性与跳出局部最优能力, 同样利用SCA策略对螺旋更新方式实行改进如下:

$ X(t + 1) = \left\{ {\begin{array}{*{20}{l}} {r_1^\prime \cdot {{\rm{e}}^{bl}} \cdot \sin (2\pi l) \cdot {D_3} + {X^*}(t),}\;\;\;{\theta < 0.5}\\ {r_1^\prime \cdot {{\rm{e}}^{bl}} \cdot \cos (2\pi l) \cdot {D_3} + {X^*}(t),}\;\;\;{\theta \geqslant 0.5} \end{array}} \right.$

(20)

$ {D_3} = \left| {{r_3}{X^ * }\left( t \right) - X\left( t \right)} \right| $

(21)

其中, ${r_3}$ 为 $\left[ {0, 1} \right]$ 之间的随机数, 通过利用正弦螺旋更新运动与余弦螺旋更新运动的随机发生, 避免种群多样性的快速丢失, 使其从全局勘探平滑地过渡到局部开发, 最终迭代收敛到最优解.

3.3.3 混合鲸鱼优化算法流程与实施

混合正余弦鲸鱼优化算法综合非线性收敛因子与SCA策略改进方式, 提高算法全局勘探能力与局部开发能力, SCWOA的框架如下:

(1) 定义目标函数, 设置算法参数, 包括种群规模N, 最大迭代次数T, 设置 $t=1$ ;

(2) 进入主循环, 根据适应度记录最优个体位置, 定义并更新非线性收敛引子 $ a^{\prime} $ , $ r_1^{\prime} $ , $ a^{\prime} $ , $ r_1^{\prime} $ 参数设置依据式(16), 式(17);

(3) 定义并更新参数 $ A $ , $ C $ , $l $ , $ \theta $ , $ r_{3} $ , $ r_{4} $ 的值, $ A $ 的数值依据式(4)所定, $ C $ 为[0, 2]内随机值, $l$ , $\theta $ , ${r_4}$ 为[0, 1]内随机值, ${r_3}$ 为 $[0, 2\pi ]$ 内随机值;

(4) 判断 $ p<0.5 $ , 若 $ |A| \geqslant 0.5 $ , 采用式(18)更新个体位置; 若 $ |A|<0.5 $ , 采用式(19)更新个体位置;

(5) 判断 $ p \geqslant 0.5 $ , 采用式(20)更新个体位置;

(6) 判断 $t = T$ , 若满足进行步骤(7), 否则返回步骤(2);

(7) 输出最优个体位置与目标函数最优解.

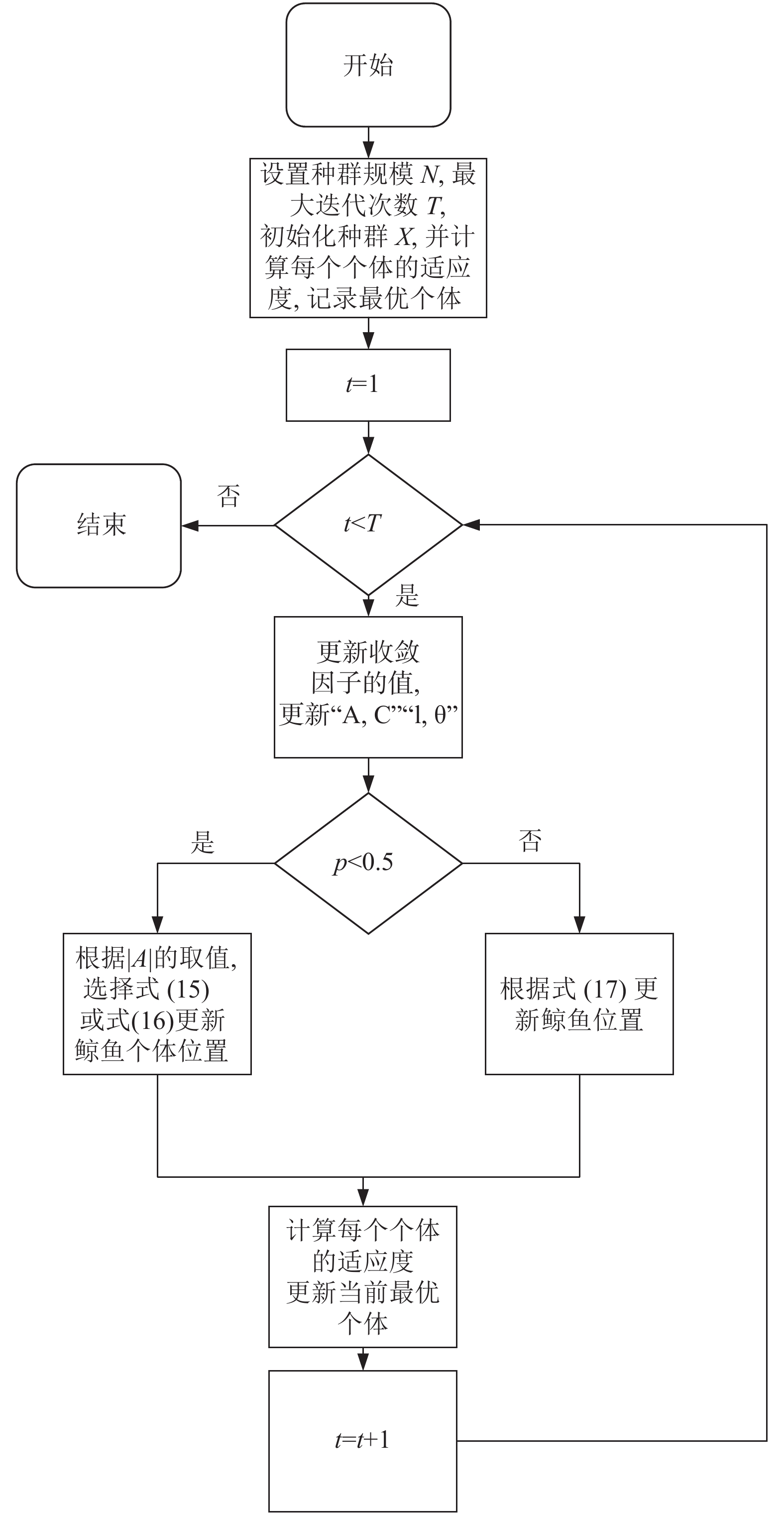
图5为SCWOA流程图.

4 实验分析

本文选取文献[23]中BRdata包含的10个FJSP标准调度实例(MK01-MK10), 与文献[24]中5个标准调度实例(kacem01-kacem05)对SCWOA实行实例验证, SCWOA由Python 3.7实现, 在Windows 10, Intel(R)Core(TM) i5-9300 CPU, 2.4 GHz主频, 16 GB内存的系统上运行. 算法参数设置种群为160, 最大迭代次数为300.

首先对基本WOA与SCWOA进行实验对比, 以验证非线性收敛因子与正余弦策略改进措施的有效性. 为避免随机性, 算法共运行10次, Time表示算法的平均运行时间, Best代表10次运行结果中最优结果, Avg代表10次实验的平均优化结果. 借鉴文献[17]的对比方法加入提升率, 其计算公式为 $(\textit{SCWOA}{_{{\rm{Best}}}} - WO{A_{{\rm{Best}}}})/ $ $ \textit{SCWOA}{_{{\rm{Best}}}}$ , 其用来表示SCWOA相较于原算法的提升水平. 其实验对比结果如表1所示.

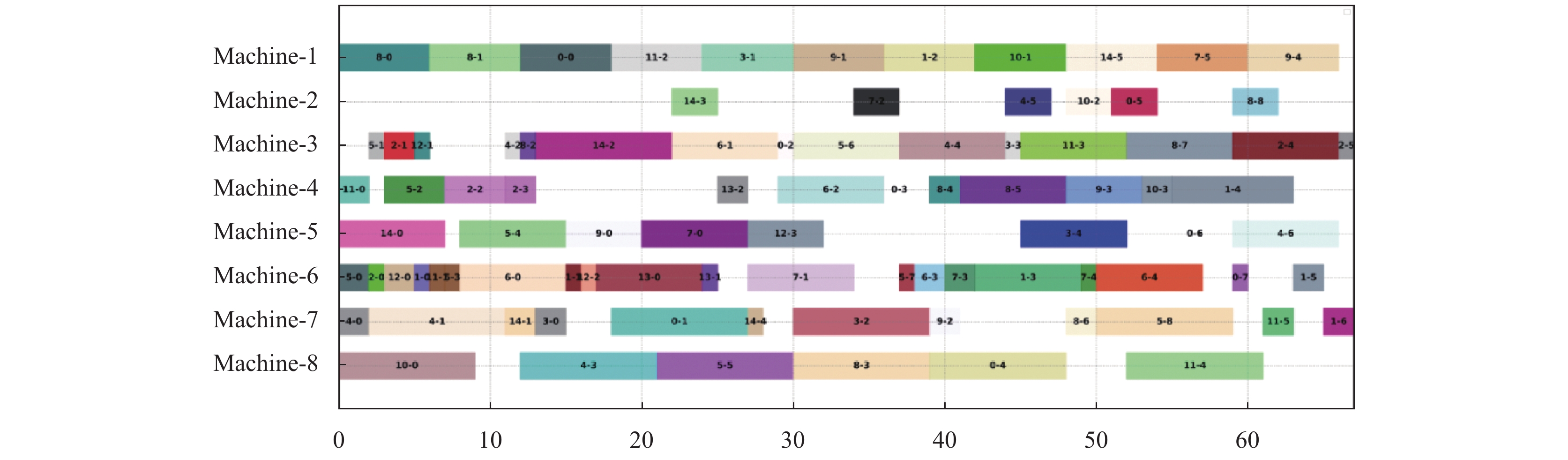
从表1对比结果可知, SCWOA相较WOA在最优寻优结果与平均寻优结果方面都获得了一定的提升, 在8个实例中优化结果得到了提升, 并且最大提升效果达到了0.1, 证明SCWOA的改进措施有效. 值得注意的是SCWOA的时间复杂度也较WOA有一定程度的提高. 如图6所示为SCWOA在MK04上的调度甘特图, MK04有8个加工机器与15个待加工工件, 求解结果C max为67, 虽未达到最优调度结果, 但调度结果仍优于大部分优化算法.

同时将SCWOA与其他元启发式算法进行实验对比, 对比算法包括基本遗传算法、文献[2]中的混合遗传算法、文献[8]的混合灰狼优化算法、文献[24]与文献[25], 最优结果以粗体表示, 对比结果如表2与表3所示.

表2对比结果表明文献[24]在缺失2个算例情况下获得最优解有1次, 文献[8]获得最优解有4次, 文献[25]获得最优解有3次, SCWOA获得最优解有4次. SCWOA表现较好. 表3对比结果表明GA获得最优解有1次, 文献[23]获得最优解1次, 文献[2]获得最优解有4次, 文献[8]获得最优解5次, SCWOA获得最优解次数最多, 并且SCWOA的寻优能力在问题规模较大时相较于其他算法表现也较好, 以上结果综合表明SCWOA应用于FJSP的有效性.

5 结束语

本文以FJSP的最大完工时间为优化目标, 对WOA进行设计改进, 提出了一种混合正余弦鲸鱼优化算法. 首先以两段式编码使鲸鱼优化算法离散化, 使其可应用于FJSP; 加入非线性收敛因子策略; 并加入SCA的优化策略, 改进鲸鱼优化算法的位置变动方式, 提高全局勘探与局部开发能力. 通过与其他算法在BRdata算例上的实验对比, 实验对比结果证明了算法设计的有效性. 下一步工作可将鲸鱼优化算法应用于更加复杂的车间调度问题, 如多目标FJSP, 进一步丰富算法的应用范围, 并且可将绿色调度目标作为算法优化目标, 响应国家碳中和、碳达峰政策.