橄榄核雕是古老的民间手工艺品, 其因精美的刀工、精致的造型、多样的艺术表现性而备受青睐. 近年来, 人们开始将数控雕刻机应用于橄榄核雕刻领域, 机器雕刻的出现解决了人工雕刻耗费工时长、品质良莠不齐、无法大规模生产以及造价高等缺点. 但是如图1所示, 橄榄核形状大小不一且中空^[1], 若将已有的三维模型直接用于橄榄核机器雕刻, 易造成雕穿的现象, 且无法发挥橄榄核雕随形雕刻的艺术特色. 目前业界在进行橄榄核机器雕刻时仍然由专业人员使用商业CAD软件手工调整三维模型再进行数控编程得到雕刻刀路. 这个过程需要较高的人力成本且具有不可复制性. 如果存在一种面向橄榄核机器雕刻的模型编辑与刀具路径规划方法, 必定会大大改善目前橄榄核机器雕刻的加工效果, 提高加工效率并可以以较低的成本实现随形雕刻.

在橄榄核机器雕刻领域, 硬件方面已相对成熟, 除了可以使用常规雕刻机搭配橄榄核专用夹具进行雕刻外, 田杰宇等^[2]研发了一种基于并联机构的核雕专用设备. 然而目前学术界对面向橄榄核机器雕刻的模型编辑与刀具路径规划研究较少, 难以对工业界提供具有针对性的指导.

1 相关基本理论

三维模型变形问题一直是国内外计算机图形学领域的研究热点, 经过众多学者多年研究已经取得了诸多研究成果. 空间变形技术最早由Sederberg等^[3]提出, 主要思想是将待变形的目标模型嵌入到某个控制网格中, 通过对控制网格顶点的操作使嵌入其中的目标模型基于函数插值进行变形. 此后学者们提出了一系列无需控制网格的方法如最小二乘法^[4]、径向基函数法(radical basis function, RBF)^[5] 及线性混合蒙皮法^[6]等. 其中, 径向基函数法基于径向基函数插值技术生成光滑的插值曲面, 是一种常用且快速的无控制网格法. Botsch等^[7]通过定义一个三维径向基函数插值变形场并求解线性方程组, 得到径向基函数混合权重以及表示仿射变换的低次多项式的系数, 从而对目标模型进行变形. Levi 等^[8]提出采用测地距离作为基函数的距离形式, 实现了较为自然的变形.

空间变形技术运算速度快, 且对目标模型的表示方式没有要求, 因此得到了广泛的应用, 然而在进行大尺度变形时, 空间变形技术不能很好地保持模型原有的局部特征. 基于曲面的变形可以很好地解决这一问题^[9]. 其主要思想是: 预先在目标模型上选择一些顶点作为变形控制顶点, 移动控制顶点, 其他顶点通过优化能量函数发生相应的变化, 从而得到最终变形结果^[10]. 在此框架下, Sorkine等^[11]提出一种近似刚性(as rigid as possible, ARAP)三维模型变形方法: 将模型中每个顶点以及该顶点1-邻域的三角面片定义为一个单元, 在变形过程中, 将单元实际变换与刚性变换的差值定义为刚性能量函数, 然后在后续操作中基于“变形-求局部旋转-再变形”的迭代过程最小化该函数, 保证每个单元近似刚性变形, 从而尽可能地保持目标模型的局部几何细节. 此后众多学者针对能量函数的定义、单元的定义等对ARAP变形方法提出了改进方案: Levi等^[12]提出一种基于旋转光滑项的改进版本的能量函数SR-ARAP, Chen等^[13]将 ARAP 方法中的单元从顶点的1-邻域三角面片扩展到r-邻域三角面片, Colaianni等^[14]在原 ARAP 的能量形式中加入各向异性的局部变换等. ARAP 算法实现简单, 易于操控, 它是目前基于曲面的变形框架下变形效果较好的算法.

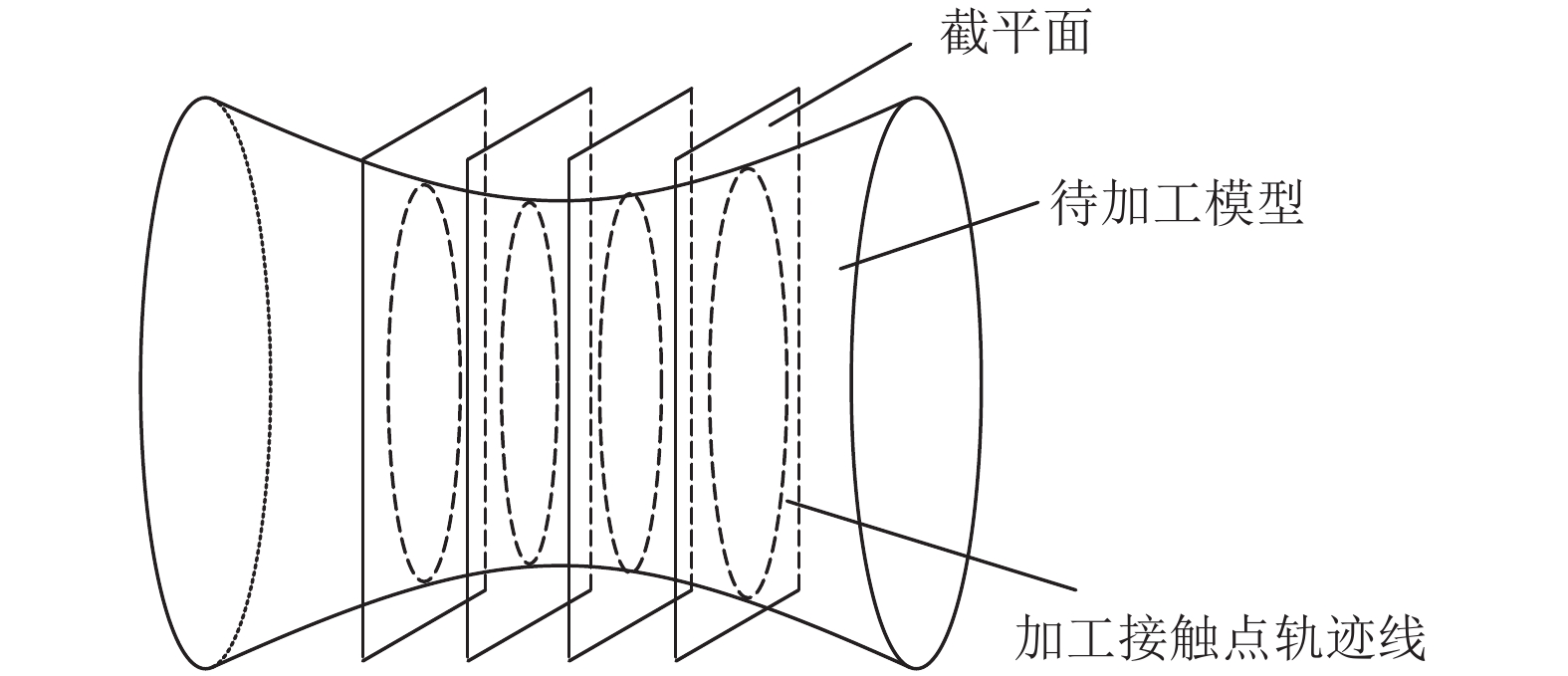
在基于三维数字模型的数控加工刀具路径规划领域, 主要方法有偏置刀位点路径截面法(cutter location, CL路径截面法)和刀触点路径截面法(cutter contact, CC路径截面法). CC路径截面法如图2所示, 用一组平行的约束面与被加工模型求交, 将交线作为刀具接触点路径来生成刀具轨迹^[15], 约束面一般是平面^[16], 也称为截平面. CC路径截面法可以灵活控制走刀路线, 生成均匀的刀具路径, 因此加工效率较高, 适合复杂模型的加工^[17]. 在对CC路径截面的研究中, 邱晓杰等^[18]采用二阶连续可导的三次B样条曲线对切片得到的刀触点轨迹进行拟合, 继而按一定的加工步长对其进行插补得到最终的刀触点轨迹. 孙殿柱等^[19]针对三角贝塞尔曲面引入R×S树快速准确地获取相交面片集, 并自适应地离散为三角网格, 然后计算截平面与离散后的三角网格的交点并进行偏置作为刀具路径; Li等^[20]针对圆角刀具的特性, 利用模型切片数据直接得到刀触点轨迹, 通过刀触点偏置计算刀位点轨迹, 然后进行干涉检测处理得到刀具路径.

虽然三维模型变形与刀具路径规划皆有诸多研究成果, 但是尚未有将二者有机结合并应用于橄榄核机器雕刻场景以及针对该应用场景进行特定优化的研究工作. 所以当前橄榄核机器雕刻领域仍存在以下不足和待解决的痛点: 若直接将标准模型应用于橄榄核机器雕刻, 如图3所示, 有一定风险出现雕穿的现象, 且不能体现橄榄核随形雕刻的艺术特色; 若由专业3D建模设计师使用商业CAD软件制作橄榄核雕刻模型, 再进行数控编程得到加工路径, 整个过程需要跨行业合作, 时间上往往需要数小时甚至数天, 有较高的人工成本与时间成本, 最终效果与设计师的技术水平、审美水平高度相关, 不具备可复制性, 不能批量生产, 同时个性化设计较为复杂.

据此, 本文基于改进的RBF变形方法与ARAP变形方法以及CC路径截面法, 提出了一种面向橄榄核雕刻的模型编辑和刀具路径规划方法, 具体技术方案流程如图4所示.

首先, 输入橄榄核模型与待雕刻模型, 基于主成分分析法对橄榄核模型与待雕刻模型进行刚性对齐, 继而使用改进的RBF变形算法与ARAP变形算法进行模型变形得到编辑后的待加工模型, 然后基于模型拓扑结构与扫描平面法对编辑后的待加工模型进行模型切片, 再由切片信息作为基数据通过干涉处理与坐标映射生成加工刀具路径, 最后进行雕刻加工, 得到加工成品.

2 模型编辑

模型编辑阶段的主要目标为: 基于橄榄核模型调整编辑待雕刻模型, 使待雕刻模型可以在保持基本形状与细节的前提下, 尽可能地填充橄榄核模型, 避免在雕刻过程中雕穿, 并做到随形雕刻. 　　

2.1 模型刚性对齐

为方便后续待雕刻模型在橄榄核模型约束下的变形操作, 首先需要将橄榄核模型 $O$ 与待雕刻模型 $G$ 调整到合适的相对位置.

根据两模型的顶点信息, 使用主成分分析法利用协方差矩阵计算得到两模型的主轴, 进而计算得到两模型的方向包围盒 ${B_O}$ 与 ${B_G}$ , 然后计算 ${B_O}$ 与 ${B_G}$ 之间的仿射变换矩阵 ${M_{\rm Affine}}$ .

对待雕刻模型 $G$ 施加上述仿射变换得到 $G'$ , 计算公式如式(1)、式(2)所示:

$ {B_O} = {B_G} \times {M_{\rm Affine}} $

(1)

$ G' = G \times {M_{\rm Affine}} $

(2)

两模型刚性对齐前后如图5所示. 此后, 为方便后续刀路生成过程中刀位点坐标计算, 再将两者共同进行仿射变换至: 主轴与坐标系z轴重合, 橄榄核模型 $O$ 中最低点z轴坐标为0.

2.2 模型变形

为使待雕刻模型更好地填充适配橄榄核模型, 在雕刻过程中更好地保留橄榄核自身的特点做到随形雕刻, 需要进行模型变形. 考虑到待雕刻模型与橄榄核模型自身的类圆柱特性, 本文使用改进的基于径向基函数(RBF)的变形算法以及尽可能刚性(ARAP)变形算法, 结合层次包围盒树(bounding volume hierarchy, BVH)进行碰撞检测, 最终实现待雕刻模型随橄榄核模型随形变形的效果.

2.2.1 RBF变形

RBF插值技术可以生成光滑的插值曲面, 被广泛应用于网格变形. 由一组变形控制点 ${c_i}$ 和相应的权重 ${w_i}$ 定义的径向基函数的一般形式为:

$ F(x) = \sum\limits_{i = 1}^N {{w_i}\varphi \left(\left\| {{c_i} - x} \right\|\right) + Mx + t} $

(3)

其中, $\left\| {{c_i} - x} \right\|$ 表示 $x$ 与 ${c_i}$ 的欧氏距离, $Mx + t$ 是一个低次多项式, 用来表示仿射变换部分. 由于待雕刻模型呈现出明显的类圆柱特性, 因此对其在同一个高度( ${\textit{z}}$ 坐标相同)的顶点进行同样的仿射变换, 会更大限度地保持原模型局部细节特征, 同时会减少时间消耗. 因此, 可以重新定义式(3)中 $\left\| {{c_i} - x} \right\|$ 的为 $\left\| {{c_i}({\textit{z}}) - x({\textit{z}})} \right\|$ , 表示 $x$ 与 ${c_i}$ 在 ${\textit{z}}$ 轴投影距离, 将式(3)改写成:

$ F(x) = \sum\limits_{i = 1}^N {{w_i}\varphi \left(\left\| {{c_i}({\textit{z}}) - x({\textit{z}})} \right\|\right) + Mx + t} $

(4)

将N个控制点处的位移带入式(4):

$ \Delta F({c_j}) = \sum\limits_{i = 1}^N {{w_i}\varphi \left(\left\| {{c_i}({\textit{z}}) - {c_j}(x)} \right\|\right) + M{c_j} + t} $

(5)

将式(5)与以下约束条件:

$ \sum\limits_{i = 1}^N {{w_i} = 0} $

(6)

$ \sum\limits_{i = 1}^N {{w_i}x_i^{\rm{T}} = 0} $

(7)

联立, 令 ${a_{i, j}} = \varphi \left(\left\| {{c_i}({\textit{z}}) - {c_j}({\textit{z}})} \right\|\right)$ 可得:

$ \left[\begin{array}{ccccc}{a}_{0, 0}& \cdots & {a}_{0, n}& & \\ \vdots& \ddots & \vdots& \vdots& \vdots\\ {a}_{n, 0}& \cdots & {a}_{n, n}& & \\ 1& \cdots & 1& 0& 0\\ {c}_{0}^{T}& \cdots & {c}_{n}^{T}& 0& 0\end{array}\right] \cdot \left[\begin{array}{c}{w}_{0}\\ \vdots\\ {w}_{n}\\ M\\ t\end{array}\right]=\left[\begin{array}{c}\Delta {c}_{0}\\ \vdots\\ \Delta {c}_{n}\\ 0\\ 0\end{array}\right] $

(8)

解该线性方程组可得一系列权重系数 ${w_i}$ 以及表示仿射变换的低次多项式系数 $M, t$ . 径向基函数 $\varphi (x)$ 有多种形式, 在本文特定网格变形的场景下, 取高斯曲面函数: $\varphi (x) = \exp ({{ - {x^2}} \mathord{\left/ {\vphantom {{ - {x^2}} {{\text{2}}{\sigma ^2})}}} \right. } {{\text{2}}{\sigma ^2})}}$ .

下一步需要确定控制点并设置控制点位移. 基于待雕刻模型的类圆柱特性以及对 $\left\| {{c_i} - x} \right\|$ 的重定义, 不需要进行复杂的控制点选取与控制点位移的设置. 只需选择 $n$ 个特定高度 ${h_1}, \cdots , {h_n}$ , 继而对待雕刻模型中与平面 ${\textit{z}} = {h_i}$ 相交的三角面片上所有顶点设为控制点, 并将控制点位移设置为待雕刻模型放缩 ${r_d} = {{{R_O}} \mathord{\left/ {\vphantom {{{R_O}} {{R_G}}}} \right. } {{R_G}}}$ 倍时控制点的位移, ${R_O}$ 与 ${R_G}$ 分别表示橄榄核模型 $O$ 与待雕刻模型 $G$ 中与平面 ${\textit{z}} = {h_i}$ 相交的所有三角面片的重心距点 $(0, 0, {h_i})$ 的平均距离, 如图6所示.

根据式(8)求解得到的权重系数 ${w_i}$ 以及表示仿射变换的低次多项式的系数 $M,\;t$ , 带入式(4)即可得到任一顶点变形后的位置, 也即得到了变形后的模型.

2.2.2 基于层次包围盒树的碰撞检测

在待雕刻模型经过一次控制点选取及模型变形后, 为保证变形后的模型仍在橄榄核模型内部, 需要将变形后的待雕刻模型与橄榄核模型进行碰撞检测.

为降低后续碰撞检测计算复杂度, 提高计算速度, 首先对两模型构建层次包围盒树. 其核心思想是使用几何特征简单的包围盒近似表示复杂的几何模型, 在进行碰撞检测时, 仅对包围盒重叠的模型进一步计算. 将包围盒嵌套而构造树状结构, 可以方便地进行逐层求精以及精确求交. 构建层次包围盒树的步骤如下.

(1)首先构建模型的AABB包围盒, 并将其作为层次包围盒树的Root节点;

(2)将当前节点包围盒中最长轴作为分割轴;

(3)使用取中点划分的分割策略, 构建当前节点的左右子节点;

(4)将当前节点的左节点和右节点分别作为当前节点, 重复步骤(2)与(3)直到所有节点包围盒都只存在一个三角面片.

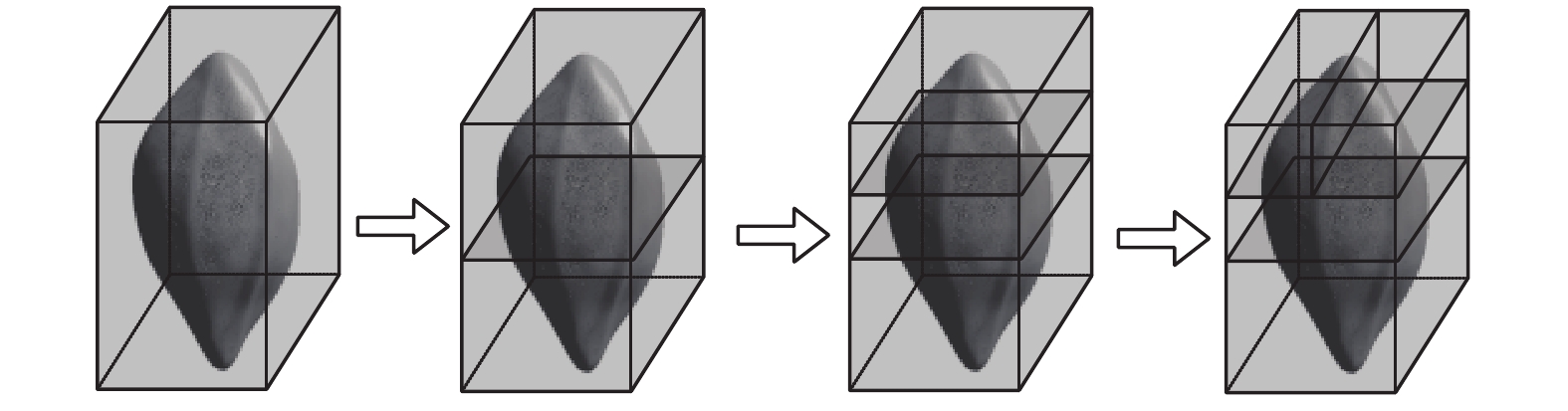
对橄榄核模型 $O$ 构建BVH树的过程示意图如图7所示, 按上述步骤构造的BVH树是一个二叉树, 其结构如图8所示.

依照上述过程完成对橄榄核模型与待雕刻模型建树后, 对两模型进行碰撞检测. 定义碰撞检测函数, 其实现逻辑如下: 输入两节点 ${N_A}$ 与 ${N_B}$ , 若两节点不相交则输出false, 结束; 若相交, 则将 ${N_A}$ 与 ${N_B}$ 依次赋值为其左右子节点, 递归调用该函数, 直至不相交输出false或 ${N_A}$ 与 ${N_B}$ 皆为叶子节点; 若 ${N_A}$ 与 ${N_B}$ 皆为叶子节点, 再精确判断两叶子节点对应的三角面片是否相交, 相交输出true, 否则输出false. 将两模型层次包围盒树的根节点 ${N_O}$ 与 ${N_G}$ 输入到该碰撞检测函数, 返回值为true则代表两模型相交, 返回值为false则代表两模型不相交.

结合第2.2.1节所述改进的RBF变形与本节所述基于层次包围盒树的碰撞检测, 将待雕刻模型进行变形. 其流程如图9所示: 将每一次RBF变形的控制点放缩倍数改为 ${{{r_d}} \mathord{\left/ {\vphantom {{{r_d}} n}} \right. } n}$ , ${r_d}$ 为第2.2.1节求得的放缩倍数. 每进行一次RBF变形后, 都进行碰撞检测, 若不发生碰撞, 则进行下一次变形, 否则结束变形并回退到上一次变形结果. 由于橄榄核模型 $O$ 在整个过程中不进行任何改变, 所以只对其进行一次BVH树的构建, 减少时间消耗.

待雕刻模型经过上述变形后效果如图10(b)所示. 模型变形前后较好地保持了局部细节, 没有出现明显的失真现象.

2.2.3 ARAP网格变形

由于橄榄核呈梭形“两头小, 中间大”的特性, 经过基于RBF的变形后, 其两端仍有部分空白空间, 针对这一问题采用ARAP变形对待雕刻模型 $G$ 进行变形使其更好地填充橄榄核模型.

首先进行ARAP变形控制点的选取: 将待雕刻模型 $G$ 与 ${\textit{z}}$ 轴求交, 得到两个相交三角面片, 将三角面片上所有顶点加入控制点集 ${V_C}$ .

对控制点集 ${V_C}$ 中每个顶点v, 取其周围半径为r的球体内的所有顶点作为与该控制顶点v对应的自由点集 ${V_F}$ . 此外, 为简化后续计算, 提升网格变形速度, 取顶点v周围半径为2r的球体内的所有顶点作为与该控制顶点对应的全部感兴趣顶点集 ${V_I}$ , $r = 0.2 \times {{\textit{z}}_{\max}}$ .

定义控制顶点 $v$ 对应的点集 ${V_I}$ 组成的网格为输入网格 $S$ . 获取输入网格 $S$ 的邻接信息, 定义单元(cell)为网格 $S$ 中顶点 ${v_i}$ 及其1-邻域顶点, 定义一个单元变形前后产生的刚性能量如式(9)所示:

$ E(C, C') = \sum\limits_{i \in {N_i}} {{w_{ij}}{{\left\| {({p_i}' - {p_j}') - R_i({p_i} - {p_j})} \right\|}^2}} $

(9)

其中, ${p_i}$ 为顶点 ${v_i}$ 的位置, ${p_i}'$ 为 ${p_i}$ 变形后的位置, ${p_j}$ 为顶点 ${v_j}$ 的位置, $ {p_j}' $ 为 ${p_j}$ 变形后的位置; ${R_i}$ 为单元 $C$ 变换前后的旋转矩阵, ${N_i}$ 为顶点 ${v_i}$ 的1-邻域顶点的集合 ${w_{ij}}$ 取余切权重公式.

而整体网格 $S$ 对应的刚性能量为所有顶点 ${v_i}$ 对应的单元刚性能量之和:

$ E(S') = \sum\limits_{i = 1}^n {{w_i}E(C, C')} $

(10)

其中, ${w_i}$ 取1, 平均权重.

当变形为刚性时, 可以找到旋转矩阵 ${R_i}$ , 使得 $({p_i}' - {p_j}') = R({p_i} - {p_j})$ , 即 $E(S') = 0$ , 当变形不是刚性的时候, 依然存在最佳旋转矩阵 ${R_i}$ , 使得 ${p_i}' - {p_j}'$ 与 $R({p_i} - {p_j})$ 差值最小, 即 $E(S')$ 最小. 因此, 通过最小化刚性能量 $E(S')$ 可以实现网格模型的尽可能刚性变形.

在式(9)中, 只有顶点变形后坐标 $p'$ 和旋转矩阵 ${R_i}$ 是未知量. 为求解 $p'$ 与 ${R_i}$ , 采用“变形-求局部旋转-再变形”的迭代方法:

(1)确定初始猜测. 对于控制点集, 其初始猜测位置为 ${p_c}' = {p_c} + a\overrightarrow n $ , $\overrightarrow n $ 为该控制点的法向量; 对于自由点, 求解拉普拉斯变形结果作为初始猜测;

(2)基于当前顶点位置 $p'$ , 求解 ${R_i}$ . 首先将式(9)带入式(10), 并进行推导化简, 再使用奇异值分解的方法估算出每个单元的最佳旋转矩阵 ${R_i}$ ;

(3)基于目前最近旋转矩阵 ${R_i}$ , 求解 $p'$ . 当 ${R_i}$ 确定后, $p'$ 的值可以通过求解线性方程组 $\dfrac{{\partial E(S')}}{{\partial p'}} = 0$ 实现;

(4)下一次迭代中, 将新求得的 $p'$ 作为已知量, 以此求解新的 ${R_i}$ 和 $p'$ , 即重复步骤(2)到(3), 直至迭代次数达到设置要求或网格刚性能量小于指定的阈值为止.

待雕刻模型进行ARAP变形后如图10(c)–图10(e)所示, 待雕刻模型可以较好地填充橄榄核模型, 达到了随形状雕刻的效果.

3 刀具路径规划

刀具路径规划阶段的主要目标为: 根据模型编辑后得到的待雕刻模型, 进行模型切片、干涉处理并根据预置的刀具信息生成可供雕刻机直接读取并执行加工的刀具路径.

3.1 模型切片

模型切片是将一组平行的截平面依次与待雕刻模型求交, 得到一系列闭合切片轮廓, 作为生成刀具路径的基数据.

3.1.1 基于扫描平面法得到相交三角面片

首先, 使用扫描平面法得到待雕刻模型 $G$ 中可能与每个截平面相交的三角面片集合 ${F_i}$ . 具体步骤为:

(1)设分层方向为 ${\textit{z}}$ 轴正方向, 分层厚度为 ${h_0}$ , 分层层数 $n = {{({\textit{z}}_{\max} - {\textit{z}}_{\min})} \mathord{\left/ {\vphantom {{({\textit{z}}_{\max} - {\textit{z}}_{\min})} {{h_0}}}} \right. } {{h_0}}}$ ;

(2)将待雕刻模型G中所有三角面片按其最低点 ${\textit{z}}$ 坐标升序排序, 记排序后集合为 ${F_{\rm order}}$ , 令遍历起始下标 $k = 0$ ;

(3)令 ${F_i} = \left\{ \begin{gathered}\varnothing , i = 0 \hfill \\ {F_{i - 1}}, {\rm{else}} \hfill \\ \end{gathered} \right.$ , 随后移除集合 ${F_i}$ 中与当前截平面 ${\textit{z}} = i \times {{({\textit{z}}_{\max} - {\textit{z}}_{\min})} \mathord{\left/ {\vphantom {{({\textit{z}}_{\max} - {\textit{z}}_{\min})} n}} \right. } n}$ 不相交的三角面片, 并赋值 $k$ 为被移除的三角面片中下标的最大值;

(4)从下标为k的三角面片开始遍历 ${F_{\rm order}}$ 中的三角面片, 添加其中与当前截平面相交的三角面片;

(5) $i$ 自增, 重复步骤(3)、步骤(4)直至 $i = n$ , 即遍历完所有层高列表.

上述步骤中对三角面片的排序仅需执行一次, 且随着 $i$ 与 $k$ 的增大, 求与当前截平面相交的三角面片所需遍历的面数会减少, 效率得到提高.

3.1.2 相交三角面片交点计算

由第3.1.1节得到的待雕刻模型与平面 ${\textit{z}} = {{\textit{z}}_i}\; ({{\textit{z}}_i} =$ $i \times {{({\textit{z}}_{\max} - {\textit{z}}_{\min})} \mathord{\left/ {\vphantom {{({\textit{z}}_{\max} - {\textit{z}}_{\min})} n}} \right. } n}$ )截平面相交的三角面片 ${F_i}$ 中, 与截平面的关系有如图11所示的7种情况.

图11中7种情况的代数特征及交点情况如表1.

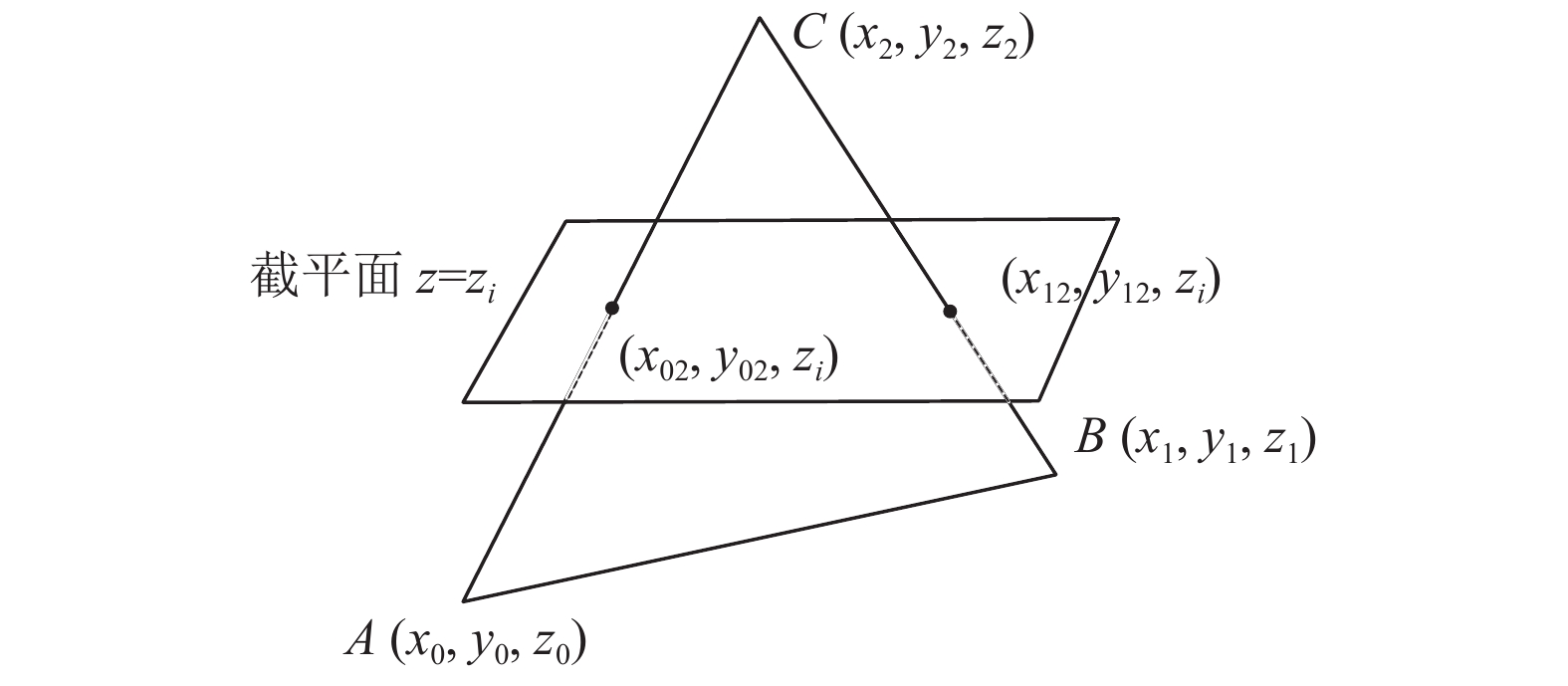
要求得具体的截交轮廓线, 需要对截平面与三角面片求交, 示意图如如图12所示.

对与任一与截平面相交的 $\vartriangle ABC$ , 将 $({x_{02}}, {y_{02}}, {{\textit{z}}_i})$ 与代入 $AC$ 所在直线方程即可求得 ${x_{02}}, {y_{02}}$ 的值:

$ \left\{ \begin{gathered} {x_{02}} = \frac{{{{\textit{z}}_i} - {{\textit{z}}_0}}}{{{{\textit{z}}_2} - {{\textit{z}}_0}}} \times ({x_2} - {x_0}) + {x_0} \hfill \\ {y_{02}} = \frac{{{{\textit{z}}_i} - {{\textit{z}}_0}}}{{{{\textit{z}}_2} - {{\textit{z}}_0}}} \times ({y_2} - {y_0}) + {y_0} \hfill \end{gathered} \right. $

(11)

同理可计算得到 ${x_{12}}, {y_{12}}$ , 即可得到截平面与相交三角面片的精确交点.

3.1.3 基于拓扑模型得到切片轮廓

第3.1.1节与第3.1.2节可以得到与当前层高 ${\textit{z}}$ 相交的三角面片集合 ${F_i}$ 以及截平面与所有三角面片的交点. 接下来需要基于模型的拓扑结构将上一小节得到的交点一定顺序排列得到切片轮廓. 在 ${F_i}$ 中选择一个未被使用过的三角面片作为种子面片, 基于待雕刻模型的拓扑关系寻找种子面片的邻接三角面片, 直至遍历 ${F_i}$ 中所有三角面片. 对于任一特定截平面 ${\textit{z}} = {{\textit{z}}_i}$ , 得到其切片数据的流程如图13所示.

首先设置 ${F_i}$ 中每一个三角面片状态为未遍历; 进行第一层循环, 在 ${F_i}$ 中任选一未遍历三角面片作为种子面片; 若能够找到种子面片, 则创建一轮廓数据contour, 并将其与截平面的交点加入当前contour; 进入第二层循环, 基于拓扑结构根据当前三角面片寻找与之相邻的未遍历三角面片, 并将其与截平面的交点加入当前contour; 若找不到种子面片则 ${F_i}$ 中所有面片均已被遍历, 则输出该层切片数据layer并结束流程.

将待雕刻模型进行切片, 结果如图14所示.

3.2 干涉处理

在得到切片数据后, 若直接将切片数据生成刀具路径, 则会在雕刻过程中出现过切干涉的现象, 为防止这一现象出现, 需要进行干涉处理.

首先, 对切片数据中每一个点, 根据其笛卡尔坐标 $(x, y, {\textit{z}})$ 求其柱面坐标 $(r, \theta , {\textit{z}})$ :

$ \left\{ \begin{split} & r = \sqrt {{x^2} + {y^2}} ,\; r \in {R^ + } \\ & \theta = \arctan ({y \mathord{\left/ {\vphantom {y x}} \right. } x}),\; \theta \in [0, 2\pi ) \\ & {\textit{z}} = {\textit{z}},\; {\textit{z}} \in R \end{split} \right. $

(12)

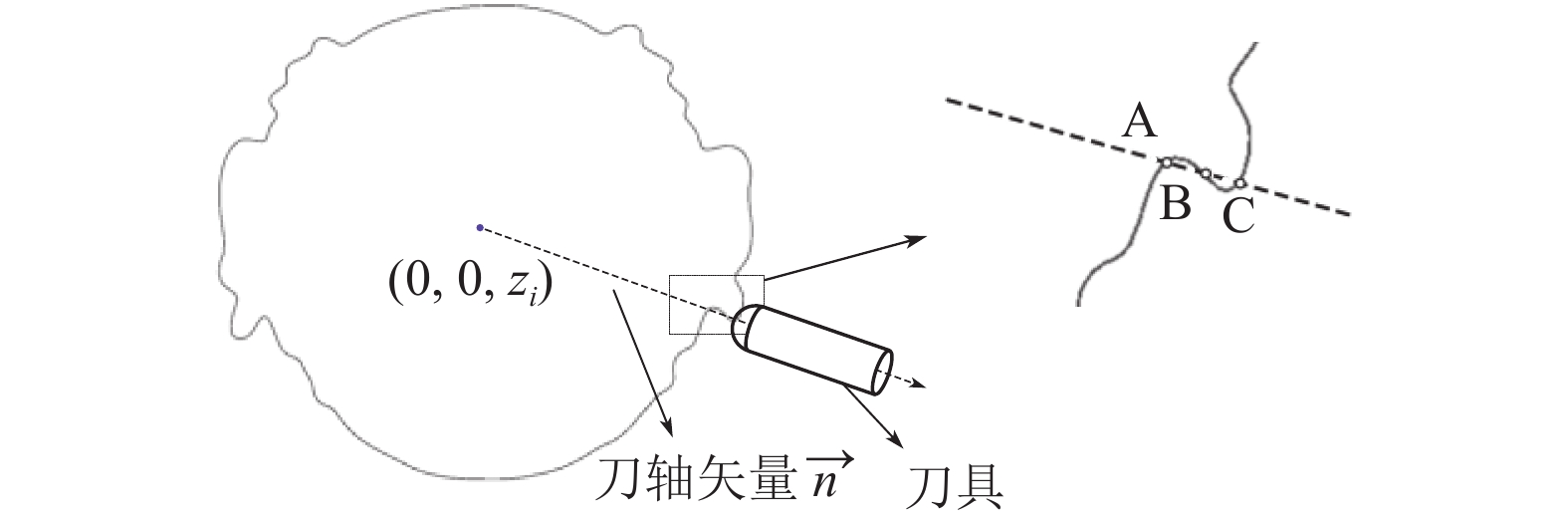
然后需要确定刀轴方向, 对于四轴三联动刀具路径, 某一准刀位点刀轴矢量为该层原点 $(0, 0, {{\textit{z}}_i})$ 指向切片数据中该点的方向 $\overrightarrow n $ . 对于切片数据中每一个点, 过点 $(0, 0, {{\textit{z}}_i})$ , 沿刀轴矢量方向做射线, 得到一个或多个交点. 若存在多个交点, 如图15所示, 交点为 $A, B, C$ , 则取其中柱面坐标 $r$ 最大的一点, 即点 $C$ 点. 对切片数据中每一个点进行上述操作则可得到无干涉的准刀位点.

进行干涉处理前后对比如图16所示.

3.3 四轴三联动刀具路径生成

生成最终四轴三联动刀具路径, 需要结合具体刀具信息. 为方便后续处理, 保证刀轴矢量竖直向上, 即 $\overrightarrow n = $ $ (0, 0, 1)$ , 将第3.2节初步干涉处理后的切片数据根据其柱面坐标进行柱面展开, 柱面展开的坐标映射关系:

$ \left\{ \begin{split} x &= {\textit{z}} \hfill \\ y &= \theta \times R \hfill \\ {\textit{z}} &= r \hfill \end{split}\right. $

(13)

其中, R为展开半径, 一般取待雕刻模型所有顶点柱面坐标中r的最大值.

接下来需要引入刀具模型, 几种常见刀具: 球头刀、角刀和平底刀模型如图17所示.

在第3.2节得到了干涉处理后的的切片数据, 其中点的坐标作为最终刀触点 ${P_c}$ , 而刀具路径中需要使用刀位点 ${P_l}$ , 由刀触点 ${P_c}$ 得到刀位点 ${P_l}$ 计算公式为:

$ {P_l} = {P_c} + (R - r) \cdot \frac{{{n_t} \times ({n_s} \times {n_t})}}{{\left| {{n_t} \times ({n_s} \times {n_t})} \right|}} + r \cdot {n_s} - r \cdot {n_t} $

(14)

其中, R为刀具半径, r为刀角半径, ${n_t}$ 为刀轴单位矢量 $(0, 0, 1)$ , ${n_t}$ 为待加工模型上该点的单位法向量. 由此可以计算出一系列刀位点数据. 但是由于式(14)的计算, 会在一些刀位点处造成刀路自交, 在另一些刀位点处造成过切, 如图18所示.

对于图18(a)的情况, 计算无干涉刀位点的过程与第3.2节的干涉处理相似, 但由于经过了柱面展开, 所以要将过准刀位点的竖直线与刀位面求交, 得到一系列的交点, 取所有交点中 ${\textit{z}}$ 值最大的交点, 即为该准刀位点所对应的无干涉刀位点.

对于图18(b)的情况, 需要为之添加点保护面, 由于在求解某一无干涉刀位点时, 其 $x$ 坐标保持不变, 仅与 $y, {\textit{z}}$ 坐标有关, 所以将保护面的三维曲面投影成二维曲线, 如图19所示. 因此, 该情况下求无干涉刀位点便转换成直线与二次曲面的求交问题, 如图19中所示, 其中 ${x_l} = {x_c}, {y_l} = {y_c}$ , 对于 ${{\textit{z}}_l}$ :

球头刀: ${{\textit{z}}_l} = {{\textit{z}}_c} + \sqrt {{R^2} - {d^2}}$

角刀: ${{\textit{z}}_l} = {{\textit{z}}_c} + \sqrt {{r^2} - {{[d - (R - r)]}^2}}$

平底刀: ${{\textit{z}}_l} = {{\textit{z}}_c}$

经如上步骤, 最终生成的刀具路径如图20所示. 随后, 为适配雕刻机, 再将柱面展开后的坐标 $(X, Y, Z)$ 映射成四轴三联动坐标 $(X, A, Z)$ , 即将Y坐标 $[0, 2\pi R)$ 映射到旋转轴成为A坐标 $[0, 360)$ , 映射公式为: $a = {\raise0.5ex\hbox{$\scriptstyle y$}\kern-0.1em/\kern-0.15em\lower0.25ex\hbox{$\scriptstyle R$}} \cdot {\raise0.5ex\hbox{$\scriptstyle {180}$}\kern-0.1em/\kern-0.15em\lower0.25ex\hbox{$\scriptstyle \pi $}}$ , 其中R为式(13)中的展开半径. 最后将得到的四轴三联动坐标数据前后加上机器能识别的特定G代码即可得到最终刀具路径.

4 实验

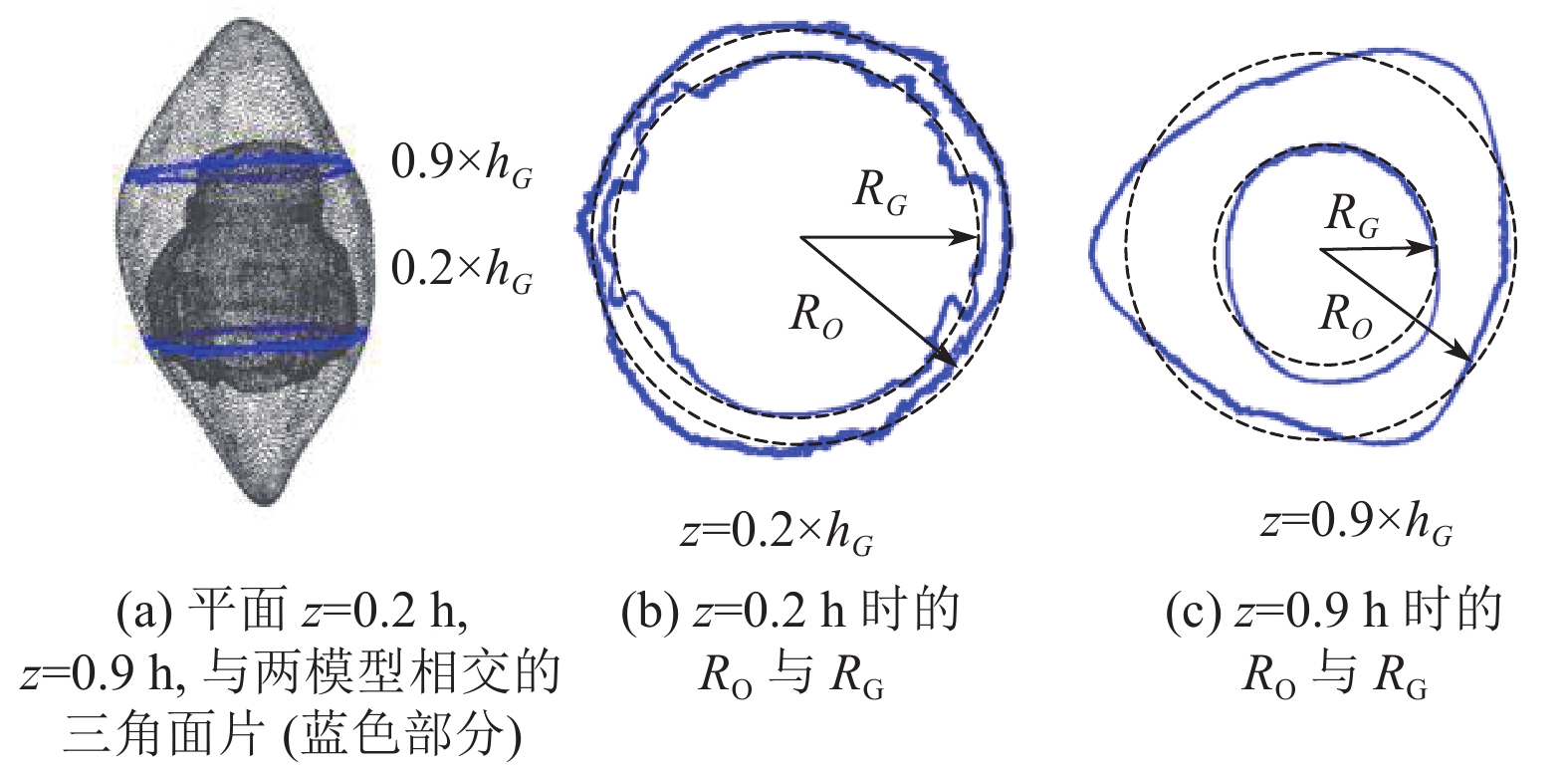
本小节将进行实验验证本文方法的有效性. 在模型编辑阶段, 为验证变形后的待雕刻模型是否可以更好地填充橄榄核模型, 在橄榄核模型与待雕刻模型模型同一高度h处分别进行采样, 得到两模型与平面 ${\textit{z}} = h$ 相交三角面片集合, 依第2.2.1节所述的方法分别计算橄榄核模型与待雕刻模型中相交三角面片重心与点 $(0, 0, h)$ 的平均距离R与r. 使用变形前后在同一采样高度h计算得到的 ${r \mathord{\left/ {\vphantom {r R}} \right. } R}$ 数值作为变形后的待雕刻模型能否更好地填充橄榄核模型的指标, ${r \mathord{\left/ {\vphantom {r R}} \right. } R}$ 越接近1, 表示填充效果越好.

在11个高度 $\left(i \times \dfrac{h}{{10}}, i = 0, \cdots , 10\right)$ 对待雕刻“财神”模型与橄榄核模型进行采样并计算变形前后 ${r \mathord{\left/ {\vphantom {r R}} \right. } R}$ 数值, 实验结果如图21所示. 由图21可以看出, 文献[8]方法在一定程度上可以使待雕刻模型在 $x, y$ 维度上更好地填充橄榄核模型, ${r \mathord{\left/ {\vphantom {r R}} \right. } R}$ 较变形前平均提高0.07; 文献[6]方法与文献[12]方法在一定程度上可以使待雕刻模型在z维度上更好地填充橄榄核模型, 其中文献[6]方法变形前后 ${r \mathord{\left/ {\vphantom {r R}} \right. } R}$ 平均提高0.16, 文献[12]方法变形前后 ${r \mathord{\left/ {\vphantom {r R}} \right. } R}$ 平均提高0.11, 但两种方法在细节方面均有一定程度的失真. 而本文方法可以在 $x, y, {\textit{z}}$ 三个维度上使待雕刻模型更好地填充橄榄核模型, 变形前后 ${r \mathord{\left/ {\vphantom {r R}} \right. } R}$ 平均提高0.28, 且模型细节保持良好.

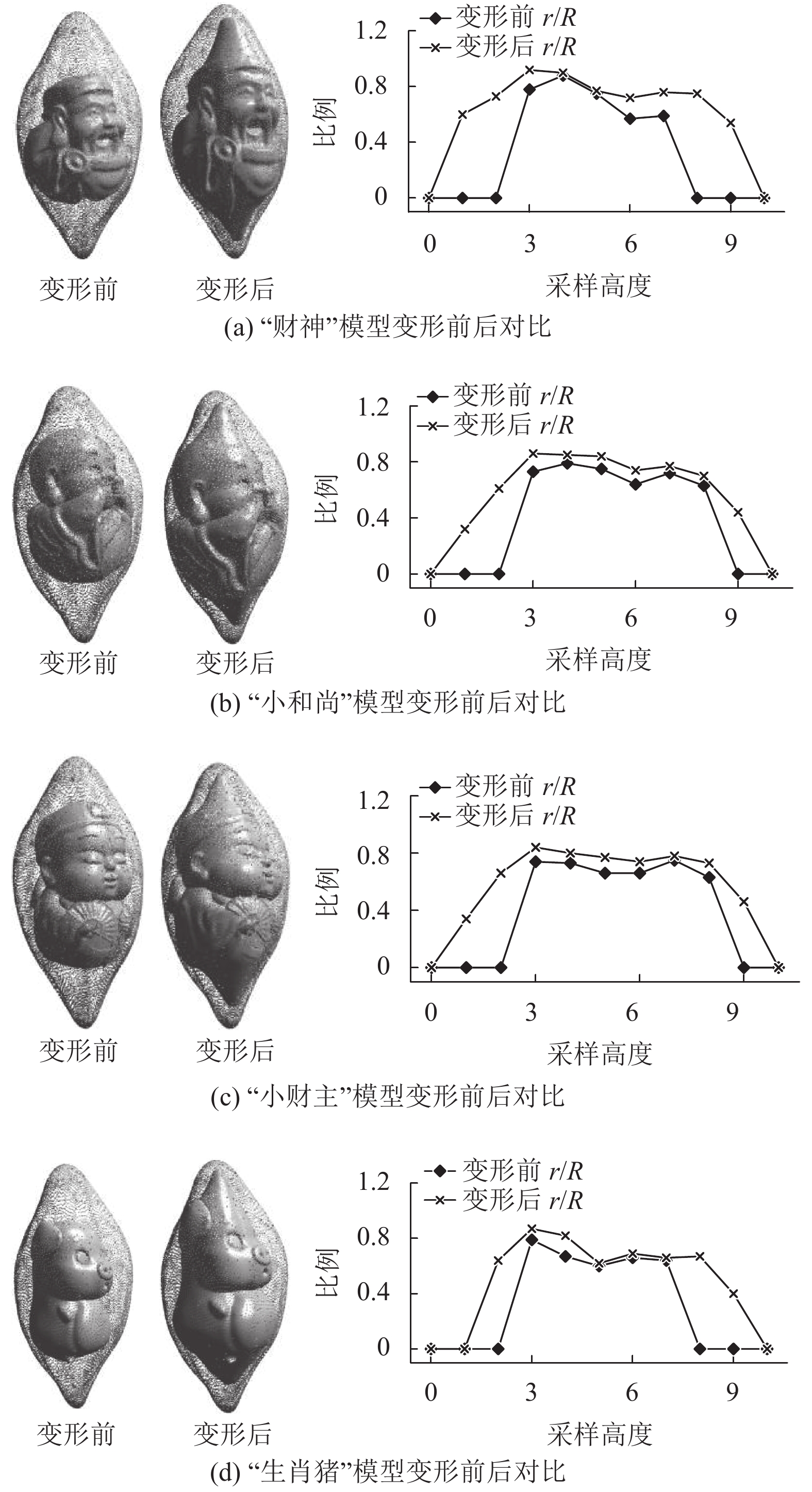
为验证本文算法的通用性, 除了对“财神”模型进行实验外, 还对另外3个模型进行了实验, 结果如图22所示. 由图22可以看出, 变形后模型r与R之比相较变形前明显提高, “财神”模型平均提高0.28, “小和尚”模型平均提高0.17, “小财主”模型平均提高0.19, “生肖猪”模型平均提高0.20, 变形后的模型能更好地填充适应橄榄核模型且能够较好的保持原模型的细节特征.

在刀具路径规划阶段, 为验证所得刀具路径的实际雕刻效果, 使用钰雕机械设备厂生产的最高支持四轴联动的雕刻机进行雕刻实验, 雕刻机如图23所示. 雕刻刀具选用常见的锥度平底刀(3.175×20°×0.2).

雕刻结果如图24所示. 由图24可以看出, 本文所述方法可以得到较好的模型变形效果, 且可以快速得到适用于机器雕刻的四轴三联动刀具路径, 实际雕刻效果良好, 没有出现雕穿的现象且能体现出橄榄核随形雕刻的艺术特色.

5 总结

本文提出了一种面向橄榄核机器雕刻的模型编辑与刀具路径规划方法, 首先, 在刚性对其后基于改进的RBF变形算法与ARAP变形算法, 结合碰撞检测算法在橄榄核模型的约束下对待雕刻模型进行变形. 再通过模型切片、干涉处理等步骤得到待雕刻模型的四轴三联动加工刀具路径. 实验表明, 本文变形方法可以更好的生成适用于橄榄核随形雕刻的三维模型, 与初始模型相比, 变形后的待雕刻模型可以更好地填充橄榄核模型, 所生成的四轴三联动刀具路径亦可以平稳快速地加工得到效果良好的随型雕刻结果, 有较强的实用价值.

但本文方法仍存在不足之处: 由于四轴三联动刀具路径刀抽始终指向圆心, 为避免发生干涉, 在干涉处理中, 部分模型细节会被舍弃. 在后续研究工作中, 可以使用四轴联动加工改善这一问题.