早产是指妊娠达到28周但不足37周而终止妊娠, 按病因分为自发性早产和医源性早产, 是新生儿死亡及病残的首要原因, 且影响新生儿的远期健康^[1].据WHO发布的《全球早产儿报告》指出, 全球每年约有1 500万早产儿出生, 发生率为5%–18%, 其中100万早产儿发生死亡^[2]. 早产是新生儿死亡的主要原因, 随着我国二胎生育政策的实施, 高龄产妇有所增多, 早产儿的发生率呈上升趋势, 出生1岁以内死亡的婴儿约2/3为早产儿^[3]. 此外, 早产儿相较于足月儿, 各器官发育不成熟, 先天畸形、神经系统发育不良如视网膜病变和脑瘫等发病率增高, 远期病死率亦高于足月儿^[4]. 因此, 在孕早期预测早产并采取预防性措施对降低早产儿病死率、提高早产儿生存率具有重要意义^[5].

目前早产的发生机制尚未明确, 临床对早产的早期风险预警仍缺乏有效的评估手段, 如何设计高效的早产筛查模型是一个具有全球意义的重大产科难题^[6]. 超声检查具有操作简便且适用性广等特点, 是临床上评估早产风险的重要手段. 其中, 经会阴超声测量孕妇的宫颈长度是一种全球公认的早产筛查方法^{[7, 8]}, 但阴道超声受限于多种因素, 例如超声设备的质量、超声医生的技术水平等, 且不适用前置胎盘和阴道出血等孕妇. 此外, 某些研究认为基因检测、某些生物标志物也可用于预测早产^{[9, 10]}. 然而以上方法所用的检测指标多为特殊检查项, 检查成本高昂, 难以进行大规模临床验证, 且方法结构简单只考虑了单一因素, 未分析各危险因素间的非线性相互作用^[7]. 早产预测模型的建立须考虑疾病的整体性、复杂性和动态性, 而机器学习技术以其独特的整体性、系统性、自学习性和极强的容错性等特点, 为复杂的疾病诊断提供支持, 成为近年来计算机与医学领域研究的热点^[11].

流行病学调查显示临床上早产高危因素主要包括社会因素、个人因素、孕妇病史因素以及本次妊娠情况等方面^[12], 结合人工智能技术可对电子病历中的体量巨大、类型异构、内部关联复杂的临床大数据进行全面客观地分析^{[13, 14]}. 针对早产问题, Koivu等人^[15]在纽约公开数据集上利用人工神经网络和梯度提升决策树(gradient boosting decision tree, GBDT)等算法构建早产预测模型. Luo等人^[16]利用弹性网络正则化逻辑回归模型, 预测一般性早产(分娩日期大于32周且小于37周)的风险. 但这些机器学习研究均未涉及到时序研究, 且模型的效果相对较差. 门控循环单元(gate recurrent unit, GRU) 是可用于处理时间序列数据的神经网络, 它是循环神经网络(recurrent neural network, RNN)的一种变体, 其结构简单、性能稳定性高, 并解决了RNN梯度消失或爆炸的问题^[17]. Ljubic等人^[18]利用RNN、长短期记忆神经网络(long short-term memory, LSTM)和 GRU预测2型糖尿病患者的并发症风险, 其中GRU时序模型整体性能最佳. 但GRU作为深度学习模型仍难以解释预测结果, 而建立疾病风险评估模型的核心是开发整体和有意义的可解释架构. 由于单一模型的局限性, 众多研究提出了将时序模型与决策树模型结合的混合模型来进行预测分析, 并广泛应用于医学领域^[19-21]. 如赖晓蓥等人^[22]将加权组合模型应用于预测肺结核发病趋势, 有效提升了模型的预测效果.

针对以上分析, 本文拟将 GRU 与 GBDT的优势结合, 将GRU和GBDT混合模型应用于早产风险预测. GRU模型挖掘产检数据中与早产相关的时间序列隐含信息, 并在28周前实现对早产的预测, 同时利用GBDT模型探究决策形成的原因, 将预测模型和医学可解释性相结合, 为提早干预和救治、降低早产发生率、改善早产人群的母婴结局提供参考依据.

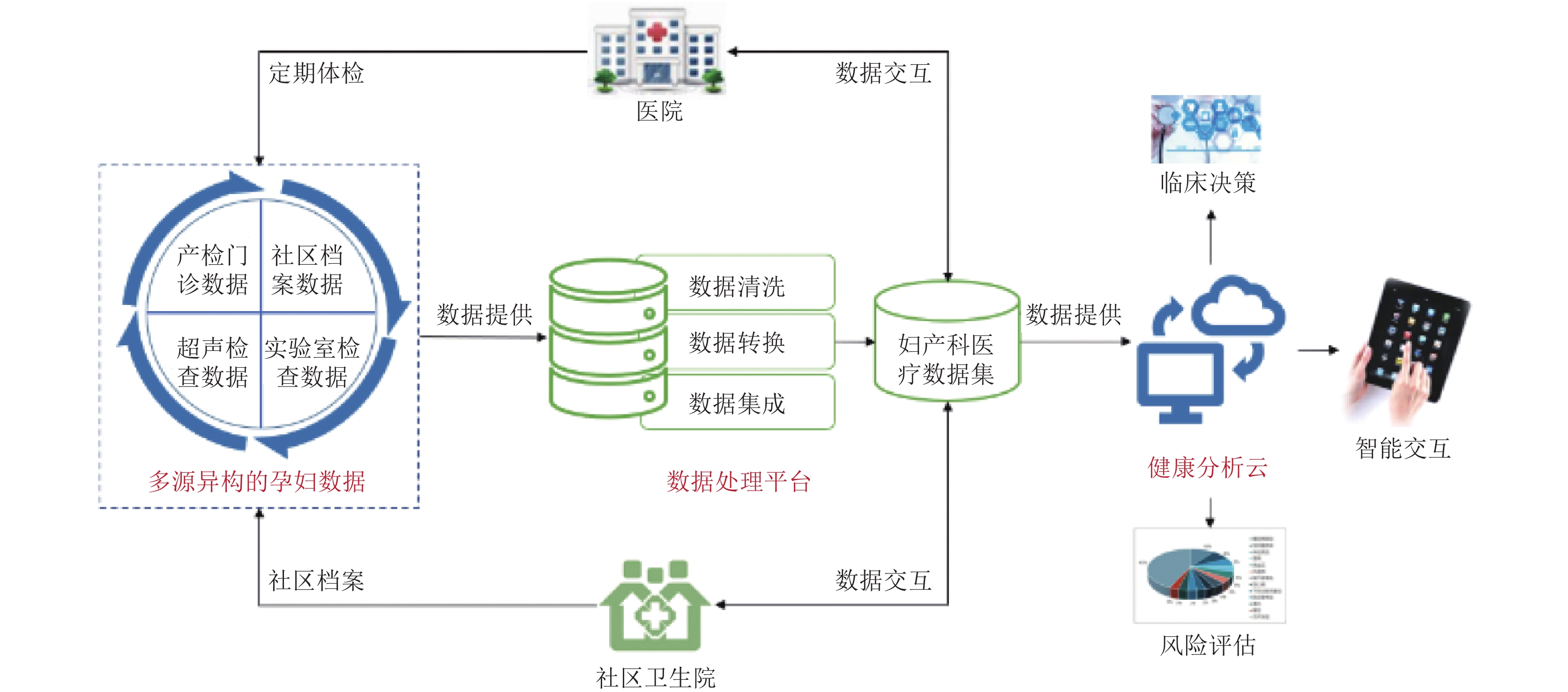
1 相关工作 1.1 数据获取平台

本项目研究团队前期建立了产科多源异构数据互通共融的产科数据科研平台, 用于孕妇产检数据的获取. 孕妇数据来源包括产检门诊、社区档案、超声检查、实验室检查等, 平台对多源异构的孕妇数据进行清洗、转换、集成, 如文本类型的超声报告结构化, 胎心信号数据的解析等, 最终形成可统一处理的结构化数据. 产科数据科研平台如图1所示.

本文的早产风险预测依托前期集成的产科医疗数据, 基于本研究可形成独立的分析模块嵌入产科数据科研平台的健康分析云模块中, 进行智能的早产风险评估, 为临床决策提供支持, 做到早产的早发现、早诊断、早干预.

1.2 GRU模型

门控循环单元(GRU)是RNN的变体, 是为了解决长期记忆和反向传播中的梯度等问题而提出的^{[23, 24]}, 能良好地拟合时序数据. 相比于LSTM, GRU只包括更新门和重置门两个门, 简化的结构使得GRU在保证预测精度的前提下能有效减少运行时间^[25]. GRU单元内部结构如图2所示.

GRU中更新门、重置门的公式如式(1)、式(2)所示:

${r_t} = \sigma ({W_r} \cdot [{h_{t - 1}},{x_t}]) $

(1)

$ \begin{split} \\ {{\textit{z}}_t} = \sigma ({W_{\textit{z}}} \cdot [{h_{t - 1}},{x_t}]) \end{split} $

(2)

其中, $ {x_t} $ 为当前的输入, $ {h_{t - 1}} $ 代表上一个节点传递下来的隐状态. $ {{\textit{z}}_t} $ 和 $ {r_t} $ 分别表示更新门和重置门. $ {W_r} $ 和 $ {W_{\textit{z}}} $ 分别代表重置门和更新门的权重矩阵. $ \sigma $ 是Sigmoid激活函数.

上一时刻隐藏数据经过重置门控得到的重置数据与当前的输入 $ {x_t} $ 相结合并通过激活函数可以得到当前时刻的候选隐藏状态 $ {\tilde h_t} $ , 公式如式(3)所示. 然后结合式(4)得到 $ t $ 时刻的隐藏状态 $ {h_t} $ , 最后得到GRU网络模型在 $ t $ 时刻的输出:

$ {\tilde h_t} = \tanh ({W_{\tilde h}} \cdot {\text{[}}{r_t}*{h_{t - 1}}, {x_t}]) $

(3)

$ {h_t} = (1 - {{\textit{z}}_t})*{h_{t - 1}} + {{\textit{z}}_t}*{\tilde h_t} $

(4)

$ {y_t} = \sigma ({W_o} \cdot {h_t}) $

(5)

其中, $ \tanh $ 为双曲正切函数. $ {W_{\tilde h}} $ 代表隐藏状态的权重矩阵. $ {W_o} $ 为隐藏层到输出层的代表权重矩阵.

1.3 GBDT模型

GBDT是于2001年被提出的以CART回归树为基学习器的Boosting算法, 具有预测精度高, 鲁棒性强, 灵活性高等特点^[26]. 其核心思想是通过损失函数的负梯度拟合前一轮基学习器的残差, 具体原理如下:

首先设训练样本为 $i \; (i = 1, 2, 3, \cdots, n)$ , 迭代次数 $j \; (j = 1, 2, 3, \cdots, m)$ , 损失函数为 $ L({y_i}, F({x_i})) $ , 设置初始常数模型来最小化损失函数, 公式如式(6)所示.

$ {F_0}(x) = \mathop {\arg \min }\limits_r \sum\nolimits_{i = 1}^n {L({y_i}, c)} $

(6)

负梯度 $ {r_{ij}} $ 的计算公式如式(7):

$ {r_{ij}} = {\left[\frac{{\partial L({{y}}, F({x_i}))}}{{\partial F({x_i})}}\right]_{F(x) = {F_{j - 1}}(x)}} $

(7)

使用基学习器 $ {h_j}(x) $ 拟合损失函数的负梯度 $ r $ , 求出使损失函数最小的最佳拟合值:

$ {r_j} = \mathop {\arg \min }\limits_r \sum\nolimits_{i = 1}^n {L(y, {F_{j - 1}}(x) + {h_j}({x_i}))} $

(8)

接着进行模型更新, 本轮的强学习器如下:

$ {F_j}(x) = {F_{j - 1}}(x) + {r_j}{h_j}({x_i}) $

(9)

输出最终的结果:

$ {F_M}(x) = \sum\nolimits_{j = 1}^m {{F_{j - 1}}(x)} $

(10)

GBDT的特征重要性计算是基于计算决策树分裂节点的增益, 并用累积求和来评估特征的重要性. 其中特征 $ j $ 的全局重要性由特征 $ j $ 重要性平均值衡量, 公式如下:

$ \hat I_j^2 = \frac{1}{M}\sum\nolimits_{m = 1}^M {\hat I_j^2({T_m})} $

(11)

其中, $ M $ 表示树的数量, $ \{ {T_m}\} _1^M $ 表示决策树的集合. 特征 $ j $ 在单棵树中的重要度如下:

$ \hat I_j^2(T) = \sum\nolimits_{t = 1}^{J - 1} {\hat i_t^21({v_t} = j)} $

(12)

其中, $ \hat i_t^2 $ 代表节点分裂后平方损失的减少值, $ {v_t} $ 代表与 $ j $ 关联的特征, $ J - 1 $ 代表非叶子节点的数量.

2 基于GRU-GBDT的早产风险预测方法

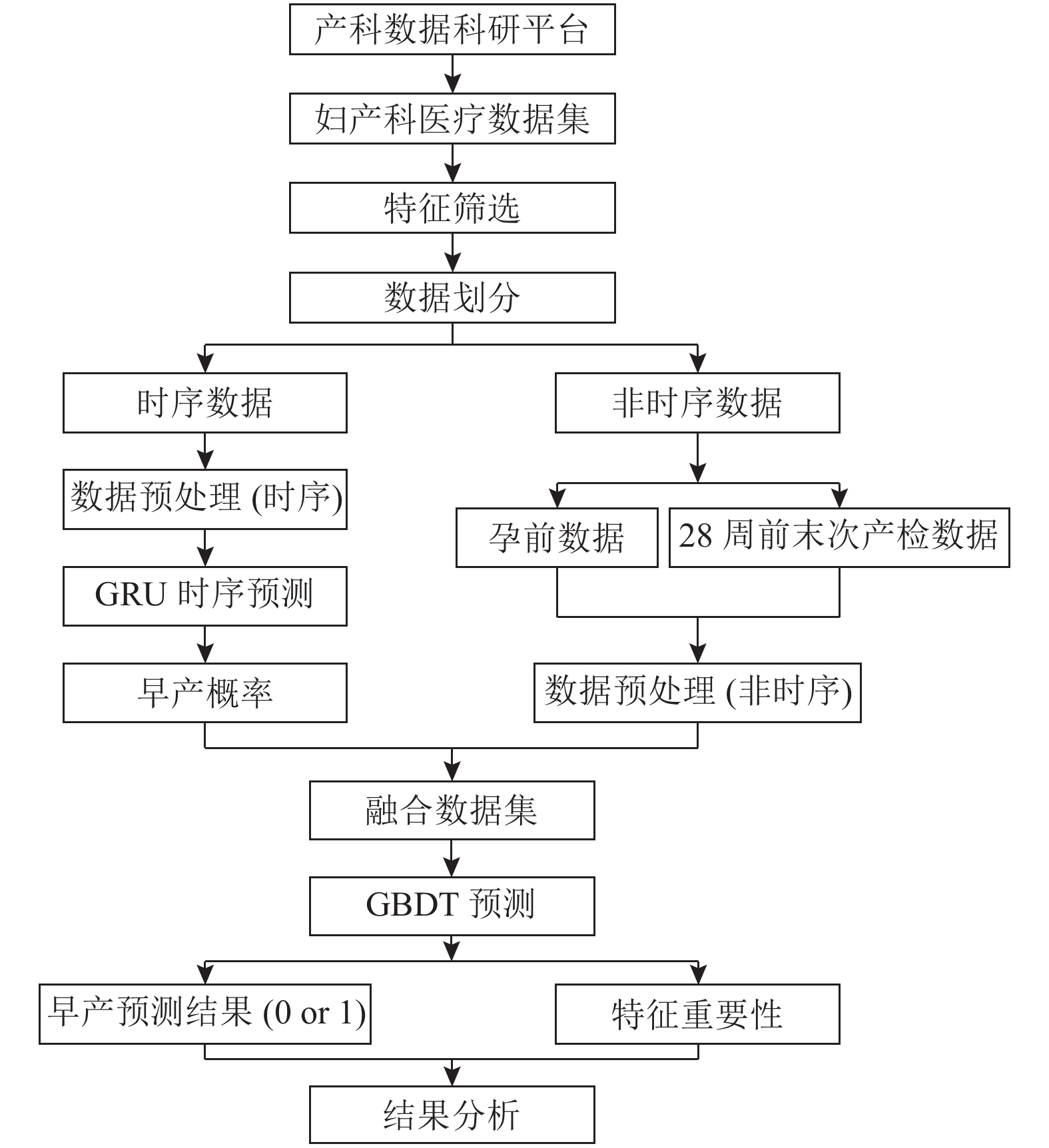
GRU模型结构简单, 运行速度快, 在时间序列预测方面具有较高的拟合能力和良好的预测效果. 然而深度学习模型难以对预测结果与输入特征之间的关系做出解释. GBDT模型能计算每个输入特征对最终预测结果的重要性, 特征重要性级别越高, 表明该特征对预测结果的影响越大, 以此解释GBDT模型的预测结果. 鉴于GRU和GBDT模型的优点, 本文旨在利用GRU和GBDT的混合模型在孕妇28周前预测早产风险, GRU模型在孕妇时序产检数据中学习并预测早产发生的概率, 结合GBDT模型实现更准确的早产风险预测, 而且在提升预测性能的同时分析输入特征在模型中的贡献程度, 实现模型的可解释性. 早产风险预测总体流程如图3所示.

首先通过产科数据科研平台获取妇产科医疗数据集, 并对获取的数据进行特征筛选、数据划分等处理. 然后将数据分为时序数据和非时序数据并分别根据两个数据集的特点进行数据预处理.

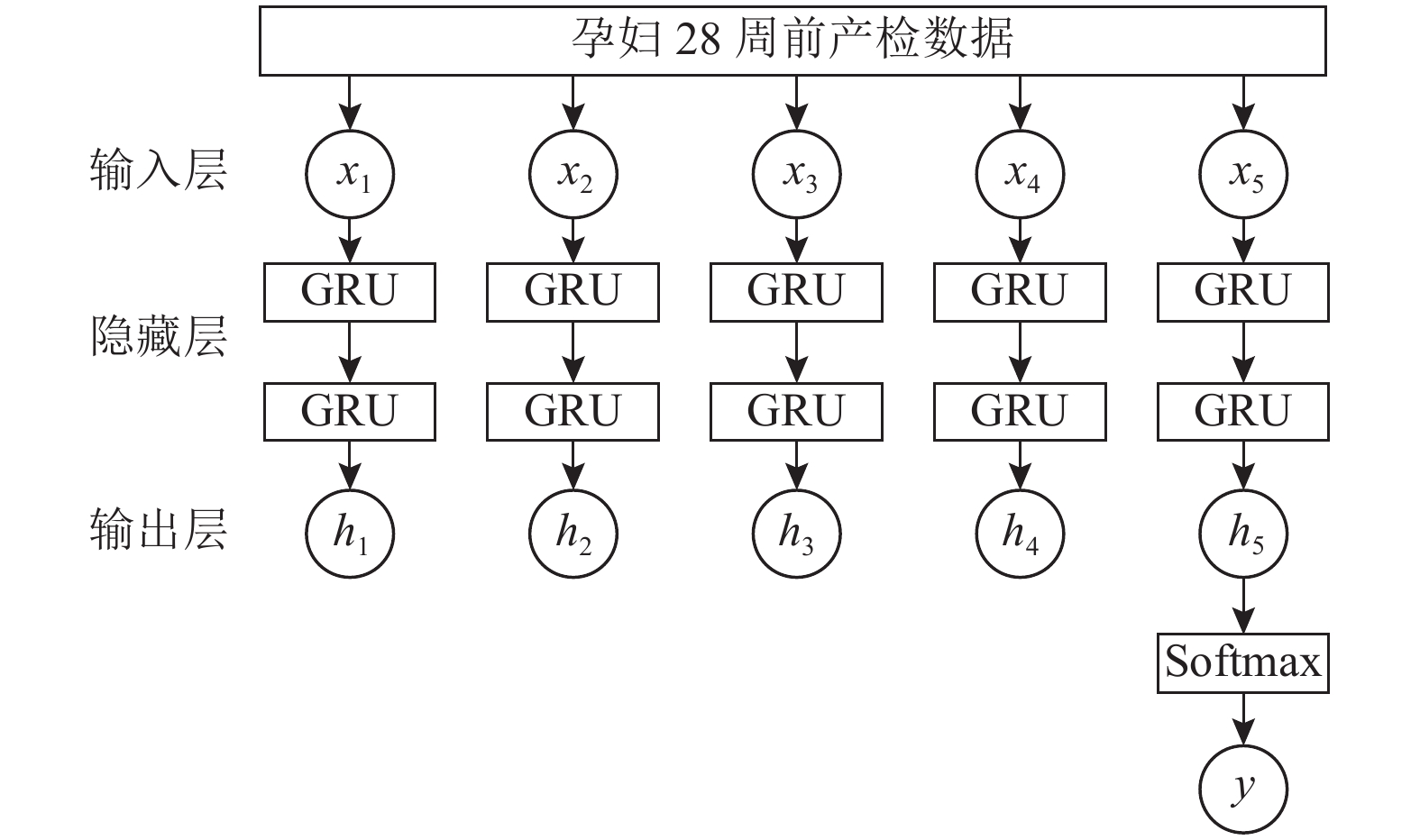
接着针对时序数据利用GRU模型得到早产发生的概率. GRU输入层为预处理后的孕妇28周前的5次产检数据, 输入序列为:

$ X = ({x_1}, {x_2}, {x_3}, {x_4}, {x_5}) $

(13)

其中, $ {x_t} $ 代表孕妇第 $ t $ 次的产检记录, GRU神经网络的隐藏层数为2层, 隐藏层的第二层连接了上一个隐藏层中保留下来的信息. 最后将输出层中最后一个时刻 $ {h_5} $ 的结果作为模型的输出, 并经过Softmax激活函数得到孕妇在不同分类结果下的概率 $ y $ . 双层GRU网络结构图如图4所示.

GRU模型的目标是利用时序数据预测出早产发生的概率. 将该早产概率作为新特征与孕前数据和28周前末次产检等非时序数据融合得到新数据集. 将新数据集输入GBDT模型中, 实现进一步的早产预测. 预测过程中GBDT模型计算输入每一个特征在预测时的贡献度. 接着, GBDT模型在得到分类结果的同时获取输入数据中每个特征的重要性. 最后对实验结果进行对比分析, 验证所用方法的有效性.

3 实验设计及分析 3.1 数据预处理

通过产科数据科研平台, 实验收集了2017年1月–2020年5月于某三甲医院产科分娩且临床资料完整的孕妇数据, 孕妇的排除标准如下: (1) 妊娠合并子宫体肿瘤; (2) 有严重的心、脑、血管、肾等内外科合并症及妊娠并发症; (3) 妊娠期间行宫颈环扎术; (4) 妊娠结局为剖宫产、引产的孕妇.

3.1.1 特征筛选

通过文献分析、专家小组会议并结合临床知识, 共纳入32个可能影响早产的相关因素, 包括孕前数据、产检数据和超声检查数据, 其中孕前数据包括年龄、孕次、产次、身高、孕前体重、文化程度、孕前收缩压、孕前舒张压、末次月经、初潮、经期、周期、月经量、痛经、是否自然妊娠、血型、流产史、早产史和其他既往史; 产检数据包括孕期体重、BMI、宫高、腹围、孕期血压和孕期血常规; 超声检查包含双顶径、胎儿头围、股骨长、胎儿腹围、羊水指数、脐动脉的血流指数和颈项透明层. 所有纳入的特征均由产科数据科研平台获取.

3.1.2 数据划分

本研究纳入的特征中产检数据和超声检查数据呈现明显的时序分布, 产检指南要求产妇在孕12周前进行登记和初检, 并在孕28周前每月1次通过门诊随访. 因此, 本研究根据产检指南规定将孕检时间初步划分为孕周12周前、13–16周、17–20周、21–24周以及25–28周, 共计5次产检信息. 但实验发现这种选取方法会丢失近80%的产妇, 2万多名孕妇中只有5 680名左右孕妇在各个划分的横断面均有孕检记录. 图5为孕妇29周前真实产检分布. 由图可知, 造成此类误差的原因可能是13–16周的部分孕妇是属于17周滞后的检查, 因此本研究根据实际产检分布略微调整, 将13–16周、17–20周和21–24周分别调整为13–17周、18–21周和22–24周. 根据调整后的横断面, 本研究最终共纳入8 140名孕妇, 包括40 700条产检记录. 此外, 本研究将纳入的8 140名孕妇的孕前数据和孕28周前末次产检的数据抽取出来作为实验所用的非时序数据.

3.1.3 数据标准化

本研究收集的诊疗数据具有明显的时序特性, 构建孕产妇早期产检的时序特征集合, 表1为其中一例产妇的时序特征集合示例, 包括其常规的体格检查、超声检查等, 其中化验数据暂未纳入时序特征集合, 原因是孕产妇早期的化验多在各自社区进行, 其检验手段和标准难以统一.

按照第3.1.2节的5个横断面筛选定时门诊且产检资料完整的孕产妇数据作为时序数据. 将孕前数据和28周前末次产检的数据作为非时序数据. 在数据使用前, 需要对数据中的缺失值和异常值进行处理.时序数据的缺失值采用线性插值法进行填充, 非时序数据采用均值填充. 结合临床中各个指标的范围, 将数据中观测极大值或极小值作为异常值, 处理方法同缺失值. 此外, 由于样本特征数据具有不同的量纲和量纲单位, 数值间的差距会对模型造成影响, 因此需要对数据进行归一化处理, 避免值域较大的特征影响其他特征, 同时提升模型的收敛速度. 本文采用min-max标准化, 使得结果映射到[0, 1]之间, 如式(14)所示:

$ {x^*} = \frac{{x - {x_{\min }}}}{{{x_{\max }} - {x_{\min }}}} $

(14)

$ y = {y_{\text{predict}}}({x_{\max }} - {x_{\min }}) + {x_{\min }} $

(15)

其中, $ x $ 为当前特征值, $ {x_{\min }} $ , $ {x_{\max }} $ 分别为当前特征的最小值和最大值, $ {x^*} $ 为标准化后的特征值. 模型得到预测结果后, 通过式(15)对结果进行反归一化处理得到真实值, 其中 $ y $ 为真实值, ${y_{\text{predict}}}$ 为预测值.

3.2 模型设置和评价指标

本研究最终纳入8 140名孕妇, 其中早产342名, 足月7 798名. 因本实验数据集样本分布不平衡, 会使预测的分类结果偏向于多数类样本点集合, 使得少数类样本点的分类正确率低. 针对样本不平衡问题, 在训练过程中将少数类样本进行随机过采样处理. 实验时使用网格搜索法选择模型的最优超参数, 并采用五折交叉验证的方法来验证结果的可靠性.

调整后的GRU和GBDT的最优参数设置如表2所示, GRU神经网络批次大小为256, 输入特征维度为32, 隐藏层层数为2, 将学习率设置为0.001, 并使用Adam优化器进一步加速训练过程, Adam优化器可以使用动量和自适应学习率来加速收敛速度. GBDT模型的损失函数采用对数似然损失函数“deviance”, 设置学习率0.01, 弱学习器的最大迭代次数为200, 子采样取值为0.8, 防止过拟合.

此外本研究采用加权平均敏感性(weighted average sensitivity, WA_Sensitivity)、加权平均特异性(weighted average specificity, WA_Specificity)、AUC和ROC曲线下面积对模型的性能进行评价. 加权平均是将每一个类别样本数量在总样本中的占比作为权重, 在样本不平衡情况下可获得更加客观的总体评价, 加权平均敏感性和加权平均特异性公式如式(16)、式(17)所示, 其中 $ s{e_0} $ 、 $ s{e_1} $ 分别代表0、1样本的灵敏度, $ nu{m_0} $ 、 $ nu{m_1} $ 分别为0、1样本的数量, $nu{m_{\text{all}}}$ 为总样本数, $ s{p_0} $ 、 $ s{p_1} $ 分别代表0、1样本的特异性.

$ WA\_{\textit{Sensitivity}} = \frac{{s{e_0} \times nu{m_0}}}{{nu{m_{\text{all}}}}} + \frac{{s{e_1} \times nu{m_1}}}{{nu{m_{\text{all}}}}} $

(16)

$\begin{split} \\ WA\_{\textit{Specificity}} = \frac{{s{p_0} \times nu{m_0}}}{{nu{m_{\text{all}}}}} + \frac{{s{p_1} \times nu{m_1}}}{{nu{m_{\text{all}}}}} \end{split} $

(17)

3.3 实验结果和分析

实验中分别选用逻辑回归(logistic regression, LR)、随机森林 (random forest, RF)、GBDT、LSTM 、GRU和GRU-GBDT进行对比, 数据集均按照8:2 划分为训练集和测试集, 并通过五折交叉验证实验结果. 表3为各模型的预测结果.

由表可知, 与单一模型相比, GRU-GBDT模型对早产的预测能力最佳, 其中加权平均敏感性为0.77, 加权平均特异性为0.84, AUC为0.647, 均优于其他方法.此外, GBDT相比较于LR和RF, 在牺牲少许运行时间的情况下各项指标均有所提高. 时序模型的AUC明显优于非时序模型, 其中GRU相对于LSTM结构更加简单, 可在保持模型性能的前提下显著提升算法运行速度.

图6为GBDT、GRU和GRU-GBDT混合模型的ROC曲线, 曲线下面积值越高模型的预测性能越佳. 由图可知, 本研究的GRU-GBDT混合模型优于对应的单一模型.

3.4 特征重要性分析

根据GBDT模型输出的特征重要性排序如图7所示, 由于所用特征较多, 本文只列出重要性排序前15名的特征.

由图7可知, GRU输出的新特征在早产预测中的重要性最高, 可见本文采用的GRU-GBDT混合模型在早产预测中的有效性. 此外, 宫高、BMI、血红蛋白、舒张压、双顶径等都是早产的重要因素. 结合GBDT模型输出的特征重要性结果, 可辅助医生临床决策, 便于医生对存在早产风险的孕妇进行及时有效的干预.

4 结论与展望

针对早产风险预测问题, 本文通过分析孕妇历次产检数据特征, 利用GRU-GBDT混合模型预测孕妇早产风险. 本实验整合多源异构的产科诊疗数据并根据产检指南以及实际情况合理获取多次产检的信息, 通过GRU模型捕捉孕妇历次产检的生理特点并得到早产发生的概率, 然后采用GBDT模型在融合数据的基础上预测最终分类结果, 并获取特征重要性. 通过与其他方法对比分析, 验证了该混合模型在早产分类效果上的优越性, 其中GRU对于时间序列信息有较强的学习能力, 该混合模型保证了孕妇多次产检数据的合理利用, 同时GBDT模型能在预测时获取每一特征对预测结果的贡献度, 特征重要性可为医生判断孕妇早产风险提供辅助决策.

本文可实现早期的早产高危人群筛选, 以建议该部分人群进行进一步的早产项目检查. 本研究不涉及特殊化验项和检查项, 在不进行额外检查项的同时基于历史诊疗数据进行早期筛查, 可节省大量资源. 然而, 本研究未加入孕妇常见的化验数据, 未来将对GRU-GBDT模型结构进一步优化, 并添加化验项来提高整体预测效果.