2. 中国科学院 沈阳计算技术研究所, 沈阳 110168;
3. 沈阳中科数控技术股份有限公司, 沈阳 110168
2. Shenyang Institute of Computing Technology, Chinese Academy of Sciences, Shenyang 110168, China;
3. Shenyang CASNC Technology Co. Ltd., Shenyang 110168, China
随着新兴物流产业的发展, 新建仓储物流系统已逐渐实现了仓储智能自动化. 作为智能仓储的重要组成部分, AGV (automated guided vehicle) 即自动导引车, 在物流行业的应用正变得越来越广泛. 但对已建成多年的老旧仓库, 由于其厂房仓库存在障碍物多杂且形状不规则等特点, 使 AGV 的寻径效率极大降低, 严重阻碍了其智能化改造的进程.
路径规划即根据 AGV 所处的环境信息、运输任务的位置信息, 依照相应评价标准, 规划的一条从起始位置到目的位置的无碰撞最佳路径[1]. 常用的路径规划算法有 Dijkstra 算法、A*算法、人工势场算法、蚁群算法、遗传算法等. 其中人工势场法(artificial potential field, APF)具有结构简单、动态适应强、计算量小等优点, 因此在实时避障与仓储物流领域得到了广泛的使用.
但传统的人工势场算法存在一定的局限性, 例如目标不可达问题、局部极小值问题等[2, 3]. 对此, 国内外的专家学者各自提出了不同的改进人工势场法来解决通用环境下的缺陷问题. 赵明等[4]创新性地提出了自适应域—人工势场改进算法, 并通过域引导势场对启发点进行了域势场传递, 此种改进算法较好地解决了局部极小值问题. 唐嘉宁等[5]在改进算法中引入了电场中的模拟等势线概念, 并对原算法中的斥力函数进行了改进, 此改进算法有效解决了局部极小值问题. Weerakoon等[6]提出了一种无死锁的改进人工势场算法, 该算法通过引入与速度方向相关联的障碍物信息, 解决了传统算法中目标点不可达与局部极小值问题. Fedele等[7]为解决多障碍物势场叠加引起的局部极小值问题, 提出了一种基于势场切换策略的改进人工势场算法.
本文拟在老旧仓库这一特定环境下进行研究, 文中提及的老旧仓库特指具有以下特点的仓库.
(1) 建成时间距今已超5年.
(2) 仓库内货架堆积无序且紧密.
(3) 仓库内杂物分布随机且与货架摆放位置无明显边界.
本文将在此处预先对下文所提及算法进行明确指代. 其中后文提及的传统人工势场法是指 Khatib于1986年首次提出的人工势场算法[8], 后文中将以T-APF (traditional artificial potential field)代指. 而针对本文所提出的新型改进人工势场算法, 后文将以I-APF (improved artificial potential field)代指.
针对传统人工势场算法(T-APF)中存在的缺陷, 本文提出了一种新型的改进人工势场算法(I-APF), 该算法通过对引力与斥力的修正, 解决了目标点不可达问题及易与远目标端障碍物相撞问题; 通过添加临时障碍物的手段, 解决了局部极小值问题. 借由上述手段, 提升了老旧仓库中人工势场算法寻径成功率. 最后使用 Matlab 软件, 对 I-APF的有效性进行了验证.
1 传统的人工势场算法人工势场算法是由 Khatib 提出的, 并首先应用于机械臂的运动规划领域[8], 后经发展现广泛应用于路径规划领域. 在路径规划问题中, 人工势场分别由目标点产生的引力势场与障碍物产生的斥力势场叠加而成. AGV 小车在人工势场中受到势场合力的作用, 避开沿途障碍物, 向目标点运动.
1.1 引力势场为使 AGV 小车能够顺利到达目标点, 引力势场的强度随与目标点的距离增大而增大. 因此, 在T-APF中引力势场
| $ {U_{\rm{att}}}(X) = \frac{1}{2}{k_{\rm{att}}}{d^2}(X, {X_g}) $ | (1) |
其中,
引力则定义为势场的负梯度其表达式为:
| $ {F_{\rm{att}}} = - \varDelta {U_{\rm{att}}} = - {k_{\rm{att}}}d(X, {X_g}) $ | (2) |
为使 AGV 可以避开障碍物, 斥力势场需要满足势能随 AGV 与障碍物的接近而增大, 远离而减小, 当二者距离增大至斥力势场所影响的最大距离
类似的, 斥力的定义为斥力势场的负梯度.
斥力势场及斥力的表达式如下:
| $ {U_{\rm{rep}}}(X) = \left\{ {\begin{array}{*{20}{l}} {\dfrac{1}{2}{k_{\rm{rep}}}{{\left(\dfrac{1}{{d(X, {X_0})}} - \dfrac{1}{{{d_0}}}\right)}^2},}&{d(X, {X_0}) \leqslant {d_0}} \\ 0, &{d(X, {X_0}) > {d_0}} \end{array}} \right. $ | (3) |
| $ \begin{split} {F_{\rm{rep}}} = - \varDelta {U_{\rm{rep}}}(X) = \left\{ {\begin{array}{*{20}{l}} {{k_{\rm{rep}}}\left(\dfrac{1}{{d(X, {X_0})}} - \dfrac{1}{{{d_0}}}\right)\dfrac{1}{{{d^2}(X, {X_0})}}\dfrac{{\partial d(X, {X_0})}}{{\partial X}}},&{d(X, {X_0}) \leqslant {d_0}} \\ 0,&{d(X, {X_0}) > {d_0}} \end{array}} \right. \end{split} $ | (4) |
其中,
由式(2)可知, 引力大小与 AGV 及目标点间的距离呈线性关系. 在路径规划初期, 由于 AGV 距离目标点较远, AGV 受到的引力较大. 因此在接近障碍物之前, AGV 已具有较大的初速度, 即使随着与障碍物的接近斥力在逐渐增大, 但引力的作用及惯性的存在仍使得 AGV 会与远目标端障碍物相撞.
1.3.2 目标点不可达由式(2)与式(4)可知, 如果目标点附近存在障碍物, 随着 AGV 逐渐向目标点与障碍物靠近, 斥力大小在逐渐增大, 引力大小在逐渐减小, 在到达某一区域时会出现斥力大于引力的情况, 使得小车背离目标点运动, 当离开此区域时, 引力再次占据主导地位, 小车重新向此区域运动, 如此循环小车只能在目标点附近振荡徘徊, 最终停在势能最低点处.
通用场景下由于障碍物分布稀疏, 在目标点处附近存在障碍物的概率很低, 实际使用中一般不考虑该问题. 而老旧仓库这一特定环境中, 由于空间狭小, 货架、货物、障碍物分布密集, 目标不可达的发生概率极大增加, 因而在该环境下目标点不可达问题成为了AGV 路径规划的严重阻碍.
1.3.3 局部极小值局部极小值的实质就是在路径某处出现了斥力与引力的平衡态, 使得AGV 陷入了局部稳定状态. 如图1所示, 本文将局部极小值分为以下两种情况: 其一为开放式障碍物影响下的局部极小值, 该类缺陷通常由多个障碍物组成, 且障碍物间存在能使 AGV 直接穿越的间距, 当 AGV 陷入其中时, 由于受到相互平衡的斥力与引力, 无法继续前进. 其二为半封闭式障碍物影响下的局部极小值, 此类缺陷由孤立障碍物或多个间距极小的障碍物组成(障碍物间距不足以使 AGV直接穿越). 当 AGV 陷入其中时, 无法通过直接穿越障碍物进行逃脱. 同前者相似, AGV 在陷阱内受到相互平衡的斥力与引力, 无法继续前进.
在老旧仓库中由于障碍物的分布较通用场景下多而密, 且分布的复杂程度、无序程度极大增加. 因而通用场景下出现频率极低的引力斥力平衡现象即局部极小值缺陷, 在老旧仓库中出现的频率极大增加, 成为了不容轻视的问题.

|
图 1 开放式及半封闭式局部极小值示意图 |
2 改进人工势场算法
现在对传统人工势场算法的主流改进方式, 多着眼于先对势场改进, 进而间接影响势场力, 最后改变 AGV 运动状态[9-11]. 以文献[10]中的改进算法为例, 其通过在T-APF 斥力势场公式, 即式(3)后添加AGV与目标点欧氏距离的n次幂作为距离因子, 使得 AGV 与目标点的距离也成为影响斥力势场的因素之一. 在对其改进的斥力势场求负梯度后得到一个复合斥力. 该复合斥力由两个分力构成, 其中一个斥力方向同原T-APF中的斥力, 由障碍物指向AGV, 另一斥力的方向由 AGV 指向目标点. 这种改进方式虽被证明是有效的, 但是通过其改进势场求得的复合斥力表达式冗余且复杂, 直接导致了路径规划效率的降低. 而本文直接对势场力进行了优化, 不再关注势场本身, 所得模型既兼顾了传统算法的简洁形式又不受到缺陷影响.
2.1 引力的改进对引力改进针对的是与远目标端障碍物相撞及目标点不可达缺陷. 针对前者缺陷, 根源在于远离目标点时引力大于斥力. 如果直接减小全局引力势场常数, 这样虽然可避免AGV 在远离目标点时与障碍物相撞, 但当接近目标点时易因引力不足而造成目标点不可达的问题. 因此, 为兼顾远距离处避碰, 近距离处目标点可达, 本文通过设定引力势场安全距离常量
| $ F_{\rm{att}}^*(X) = \left\{ {\begin{array}{*{20}{c}} { - k_{\rm{att}}^*d(X, {X_g})},&{d(X, {X_g}) \geqslant {d_s}} \\ { - j_{\rm{att}}^*d(X, {X_g})},&{d(X, {X_0}) < {d_s}} \end{array}} \right. $ | (5) |
其中,
对斥力的改进针对的同样是与远目标端障碍物相撞及目标点不可达缺陷. 同时解决这两个缺陷的关键在于, 要确保 AGV 在路径规划途中, 非碰撞的情况下引力始终略大于斥力, 从而使AGV 持续向目标点运动. 由引力表达式(5)可知, 随着 AGV 与目标点的靠近, 引力大小在不断减小, 此时若不对斥力大小进行削减, 极易造成靠近目标点时, 斥力大于引力, 出现目标点不可达现象. 若直接减小斥力势场常数, 由式(5)可知, 在路径规划初期引力极大, AGV 易与远目标端障碍物相撞. 因此斥力的变化趋势需同引力一致. 于是在原斥力表达式中, 加入 AGV 当前位置与目标点的欧式距离作为因数, 使引力与斥力的变化趋势基本一致. 在此基础上, 通过调整斥力势场常数使斥力略小于引力, 即可顺利规划路径. 改进后的斥力表达式如式(6)所示:
| $ F_{\rm{rep}}^* = \left\{ {\begin{array}{*{20}{l}} {{k_{\rm{rep}}}\left(\dfrac{1}{{d(X, {X_0})}} - \dfrac{1}{{{d_0}}}\right)\dfrac{1}{{{d^2}(X, {X_0})}}\dfrac{{\partial d(X, {X_0})}}{{\partial X}}d(X, {X_g})},&{d(X, {X_0}) \leqslant {d_0}} \\ 0,&{d(X, {X_0}) > {d_0}} \end{array}} \right. $ | (6) |
其中,
AGV 陷入局部极小值的原因是路径规划途中出现了斥力大于等于引力的区域(也称陷阱区域), 导致 AGV 在该区域内出现局部振荡现象, 无法逃离. 本文拟采用添加临时障碍物的方式破坏 AGV 在陷阱区域内力的平衡态, 实现 AGV 的逃离, 随后再删去临时障碍物. 具体逃离策略分直接穿越陷阱区域与绕行陷阱区域两种.
对于半封闭式局部极小值问题, 由于障碍物分布极为连续, AGV 无法做到直接穿越, 因此只能选用绕行方式逃离陷阱区域. 对于开放式局部极小值陷阱, 由于障碍物分布较为稀疏, 为使规划路径尽可能短, 采用直接穿越方式逃离陷阱区域.
2.4 改进人工势场算法的步骤算法1. 改进人工势场算法
1) 参数初始化. 首先初始化位置参数, 包括 AGV 的起始位置
2) 进入循环体, 并计算 AGV所受合力. 分别计算目标点对当前位置处AGV的引力及 AGV 受到的所有障碍物产生的斥力, 并对引力与所有斥力求和.
3) 计算 AGV 经过迭代后的坐标. 通过合力与当前位置坐标, 依据牛顿运动定律, 计算下一路径点 AGV 坐标, 并将其置为AGV当前位置点.
4)判断AGV 是否达到目标点. 本算法规定当AGV 与目标点距离小于迭代步长
5) 判定 AGV 是否与障碍物相撞. 本算法规定当AGV 与障碍物距离小于步长
6) 判定 AGV 是否陷入局部极小值. 若当前迭代次数大于最大逃离迭代数
本文使用 Matlab 对所提出的改进人工势场算法进行仿真实验, 其中测试主机为 Acer Aspire VN7-591G, 配置为 Intel(R) Core(TM) i5-4210H 2.90 GHz , 内存为12 GB, 并在 Windows 10 操作系统下进行仿真, 测试算法的有效性.
图2针对的是与远目标端障碍物相撞缺陷的路径规划仿真. 该组仿真的参数如下: 起点(0, 0), 终点(10, 10)
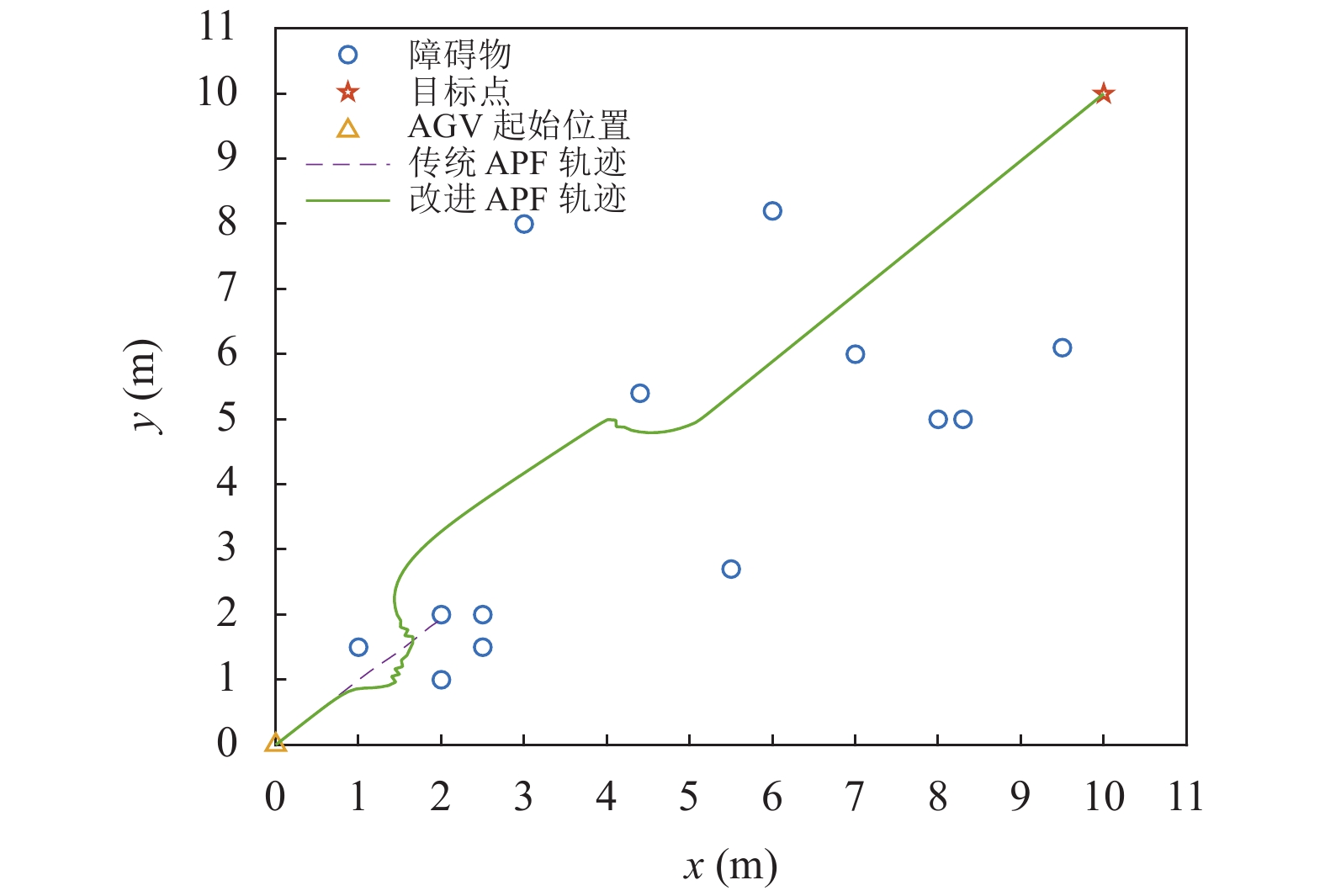
|
图 2 与远目标端障碍物相撞缺陷环境中的路径规划 |
图3针对的是老旧仓库中易出现的目标点不可达缺陷的路径规划仿真. 该组仿真参数如下: 起点(0, 0) 终点(3, 3)
图4图5分别针对的是局部极小值中的半封闭式障碍缺陷与开放式障碍缺陷的路径规划仿真, 其中对半封闭式障碍采用绕行逃脱策略, 对开放式障碍采用直接穿越的逃脱策略. 开放式障碍组仿真参数如下: 起点(0, 0) 终点(3, 3)

|
图 3 目标点不可达缺陷环境中的路径规划 |

|
图 4 局部极小值中半封闭式缺陷环境的路径规划 |

|
图 5 局部极小值中开放式缺陷环境的路径规划 |
除对上述 T-APF 算法的典型缺陷环境进行路径规划仿真外, 本文也对无陷阱环境进行了路径规划仿真. 该组仿真参数如下: 起点(0, 0) 终点(10, 8)
本节共进行了4组实验, 前3组实验对前文中提到的3种常见缺陷进行了陷阱障碍物仿真, 并在其上分别使用 I-APF 与 T-APF 进行路径规划, 实验结果显示 T-APF 无法成功规划完整路径, I-APF可使 AGV 成功到达目标点. 最后一组实验是在无陷阱障碍物情况下进行的, 目的是为了比较在无陷阱情况下, 两种算法的优劣情况, 实验结果显示, 二者均可使 AGV 成功到达目标点. 但对路径长度与程序运行时间两个评价指标进行对比发现, I-APF优于T-APF.

|
图 6 无陷阱环境中的路径规划 |
| 表 1 对T-APF与I-APF的算法评估 |
4 结语
为解决老旧仓库中人工势场算法易陷入陷阱的问题, 本文提出了一种新型的改进人工势场算法(I-APF). 并在仿真环境下对传统人工势场算法(T-APF)与改进人工势场算法进行了实验, 结果表明改进人工势场算法优于传统人工势场算法. 下一步研究中将计划使改进人工势场算法支持对动态障碍物的避障, 使改进人工势场算法可以更好地适用于老旧仓库中 AGV 的路径规划.
| [1] |
葛研. AGV自动导引车在国内的发展前景探讨. 设备管理与维修, 2021(S1): 157-159. DOI:10.16621/j.cnki.issn1001-0599.2021.02.81 |
| [2] |
付泽民, 吴力杰, 乔涛涛, 等. 基于改进人工势场法的搬运机器人避障算法研究. 机床与液压, 2021, 49(5): 25-29. DOI:10.3969/j.issn.1001-3881.2021.05.005 |
| [3] |
霍凤财, 迟金, 黄梓健, 等. 移动机器人路径规划算法综述. 吉林大学学报(信息科学版), 2018, 36(6): 639-647. DOI:10.3969/j.issn.1671-5896.2018.06.007 |
| [4] |
赵明, 郑泽宇, 么庆丰, 等. 基于改进人工势场法的移动机器人路径规划方法. 计算机应用研究, 2020, 37(S2): 66-68, 72. |
| [5] |
唐嘉宁, 潘蓉, 周思达, 等. 融合模拟电势场的改进人工势场法研究. 电光与控制, 2020, 27(12): 69-73. DOI:10.3969/j.issn.1671-637X.2020.12.015 |
| [6] |
Weerakoon T, Ishii K, Nassiraei AAF. An artificial potential field based mobile robot navigation method to prevent from deadlock. Journal of Artificial Intelligence and Soft Computing Research, 2015, 5(3): 189-203. DOI:10.1515/jaiscr-2015-0028 |
| [7] |
Fedele G, D’Alfonso L, Chiaravalloti F, et al. Obstacles avoidance based on switching potential functions. Journal of Intelligent & Robotic Systems, 2018, 90(3): 387-405. DOI:10.1007/s10846-017-0687-2 |
| [8] |
Khatib O. The potential field approach and operational space formulation in robot control. In: Narendra KS, ed. Adaptive and Learning Systems. Boston: Springer, 1986. 367–377.
|
| [9] |
程紫云. 基于人工势场法的机器人路径规划研究[硕士学位论文]. 秦皇岛: 燕山大学, 2016.
|
| [10] |
汪俊杰, 陈凌珊, 盛铭, 等. 基于改进人工势场法的机器人路径规划研究. 农业装备与车辆工程, 2020, 58(7): 66-70. |
| [11] |
Sun JY, Tang J, Lao SY. Collision avoidance for cooperative UAVs with optimized artificial potential field algorithm. IEEE Access, 2017, 5: 18382-18390. DOI:10.1109/ACCESS.2017.2746752 |
 2022, Vol. 31
2022, Vol. 31



