医学图像分割是指用具有生物学意义的标签标记图像像素或体素的过程^[1]. Rohlfing等人^[2]在2004年首次引入的, Klein等人^[3]和Heckemann等人^[4]分别在2005年和2006年推广的多图谱分割(multi-atlas segmentation)方法是目前生物医学领域应用最广泛、最成功的图像分割技术之一.

基于多图谱的医学图像分割的基本过程包含图像配准和标签融合两部分, 其中标签融合的部分常采用基于相似度加权融合的方法. 传统的基于相似度加权融合的方法存在两个不足: (1)该方法没有考虑图谱集的干扰性. 图谱集中存在一些相对于目标图像而言属于干扰的图谱. 这些干扰图谱的目标组织在形态上可能与目标图像会有较大的差异, 从而导致标签映射结果与实际结果有很大的差异. (2)该方法没有考虑图谱集的冗余性. 图谱集中图谱图像具有多样性的同时也具有相似性, 即图谱集中会存在很多较为相似的图谱, 图谱集因此具有较高的冗余性. 如果用于融合的图谱集中大部分是这些相互之间较为相似的图谱, 则最后得到的结果肯定与这些图谱一致, 从而失去了多图谱融合的意义. 对图谱集中的图谱进行选择后用于标签融合可以弥补这两个不足, 进而提高分割精度.

目前已经有很多学者采用选择的策略来对图谱集中的图谱图像进行初步的筛选后再进行后续的标签融合操作. Aljabar等人^[5]对一个包含275个图谱的数据集采用留一法(leave-one-out)研究了基于图像相似度选择策略和基于年龄段选择策略的图谱选择方法以及图谱数量对最终分割结果的影响等问题. Zhao等人^[6]提出一种两步子图谱集选择方法用于基于多谱图的图像分割. Karasawa等人^[7]针对传统基于强度的图谱选择方法往往不能选到在位置和形状上都与待分割的目标图像较为相似的胰腺图谱的问题, 提出一种新的基于胰腺组织周围血管结构的图谱选择策略. Langerak等人^[8]使用了迭代的策略来对采用不同选择策略得到的分割性能进行评级. Sanroma等人^[9]认为图谱与目标图像相似性包含两方面, 即图谱图像与目标图像的相似性以及图谱标签图像与目标标签图像的相似性, 进而从机器学习的角度提出了一种新的图谱选择方法. 唐慧慧等人^[10]使用正规化的交互信息从图谱集中获得“最优”模板, 然后将水平集的方法用于图谱分割之中, 获得比传统的图谱分割方法更精确的分割结果.

图谱选择的关键就是找到合适的相似度度量准则来度量各个图谱与待分割的目标图像的相似度. 除了上述文献给出的相似性度量方法外, 还有一些其他的相似性度量方法, 比如平方差之和^[11]、互相关^[12]、互信息^{[13, 14]}、归一化互信息^{[15, 16]}以及图谱图像与待分割的目标图像所对应主体的性别、年龄、临床状态等属性作为图谱图像与待分割的目标图像相似度度量. 利用相似度度量方法, 上述这些图谱选择方法可以从图谱集中选择相似度最高的若干图谱来构造基于多图谱分割方法所需的子图谱集, 可以克服图谱集的干扰性. 但是这种依据图谱图像和待分割的目标图像整体相似度的图谱选择方法仅仅考虑了图像之间的相关性, 仍然没有考虑图谱集内部的冗余性. 同时, 这些方法是在整体上计算图谱集中图谱图像与目标图像之间的相似性, 没有考虑目标分割的局部性. 对于脑MR图像而言, 由于年龄、形态或病理等方面的原因, 脑内部可能存在个别组织差异比较大而其他组织差异比较小的情况. 这样, 对于这些差异比较大的组织而言, 采用整体相似性度量的方法可能会存在整体比较相似但该目标组织却不相似的情况. 因此, 将这些方法直接用于特定目标组织的分割可能获得不准确的分割结果.

基于上述分析, 结合Zhao等人^[6]提出的两步子图谱集选择的思想, 本文提出一种基于两步图谱选择策略的脑MR图像分割方法. 该方法的整体属于一种由粗到精的选择策略. 第一步采用一种基于最小角回归的方法进行图谱粗选择, 第二步则采用基于豪斯多夫距离的以目标为导向的图谱精选择.

1 基于最小角回归的图谱选择方法

最小角回归(least angle regression, LAR)是Efron等人^[17]在2004年提出的一种基于变量选择的回归方法. 该回归模型可以用式(1)表示^[18].

$ \left\{ {\begin{split} & \min {\text{ }}S(\bar \beta ) = \sum\limits_{i = 1}^n {{{({y_i} - {{\bar \mu }_i})}^2}} = \sum\limits_{i = 1}^n {{{\left({y_i} - \sum\limits_{j = 1}^p {{x_{ij}}{\beta _j}} \right)}^2}} \hfill \\ & {\text{s.t.}} \sum\limits_{j = 1}^p {\left| {{\beta _j}} \right|} \leqslant t \hfill \end{split} } \right.$

(1)

其中, ${{{x}}_i} = {[{x_{i1}}, {x_{i2}}, \cdots , {x_{ip}}]^{\text{T}}}$ 和 ${y_i}$ 分别表示第 $i$ 个样本对应的自变量和响应变量, $\;{\bar \mu _i}$ 表示第 $i$ 个样本对应的回归变量, $\;{\beta _j}$ 是第 $j$ 个自变量的回归系数, $t$ 为约束值. 最小角回归算法就是通过寻找合适的回归系数来让回归变量 $\;{\bar \mu _i}$ 与响应变量 ${y_i}$ 尽可能接近. 当约束值较小时, 某些与因变量相关度较低的自变量的回归系数将会被置零, 因此, 最小角回归算法可以删除某些无效变量. 最小角回归的基本思想可以描述为: 每次先找出和因变量相关度最高的那个变量, 再沿着最小二乘估计的方向一点点调整这个变量的系数. 在这个过程中, 这个变量和残差的相关系数会逐渐减小, 等到这个相关性没那么显著的时候, 就要选进新的相关性最高的变量, 然后重新沿着最小二乘估计的方向进行变动, 在行径过程中残差与入选变量的相关度将逐渐减小. 以此类推, 直到选择出所有所需的变量. 很显然, 最小角回归在选择变量的时候充分考虑了所选变量的冗余性, 因此可以用来解决传统的基于相似度加权融合的方法中存在干扰性和冗余性的不足. 基于该原理, 参照Shen等人^[19]提出的图谱选择方法, 本文采用基于最小角回归的图谱选择方法作为一种粗略选择的方法用于基于多图谱的图像分割. 假定 $\Omega $ 表示相似图谱的图谱集, 即经过选择用于目标图像分割的图谱集, 基于最小角回归的图谱选择的过程可以用算法1来描述.

算法1. 基于最小角回归的图谱选择方法

输入: 目标图像 $\scriptstyle I$ , 配准后的图谱图像集 $\scriptstyle\{ {I_k} \circ {T_k}\} $ , 输出图谱集中图谱的数量.

输出: 选择用于目标图像分割的图谱集 $\scriptstyle\Omega $ , 估计图谱 $\scriptstyle{\hat I_\Omega }$ .

步骤:

Step 1. 对于 $\scriptstyle k$ 个图谱图像, 计算其与残差图像相关系数: $\scriptstyle {\hat c_k} = $ corr $ \scriptstyle ({I_k} \circ {T_k}, I - {\hat I_\Omega }) $ ;

Step 2. 根据相关系数为对应的图谱设置标签 $\scriptstyle{s_k}$ , 并找出最大相关系数: $\scriptstyle{s_k} = sign({\hat c_k})$ $\scriptstyle \hat C = \max \{ {\hat c_k}\} $ ;

Step 3. 得到有效图谱矩阵 $\scriptstyle{{{X}}_\Omega }$ , 其中每一列代表一个图谱: $\scriptstyle({s_k} \cdot $ $ \scriptstyle {I_k} \circ {T_k}) \to {{{X}}_\Omega } $ , $\scriptstyle k \in \Omega $ ;

Step 4. 计算最佳相关系数 $\scriptstyle{A_\Omega }$ : $\scriptstyle{A_\Omega } = {\left( {{{e}}_\Omega ^{\text{T}}{{({{X}}_\Omega ^{\text{T}}{{{X}}_\Omega })}^{ - 1}}{{{e}}_\Omega }} \right)^{ - \frac{1}{2}}}$ , 其中 $\scriptstyle{{e}}$ 是长度为 $\scriptstyle\left| \Omega \right|$ 的全1向量;

Step 5. 计算最小角图像 $\scriptstyle{U_\Omega }$ : $\scriptstyle corr({I_k} \circ {T_k}, {U_\Omega }) = {A_\Omega }, \forall k \in \Omega $ ;

Step 6. 对于 $\scriptstyle k$ 个图谱图像, 计算其与最小角图像相关系数 $\scriptstyle{a_k} = $ corr $ \scriptstyle ({I_k} \circ {T_k}, $ $ \scriptstyle {U_\Omega }) $ ;

Step 7. 找到最佳的回归系数 $\scriptstyle\hat \gamma $ : $\scriptstyle\hat \gamma = \min _{k \notin \Omega }^ + \left\{ {\frac{{\hat C - {{\hat c}_k}}}{{{A_\Omega } - {a_k}}}, \frac{{\hat C + {{\hat c}_k}}}{{{A_\Omega } - {a_k}}}} \right\}$ , 其中 $\scriptstyle{\min ^ + } \{ \} $ 表示只取正数部分进行操作;

Step 8. 选择相似图谱, 并更新图谱集 $\scriptstyle\Omega $ : $\scriptstyle\hat k = \arg \min _{k \notin \Omega }^ + \left\{ {\frac{{\hat C - {{\hat c}_k}}}{{{A_\Omega } - {a_k}}}, \frac{{\hat C + {{\hat c}_k}}}{{{A_\Omega } - {a_k}}}} \right\} $ , $ \scriptstyle \Omega $ = $ \scriptstyle \Omega \cup \{ \hat k\} $ ;

Step 9. 更新估计图谱: $\scriptstyle{\hat I_\Omega } = {\hat I_\Omega } + \hat \gamma {U_\Omega }$ l;

Step 10. 重复Step 1–9, 直到图谱集的相似图谱数量满足要求.

2 以分割目标为导向的图谱选择方法

由于图谱集中的图谱所代表的年龄、形态或病理等方面的信息是多种多样的, 可能存在图谱图像与待分割的目标图像整体比较相似, 但在待分割的目标组织却不相似的情况. 如果选择这类的图谱参与分割, 会影响目标组织的最终分割结果. 以分割目标为导向的图谱选择方法可以弥补这个不足. 以分割目标为导向的图谱选择方法是以目标组织为导向来计算图谱图像与参考图像的相似度, 然后根据这个相似度来选择合适的图谱进行进一步的处理. 但是, 由于目标组织形态的不规则性和不一致性, 传统的诸如平方差之和、互相关和归一化互信息等度量方法不能用于目标组织之间相似性的度量. 为了解决这个问题, 本文将采用豪斯多夫距离来度量两个目标组织之间最大不匹配程度, 并进一步提出基于豪斯多夫距离的以目标为导向的图谱选择方法.

对于两个目标组织 $A = \{ {a_1}, {a_2}, \cdots , {a_m}\} $ 和 $B = \{ {b_1}, {b_2}, $ $ \cdots , {b_n}\} $ , 它们之间的豪斯多夫距离如式(2).

$ \left\{ {\begin{split} & H(A, B) = \max \left[ {h(A, B), h(B, A)} \right] \hfill \\ & h(A, B) = \mathop {\max }\limits_{a \in A} \mathop {\min }\limits_{b \in B} \left\| {a - b} \right\| \hfill \\ & h(B, A) = \mathop {\max }\limits_{b \in B} \mathop {\min }\limits_{a \in A} \left\| {b - a} \right\| \hfill \end{split}} \right. $

(2)

其中, $h(A, B)$ 表示从集合 $A$ 到集合 $B$ 的有向豪斯多夫距离, 即集合 $A$ 中的点到集合 $B$ 中的任意一个点的最长距离; 同理, $h(B, A)$ 表示的是集合 $B$ 中的点到集合 $A$ 中的任意一个点的最长距离.

很显然, 基于豪斯多夫距离的相似性度量方法可以度量两个元素个数不一样的点集的最大不匹配程度, 进而可以用这个最大不匹配程度来作为两个点集相似度的衡量标准, 即最大不匹配程度越小, 则说明两个点集越相似, 反之亦然. 当两个点集完全重合时, 其豪斯多夫距离为0. 另外, 采用豪斯多夫距离作为两个点集相似度度量标准还有一个优势就是, 点集内元素的顺序对于最后的结果没有影响. 这两个优势表明, 采用豪斯多夫距离作为相似度度量的标准所得到的相似度计算的结果不受待分割的目标组织尺寸和位置的影响, 具有更高的鲁棒性, 因此有利于后续的以分割目标为导向的相似度的计算.

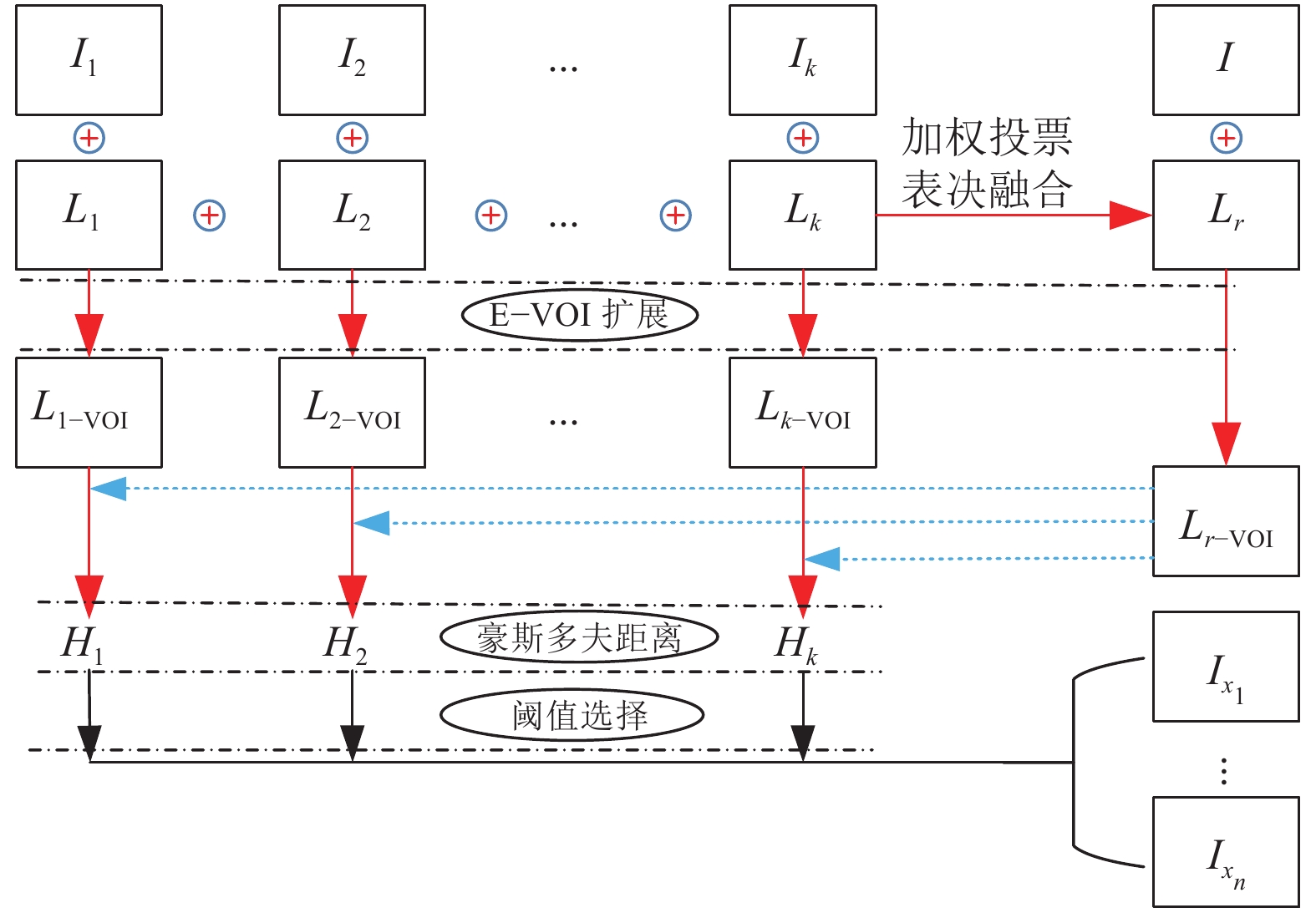
对于某一个分割目标, 图谱集中的会有精确的人工标注的分割结果与之对应. 但是, 对于待分割的图像而言, 这个分割目标是未知的. 本文采用基于多数表决法MV (majority voting)^{[4, 20]}的融合方法来初步确定分割目标. MV方法得到的结果往往与实际结果有较大差异, 为了降低这个差异对于计算目标相似度的影响, 本文采用形态学膨胀的方法对该分割结果以及图谱集中的目标进行边界扩充后再进行相似度的计算. 综上所述, 以分割目标为导向的图谱选择方法的工作原理可以用如图1所示的示意图来表示, 其实现步骤可以用算法2来描述.

算法2. 以分割目标为导向的图谱选择方法

输入: 目标图像 $\scriptstyle I$ , 配准后的图谱图像集 $\scriptstyle{I_k}$ 和标签集 $\scriptstyle{L_k}$ .

输出: 选择用于目标图像分割的图谱集 $\scriptstyle{I_{\text{Out}}}$ 和对应的标签集 $\scriptstyle{L_{\text{Out}}}$ .

步骤:

Step 1. 采用多数表决的标签融合方法得到初始的分割结果 $\scriptstyle{L_r}$ ;

Step 2. 对于第 $\scriptstyle k$ 个图谱图像的标签集, 采用形态学方法对其进行扩展, 得到对应的VOI区域 $\scriptstyle{L_{k - {\rm{VOI}}}}$ , 并根据 $\scriptstyle{L_{k - {\rm{VOI}}}}$ 提取出该图谱的目标组织数据, 用点集 $\scriptstyle{B_k}$ 表示;

Step 3. 对于初始分割结果 $\scriptstyle{L_r}$ 也采用同样的方法进行扩展, 得到对应的E-VOI区域 $\scriptstyle{L_{r - {\rm{VOI}}}}$ , 并根据 $\scriptstyle{L_{r - {\rm{VOI}}}}$ 提取出初始的目标组织数据, 用点集 $\scriptstyle{B_r}$ 表示;

Step 4. 对于第 $\scriptstyle k$ 个图谱图像目标组织数据 $\scriptstyle{B_k}$ , 计算其与初始的目标组织数据 $\scriptstyle{B_r}$ 的豪斯多夫距离 $\scriptstyle{H_k}$ ;

Step 5. 保留豪斯多夫距离最小的 $\scriptstyle n$ 个图谱, 剔除其余图谱, 得到最终的有效图谱集 $\scriptstyle{I_{\rm{Out}}}$ 及对应标签集.

3 基于两步图谱选择策略的分割方法

基于最小角回归的图谱选择方法是从整体上选择与待分割的目标图像较为相似的图谱来构造基于多谱图分割方法的图谱集, 与仅用相似度排序进行图谱选择的方法相比, 该方法既考虑了图谱之间的相似性, 也考虑了图谱内部的冗余性, 因此得到的结果更有利于后期的基于相似图谱的多图谱分割方法的分割, 但是该方法是从整体上来寻找相似图谱的, 没有考虑待分割目标图像的局部性, 因此有必要采用局部相似度量的方法来对这些相似图谱集进行进一步的筛选, 以便能选出与待分割的目标图像在分割区域较相似的图谱. 基于上述分析, 本文提出一种基于两步图谱选择策略的脑MR图像分割方法. 第1步采用基于最小角回归的方法进行图谱的粗选择, 第2步则在第1步得到的图谱集中采用以分割目标为导向的图谱选择方法进行图谱的精选择, 最后利用得到的图谱集结合现有的标签融合方法来得到最终的分割结果.

4 实验与分析

为了准确地评估基于两步图谱选择的脑MR图像分割方法的有效性, 本文在IXI图谱数据集^[21]上进行相关实验. 实验环境为一台标准的台式电脑, 其配置为CPU i5-4570, 内存大小为16 GB, 没有使用GPU加速, 编程环境为Matlab 2016b. IXI数据库中含有30例完整的脑MR图谱. 本文通过交叉实验验证, 在基于最小角回归的图谱选择方法挑选出20例相似图谱的基础上, 通过以分割目标为导向的图谱选择方法确定最终的10例图谱用于基于多图谱的脑MR图像分割能够获得较好的分割效果(图谱数的选取一般都是根据经验进行设置, 此外还与参与标签融合的方法有关, 目前还没有一种自适应的方法来确定最优图谱数量参与分割. 本文通过大量的实验进行验证, 最终确定图谱数量为10时, 大多数的标签融合方法能获得较好的分割结果).

本次实验主要是对海马体、杏仁核、尾状核、伏隔核、壳、丘脑、苍白球这7种组织采用基于多数表决法(MV)^{[4, 20]}、精确度与性能水平联合评估法 (simultaneous truth and performance level estimation, STAPLE)^[22]、基于非局部加权的图谱标签融合方法(NPBL)^{[23, 24]}和基于图谱灰度块稀疏表示的图谱标签融合方法(SPBL)^{[25, 26]}这4种方法进行分割实验. 实验将统计以图谱集中任意一个图谱图像作为目标图像时不同分割方法对这7种组织分割结果的重叠率, 并画出这些重叠率分布的盒形图.

基于两步图谱选择的脑MR图像分割方法是通过两次图谱选择策略(two steps select, TSS)挑选出适当数量的图谱后再采用上述这些标签融合方法来实现分割, 本次实验将根据标签融合方法的不同, 对基于相似图谱的脑MR图像分割方法分别命名为TSS_MV、TSS_STAPLE、TSS_NPBL和TSS_SPBL. 因此, 本次实验可以分为MV、STAPLE、NPBL和SPBL这4种分割方法使用全部图谱和使用相似图谱这两种情况分割脑MR图像的7种组织.

表1展示了IXI图谱集中任意一个图谱图像作为目标图像时, 这4种分割方法使用全部图谱和使用相似图谱对不同脑部组织进行分割所得到的平均重叠率. 从表1可以看出, TSS_MV和TSS_STAPLE采用两次图谱选择策略分割7种脑组织获得的平均重叠率总体比不使用图谱选择策略得到的平均重叠率要高. TSS_SPBL仅在分割海马体和伏隔核组织时, 所获得的平均重叠率低外, 对于分割其余6种组织的分割结果要优于不使用图谱选择策略所得到的分割结果. 但是TSS_NPBL仅在杏仁核、和丘脑组织分割上要优于不使用图谱选择策略所得到的分割结果, 而在分割海马体、尾状核、伏隔核、壳和苍白球这5种组织的分割结果要比不使用图谱选择策略所得到的分割结果差. 我们仔细研究TSS_NPBL方法不能获得较好分割结果的原因是由于NPBL标签融合方法是一种基于非局部加权的标签融合方法. 当用于非局部相似度和权重计算的样本数量太少时, 从而影响标签加权的权重计算进而影响了最终的分割结果. 因此, 从总体数据分析来看, 除了TSS_NPBL方法外, 其余3种分割方法使用两次图谱选择策略能够获得较高的平均重叠率, 这在一定程度上验证了本文方法的有效性.

表2展示了IXI图谱集中任意一个图谱图像作为目标图像时, 这4种分割方法使用全部图谱和使用相似图谱对不同脑部组织进行分割所消耗的平均时间, 其中采用两次图谱选择策略的方法消耗的时间包含图谱选择的时间. 从表2可以看出, 除了TSS_MV方法消耗的时间比使用全部图谱进行脑组织分割的MV方法所消耗的时间要长外, TSS_STAPLE、TSS_NPBL和TSS_SPBL这3种方法由于采用两次图谱选择策略极大地缩短了脑组织分割所消耗的时间, 这在一定程度上说明了本节提出的基于相似图谱的脑MR图像分割方法能提高脑组织的分割效率.

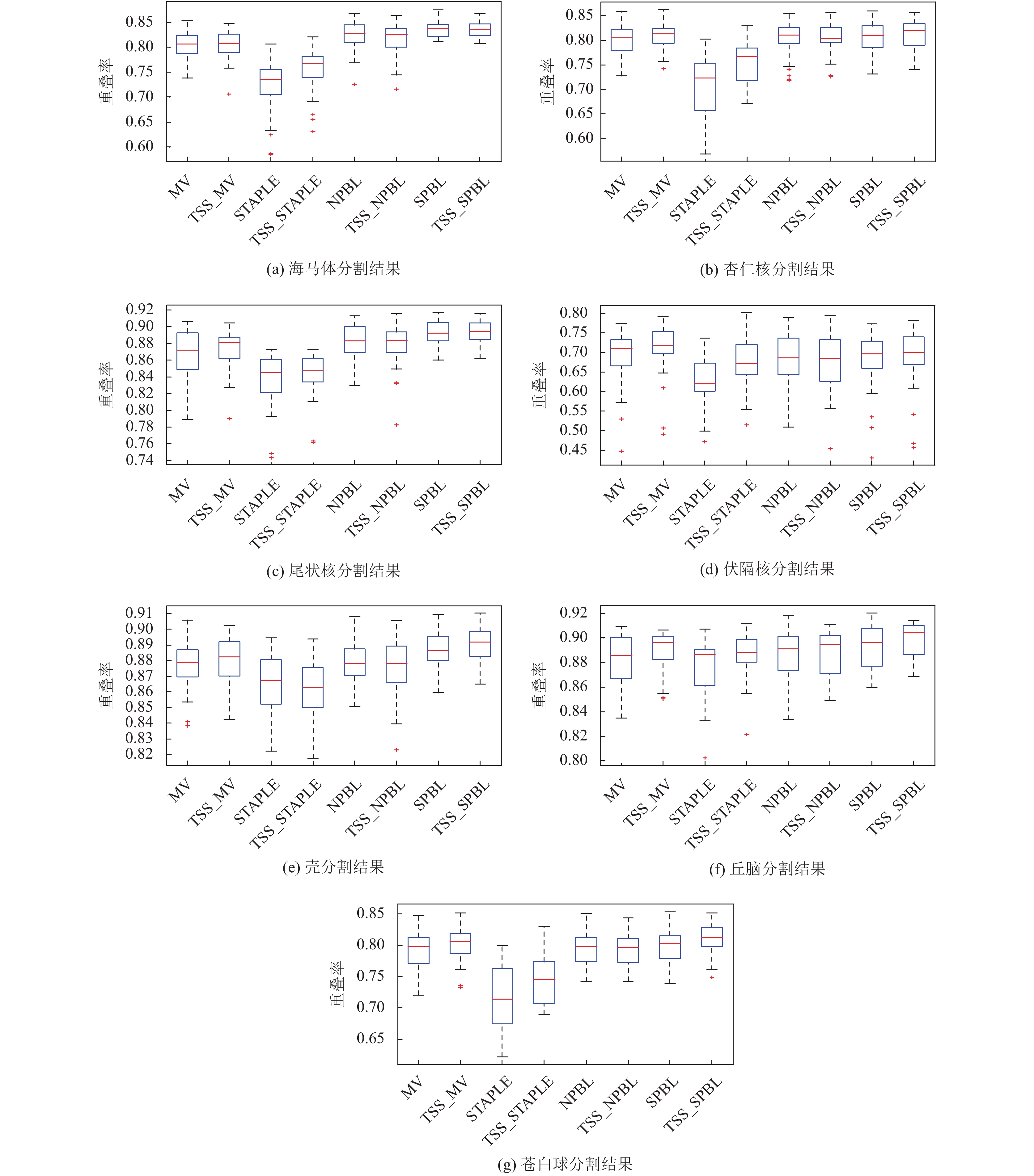
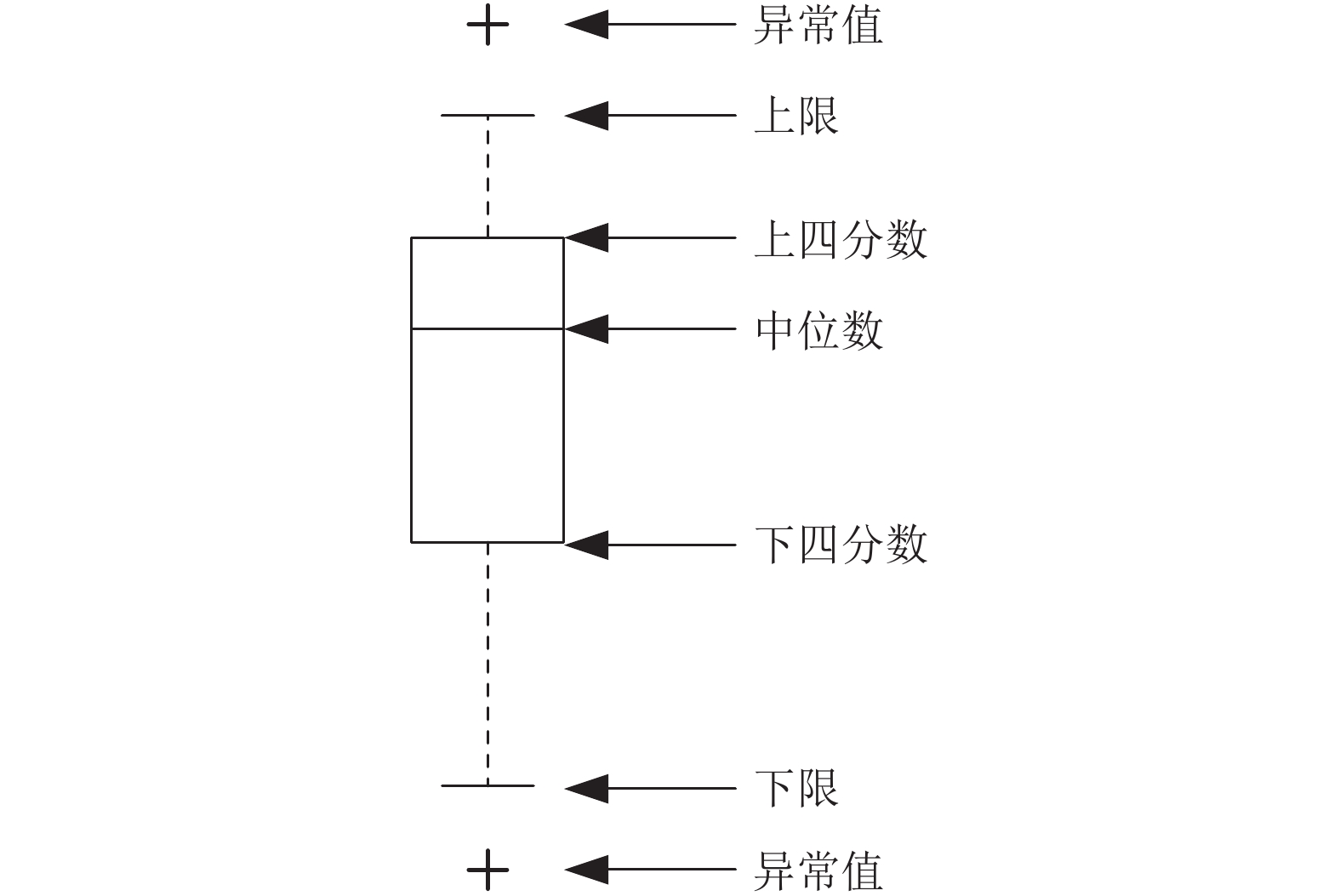
图2展示了IXI图谱集中任意一个图谱图像作为目标图像时, 这4种分割方法使用全部图谱和使用相似图谱对不同脑部组织进行分割结果的盒形图(blox plot). 盒形图能够很好地反映数据的离散分布情况, 它由5个数值点组成: 非异常范围内的最小值(下限), 非异常范围内的最大值(上限), 中位数, 下四分位数, 上四分位数和异常值. 图3给出了盒形图的详解图.

综合表1、表2和图2对30例脑MR图像中7种不同脑组织的分割情况, 可以得出如下结论: 基于多数表决法得到的分割结果比基于精确度与性能水平联合评估算法得到的分割结果更为准确, 基于非局部加权的图谱标签融合方法得到的分割结果比基于多数表决投票的图谱标签融合方法得到的分割结果更为准确; 基于图谱灰度块稀疏表示的图谱标签融合方法得到的分割结果比基于非局部加权的图谱标签融合方法得到的分割结果更为准确. 但是基于图谱灰度块稀疏表示的图谱标签融合方法和基于非局部加权的图谱标签融合方法所需要的分割时间要远远大于其他两个方法. 总的来说, 采用本文提出的两次图谱选择策略能够在提高分割精度的同时大大缩短分割的时间.

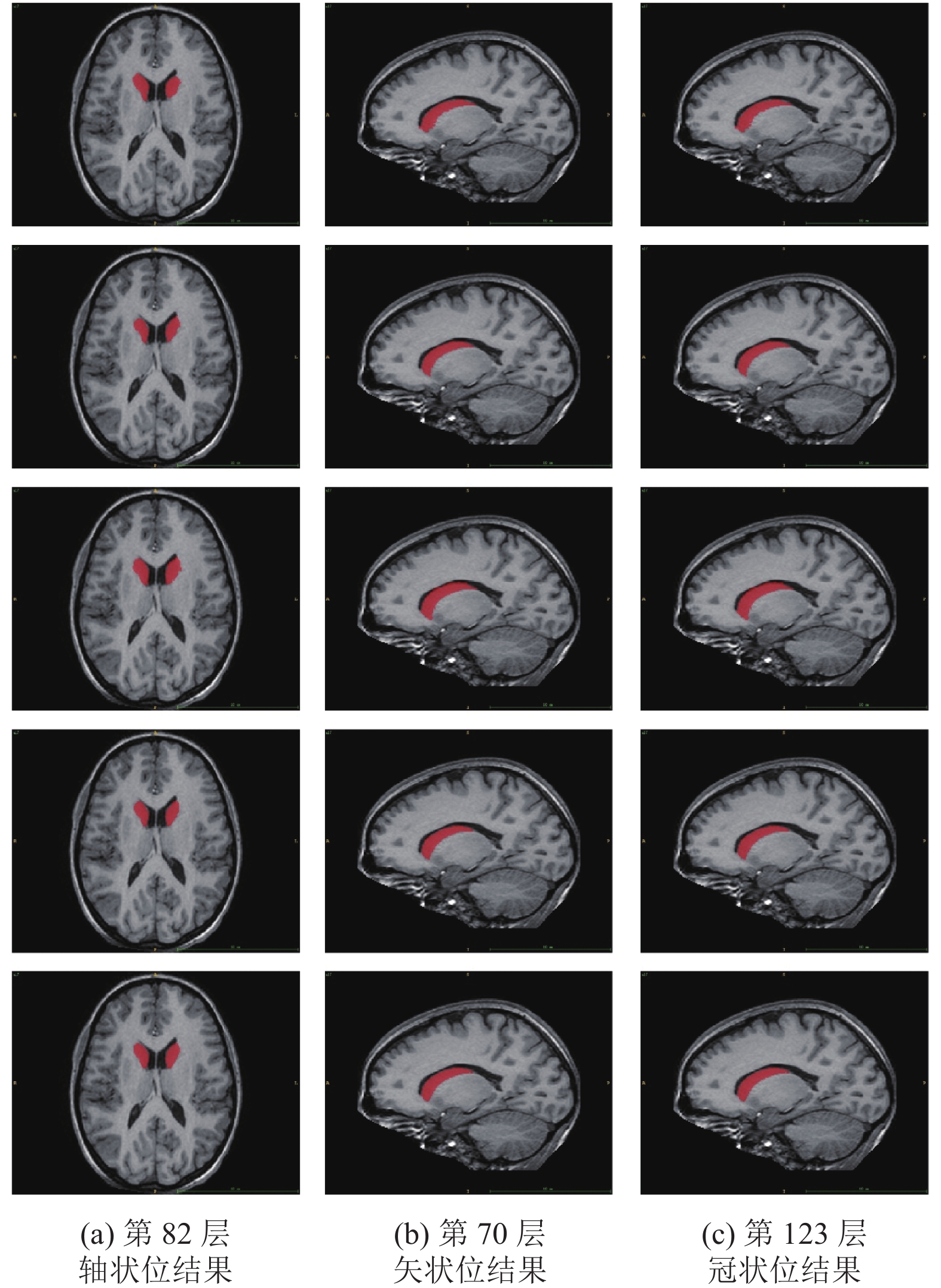
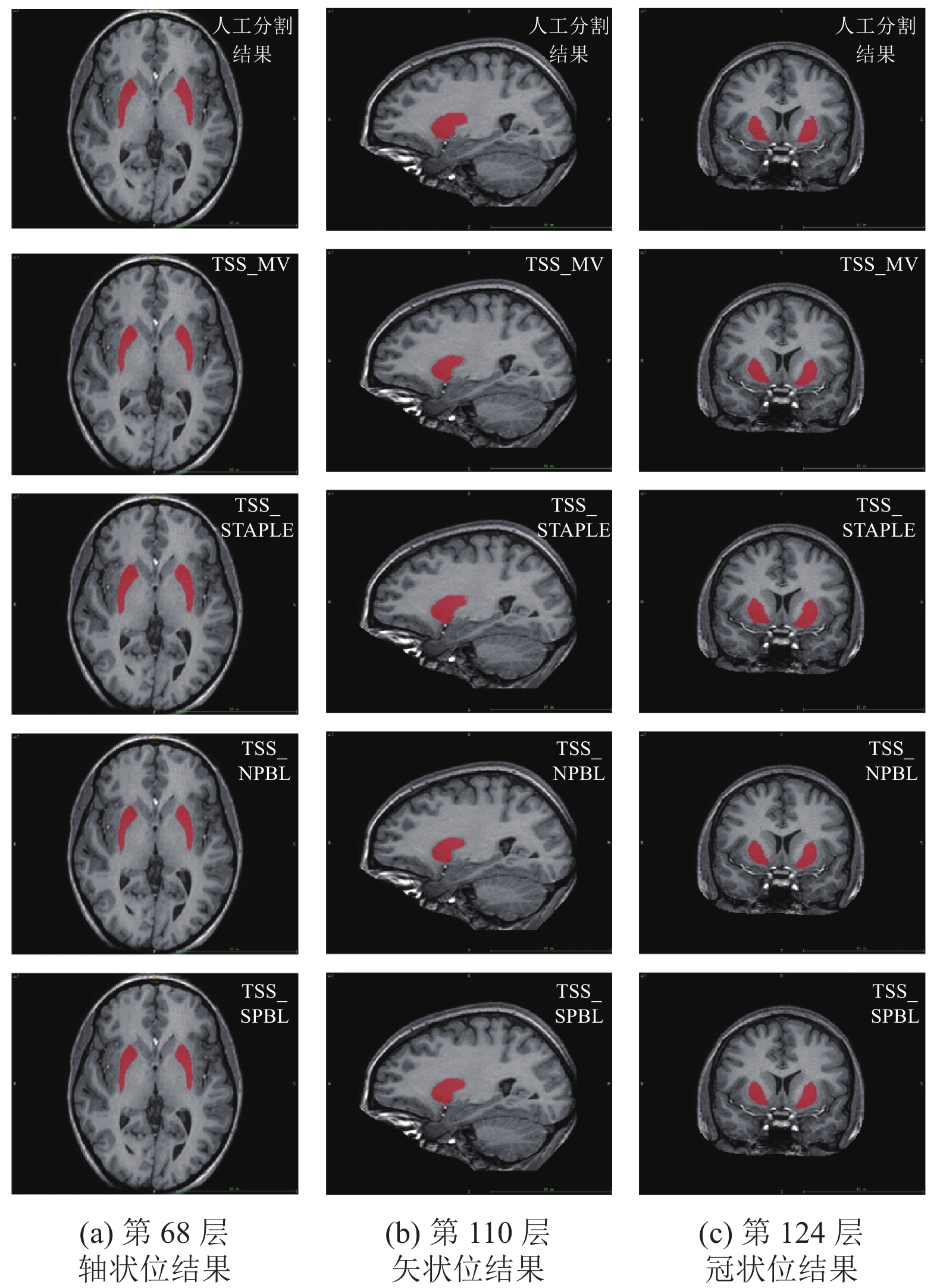
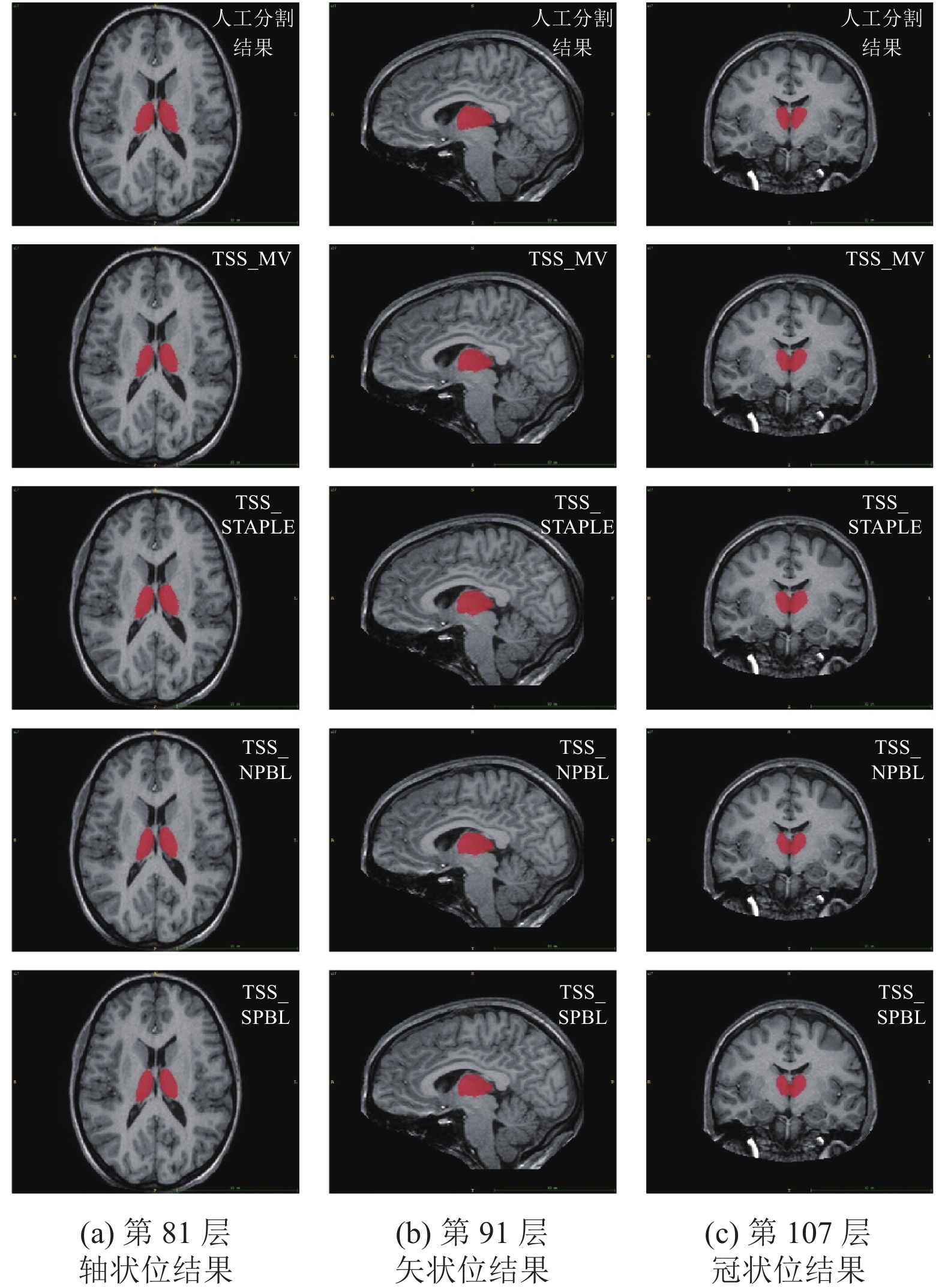
图4–图6分别展示了IXI图谱集中以第17号脑MR图像作为待分割的目标图像时, 利用TSS_MV、TSS_STAPLE、TSS_NPBL和TSS_SPBL这4种方法对尾状核、壳和丘脑3种不同脑组织进行分割得到的结果在相应层的二维剖面图. 从二维剖面图可以看出, 利用本文提出的基于两步图谱选择的脑MR图像分割方法得到的分割结果与金标准的相符程度是比较好的. 该结果进一步验证了本文所提方法的有效性.

综上所述, 从实验结果可以看出本章所提出的方法能获得更可靠的子图谱集, 从而提高脑MR图像中脑组织的分割精度.

5 结论与展望

本文针对传统的基于相似度加权融合的方法存在两个不足提出了一种基于两步图谱选择的图谱分割方法. 该方法首先采用基于最小角回归的图谱选择方法来对图谱集中的图谱进行粗略选择, 然后再采用以分割目标为导向的图谱选择方法来对粗略选择的结果进行精细选择, 最后将精细选择得到的图谱集应用于基于多图谱的脑MR图像分割方法. 该方法在从整体上选择与目标图像更为相似的图谱的同时能够避免图谱集的冗余性, 同时采用以分割目标为导向基于豪斯多夫距离的图谱选择方法既满足了局部计算相似度的原则, 在计算过程中又保持了目标组织原有的形状. 因此, 该方法相比于传统的方法具有更高的鲁棒性, 得到的相似度也更为可靠. 实验结果也验证了本文提出的方法的有效性.