社交网络(social networks, SNs)是一种人与人之间的关系与互动的结合^[1]. 社交网络把网络中的每个节点看作参与这个网络中人的抽象, 每个人之间的关系则抽象成节点之间的连边, 网络中每个人的行为不同且具有不同的属性特征. 在线社交网络的起点是电子邮件的出现, 早期的电子邮件解决了远程的邮件传输问题, 人们用电子邮件交换信息所构成的关系网络就是在线社交网络的最早形式.

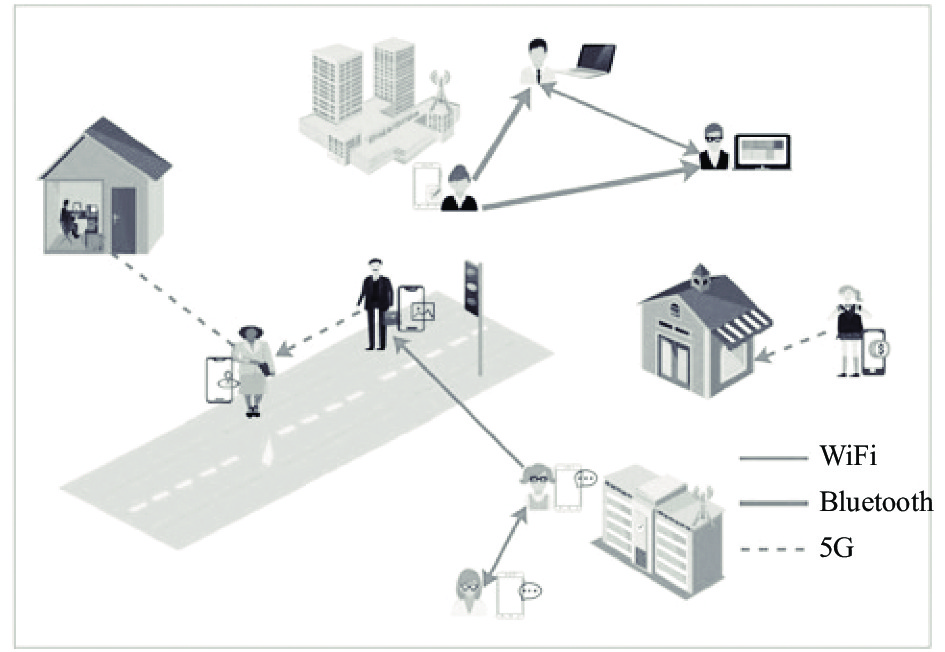
随着互联网技术和无线技术的迅猛发展, 移动社会网络(mobile social networks, MSNs)应运而生^[2]. 如图1, 移动社会网络是从在线社交网络演化而来的一种用户驱动的移动通信网络. 这种网络具有更加显著的泛在性和移动性, 其中包括节点(用户)的社交连接^[3]. 同时, 移动社会网络也具有移动通信网络和在线社交网络的一些基本属性, Dong等^[4]发现移动社交网络具有典型的无尺度网络和小世界网络属性. Pietilänen等^[5]发现移动社会网络中人们表现出空间上复杂的移动性以及各个用户具有复杂的个人属性. 移动社会网络的发展给人们的日常生活带来很多便利的服务, 例如基于位置的可穿戴设备, 医疗保健以及移动社会网络服务等.

高影响力节点挖掘是移动社会网络分析中的重要内容. 通过从网络中识别前 $ k $ 个高影响力节点, 使得在网络中利用这 $ k $ 个节点产生的影响传播范围最大速度最快. 影响力节点挖掘在控制舆情传播、扼制病毒传染等领域有着广泛应用. 对于移动运营商, 通过挖掘影响力节点能够以较少的代价得到高效的信息传播能力从而获得更高的效益. 近年来大量学者从不同角度提出了不同算法进行影响力分析, 影响力节点的挖掘依然是热门研究方向. 由于真实网络中节点数量巨大、节点间关系复杂且节点属性繁多, 移动社会网络中的最大化影响力节点挖掘仍然面临着巨大的挑战. 目前, 大多的节点影响力计算方法可以分为基于网络拓扑特性的启发式算法和基于传播的贪心算法.

启发式算法通过考虑网络的拓扑结构来衡量网络中节点的重要性, 并把重要性高的节点作为高影响力节点. Freeman^[6]首先提出用度中心性(degree centrality, DC)衡量网络中节点的重要性, 按照节点的度中心性大小衡量节点的影响力强度. 以图中的最短路径经过一个节点的次数表现了该节点与其他节点的互动程度这一观点提出了介数中心性(betweenness centrality, BC)^[7]这一指标来评价节点在网络中的影响力强度. PageRank (PR)算法^[8]属于特征向量中心性的一种变体. 节点的影响指标定义为PR值, 如果一个网页被很多其他网页链接到的话这个网页的PR值会相对较高, 也就是更加重要. 陆晓野等^[9]从社区的角度提出基于节点频度中心度的挖掘算法. 张宪立等^[10]在PageRank基础上提出反向PageRank算法并与度中心性结合得到一种混合的启发式算法(heuristic algorithm of mixed PageRank and degree, MPRD). Kitsak等^[11]提出了核心度(coreness)作为评价节点在网络中影响力的指标, 利用k-核分解^[12]计算在网络中各个节点的影响力. Morone等^[13]基于渗透理论提出了集体影响(collective influence, CI)这一网络拓扑指标, 利用渗透模型找出被破坏就会使整个网络崩溃的节点, 把这些节点集作为影响力前k节点. 宋甲秀等^[14]在集体影响的基础上提出了局部集体影响算法(local collective influence rank algorithm, LCIR)使得影响力的传播更加稳定. 康玲等^[15]对网络中的节点根据紧密度情况重新排序, 并绘制网络的区域密度曲线, 在密度图中波谷点两侧选取一定比例的节点作为影响力节点. 杨树新等^[16]考虑局部方法的适宜度量层级与网络拓扑的差异性, 提出一种新的基于3级邻居的节点影响力度量法(three-level influence measurement, TIM).

基于传播的贪心算法通过贪心策略近似的追求最优解: 初始设置空的影响力节点集, 并不断向节点集中添加当前网络中最具影响力的节点. Kempe等^[17]证明影响力最大化问题是NP-hard问题, 并提出原始贪心策略用于求影响力前k节点. 使用基于子模块函数的分析框架证明了原始贪心策略所获得的解决方案对于几种类型的模型而言, 在最优值的63%之内. Leskovec等^[18]提出CELF (cost-effective lazy-forward)方法根据影响力扩散的子模态特性来避免影响范围的冗余计算从而提高了贪心算法的计算效率. Kim等^[19]基于IC模型提出一种独立路径算法(independent path algorithm, IPA)来近似计算节点的影响力传播能力. Kianian等^[20]在IPA的基础上考虑到两条影响路径的相关性并与启发式算法结合提出一种高效的启发式独立路径算法(heuristic independent path algorithm, HIPA). 李国良等^[21]针对多社交网络中影响力传播问题, 使用节点间具有最大传播概率的路径来近似衡量节点间的传播概率.

上述方法虽然在影响力最大化研究上做出了重要贡献, 但是实际社会网络中信息传播并不完全基于网络的拓扑特性, 它们未考虑到信任对于用户间交互的重要性. Asim等^[22]根据多种信任度计算方法提出了一种社会网络信任模型(SNTrust model)揭示了在本地网络中节点的影响力和信任度是存在着联系的. 例如: 若两个人之间具有更高的相似度, 则相互之间的信任度越高, 也越有利于两者间信息的交换. 因此, 可以用信任度来评价节点在其相邻节点中的影响力, 并且节点的偏好以及节点间的信任关系在很长一段时间内是一种较为稳定状态, 只有当外界环境发生重大变化时才会改变, 所以静态网络中节点的信任度可以用于刻画这个网络一段时间内网络中节点的状态以及节点间的关系. 然而, 尽管某一用户节点在其邻居节点中信任度高, 但是并不能证明它就是整个网络中的高影响力节点. 为了解决这些问题, 我们提出一种基于邻居节点间信任度和Beta信誉模型^[23]的全局信任模型(global trust model, GTM)用于计算网络中节点的影响力. 利用SI模型, 在真实网络数据集中与启发式算法所挖掘的影响力节点集合和其传播效果进行比较, 证明了本文所提出模型在保证精确性和传播能力的同时, 还具有更低的时间复杂度.

1 全局信任模型概述

为解决影响力最大化选择前 $ k $ 节点问题, 本文提出了一种基于邻居节点间信任度和Beta信誉模型的影响力节点挖掘全局信任模型. 该模型分为3部分: 节点局部信任度的计算, 节点全局信任度计算, 影响力节点选择.

(1)节点局部信任度计算阶段. 计算节点与邻居节点间的属性信任度和共同好友相似信任度, 结合一起得到节点在邻居节点中的局部信任度.

(2)节点全局信任度计算阶段. 利用Beta信誉模型, 在节点的局部信任度的基础上得到节点的全局信任度.

(3)影响力节点选取阶段. 通过对节点的全局信任度大小排序, 选取全局信任度最大的前 $ k $ 节点, 把这些节点作为影响力前 $ k $ 节点.

2 全局信任模型设计

在本节我们提出一种新的信任模型设计方式. 首先从局部的角度计算节点的初始信任值, 再从全局的角度对节点的信任值进行再计算得到节点的全局信任值, 最后选取其中的前 $ k $ 节点作为最大影响力节点.

本文中, 网络由 $ G=\left(V, E\right) $ 组成, 其中 $ V $ 是指网络中的节点集, $ E $ 是指节点的边集. 模型设计中 $ {{X}_{v}}_{1} $ 表示节点 $ {v}_{1} $ 的属性列表, $ {N}_{{v}_{1}} $ 表示节点 $ {v}_{1} $ 的邻居节点列表.

2.1 局部信任度计算

在计算局部信任度中, 我们考虑两个因素来计算: 属性信任, 共同好友相似信任.

(1)属性信任

Baek等^[24]发现当两个人之间相似的特征更多时, 会使得双方在一起交流更加舒服并有进一步接触的趋势. Golbeck^[25]发现用户大多信任具有相似属性的其他人. 因此可以通过用用户间属性相似度来计算他们的信任度. 我们通过Pearson相关系数^[26]来计算两节点间的属性序列相似度:

$ {\rho }_{{X}_{{v}_{1}}, {Y}_{{v}_{2}}}=\frac{cov({X}_{{v}_{1}}, {Y}_{{v}_{2}})}{{\sigma }_{{X}_{{v}_{1}}}{{\sigma }_{y}}_{{v}_{2}}} $

(1)

其中, $ {{X}_{v}}_{1} $ 和 $ {{Y}_{v}}_{2} $ 分别为节点 $ {v}_{1} $ 和 $ {v}_{2} $ 的属性序列, $ \;{\rho }_{{X}_{{v}_{1}}, {Y}_{{v}_{2}}} $ 表示节点 $ {v}_{1} $ 和 $ {v}_{2} $ 之间的属性信任相似度.

(2)共同好友相似信任

Lo等^[27]提出当两用户都对第3个用户有良好的关系, 则这两个用户就可能建立起良好的关系. 因此, 我们通过共同好友的相似度来计算节点间的信任值. 该模型中利用Jaccard系数^[28]来计算两用户之间的共同好友相似度:

$ J({N}_{{v}_{1}}, {N}_{{v}_{2}})=\frac{|{N}_{{v}_{1}}\cap {N}_{{v}_{2}}|}{|{N}_{{v}_{1}}\cup {N}_{{v}_{2}}|} $

(2)

其中, $ {N}_{{v}_{1}} $ 为节点 $ {v}_{1} $ 的邻居节点集合, $ {N}_{{v}_{2}} $ 是节点 $ {v}_{2} $ 的邻居节点集合, $ J({N}_{{v}_{1}}, {N}_{{v}_{2}}) $ 表示节点 $ {v}_{1} $ 和 $ {v}_{2} $ 之间的共同好友相似信任度.

最后, 节点的初始信任度通过属性信任与共同好友相似信任结合计算:

$ {T}_{{v}_{1}{v}_{2}}=\alpha \left({\rho }_{{X}_{{v}_{1}}, {Y}_{{v}_{2}}}\right)+\beta \left(J\right({N}_{{v}_{1}}, {N}_{{v}_{2}}\left)\right) $

(3)

$ {T}_{{v}_{1}}=\left(\sum _{i=1}^{n}{T}_{{v}_{1}{v}_{i}}\right) $

(4)

$ L{T}_{{v}_{1}}=\frac{{T}_{{v}_{1}}}{n} $

(5)

其中, $ {T}_{{v}_{1}{v}_{2}} $ 是节点 $ {v}_{1} $ 和 $ {v}_{2} $ 之间的信任度, $ \alpha $ 为属性信任占的比例, $\; \beta $ 为共同好友相似信任的占比, $ \alpha $ 和 $ \;\beta $ 都选取0.5. $ {T}_{{v}_{1}} $ 为节点 $ {v}_{1} $ 与其邻居节点信任度的总和, $ n $ 是节点 $ {v}_{1} $ 的邻居节点数, 以节点 $ {v}_{1} $ 与其邻居节点信任度总和的均值作为其局部信任度 $ L{T}_{{v}_{1}} $ .

2.2 利用Beta信誉模型进行全局信任度计算

尽管节点的局部信任度可以反映出其在本地网络中的影响力大小, 但并不能代表它在整个网络中的重要性程度. 目前大多的信任模型通过计算节点在本地网络中与相连邻居节点集的信任度大小来评价节点的影响力, 但是这种方法可能会导致由于节点的邻居节点较少使得尽管节点在本地网络中的信任度很高, 但是在整个网络中却并没有相应的影响力. 针对这一问题, 我们利用Beta信誉模型来解决.

Beta信誉模型是一种结合用户对目标给出的反馈来计算用户信誉值的基于Beta分布的概率密度函数^[29]. 该模型被用来表述无线通信节点之间网络安全模型, 而移动社会网络是社会网络和移动通信网络结合形成的交叉网络所以在本文的背景下也同样适用. 如果令 $ r_{T} $ 和 $ s_{T} $ 分别表示目标实体 $ T$ 的正面评价和负面评价的个数, 则实体 $ T $ 的信誉值函数可以表示为:

$ \left.\varphi \left(p\mid {r}_{T}, {s}_{T}\right)\right)=\frac{\varGamma \left({r}_{T}+{s}_{T}+2\right)}{\varGamma \left({r}_{T}+1\right)\varGamma \left({s}_{T}+1\right)}{p}^{{r}_{T}}(1-p{)}^{{s}_{T}} $

(6)

那么信誉值的期望为:

$ E\left(\varphi \left(p\mid {r}_{T}, {s}_{T}\right)\right)=\frac{{r}_{T}+1}{{r}_{T}+{s}_{T}+1} $

(7)

此时, 实体信誉值的大小可以用其信誉值的期望来表示. 在移动社会网络中, 度更大的节点能够将自己的信息传播到更多的节点上, 则其在整个网络中具有更高的信誉度, 根据式(4)和式(7)我们得到下列公式. 我们基于节点局部信任度的计算得出节点在网络中的全局信任度:

$ G{T}_{{v}_{1}}=\frac{{d}_{{v}_{1}}}{D}\left({T}_{{v}_{1}}\right) $

(8)

其中, $ D $ 为网络中的节点数总和, $ {d}_{{v}_{1}} $ 为节点 $ {v}_{1} $ 的度数, 以 $ {d}_{{v}_{1}} $ 和网络中总节点数的比值作为节点 $ {v}_{1} $ 在整个网络中的信誉度, 并将节点与邻居节点的信任度总和 $ {T}_{{v}_{1}} $ 与信誉度相乘得到节点的全局信任度.

3 实验与结果分析

实验数据集来源是斯坦福大学Facebook网络( http://snap.stanford.edu/data/ego-Facebook.html), 对本文提出的模型进行实验分析, 并与传统的选取影响力节点算法进行实验对比评估模型的精确度与影响力最大化效果. 实验环境为MacBook Pro (16-inch, 2019), 2.6 GHz hexa-core Intel Core i7处理器, 16 GB 2667 MHz DDR4内存以及Intel UHD Graphics 630 1536 MB图形卡. 数据集包括节点的部分属性以及节点间的社交关系, 考虑到数据集中节点属性数量并不一致, 我们选择整个数据集其中的5个子网进行实验, 并且每个子网中各个节点的属性数量相等, 表1展示了数据集的相关信息, 图2–图6展示了5个网络的拓扑结构.

实验利用SI传染病模型来模拟现实中传播的影响, 并选取度中心性(DC), 介数中心性(BC), PageRank算法(PR)以及紧密度中心性(CC)^[30]4个标志性算法与本文提出的方案进行实验对比, 表2–表6中列出了每个算法所选取的前10节点.

表7展示了各个算法与GTM得到的前10个影响力节点的交集情况. ${N_{\rm{DC}}}$ 、 ${N_{\rm{BC}}}$ 、 ${N_{\rm{PR}}}$ 、 ${N_{\rm{CC}}}$ 和 ${N_{\rm{GTM}}}$ 分别代表各个算法以及GTM得到的前10影响力节点集, 例如在3980.circles网络中: ${N_{\rm{DC}}}$ ={4030, 4023, 3998, 3982, 4014, 3997, 4031, 4021, 3994, 4004}、 ${N_{\rm{BC}}}$ ={4023, 4030, 3998, 4031, 4014, 4027, 4002, 4017, 4038, 4020}、 ${N_{\rm{GTM}}}$ ={4030, 4023, 3998, 3982, 3997, 4021, 4014, 4009, 3994, 4031}. 从表中可以发现GTM与DC具有高度相似性, 跟CC的重合度也较高. 在前3个网络中GTM和PR也具有不错的相似度, 整体上跟BC的结果较为不同. 由于各个算法寻找影响力节点的出发角度不同, 所以GTM在结果上与个别算法存在差异性, 但是从表中可以发现GTM的整体精确度是在可接受范围内.

本文算法时间复杂度如下:

(1)在计算局部信任度时复杂度为 $ {\text{O}}\left(n\times m\right) $ .

(2)在计算全局信任度时复杂度为 ${\text{O}}\left(n\right)$ .

(3)在选择最大影响力节点时复杂度为 ${\text{O}}\left(k\right)$ .

表8列出GTM与另外4个算法的时间复杂度对比, 从表中可以看出GTM相比其他算法具有更低的时间复杂度.

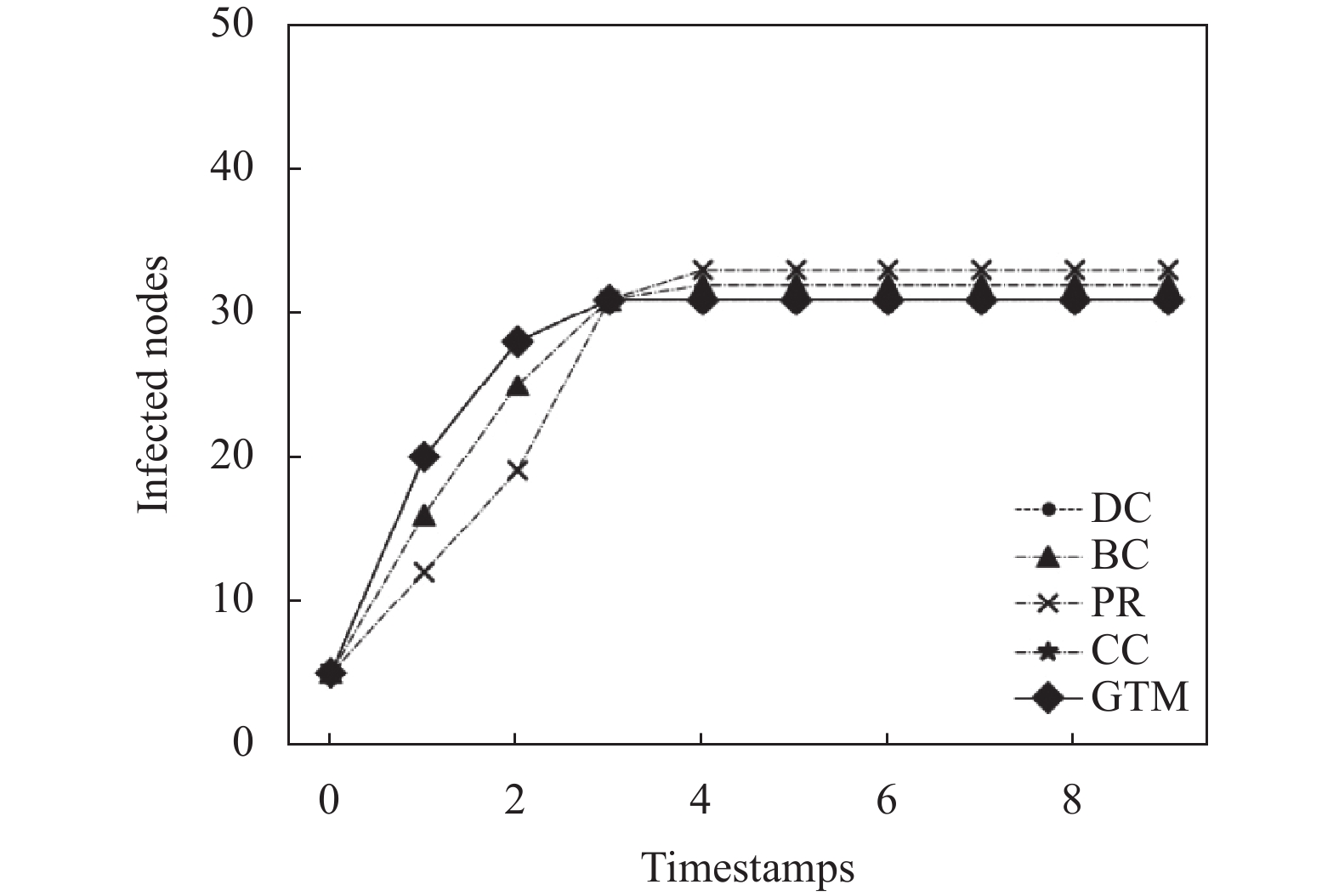
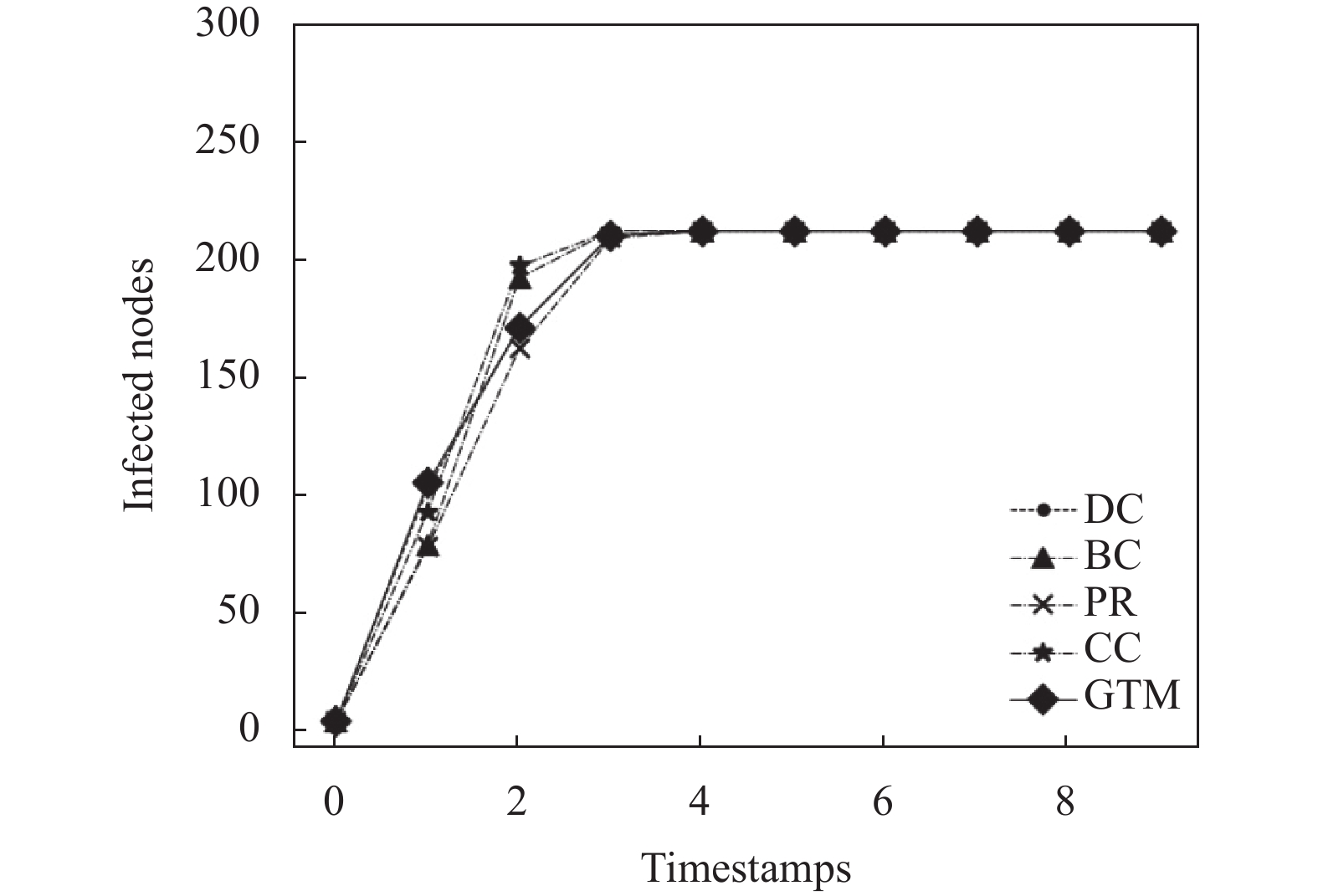
SI 模型^[31]是经典的传染病传播模型, 用来模拟那些感染后不能治愈的疾病在网络中的传播情况. 在SI 模型中, 人群数量的总和不变, 把人群划分为易感染者(susceptible, S)和感染者(infected, I)两类, 其中S用来表示还未被感染的人, I用来表示已被感染的人. 我们选取每个算法所得的前5个最大影响力节点作为初始影响力节点, 将其状态设置为I, 根据这些算法选出来的影响力节点在网络中的影响传播能力进行比较可以发现, 我们方案的节点在网络中具有不错的传播能力.

考虑到真实网络中人们的交互依赖于相互间的信任度, 人们对信任度较大的人所提出的意见会更容易接纳, 也更有力于信息的传播, 而信任度较小的人意见并不能被很好地传播. 即若一个节点局部信任度较大可以很好地将信息传播给邻居节点, 而信任度较小的节点只能够接受信息而不能够传播信息. 所以我们选取网络中节点局部信任度的均值作为两节点间是否有信息传播的阈值 $ \gamma $ . 当信息从 $ {v}_{1} $ 向 $ {v}_{2} $ 传播时, 若 $ {v}_{1} $ 的局部信任度大于 $ \gamma $ 则 $ {v}_{2} $ 接受信息, 信息传递成功. 图7–图11展示了在5个网络中每个算法的传播率. 图7可以看出DC跟GTM具有最大的传播率; 图8中发现, GTM相比其他算法的初始传播速度要更快, BC算法尽管传播速度上最慢, 但是在传播范围上最大; 图9观察到GTM的传播速度在最初处于领先位置之后趋于中流水平; 图10中GTM跟DC具有同样的传播率并且都明显优于别的算法, 其中BC的传播率最低; 图11看到GTM在传播的初期具有最快的传播效率, 尽管之后传播速度低于BC和CC, 但在最终的传播范围上都相同. 综上所述, 我们可以发现GTM在5个网络的传播率都有着良好且稳定的效果.

4 总结

用户影响力分析依然是移动社会网络领域中的一个重要研究方向, 不仅涉及网络自身的拓扑性质还与社会属性息息相关. 本文考虑了节点间信任度的影响, 建立全局信任模型计算节点的局部信任度, 并利用Beta信誉模型从局部信任度得到节点的全局信任度, 根据全局信任度大小评估节点在网络中的影响力大小. 本文从局部的角度出发计算节点在本地网络中的信任度大小从而减少了计算开销, 并在局部信任度的基础上考虑了节点在整个网络中的信誉值, 将两者相结合得到节点在网络中的全局信任度大小. 方案既保证了算法的较低时间复杂度也保证了能得到节点在整个网络中的信任度的大小. 本文在真实的网络数据集上对该模型与经典影响力算法进行实验对比, 结果表明, 本文提出的全局信任模型不仅具有更低的时间复杂度, 并且在保证节点高可信度与合理精确度的同时也具有良好的影响传播能力.