对于移动机器人来说, 最重要的是解决如何识别周围的环境情况、如何移动到目标位置、以及如何避开障碍物3个问题. 这些问题的关键都在于如何在环境中实现移动机器人的精确定位^[1], 可以说, 高精度的定位是机器人控制系统中最重要的部分. 因此, 近年来, 移动机器人的定位技术逐渐成为机器人相关领域的研究热点. 尽管在定位技术上已经有很多方面的研究, 但依旧存在着各种挑战与问题.

在实际定位中, 不同的传感器对于位姿和姿态的测量精度各有优劣, 可以利用各传感器的优势估计机器人位姿, 因此, 基于多传感器数据融合的定位方法^[2,3]受到了广大专家学者的青睐. Du等^[4]提出了一种基于仿生极化天窗传感器的多传感器融合SLAM方法, 减少了定位误差和航向角误差. 柯显信等^[5]设计的多传感器定位系统, 由红外定位系统、听觉定位系统和视觉定位系统融合而成, 可适应复杂场景, 提高了机器人的定位精度和可靠性. 但其中的视觉传感器容易受到光照强度的影响. 尹皓等^[6]提出一种基于高斯牛顿方程的多传感器非线性融合定位算法, 该算法非线性融合轮式里程计、惯性测量单元 (inertial measurement unit, IMU) 和激光雷达的测量信息, 从而得到最优位姿估计, 然而却面临算法运算量大, 定位速度慢等问题. He等^[7]以激光传感器为核心设计了多传感器融合定位导航系统, 通过实验验证了系统的可行性和可靠性. Rigatos等^[8]分别利用EKF和PF两种滤波算法融合里程计和声呐的测量数据, 针对实验的传感器融合问题, 表明了粒子滤波具有更好的性能, 而蒙特卡洛定位算法便是基于粒子滤波. 此外, 在静态环境下, 基于地图匹配的定位方法也可以提高机器人的定位精度, 将传感器的扫描信息与先验地图信息做匹配, 得到最相符的匹配结果, 从而提高精度^[9–11].

综上所述, 本文考虑是否已知环境信息以及针对不同传感器定位效果的情况下, 提出了基于里程计、IMU和激光雷达的多传感器融合移动机器人定位方法. 所提出的定位方法具有以下贡献: 1)将定位实现分为是否已知先验环境地图信息进行, 突出了环境对定位的重要性; 2)将EKF融合里程计和IMU的位姿作为AMCL算法粒子集预测的初始位姿, 并辅助粒子更新; 3)利用激光雷达获取的地图环境信息, 弥补了里程计和IMU只适用于短时间, 短距离内位姿估计的缺点.

1 移动机器人定位系统 1.1 机器人运动学模型

对于常用的两轮差速移动机器人, 由于噪声、传感器等因素的影响, 机器人的运动状态难以描述, 通过对机器人建立恰当的运动学模型, 可以更加准确地模拟其运动过程. 本文研究机器人在二维平面内的运动情况, 将传感器坐标系与机器人坐标系合并, 机器人坐标系建立在机器人中心位置并随其移动, 全局坐标系保持固定. 移动机器人的运动学模型如图1所示.

在图1中, X_g–Y_g为全局坐标系, X–Y为机器人坐标系, 用 ${(x, y, \theta )^{\text{T}}}$ ( ${\text{T}}$ 表示矩阵转置)表示移动机器人在全局坐标系下的位姿, 其中 $(x, y)$ 表示机器人的位置信息, $\theta $ 表示机器人的朝向信息(航向角). 假定移动机器人左右两轮的中心距离为 $ 2d $ , 车轮半径为 $r$ , 线速度分别为 $ {V_L} $ 、 $ {V_R} $ , 则可得其运动学方程:

$ \left[ {\begin{array}{*{20}{c}} v \\ \omega \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\dfrac{{{V_L} + {V_R}}}{2}} \\ {\dfrac{{ - {V_L} + {V_R}}}{{2d}}} \end{array}} \right] $

(1)

$ \left[ {\begin{array}{*{20}{c}} {\dot x} \\ {\dot y} \\ {\dot \theta } \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\cos \theta } \\ {\sin \theta } \\ 0 \end{array}}&{\begin{array}{*{20}{c}} 0 \\ 0 \\ 1 \end{array}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} v \\ \omega \end{array}} \right] $

(2)

其中, $v$ , $\omega $ 分别为移动机器人绕其旋转中心的线速度和角速度.

1.2 机器人定位模型

由于最终要求解的是移动机器人在全局坐标系下的位姿数据^[12], 而传感器测量的数据是在机器人坐标系下的数据, 因此定位问题可以看作是机器人坐标系至全局坐标系的转换问题. 机器人坐标系下的任意一点坐标 $({x_a}, {y_a})$ 通过旋转变换矩阵 $ R $ , 平移变换矩阵 $ T $ 可转换至全局坐标系下. 其中, 矩阵 $ R $ , $ T $ 分别为:

$ R = \left[ {\begin{array}{*{20}{c}} {\cos \theta }&{ - \sin \theta }&0 \\ {\sin \theta }&{\cos \theta }&0 \\ 0&0&1 \end{array}} \right] $

(3)

$ T = \left[ {\begin{array}{*{20}{c}} 1&0&x \\ 0&1&y \\ 0&0&1 \end{array}} \right] $

(4)

此外, 在移动机器人定位中, 基于概率的估计方法经常被使用, 常用的概率定位方法有卡尔曼滤波^[13]和粒子滤波^[14], 他们的主要区别是概率分布函数的不同. 机器人的条件概率可表示为:

$ P({x_t}{\text{|}}{u_t}, {x_{t - 1}}) $

(5)

其中, ${x_{t - 1}}$ 表示机器人在 $t - 1$ 时刻的位姿; ${x_t}$ 表示机器人在 $t$ 时刻的位姿; ${u_t}$ 表示 $t$ 时刻的运动控制. 模型表示在 $t - 1$ 时刻, 已得机器人的位姿时, 对其执行 ${u_t}$ 后, 所得到的后验概率分布. 假设 $m$ 为周围环境地图信息, $ {\textit{z}} $ 为观测状态信息, 则可得图2所示的机器人定位模型.

2 传感器定位原理 2.1 里程计定位原理

里程计(odometer)结构简单, 可以在短时间内较精确地测量到移动机器人的位姿. 理论上, 若里程计没有各因素的影响, 仅使用单一里程计就可以实现精确定位. 但在实际情况下, 机器人的轮子难免会发生漂移或打滑等现象, 因此仅使用里程计定位并不准确, 与机器人的真实位姿会有较大的差别.

假设轮子的编码器参数为 $ K $ 线/转, 在 $ \Delta t $ 时间内输出 $ N $ 个脉冲, 则车轮的移动距离 $ \Delta S $ 为:

$ \Delta S = 2\pi r\frac{N}{K} $

(6)

由式(6)可得机器人左轮移动距离 $ \Delta {S_L} $ , 右轮移动距离 $ \Delta {S_R} $ , 则可得:

$ {V_L} = \frac{{\Delta {S_L}}}{{\Delta t}} ,\; {V_R} = \frac{{\Delta {S_R}}}{{\Delta t}} $

(7)

将式(7)代入式(1), 可得移动机器人绕其旋转中心的线速度 $v$ 和角速度 $\omega $ . 此外, 根据几何关系, 移动机器人的移动距离 $ \Delta {S_t} $ , 旋转角度 $ \Delta \theta $ 和旋转半径 $ R $ 可分别表示为:

$ \Delta {S_t} = \frac{{\Delta {S_L} + \Delta {S_R}}}{2} $

(8)

$ \Delta \theta = \frac{{ - \Delta {S_L} + \Delta {S_R}}}{{2d}} $

(9)

$ R{\text{ = }}\frac{v}{\omega }{\text{ = }}\frac{{\Delta {S_t}}}{{\Delta \theta }} $

(10)

假设 $ \Delta t $ 很小, 机器人在 ${t_1}$ 时刻的位姿为 ${({x_1}, {y_1}, {\theta _1})^{\text{T}}}$ , 可得与之时长相差 $ \Delta t $ 的 ${t_2}$ 时刻的位姿 ${({x_2}, {y_2}, {\theta _2})^{\text{T}}}$ 为:

$ \left[ {\begin{array}{*{20}{c}} {{x_2}} \\ {{y_2}} \\ {{\theta _2}} \end{array}} \right]{\text{ = }}\left[ {\begin{array}{*{20}{c}} {{x_1}} \\ {{y_1}} \\ {{\theta _1}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {R(\sin ({\theta _1} + \omega \Delta t) - \sin {\theta _1})} \\ {R(\cos {\theta _1} - \cos ({\theta _1} + \omega \Delta t))} \\ {\omega \Delta t} \end{array}} \right] $

(11)

机器人的轮子不可避免会发生磨损变形, 从而导致轮子半径 $r$ 发生变化, 所以单一里程计定位会出现定位误差, 且误差会随着移动的时间和距离不断累积.

2.2 IMU定位原理

IMU体积小、成本低, 通过加速度计, 陀螺仪和磁力计的测量数据计算得出移动机器人的位姿信息.

机器人的位姿信息可以看作是在空间内经过一系列旋转平移而得到的结果. 假设机器人绕Z轴旋转 $\alpha $ 角度, 绕X轴旋转 $\;\beta $ 角度, 绕Y轴旋转 $\delta $ 角度, 可得变换矩阵分别为:

$ \left\{ {\begin{array}{*{20}{c}} {{C_1} = \left[ {\begin{array}{*{20}{c}} {\cos \alpha }&{\sin \alpha }&0 \\ { - \sin \alpha }&{\cos \alpha }&0 \\ 0&0&1 \end{array}} \right]} \\ {{C_2} = \left[ {\begin{array}{*{20}{c}} 1&0&0 \\ 0&{\cos \beta }&{\sin \beta } \\ 0&{ - \sin \beta }&{\cos \beta } \end{array}} \right]} \\ {{C_3} = \left[ {\begin{array}{*{20}{c}} {\cos \delta }&0&{ - \sin \delta } \\ 0&1&0 \\ {\sin \delta }&0&{\cos \delta } \end{array}} \right]} \end{array} } \right.$

(12)

则机器人坐标系至全局坐标系的变换矩阵 $C_b^n$ 为:

$ C_b^n{\text{ = }}{C_3}{C_2}{C_1} $

(13)

2.3 激光雷达定位原理

结合图2, 对激光雷达测量值建立概率学模型, 可以用条件概率分布来表示其数据观测模型:

$ P({{\textit{z}}_t}{\text{|}}{x_t}, m) $

(14)

其中, ${{\textit{z}}_t}$ 为 $ t $ 时刻的激光雷达观测状态; $ {x_t} $ 为 $ t $ 时刻的机器人位姿; $ m $ 为周围环境地图信息. 由于激光雷达在某个测量时刻会得到一系列的测量值, 因此可得:

$ {{\textit{z}}_t} = \{ {\textit{z}}_t^1, {\textit{z}}_t^2, {\textit{z}}_t^3, \cdots, {\textit{z}}_t^j\} $

(15)

其中, $j$ 为 $ {{\textit{z}}_t} $ 状态测量值的数目. 假设激光雷达得到的每个测量值之间相互独立, 则激光雷达的数据观测模型条件概率分布可表示为:

$ P({{\textit{z}}_t}{\text{|}}{x_t}, m){\text{ = }}\prod\limits_{j = 1}^j {P({\textit{z}}_t^j{\text{|}}{x_t}, m)} $

(16)

3 定位实验和结果分析

移动机器人定位实验基于ROS (robot operating system)系统平台^[15]进行, 分为未知环境定位与已知环境定位. 实验对robot_localization功能包^[16]进行了一定的改进设置, 功能包的每个状态估计节点在收到传感器的测量结果后便会估计机器人状态. 根据机器人实际的传感器模型参数进行配置, 修改了功能包原有的参数配置文件, 保证了与实际机器人的物理模型参数一致.

实验选用定位误差作为定位精度的评价指标, 定位误差指的是机器人的估计位置与真实位置之间的偏差. 假设移动机器人的真实位姿为 ${({x_m}, {y_m}, {\theta _m})^{\rm{T}}}$ , 估算所得位姿为 ${({x_n}, {y_n}, {\theta _n})^{\rm{T}}}$ , 则两者之间的定位误差 $ {d_e} $ , 航向角误差 ${\theta _{{e}}}$ 表达式为:

$ {d_e} = \sqrt {{{({x_m} - {x_n})}^2} + {{({y_m} - {y_n})}^2}} $

(17)

$ {\theta _{{e}}}{\text{ = }}\left| {{\theta _m} - {\theta _n}} \right| $

(18)

3.1 未知环境定位

在未知环境地图的情况下, 首先利用单一里程计对移动机器人进行定位研究, 然后利用EKF算法^[17]融合里程计和IMU进行定位研究. EKF是借助线性滤波理论求解非线性问题的算法, 如图3所示, 算法可以分为两部分, 一是状态预测, 二是观测更新:

$ \left\{ \begin{gathered} {{\bar x}_{k|k - 1}}{\text{ = }}f({{\bar x}_{k - 1}}, {u_{k - 1}}) \hfill \\ {P_{k|k - 1}} = A{P_{k - 1}}{A^{\rm{T}}} + {Q_{k - 1}} \hfill \\ \end{gathered} \right. $

(19)

$ \left\{ \begin{gathered} {K_k} = {P_{k|k - 1}}{H^{\rm{T}}}{(H{P_{k|k - 1}}{H^{\rm{T}}} + {R_k})^{ - 1}} \hfill \\ {{\bar x}_{{{k|k}}}} = {{\bar x}_{k|k - 1}} + {K_k}({Z_k} - h({{\bar x}_{k|k - 1}})) \hfill \\ {P_{{{k|k}}}} = (I - {K_k}H){P_{k|k - 1}} \hfill \\ \end{gathered} \right. $

(20)

其中, 式(19)是状态预测方程, $ {\bar x_{k|k - 1}} $ 为先验估计, $ {P_{k|k - 1}} $ 为先验估计误差协方差矩阵; 式(20)是观测更新方程, $ {K_k} $ 为卡尔曼增益, ${\bar x_{k{{|k}}}}$ 为更新后验估计, ${P_{k{{|k}}}}$ 为更新误差协方差矩阵.

为了验证所提出的定位方法的有效性, 进行了对比实验. 控制机器人沿着既定的路线移动, 比较单一里程计定位轨迹, EKF算法融合里程计、IMU定位轨迹和真实轨迹之间的差异, 如图4所示.

从图4可以看到, 在移动机器人只有单一里程计定位时, 定位轨迹与真实轨迹之间的差距逐渐增大, 存在较大的定位误差, 这会对后续的导航避障工作造成很大的不利影响. 当利用EKF算法融合里程计和IMU定位后, 定位轨迹虽与真实轨迹仍有差距, 但与单一里程计的定位轨迹相比, 与真实轨迹明显相近, 定位误差有所降低. 根据轨迹图可发现每当机器人改变航向角时, 其定位误差会明显增加.

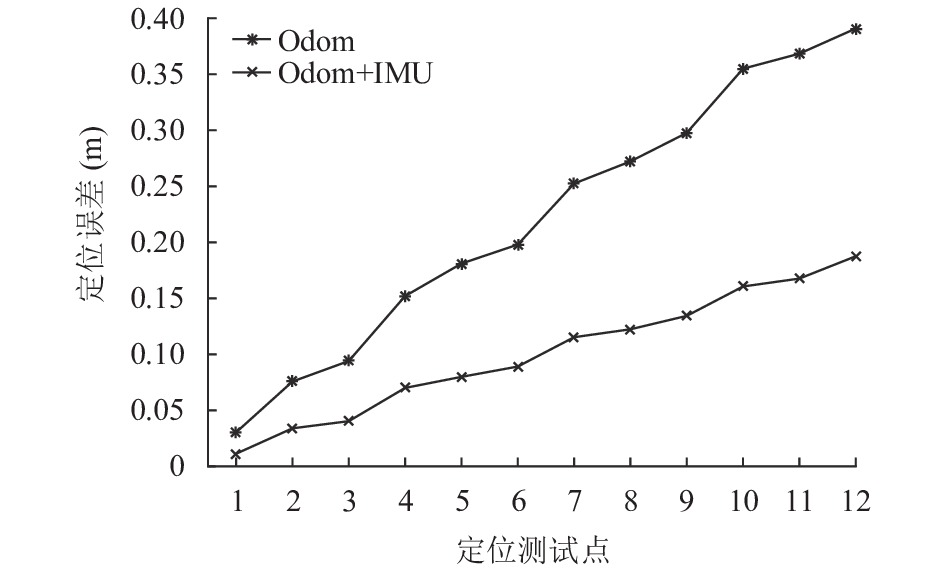
为进一步验证分析未知环境地图下的定位效果, 根据所测得的机器人的位姿数据, 选取12个定位测试点进行对比, 分别记录真实位置与估计位置, 如表1所示. 比较这两种定位方法所估计的位置分别与真实位置之间的误差以分析定位精度, 处理结果如图5所示.

由上述实验结果可知, 移动机器人在未知环境下, 单一里程计定位存在较大的定位误差, 且会随着移动的时间和距离不断累积, 所取定位测试点的定位误差均值为0.22 m左右; EKF算法融合定位后的定位误差均值为0.1 m左右, 相对而言明显降低, 定位精度比单一里程计的精度高, 但误差仍会不断累积, 不能通过先验环境地图信息进行校正.

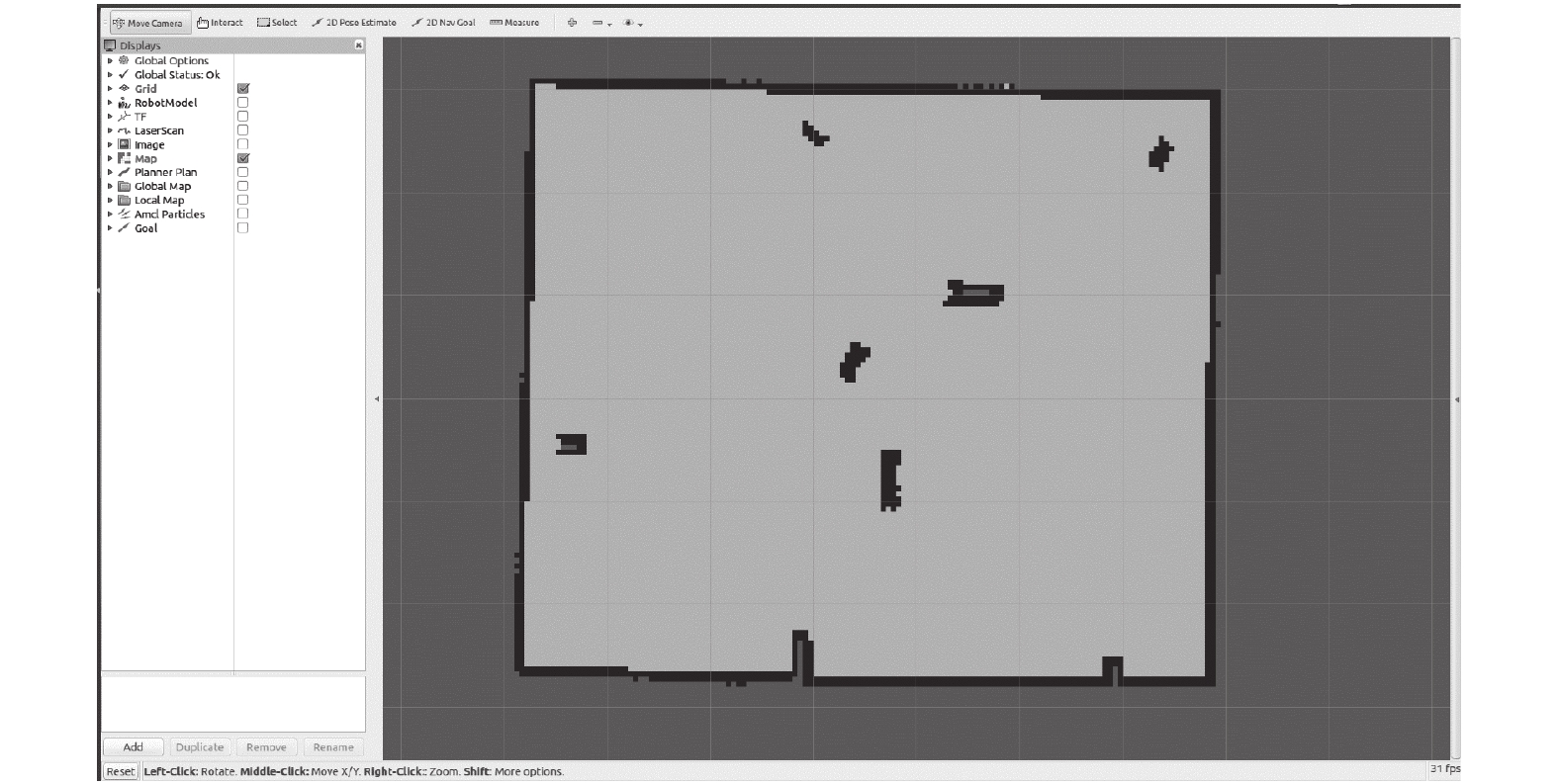
3.2 已知环境定位

实验利用ROS开源社区中SLAM算法Gmapping功能包^[18]构建环境地图, 如图6所示. Gmapping对于小环境地图的构建计算量小且精度高, 所得到的实验环境地图如图7所示.

对于已知环境地图定位, 利用AMCL算法对移动机器人进行定位研究. AMCL算法是一种基于粒子滤波的, 适用于二维环境下移动机器人的概率统计定位方法^[19].

AMCL算法是MCL (Monte Carlo localization)算法的一种改进^[20]. MCL算法在对移动机器人进行定位时, 会将粒子均匀的散布在已知的环境地图上, 表示着机器人此时刻所有可能的位姿信息. 当机器人移动时, 粒子均会随之移动, 但会存在与机器人移动方向不一致的粒子. 然后, MCL算法会逐渐去除这些粒子, 保留与机器人移动方向一致的粒子. 经过这些粒子的收敛, 从而得到机器人所处的实际位置. 然而, MCL算法将粒子去除后, 无法注入新的粒子, 可能会在粒子数量很小的情况下, 丢失正确位置附近的粒子, 这样就无法解决机器人绑架问题. 而AMCL算法解决了这一问题, 该定位算法在机器在面对机器人绑架问题时, 会注入新的粒子. AMCL算法在已知环境地图的情况下, 通过激光雷达对环境的扫描观测信息, 会去除与观测结果不一致的粒子, 同时生成与结果一致的粒子. 最终随着机器人的移动, 粒子收敛至其附近, 从而获得机器人的实际位置.

AMCL算法采用粒子集合来描述机器人所处的所有可能的位置, 且这些粒子带有不同的权重信息. 粒子集合 ${S_{{t}}}$ 可表示为:

$ {S_{{t}}} = \{ x_t^{(i)}, \omega _t^{(i)}\} \;(i = 1, \cdots , N) $

(21)

其中, $ x_t^{(i)} $ 是当前 ${{t}}$ 时刻第 ${{i}}$ 个粒子, $ \omega _t^{(i)} $ 为该粒子的权重, 并且满足归一化条件 $\displaystyle\sum\limits_{{{i = }}1}^{{N}} {\omega _t^{(i)}} {\text{ = }}1$ , ${{N}}$ 为粒子集合中的粒子数量. 算法具体执行以下步骤.

1)预测阶段. 首先, 将粒子散布在已知的环境地图上; 然后, 基于机器人的运动学模型, 根据里程计的定位原理, 结合式(5)对每个粒子的状态进行预测.

2)权值更新阶段. 该阶段需要激光雷达的扫描信息作为输入. 由式(14)–式(16)得到激光雷达的观测数据, 对粒子的权重进行更新, 并进行归一化处理.

3)采样更新阶段. 随着机器人的移动, 权重大小发生改变. 从而去除权重小的粒子, 保留权重大的粒子, 同时产生新的预测粒子避免粒子退化现象. 经过反复迭代, 使得多数粒子收敛至机器人的实际位置, 实现对其定位.

传统的AMCL算法是利用单一的里程计测量模型作为运动模型采样, 但由于里程计容易受到多种因素的影响, 其采样结果与真实值有一定的误差, 导致定位效果较差. 为了改善AMCL的定位效果, 在已知环境地图的定位过程中, 本文的具体的算法流程如图8.

首先在预测阶段, 利用EKF算法融合里程计和IMU的测量信息得到的移动机器人位姿数据作为AMCL算法运动模型的采样源; 然后在权值更新阶段, 充分利用激光雷达扫描的点云信息和先验地图信息, 更新给定粒子权值, 并基于粒子的权重不断迭代估计当前位姿, 最终得到移动机器人在全局环境地图下的最优位姿. 该方法的定位效果如图9、图10所示, 图中的粒子表示机器人此刻可能的位姿状态. 从图10中可以看出随着机器人的运动, 粒子收敛至机器人的实际位置周围, 改进后的AMCL算法可以有效地对机器人定位.

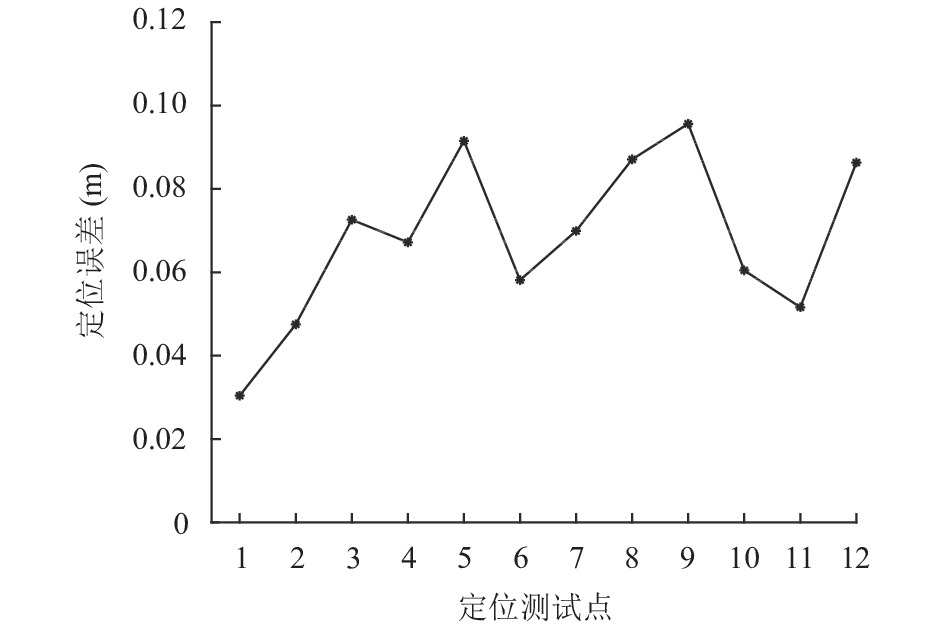
为验证分析已知环境地图下的定位效果, 控制机器人移动并从中选取定位测试点进行对比, 记录所测得的位置数据, 如表2. 比较该方法所估计的位置与真实位置之间的误差以分析定位精度, 处理结果如图11.

由上述实验结果可得, 移动机器人在已知环境下, AMCL算法所得的定位误差均值为0.07 m左右, 相对于未知环境下的两种定位方法的定位误差明显降低. 由于已知先验环境地图信息, 因此该方法的定位误差较小, 校正了未知环境定位下的累积误差, 有效地提高了定位精度.

3.3 定位结果分析

针对移动机器人单一传感器定位精度低与环境地图的重要性问题, 实验分为未知环境定位与已知环境定位两种情况. 对于未知环境下的单一里程计定位、EKF算法融合定位, 环境地图构建以及已知环境下的AMCL算法做出了一定的理论分析与实验研究. 实验结果表明, 未知环境定位会产生明显的累积误差, 与真实位置有较大的差别, 因此不适用于远距离定位; 已知环境定位利用本文方法可以对累积误差进行一定的校正, 相较于未知环境下的单一里程计定位与EKF算法融合定位, 误差均值分别减少了68%、30%, 提高了移动机器人的定位精度, 改善了定位效果, 验证了所提出定位方法的有效性以及环境地图的重要性.

4 结语

本文提出了基于里程计、IMU、激光雷达融合的移动机器人定位方法, 并通过实验加以验证. 相较于未知环境定位, 所提出的方法具有较高的定位精度, 其具有以下特点: 1)多传感器融合定位方法利用了各传感器的优势, 克服了单一传感器定位精度低的问题; 2)通过激光雷达构建环境地图, 校正了未知环境下定位的累积误差.

为了进一步研究所提出的多传感器融合定位方法并提高移动机器人定位的准确性, 后续计划进行以下工作: 1)增加GPS传感器, 以提高机器人的定位精度; 2)增加环境的复杂性, 研究机器人在表面不平整环境中的定位精度.