2. 渤海装备 华油钢管有限公司, 沧州 062658
2. North China Petroleum Steel Pipe Co. Ltd., CNPC Bohai Equipment Manufacturing Co. Ltd., Cangzhou 062658, China
无人机作为一种现代航空设备, 不仅作业速度快, 成本低, 还具有卓越的灵活性和时效性. 常用于完成那些繁冗、危险、对灵活性要求较高、作业范围较大的任务, 比如航空拍摄、农药喷洒、边防检查、电力检测、防汛扛旱等领域[1]. 随着技术的发展, 将无人机独特的优势和不同的行业技术相结合, 可以应用到不同的行业. 比如, 无人机搭载成像传感器, 可以组成一种可以捕获目标图像的新型监视设备[2]. 目前, 许多国家都在积极拓展无人机与工业应用相结合的技术, 因此无人机应用的研究一直备受关注.
稳定的用电需求是当今社会的基础需求, 因此, 输电线路检测在电力行业显得尤为重要. 输电线路检测的主要工作是工人利用眼睛、望远镜以及其他工具和手段观察并检测输电设备, 跟踪设备的运行状况, 发现威胁输电设备和输电安全的缺陷和问题. 输电线路分布很广, 通常跨越高山、海域、平原及交通要道, 且很大部分是露天下的高压或超高压传输, 这使得输电线路的检测更加危险和困难. 据统计, 我国现有总长达68.8万千米的220千伏及以上的输电线路, 相当于绕地球17圈[3]. 目前电力巡检依旧是以传统的人工巡检为主, 人工巡检不仅耗费大量的人力、物力、效率低、作业局限性大、还存在安全隐患. 而无人机凭借其独特的优势和性能, 能使这一问题的解决更加高效、简单和安全, 因此无人机巡检是未来电力巡检的重要方式之一[4].
无人机路径规划是保证无人机作业的关键步骤. 典型的路径规划问题有车辆路径问题(vehicle routing problem, VRP)、带有多车场的车辆路径问题(multi-depot vehicle routing problem, MDVRP)[5]和多旅行推销员问题 (multiple travelling salesman problem, MTSP)[6]. 无人机路径规划问题(unmanned aerial vehicle routing problem, UAVRP)是VRP衍生出来的问题. 相对于地面作业而言, 无人机作业有着以下特点: (1)续航时间有限, 需及时补充能耗; (2)单站点时作业里程受限, 对于大规模问题无法高效解决; (3)负载能力有限且续航时间与负载能力有关[5]. 通常供无人机搭载的图像传感器体积和重量都很小, 所以用于巡检或监视的无人机可以不考虑负载[2]. 在现有无人机路径规划的研究中, 有要求无人机必须离开并返回一个仓库的[1, 7], 有允许无人机在不同仓库起飞和降落的, 但是一次只能服务一个客户的[5]; 有无人机和地面车辆合作才能完成任务的[7, 8]. 而本文考虑的无人机群巡检系统具有以下特点: (1)带有多个站点, 可以有效解决无人机续航受限的问题; (2)无人机群协同作业, 能更快速地完成任务; (3)允许无人机在不同的站点起飞和降落, 可以提高无人机自身的工作效率与工作范围, 结合(1)和(2)可以有效解决覆盖范围较大的任务; (4)同时包含点和线两种类型的巡检任务, 可以用于更复杂的巡检系统, 扩大其应用范围.
本文的目的是提出一种有效的解决方案来应对带有多站点的无人机群巡检系统. Kuhn等人[9]在2020年在自适应大邻域搜索算法(adaptive large neighborhood search, ALNS)的框架下调用了两个变邻域下降搜索(variable neighborhood descent , VND)提出了一种通用ALNS (GALNS)算法, 该算法用于求解具有时间窗和批量订单要求的车辆路径问题, 得到了较好的结果. 因此, 本文结合ALNS和VND提出了一种混合式元启发式算法用于解决本文考虑的无人机群巡检系统. ALNS和VND都是路径规划中比较常用的方法. ALNS是大邻域搜索算法(large neighborhood search, LNS)的扩展, 是一种基于个体解去搜索更好解的局部启发式搜索算法, 通过不同的搜索策略可扩大搜索解空间[10]. VND常用于在相对较短的计算时间内提升当前解的质量, 可以有效地提高算法的收敛时间[11].
1 问题描述本文研究的问题是通过算法找出无人机群在任意站点之间巡检代价最小的飞行路径. 本文以输电线路中的输电线和电力塔杆为巡检对象, 将每个电力塔杆视为一个独立的任务点, 两塔杆之间的输电线缆视为为独立的任务线段. 假设待巡检区域有多个站点可供无人机充电和存放, 并允许每个无人机在任意的站点起飞和降落; 假设供巡检的无人机均为充电式无人机, 单次飞行续航时间有限. 为了保证完整并高效地完成巡检任务, 无人机群路径规划是必不可少的工作.
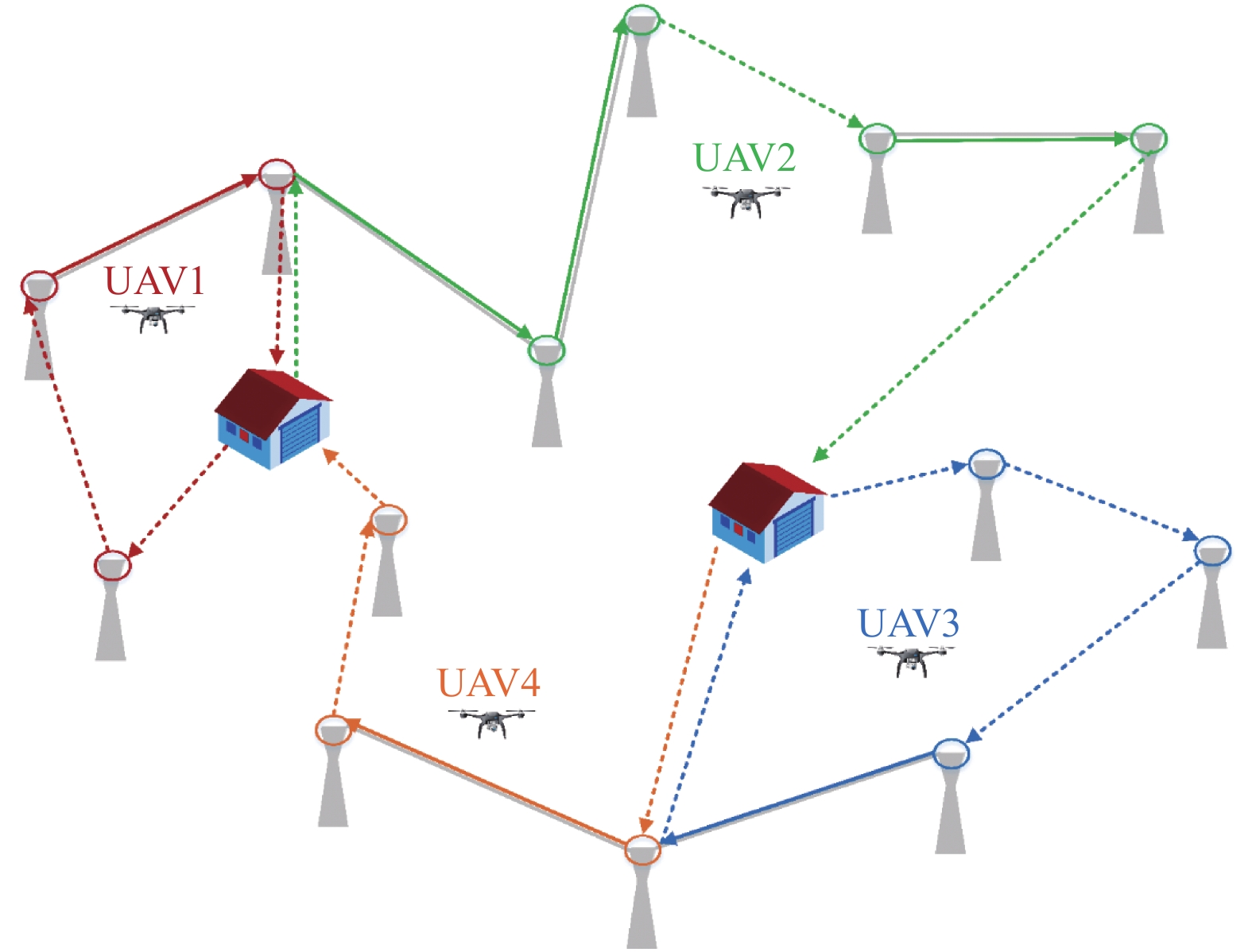
无人机群路径规划要满足以下约束: (1)每个任务服务时间不定, 参与任务的无人机要在最大续航时间到达之前回到站点; (2)规划得到的路线应是从任意站点起飞在任意站点降落的完整路径; (3)任务结束后, 每个仓库原有的无人机数量不变, 保证路径规划方案可周期性使用. 图1给出了无人机群巡检本问题的示意图. 图中的4种颜色代表4个无人机的飞行路线, 实线表示无人机正在巡检目标任务, 虚线表示无人机正飞往下一目标的路途中.
|
图 1 无人机群巡检示意图 |
本文的目标函数是在满足上述约束条件的前提下, 最小化所使用的无人机数量(NV)和总巡检时间(T). 一条从站点起飞后在站点降落的路径定义为一架无人机的飞行路径, 即使用一架无人机; 一架无人机的巡检时间从起飞开始计算直到降落, 所有无人机的巡检时间之和为总巡检时间. 为了区分优化目标的优先级, 我们将无人机的数量设为本问题的主要优化目标, 总巡检时间设为次要优化目标, 目标函数表达式如式(1).
| $ obj=NV+\frac{T}{M} $ | (1) |
其中, M为一个总是大于总飞行时间的数, 即第二项的值总是介于0到1之间, 以此保证优化目标的主次性.
2 算法设计自适应大邻域搜索算法是一种源于大邻域搜索算法的元启发式算法, 能有效地解决路径规划问题[9]. 其与大邻域搜索算法的区别在于加入了自适应机制, 该机制根据破坏算子和修复算子的作用效果, 动态调整权重并选择不同的搜索算子来寻找更好的解. 该方法通过设计多种破坏算子和修复算子, 扩大解空间的搜索范围, 在每次迭代中, 算法会根据过去的效果对各个算子进行权重和选择的调整, 表现好的算子就会得到更高的选择权重, 根据权重选择更有效的算子组合方法来提高算法本身的寻找最优解的能力. 相比同类算法, 如模拟退火算法, 只调用了一种邻域, 其解空间的搜索范围很小, 很容易陷入局部最优, 而大邻域搜索算法具有多种搜索算子, 就能有效地避免陷入局部最优.
变邻域下降是一种强化版的局部改进策略, 近年来该算法已经被成功用于求解不同的组合优化问题, 具有算法结构简单、鲁棒性强、计算效率高、易于实现等优点, 在变邻域搜索和其他元启发式方法中常作为下属策略[9].
本文将变邻域下降作为自适应大邻域搜索算法的下属策略, 提出一种新的元启发式算法来解决本问题. 本算法设计了4种破坏算子和4种修复算子用于扩大解空间. 在变邻域下降中, 本文采用了5种局部搜索方法增强局部改进, 提高算法的收敛性. 此外, 在每次迭代中, 本文采用模拟退火原则来保留进化过程中解的多样性[11].
2.1 个体表示与初始解本问题由n+m个任务和d个无人机站点组成, 其中n表示电力塔杆数量, m表示输电线段数量, 每个任务必须检查一次且只能检查一次. 本文采用二维序列编码方法来表示一个个体, 个体由多条路径组成, 每条路径中存放一架无人机完整的飞行序列, 该序列的首尾表示无人机的起降站点, 中间代表该无人机需要访问的任务序列.
本文的初始个体是随机生成的. 个体由若干飞行路径组成, 所以每条路径必须保证无人机有足够的电量安全降落, 并满足前述无人机群路径规划的所有约束. 初始解的生成可分为以下步骤: (1)对于个体中的第一条路径, 随机选择两个站点作为起飞点和降落点, 再随机选择任务插入到两个站点中间; (2)下一条飞行路径的降落点随机选择, 起飞点为上一条路的降落点, 同样随机选择剩余的任务插入到起飞点和降落点之间; (3)重复步骤(2), 直到所有的任务被访问完毕; (4)判断每个站点的无人机数量是否保持不变, 如果不是则需要进行调整, 即为了满足此约束可能会出现无人机从这个站点起飞不执行任务, 直接降落到另一个站点的空飞路径. 存在空飞路径的解也是一种可行解, 所以我们是允许它存在的.
2.2 破坏算子破坏算子通过删除任务序列的方法来破坏一个解的完整性, 删除任务序列的方法不同, 构成的破坏算子不同. 本算法设计了4种破坏算子, 其描述如下:
(1)随机破坏: 随机破坏是此类算法中一种常见的破坏算子, 它是从个体中随机的删除β个任务.
(2)聚类破坏: 该方法是Sacramento等人[7]提出的一种聚类删除方法. 具体操作是随机选择一个任务点, 以该点为中心删除一定范围内的所有任务.
(3)删除最差的任务: 该方法是去除耗费成本最多的一个任务, 由Li等人[12]提出的. 在本文中, 是去除每条路径中耗费时间成本最大的一个任务, 因为时间和距离成正比, 所以我们定义最差的任务是在该条路径上到前一个节点和下一个节点的旅行距离之和最大, 即无人机为了访问该任务, 飞行的距离更长. 例如, 现有一条路径为R1<…,i , j, k , …>,dij是无人机从任务j到前一任务i之间的飞行距离, djk是无人机从任务j到下一任务k之间的飞行距离, dij与djk的和是该路径中最大的, 则任务j作为最差的任务被删除.
(4)删除效率最差的路径: 将个体内具有效率比最低的路径删除. 效率比α的计算方法如式(2). 例如, 个体中有一条路径R1, 无人机完整飞行完该路径的时间是T(R1), 除去无人机在飞往目标任务路上的飞行时间外, 纯用于巡检任务的时间为p(R1), 则效率比α为:
| $ \alpha =\frac{p\left({R}_{1}\right)}{T\left({R}_{1}\right)} $ | (2) |
修复算子是专门修复被破坏算子破坏后的解, 通过不同修复方法, 将被破坏算子删除的任务重新插入到个体中, 通过这样的方式来生成一个新的解. 本文采用了4种修复算子, 其描述如下.
(1)随机插入: 该方法是将被删除的任务随机插入到被破坏的解中, 可以增加搜索解空间的多样性.
(2)最佳插入: 该操作将待插入的任务插入到最佳位置, 即在该位置插入后增加的飞行时间最小.
(3)次优插入: 这种修复方法的工作方式与最佳插入相似. 但是, 并不总是选择最佳位置插入, 而是随机选择一个相对于插入之前成本不超过10%的位置插入. 这种方法和随机插入方法一样, 在搜索时能表现出更优的多样性, 增加找到最优解的可能性[7].
(4)插入效率最差的路径: 对于每个待插入的任务, 选择如式(2)所示效率比最差的一条路, 插入该路径中的最佳位置. 重复该过程, 直到所有的任务都包含在新的解决方案中.
2.4 可行性修复个体在不断进化过程中得到的新解, 并不一定总是满足约束的, 所以我们需要判断新得到的解的可行性, 如果是一个不可行的解, 则需要进行可行性修复. 可行解修复是在不改变当前任务序列的情况下, 将不可行解转化为可行解. 其修复算法如算法1所示, 其中第一步是从不可行解中提取一个完整的任务序; 第2)–4)步是生成第一条路径; 第5)步是生成第二条及以后的飞行路径; 第6)步是使其满足问题描述中的约束(3).
算法1. 可行性修复算法
输入: 一个不可行解X
输出: 可行解S
1)移除不可行解中包含的所有站点, 形成一个完整的任务序列.
2)选择距离任务序列中第一个任务和最后一个任务最近的一个站点, 作为第一条路的起点.
3)对于待分配任务序列<i, j, k, …>, 判断是否分配任务i. 假设距离i, j最近的站点为h, 计算无人机的剩余时间是否足够执行完任务i后回到站点h; 如果足够则分配任务i到当前路径, 继续判断下一个任务j; 否则直接返回最近的站点.
4)将新生成的完整路径加入S.
5)下一条路的起飞点为上一条路的降落点; 重复步骤3)和4)直到所有的任务配分配完.
6)调整每个站点的无人机数使之与任务开始前的数量保持一致.
7)返回可行解S.
2.5 变邻域下降本文在变邻域下降中采用了五种邻域搜索结构, 在调用变邻域下降的过程中, 仍然需要判断解的可行性, 如果是不可行解也要进行可行性分割. 变邻域下降算法伪代码如算法2所示. 5种邻域结构简单解释如下.
2-opt: 该方法是反转一段任务序列后该路径会变得更优, 是一种著名的可解开交叉的邻域搜索结构; 在本文中每一条飞行路径都有一段任务序列, 遍历个体中的每条路径, 如果反转i和j之间的任务序列后路径会变得更优, 则接受反转.
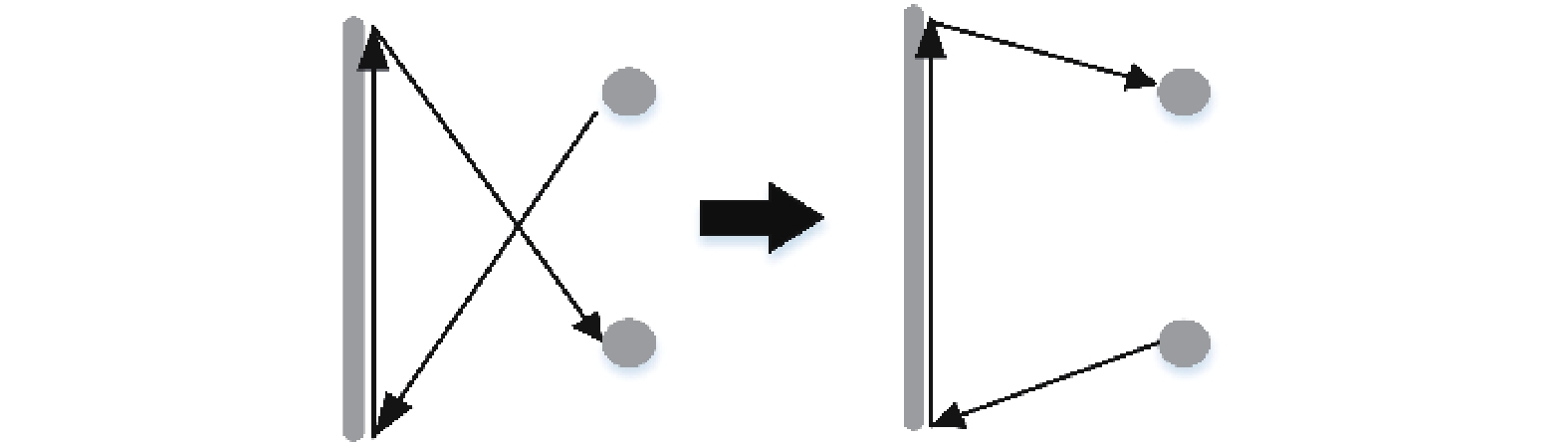
颠倒线段走向: 本结构是专门针对本文题中的任务线段的, 线段的访问方向与飞行距离直接相关, 所以颠倒线段的访问方向可能会节省更多的成本. 具体操作如图2所示.
|
图 2 颠倒线段走向 |
Swap: 通过删除最差的任务方法分别从两条路径中选出最差的任务两个任务, 交叉插入最佳位置.
算法2. 变邻域下降主要伪代码
输入: 可行解X
输出: 局部增强后的可行解X'
Begin
k←1
While k ≤ kmax do
X' ← 第k个邻域结构(X)
if X'是不可行解 then
X' ←可行性修复(X)
if f(X')<f(X) then
X←X'
k←1
else k←k+1
end while
返回X'
end
Exchange: 遍历每条路径, 交换其中两个任务的位置.
Migration: 在两条路径中, 将其中一条路的一个任务, 在可行的情况下转移至另一条路, 即转移之后, 该条路径的飞行时间仍然满足最大飞行时间约束.
2.6 完整算法描述本算法主要步骤描述如下: (1)生成初始解. (2)更据各个破坏算子和修复算子的权重, 轮盘赌选择出一组破坏算子和修复算子对当前解进行改进得到新解; 判断新解的可行性, 如果修复后得到的新解是不可行解, 则需要进行可行性分割, 保证新解是一个满足约束的可行解. (3)变邻域下降增强局部改进. (4)更新当前最优解, 如果当前解优于最优解, 则无条件更新, 如果当前解不是最优解, 则根据模拟退火准则接受. (5)重复(2)–(4)直到满足算法终止条件. 对应的伪代码如算法3所示.
算法3. 完整算法主要伪代码
输入: 相关任务信息及参数
输出: 最优解
Begin
生成初始解S
记录局部最优pbest←S, 全局最优gbest←S
While 终止条件为满足 do
X← pbest
轮盘赌选择一种破坏算子Destroy( )和一种修复算子Repair( );得到新的解X'← Repair(Destroy(X))
if X'是不可行解 then
X' ←可行性修复X
X'← 变邻域下降(X')
if f(X')<f(gbest) then
gbest ← X'
pbest ← X'
else if f(X')<f(gbest) then
pbest ← X'
else 模拟退火准则更新pbest
end while
返回最优解gbest
end
3 实验验证我们对所设计的算法进行了实验验证, 所有的实验都采用C++语言编写, 在Microsoft Visual Studio 2019上编译, 所用到的计算机参数为Intel (R) Core (TM) i7-8700 CPU 3.20 GHz, 16.0 GB的RAM, 64位的Windows 10操作系统. 由于本文解决的是一种同时包含点和线的问题, 没有现存的测试数据, 但是本问题又是从经典的MDVRP拓展过来的, 所以本文的测试数据是根据Cordeau在VRP bench mark中给出的Multiple Depot VRP测试实例[13]的基础上修改得到的. 因为Cordeau给出的数据中只包含了客户的坐标信息, 该信息可对应于本文题中的任务点的信息, 我们随机连接两点间的直线作为任务线段信息, 只要求其互不交叉, 修改后的数据信息可在
根据常用电力巡检无人机的参数, 我们设置无人机匀速飞行, 速度为1 500单位每分钟, 最大飞行时间为90分钟, 在每个任务点的执行任务时间为2分钟, 对每个任务线段的巡检时间取决于线段的长短. 所测试的数据中, 相邻两点间的距离放大了50倍, 其他点的距离按照同样的比例缩放. 本算法中随机剔除数量β为总任务数量的0.3倍, 即β= 0.3×(n+m); 对于任务点数量在100及以下的M设为999, 其他的M为9 999; 由于本算法是在一次次迭代中寻找更优解, 随着迭代次数的增加, 找到最优解的可能性越大, 本算法设置的最大迭代次数为1 000次. 此外本文在实验时, 还设计了离散的粒子群算法(PSO)和标准文化基因算法(MA)两个对比算法, 两个算法的种群大小为200, 交叉概率为0.95, 变异概率为0.2.
3.2 实验结果我们根据数据集对该算法进行了测试, 实验结果如表1所示. 表中Instance表示被测数据的名称; n、m和d分别表示任务点的数量、任务线段的数量和站点的数量; AVG、BEST、SD分别表示每个数据运行10次后得到的平均值, 最佳值和标准差; NV和T为该数据的最佳值对应的无人机数量和总飞行时间. 从表1我们可以看出, 对于表中不同规模的问题而言, 本算法都能找到有效解, 这表明本算法能够求解大规模问题; 此外, 随着问题规模的增加, 算法的标准差依旧很稳定, 这表明了本算法具有很强的稳定性和鲁棒性.
| 表 1 实验结果 |
为了进一步验证本文所设计的算法解决问题的能力, 我们将所设计的算法与离散的PSO和标准的MA算法进行了对比, 其中离散的PSO和MA都是路径规划相关文献中常用的算法. 在离散的PSO中只采用了交叉和变异两种邻域, 本文中的交叉方法是常见的Recombine, 变异方法是采用的变邻域下降里面的Swap操作. MA中采用同样的Recombine和Swap作为交叉和变异, 邻域搜索结构用的变邻域下降中的2-opt. 因为3种算法的执行框架是不同的, 为了保证对比结果的有效性, 我们将这3个算法放在同样的搜索时间内去测试, 即判断在同样的时间内哪个算法找到的解更优. 我们设置的搜索时间为10分钟, 同样每个案例测10次, 得到的数据如表2所示.
| 表 2 对比实验结果 |
表2中加粗的字体为3个算法在同样的寻优时间内找到的最佳结果, 从上可看出, 在同等时间内, 本文所设计的算法均得到了更好的结果, 这表明本文设计的算法比离散的PSO和MA能更好地节省巡检中使用的无人机数量成本和时间成本. 进一步分析3个算法的标准差可看出, 在解决此问题时, 本文的算法比其他两种算法具有更好的鲁棒性和稳定性, 并且随着问题规模的增加, 算法依然具有较好的稳定性.
上述实验结果表明, 本算法能有效地解决该问题, 能够应用于大规模问题的求解; 并且随着问题规模的增加, 本算法依旧具有较好的稳定性和鲁棒性. 此外, 相比离散的PSO和标准的MA来说, 本算法具有更强的寻优能力和稳定性, 能够找到更优的解.
4 结论与展望本文考虑了一种带有多个站点的无人机群巡检系统, 该系统中同时包含任务点和任务线两种巡检任务. 本文在ALNS算法的框架下加入VND为下属策略, 提出了一种新的混合式元启发式算法来解决该问题中的无人机群路径规划问题. 实验结果表明该算法成功地解决了无人机群在巡检过程中的路径规划问题, 表明了算法的有效性. 此外我们还同优化算法中常见的离散PSO和标准的MA算法进行了对比实验, 实验结果表明本算法具有更好的寻优能力, 并且随着问题规模的增加, 本算法依旧具有较好的稳定性和鲁棒性. 这表明了本算法能高效地解决该问题. 接下来, 我们将尝试解决环境更复杂、规模更大的巡检系统中的问题.
| [1] |
Xu C, Xu M, Yin CJ. Optimized multi-UAV cooperative path planning under the complex confrontation environment. Computer Communications, 2020, 162: 196-203. DOI:10.1016/j.comcom.2020.04.050 |
| [2] |
Zhen L, Li M, Laporte G, et al. A vehicle routing problem arising in unmanned aerial monitoring. Computers & Operations Research, 2019, 105: 1–11.
|
| [3] |
张志鹏. 面向电力杆塔的无人机自主巡检系统设计与实现[硕士学位论文]. 成都: 电子科技大学, 2020.
|
| [4] |
王建沣, 王春百, 李卫华. 无人机输电线路巡检技术研究. 科技视界, 2021(8): 174-175. |
| [5] |
Song BD, Park K, Kim J. Persistent UAV delivery logistics: MILP formulation and efficient heuristic. Computers & Industrial Engineering, 2018, 120: 418-428. |
| [6] |
Chen YB, Jia ZY, Ai XL, et al. A modified two-part wolf pack search algorithm for the multiple traveling salesmen problem. Applied Soft Computing, 2017, 61: 714-725. DOI:10.1016/j.asoc.2017.08.041 |
| [7] |
Sacramento D, Pisinger D, Ropke S. An adaptive large neighborhood search metaheuristic for the vehicle routing problem with drones. Transportation Research Part C: Emerging Technologies, 2019, 102: 289-315. DOI:10.1016/j.trc.2019.02.018 |
| [8] |
Ding YL, Xin B, Chen J, et al. Path planning of messenger UAV in air-ground coordination. IFAC-PapersOnLine, 2017, 50(1): 8045-8051. DOI:10.1016/j.ifacol.2017.08.1230 |
| [9] |
Kuhn H, Schubert D, Holzapfel A. Integrated order batching and vehicle routing operations in grocery retail—A General Adaptive Large Neighborhood Search algorithm. European Journal of Operational Research, 2021, 294(3): 1003-1021. DOI:10.1016/j.ejor.2020.03.075 |
| [10] |
Shaw P. Using constraint programming and local search methods to solve vehicle routing problems. Proceedings of the 4th International Conference on Principles and Practice of Constraint Programming. Pisa: Springer, 1998. 417–431.
|
| [11] |
Goksal FP, Karaoglan I, Altiparmak F. A hybrid discrete particle swarm optimization for vehicle routing problem with simultaneous pickup and delivery. Computers Industrial Engineering, 2013, 65(1): 39-53. |
| [12] |
Li HQ, Wang HT, Chen J, et al. Two-echelon vehicle routing problem with time windows and mobile satellites. Transportation Research Part B: Methodological, 2020, 138: 179-201. DOI:10.1016/j.trb.2020.05.010 |
| [13] |
Multiple Depot VRP Instances. https://neo.lcc.uma.es/vrp/vrp-instances/multiple-depot-vrp-instance.
|
 2022, Vol. 31
2022, Vol. 31



