子群发现是一种数据挖掘技术, 它基于给定目标特征, 挖掘不同特征间的有趣关联^[1]. 提取的模式通常用规则表示, 规则定义为:

$ R:Cond \to Targe{t_{\rm{value}}} $

(1)

$Cond$ 是由一组属性键值对组成, 称为规则前件; $Targe{t_{\rm{value}}}$ 是目标特征值, 称为规则后件.

尽管子群发现算法在过去得到了足够的发展, 但仍存在一些不足. 传统子群发现算法通常是将连续型数值数据直接离散化, 导致了精度损失和次优结果; 并且是基于局部模式挖掘, 导致模式集缺乏多样性^[2]. 对于这些问题, Millot等人^[3]提出OSMIND (optimal subgroup discovery in purely numerical data)算法, 利用闭合间隔模式避免连续型数值数据离散化, 但是忽略了模式集挖掘. Bosc等人^[4]提出MCTS4DM (Monte Carlo tree search for pattern mining)算法, 在使用闭合间隔模式的基础上, 增加相似性度量函数, 对MCTS (Monte Carlo tree search)输出的候选模式集进行后处理, 从而获得多样性的模式集, 但是需要消耗大量内存来存储候选模式集. Belfodil等人^[5]提出FSSD算法, 使用闭合间隔模式和子群集质量度量函数, 后者用来评估模式集的多样性, 同时在每次迭代过程中只存储最优模式, 避免了消耗大量内存. 但是FSSD算法为了减少运行时间, 选择特征域数量少的特征子集, 此特征选择方法没有考虑数据集中的监督信息, 属于无监督特征选择, 当选择的特征子集与目标类不相关或弱相关时, 模式集质量下降, 因此研究如何选择FSSD算法的特征子集具有重要意义.

特征选择是根据某些特征选择标准从原始特征集中获取特征子集的过程^[6]. 现有特征选择主要用在分类、聚类上, 用在子群发现上的研究较少. 在子群发现上的特征选择只找到文献[7], 它提出基于相关性约束的过滤式特征选择, 将特征-值对的覆盖关系作为相关性约束, 当特征的所有特征-值对满足相关性约束时, 才被定义为不相关并且去除, 在最坏的情况下, 每个特征都存在一个特征-值对不满足相关性约束, 此时无法去除任何特征, 同时单一的特征选择方法生成的特征子集缺少多样性和稳定性^[8].

分类、聚类特征选择与子群发现特征选择的原则有些不同: (1) 前者是将类和类区分开, 后者是将目标类和非目标类区分开, 在多类情况下, 两者差别比较明显; (2) 前者需要去除不相关和冗余特征, 而后者只去除不相关特征, 不去除冗余特征, 这点在医学领域尤其明显, 在文献[9]中, 使用子群发现挖掘初次使用合成阿片类药物后, 出现不良后果的患者特征, 挖掘结果认为有慢性疼痛病史的患者, 会增加药物上瘾风险, 与合成阿片类药物处方指南相吻合. 由于慢性病与疼痛病存在强相关, 如果考虑去除冗余特征, 子群发现挖掘结果会变成有慢性病史或者疼痛病史的患者, 会增加药物上瘾风险.

为了解决FSSD算法的特征子集选择问题, 本文引入基于ReliefF和方差分析的集成特征选择算法, 获得具有多样性、稳定性以及与目标类相关性强的特征子集. 第2节介绍FSSD算法, 第3节介绍改进的FSSD算法, 第4节对改进的FSSD算法进行实验并且对实验结果做分析, 第5节对所做的工作进行总结和未来进一步的研究方向.

1 FSSD算法简介

FSSD算法旨在使用少量内存和短时间内提供多样性的模式集^[5]. FSSD是基于穷举搜索的子群发现算法, 穷举搜索的运行时间与模式数量成正比, 当搜索空间很大时, 运行时间变长, 所以在文献[5]中, 先选择特征子集, 再使用FSSD算法来提取模式集.

1.1 特征子集选择

在运行FSSD算法前, 数据集的特征先按照名义型、数值型排序, 再按照特征域数量从小到大排序, 然后根据用户给定的特征子集数量选择特征子集, 此特征选择方法是为了尽可能选择特征域数量少的特征子集, 随着特征子集的域数量减少, 模式数量就减少, 运行时间就缩短. 然而此方法忽视了数据集中的监督信息, 没有考虑特征与目标类的相关性, 特征与目标类的相关性就完全取决于数据集分布情况, 当特征子集与目标类相关性不佳时, 模式集质量下降, 当特征子集与目标类相关性强时, 模式集质量上升, 模式集质量随着特征子集与目标类的相关性而变化, 让模式集质量充满不确定性.

1.2 FSSD算法

在FSSD算法中, 子群 $ s $ 是子群集合 $\mathbb{S}{{ = ext }}\left[ {{D}} \right]{{ = }} $ $ \left\{ {{{ext}}({{d}}){{| d}} \in {{D}}} \right\}$ 的任何子集, 模式 $ {{d}} \in D $ 提供了对子群的描述. 模式结构是三元组(G, (D, $\sqsubseteq $ ), $\delta $ )形式, G是样本集, $D$ 是模式集, $\sqsubseteq $ 是偏序关系, 模式集 $D$ 的模式通过偏序关系 $\sqsubseteq $ 从最普通限制到最严格限制进行排序, 即 $c \sqsubseteq d $ $ \Leftrightarrow $ $ {{ext}}(d) \subseteq {{ext}}(c)$ , 表示模式d覆盖的子群是模式c覆盖的子群的子集. $\delta $ 将样本映射到最严格模式上, 例如: $\delta (g)$ 是样本g的最严格模式, 称为闭合间隔模式, 只要修改模式 $\delta (g)$ , 至少会丢弃一个样本. 与模式结构相关的两个映射: (1) $ext{{:D}} \to \wp (G)$ , $ext(d) = \{ g \in $ $ G|\forall d \in D, d\sqsubseteq \delta (g)\} $ , $\wp (G)$ 是样本集G的幂集, $ ext(d) $ 表示模式 $d$ 覆盖的子群; (2) $int:\wp (G) \to D$ , $int(E) = $ $ {\prod _{{{g}} \in {\rm{E}}}}\delta (g)$ , 其中 ${{E}} \subseteq G$ , $int(E)$ 表示覆盖样本子集E的闭合间隔模式.

给定子群 $ s $ 和子群集 $S \subseteq \mathbb{S}$ , 计算子群 $ s $ 给 $S$ 带来的质量增益可以表示为:

$ WRAc{c_S}(s) = \alpha \cdot (1 - \alpha ) \cdot [{{TPR}}(s, {G_S}, G) - {{FPR}}(s, {G_S}, G)] $

(2)

$ TPR(s, {G_S}, G) = tpr({G_S}, G) \cdot tpr(s, {G_S}) $

(3)

$ {{FPR}}(s, {G_S}, G) = fpr({G_S}, G) \cdot fpr(s, {G_S}) $

(4)

$ {{tp}}r(s, {G_X}) = \frac{{|s \cap {G^ + } \cap {G_X}|}}{{|{G^ + } \cap {G_X}|}} $

(5)

$ {{fp}}r(s, {G_X}) = \frac{{|s \cap {G^ - } \cap {G_X}|}}{{|{G^ - } \cap {G_X}|}} $

(6)

$ \alpha = {{\left| {{{{G}}^ + }} \right|} \mathord{\left/ {\vphantom {{\left| {{{{G}}^ + }} \right|} {\left| {{G}} \right|}}} \right. } {\left| {{G}} \right|}} $ 是正样本比例, $ {{{G}}_S} = {{G}}\backslash \cup S $ 是未被子群集 $ {{S}} $ 覆盖的样本集, $TPR(s, {{{G}}_S}, {{G}})$ 和 $FPR(s, {{{G}}_S}, {{G}})$ 分别表示在 $ {{G}} $ 中未覆盖样本 ${{{G}}_S}$ 的子群 $ s $ 的真阳性率和假阳性率. $ {{{G}}^ + }, {{{G}}^ - } $ 分别表示样本集 $ {{G}} $ 中的正、负样本, $ {G_X} $ 是样本集 $ {{G}} $ 中的非空子集, $ tpr(s, {G_X}) $ 和 $ fpr(s, {G_X}) $ 分别表示在 $ {G_X} $ 中子群 $ s $ 的真阳性率和假阳性率.

与式(2)对应的严格乐观估计:

$ {{WRA}}cc_S^{oe}({{s}}) = {{\alpha}} \cdot (1 - {{\alpha}} )[TPR(s, {G_S}, G)] $

(7)

FSSD算法框架如算法1.

算法1. FSSD $\scriptstyle (G, {{{A}}_n}, k)$

输入: 数据集 $\scriptstyle ({{G}}, {{{A}}_n})$ , 子群数量 $\scriptstyle {{k}}$

输出: 子群集 $\scriptstyle {{S}}$

1) $\scriptstyle {{S}} = \phi$ , $\scriptstyle {{{G}}_S} = {{G}}$ // $\scriptstyle {{{G}}_S}$ 是当前样本集

2) while $\scriptstyle {{|S| \lt k}}$

3) 在模式结构( $\scriptstyle {{{G}}_S}$ , (D, $\sqsubseteq $ ), $\scriptstyle \delta$ )中寻找子群 $\scriptstyle {s^*}$ 使得增益最大WRA $\scriptstyle {{c}}{{{c}}_S}(ext(int({s^*})))$

4) if $\scriptstyle {{WRAc}}{{{c}}_S}(ext(int({s^*}))) \leqslant 0$ then break

5) $\scriptstyle {{S}} = {{S}} \cup \{ ext(int({s^*}))\} ,\; {G_S} = {G_S}\backslash {s^*}$

6) end while

对于算法1, 在第1)行中初始化子群集 $ {{S}} $ 为空和当前样本集 ${{{G}}_S}$ 为 $ {{G}} $ ; 第2)行和第4)行是控制迭代次数, 当 $ |S| = k $ 或者最大增益小于0时, 算法终止并返回子群集 $ S $ ; 在每次迭代过程中, 第3)行是在未覆盖样本集 ${{{G}}_S}$ 的模式结构( ${{{G}}_S}$ , (D, $\sqsubseteq $ ), $\delta $ )中选择最大化增益 $WRA $ $ c{c_S}({{ext}}({{int}}({{{s}}^*})))$ 的子群 $ {s^*} $ , 由于 ${s^*} \subseteq {G_S}$ 但不一定 ${s^*} \in \mathbb{S}$ , 所以通过映射关系使得 ${{ext}}({{int}}({{s^*}})) \in \mathbb{S}$ , 在寻找子群 $ {s^*} $ 过程中, 使用严格乐观估计式(7)进行剪枝, 从而缩小搜索空间; 在第5)行中更新子群集 $ {{S}} $ 和当前样本集 ${{{G}}_S}$ , ${{ext}}({{int}}({{s^*}}))$ 添加到子群集 $ {{S}} $ 并且将 $ {s^*} $ 从当前样本集 ${{{G}}_S}$ 中去除.

2 基于集成特征选择的FSSD算法

当FSSD算法的特征子集与目标类相关性不强时, 模式集质量下降, 而单一特征选择方法获得的特征子集缺乏多样性和稳定性. 为此, 本文提出基于集成特征选择的FSSD算法, 简称FSSD++算法. FSSD++算法通过集成ReliefF和方差分析方法获得多样性、稳定性以及与目标类相关性强的特征子集, 再使用FSSD算法返回高质量子群集. 在设计集成特征选择时, 需要确定以下几个方面: (1)集成方法; (2)确定特征选择器的返回形式和使用的特征选择器; (3)组合方式.

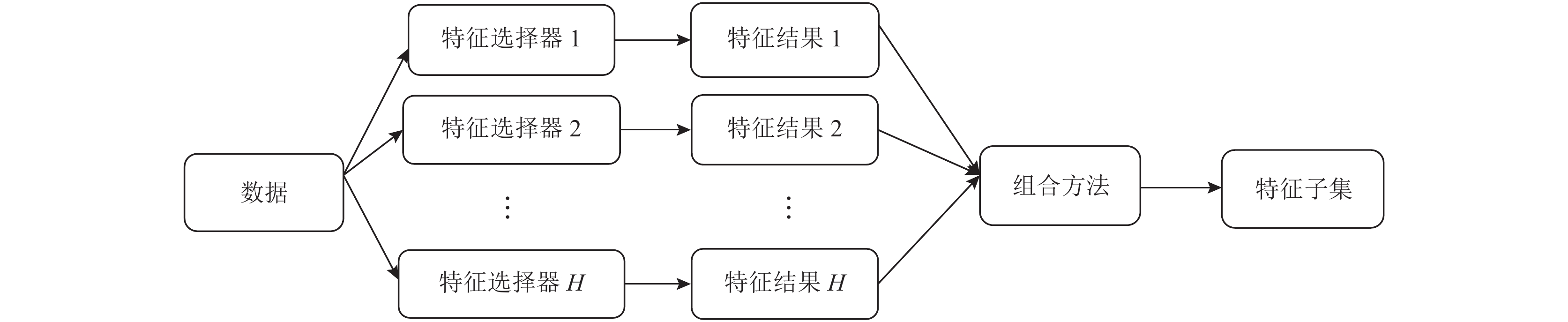
2.1 集成方法

集成特征选择的集成方法主要有两种: 同构集成和异构集成, 如果使用相同的基本特征选择器, 称为同构集成, 否则称为异构集成. 在同构集成特征选择中, 使用相同的特征选择器和不同的数据子集, 可以使用自举法抽样得到数据子集; 在异构集成特征选择中, 使用不同的特征选择器和相同的数据, 如图1所示. 前者用于大规模数据集, 通过在并行节点中处理数据来缩短计算时间; 后者确保稳定、鲁棒的特征选择^[10], 由于本文的实验数据集规模不大, 所以采用异构集成方法.

2.2 特征选择器

特征选择器的返回形式分为特征子集和特征排名, 特征子集是先根据预先定义的搜索策略生成特征子集, 再使用最优原则对特征子集进行评估, 最终获得局部最优特征子集; 特征排名是根据特征相关性或者重要性返回所有特征排名, 再使用阈值确定最终特征子集^[10]. 返回特征子集的特征选择器需要搜索所有特征子集, 计算量大, 为了避免此问题, 本文选择返回特征排名的特征选择器. 此外, 为了缩短运行时间和有效利用监督信息, 所选的特征选择器还应该是基于过滤式和监督的特征选择器.

本文选择ReliefF^[6]和方差分析^[11]作为基本特征选择器, 它们既是返回特征排名, 又是基于过滤式、监督的特征选择器. 同时它们都是单独评估每个特征与目标类的相关性, 并且不去除冗余特征^{[6, 11]}, 这与子群发现特征选择原则相符合. 下面具体介绍ReliefF和方差分析.

ReliefF是根据特征区分不同类别样本的程度, 对特征进行加权, 它为每个特征分配一个相关权重来表示特征与目标类的相关性. 假设在n个样本中随机选择 $l$ 个样本, 每个特征 ${f_i}$ 的计算公式:

$ {Re} liefF\_score({f_i}) = \frac{1}{l}\sum\limits_{j = 1}^l {W(j, i)} $

(8)

$ {{W}}(j, i) = - {d_i}(H({x_j}, {y_j}), {x_j}) + \sum\limits_{y \ne {y_j}} {\left[\dfrac{{p(y)}}{{1 - p(y_j)}}{d_i}(H({x_j}, y), {x_j})\right]} $

(9)

$ {d_i}(H({x_j}, {y_j}), {x_j}) = \dfrac{1}{{{{|H}}({x_j}, {y_j}){{|}}}}\sum\limits_{r = 1}^{{{|H}}({x_j}, {y_j}){{|}}} {{{|}}{{{x}}_{{{ji}}}} - {x_{ri}}|} $

(10)

$ {d_i}(H({x_j}, y), {x_j}) = \dfrac{1}{{{{|H}}({x_j}, y){{|}}}}\sum\limits_{r = 1}^{{{|H}}({x_j}, y){{|}}} {{{|}}{{{x}}_{{{ji}}}} - {x_{ri}}|} $

(11)

$ {{c}} $ 是类别数量, ${{{y}}_j}$ 是样本 $ {x_j} $ 的类别, $W(j, i)$ 是样本 $ {x_j} $ 与同类样本和不同类样本在特征 $ {f_i} $ 上的距离之和, ${d_i}(S, {x_j})$ 是样本 $ {x_j} $ 与样本集 $ {{S}} $ 在特征 $ {f_i} $ 上的距离, $H({x_j}, t)$ 是样本 $ {x_j} $ 的近邻 $t$ 类样本集, $|H({x_j}, t)|$ 是 $H({x_j}, t)$ 样本集的数量, $ {{p}}(y) $ 是 $ y $ 类样本的比例.

方差分析是研究每个特征对目标类是否产生显著影响, 它使用F统计的值作为每个特征得分, 得分越高, 类间特征均值差异越大, 说明特征变化引起了目标类变动. 每个特征 $ {f_{\text{i}}} $ 的计算公式:

$ {{F}}\_score({f_i}) = \frac{{\displaystyle\sum\nolimits_{j = 1}^c {{n_{{j}}}{{({\mu _{ij}} - {\mu _i})}^2}/(c - 1)} }}{{\displaystyle\sum\nolimits_{j = 1}^c {\displaystyle\sum\nolimits_{k = 1}^{{n_j}} {{{(x_{ij}^k - {\mu _{ij}})}^2}/(n - c)} } }} $

(12)

$ {{c}} $ 是类别数量, $ {{n}} $ 是样本总数量, $ {n_{{j}}} $ 是 $ {{j}} $ 类别的样本数量, $\; {\mu _{ij}} $ 是 $ {{j}} $ 类样本中特征 $ {f_{{i}}} $ 的平均值, $ {\mu _i} $ 是全部样本中特征 $ {f_{{i}}} $ 的平均值, $ x_{ij}^k $ 是 $ {{j}} $ 类样本中第 $ {{k}} $ 个样本在特征 $ {f_{{i}}} $ 上的值.

2.3 组合方式

参考文献[12]中的组合方式, 使用min函数获取每个特征在所有特征选择器的特征排名中的最小排名, 排名越小, 特征越重要, 重复此过程获得所有特征的最小排名, 再将所有特征的最小排名按进行二次排序: 先按排名从小到大排序, 再按特征域数量从小到大排序, 最后得到所有特征最终排名. 假设ReliefF返回所有特征排名 $Ran{k_1}$ , 方差分析返回所有特征排名 $Ran{k_2}$ , 首先获取特征 ${a_j}$ 在所有特征选择器的排名 $Ran{k_{*, j}} = \{ Ran{k_{1, j}}, $ $ Ran{k_{2, j}}\} $ , 然后使用min函数获取特征 ${a_j}$ 在所有特征选择器的最小排名, 即特征 ${a_j}$ 的最终排名 ${{min}}\_{{{a}}_{{j}}} = $ $ {\text{min}}({{Ran}}{{{k}}_{{{*}}, {{j}}}})$ , 重复此步骤直到获得所有特征的最小排名 ${{A'}} = \{ {{min}}\_{{{a}}_{{j}}}|j = 1, \cdots, J\} $ , 再将排名先按从小到大排序, 再按特征域数量从小到大排序得到所有特征最终排名 ${{A''}}$ .

2.4 算法

FSSD++算法框架如算法2.

算法2. FSSD++算法

输入: 数据集 $\scriptstyle ({{G}}, {{A}})$ , 子群数量 $\scriptstyle{{k}}$ , 特征子集大小 $\scriptstyle{{n}}$

输出: 子群集 $\scriptstyle{{S}}$

1) for h=1to H //H个特征选择器

2) $\scriptstyle Ran{k_h}$ =第h个特征选择器获得特征集A的排名

3) end for

4) for j=1to J //组合所有特征排名, J是特征集A的数量

5) $\scriptstyle Ran{k_{*, j}} = \{ Ran{k_{h, j}}|h = 1, \cdots, H\}$

//获取特征 $\scriptstyle {{{a}}_j}, {{{a}}_j} \in A$ 在所有特征选择器中最小的特征排名

6) $\scriptstyle {{min\_}}{{{a}}_{{j}}} = min({{Ran}}{{{k}}_{{{*}}, {{j}}}})$

7) $\scriptstyle{{A'}} = {{A'}} \cup {{min\_}}{{{a}}_{{j}}}$

8) end for

9) $\scriptstyle {{A''}} =$ 对 $\scriptstyle{{A'}}$ 进行二次排序, 先按排名从小到大排序, 再按特征域数量从小到大排序

10) $\scriptstyle {{{A''}}_n} =$ 从 $\scriptstyle {{A''}}$ 中取前n个特征

11) FSSD $\scriptstyle (G, {{t{A''}}_n}, k)$

对于算法2, 在第1)–3)行中获取每个特征选择器返回的特征排名; 在第4)–8)行中使用min函数获取在所有特征选择器中每个特征的最小排名, 直到获得全部特征的最小排名 ${A'}$ ; 在第9)行中对组合排名 ${A'}$ 先按排名升序, 再按特征域数量升序获得最终排名 ${{A''}}$ ; 在第10)行中根据用户给定数量 $n$ , 从 ${{A''}}$ 中获取前 $n$ 个特征子集 ${{{A''}}_n}$ .

3 实验与分析 3.1 实验数据集

实验选择7个UCI数据集和1个NHANES (national health and nutrition examination survey)数据集, 如表1所示. abalone、adult、autos、credit、dermatology、mushrooms和sonar 来自UCI数据集, 1999_2004_Audiometry来自NHANES数据集.

NHANES是一项连续的横断面健康访问和调查研究, 旨在评估美国人民的健康和功能状况. 该研究每两年周期收集一次数据, 本文重点分析1999–2004年参加听力检测和听力问卷调查的20–69岁人群的数据, 研究在自我报告听力损失人群中, 不同特征之间的关联. 根据测试者编码(SEQN)连接听力检测数据(audiometry examination data)、听力问卷数据(audiometry questionnaire data)、糖尿病数据(diabetes questionnaire data)、高血压数据(blood pressure questionnaire data)和人口统计数据(demographics data)生成5 417条数据. 样本排除标准如下: (1)变量数据缺失, (2)在第1次1 kHz和第2次1 kHz频率下, 听力阈值的差值超过10 dB, (3)自我报告听力损失程度为耳聋, (4)血糖水平介于正常和糖尿病之间的数据, 根据上述标准排除280条数据, 最终纳入5 137条数据, 被命名为1999_2004_Audiometry. 同时作者将自我报告听力损失程度(good、little of trouble hearing、a lot of trouble hearing)重新分类: good表示未自我报告听力损失, little 、a lot of trouble hearing表示自我报告听力损失. 1999_2004_Audiometry数据集的特征有性别、年龄、种族、国家、学历、24小时内有没有听音乐、糖尿病、高血压、在0.5、1、2、3、4、6、8 kHz下左右耳的听力阈值, 目标变量是自我报告听力损失, 它的取值范围是{Yes, No}, Yes表示自我报告听力损失, No表示未自我报告听力损失.

3.2 实验参数

FSSD++算法实验选择FSSD算法实验中特征子集数量与特征总数量不同的7个UCI数据集, 并在此基础上增加1999_2004_Audiometry数据集. 特征子集数量与特征总数量相同的数据集, 无法突显出特征选择的意义, 所以在此不做实验对比. 在FSSD++算法对比实验中, FSSD++算法的参数有最大规则数量 ${{k = }}5$ 、特征子集数量n、最大搜索深度 ${{Dept}}{{{h}}_{{\text{max}}}} = 8$ . 除了1999_2004_Audiometry数据集的特征子集数量 $ n = 6 $ 由作者给定外, 其他数据集的特征子集数量与文献[5]中FSSD算法实验给定特征子集数量一致, FSSD算法实验的最大规则数量 ${{k = }}5$ 和最大搜索深度 ${{Dept}}{{{h}}_{{\text{max}}}} = 8$ , 所以FSSD++算法实验也选择此值. MCTS4DM算法的参数除了最大规则数量 ${{k = }}5$ 、特征子集数量n外, 还有最大迭代次数 ${{n}}{{{b}}_{{{iter}}}}{{ = }}5\;000$ , 最大冗余 ${{maxRedundancy = }}0.25$ . 每个数据集指定特征子集数量n后, 表示为数据集-特征子集数量, 例如: abalone-5, 具体如表2所示. 表2 中“–”表示WRAcc质量小于0.

3.3 实验分析

表2是FSSD++算法与FSSD算法、MCTS4DM算法的对比实验结果, 使用WRAcc作为评估指标. 对比FSSD++和FSSD算法, 在大部分数据集中FSSD++提供更优的WRAcc质量, 除了数据集dermatology-10提供相等WRAcc质量, 这个结果表明使用集成特征选择的FSSD++算法能够提高WRAcc质量, 验证了FSSD++算法的有效性. 同时FSSD++和FSSD算法都优于MCTS4DM算法.

表3是在自我报告听力损失中, FSSD和FSSD++算法的特征子集和阳性预测值对比. 表4对表3中特征子集进行了具体描述, 从表3可以看出, FSSD和FSSD++算法的特征子集都有DIQ010 (糖尿病)、BPQ020 (高血压)和AUQ030 (24小时内有没有听音乐), FSSD算法是根据特征域数量来获取特征, 而FSSD++算法是根据特征与目标变量的相关性来获取特征, FSSD++算法认为自我报告听力损失与3 kHz 、4 kHz、6 kHz、糖尿病、高血压、24小时内有没有听音乐有关. 文献[13]验证了4 kHz是自我报告听力损失最重要的个体频率, 但是目前还没有文献表明自我报告听力损失与3 kHz 、6 kHz相关, FSSD++算法为研究自我报告听力损失的相关知识提供了新思路. 文献[14]和文献[15]表明糖尿病和高血压与听力损失有关, 听力损失与自我报告听力损失存在中等一致性^[16], 所以糖尿病和高血压与自我报告听力损失有关, 进一步说明FSSD++算法挖掘自我报告听力损失人群特征的有效性.

在文献[13]中听力损失定义: 在0.5、1、2、4 kHz下较差耳朵的纯音平均听力阈值>25 dB (WE4FA >25 dB)或者在4、6、8 kHz下较差耳朵的纯音平均听力阈值>35 dB (WEHFA >35 dB).表3中n(WE4FA >25 or WEHFA >35)/n(class= Yes)表示模式集覆盖人群中WE4FA >25 dB 或者WEHFA >35 dB的数量占自我报告听力损失总数量的比, 即对于WE4FA >25 dB 或者WEHFA >35 dB, 自我报告听力损失的阳性预测值, n(class =Yes)是自我报告听力损失总数量. 与FSSD算法相比, FSSD++算法挖掘自我报告听力损失的阳性预测值更高, WE4FA >25 dB 或者WEHFA >35 dB的人数也更多, 因为FSSD++算法的特征子集包含4 kHz, 4 kHz听力下降是导致自我报告听力损失的重要因素, 所以FSSD++算法挖掘自我报告听力损失人群在4 kHz的听力损失比较高, WE4FA >25 dB 或者WEHFA >35 dB的人数就增多, 自我报告听力损失的阳性预测值也就变高.

4 总结与展望

针对FSSD算法选择特征域数量较少的特征子集, 导致模式集质量下降的问题, 提出一种基于集成特征选择的FSSD算法. 该算法在预处理阶段, 根据min函数组合ReliefF和方差分析的输出结果, 对组合结果先按排名升序, 再按特征域数量升序, 最后获得前n个特征. 此特征子集作为FSSD算法的输入参数, 从而获取更优的模式集. 在UCI数据集和NHANES数据集中进行实验, 对比FSSD++、FSSD和MCTS4DM算法的WRAcc; 对比FSSD和FSSD++算法的自我报告听力损失的特征子集和阳性预测值. 实验结果表明, 与MCTS4DM和FSSD算法相比, FSSD++算法归纳的模式集WRAcc值更优; 与FSSD算法相比, FSSD++算法挖掘自我报告听力损失人群的特征有效性和阳性预测值更高. 在未来工作中将侧重研究如何自适应选择特征数量.